お詫び
私のGithub Pagesに公開したものを、Qiita の Advent Calendar 2017 の 12/1 のエントリ記事としていました。
この Advent Calendar 2017 に量子コンピューターの話題があるのを知ったのが当日(12月1日)でした。そしてその日の枠が当日でも空いていたため、慌てて、有りもので参加しました。その後、友人から Qiita に書き直しを勧められましたので、後日ではありますが、Qiitaにあらためて投稿いたします。
また、内容につきましては、ある量子コンピューターの勉強会向けに作成したものです。話題の展開が分かりづらい箇所も多いと思います。ご容赦ください。
はじめに TL; DR;
Google や IBM、Microsoft などコンピューター分野で巨人と呼ばれる企業が量子コンピューターの実現に向けて取り組んでおり、実際の量子コンピューターを触れる機会も出てきました。そんな中、量子コンピューターを利用するための活動は未成熟です。
量子コンピューターを利用する様々なアルゴリズムが提案されていますが、その中で、量子コンピューターで素因数分解を行う Shor アルゴリズムと、探索のための Grover のアルゴリズムが有名です。
このエントリでは、Grover のアルゴリズムについてご紹介します。
Grover アルゴリズムの概要
Grover のアルゴリズムの原論文を引用して紹介します。
1996、Lov Grover、"A fast quantum mechanical algorithm for database search" quant-ph/9605043
Imagine a phone directory containing N names arranged in completely random order。In order to find someone's phone number with a 50% probability、any classical algorithm (whether deterministic or probabilistic) will need to look at a minimum of N/2 names。Quantum mechanical systems can be in a superposition of states and simultaneously examine multiple names。By properly adjusting the phases of various operations、successful computations reinforce each other while others interfere randomly。As a result、the desired phone number can be obtained in only O(sqrt(N)) steps。The algorithm is within a small constant factor of the fastest possible quantum mechanical algorithm。
完全にランダムな順序で並べられたN個の名前を含む電話帳を想像してみてください。50%の確率で誰かの電話番号を見つけるためには、古典的なアルゴリズム(決定論的であろうと確率的であろうと)は、少なくとも N/2 名を見る必要があります。量子力学的システムでは、状態の重ね合わせにあり、複数の名前を同時に調べることができます。さまざまな操作のフェーズを適切に調整することによって、成功した計算は互いに強化し、他はランダムに干渉します。その結果、所望している電話番号は $ \mathcal{O}( \sqrt{N})$ ステップだけで計算できます。このアルゴリズムは、最も高速な量子力学アルゴリズムの定数倍の範囲の計算速度です。
グローバー自身が論文の概要で示しているとおり、グローバーアルゴリズムの用例として、「整列化されていないアドレス帳から、知り合いの携帯番号を探す」のに使われると紹介されているとおり、一般的には「データベースの探索」と説明されています。
しかし、この具体例を想像しながらこのアルゴリズムを学ぶと、少し戸惑うかもしれません。グローバーアルゴリズムは、「逆関数の導出」と言うほうがより正確かもしれません。
すなわち、量子コンピューターで処理できる関数 $ y = f(x) $ があるとき、グローバーアルゴリズムを使うと、ある $ y $ を与える $ x $ の値を計算することができます。
例えば、重ね合わせられた量子状態 $ \psi $ が特定の状態 $ x $ を含んでいる場合には、$ 1 $ を返し、含まない場合は $ 0 $ を返すような関数 $ f(x、\psi) $ を考えたとき、$ x = \phi $ の答え $ f(\phi、\psi) $ が $ 0 $ か、$ 1 $ かを判定するときに、使える最も効率的な量子アルゴリズム。これがグローバーアルゴリズムです。
4-qubit の例 : $ \psi = \alpha \lvert0000\rangle + \beta \lvert0001\rangle + \gamma \lvert0010\rangle + \cdots $
のような $ \psi $ に、$ \phi = \lvert0101\rangle $ が、含まれるかどうかを調べる問題がこのアルゴリズムの対象です。
それでは、Grover アルゴリズムの特徴をみていきましょう。
Grover アルゴリズムは、振幅増幅手法と呼ばれる操作を行い、目的の値 $ x $ を検出します。
振幅増幅手法 [Amplitude Amplification] とは、欲しい解の確率振幅をマイナスにマーキングし、全確率振幅の平均値の周りで逆転させる計算手法です。
この手法を手順を追ってみてみましょう。例として 2-qubit の場合を使って計算してみます。
(問題) $ \lvert\phi\rangle = \frac{1}{2}\left( \lvert00\rangle + \lvert01\rangle + \lvert10\rangle + \lvert11\rangle \right) $ という重ね合わせられた量子ビットがあるときに、この中から $ \lvert10\rangle $ を探したいという問題とします。
手順1) 欲しい解の確率振幅をマイナスにマーキング
\lvert\phi\rangle_{marked} = \frac{1}{2}\left( \lvert00\rangle + \lvert01\rangle \textstyle - \lvert10\rangle + \lvert11\rangle \right)
手順2) 全確率振幅の平均値の周りで逆転
マーキングされた状態の全確率振幅 $ \langle\alpha\rangle $ は、$ \left( \frac{1}{2} + \frac{1}{2} - \frac{1}{2} + \frac{1}{2} \right) / 4 = \frac{1}{4} $ です。
\lvert\phi\rangle^{\prime}_{marked} = \left(\frac{1}{4}-\frac{1}{2}+\frac{1}{4}\right) \lvert00\rangle + \left(\frac{1}{4}-\frac{1}{2}+\frac{1}{4}\right) \lvert01\rangle \\
+ \left(\frac{1}{4}+\frac{1}{2} +\frac{1}{4}\right) \lvert10\rangle + \left(\frac{1}{4}-\frac{1}{2}+\frac{1}{4}\right) \lvert11\rangle = \lvert10\rangle
この状態 $ \lvert\phi\rangle^{\prime}_{marked} $ を観測すると、$ \lvert10\rangle $ の確率が $ 1 $ となり、$ \lvert10\rangle $ の状態を探しだすことができます。
2-qubit では、この手順1)、2)を1回行えば、マーキングされた量子状態の確率振幅が 1 になりますが、N-qubit のときには、この方法を反復してマーキングした振幅を増幅します。
このように2つの手順で、検索したい目的の状態の確率振幅を 1 に近づけて、検出されるようにします。
これが、Grover アルゴリズムです。
また、問題の初期量子状態に探したい状態がわずかな確率で含まれている場合でも、次の例のように、この手法は有効に作用します。
2-qubit の例(わずかな確率で検索対象が含まれている例) :
(問題)
\begin{align*} \lvert\phi\rangle &= \frac{400\sqrt{3}}{1201} \lvert00\rangle + \frac{400\sqrt{3}}{1201} \lvert01\rangle + \frac{49}{1201} \lvert10\rangle + \frac{400\sqrt{3}}{1201} \lvert11\rangle \\
\lvert\phi\rangle &= 0.0407 \dots \lvert10\rangle + 0.5768 \dots \left( \lvert00\rangle + \lvert01\rangle + \lvert11\rangle \right)
\end{align*}
問題の $ \lvert10\rangle $ の確率は、$ \left(0.0407 \cdots\right)^{2} \approx \textstyle \class{mathfont-r}{0.166 %} $
(手順1)
\lvert\phi\rangle_{marked} = \frac{400\sqrt{3}}{1201} \lvert00\rangle + \frac{400\sqrt{3}}{1201} \lvert01\rangle - \frac{49}{1201} \lvert10\rangle + \frac{400\sqrt{3}}{1201} \lvert11\rangle
全確率振幅平均は、$ \langle\alpha\rangle = \frac{1200\sqrt{3}-49}{1201\times 4} $
(手順2)
\begin{align*} \lvert\phi\rangle^{\prime}_{marked} &= \frac{400\sqrt{3}-49}{1201\times 2} \lvert00\rangle + \frac{400\sqrt{3}-49}{1201\times 2} \lvert01\rangle + \frac{1200\sqrt{3}+49}{1201\times 2} \lvert10\rangle + \frac{400\sqrt{3}-49}{1201\times 2} \lvert11\rangle \\
\lvert\phi\rangle^{\prime}_{marked} &= \frac{1200\sqrt{3}+49}{1201\times 2} \lvert10\rangle + \frac{400\sqrt{3}-49}{1201\times 2} \left( \lvert00\rangle + \lvert01\rangle + \lvert11\rangle \right) \\
\lvert\phi\rangle^{\prime}_{marked} &= \textstyle \class{mathfont-r}{0.8857 \cdots} \lvert10\rangle + 0.2680 \cdots \left( \lvert00\rangle + \lvert01\rangle + \lvert11\rangle \right)
\end{align*}
操作後の $ \lvert10\rangle $ の確率は、$ \left(0.8857 \cdots\right)^{2} \approx \textstyle \class{mathfont-r}{78.44 %} $
Grover アルゴリズムの数理
Grover アルゴリズムの数理的な背景を数式で説明します。
$ f(x) := \begin{cases}
1 & (x = z) \cr
0 & (x \neq z) \
\end{cases}
x \in \mathbb{Z}
$ を考えるとき、次の 2 つのオペレーター行列を考えます。
【オペレーター $ R_f $ :選択的回転】
R_f(m,n):= e^{i\pi f(x)} \delta_{mn} = (-1)^{f(x)} \delta_{mn} = \mathcal{I} - 2 \lvert z \rangle \langle z \rvert
【オペレーター $ D $ :平均値まわりの反転】
D := - \mathcal{I} + 2 \lvert \phi_0 \rangle \langle \phi_0 \rvert
\;\;\; \Bigg( \texttt{ここでの} \displaystyle \lvert \phi_0 \rangle = \frac{1}{\sqrt{N}} \sum_{x=0}^{N-1} \lvert x \rangle \Bigg)
ここで、選択的回転 $ R_f $ と、平均値まわりの反転 $ D $ の合成を考えると、
U_f := D R_f = \left( - \mathcal{I} + 2 \lvert \phi_0 \rangle \langle \phi_0 \rvert \right)
\left( \mathcal{I} - 2 \lvert z \rangle \langle z \rvert \right)
これを、状態 $ \displaystyle \lvert \phi \rangle := \sum_{x=0}^{N-1} w_x \lvert x \rangle ;;; \Bigg( \texttt{ここでは} \left( \sum_{x=0}^{N-1} \lvert w_x \rvert^{2} = 1 \right) \Bigg) $ に施すと、状態 $ \lvert \phi \rangle $ は、次で示す状態に遷移します。
\displaystyle U_f \lvert \phi \rangle =
\sum_{x=0,x \neq z}^{N-1} ( 2 \overline{w} - w_x ) \lvert x \rangle + ( 2 \overline{w} + w_z ) \lvert z \rangle
すなわち、目的の $ \lvert z \rangle $ の確率振幅が増加し、それ以外の $ \lvert x \rangle、( x \neq z )$ では確率振幅が減少します。
そして、目的の $ \lvert z \rangle $ の確率振幅が十分に大きくなるまで、この操作 $ U_f $ を繰り返します。
反復回数についての考察
次に、どの程度の回数を繰り返せばよいかを考察します。
操作 $ U_f $ を繰り返す回数を $ k $ として、$ k $ 回の $ U_f $ の操作をまとめて、$ U_f^{k} $ とおきます。
ここで、$ \lvert \phi \rangle $ として、平均値まわりの反転のときに使った $ \lvert \phi_0 \rangle $ を考えてみます。
状態 $ \lvert \phi_0 \rangle $ に $ U_f^{k} $ を施すと、$ \displaystyle sin \theta = \sqrt{\frac{1}{N}}、cos \theta = \sqrt{ 1 - \frac{1}{N}} $ とおいて、
U_f^{k} \lvert \phi_0 \rangle =
sin((2k+1)\theta) \lvert z \rangle + \sum_{x \neq z}^{N-1} \frac{1}{\sqrt{N-1}}cos((2k+1)\theta) \lvert x \rangle
となります。
$ m := \lfloor \frac{\pi}{4 \theta} \rfloor $ とおき、$ U_f $ を $ m $ 回施して観測したときに期待どおりの結果が得られる確率 $ P_c $ とすると、 $ P_c \geq 1 - \frac{1}{N} $ で抑えられ、このとき、 $ m = \mathcal{O}( \sqrt{N})$ です。
Grover アルゴリズム を試してみる
さて、Grover アルゴリズムの手順を、実際の量子計算として活用することを考えてみましょう。
具体的な例として「$ \lvert\phi\rangle = \frac{1}{2}\left( \lvert00\rangle + \lvert01\rangle + \lvert10\rangle + \lvert11\rangle \right) $ で表された量子ビット状態があるときに、この中から $ \lvert11\rangle $ を探したい」という問題を考えます。
手順1)欲しい解の確率振幅をマイナスにマーキング
$ CZ (Controlled-Z) $ オペレータを作用させれば、$ \lvert 11\rangle $ の符号を入れ替えられます。
$ 2^{2}\times2^{2} $ の行列で表すと、
CZ = \left( \begin{array}{cc} I & 0 \\ 0 & Z \end{array} \right)
ここでの $ I、Z $ は,それぞれ
\begin{align*}
I = \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) ,
Z = \left( \begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right)
\end{align*}
の $ 2 \times 2 $ の行列。
この行列 $ CZ $ を $ \lvert\phi\rangle $ に作用すると、
CZ \lvert\phi\rangle = \frac{1}{2}\left( \lvert00\rangle + \lvert01\rangle + \lvert10\rangle - \lvert11\rangle \right)
手順2)全確率振幅の平均値の周りで逆転
\displaystyle D = \frac{1}{2} \left( \begin{array}{cccc} -1 & 1 & 1 & 1 \\ 1 & -1 & 1 & 1 \\ 1 & 1 & -1 & 1 \\ 1 & 1 & 1 & -1 \end{array} \right) =
\frac{1}{2} \left( \begin{array}{cc} X-I & X+I \\ X+I & X-I \end{array} \right) =
\frac{-1}{\sqrt{2}} \left( \begin{array}{cc} H & H \\ H & -H \end{array} \right)
\left( \begin{array}{cc} 0 & X \\ X & 0 \end{array} \right)
\left( \begin{array}{cc} I & 0 \\ 0 & Z \end{array} \right)
\left( \begin{array}{cc} 0 & X \\ X & 0 \end{array} \right)
\frac{1}{\sqrt{2}} \left( \begin{array}{cc} H & H \\ H & -H \end{array} \right)
最終的な右辺には、-1 が全体に掛かっています。これは、グローバル位相、または絶対位相(global phase)と呼ばれています。 グローバル位相は、測定段階で絶対値の二乗をとるため、量子計算としては、+1 との区別ができません。 そのため、一般的に無視しても良いとされています。 量子回路にする以降の例ではこの -1 は省略して検証を進めます。
D \cdot CZ \lvert \phi \rangle = \frac{1}{4}\left( (-1 + 1 + 1 - 1) \cdot \lvert00\rangle + (1 - 1 + 1 - 1) \cdot \lvert01\rangle + (1 + 1 - 1 - 1) \cdot \lvert10\rangle + (1 + 1 + 1 + 1) \cdot \lvert11\rangle \right)
ここで、$ Z = H \cdot X \cdot H $ を使うと、$ CZ = ( I \otimes H ) \cdot CX \cdot ( I \otimes H ) $ と書けます。
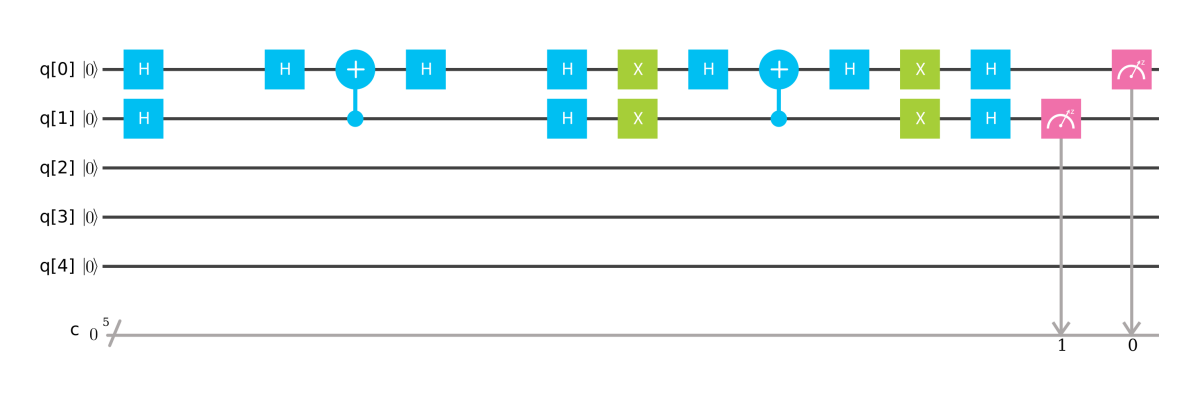
IBM Q を使った検証
これを IBM Q 上で表現すると以下のようになります。 実行すると、$ \lvert 11 \rangle $ の確率が $ 1 $ となります。
次に 3-qubit の例は以下のようになります。
* 3-qubit で $ \lvert 111 \rangle $ を $ 1 $ 回の試行を行なう例
* 3-qubit で $ \lvert 111 \rangle $ を $ 2 $ 回の試行を行なう例
【補足】 手順2)の別解
手順2での行列の式の変換は、執筆者の力では導出が難しく、参考書のお手本を元にしております。執筆者の行なった違う計算を次に記します。
\begin{align*} D &= \frac{1}{2} \left(
\begin{array}{cc}
X-I & X+I \\
X+I & X-I
\end{array} \right) \end{align*}
この行列の固有値を $ \lambda $ とすると、固有値を求める式は、
\begin{align*} 4\lambda^2 - 4\left(X-I\right)\lambda + \left(X-I\right)^2 - \left(X+I\right)^2 = 0 \\
\longrightarrow 4\lambda^2 - 4\left(X-I\right)\lambda - 4 \cdot X = 0 \\
\longrightarrow \left(\lambda + I\right)\left(\lambda - X\right) = 0
\end{align*}
となり、固有値は、$ \lambda = -I、X $ 。
$ \lambda = -I $ の固有ベクトルは、
\frac{1}{\sqrt{2}}\left( \begin{array}{cc} I \\ -I \end{array} \right)
$ \lambda = X $ の固有ベクトルは、
\frac{1}{\sqrt{2}}\left( \begin{array}{cc} I \\ I \end{array} \right)
です。
ここで、固有値ベクトルで作られる行列
U = \frac{1}{\sqrt{2}} \left( \begin{array}{cc} I & I \\ I & -I \end{array} \right)
を考えると、 これは、$ 2 \times 2 $ 行列の Hadamard 演算子 $ H $ を使って、$ H \otimes I $ と表せます。
また、この $ U $ は、逆行列も同じ行列 $ U^{-1} = U $ という特徴もあり、この性質を使って、
U^{-1}DU = \left( H \otimes I\right) \cdot D \cdot \left( H \otimes I \right) = \left( \begin{array}{cc} X & 0 \\ 0 & -I \end{array} \right)
が得られます。
次に、右辺の
\left( \begin{array}{cc} X & 0 \\ 0 & -I \end{array} \right)
の展開を考えてみます。 形が
CNOT = \left( \begin{array}{cc} I & 0 \\ 0 & X \end{array} \right)
に似ていますので、単にこの2つをかけてみます。
\left( \begin{array}{cc} X & 0 \\ 0 & -I \end{array} \right) \cdot \left( \begin{array}{cc} I & 0 \\ 0 & X \end{array} \right) = \left( \begin{array}{cc} X & 0 \\ 0 & -X \end{array} \right) = Z \otimes X
偶然にもうまく量子回路にできる形がでてきました。そこで、両辺に、CNOT を掛けると次式が得られます。
\left( \begin{array}{cc} X & 0 \\ 0 & -I \end{array} \right) = \left(Z \otimes X \right) \cdot CNOT
この式を使って、$ U^{-1}DU $ の左右から、$ U = U^{-1} = H \otimes I $ を掛けると、$ D $ を表す式が得られます。
D = \left(H \otimes I \right) \cdot \left(Z \otimes X \right) \cdot CNOT \cdot \left(H \otimes I \right)
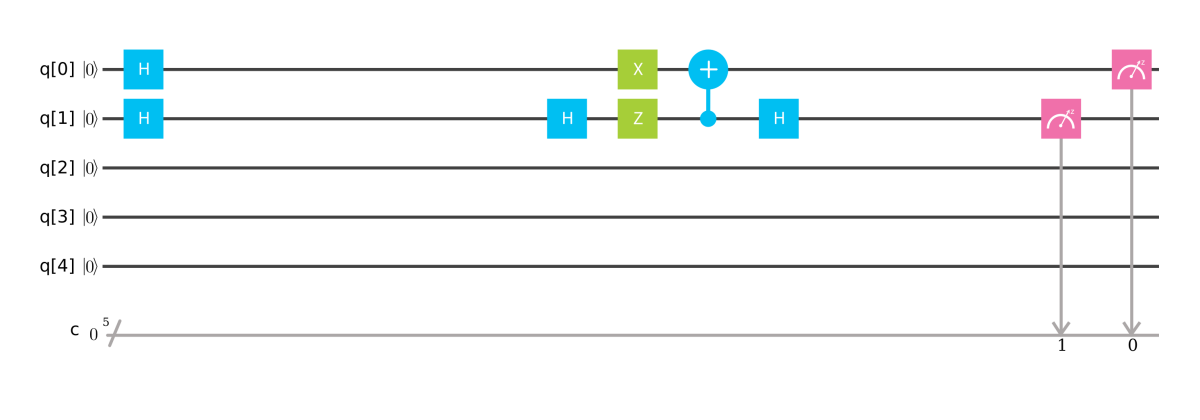
これを IBM Q 上で表現すると以下のようになります。
(Rigetti製) pyquil を使った検証
python環境に pyquil をインストールします。
$ pip install pyquil
* 2-qubit から、$ \lvert 11 \rangle $ があるか検索する量子プログラム。
import pyquil.quil as pq
import pyquil.api as api
from pyquil.gates import *
qvm = api.SyncConnection()
p = pq.Program()
p.inst(
H(0),
H(1),
H(0),
CNOT(1,0),
H(0),
H(0),
H(1),
X(0),
X(1),
H(0),
CNOT(1,0),
H(0),
X(0),
X(1),
H(0),
H(1),
MEASURE(0,0),
MEASURE(1,1))
result = qvm.run(p,[0,0],20)
print(result)
参考書籍
量子コンピュータと量子通信〈2〉量子コンピュータとアルゴリズム
量子アルゴリズム
クラウド量子計算入門
量子コンピュータの基礎数理
今度こそわかる量子コンピューター
量子情報科学入門
量子計算 (ナチュラルコンピューティング・シリーズ)
量子情報理論 第2版
量子コンピューティング
量子計算と量子情報の原理
付録: sympy で Grover アルゴリズムを計算してみましょう
本編では、IBM Q や pyquil で検証しましたが、python 製のライブラリ sympy でも簡単に検証ができます。
まず、python環境に sympy をインストールします。
$ pip install sympy
sympy.physics.quantum パッケージをインポートします。
>>> from sympy.physics.quantum import *
>>> from sympy.physics.quantum.gate import X,Y,Z,H,T,S,CNOT,SWAP
>>> from sympy.physics.quantum.qubit import Qubit
* 2-qubit から、$ \lvert 11 \rangle $ があるか検索する量子プログラム。
>>> qi = qapply(H(0)*H(1)*Qubit('00'))
>>> rf_3 = H(0)*CNOT(1,0)*H(0)
>>> d_2 = (H(0)*H(1))*(X(0)*X(1))*(H(0)*CNOT(1,0)*H(0))*(X(0)*X(1))*(H(0)*H(1))
>>> grover = d_2 * rf_3
>>> qapply( grover * qi)
-|11>
別解したグローバル位相が +1 のケースの用例も記します。
>>> from sympy.physics.quantum.gate import IdentityGate as I
>>> qi = qapply(H(0)*H(1)*Qubit('00'))
>>> rf_3 = H(0)*CNOT(1,0)*H(0)
>>> d_2 = (H(1)*I(0))*(Z(1)*X(0))*CNOT(1,0)*(H(1)*I(0)) # 別解の行列
>>> grover = d_2 * rf_3
>>> qapply( grover * qi)
|11> # ←グローバル位相が正の値
更新記録
2017/11/15 初版
2017/11/27 追記
2017/12/01 Advent Calendar 2017 向けに「はじめに」を追記
2017/12/12 Github Pages で公開していた記事を Qiita に移行
2018/12/03 数式が見えなくなっていたようなので修正(Texの表示が初稿のときと変わっていました)