4qubitのGroverのアルゴリズムを実装してみる
今更Gloverやります!笑
書いた理由は4qubitのGloverがどこにも見当たらなかったのと、年初に大学の研究発表にて色々調べたので理解のアウトプットのためにもこの記事でまとめてみました。
ついでにblueqat新機能にも触れてみました!
Gloverのアルゴリズムとは
Imagine a phone directory containing N names arranged in completely random order. In order to find someone's phone number with a 50% probability, any classical algorithm (whether deterministic or probabilistic) will need to look at a minimum of N/2 names. Quantum mechanical systems can be in a superposition of states and simultaneously examine multiple names. By properly adjusting the phases of various operations, successful computations reinforce each other while others interfere randomly. As a result, the desired phone number can be obtained in only O(sqrt(N)) steps. The algorithm is within a small constant factor of the fastest possible quantum mechanical algorithm.
上記の引用はアルゴリズムの考案者Gloverの導入で、簡単に日本語にすると以下のようになっています。
N個の名前を含む電話帳を考えましょう。50%の確率で誰かの電話番号を見つけるためには、古典アルゴリズムで少なくとも N/2 名を見る必要があります。量子アルゴリズムでは、重ね合わせで複数の電話番号を同時に調べることができます。その結果、電話番号は O(√N) ステップだけで計算できます。
ですが、現状の量子コンピュータの量子ビット数では本来実現したいような上記のアルゴリズムは実装できません。実際に実装してみての、自分なりの言葉で説明すると、
各データが等確率で存在するデータの集まりから任意の探したいデータが存在するか否かを判断するアルゴリズム
という感じでした。
簡単な仕組みを2qubitで説明




重ね合わせともつれがわかりやすく反映されていて勉強するにはいいアルゴリズムだと思います。
blueqatを用いてIBM Qを動かして行います(シミュレータと実機を比較しながら)
準備します。
from blueqat import Circuit
import math
手始めの2qubit
IBM Qの回路を表示してみます。
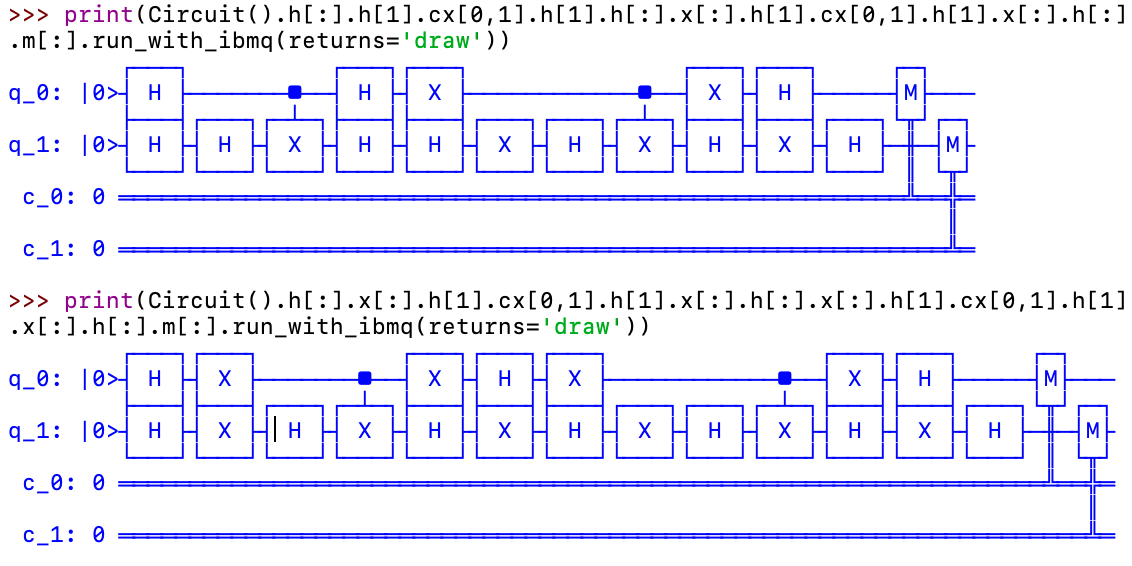
blueqat新機能すげえ、、!!
Circuit().h[:].h[1].cx[0,1].h[1].h[:].x[:].h[1].cx[0,1].h[1].x[:].h[:].m[:].run(shots=100)
Counter({'11': 100})
# 上で説明したようにxgateを噛ませてあげると...
Circuit().h[:].x[:].h[1].cx[0,1].h[1].x[:].h[:].x[:].h[1].cx[0,1].h[1].x[:].h[:].m[:].run(shots=100)
Counter({'00': 100})
IBMQ実機で実行
pprint(Circuit().h[:].h[1].cx[0,1].h[1].h[:].x[:].h[1].cx[0,1].h[1].x[:].h[:].m[:].run_with_ibmq(backend))
Counter({'11': 467, '10': 277, '01': 150, '00': 130})
一応観測したい|11>が最も多く観測されたもののこの精度、、
3qubitやってみます。IBMQを使って結果を返してみます。(111を探します)
Circuit().h[:].h[2].ccx[0,1,2].h[2].h[:].x[:].h[2].ccx[0,1,2].h[2].x[:].h[:].m[:].run_with_ibmq(returns='shots')
Counter({'111': 812, '100': 34, '011': 31, '101': 30, '001': 30, '110': 29, '010': 29, '000': 29})
111は812回。1024回中なので、正解率80%くらいか。
上で説明したように、繰り返して確率振幅を増大させます。
Circuit().h[:].h[2].ccx[0,1,2].h[2].h[:].x[:].h[2].ccx[0,1,2].h[2].x[:].h[:].h[2].ccx[0,1,2].h[2].h[:].x[:].h[2].ccx[0,1,2].h[2].x[:].h[:].m[:].run_with_ibmq(returns='draw')

気になる結果は...
Circuit().h[:].h[2].ccx[0,1,2].h[2].h[:].x[:].h[2].ccx[0,1,2].h[2].x[:].h[:].h[2].ccx[0,1,2].h[2].h[:].x[:].h[2].ccx[0,1,2].h[2].x[:].h[:].m[:].run_with_ibmq(returns='shots')
Counter({'111': 968, '110': 12, '011': 9, '010': 9, '001': 9, '000': 9, '100': 5, '101': 3})
968/1024!! かなりの精度で観測できました。
見つけたいデータが観測される確率は繰り返し回数に対してsin関数を描くため、さらに繰り返すと確率は小さくなってしまいます。
IBMQ実機で実行
pprint(Circuit().h[:].h[2].ccx[0,1,2].h[2].h[:].x[:].h[2].ccx[0,1,2].h[2].x[:].h[:].h[2].ccx[0,1,2].h[2].h[:].x[:].h[2].ccx[0,1,2].h[2].x[:].h[:].m[:].run_with_ibmq(backend))
Counter({'111': 194,'010': 135,'101': 128,'011': 127,'110': 120,'000': 117,'001': 106,'100': 97})
正解率20%にも満たない(笑)
4qubitに挑戦。
2qubit,3qubitの回路を見ますと法則性があるため、4qubitも行けそうなわけです。
しかし、2qubit,3qubitでもつれを作るキーマンとなるゲートはそれぞれcx,ccxゲートなわけですが、cccxは使用可能ゲートには存在しません。ccxをcxゲート、Hゲート、Tゲートで表現できるように、cccxも既存のゲートで構成することができます。
Circuit().x[0,1,2].cx[0,3].ry(-math.pi*1/4)[3].cx[0,3].ry(math.pi/4)[3].cx[0,3].ccx[0,2,3].crz(-math.pi*1/4)[0,3].ccx[0,1,3].crz(math.pi/4)[0,3].ccx[0,2,3].crz(-math.pi*1/4)[0,3].ccx[0,1,3].crz(math.pi/4)[0,3].crz(math.pi/4)[0,2].cx[0,3].ry(-math.pi*1/4)[3].cx[0,3].ry(math.pi/4)[3].cx[0,3].ccx[0,1,2].crz(-math.pi*1/4)[0,2].crz(math.pi/4)[0,1].ccx[0,1,2].m[:].run_with_ibmq(returns='shots')
Counter({'1111': 1024})
# |1110>をこれらのゲートに通すと|1111>となっています。
cccxが完成しました。こいつを使って4qubitのGloverのアルゴリズムを実装していきます。
print(Circuit().h[:].h[3].cx[0,3].ry(-math.pi*1/4)[3].cx[0,3].ry(math.pi/4)[3].cx[0,3].ccx[0,2,3].crz(-math.pi*1/4)[0,3].ccx[0,1,3].crz(math.pi/4)[0,3].ccx[0,2,3].crz(-math.pi*1/4)[0,3].ccx[0,1,3].crz(math.pi/4)[0,3].crz(math.pi/4)[0,2].cx[0,3].ry(-math.pi*1/4)[3].cx[0,3].ry(math.pi/4)[3].cx[0,3].ccx[0,1,2].crz(-math.pi*1/4)[0,2].crz(math.pi/4)[0,1].ccx[0,1,2].h[3].h[:].x[:].h[3].cx[0,3].ry(-math.pi*1/4)[3].cx[0,3].ry(math.pi/4)[3].cx[0,3].ccx[0,2,3].crz(-math.pi*1/4)[0,3].ccx[0,1,3].crz(math.pi/4)[0,3].ccx[0,2,3].crz(-math.pi*1/4)[0,3].ccx[0,1,3].crz(math.pi/4)[0,3].crz(math.pi/4)[0,2].cx[0,3].ry(-math.pi*1/4)[3].cx[0,3].ry(math.pi/4)[3].cx[0,3].ccx[0,1,2].crz(-math.pi*1/4)[0,2].crz(math.pi/4)[0,1].ccx[0,1,2].h[3].x[:].h[:].m[:].run_with_ibmq(returns='draw'))
crzゲート(制御位相ゲート)は仕様上分解されて表示されます。




綺麗なIBMQ手動量子回路が欲しかったので...

2回繰り返しverは...(途中で泣きそうになりました)

繰り返し部分をRとおいて繰り返し、精度を上げていきます。
(Circuit().h[:] +R).m[:].run_with_ibmq(returns='shots')
Counter({'1111': 439, '0111': 64, '0001': 51, '0000': 49, '0110': 47, '0100': 47, '0011': 43, '0010': 42, '0101': 39, '1001': 35, '1101': 34, '1110': 31, '1000': 29, '1011': 29, '1100': 24, '1010': 21})
>>> (Circuit().h[:] +R+R).m[:].run_with_ibmq(returns='shots')
Counter({'1111': 922, '1100': 15, '1101': 13, '1110': 12, '1001': 8, '1010': 8, '1000': 7, '1011': 7, '0111': 6, '0110': 5, '0101': 5, '0010': 4, '0011': 3, '0001': 3, '0100': 3, '0000': 3})
>>> (Circuit().h[:] +R+R+R).m[:].run_with_ibmq(returns='shots')
Counter({'1111': 953, '0111': 17, '1000': 11, '1110': 8, '1011': 8, '1100': 7, '1001': 7, '1010': 6, '1101': 5, '0010': 2})
>>> (Circuit().h[:] +R+R+R+R).m[:].run_with_ibmq(returns='shots')
# 4回目の繰り返しで確率は下がってしまいました。最適繰り返し回数は3回のようです。
Counter({'1111': 645, '0110': 42, '0101': 42, '0111': 40, '0001': 35, '0100': 30, '0000': 29, '0010': 27, '0011': 27, '1011': 19, '1110': 18, '1100': 16, '1000': 15, '1001': 14, '1010': 14, '1101': 11})
IBMQ実機で(一応)実行
結果はお察しですが、、
pprint((Circuit().h[:] +R+R+R+R).m[:].run_with_ibmq(backend))
Counter({'0000': 88,
'1000': 82,
'0100': 80,
'1001': 75,
'1100': 74,
'0010': 74,
'1110': 68,
'0101': 65,
'1101': 65,
'0110': 64,
'1010': 61,
'1011': 60,
'0001': 50,
'0011': 43,
'0111': 38,
'1111': 37})
もはや笑うしかない。実機のバックエンドを変えても何故だか|1111>が最も観測されませんでした。
ちなみにノイズなしシミュレータで確認してみたところ、

blueqatでIBMQを動かした時同様、3回が最適繰り返し回数でした。
このような結果になり、qubit数を増やすほどsin関数が綺麗に見えてきます。
同時にデータ数をNとするとO(√N)に比例することも示せます。

感想
結構大変だった。
暗号技術と量子アルゴリズム
個人的な興味として、RSAであったり、ビットコインに用いられている楕円曲線であったりする暗号がいかにして破られるかというものがありますが、わかりやすいものはあまりなかったです。
Googleの論文ではRSA2048が2000万qubitのShorが必要とありましたが、公開鍵とは異なる共通鍵方式のAESはGloverによって3000~7000qubitで攻撃が可能なようだったりするようです。
参考
更新
2020 2/25 IBMQ実機との比較