はじめに
Adventカレンダー、初参加ですがよろしくお願いいたします。
プロフィールに記載の通り、私は55歳から趣味で量子コンピュータの勉強を始めたSE歴3x年(現在58歳)のSEです。
これまで、Groverに関する投稿を2件ほどしましたが、線形代数が苦手で数式が読めない私が昨年7月にグローバーアルゴリズムの使い方を(我流で😅)習得するまでの試行錯誤(失敗の連続🤣)を年末の余興としてご笑納ください。
なお、毎度のことですが素人ゆえの不適切な用語の用法や表現が散見されてお見苦しい点が多々あると思いますがご容赦下さいませ。(コメントでのご指摘、大歓迎です)
[過去の投稿]
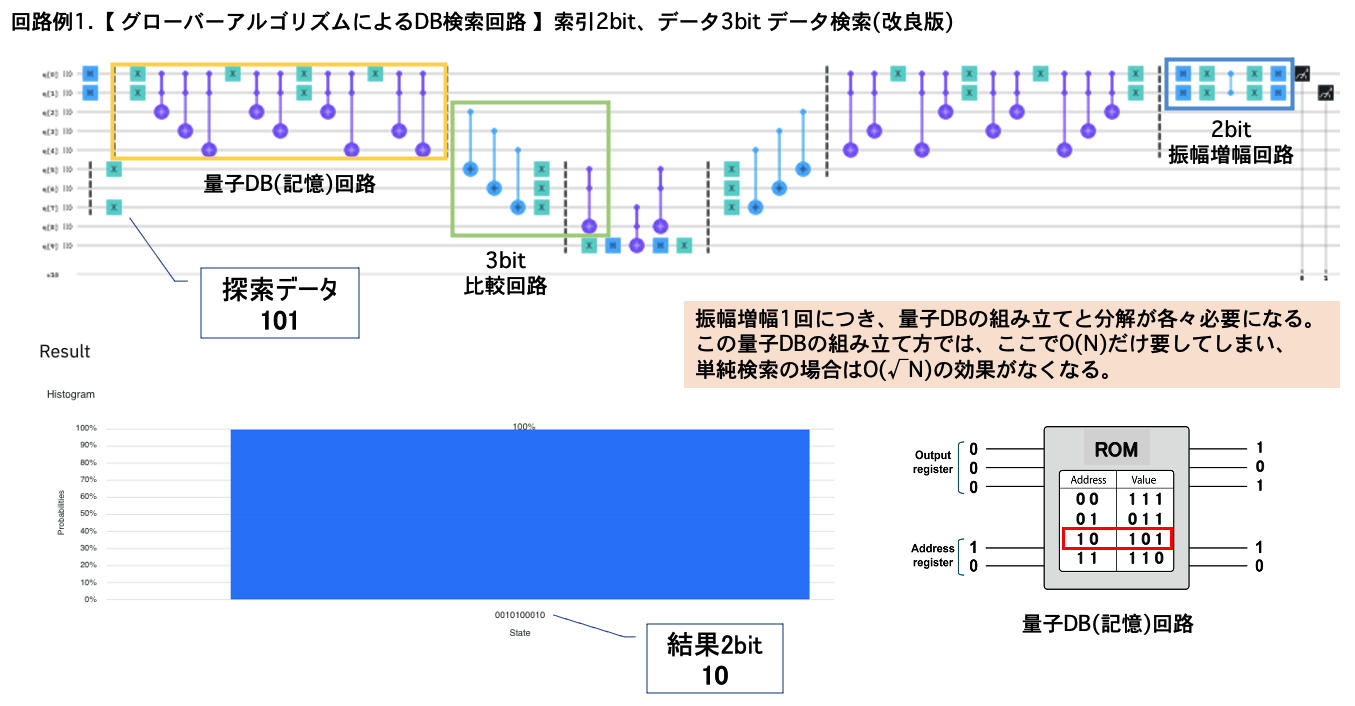
・Groverアルゴリズムで実際にデータを検索(!?)
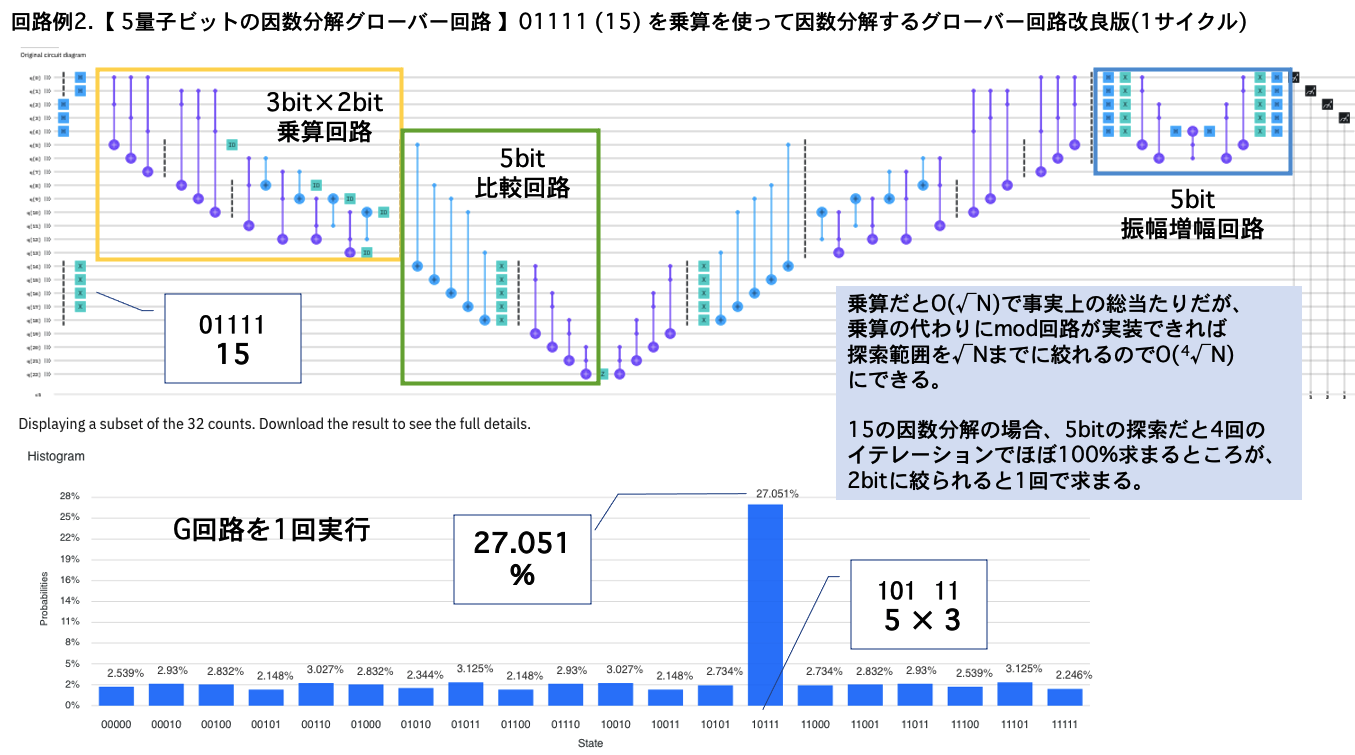
・Groverアルゴリズムで15を因数分解
(記事中の図はIBM Quantum Experienceの画面から切り抜いたものですが、2019年当時のもので現在とは色使いやゲートのシンボルが異なります。)
越えられない谷(壁)
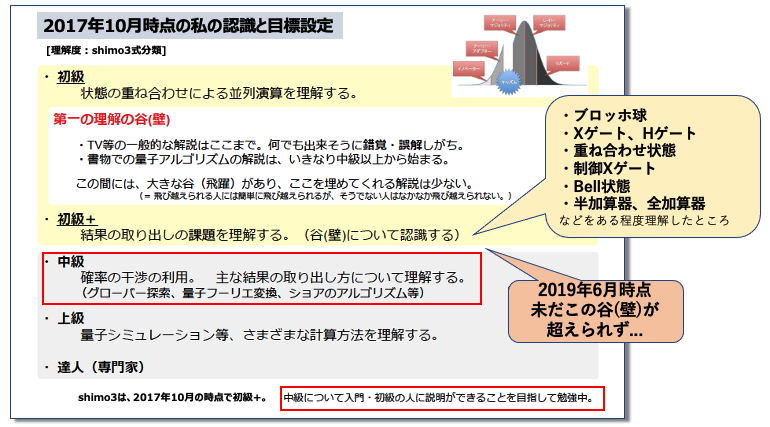
私が量子コンピュータの勉強を始めた2017年6月から2019年初頭あたりまでは、shimo3式分類(😅)で言うところの初級と中級の間を埋めてくれる素人向けの情報がほとんどありませんでした。
(料理の作り方が知りたいのに、料理についての説明と出来た料理に若干のアレンジを加える方法だけ教えられている気分)
Groverについて当時見た動画はこんな感じですが、これが全く理解できなかったんですね。😅
・Running an experiment in the IBM Quantum Experience
・慶應大学 量子コンピュータ授業 #4 グローバーのアルゴリズム
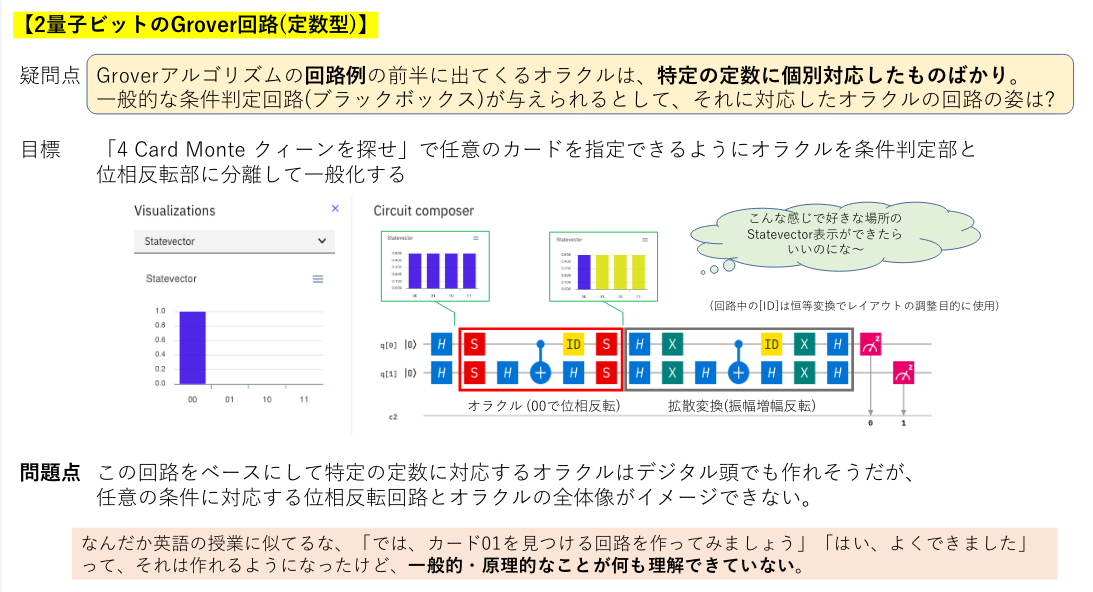
殆ど理解が進まないまま迎えた2019年6月、社内の量子コンピュータの勉強会で2量子ビットのグローバーアルゴリズムの解説がありました。何度も目にして理解できなかった回路ですが、この「最も単純な回路」を理解できなければ谷(壁)は越えられないと読解(リバースエンジニアリング?) に取り組む覚悟(😅)を決めました。
ドンキホーテ、Groverに挑む
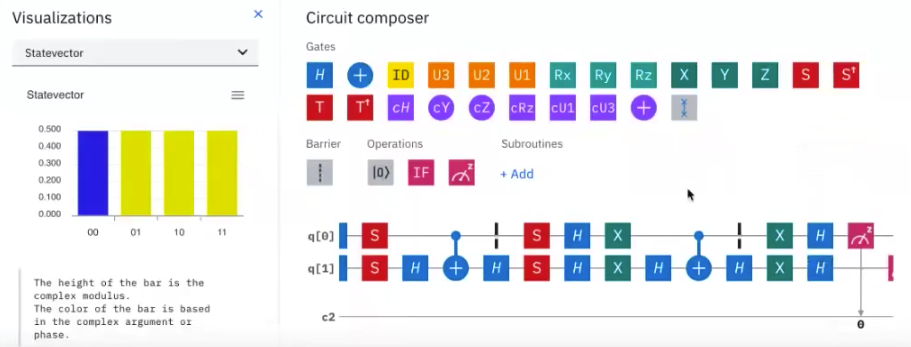
挑戦の意志を強く後押ししてくれたのが、IBM Quantum Experienceのサーキットコンポーザーに追加された「Statevector」表示の存在でした。
それまで、回路をいじってはシミュレーションを実行し、測定結果を見ることしかできなかったので、位相についてはブラインド状態だったわけですが、回路を作りながら 「計算過程の状態の振幅と位相(色)が見える」 ようになったことは、数式から意味を読み取れない私にとって最大の武器になりました。
答えを知っている前提のサンプル回路では!!
チャレンジ#1: 試行錯誤と迷走の日々
位相反転の意味やその方法について何も理解しないままの無謀な特攻。🤣
さらっと書いていますが、ここは試行錯誤と迷走に次ぐ迷走の日々でした。
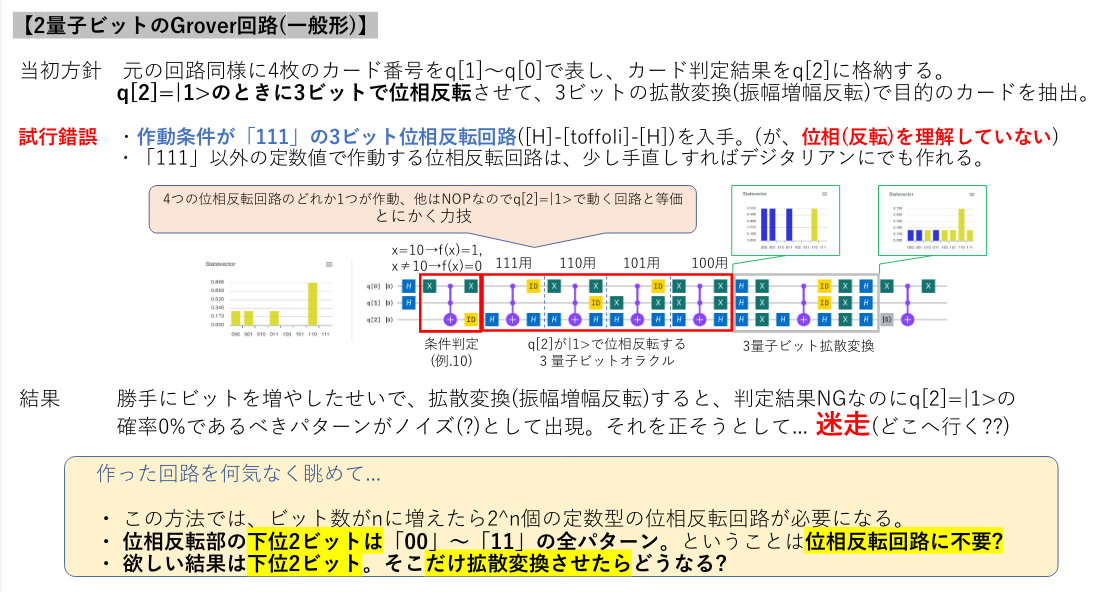
チャレンジ#2: 迷走中、しかし一歩前進
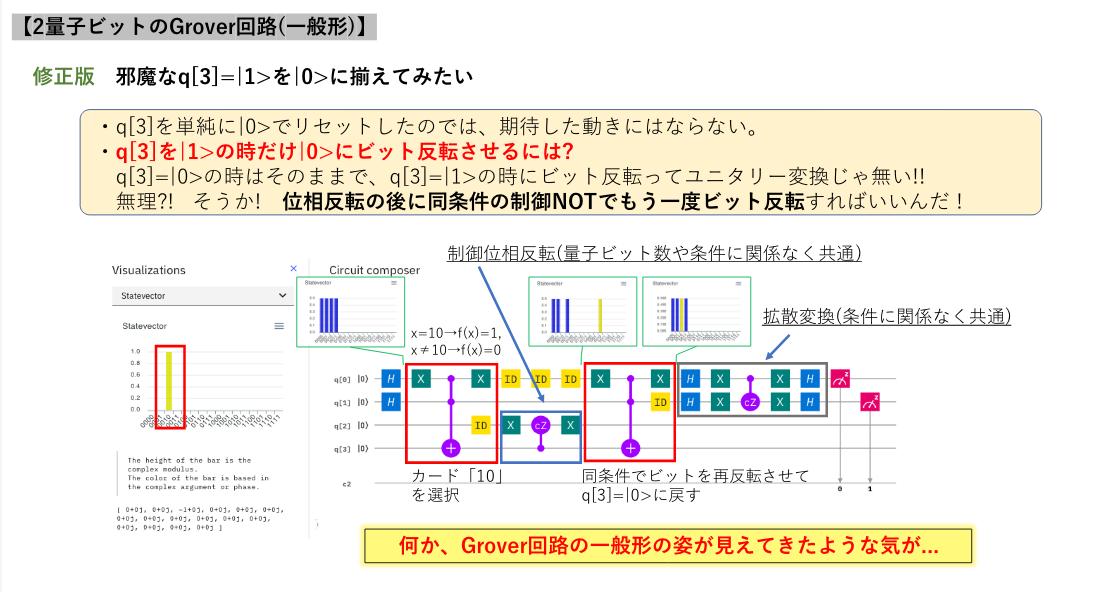
理屈を何も知らないまま、ブロックごとにStatevectorで動きを確認しながら理解を進めていきます。

位相反転部の回路がシンプルになったことで、それまで訳も分からず模倣するしかなかった位相反転のコアパーツが手に入りました。そして、拡散変換の方も微かな光が見えた気が。
チャレンジ#3: 一筋の光明、何か掴んだ気が
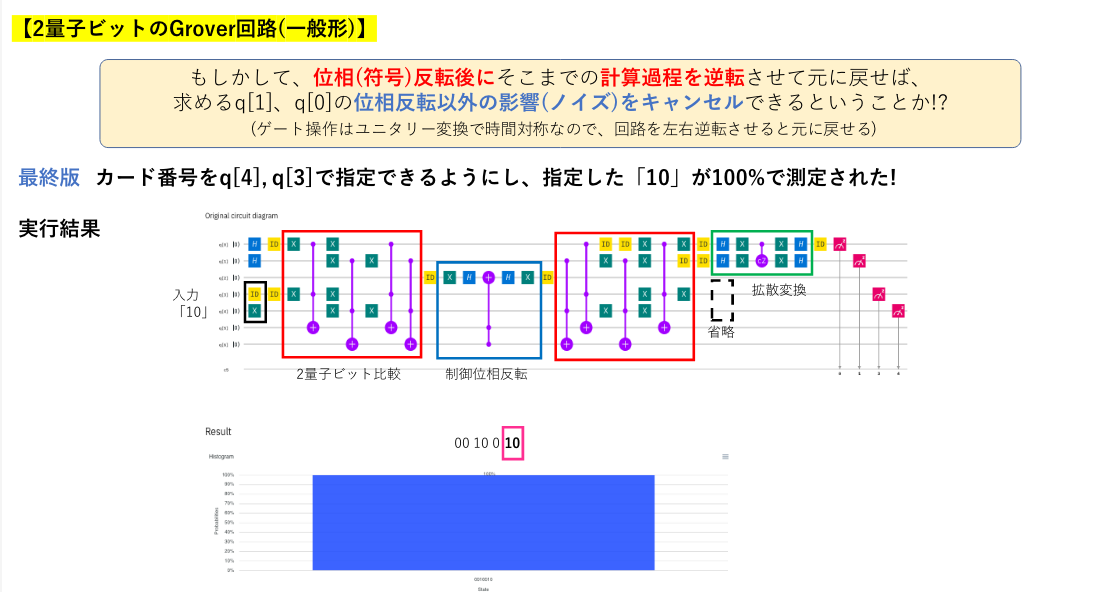
チャレンジ#4: オラクルの作り方が理解できた?!
チャレンジ#5: 振幅増幅の理解(アダマール行列、拡散、干渉)
ここまでのチャレンジを終えた私は、堰を切ったように「Groverアルゴリズムで実際にデータを検索(!?)」と「Groverアルゴリズムで15を因数分解」を着想して取り組みオラクルの作り方については自信を得ましたが、振幅増幅回路の理解については先送りにしていたので、次はこれに取り組むことにしました。
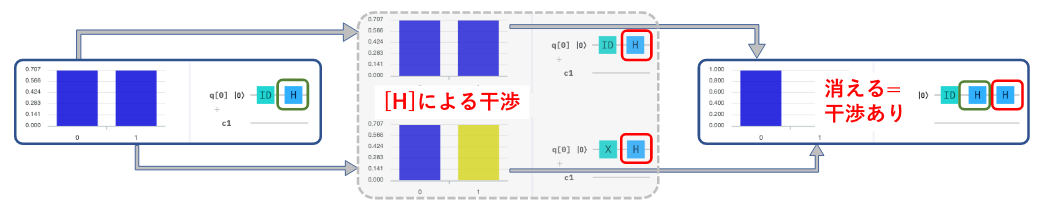
|0>にHゲートを作用させると|0>と|1>の重ね合わせ状態になり、さらにHゲートを作用させると|0>成分と|1>成分の各々にHゲートを作用させたものが干渉により打ち消しあって|0>のみが残るところまでは理解していました。
そこで、同様に2量子ビットの場合で拡散と干渉の過程を計算で追ってみることにしました。😭😭😭
|00>、|01>、|10>、|11>の状態がアダマール行列の拡散変換でどのようになり、再変換でどのように元に戻るのか。
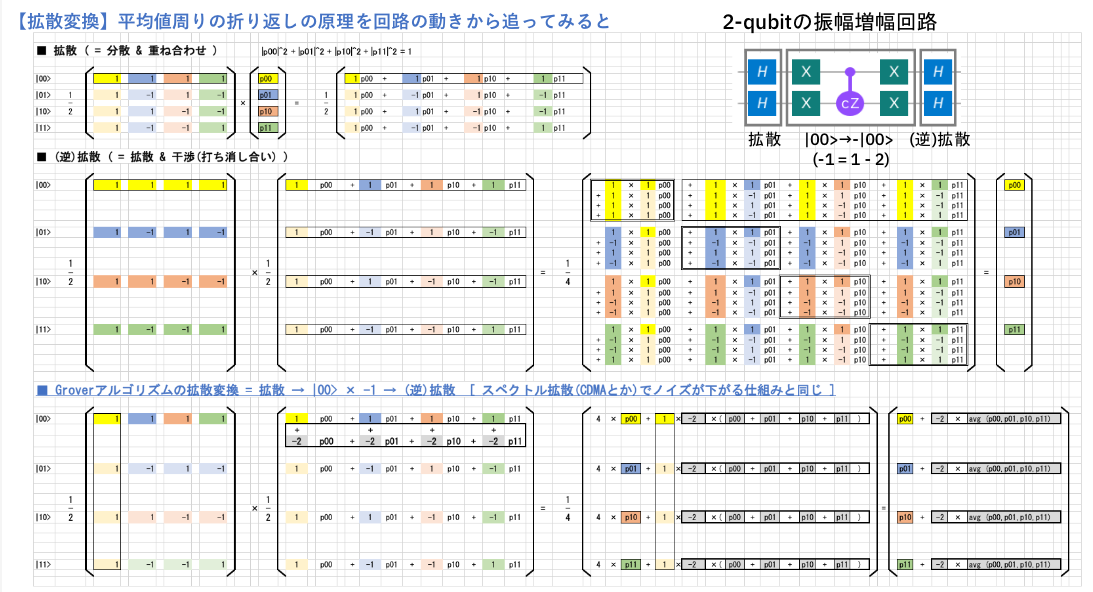
Hゲートについてブロッホ球での単一量子ビットの動きでしか把握していなかった自分には、複数量子ビット状態でのアダマール行列による干渉が見えた事が新鮮でした。
また、アダマール行列の1行(列)目(全て1)と他の行(列)(1が半分、-1が半分)の違いを認識したことで、振幅増幅回路の二つの拡散(逆拡散)回路の間にある|00>の符号反転の意味が理解できました。
・最初の拡散過程で|00..0>の状態は、元の全状態の合計になる
・|00..0>の符号反転により|00..0>に|00..0>の-2倍を加えたことと同じになり
・後ろの逆拡散過程で元に戻った全ての状態に合計の-2倍を拡散(平均)したものが付加される
試行錯誤しながら学習したこと(我流)のまとめ
Boolean(二進数)での演算は、(制御)Xゲートのみで構成できる
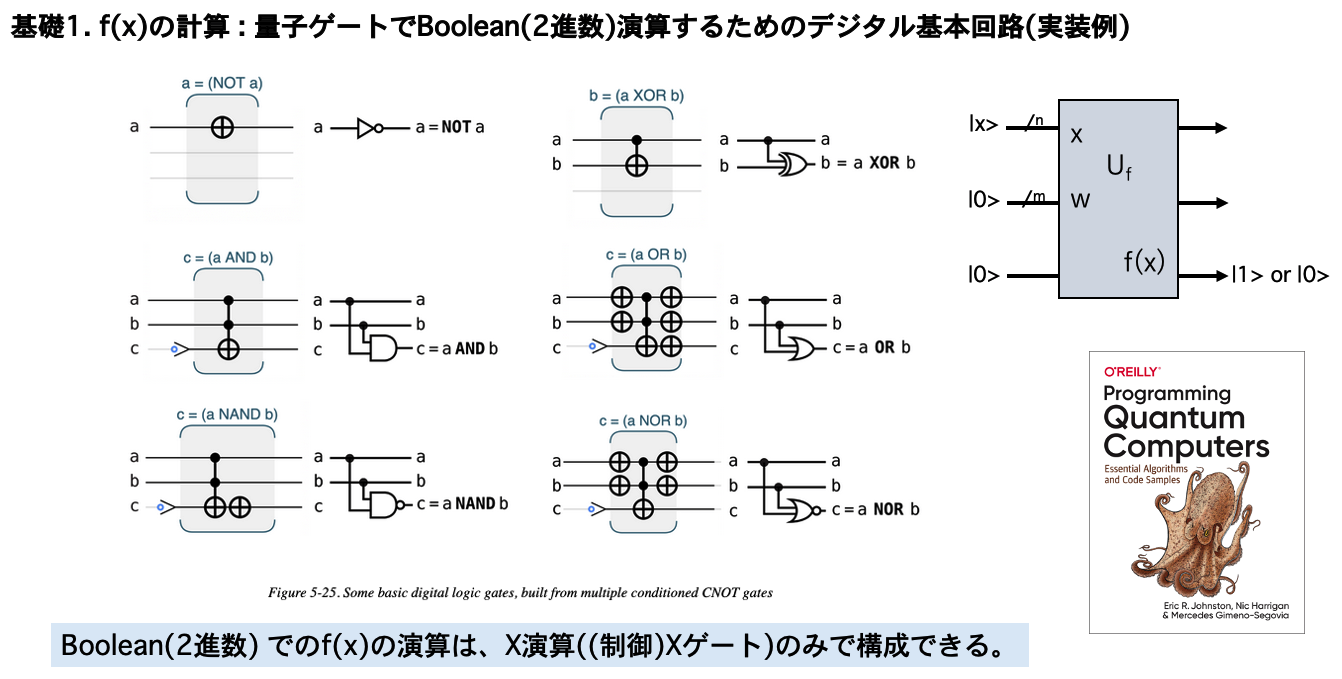
・Programming Quantum Computers
・動かして学ぶ量子コンピュータプログラミング
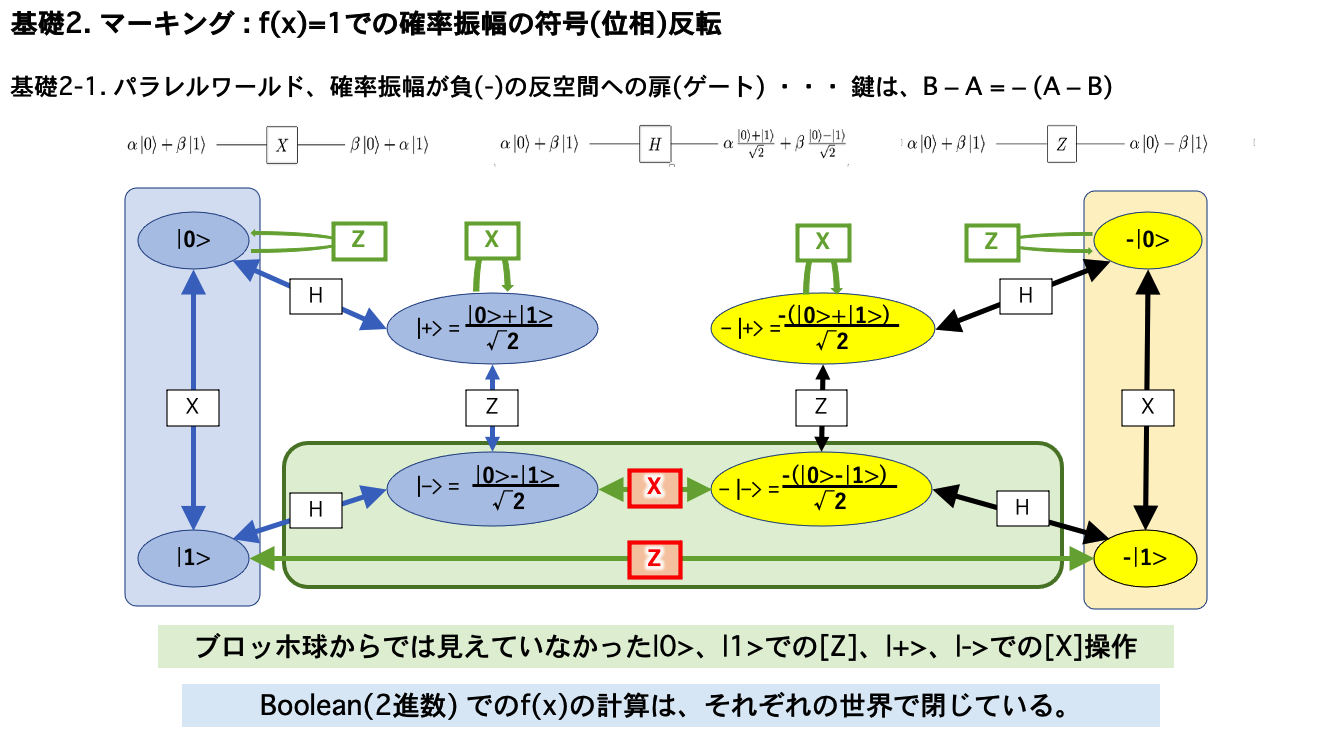
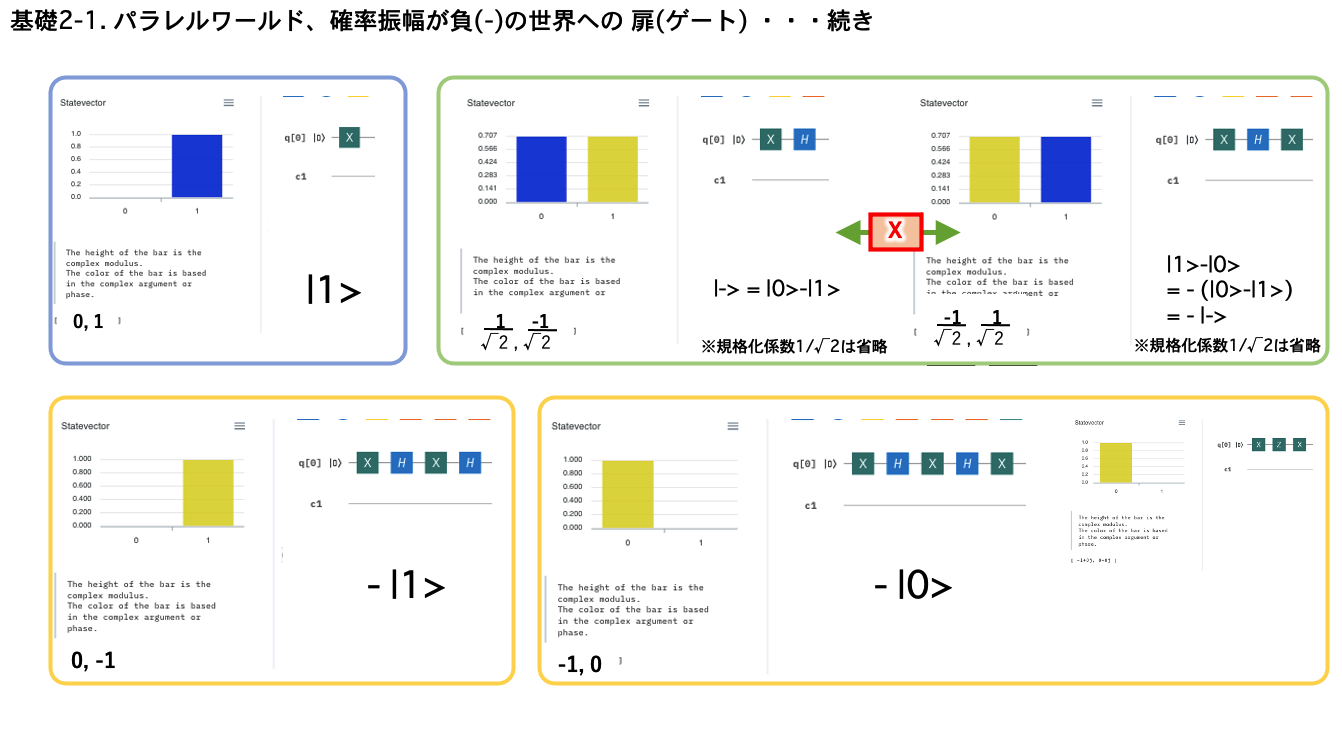
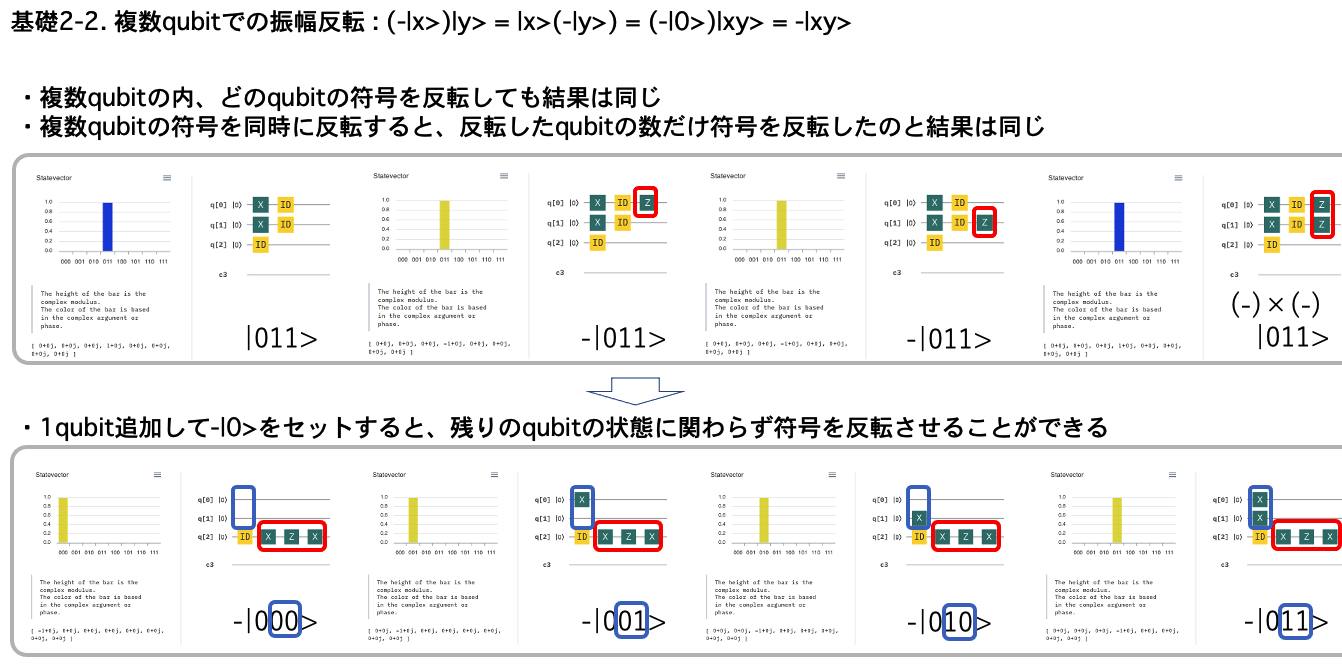
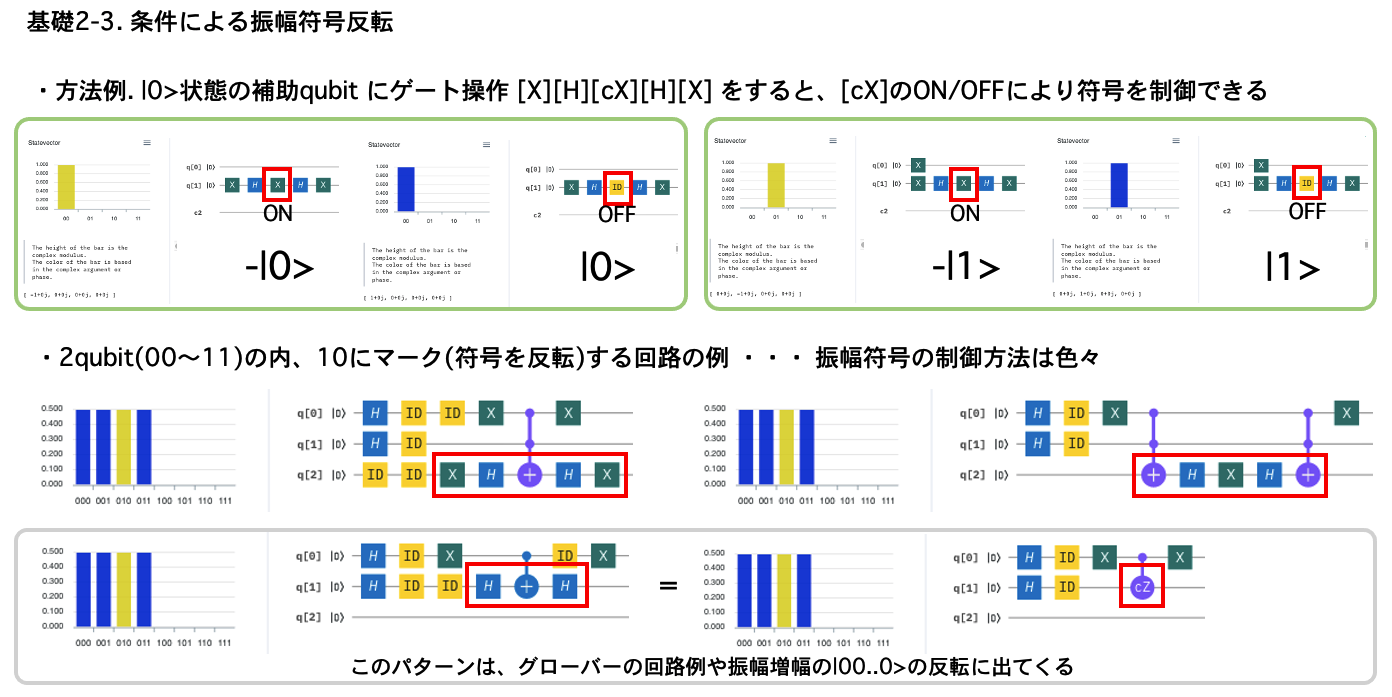
マーキング: 並行(反)宇宙への扉(ゲート)の鍵は B-A = -(A-B)
振幅増幅: アダマール行列による拡散と干渉
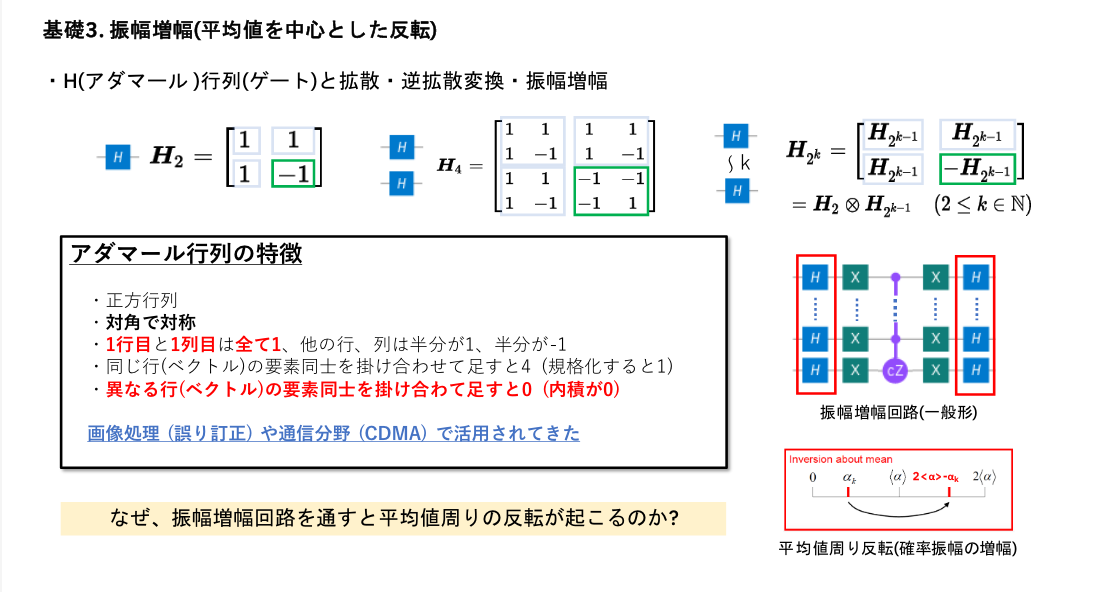
「平均値を中心とした反転」は、平均値の二倍から元に値を引くことと同じで、教科書に出てくるような数式ではそのように書かれています(数式的にはこちらがシンプル)。しかし量子回路を読解してみると「元の値から平均値の二倍を引く」回路になっています(回路的にはこちらがシンプル)。確率振幅の二乗が測定結果に現れるので結果は同じになりますが、これも数式と回路の関係の理解の妨げになっていました。
振幅増幅の前に: もつれた糸を解きほぐせ
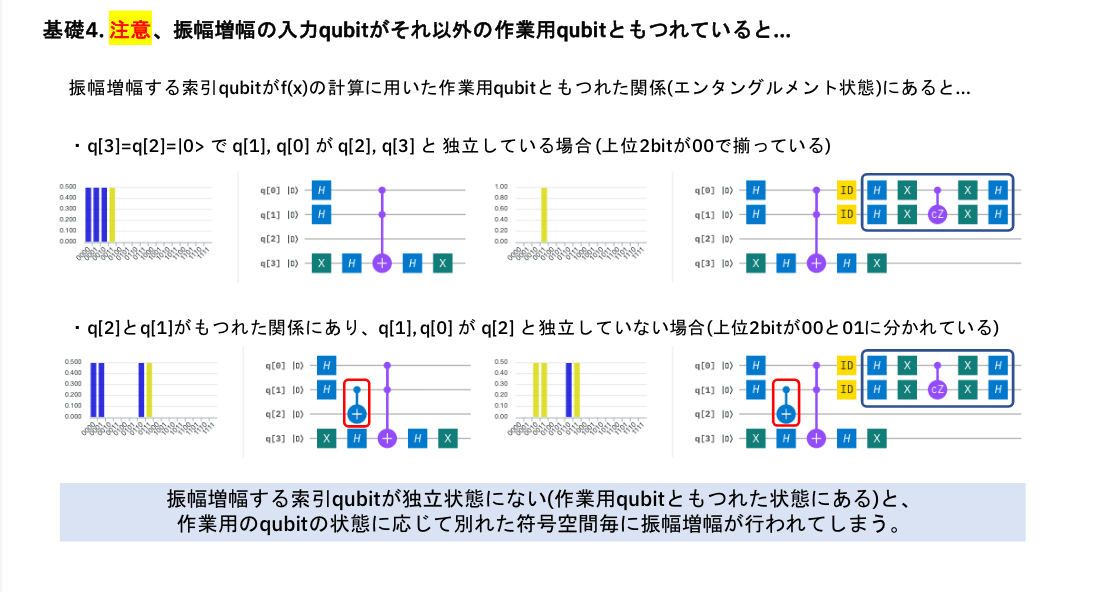
糸が絡まっていると干渉できない。ステートベクトル表示が無ければ気付けなかったポイントです。
こうしてたどり着いた一つの形
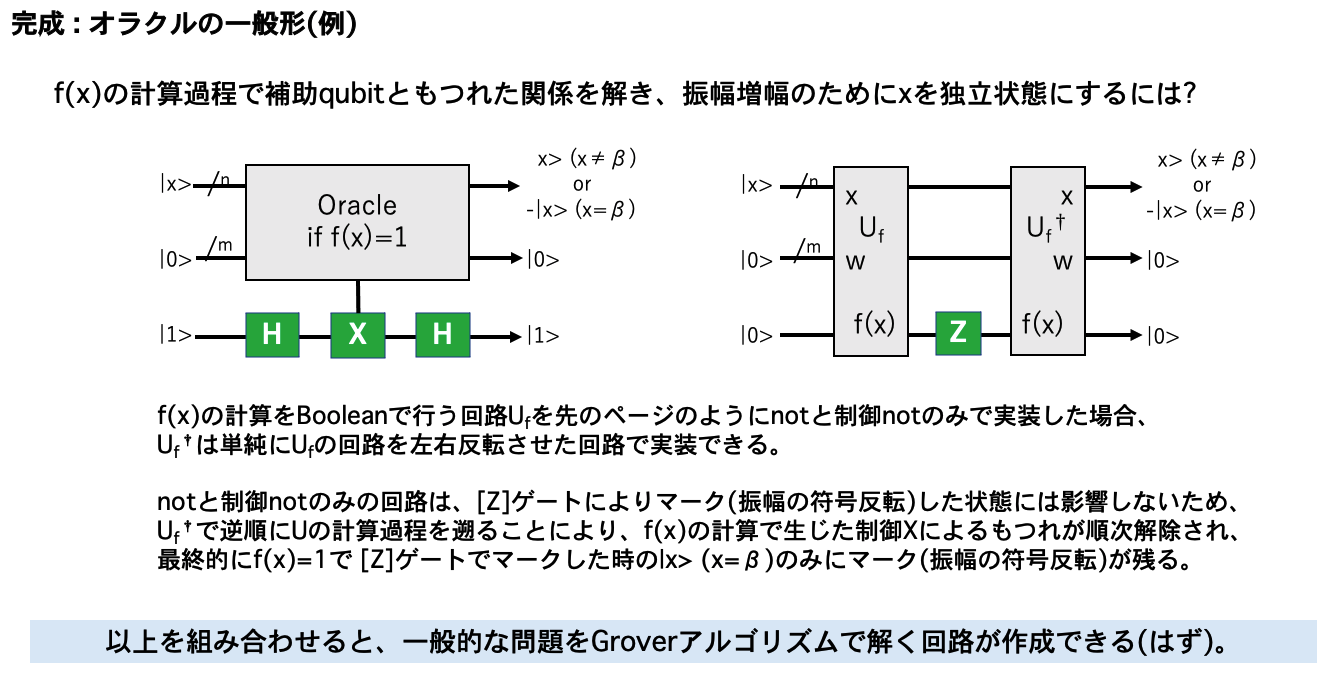
こうして、我流で習得した自分の理解が正しいか確認する意味で作成したのが、冒頭で紹介した「Groverアルゴリズムで実際にデータを検索(!?)」と「Groverアルゴリズムで15を因数分解」でした。

終わりに
理論について正しく書かれた書籍や記事は、より分かり易いものがたくさんあると思いますし、数式などから理論や使い方を理解できる人は、そちらからアプローチする方が圧倒的に楽です。
(私の場合は、外国語の映画みたいに一旦理解してから原文(数式)を見てはじめて少しだけ分かるようになりましたが😅)
一方、回路(コード)を間違えると何が起こるのかといった(失敗😅)事例の解説は皆無だと思います。
ということで、こういった変わった投稿も年末の余興としてだったらありですよね?!
(ほぼほぼ、昨年作ったパワポの寄せ集めと再編だけど、期日に無事間に合わせることができてホッとしました👏)
参考
・慶應大学 量子コンピュータ授業 #4 グローバーのアルゴリズム
・Qiskit Textbook - Grover's Algorithm
・Groverアルゴリズムで実際にデータを検索(!?)
・Groverアルゴリズムで15を因数分解