量子コンピュータで因数分解が高速に解ける？〜 ショアのアルゴリズム 〜

！！注意事項！！

本記事は、国内の量子情報の市販本を読んで、私なりに理解した情報を、敢えて専門書には書いていない用語も使ったプローチで解説を試みています。正確ではない記述もあり、ご批判はあるとは思います。その点を差し引いて、お読みいただけると嬉しいです。

はじめに

今年も残すところあと僅かです。2017年を振り返ると、量子コンピューター関連のニュースとして大きなトピックといえば、2017年3月の**「IBM Q」の登場**でしょう。IBM¹ により、ユニバーサル量子コンピューターがクラウドで商用利用できるようになりました。利用できる量子ビット数が少ないとはいえ、この分野に関わる多くの人たちに刺激と希望を与えました。

話が飛びますが、インターネットを利用している私たちにとって、SSL（Secure Socket Layer）という暗号化通信の技術によって、一般的なWebサービスの通信経路のセキュリティが保証されてることは、皆さんもご存じのとおりです。安全にインターネットショッピングができるのは、この技術のおかげです。SSL の暗号方式（ RSA 暗号）は「因数分解が多項式時間では解けない」という情報科学の理論に裏づけられており、私たちはこの方式が安全であると信じています。ここで言う「多項式時間では解けない」とは、現在のコンピューターでは現実的に有効な時間で解を求められないということです。

さて、ここで本記事の主役の量子コンピューターの登場です。
実は、この因数分解の問題は「ユニバーサルな量子コンピューターでは多項式時間で解ける」ことが知られています。つまりは、この暗号技術が役に立たなくなるとも言われています。

はたして、本当なのでしょうか？

（言い切る人はいないので、敢えて言い切ります）違います！
これはあくまでも理論的な話しであって、現時点では現実的には誤ったイメージだと私は考えています²。実は、国内でこの手の情報を見つけようとすると、きちんと説明されたものは専門書しかなく、その専門書ですら、うまく解説されているものはほとんどありません。現実的な解釈として表立った情報が少ないために、「○○ビットの量子コンピューターが開発された」というニュースが流れるたびに、暗号が破られるのでは？とか、ネット通販はオワコン？とか、漠然とした不安を煽るような話しが出たりしているのではないでしょうか。

おそらく、どのような条件の量子コンピューターがあれば、現実的に解けることになるかを判断するための情報が一般的に不足していて、話題性が先行してしまうがゆえに、こういった認識のずれが起きているのだと私は思います。その判断材料の１つになればと思い、このエントリでは「量子コンピューターで因数分解が高速に解ける」の理論的な解説を紹介したいと思います。

ショアのアルゴリズム

量子コンピューターを使った因数分解ができるのが、「ショアのアルゴリズム」と呼ばれている方法です。簡単な図でその手順を見てみましょう。
ショアのアルゴリズムは、古典コンピューター³を使って処理ができる部分（図の（１）、（３））と量子コンピューターを使う必要のある処理の部分（図の（２））で構成されます。

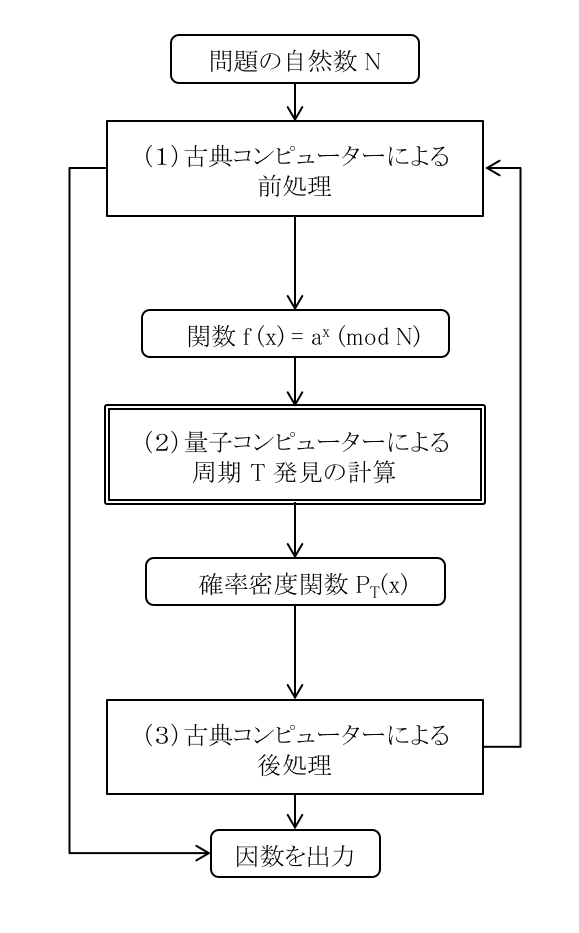
（１）古典コンピューターによる前処理
問題となる自然数 $ N $ より小さい、$ N $ と互いに素である^(*)適当な $ a $ を選択する処理です。この処理で、$ N $ を割り切る因数がたまたま見つかることもあり、そのときは、以降の処理は不要となります。

（２）量子コンピューターによる処理
（１）で選択した $ a $ を使った「関数：$ f(x) = a^x\pmod{N} $」を入力にして、周期 $ T $ を発見するための処理です。
この処理の出力は、あとで周期 $ T $ を計算で求められるような確率密度関数 $ P_T(x) $ です。

（３）古典コンピューターによる後処理
確率密度関数 $ P_T(x) $ から $ T $ を計算し、それが偶数かどうかを判定します。
$ T $ が奇数であれば、（１）からやり直します。
$ T $ が偶数であれば、$ a^{T/2} \pm 1 $ と $ N $ が互いに素^(*)か調べます。
互いに素であれば、（１）からやり直します。
互いに素でなければ、因数が求められます。
そして、この手順で（２）で発見した $ T $ を使うと、「互いに素にならないことが多い」ということが分かってます。よって、手順が効率的に終了して、速く計算できるということです。

(*) 上記手順で、「互いに素」かどうかの判定は、「ユークリッドの互除法」で計算されます。これは、古典コンピューターでも多項式時間で解を求められる計算です。

ここで、気になる計算時間に関して整理してみましょう。
（１）の前処理　＝　多項式時間で処理が終わる
（２）の量子計算＝　多項式時間で処理が終わる⁴
（３）の後処理　＝　多項式時間で処理が終わる
ことが知られています。このことから、（１）〜（３）までの全体処理である「ショアのアルゴリズムは多項式時間で解を求められる」のです。

周期 T 発見のための計算

次に、気になる量子コンピューター上の計算はどのようなことが行われているのでしょうか。見てみましょう。
「関数」を入力して「密度関数」を出力すると解説していますが、なんだか関数型言語を知っていれば、分かるようで、分かりにくい話しに聞こえます。意訳した下図を使って説明します。

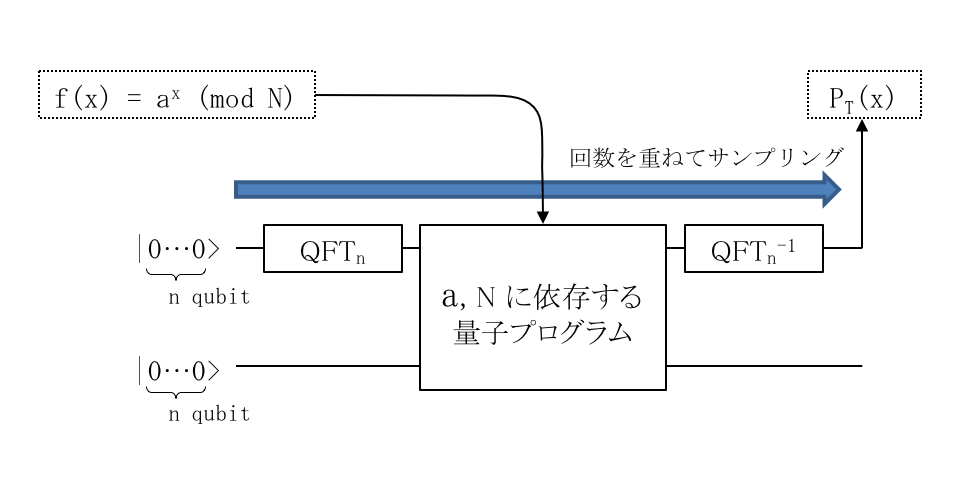
【入力】
古典コンピューターの前処理で選択された $ a $ と問題 $ N $ が与えられます。この２値を使った関数 $ a^x\pmod{N} $ がこの量子コンピューターの入力になります。関数とは、ある計算ができる量子プログラム⁵と考えてください。

【演算】
演算は、$ N $ を２進数で表すのに十分な量子ビット数 $ n $（$ N \le 2^n \lt 2N $ を満たす $ n $）を２つ準備します。この $ 2n $個の量子ビットを使って、図のような量子プログラム（量子回路ともいう）を左から右に操作して計算します。その結果は、量子計算ですから、確率的に値が得られます。その結果を適切な回数サンプリングします。

図にある「$ QFT_n $」と「$ QFT_n^{-1} $」は、それぞれ「量子フーリエ変換」と「逆量子フーリエ変換」の演算を行う量子プログラムです。本記事では、量子フーリエ変換については詳しく説明しません。ここでは、ある$ n $に応じて決まった操作が入力関数 $ f(x) $ の前後で行われるのだと受け入れましょう。なお、「$ QFT_n $」は、$ \lvert 0 \dots 0 \rangle $ ケットベクトルに作用させるときには、アダマール変換（Hadamard）と同じ結果になります。そのため、「$ QFT_n $」を「$ H_n $」で代用されることも多いです。

【出力】
演算を繰り返して得られた結果は、得られた値 $ x $ とその $ x $ が得られる確率 $ P_T(x) $ として、出力されます。$ P_T(x) $ は、入力された関数 $ f(x) $ に周期性の性質があると、その周期 $ T $ で特徴づけられる構造の関数となるようです。
理論的にはもっと複雑ですが、ある結果のパターンを分かりやすくグラフで示すと次のような関数になります。横軸が観測された値 $ x $ で、縦軸がその観測確率です。

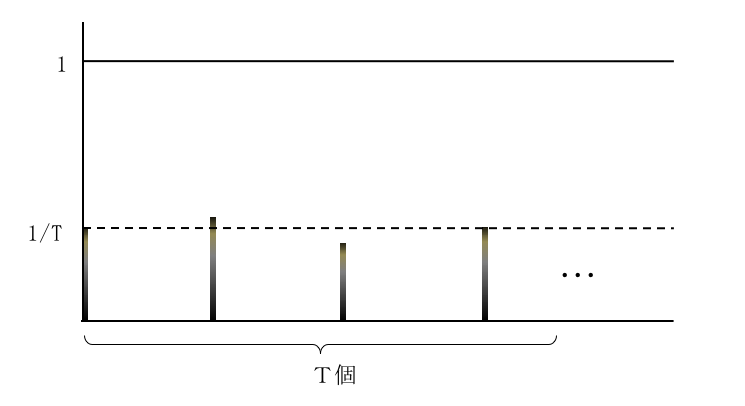
この例は分かりやすく、サンプリングもよくて、$ T $ が見つけやすいケースでした。
前処理で適切に選択された $ a $ に対しては、多くの場合がこのように $ T $ が見つけやすい形で出力を得られそうです。

ここまでで、ショアのアルゴリズムの説明は終わりです。
概要は、それほど難しい感じではないかと思いますが、いかがでしょうか。
次に、これをふまえた上で、２つの疑問について考えながら、量子コンピューターの現状を考えてみましょう。

２つの疑問に対する答え

量子コンピューターで因数分解が高速に解けるのか？（疑問１）

理論的には高速に解けるはずです。そして、それには量子コンピューターだけではなく、古典コンピューターも使って、両者を組み合わせて計算します ⁶。
ただ、高速といっても「それがどれ程速いのか？」という疑問については、計算量に関する理論式はありますが、実機がないので、正直なところわかりません。
量子回路がどれくらいの時間で動くのか、そのためのプログラムがどのようにコンパイルされて実行されるのか（コンパイル時間やプログラムのロード時間）という肝心なところが、現時点では全て不明瞭です。

どういう条件の量子コンピューターが必要なのか？（疑問２）

量子ビットの前提条件

上記のとおり、一般に純粋なショアのアルゴリズムでは、ある自然数 $ 2^n $ の因数分解をするためには、$ 2n $ 個の量子ビットが必要になります。
例えば、$ 50 $ 量子ビットの量子コンピューターが出現したとしましょう。すると、$ 25 $ ビットの暗号が多項式時間で解けるようになるということを意味します。現時点ではRSA暗号の鍵長は、$ 2048 $ ビットですから、どれ程の隔たりがあるか想像してみてください。
更には、この量子コンピューターには、不安定な物理現象を使うために、使える量子ビットを犠牲にして確実性を上げる（エラー訂正という）必要があります。$ 50 $ 量子ビットの量子コンピューターと呼ばれたとき、このエラー訂正のための量子ビットが含まれているかは、注意する必要があります。つまり、$ 50 $ 量子ビット実現といっても、有用な量子ビットは、その半分程度かもしれません。
そして、もう一つ注意しなければならないのが、ニュースなどで「量子コンピューター」と表記されるもののなかに、ユニバーサルではないものが量子コンピューターと呼ばれているということです。いわゆる「イジングマシン」といわれるマシンがそれです。このマシンにも量子ビットという単位が使われています。こちらは方式が異なるため、数千量子ビットを扱える実機が存在します。しかし、上記のショアのアルゴリズムは、あくまでユニバーサルな量子コンピューターについての話しで、この種類のマシンには当てはまりません。5000量子ビットのイジングマシンが登場したからといって、RSA暗号が危険になるようなアルゴリズムが動くかは見極めが必要です。

量子プログラムの前提条件

ショアのアルゴリズムは、まさに論文や教科書にあるアルゴリズムです。
これを動くプログラムにして、量子コンピューターで動かすという仕組みは、未成熟です。ユニバーサル量子コンピューターである「IBM Q」を動かすためには、OpenQASM という記述言語⁷（量子アセンブリ言語）があります。しかし、これは私たちが慣れ親しんでいる高級言語⁸ではありません。プログラムを記述するのは、それなりにハードルが高いのです。
また、アルゴリズムに注目してください。「関数 $ f(x) = a^x\pmod{N} $ を入力して、確率関数 $ P_T(x) $ が出力されます」と解説していますが、このブラックボックスをプログラムすることが必要になります。この部分を（任意の）$ ^\forall N $ に対して書いてあるプログラムは数少ないです。
その理由は、簡単な開発環境が整っていない点が大きいです。もう一つの理由としては、プログラミングに精通した量子情報分野の研究者と、量子情報に詳しいIT業界のエンジニアの人口が圧倒的に足りていません。プログラム開発ができる人が少なくて、このような一見簡単そうなプログラムもプログラミングする人がとても少ないのが現状です。
今後、目的に近い形で量子プログラミングができる環境が整備されていく⁹ことと量子プログラムに関わる人が増えることが重要だと思います。

まとめ（感想）

現実的には数万個の量子ビットを備えたユニバーサル量子コンピューターが実現しない限り、 RSA 暗号が解けるものではない、と私は見ています。しかし、安心はできません。もっと少ない量子ビットで因数分解を解くような手法や効率的なエラー訂正の手法が発見されるかもしれません。そもそもエラー訂正をしないでも動作するハードウェアが開発されるかもしれません。これからの量子コンピューターの発展に期待したいと思います。
そして最後に、量子コンピューターを見るときには、量子ビット数だけではない複合要因があるのだということを知っていることが大切だと思います。

---

私は、Qiitaのアドベンドカレンダー2017に量子コンピュータが立ち上がったのを 12月1日に知りました。その時には、参加枠がほとんど空いている状態でした。量子コンピューターの進歩のために活動している者としては、その状況は寂しくもあり、今のこの分野における現実を突きつけられたようでもあり、焦りも感じました。ですから、慌てて、有りものではありましたが、その12月1日に参加させて頂きました。

そんな状況のなか、今日まで途切れることなく、リレーできているのは、奇跡的なことのように思います。アドベントカレンダーは、様々な人がワイワイやって楽しむイベントであるにも関わらず、複数回投稿を予定してしまって申し訳ないです。ただ、リレーが途切れるのも辛いので、お許しください。

アドベントカレンダーはそろそろ中盤ですが、後半には未だ空き枠がございます。同じ興味がある仲間が少しでも増えると嬉しいです。

---

脚注

1. https://www.research.ibm.com/ibm-q/ ↩

2. 私は、量子情報の専門家でも、暗号の専門家でもありません。ただ好きで量子コンピューターの実現と進歩に関わる活動をしています。その立場から個人的な意見を述べさせていただくと「量子コンピューターが因数分解を高速にできる」という理論的な事実は、量子コンピューターの研究を進めるためのとても良い動力源となっているように感じます。専門家であれば、現時点では現実的でないことは言うまでもない当たり前のことだと思います。勿論、取り組んでいる側としては、出来ることを出来ないとは言いません。ただ、それが出来ることを示すだけのハードがないだけです。その可能性を前面に出すことで、この分野に注目してもらい、探求しつづけたいという思いがあるのかもしれません。ただ、量子アルゴリズムの研究はこれからの分野であり、今後いつ素敵な問題解決の手法が見つかるかわからない、可能性を秘めた研究分野でもあります。 ↩

3. 量子コンピューターに対して、従来のコンピューターを「古典コンピューター」（classical computer）と呼びます。いま現役のコンピューターを「古典」と呼んでしまうのは、なんだか可哀想です。物理の分野では、量子力学が確立されてから、それまでの力学を古典力学と呼んでいます。この呼び名は、それに習っているそうです。 ↩

4. 少し難しい計算が必要になります。興味がある方は「量子コンピュータの基礎数理」（上坂吉則 著、コロナ社、ISBN:4339023760）がお薦めです。 ↩

5. ここでは量子アセンブラなど何らかの方法で、量子アセンブリ・プログラムにできるとします。ちなみに、この量子プログラムは、具体的には、$ 2n \times 2n $ のUnitary行列演算の積で表される計算です。 ↩

6. ユニバーサルな量子コンピューターは古典コンピューターと同等の計算もできますから、古典コンピューターを使わずに、量子コンピューターだけでも計算はできます。 ↩

7. Advent Calender 2017 の他の方の記事で、使い方が解説されていると思います。 ↩

8. これを扱うための python ライブラリ QISKit が IBM からオープンソースとして提供されてますが、核となる部分は、アセンブリ言語のままです。 ↩

9. 私は、この課題を解決したいと、OpenQL ProjectというOSSプロジェクトで、草の根的な活動を行っております。 ↩