セルオートマトンの量子アルゴリズム
今回は一連の投稿の核心の一つ、セルオートマトンの量子アルゴリズム!1回目、2回目、3回目とも文が長すぎたので、今回は文を減らし図表やコードを増やした。
4-1. ウルフラムコード
セルオートマトン
格子状にセルあるいは箱の並びがあり、セルには、1(玉有)状態、あるいは0(玉無)状態がある。その1と0が単純なルールに従って移っていく。移ることを遷移と表現し、移る前後で時間が(1ステップ)経過したと言う。この時間経過とともに1と0は遷移を繰り返して全体としての1と0の並びの様相は変化していく。この時間経過での変化を時間発展と称する。
玉を動かすルール
単純なルールとして、セルが一直線に並んでいて、あるi番目のセルとその両隣のセル(i-1番とi+1番)の3つの状態で決定するものが有名である。
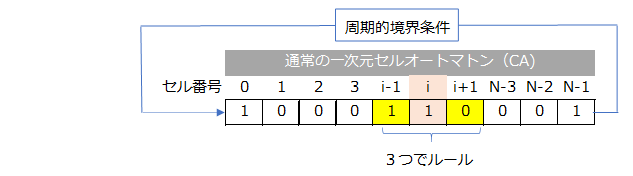
時刻(t)での3つのセルの 1,0 のとり得るパターンは、$2^3=8$ である。(下の左の表)。尚表ではルールの対象となるセルを C(Center)、左隣りを L(Left)、右隣りを R(Right) で示している。前述の8パータンに対して次の時刻(t+1)でCはLCRの状態に応じて1,0をとり得るので、ルールとしては$2^8=256$ 通り存在し得る。下表はその中で代表的なもの6つを示した。
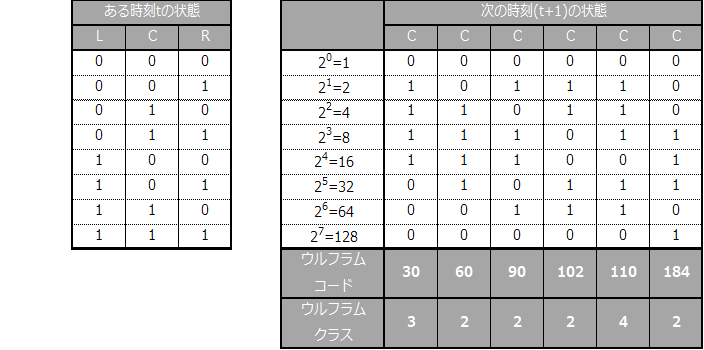
ウルフラムコードとクラス
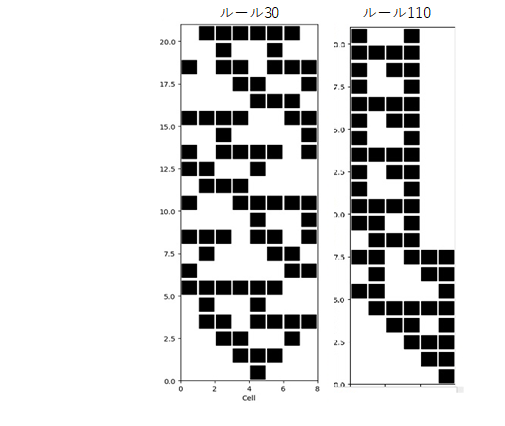
各ルールにはコード番号が付けられている。かつてセルオートマトンを研究したウルフラムさんにちなんでウルフラムコードと称する。コード番号は時刻t+1でのCを二進数と見立てたときの十進数である。表中の30番、90番、110番、184番はググルと出てくるほど有名なルールである。ルール30は時間発展がカオスになることで有名で、時間発展で出る模様がイモ貝の文様と類似しているとか。ルール90は時間発展で出る模様が典型的フラクタル図形のシェルピンスキーギャスケットとなる。さらにルール110はチューリング完全と言われている、って? ウルフラムさんはルールによって異なるセルオートマトンの時間発展の様子を次の4つのクラスに分類していてる。
- クラス1 初期状態は時間発展に伴い安定状態(均質状態)へと発展する
- クラス2 初期状態は時間発展に伴い複数パターンが繰り返す振動状態へと発展する
- クラス3 初期状態は時間発展に伴い擬似的ランダムあるいはカオス的挙動となる
- クラス4 初期状態は時間発展に伴い長期間存続可能な局所的パターンが相互作用をする構造に発展する(クラス2とクラス3の中間的クラス)=カオスの淵と称される
256種あるルールの中で半数はクラス3で、クラス4となるルールは稀であるらしい。
4-2. 周期的境界条件
今までセルは一直線に並んでいて無限に続いているイメージで語ってきた。が残念ながら計算上無限とすることはできない。2回目で詳述した通り、Blueqatの場合、量子ビット数の上限は32bitなので、NR≦32(Nはセル数、Rはレジスタ数)だが、24ぐらいを超えると計算時間が長くなる上メモリー不足でエラーを生じてしまう。もしレジスタ数R=4ならセル数は高々N=6程度が限界。そのためセル数は有限で、始点と終点を持つ。一方、ルールは左右両隣のセルの状態を見るため始点や終点では特別な扱いが必要となる。要は、終点(右端)のセルは右隣りとして始点(左端)のセルを想定する。逆も同様。4-1の図で言うとセル番号N-1の右はセル番号0と言うことである。つまりセルが環状になっているイメージである。このことを周期的境界条件と言う。
4-3. ルール102 ルール60 ルール90
ルール102
先ほどの表のルール102は、実は、Lは無関係でCとRの排他論理和が遷移後のCの状態となっている。Cをi番目のセルとした場合、セルiとセルi+1の状態の排他論理和がセルiの遷移状態となる。これらをqubitに置き換えてblueqatのコードで記せば、 c.cx[1+i, i] まさに、1回目の冒頭で示したものである。このアルゴリズムでは、補助目的のレジスタ用qubitを必要としない。以下に量子プログラム部のみのコードを示す。
def qproc():
for i in range(N):
c.cx[1+i, i]
return
フルコードはGithubのリポジトリ q-cams 内のq-cam102r.py。量子プログラムの中にpythonのループ構造があるため純粋な量子プロセスではないと思われるかもしれないが、実はループは記述の手間を省略するためで、特別な制御構造を使用していない。つまりblueqatのコードのみに展開可能であり純粋な量子プログラムとなっている。
セル数20でレジスタは1(N=20、R=1)。初期状態として右端のセルのみ1とし実行してみる。コンソールの中に色々な結果が出力されるがそれは後述するとし、時間発展の絵を見てみよう。(q-camでは最後にグラフィック出力をするようにしてい) 横軸がセル番号、縦軸が時刻で、下が0で上に向かって時間発展していく。黒が1、白が0で出力している。ルール102の結果は下図の左半部である。
ルール60
次にルール60。ルール102とは対照関係で、CとLの排他論理和が遷移後のCの状態となっている。c.cx[i-1, i]がコードだが、注意が必要でルール102のようにループでカウントアップすると遷移した状態で遷移を起こすことになり、まともな結果にならない。したがってループはfor i in range(N,0,-1):のようにカウントダウンにする。ルール60の結果は下図の右半部である。尚、条件は N=20、R=1、 初期状態は左端のみ1とした。フルコードはGithubのリポジトリ q-cams 内のq-cam60r.py
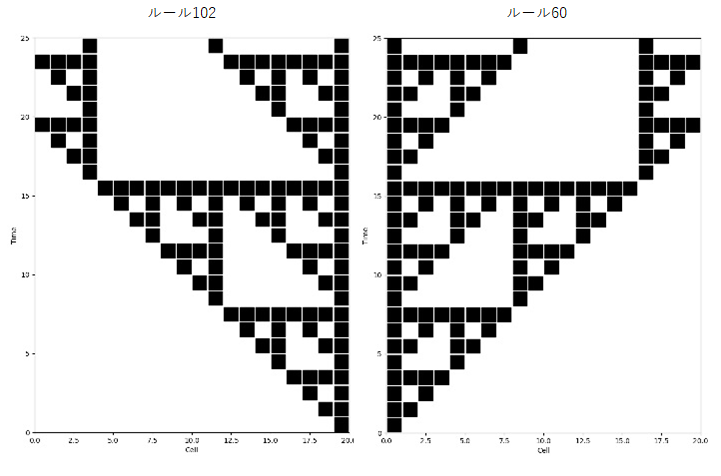
ルール90
上図の左右を合体すると、ルール90となる。しかしアルゴリズムは単純合体とはいかない。下の表がアルゴリズムの考え方を示している。表の②では表の①のL(L①)を制御ビット、表①のC(C①)を標的ビットとして制御NOTゲートを実施していて、その結果をC②に記している。実際にはC①がC②に変化する。表の③ではR①を制御、C①を標的として制御NOTを実施しC③を得る。えっ!C①の中身は表②のプロセス実施後はC②に書き換えられているのでは?その通り!そこで登場するのが補助用のレジスタ。0~N-1番をN個のセルに見立てメインレジスタとし、N~2N-1番を補助レジスタとして、初めに0~N-1番の状態をそっくりコピーする。(3回目の3-1参照)このレジスタにコピーされた状態をC①とすればよく、得られるC③もこのレジスタの中にあることになる。次に表④ではC③を制御、C②を標的して制御NOTを行うと求める結果となる。
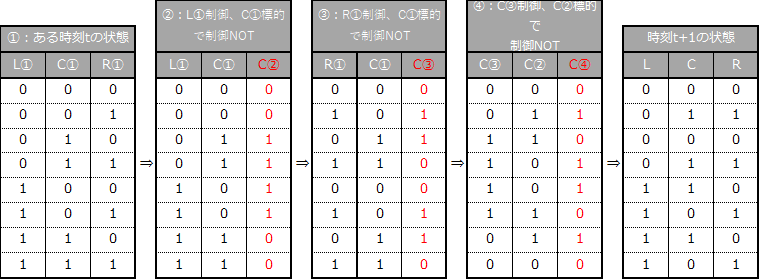
これをコードで書くと以下の通りである。尚、Reg1sb=Nはレジスタ1のスタートビット番号である。
def qproc():
for i in range(N):
c.cx[i, Reg1sb+i]
for i in range(N,0,-1):
c.cx[Reg1sb+i-1,Reg1sb+i]
for i in range(N):
c.cx[i+1, i]
for i in range(N):
c.cx[Reg1sb+i,i]
return
フルコードはGithubのリポジトリ q-cams 内のq-cam90r.py。N=12(セル数)、R=2(メインレジスタ1個+補助レジスタ1個)、初期状態[0,0,0,0,0,0,1,0,0,0,0,0]の時のグラフィック結果が下図である。
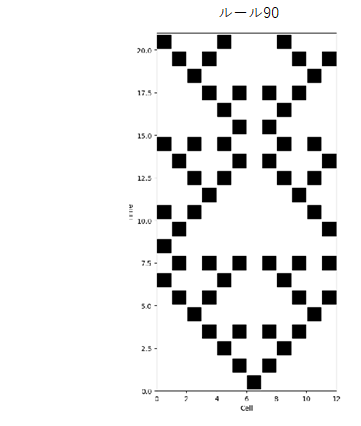
実は周期的境界条件に達しところで正しい結果ではなくなっている。また厳密にはルール60と102の合体とは異なっている。とは言え対照性は見て取れる。
4-4. ルール30とルール110
ウルフラムクラス3でカオスになるルール30やクラス4であるルール110は、前のルール90等より複雑なアルゴリズムとなり、補助のレジスタも2個(2N個 ⇒ R=3)必要となる。さらに、制御NOTゲートだけではなくトフォリゲートが必要となる。そこで、まずアルゴリズムを組み立てていく考え方を説明しよう。
量子アルゴリズムを作る考え方( 30,110 含む多くのルールで)
Ⅰ(アプローチ): スタートのC列(列:表の縦、行:表の横)にL列あるいはR列さらにはその両方を用い何某かの量子ゲート(原則制御NOT)を作用させ、できるだけゴールのC列に近いものを得る
Ⅱ(フラグ付け): ゴールと状態が異なる行を他行にはない特徴的なパターンを見出し量子ゲート(原則トフォリゲート)を作用させフラグ(目印)をつける。フラグは補助レジスタに格納する
Ⅲ.(補正): 抽出された特徴行のC列の状態をフラグで反転させる
ルール30
一連の流れは下表参照。まずアプローチとして、左隣(L①)と制御NOTを実施(②)さらにこのC②の結果に右隣(R①)を制御ビットとして制御NOTを作用させる(③)。次にフラグ付けとして、C③とゴールを比べると、下表の黄色にした行だけが異なっている。この行に他行にはない特徴的パターンを検討すると、C①とR①がこの行のみ共に1であることが分かる(青色)。従って、C①とR①を制御ビット、補助のレジスタXを標的にトフォリゲートを作用させると、この行のみが1状態となりフラグ付けされる。最後に補正としてフラグで反転させる。つまりXレジスタのビット列を制御ビット、C③を標的に制御NOTを作用させゴールとなる。
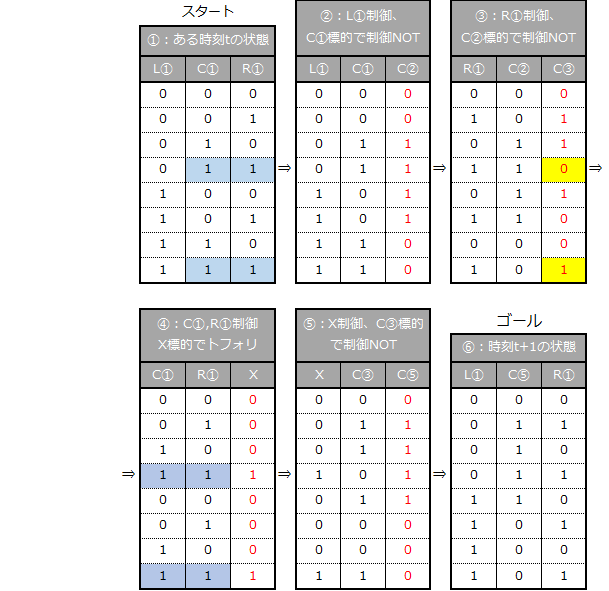
実際のコードに書き下すには上のフローのままでは困難である。はじめに補助レジスタXに、C①とR①制御としたトフォリゲートの結果(フラグ)を格納する。次に、スタートの状態であるC①を別の補助レジスタYにコピーする。何故なら、上表では変化が分かりずらいが、アプローチの第2弾目ではR①を制御ビットとし制御NOTを作用させるが、この時R①の状態は、第一弾目の制御NOTを作用させた段階で変化してしまっている。そのため変化前のR①状態が必要なためコピーが必要となる。わかりづらいので実際のセルとレジスタを想定したフローを下表に示した。
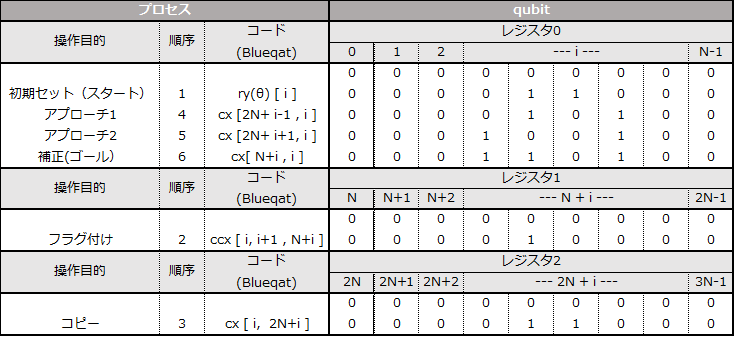
この表を基にコードに書き下すと以下のようになる。ループ外の記述は周期的境界条件のためである。
Reg0sb=0 # start qubit number of Reg0
Reg1sb=N # start qubit number of Reg1
Reg2sb=N*2 # start qubit number of Reg2
Reg3sb=N*3 # start qubit number of Reg3
Reg0lb=N-1 # last qubit number of Reg0
Reg1lb=N*2-1 # last qubit number of Reg1
Reg2lb=N*3-1 # last qubit number of Reg2
Reg3lb=N*4-1 # last qubit number of Reg3
def qproc():
for i in range(N-1):
c.ccx[i, 1+i, Reg1sb+i]
c.ccx[Reg0lb,Reg0sb,Reg1lb]
for i in range(N):
c.cx[i, Reg2sb+i]
for i in range(N-1):
c.cx[Reg2sb+i,i+1]
c.cx[Reg2lb,Reg0sb]
for i in range(N-1):
c.cx[Reg2sb+i+1, i]
c.cx[Reg2sb,Reg0lb]
for i in range(N):
c.cx[Reg1sb+i,i]
return
フルコードはGithubのリポジトリ q-cams 内のq-cam30r.py。N=8(セル数)、R=3、初期状態[0,0,0,0,1,0,0,0]の時のグラフィック結果を下図(ルール110の下)に示した。
ルール110
ルール30よりさらに複雑となる。しかし実はアプローチは下表の⑥だけでR①を制御、C①を標的した制御NOTだけである。しかもゴールとの比較で補正が必要な行は1か所のみ。ところが、この行に特徴的なパターンは直ぐにはなく、トフォリゲートを繰り返すことで特徴を付け補正フラグをつける。それに②~⑤までかかる。そして⑦で反転し完成する。
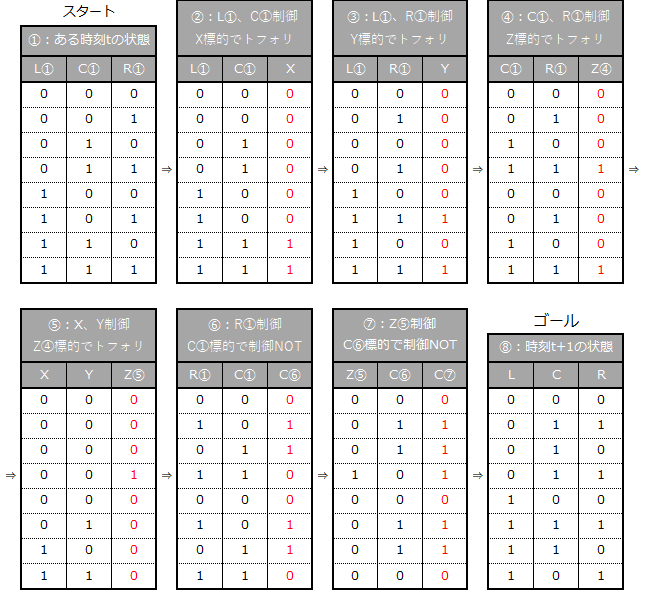
ルール30と同様コードの前にセルとレジスタを想定したフローに直す。
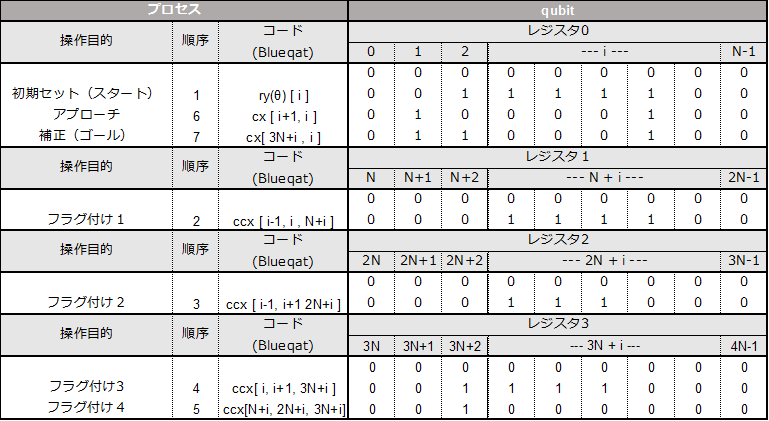
この表を基にコードに書き下すと以下のようになる。ループ外の記述は周期的境界条件のためである。
def qproc():
c.ccx[Reg0sb,Reg0lb,Reg1sb]
for i in range(1,N):
c.ccx[i-1, i, Reg1sb+i]
c.ccx[Reg0lb,Reg0sb+1,Reg2sb]
for i in range(1,N-1):
c.ccx[i-1, i+1, Reg2sb+i]
c.ccx[Reg0sb,Reg0lb-1,Reg2lb]
for i in range(N-1):
c.ccx[i,i+1, Reg3sb+i]
c.ccx[Reg0sb,Reg0lb,Reg3lb]
for i in range(N):
c.ccx[Reg1sb+i,Reg2sb+i,Reg3sb+i]
for i in range(N):
c.cx[i+1,i]
for i in range(N):
c.cx[Reg3sb+i,i]
return
フルコードはGithubのリポジトリ q-cams 内のq-cam110r.py。N=6(セル数)、R=4、初期状態[0,0,0,0,0,1]の時のグラフィック結果が下図の右(ルール110の下)である。
qubit数の制約、メモリーの制約、計算時間の制約からセル数としてこの程度しかとることができないため、意味不明の時間発展となっている。
4-5. 1, 0 の重ね合わせ初期状態からの時間発展
1,0の重ね合わせの初期状態、つまり、2回目の2-2で詳述した、「1,0ではない確率的初期状態」をセルに適用してみると何が起こるのか議論である。初期状態のセットの方法論も2-2を参照されたし。
ルール110で初期状態として、[0,0,0,0,0,1] に代えて [0,0,0,0,0,0.9] としてみる。後は全く同様にコンソールからq-cam110r.pyを実行する。今までより、コンソールに出る結果が多少うるさく以下のようになる。
コンソール結果例
原理的なことに関しては、2回目の2-4. 「Blueqatのベクトルと観測」を参照されたし。時間発展1ステップ分ごとに出力が有り、Timeの右に各セルの「1」状態である確率を示し、その右のsumに全セルの確率の合計値、さらにその右のstdevにはセルの確率の標本標準偏差を示している。その下からはそのステップで考えうる状態ベクトルとその状態ベクトルが出現する確率を示している。ただこれは、セル数N場合、最大 $2^N$ 個、例えばルール60と102ではのN=20。よって$2^{20}=1048576$個,
これが、20ステップ以降毎回出力されることになってしまう。このような場合は、出力用の関数を呼び出さないようにする。
出力を呼び出さない代表的コード例
pstep=0
ret='y'
while ret=='y':
pstep+=1
c=Circuit(N)
pinitial_a=probability_a
if pstep==1:
pinitial_a=initial_a
qcam.propinit(N,c,pinitial_a)
qproc()
master_a=np.array(c.run())
num,vector_a,prob_a=qcam.qvextract(N,R,1,master_a)
stdev,probability_a=qcam.qcalcd(N, num,vector_a,prob_a)
#qcam.qcresultout(N, pstep, num,pinitial_a,vector_a,prob_a,stdev,probability_a)ここを除外
stepdist_a[pstep,0:N]=probability_a[0:N]
stdev_a[pstep]=stdev
ret=input(' NEXT(Y/N)?')
qcam.qcfinal(N, pstep, initial_a ,stepdist_a, stdev_a )
qcam.qcamplot(N, pstep, stepdist_a)
ステップを進めるには NEXT(Y/N)?でyを入力する。それ以外の文字を入力、あるいはEnterのみを入力すると次のステップには進まず、時間ごとの各セルの確率、合計と標本標準偏差を一覧として出力する。また同時にグラフィック出力を行う。グラフィック出力を終了すると、プログラムは停止する。
以下のグラフィックの一番左ががルール110で初期確率状態として [0,0,0,0,0,0.9]を与えた場合(量子)、その右横は[0,0,0,0,0,1]を与えた場合(古典)である。同様にルール30で初期確率状態として[0,0,0,0,0.9,0,0,0]と同古典の結果である。黒が1、白が0、また1,0の中間はグレーの階調表現としてる。
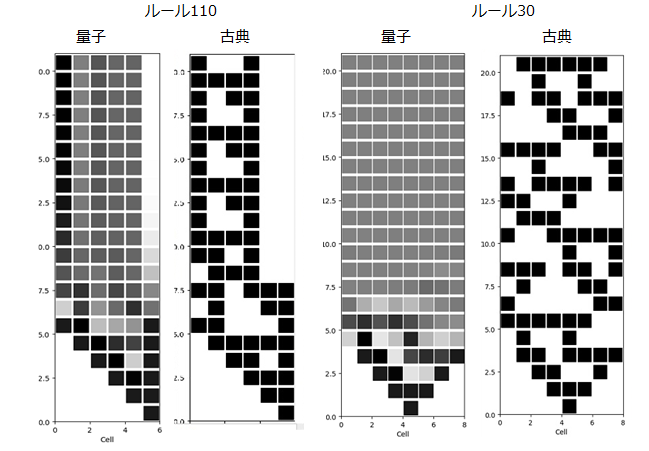
ルール30の場合、途中からすべてのセルで確率が0.5の状態になっている。さらにルール90において初期確率状態として[0,0,0,0,0,0,0.9,0,0,0,0,0]を与えた場合を示す。
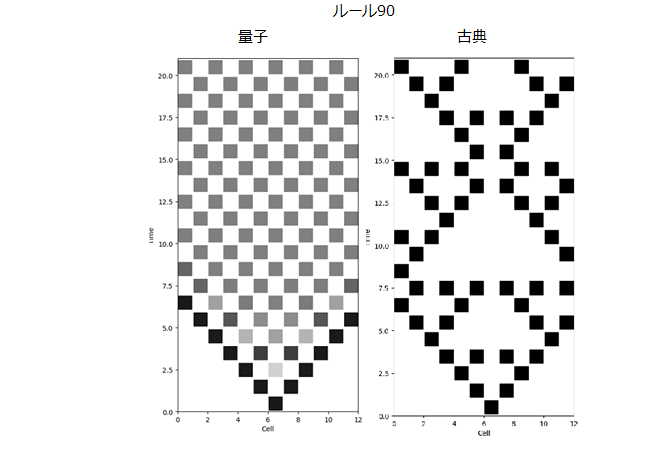
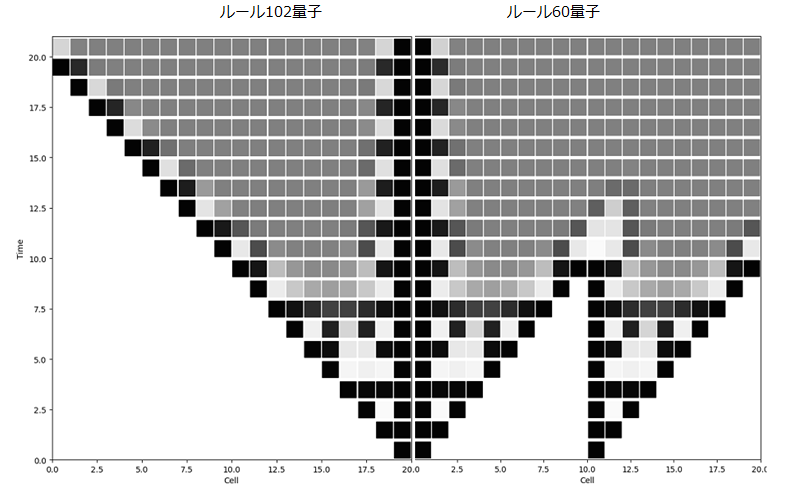
最後に、ルール102とルール60だが、ルール102では右端の1の代わりに0.99を、その差僅かに1%。そしてルール60では左端以外にもう一か所に0.99をセットして時間発展させてみた。よく見ると存外複雑である。
4-6.サマリー
一次元の単純なセルオートマトンのセルに量子アルゴリズムで1,0の重ね合わさった状態をセットして時間発展させてみた。今回のルールではその性質に関しては特に検討していない。次回の投稿は本命のルール184!そのセルに1,0の重ね合わさった状態をセットして時間発展させたときの性質を考察しているが、それはそれは摩訶不思議なことが生じている。