前回の投稿から2か月近くが経ってしまった。そもそも渋滞が気になるゴールデンウィークに全8回の連載投稿をお盆までに完了させるつもりが、今回の主題とも言える**「緩和時間」**で、当初の考えとは異なる深みにはまって、気づいたらもうお盆である。暮れまでに解消できるのか疑問。それで不明点多々あるが投稿再開決心。むしろ謎を教えて下さる方に期待しつつ。
5-1. ルール184(渋滞系)の量子アルゴリズム (交通流量計算付き)
ルール184をなぜ渋滞系と称するのか。このルールが交通渋滞をよく再現するからに他ならない。詳しくは西成活裕東大教授の著書に記載されている。また文献にも多い。例えばこれ。ルールそのものは前回の4回目で紹介した通りで、ウルフラムコードが184となるものである。それで前回のような考えでこの量子アルゴリズムも考えることができるが、もっと渋滞に即した簡単なルール表記がある。**「自分の前のセルが空いていれば進める、逆に前のセルに他の車がいれば進めない」**今回はこの言葉通りのアルゴリズムに落とし込みBlueqatでの実装を行う。
まず、すべてのセルの中で、前に進めない車はどれか?つまり、どのセルの車は前に進めないのかを調べる。i番目のセルに車がいた場合、その車が前進できるのはi+1番目のセルが空の場合だけである。車有を1、空を0とした場合、下表5-1-1のように前進不可の車はトフォリゲートで表現できる。この結果を反転し2N-1番に割り当てる第1レジスタに格納する。レジスタの考え方は2回目を参照。いきなり今の結果を制御ビット、元の車列を標的ビットとして制御NOTすると、都合が良いことに、前進できない車はそのままそのセルに留まり、前進できる車は一つ前のセルに移り、さらに前進前のセルは空にしてくれる。(表5-1-2内のブルーの網掛け)だが、残念なことに、元の車列に車がいなくて、かつ新たに車が後ろから前進してこなかったセルは表5-1-2内で黄色で示したように空(=0)であるべきだが、1となってしまう。

このエラーの補正を考える。このエラーが生ずるセルとは、時刻tで空セルで、時刻t+1でも不変の空セルであるべきセルである。先ほどは、車があるセルにおける前進不可を探した。つまり時刻tで1、時刻t+1でも1という不変を探した。今回はその逆を行えばよい。逆とは車がない空セルでの空まま不変であるセル探しの意味である。つまり時刻tで0、時刻t+1でも0という不変探しだ。これは簡単で、まず元の車列を、先ほどの制御NOTを行ってしまう前に第2レジスタにコピーする。コピーの概要は3回目参照。**逆(車有がなし、無しがあり)**にするためにこれを反転し、左隣りとトフォリをとり、結果を第3レジスタに格納する。ここでは前と異なり反転させず不変セルは1とする。この結果を制御ビットにして先のエラー含みの結果を標的ビットに制御NOTを実施するとルール184は完結する。(表5-1-3:周期的境界条件であることを注意)

このアルゴリズムをqcamを用いてBlueqatで実装した量子プログラム部分の関数を以下に掲載する。尚、レジスタを4個使用しているため、セル数はN=7が限界である。実質的にはN=6がせいぜいである。まあ、このセルオートマトンを量子化すること自体ナンセンス極まりないことなので仕方がない。
def proc():
for i in range(N-1):
c.ccx[i, 1+i, Reg1sb+i].x[Reg1sb+i] #indicating congestion cells
c.ccx[Reg0lb,Reg0sb,Reg1lb].x[Reg1lb]
for i in range(N):
c.cx[i, Reg2sb+i].x[Reg2sb+i]
c.ccx[Reg2lb,Reg2sb,Reg3sb]
for i in range(1,N):
c.ccx[Reg2sb+i, Reg2sb-1+i, Reg3sb+i] #indicating hopping correction cells
for i in range(N):
c.cx[Reg1sb+i,Reg0sb+i] # hopping with error
c.cx[Reg3sb+i,Reg0sb+i] # error correction
return
フルコードはGithubのリポジトリ q-cams 内のq-cam184r.pyで公開している。
交通流量の計算
渋滞系で重要な概念に交通流量がある。これはあるポイントを一定時間で通過した車の台数のことである。従って、このプログラムq-cam184r.pyでも、交通流量=flow rate を計算し出力するようにした。ただ、世間では車の有り=1と無し=0の状態だけだが、このqcamでは、1でも0でもない、確率のような、例えば車0.3台などと言う幻を用いるのが真骨頂であるため、流量もやや異なる概念となる。とは言え要は、時刻tからt+1でセル全体で何台動いたかで表現する。例えば、初期状態のセル列を確率で、0.0, 0.4, 0.0, 0.8, 1.0 とし計算した時の出力で Final Cell Probability 下に Flow-Rate /Cell で示した値がそのセルで前進した車の量であり、それを全セルで合計したものを Total で示している。この値は時刻tからt+1の遷移で動いた車の全部の量である。

では、どうやって計算するのか?ここで非常に役立つのが、前進不可のセルを探したトフォリを反転させた結果である。つまりこれは動かなかった車を'0'で現しているので、上の出力結果で、各Result に出ている1,0から成る状態ベクトルに乗ずれば、動いた車のみ1で他は0の状態ベクトルが作られる。それにその状態ベクトルが出現する確率(出力結果の Probability )をかけて、それをセル番号ごとに和をとれば、そのセルで前進した車の量となり、さらにそれらを全セルで合計したものが、時刻tからt+1で全セルで何台動いたかの流量として計算できる。この値は上の例で見てわかる通り時間とともに単調に減少するとは限らない。
5-2. 時間発展させると(セル数が偶数か奇数で異なる結果)
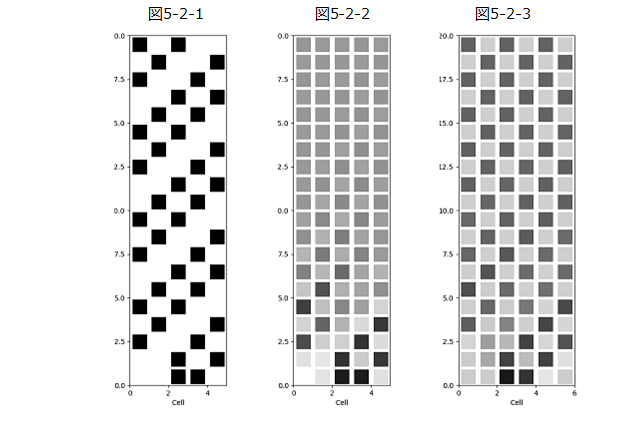
いわゆる 普通の初期状態、つまり1,0のみの車列で周期的境界条件の場合、当たり前だが、同じパターンの繰り返しとなる。例えば、初期状態が 0, 0, 1, 1, 0 の時間発展のプロットを図5-2-1で示した。プロットの見方は4回目参照。時刻2以降、5時間単位ごとに同じパターンが繰り返し現れていることが分かる。これはウルフラムクラスでいうクラス2で、「初期状態は時間発展に伴い複数パターンが繰り返す振動状態へと発展する」である。ウルフラムクラスも4回目参照。尚、ルール184は、前回までのルールと異なり周期的境界条件の場合は、’1’と’0’の数は変化することがなく、セルの値の合計値は常に等しい。従って、同じパターンで繰り返すことは分かりやすい。ただし、全て’1’あるいは全て’0’は不動である。不動とは交通流量ゼロの状態である。
ところが 初期状態に’1’でも’0’でなもない「確率」にすると話は異なる。例えば 0.00, 0.11, 0.89, 0.89, 0.12 にした場合どのような時間発展をするのであろう? 尚、0,1の場合と同じでセルの値の合計値は常に等しく、この場合の合計値は $2.00=( 0.00+0.11+0.89+0.89+0.12)$ であり、どのように時間発展していこうが、この合計値2.00は不変である。
?の答えは、図5-2-2。全てのセルでセルの値の平均値である $0.4(=2/5)$ に収束していってしまう。これはウルフラムクラスでいうクラス1で、「初期状態は時間発展に伴い安定状態(均質状態)へと発展する」である。ただし例外有り。初期の確率値が特定の条件で1または0に囲まれている場合、収束せずクラス2としての時間発展となる場合があり。
全てのセルで同じ値になってしまうと交通流量はゼロになってしまうかというとそうではない。ちゃんと流れている!交通流量も最終的にはある一定の値に収束する。尚、セルの合計値を増やしていった場合、つまり車の台数を増やしていった場合、中間の値(N/2=5/2=2.5)のとき流量が最大となる。
さらにところが 今までセル数Nは5であったが、それを6にして初期状態を例えば、0.2, 0.2, 0.9, 0.8, 0.1, 0.2 (セル値合計2.4)とした場合、図5-2-3となり、N=5とは様相が異なる。実は収束値が0.19と0.61の二値となっており、これらは一つのセルに留まるのではなく交互に入れ替わる。つまりウルフラムクラスは2となる。このことは実はセルの数Nが偶数の時生じ、奇数の時は生じない。ただし、初期状態の値の分散が小さいなどの特殊な条件下では偶数でも一つの値となる。(少なくともNが3から7で確認)
5-3. 緩和時間(τ)
非平衡だった初期状態が時間経過(発展)で平衡に達することを緩和と言うが、それに要する時間を緩和時間と言う。だとすれば少なくともNが奇数の時はこの緩和時間を考えることができる。(実際には偶数でも考えられる)以下、緩和時間を τ で表そう。では、この緩和時間を決定ずける初期状態の因子は何であろう? 尚、残念ではあるがこれは渋滞が緩和していくこととは異なる。
平均(A)
色々な初期状態からスタートさせて収束までの時間(=ステップ数)を眺めていると、どうやら各セルの値の和が相当影響していることに気が付く。この和をSで表そう。Sをセル数Nで割れば平均値である。これをAとしよう。$A=S/N$ である。こうすればセル数Nの大小に影響されずに最大値は1、最小値は0となる。つまり、$0≦A≦1$である。A=0 あるいは A=1 の時、どちらも緩和しないので $τ=∞$ である。だとするとA=0.5がτの最小値になりそうである。また、これらS,Aは全ての時間ステップで不変である。
標準偏差(σ)
平均が関連しているとすれば、初期状態の分散(バラツキ度)も関連しているのでは? 時間発展していくと次第に、バラついていた各セルの値(確率)が次第に均一化され、最終的にはバラツキがなくなるのだから、当然はじめからバラツキが小さいもの、つまり初期状態の分散あるいは標準偏差が小さいものほど、早く収束することは容易に想定される。今、標準偏差(母集団の標準偏差)をσで表そう。このσは議論を進めるのには実は便利で、時間ステップt=0が最大値で時間発展するに従って単調に減少していきゼロに収束していく。緩和時間τを実際に計算機で求める際も、このσの値が、例えば0.001以下になった時間ステップなどと定義し計算を止めることができる。
**標準偏差(σ) or 変動係数(CV)**
標準偏差でバラツキを現した時、平均値が大きいとバラツキも大きくなっていく。そこで標準偏差を平均でわった変動係数(CV)というものがある。$ CV=σ/A $。τの変数として、σとCVどちらを用いるのがより妥当であろうか。計算上の問題であればどちらでもよいが、σのほうがなじみ深いので、ここではσを使っていく。 $0.200, 0.200, 0.338, 0.562, 0.700 A=0.4, σ=0.2 (L並びと呼ぼう) $
$0.200, 0.200, 0.700, 0.562, 0.338 A=0.4, σ=0.2 (S並びと呼ぼう) $
でのσと交通流量(Flow Rate)の時間発展のグラフを以下に示した。σ<0.002を緩和時間τとすると、L並びでは τ=23、S並びでは τ=11 と倍半分である。これでは τ を A と σ で表すことはできない。

では、初期状態 0.200, 0.338, 0.562, 0.700, 0.200 はどうなるのだろう? L並びと全く等しい結果となる。これは先のL並びを左に1個ローテートした並びである。(ローテートは3回目参照)結論から言ってしまうと、ある並びをどんなにローテートさせても同じ結果となる。N=5の場合、すべての並びの数は $5!=120$ 通りであるが、この中からローテート同一の並びを除く。例えば最小値(上の例では0.200)を先頭で固定し、残り4つのセルに残り4つの数値を全ての組み合わせてできた並びは、まさにローテート同一を除いた場合となる。兎に角一つだけ固定すれば良い。だとすると $4!=24$ 通りとなる。一般的にセル数Nにした場合は、 $(N-1)!$ 通りとなる。
流量(FR)は不思議な動きをする。緩和時間の長いL並びでは初期的に流量があがり、その後エクスポーネンシャルに減少していく。一方、緩和時間の短いS並びでは増加し直ぐに飽和してしまう。ただ、どちらの並びでも飽和後のFRは同一である。流量が大きくなることは渋滞の緩和にとっては重要なことであるがここでは議論しない。
同じ初期状態でありながらその並びで緩和時間がどう影響されるか、未だ十分に解析できておらず、何故そうなるのかも分からないが、分かったことだけ列記しておく。
・並びでセルの値をローテートさせた初期状態の緩和時間はローテート前と変わらない
・並びが昇順の時は概して緩和時間が長く、降順の時は概して緩和時間は短い
・緩和時間が短いものの並びは概して、値の大きさを小さい順に1,2,3,4,5とした時、以下の並びとなる
1,2,4,5,3 1,2,5,4,3 1,4,5,3,2 1,5,4,3,2
・緩和時間が短い並びの時の緩和時間が例外的(平均値からのズレが大きい)に見える
・初期状態の並びに緩和時間が依存しない場合もある
セルの値
A、σ、並びが同じでもセルの値そのものが異なれば緩和時間も異なる。ただし、その差は倍半分などと大きくない。例えば、以下のセルの値の組み合わせを比較してみる。
$0.340, 0.398, 0.400, 0.662, 0.700 A=0.5, σ=0.15 (系列1と呼ぼう)$
$0.263, 0.500, 0.500, 0.500, 0.737 A=0.5, σ=0.15 (系列2と呼ぼう)$
それぞれの系列で全24通りの並びに対して緩和時間を計算し、24個のτの結果の概要(平均値:av、最大値:max、最小値:min)は以下の通りとなった。
系列1 τav=19.1 τmax=20 τmin=17
系列2 τav=18.7 τmax=21 τmin=17
A、σ、並びに比べると影響は小さい。
初期状態からの緩和時間τの大体の予測
Aを0.1~0.9まで0.1刻みで9変数分、かつそれぞれのAでσを0.05~0.45まで0.05刻みとなるよう9変数分、5個1組の確率値を組み合わせてデータを61通り作った。81通りではなく61通りなのは、Aの値が末端に近いと大きな値のσは生成できないからである。また、手間を省くために A>0.5の組のは、(1-A)の組の確率値を1から引いた値とした。すると自動的に同じσとなる。例えば、A=0.7の組はAが0.3の組の各確率値のデータを1から引いたもので構成した。さらに各組でローテート重複をさけた24通りの並びで全1464通りの初期状態のデータセットを準備した。
このデータセットで、一度に計算できるようにq-cam184rをモディファイしたプログラムを用い、セルの値や交通流量などの値を一時間ステップ毎に計算し、またσ<0.002となる緩和時間τを求めた。これら全てのデータセットと結果は膨大なため、この投稿ではエッセンスだけとし、全データはGithubのリポジトリ q-cams 内のq-cam184-propagation-N5-data.xlsxに公開した。
A、σ、並びが同じでセルの値そのものの差による緩和時間差は対象外とし、また並び差の結果は前述のファイル内には記載したが、現時点では、A、σ同一で並び差がもたらす緩和時間への理屈が不明確なため、24通りの並びの平均緩和時間τavから大体の予測式を考えることにした。まずはそのτavの結果を以下に示す。
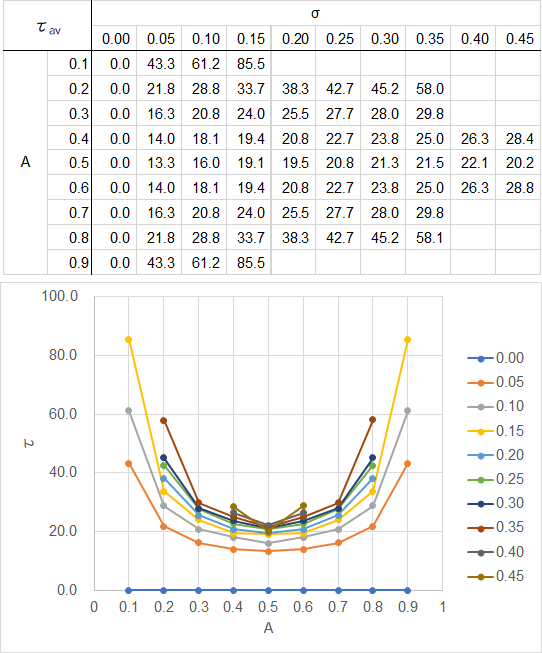
同じAでσを変数とした場合、つまり上表を横一列でみた場合、下図の実線のようになる。
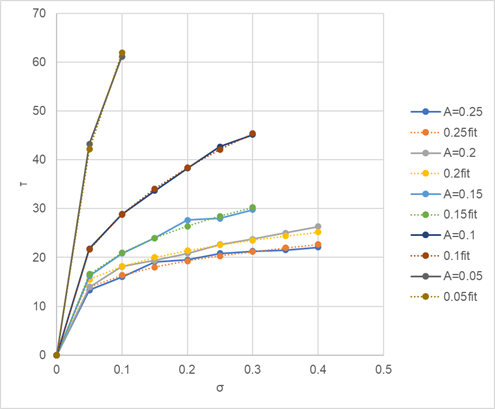
このτに対するσ依存性を各Aごとに次式のような累乗の関数で表せると考え、最小二乗法からx,yを決めた。(ソルバー使用)
$$τ_{av}=yσ^x$$
ここで得たx,yを用いて計算した結果は上図の点線である。
次にxはAに対して二次関数に見事とにフィッティングでき次の関係式が得られる。
$$x=2(A-0.5)^2+0.2338$$
さらにyもAに対して指数関数でフィッティングさせることで次の関係式が得られる。
$$y=23.868exp\{13.88(A-0.5)^2\}$$
これらの式から計算した結果を以下に示した。
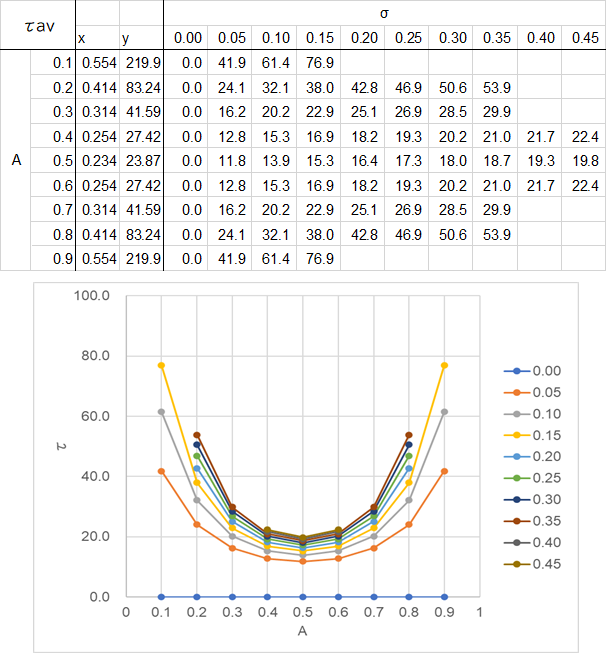
実際の結果に比べるとAの値が0又は1に近ければ近いほどτが小さく出ているようである。まっ、大体の予測であるので・・・
5-1. サマリー
ルール184渋滞系の量子アルゴリズムをBlueqatで実装し色々な1,0でない確率を入れて試してみた。セル数が奇数で周期的境界条件では時間発展でウルフラムクラス1になるが、偶数では2値に収束していく。緩和時間τはA、σから大体予測できるのだが、「並び」に対しての理解が現時点ではできていない。また。渋滞系で最も重要な交通流量に関しての議論も不十分な状態である。そもそもあるセルに車がありなしではなく確率的に存在しているというのは、多分、セルは一台分の区間ではなく、複数台、例えば10台入る一定区間で、車の密度を表現しているのか・・・いずれにせよ今回は渋滞としての議論には至らなかった上、未解決事項もある尻切れトンボ状態で・・・すみません。
次回(6回目)は今までのセルオートマトンとはかなり異なるソリトンセルオートマトン(箱玉系)に関してである。時間発展云々よりも、系を如何に量子アルゴリズムに落とし込んだのかが主題のつもりである。
次々回(7回目)は逆に量子アルゴリズム的には著名なグローバーアルゴリズムを多少視点を変えて、ある意味時間発展を、今回のように予測することが主題のつもりである。6回目、7回目では3回目で紹介した、マルチ制御NOTゲートが活躍する。
最終回(8回目)では今回の未解決事項や渋滞としての議論に触れられたら触れたい。本当はこの8回目までがお盆の予定だったのだが?次の渋滞の季節(コロナ禍で渋滞しないかもしれないが)、年末までには終わらせたい。
8回目は量子位相推定(QPE)をセルオートマトンやグローバーアルゴリズムに適用してみた話となりました。