6回目より先に7回目のグローバーアルゴリズム一考を投稿してしまった。アドベントカレンダーに登録してしまっていた故・・・で、戻っての今回は、5回目までと異なり時間発展とか緩和時間云々よりアルゴリズムの腐心の話。なんせ量子ゲートのプログラミングには制御構造がない故、いきおいマルチ制御NOTゲートを連ならせ複雑怪奇となっていく。たった7セルで1ステップ遷移するのにSDK(blueqat)での計算時間は1時間越え、量子コストは計り知れず。尚且つ今回のアルゴリズム由来なのか?確率的初期状態からだとセルから玉(車)が消えていく。本来、箱玉系(ソリトンセルオートマトン)では玉数不変のはずなのに。このような量子プログラミングの不便さは@notori48さんの「素人が量子プログラミングをやって感じたこと」によく記述されていてる。
6-1. 箱玉系のいくつかのルール表現
4回目、5回目では、玉あるいは車の遷移は、時刻 t でのそのセルの状態とその両隣のセルの状態から決まる、256 ($=2^8$) 番までのウルフラム番号の付いた比較的単純なルールのセルオートマトンで、ECA (Elementaly Cellular Automata)と言われるものであった。今回取り組んだのはもう少し複雑なFCA(Filter Cellular Automata)と称されるもので、時刻 t+1 への遷移のルールに時刻 t+1 の状態が関係する。具体的にはソリトンセルオートマトン、別名、箱玉系と言われるもの。その量子アルゴリズムを考えblueqatで実装してみる。
実のところ「時刻 t+1 への遷移のルールに時刻 t+1 の状態が関係」するといっても箱玉系(ソリトンセルオートマトン)のルール自体は簡単なものである。特にセルが無限につらなっていて、玉が有限個の時など。左の玉から順に、空いている一番近い右のセルに移す。一度動かしたものは動かさない。以上! qiita内では、@massss 氏の ”箱玉系について” で図説されていて、これを参照いただければイメージをつかみやすい。ただ、セルが有限の時、つまり周期的境界条件がある時、この単純なルールだけでは表現できず、別のルール表現が必要となる。ネットで”箱玉系”と入れて検索するといくつかの異なるルール表現が見つかる。いずれも引用元に行くと図説されているので、ここでは動きを図示しない。
その1 : 時弘哲治氏
( https://mathsoc.jp/meeting/kikaku/2008aki/2008_aki_tokihiro.pdf )
- 玉のコピーをつくる
- コピーの中の1つを最も近い右の空箱に移動させる
- 残りのコピーの中の1つを最も近い右の空箱に移動させる
- すべてのコピーを移動させるまで 3. の操作を繰り返す
- もとの玉を消去すると,1(時間)ステップが進んだものとする
その2 : 前田一貴氏
( https://kmaeda.net/kmaeda/demo/bbs/ )
1.玉が入っている箱が左に,空き箱が右に隣り合っている対を見つけて線で結び,左の箱から右の箱へと玉を動かす
2.線で結ばれた箱は以降無かったものとして,上の操作を玉の入っている箱が無くなるまで繰り返す
その3 : 由良文孝氏
( https://www.rikkyo.ac.jp/science/math/math/kakei/public_html/RIMS2000/yura.pdf )
- 箱に玉が入っているならば (a) 運搬車に空きがあれば、玉を載せる。 (b) 運搬車に空きがなければ、そのまま通過する
- 箱に玉が入っていなければ (a) 運搬車に玉があれば、玉を降ろす。 (b) 運搬車に玉がなければ、そのまま通過する
- ただし、初期状態と遷移完了後の状態において運搬車は空でなければならない。
ところで、この「その3」は、古い文献ながら、「ソリトンセルオートマトンと量子コンピューティング」と題されていて、当時、実装はあり得なかったであろうが量子回路まで描かれている。尚、この記事のアルゴリズムは全く別ものである。
6-2. 量子アルゴリズム
***その3のルールを選択***
ソリトン特有の挙動を見ようとした場合、最低でもセルは7箱、玉は3個欲しい。はじめ上記その1で量子アルゴリズムを考えた挙句、必要量子ビット数が34ビット(セルに7量子ビット、レジスタに21量子ビット、玉個数(3個)X2のフラグ用ビットが6量子ビット、合計34量子ビット)。blueqatでの上限を超えている。これでは動かない。その2でも同様な状況に陥った。で結局その3でどうにかこうにか、2レジスタ、6フラグ、つまり (1+2)X7+6 = 27 量子ビットに収めた。***準備(量子ビットの用意)***
その3に従い運搬車(キャリア)として量子ビット3個を用意する。これを```CA0,CA1,CA2```とする。初期状態では当然、玉を載せていない。そこで全て'0'とする。後に説明する必要性から、このキャリアの常に反転状態にある反キャリアを3個を用意する。これを```XC0,XC1,XC2```とし、初めからフリップして初期状態'1'をセットする。7個のセルを表現する7量子ビットは```R0[i] i=0~6```とする。このR0の初期状態としてセットするのは、玉数が3以下の任意の確率的初期状態である。セットの方法は[2回目の2-2](https://qiita.com/gigagulin/items/634744f9038cd843f8ce)を参照されたし。セルのコピーで最初から最後まで不変のレジスタとして、```R1[i] i=0~6```を準備する。コピーは単純に```R0[i] ```を制御、```R1[i] ```を標的とした制御NOTを行えばよい。また、初期は空、つまり'0'状態のレジスタとして```R2[i] i=0~6```を準備する。全体の流れ
まず図1を見て欲しい。セルR0[0]-R0[6]に黒玉が3つ入っている。セルの下の小さな3個の箱はキャリアでCA0,CA1,CA2を現している。これを図の左から右に移動させていく。左右というのは架空で、実際にはセルR0の[0]から[6]への順次実行であって、図では1段目から7段目への移り変わりを意味している。
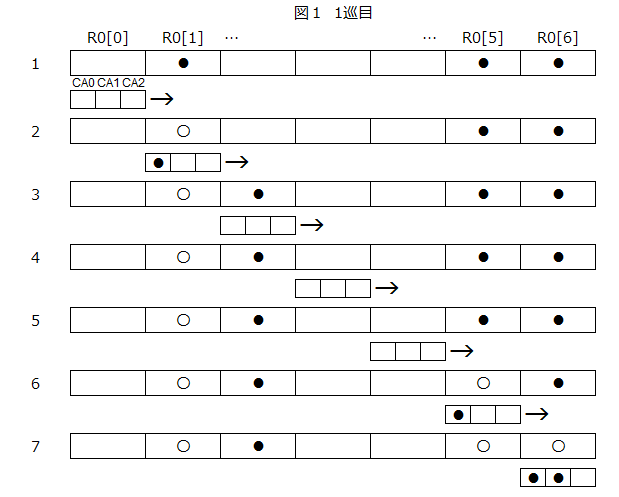
キャリアが移動したセルに玉があったら空いているキャリアに玉を載せる。勿論キャリアが満杯だったら載せられない。載せる順はCA0からである。次にキャリアが移動したセルが空で、キャリアに玉が載っていたら玉を降ろす。当然、キャリアが空なら降ろせない。降ろすのはCA2から、つまり、後乗せ先降りである。これらを、右端の最後のセルR0[6]にたどり着くまで行う。実はこれで終わりではない。図1の例の場合、キャリアが右端に達した7段階目でも玉が2個載ったままである。ルール「その3」の3.にあるように、遷移完了後にはキャリアは空でなければならいので、全ての玉を降ろすには左端から2巡目を行う必要がある。

2巡目ではもう玉を載せる必要はなく降ろすだけである。1巡目と同様でキャリアが空いているセルに遭遇したら玉を降ろせば良いかと言うとそこまで単純ではない。過去に玉があったところでは空いていても降ろしてはいけない。図2では9段目がそのような状況である。そこで初期状態では玉があってキャリアに載せてしまったセルに目印として白丸〇を記している。つまり白丸のセルには玉をおろしてはいけない。白丸でも黒丸でもないセルであれば玉が降ろせる。この2巡目でキャリアが空になったら遷移は完了である。従って図2の11段目で元来実行完了である。しかし、その状況を判断して止められるほどの制御は量子ゲートの組み合わせでは困難で、最初から2巡目の最後のセルまで実行、つまり1段目から14段目までを素直に実行し完了させることになる。
2巡目で図の白丸のセルにキャリアが来た時、玉を降ろせないがそれを判断するのは、初期状態を参照し、初期に玉があったセルでは降ろさなくすればよい。その初期状態を不変的に記憶させておく領域としてとしてセルであるR0[0]~R0[7]のコピーR1[0]~R1[7]をレジスタとして確保しておく。現実的には、1巡目でキャリアに玉を載せた時、そのセルの玉は消去せずにおけば、2巡目でそこに玉を降ろすことは生じない。すると、図3のセルAに示しているように最終段14段目に達した時、セルであるR0には、玉が移動してきたセルにも、その玉が移動する前のセルにも玉があることになる。しかし、レジスタR1には移動前の状態が記憶されているので、14段目が終了した後にR1に玉があるセルの玉を消去すれば良い。これは、R0を標的、R1を制御とした制御NOTで記述でき図3のセルBとなる。

1巡目の玉載せ
1巡目において、キャリアが移動したセルに玉があれば必ずキャリアに玉載せする。キャリアが満杯でスルーはあり得ない。なぜならキャリアに3個まで玉が入り、かつ前提条件としてセルの配列上には3個までしか玉がないのだから。もしキャリアCA0が空いていれば、つまりCA0の状態が'0'であれば、玉をCA0に載せる。載せるとは、CA0の状態を'0'から'1'にすることである。載せるかどうかには、複数の条件があり、それが全て満たされているときに、'0'を'1'にする。
**今、n個の条件を条件1,..., 条件nとしよう。全ての条件が満たされている、つまり真のとき、言い換えれば、全ての条件である量子ビットの状態が'1'の時、標的となる量子ビット(この場合CA0)の'0'を'1'にする。これはまさにn個のマルチ制御NOTゲートで表現できる。**尚、条件が一つだけであれば、単なる制御NOTゲートであるし、条件が二つであればトフォリゲートである。条件が3以上の場合はマルチ制御NOTゲートであるが、これに関しては 第3回を参照されたし。
CA0に載せる場合 i番目のセルにキャリアが来た時(単にi番目の実行の時)セルが空きかどうかはR1[i]を見ればよい。R1[i]が1(玉あり)でかつCA0が空いていればCA0に玉を載せる。この時CA0を調べてCA0を変化できるゲートなどありえない**(つまり自分を制御とし自分を標的とするゲートはありえない)**ので、CA0の反キャリアXC0が必要となる。XC0はCA0が空いているときに1になっている。従って、R1[i]とXC0を制御ビットとしてCA0を標的ビットとした制御NOT、ここではトフォリゲートを用いれば、目出度くCA0に玉を載せることができる。当然R[i]が0(玉がセルにない)であったり、XC0が0(CA1には既に玉が積まれている)の場合はCA0には玉を載せない。コードで記せばccx[R1[i],XC0,CA0]である。CA0が1になった以上、反キャリアであるXC0も反転しておかなければならない。R1[i]が空の時にはキャリアに玉を積むことはあり得ないため、R1[i]とCA0を条件に、つまり制御にして、XC0を反転させる。コードで記せばccx[R1[i],CA0,XC0]である。ただし、もともとCA0に玉が積まれていた(CA0=1)時、XC0は0なのだが、もしこの時R[i]に玉があった場合XC0は反転してしまい1となる。CA0もXC0も1となってしまいXC0は反キャリアとはならなずにエラー状態となる。実は、これは後々に補正することができる。これらのことを示すために状態表があるとわかりやすい。この部分の状態表を表1(以下の折り畳み)に示した。
表1
CA1に載せる場合 もし、R1[i]には玉があるのだが、CA0は既に玉が載っている(CA0=1)場合、つまりXC0=0の場合、次のキャリアCA1に空きがあればCA1に玉を載せる。要するに R1[i]=1 でかつ XC0=0 (又はCA0=1) でかつ XC1=1 が条件であり、この条件が真の時CA1を反転させる。従ってマルチ制御NOTを使用し3つの条件ビットともに1でCA1は反転できるが、括弧内CA0=1を条件として選択すると後々のエラー補正等に問題を起こす。ではXC0は?玉が載っていたら0、これではマルチ制御NOTで反転できない。がしかし、実は表1を見直すと、XC0はエラーで1(赤字)となっている。これは好都合でCA1に玉を載せるのに使える。従ってコード記せばcccx[R1[i],XC0,XC1,CA1]となる。CA1に玉を積んだらXC1をフリップさせる。これはCA0に玉を積んだ場合と同じ原理でccx[R1[i],CA1,XC1]でできる。しかし、表2(折りたたみ)の赤字で示したようにいくつかの組み合わせにおいてXC1はエラー状態となる。
CA2に載せる場合 もし、R1[i]には玉があるのだが、CA0,CA1ともに玉が載っている場合、次のキャリアCA2に載せることになる。原理はCA1に載せる場合と同様だが、条件は4つ。条件は、R1[i]=1 でかつ XC0=1 でかつ XC1=1 でかつ XC2=1 であり、コードで記せばcccx[R1[i],XC0,XC1,XC2,CA2]となる。そして、XC2をccx[R1[i],CA2,XC2]でフリップさせる。結果は表2の通り。ただし、今までとは多少異なり、一番下段のXC2でそもそもエラーしていた値が正しく戻っている。
表2
エラー修正 表2の最後の結果(右下側)のXC0とXC1のエラー(赤字値は当然1)を、他の組み合わせに影響なく0にすることができれば修正できたことになる。果たして、エラー部分だけをフリップさせられるのか?エラーはR1[i]=1だけで生じている。XC1のエラーの組み合わせはCA2の1と一致している。ということはR1[i]とCA2を制御としてXC1を標的にすれば他の組み合わせには影響せずにXC1は修正可能となる。同様にしてXC0ではR1[i]とCA1を制御にすればよい。これらの状態表を表3上段に示した。結果をコードで記述すれば、ccx[R1[i],CA2,XC1] ccx[R1[i],CA1,XC0]である。また、表1でXC2の最下段を故意にエラーさせているが、これは表1のプロセスの前に、R1[i]、CA1、CA2を制御にXC2を標的にマルチ制御NOTを適用させることで実現している。表3下段に示した通り、他の組み合わせに影響を与えていない。コードで記せばcccx(c,R1[i],CA1,CA2,XC2)となる。
表3
# 1巡目玉載せ
q.cccx(c,R1[i],CA1,CA2,XC2) # XC2故意にエラーさせる
c.ccx[R1[i],XC0,CA0] # CA0が空いておりCA0に玉載せ
c.ccx[R1[i],CA0,XC0]
q.cccx(c,R1[i],XC0,XC1,CA1) # CA0に既が玉がありCA1に玉載せ
c.ccx[R1[i],CA1,XC1]
q.ccccx(c,R1[i],XC0,XC1,XC2,CA2) # CA0とCA1に既が玉がありCA2に玉載せ
c.ccx[R1[i],CA2,XC2]
c.ccx[R1[i],CA2,XC1].ccx[R1[i],CA1,XC0] # XC1とXC0のエラーを補正
1巡目の玉降ろし
玉降ろし キャリアが移動したセルに玉がなくかつキャリアに玉があれば玉を降ろす。1巡目なので「過去に玉があったところでは空いていても降ろしてはいけない」という事態にはならない。そこで、セルR0[i]に玉がない(つまり'0')ことが条件だが、制御が0では標的ビットを変化させられないので、まずR0[i]をxゲートで反転させる。さらに後で説明するがキャリアCAも反キャリアXCも同時に反転させておく。これで、まずキャリアとしては2番、つまりCA2から玉降ろしを行う。セルが空いている(反転しているR0[i]が1)、CA2に玉が載っている(反転しているXC2が1)ときにCA2を反転させる。これをコードで記述すればccx[R0[i],XC2,CA2]となる。キャリアーから玉を降ろした以上、そのセルには新たに玉を置くことになる。この時に玉を置くと言うことは、直前でキャリアから玉を降ろしているので、CAは(反転しているので)1、XCも1である。ここで初めにキャリアCAも反キャリアXCも反転させておいた意味が出てくる。つまり、CAとXCを制御としてR0[i]を標的にすればR0[i]への玉降ろしができる。コードで記述すればccx[XC2,CA2,R0[i]]となる。セルもキャリアも玉降ろしは以上で終了だが、このままでは反キャリアがエラーしたままである。つまり玉降ろしが生じた場合に限りXCも反転しておかなければならない。今の状態は以下に示した表4の右側となっている。キャリアのサフィックスmは0~2で、今は2として見ればよい。尚、表の最下段2行は、スタート状態の時セルに玉があり、コピーのレジスタR1には玉がない状態だが、このような状態になり得るのはm=2で玉を降ろした時のm=1、あるいはm=1で玉降ろした時のm=0の状態の時だけで、それは下から2番目の状態のみであり、よく考えると最下段の状態は存在し得ないことが分かる。
表4
エラー修正 ここで、エラーをしている上から2番目のxcを他には影響を与えずにフリップさせる操作を考える。ただし、最下段の状態は存在し得ないので考慮から外して、この上から2番目だけXC以外のビットが特徴的な組み合わせを見出せばよく、幸い、R0が0、R1が0、CAが1という組み合わせがそれに当たる。これを制御ビットとして利用するが、そのためにはR0とR1を反転させておく必要がある。その後にR0,R1,CAを制御ビットとして、XCを標的ビットとしてマルチ制御NOTをとれば、エラーの修正は完了する。最後にR0(R0は先ほど再反転済み)以外のビットは反転されているので、それらを再度反転し完了である。表5にエラー修正の状態を示した。最下段は最終的に逆にエラーを生ずるが存在しないので無関係である。
表5
# 1巡目玉降ろし
# m=2
c.x[R0[i],CA2,XC2].ccx[R0[i],XC2,CA2] # セルが空き、キャリアに玉がるとき、キャリアから玉を降ろす
c.ccx[XC2,CA2,R0[i]].x[R0[i],R1[i]] # iキャリアから玉を降ろした場合、セルに玉を置く
q.cccx(c,R0[i],R1[i],CA2,XC2) # 反キャリアのエラーを修正
c.x[R1[i],CA2,XC2]
# m=1
c.x[R0[i],CA1,XC1].ccx[R0[i],XC1,CA1]
c.ccx[XC1,CA1,R0[i]].x[R0[i],R1[i]]
q.cccx(c,R0[i],R1[i],CA1,XC1)
c.x[R1[i],CA1,XC1]
# m=0
c.x[R0[i],CA0,XC0].ccx[R0[i],XC0,CA0]
c.ccx[XC0,CA0,R0[i]].x[R0[i],R1[i]]
q.cccx(c,R0[i],R1[i],CA0,XC0)
c.x[R1[i],CA0,XC0]
2巡目の玉降ろし
さらなるレジスタR2の必要性 前にも記したが2巡目ではもう玉を載せる必要はなく空きのセルに玉を降ろすだけである。いかにも単純そうだが存外ややこしい。1巡目の玉降ろしと同様のアルゴリズム適用では?と思うがそうはいかない。2巡目では表4や5の最下段の1と0の組み合わせ状態が生じ、表5の一番右側の通り1巡目の玉降ろし方法ではエラーが残ってしまう。そこで新たにレジスタR2を使用することになる。R2はセルのコピーではなく初期的には全て0としておく。逆に2巡目では反キャリアは不使用となる。
CA2からの玉降ろしまずセルが空きで玉降ろしをするために、セルR0を反転させる。キャリアからの玉はセル(R0)に直接降ろさずレジスタR2に降ろす。コードで記述するとccx[R0[i],CA2,R2[i]]である。次にCA2から玉を消す。R2と反転しているR1を制御としてCA2を標的にすれば玉を消すことができる。コードで記述するとccx[R0[i],R2[i],CA2]である。表6(最初のR0の反転は省略している)で見ての通り何のエラーも生じていない。単純?
表6
CA1,CA0からの玉降ろし
エラーが生じてしまうこと以外はCA2の玉降ろしと変わらない。つまりR2への玉降ろしはコードでは、ccx[R0[i],CAm,R2[i]]であるし、キャリアの玉消しもccx[R0[i],R2[i],CAm]である。しかし、表7の「ここの状態に注目」を見ると、CA1からの玉降ろしでは最下段のR2[i]が、またCA0からの玉降ろしでは下2段のR2[i]がエラーしている。そこで、このエラー行だけにR2[i]を除いたビットで特徴的な組み合わせ(できれば1)を見つけ、それを条件に制御NOTでエラーをフリップさせ修正する。CA1の場合はR0,CA0,CA1がそれに該当する。従ってコードで記せばcccx[R0[i],CA0,CA1,R2[i]]となる。また、CA0の場合は下2段だけに共通で他の行にはない組み合わせは、うまい具合にR0[i]とCA0の2個がそれに該当する。条件ビットが2個だけなのでトフォリゲートでccx[R0[i],CA0,R2[i]]とかける。CA2からの玉降ろしの前にR0を反転させているので、最後に、再反転して元に戻す。
表7
# 2巡目玉降ろし
c.x[R0[i]]
c.ccx[R0[i],CA2,R2[i]].ccx[R0[i],R2[i],CA2] # CA2からR2へ玉降ろし
c.ccx[R0[i],CA1,R2[i]].ccx[R0[i],R2[i],CA1] # CA1からR2へ玉降ろし
q.cccx(c,R0[i],CA0,CA1,R2[i]) # エラー修正
c.ccx[R0[i],CA0,R2[i]].ccx[R0[i],R2[i],CA0] # CA0からR2へ玉降ろし
c.ccx[R0[i],CA0,R2[i]] # エラー修正
c.x[R0[i]]
プロセスの最後に、元来2巡目で玉が降ろされているべきセルに玉を加え、さらに元々玉があったセルから玉を消す。つまり、レジスタR2を制御にセルR0を標的に、またレジスタR1を制御にセルR0を標的に、それぞれ制御NOTを行う。コードではcx[R2[i],R0[i]].cx[R1[i],R0[i]]である。以上で全プロセスが完了となる。以下に、量子プロセス部分のコードをまとめて記述しておく。尚、1巡目の玉載せ玉降ろし部分をProc1、2巡目の玉降ろしをProc2、最後のセルのレジスタによる修正をProc3というモジュールにしている。
def Proc1():
for i in range(N):
c.cx[R0[i],R1[i]] # copy to R1
c.x[XC0,XC1,XC2] # carrier flag sets XCm=1
# first round
for i in range(N):
# first round loading
q.cccx(c,R1[i],CA1,CA2,XC2) # XC2 error correction
c.ccx[R1[i],XC0,CA0] # if R1=1 and XC0=1,loading to CA0
c.ccx[R1[i],CA0,XC0] # if CA0 is loaded, XC0 turns
q.cccx(c,R1[i],XC0,XC1,CA1) # if R1=1 and XC1=XC0=1, loading to CA1
c.ccx[R1[i],CA1,XC1] # if CA1 is loaded, XC1 turns
q.ccccx(c,R1[i],XC0,XC1,XC2,CA2) # if R1=1 and XC2=XC1=XC0=1, loading to CA2
c.ccx[R1[i],CA2,XC2] # if CA2 is loaded, XC2 turns
c.ccx[R1[i],CA2,XC1].ccx[R1[i],CA1,XC0] # XC1 and XC0 error correction
# first round unloading
c.x[R0[i],CA2,XC2].ccx[R0[i],XC2,CA2] # if R0 and R1 are empty and CA2 is occupied, unloading from CA2
c.ccx[XC2,CA2,R0[i]].x[R0[i],R1[i]] # if CA2 is changed, R0 turns
q.cccx(c,R0[i],R1[i],CA2,XC2) # if CA2 is changed, R0[i] are occuppied and R1[i] is empty, XC2 turns
c.x[R1[i],CA2,XC2]
c.x[R0[i],CA1,XC1].ccx[R0[i],XC1,CA1] # if R0 and R1 are empty and CA1(XC1=0) is occupied, unloding from CA1
c.ccx[XC1,CA1,R0[i]].x[R0[i],R1[i]] # if CA1 is changed, R0 turns
q.cccx(c,R0[i],R1[i],CA1,XC1) # if CA1 is changed, R0[i] are ocuippied and R1[i] is empty, XC1 turns
c.x[R1[i],CA1,XC1]
c.x[R0[i],CA0,XC0].ccx[R0[i],XC0,CA0] # if R0 and R1 are empty and CA0(XC0=0) is occupied, unloding from CA0
c.ccx[XC0,CA0,R0[i]].x[R0[i],R1[i]] # if CA0 is changed, R0 turns
q.cccx(c,R0[i],R1[i],CA0,XC0) # if CA0 is changed, R0[i] are ocuippied and R1[i] is empty, XC0 turns
c.x[R1[i],CA0,XC0]
return
def Proc2():
# second round (unloading only)
for i in range(N):
c.x[R0[i]]
c.ccx[R0[i],CA2,R2[i]].ccx[R0[i],R2[i],CA2] # Unloading from CA2 to R2[i]
c.ccx[R0[i],CA1,R2[i]].ccx[R0[i],R2[i],CA1] # Unloading from CA1 to R2[i]
q.cccx(c,R0[i],CA0,CA1,R2[i]) # error correction
c.ccx[R0[i],CA0,R2[i]].ccx[R0[i],R2[i],CA0] # Unloading from CA0 to R2[i]
c.ccx[R0[i],CA0,R2[i]] # error correction
c.x[R0[i]]
def Proc3():
for i in range(N):
c.cx[R1[i],R0[i]]
c.cx[R2[i],R0[i]]
return
量子プロセス以外も含めたフルコードはGithubのリポジトリ q-cams 内のq-cambbs1.pyに保管している。使用方法とりわけ確率的初期状態のセットに関しては2回目の「2-1.q-camの構造とモジュール」に記載しているのでそちらを参照されたし。
6-3. 確率初期状態からの時間発展
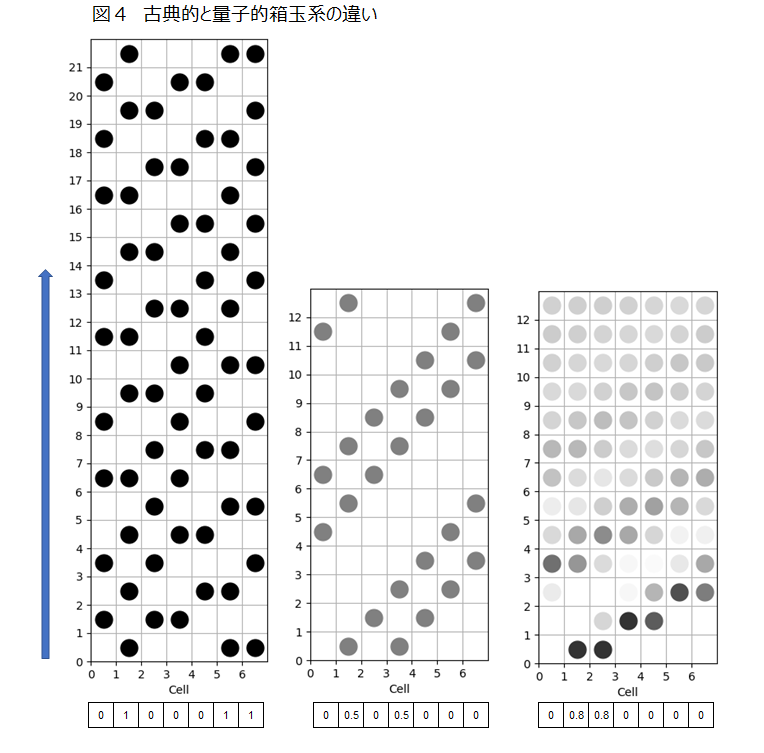
完成したプログラムq-cambbs1.pyを用いて、いくつかの例での時間発展と性質をみてみよう。尚、結果はプロットした図で示している。図の見方は下から上への1ステップ(時間)単位での発展で、横軸は軸ではなくてセル列である。玉の色の濃淡は確率に比例させていて、1の時が黒、0の時が白である。尚、玉の確率とは、セルに玉が存在する確率の意味である。
古典と量子の違い
図4の左は初期値として7つのセルを0,1,0,0,0,1,1 とした場合で、セルの値が1と0のみなので従来からのソリトンセルオートマトンであり、ここでは古典(的)と称する。この場合、最下段の初期値と同配置に戻るのは、21ステップ目である。それ以降は当然、同じことを繰り返しとなる。つまり古典の場合は周期性があり、この例では21である。尚、各プロットに下には初期値(確率的初期状態のセット)を数値で示した。図4の中央のプロットは初期確率0.5の玉を離して2個配置したものである。これは2個の玉の間で何の相互作用もないので、お互い単純に一セルづつ移動していくだけで古典的なものと変わりはない。また周期性があり、この例では周期は7である。一方、図4の右のプロットは初期確率0.8の玉を隣り合わせて配置したものである。この場合、時間発展とともに次第に全てのセルが均一でより小さい確率となっていくように見え、いかにも量子的である。周期性は全くない。
問題点
図4の右と図5の左のプロットは同じものである。初期での玉の合計数(確率的初期状態のセルの値の合計値)は1.6(0.8+0.8)である。一方、第12ステップ目の合計値は1.2となっている。初期から時間発展する従って単調に減少している。本来、箱玉系では玉数は遷移によって減らない。これは量子の場合の特有の性質ではないと思われる。これは詰まる所アルゴリズム上の欠陥と考えている。
推定原因
誤っているかもしれないが、原因は量子の場合、ゼロではない玉の存在確率が3個以上のセルに広がっており、一方キャリアは3つしか準備していない。あるセルにキャリアが既に満タンで到達した時で、そのセルの玉の存在確率があればキャリアに載せることができない。量子コンピューティングで0と1の中間の値をとるようであるが、実際は0と1だけでそれが重ね合わせっているだけである。結局、キャリアに乗れなかった分づつ減少していくと思われる。もしキャリアがセル数と同じ分だけあればこのような問題は生じないと考えられるが、量子ビットの制限から未検証である。やむを得ずの応急処置として、各ステップでセルの値の合計値が初期での合計値と等しくなるように規格化する。つまり、jステップ目のi番目のセルの玉確率を$P_{ji}$とし、規格化後のセルの玉確率$P’$を次式で与える。
$$P'_{ji}=\frac{\sum P_{0i}}{\sum P_{ji}} P_{ji}$$
このようにして得た結果を図5の右に示した。右のプロットでは初期値1.6、第12ステップ目の合計値も1.6となっている。差が0.4程度しかないので、これらのプロットでは濃淡の差は分かりずらい。

初期同玉配置での玉存在確率違い
初期の玉配置として、0,1,0,0,0,1,1 として、玉存在確率(確率的初期状態)を1から0.8と0.5と変えた場合の時間発展を比較したプロットを図6に示した。尚、0.8と0.5では規格化している。0.8と0.5では濃淡が薄くなり比較しづらいが、それとなく似たパターンでかつ古典を引きづっている。がしかし、よーく見ると、0.8と0.5では3ステップ以降、セル毎の濃淡の順が入れ替わっている。

6-4. サマリー
・今回は冒頭で述べた通り、アルゴリズムの腐心の話なので時間発展での結果を云々していない。
・玉数減少がアルゴリズム由来なのか、量子としての真実なのか投稿者にはわからない。
・強調したいのは、分岐構造を持たない量子プログラミングでマルチ制御NOTを多用しあたかもif文のような働きさせてみたことである。
ところで量子でのifとは何を意味しているのだろうか? 次回8回目はこの投稿シリーズ(【数式なしの量子コンピュータ】 新視点セルオートマトンとグローバー)の最終回であり、締めとして***量子でのifとは何を意味しているのだろうか?***を記したい。
8回目は量子位相推定(QPE)をセルオートマトンやグローバーアルゴリズムに適用してみた話となりました。