Cirq で Grover アルゴリズムを実装

Grover アルゴリズムを Cirq を利用して実装してみました。

Grover アルゴリズムとは

概要

量子コンピュータ用の未整序データベースの検索アルゴリズムです。
未整序データベースの検索は、古典コンピュータでは $O(N)$ の計算時間がかかるところ、量子コンピュータ上で Grover アルゴリズムを利用すると $O(N^{1/2})$ の計算時間で検索が行えるようになります。

アルゴリズムの理論

Grover アルゴリズムの理論を説明します。
※ @kyamaz さんの Grover アルゴリズムについてにわかりやすく書いてありますので参考にすると良いと思います。

アルゴリズムは以下のステップで実行されます。

全状態を均等に重ね合わせておく
検索したい量子ビット列だけの確率振幅を -1 にする
演算子 $g = 2 \left| \psi \right>\left< \psi \right| - \bf{1} $を Step 2. で作った状態に作用させる。
量子ビット数 $N$ とした場合、$\sqrt[]{\mathstrut N}$ 回だけ Step 2. から Step 3. の処理を繰り返す
すべての量子ビットを測定する

ここで、3 で定義した $\left| \psi \right>$ は以下で定義されます。

\left| \psi \right> = \frac{1}{N^{1/2}}\sum_{x=1}^{N} \left| x \right>

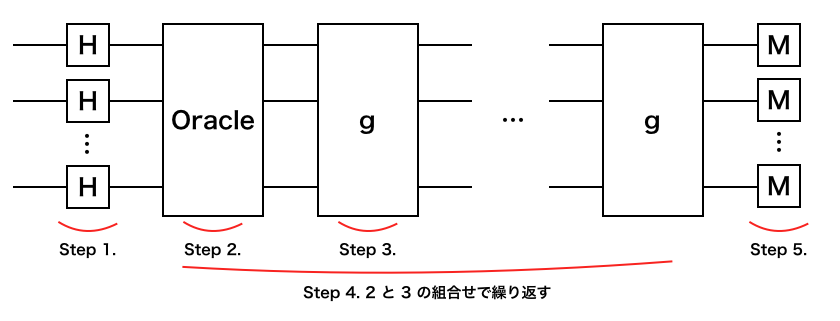
アルゴリズムの概要を回路に落とすと以下になります。

オラクル

Step 2. の演算のことをオラクルといい、量子ビット数に応じて適当な回路を組んで検索対象の状態の確率振幅に -1 をつけるようにする操作を指します。

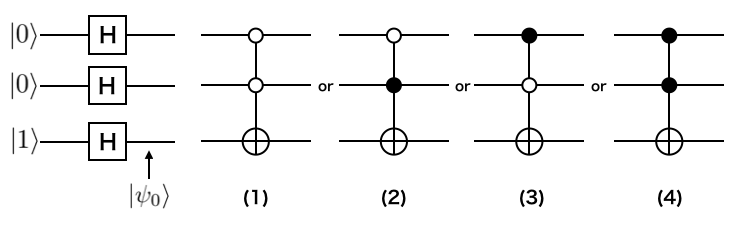
2 量子ビットの Grover では Oracle Work Space として、オラクルを実行するために新たに 1 量子ビットを追加します。そして、検索対象の量子ビットを $\left| 0 \right>$ で Oracle Work Space の量子ビットを $\left| 1 \right>$ で初期状態を用意します。

上記の図のようにハダマールゲートをすべての量子ビットに作用させると $\left|\psi_{0}\right>$ は以下のようになります。

\begin{align}
\left| \psi_{0} \right> &= \frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 0 \right> + \left| 1 \right> \right) \otimes \frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 0 \right> + \left| 1 \right> \right) \otimes \frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 0 \right> - \left| 1 \right> \right) \\
&= \frac{1}{2}\left(\left| 00 \right> + \left| 01 \right> + \left| 10 \right> + \left| 11 \right> \right) \otimes \frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 0 \right> - \left| 1 \right> \right)
\end{align}

オラクルで行いたい操作は、次の4つの $\left| 00 \right>, \left| 01 \right>, \left| 10 \right>, \left| 11 \right>$ のどれかの確率振幅を -1 にすることなので、 Oracle Work Space の量子ビット $\frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 0 \right> - \left| 1 \right> \right)$ の状態に $X$ ゲートを作用させて反転させることを考えます。
例えば、 1 量子ビット目と 2 量子ビット目が 1 の場合にだけ $X$ を操作する 3 量子ビットゲート(Toffoli ゲート)を定義します。

各状態$\left| 00 \right>, \left| 01 \right>, \left| 10 \right>, \left| 11 \right>$に対する3量子ビットゲートはそれぞれ図の (1) ~ (4) になります。

$\left| 01 \right>$ の場合だけ、計算してみると

\begin{align}
\frac{1}{2}\left(\left| 00 \right> + \left| 01 \right> + \left| 10 \right> + \left| 11 \right> \right) \otimes \frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 0 \right> - \left| 1 \right> \right) &\rightarrow \frac{1}{2}\left(\left| 00 \right> + \left| 10 \right> + \left| 11 \right> \right) \otimes \frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 0 \right> - \left| 1 \right> \right) + \frac{1}{2} \left| 01 \right> \otimes \frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 1 \right> - \left| 0 \right> \right) \\
&= \frac{1}{2}\left(\left| 00 \right> + \left| 10 \right> + \left| 11 \right> \right) \otimes \frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 0 \right> - \left| 1 \right> \right) - \frac{1}{2} \left| 01 \right> \otimes \frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 0 \right> - \left| 1 \right> \right) \\
&= \frac{1}{2}\left(\left| 00 \right> - \left| 01 \right> + \left| 10 \right> + \left| 11 \right> \right) \otimes \frac{1}{\sqrt[]{\mathstrut 2}}\left(\left| 0 \right> - \left| 1 \right> \right)
\end{align}

となり、確かに狙った $\left| 01 \right>$ の確率振幅だけを -1 にすることができます。

ゲート

Grover アルゴリズムで使用する演算子は$2 \left| \psi \right>\left< \psi \right| - \bf{1}$ でしたが、これを回路図にしていきます。

まず、$\left| \psi \right> = \frac{1}{N^{1/2}}\sum_{x=o}^{N} \left| x \right>$で、2 量子ビットの場合、$N=2^{2} = 4$ なので、 $\left| \psi \right>$ は以下のように表せます。

\begin{align}
\left| \psi \right> &= \frac{1}{\sqrt[]{\mathstrut 2^{2}}} \sum_{x=1}^{2^{2}} \left| x \right> \\
&= H^{\otimes 2} \left| 0 \right>
\end{align}

そのため、 $2 \left| \psi \right>\left< \psi \right| - \bf{1}$ は

\begin{align}
2 \left| \psi \right>\left< \psi \right| - \bf{1} &= 2 H^{\otimes 2} \left| 0 \right>\left< 0 \right| H^{\otimes 2} - \bf{1} \\
&= H^{\otimes 2} \left(2 \left| 0 \right>\left< 0 \right| - \bf{1}\right) H^{\otimes 2}
\end{align}

となります。

$2 \left| 0 \right>\left< 0 \right| - \bf{1}$ は 4×4の行列であることに注意すると以下のような正方行列になります。

\begin{align}
2 \left| 0 \right>\left< 0 \right| - \bf{1} & =
\left( 
\begin{array}{cccc}
1&  0& 0& 0\\
0& -1& 0& 0\\
0&  0& 1& 0\\
0&  0& 0& 1\\
\end{array} 
\right) \\

& = 
\left( 
\begin{array}{cc}
     Z&  \bf{0}\\
\bf{0}& -\bf{1}\\
\end{array} 
\right) \\
& = 
\left( 
\begin{array}{cc}
  -XZX&  \bf{0}\\
\bf{0}& -\bf{1}\\
\end{array} 
\right) \\

& = -
\left( 
\begin{array}{cc}
  XZX&  \bf{0}\\
\bf{0}& \bf{1}\\
\end{array} 
\right) \\

\end{align}

行列内の符号を全体にかかるようにしたいために、$Z = -XZX$ の関係を使用ししました。この行列全体にかかった -1 は量子計算には寄与しないため、今後は無視して、計算を進め、Xゲートと Control-Z ゲートで上記の行列を分解すると

\begin{align}
\left( 
\begin{array}{cc}
  XZX&  \bf{0}\\
\bf{0}& \bf{1}\\
\end{array} 
\right)
&=
\left( 
\begin{array}{cc}
  \bf{0}&  X\\
X& \bf{0}\\
\end{array} 
\right)
\left( 
\begin{array}{cc}
  \bf{1}&  \bf{0}\\
\bf{0}& Z\\
\end{array} 
\right)
\left( 
\begin{array}{cc}
  \bf{0}&  X\\
X& \bf{0}\\
\end{array} 
\right) \\
&= 
X^{\otimes2}C_{Z}X^{\otimes2}
\end{align}

の形になります。そして、全体の回路としては以下のようになります。

2 \left| \psi \right>\left< \psi \right| - \bf{1} = H^{\otimes2}X^{\otimes2}C_{Z}X^{\otimes2}H^{\otimes2}

上記及びオラクル等を含め、回路図にすると以下になります。

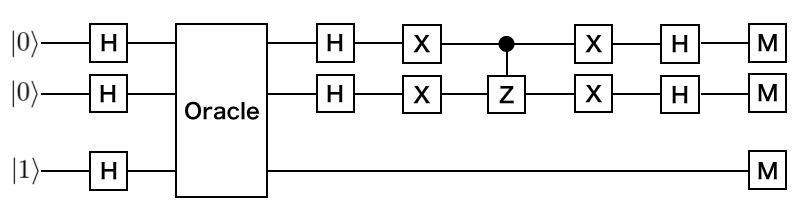
※ Oracle と書かれたボックスの右側からが $2 \left| \psi \right>\left< \psi \right| - \bf{1}$ になります。

ゲートの実装

Criq で実装した場合は以下になります。
※ q0 及び q1 を検索対象の量子ビット、q2 を Oracle Work Space としてます。

from cirq import LineQubit, Circuit, Simulator, measure
from cirq.ops import X,  H, CNOT, TOFFOLI
from cirq.google import XmonSimulator

q0, q1, q2 = [LineQubit(x) for x in range(3)]

def oracle(search_bit):
    if search_bit == '00':
        yield X(q0), X(q1)
        yield TOFFOLI(q0, q1, q2)
        yield X(q0), X(q1)
        return

    if search_bit == '01':
        yield X(q0)
        yield TOFFOLI(q0, q1, q2)
        yield X(q0)
        return

    if search_bit == '10':
        yield X(q1)
        yield TOFFOLI(q0, q1, q2)
        yield X(q1)
        return

    if search_bit == '11':
        yield TOFFOLI(q0, q1, q2)
        return

def unit_of_grover(search_bit):
    yield oracle(search_bit)
    yield H(q0), H(q1)
    yield X(q0), X(q1)
    yield H(q1)
    yield CNOT(q0, q1)
    yield H(q1)
    yield X(q0), X(q1)
    yield H(q0), H(q1)

def create_circuit_of_grover(search_bit):
    yield X(q2)
    yield H(q0), H(q1), H(q2)
    yield unit_of_grover(search_bit)
    yield H(q2)
    yield measure(q0, key='q0'), measure(q1, key='q1'), measure(q2, key='q2')

実行すると以下になります。

SEARCH_BIT = '00'
circuit = Circuit()
circuit.append(create_circuit_of_grover(SEARCH_BIT))
simulator = Simulator()
print(circuit)
print(simulator.run(circuit))

0: ───H───X───@───X───H───X───────@───X───H───M('q0')─────────────
              │                   │
1: ───H───X───@───X───H───X───H───X───H───X───H─────────M('q1')───
              │
2: ───X───H───X───────────────────────────────H─────────M('q2')───
q0=0
q1=0
q2=1

Cirq で実装する際に、Oracle Work Space の初期状態が $\left|0\right>$ が始まるので、$X$ ゲートを作用させて $\left|1\right>$ に反転させ、$C_{Z}$ を $H$ ゲートと $CNOT$ ゲートで表現しています。

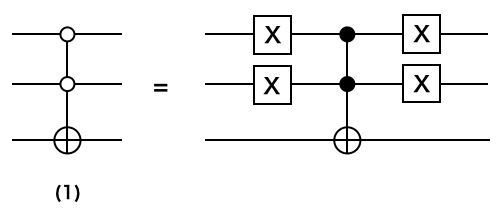
また、上記の実行は $\left|00\right>$ を検索する回路を組んでいるため、オラクルは (1) を採用し、以下の関係を利用しています。

まとめ

Cirq で Grover アルゴリズムを実装してみました。量子ビット数は増えてしまいますが、今回のように Oracle Work Space 導入し、 Toffoli ゲートを利用するとオラクル部分がスッキリとして、理解しやすいように思いました。

また、今回実装したものはいつも通り github にあげています。

Cirq で Grover アルゴリズム を実装

Cirq で Grover アルゴリズムを実装

Grover アルゴリズムとは

概要

アルゴリズムの理論

オラクル

ゲート

ゲートの実装

まとめ

Cirq で Grover アルゴリズムを実装