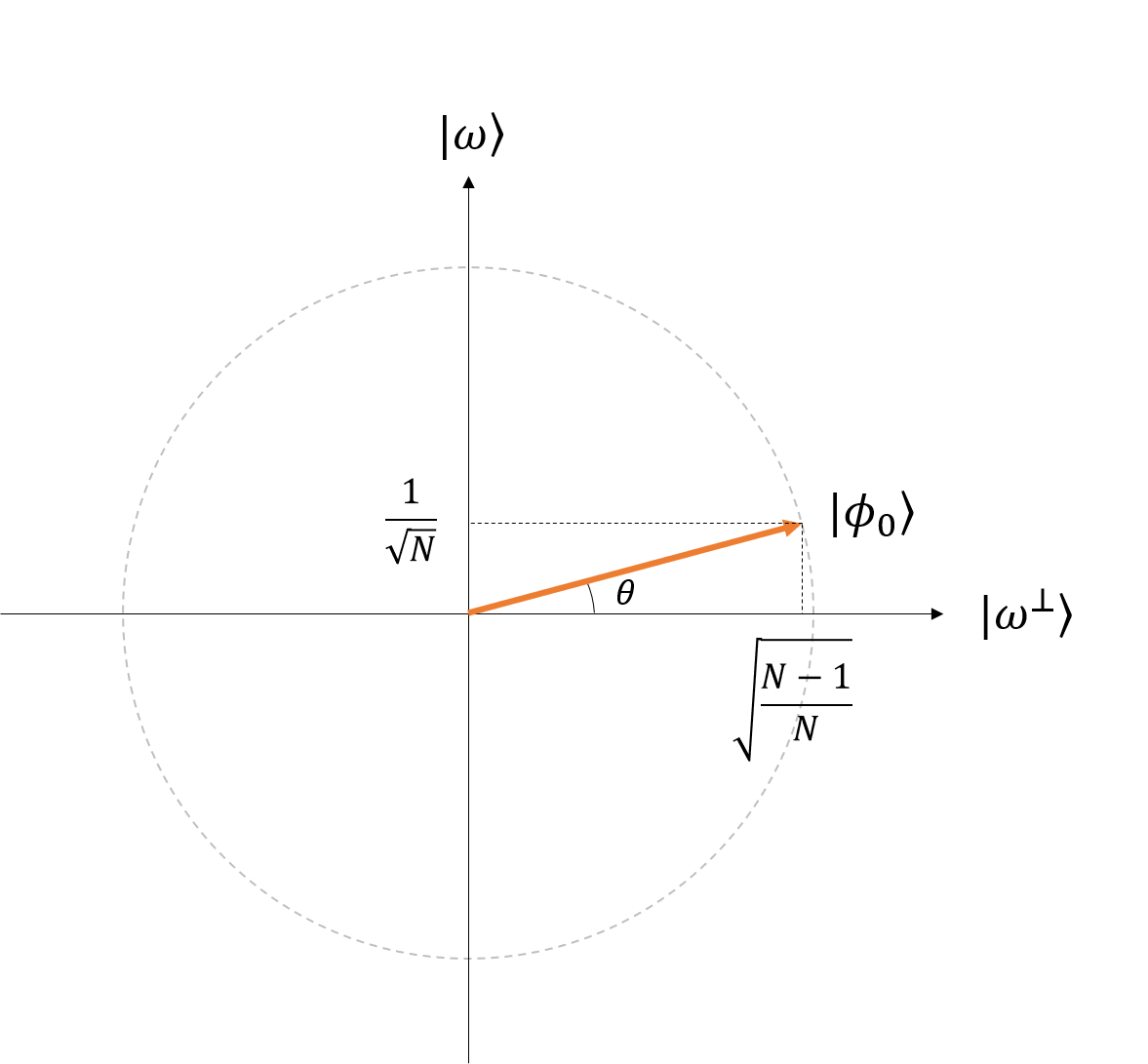前書き
本記事では、Quantum Katas の Grover's algotithm について解説します。Q# や Quantum Katas って何よという方は Quantum Katas で始める量子コンピュータ入門 |0⟩ をご参照ください。
さて、勝手にまとめて来た Quantum Katas のまとめも今回で $|10⟩$ 回目となりました。各種アルゴリズムや観測、誤り訂正などを一通りこなすことで、なんとなく量子プログラミングってこんなもんなんだなという感じが見えてきているのではないかと思います。
今回は Grover's アルゴリズムです。量子コンピューターをよく知らない人でも、Shor と Grover くらいは知っているという方もいらっしゃるかもしれません。それくらい有名な、重要性の高いアルゴリズムです。Grover のアルゴリズムは未ソートのデータの集合からリーズナブルな計算量で目的のデータを探索するアルゴリズムで、量子コンピューターが実現された暁には幅広い応用が期待されるアルゴリズムです。
いつも通り最初のほうのタスクはあくまで導入で直接的にアルゴリズムとは関係ないものも含まれますが、早速進めていきましょう。
各 Task の解説
Task 1.1. The |11...1〉 oracle
問題
入力: 任意の状態の N 量子ビット $|x\rangle$ と 1 量子ビット $|y\rangle$
ゴール: $|x\rangle = |11\dots11\rangle$ のとき、$|y\rangle$ を反転せよ。
解説
そんなに難しい問題じゃないですね。Controlled ファンクタで X ゲートの処理をすれば終了です。
operation Oracle_AllOnes (queryRegister : Qubit[], target : Qubit) : Unit {
body (...) {
Controlled X(queryRegister, target);
}
adjoint self;
}
Task 1.2. The |1010...〉 oracle
問題
入力: 任意の状態の N 量子ビット $|x\rangle$ と 1 量子ビット $|y\rangle$
ゴール: $|x\rangle = |1010\dots\rangle$ のように 1 と 0 が交互に現れる場合に、$|y\rangle$ を反転せよ。 例えば、$|x\rangle = |10101\rangle$ なら $|y\rangle$ を反転するが、$|x\rangle = |000000101\rangle$ なら $|y\rangle$ を反転しない。
解説
さっきの問題の亜種です。いかようにも処理できそうですが、$|x\rangle$ の奇数ビットをすべて反転して Controlled X で処理するのが楽そうですかね。1..2.. のように Step として 2 を指定すれば場合分けもいらなそうです。回答は以下となります。
operation Oracle_AlternatingBits (queryRegister : Qubit[], target : Qubit) : Unit {
body (...) {
// 1, 3, 5,... ビット目を反転
for(i in 1..2..Length(queryRegister)-1) {
X(queryRegister[i]);
}
// 入力が 1010101... ならこの時点ですべて 1 になっているので Controlled X で処理
Controlled X(queryRegister, target);
// 反転したビットをもとに戻す
for(i in 1..2..Length(queryRegister)-1) {
X(queryRegister[i]);
}
}
adjoint self;
}
Task 1.3. Arbitrary bit pattern oracle
問題
入力: 任意の状態の N 量子ビット $|x\rangle$ と 1 量子ビット $|y\rangle$、および N 古典ビット
ゴール: $|x\rangle$ のビットパターンが古典ビットと同じなら $|y\rangle$ を反転せよ。
解説
さらに亜種が続きます。これも同じ方法でやっつけましょう。今回は古典ビットの状態による場合分けで処理します。
operation Oracle_ArbitraryPattern (queryRegister : Qubit[], target : Qubit, pattern : Bool[]) : Unit {
body (...) {
// 古典ビットが 0 の時はビットを反転
for(i in 0..Length(pattern)-1) {
if(pattern[i] == false) {
X(queryRegister[i]);
}
}
// 古典ビットと x が同じパターンを持っている場合はこの時点ですべて 1 になっているので Controlled X で処理
Controlled X(queryRegister, target);
// 反転したビットをもとに戻す
for(i in 0..Length(pattern)-1) {
if(pattern[i] == false) {
X(queryRegister[i]);
}
}
}
adjoint self;
}
Task 1.4*. Oracle converter
問題
入力: N ビットの入力レジスタとターゲットが与えられた際に、入力レジスタが特定の条件を満たす際にターゲットを反転するオラクル
出力: 特定の条件が満たされた際にターゲットを反転するのではなく、入力レジスター自身の位相を反転するオラクルを出力せよ。
解説
これまでの問題とはかなり毛色が変わりました。今回は入力として (特定の条件というものが何なのか全く分からない) オラクル自身が与えらた際に、オラクル自体を変換して出力せよという問題となります。個人的には非常にとっつきにくい問題に思いますが、皆さんにとってはどうでしょうか。問題文にもある通り、Wikipedia の Grover's algorithm の記事 にもこのオラクルについての説明がありますので、必要に応じてみてみてください。(2019 年 1 月現在では日本語版には $U_\omega$ についての記載がないので英語版のリンクを貼っています)
与えられるオラクルを $U$、出力する変換後のオラクルを $U_\omega$、この問題で行う処理を $F_U$ とすると、それぞれ以下のような変換を行うこととなります。
\begin{align}
&U: \{0, 1\}^n, \{0, 1\}\rightarrow \{0, 1\}^n, \{0, 1\} \\
&U_\omega: \{0, 1\}^n \rightarrow \{0, 1\}^n \\
&F_U: U \rightarrow U_{\omega}
\end{align}
まず、この問題では関数の部分適用が必要になります。部分適用ってなんだっけという方は Q# の Operation と Function についてのメモ をご参照ください。
今回与えられるオラクル $U$ はターゲット自体を反転するので、それを位相の反転に変えなければいけないのですが、どうすればいいでしょうか。ドイチェ・ジョザなんかでもやった通り、$|-⟩$ を使えばよさそうです。すなわち、
$$
|x⟩|-⟩ = \frac{1}{\sqrt 2}|x⟩(|0⟩ - |1⟩)
$$
とすると
U|x⟩|-⟩ =
\begin{cases}
-\frac{1}{\sqrt 2}|x⟩(|0⟩ - |1⟩) & \text{If conditions are satisfied,}\\
\frac{1}{\sqrt 2}|x⟩(|0⟩ - |1⟩) & \text{otherwise,}
\end{cases}
となるため、最後のアンシラ ビットを捨ててやれば $-|x⟩$ が得られます。あとは上記を実装してやれば終了です。
// 自分で作成したオラクル (今回のタスクの回答)
operation MyCustomOracle (markingOracle : ((Qubit[], Qubit) => Unit), qs: Qubit[]) : Unit {
body (...) {
using(q = Qubit[1]) {
// アンシラ ビットを |-⟩ に変換
X(q[0]);
H(q[0]);
// 与えられたオラクルで処理
markingOracle(qs, q[0]);
// アンシラ ビットをリセット
Reset(q[0]);
}
}
adjoint self;
}
// オラクルの変換を行う関数
function OracleConverter (markingOracle : ((Qubit[], Qubit) => Unit : Adjoint)) : (Qubit[] => Unit : Adjoint) {
// 与えらえた matkingOracle を適用したオラクルを返す
return MyCustomOracle (markingOracle, _);
}
グローバーのアルゴリズム
さて、ここまでで準備が一旦完了です。今回のグローバーのアルゴリズムで解決する問題を定義しておきます。
グローバーの探索問題
関数 $f: {0, 1}^n \rightarrow {0, 1}$ が与えられたとする。$f(\omega) = 1$ を満たす解 $\omega \in {0, 1}^n$ がただ一つ存在する場合に、解 $\omega$ を求めよ。
ただし、関数 $f$ はオラクル $U_\omega$ を用いて以下の形式で与えらえる。
$$U_\omega|x⟩|y⟩ = |x⟩|y \oplus f(x)⟩$$
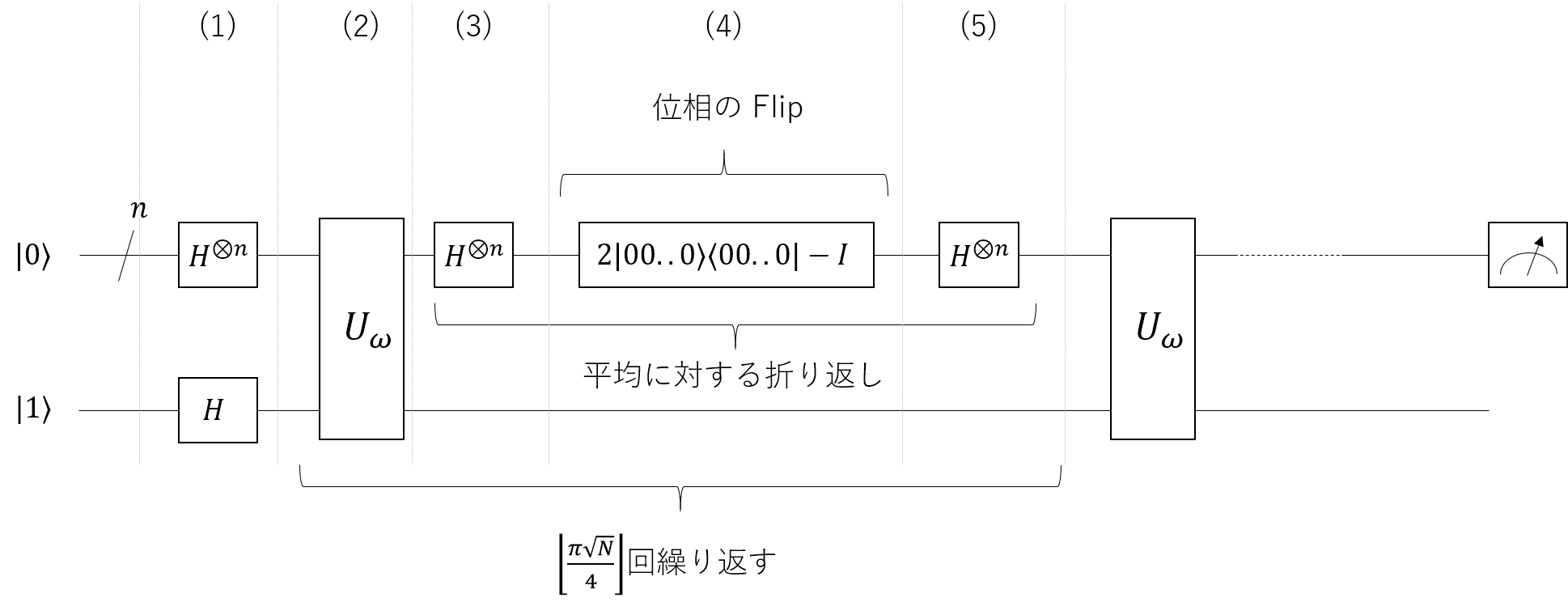
問題としてはこれまでのアルゴリズムに比べてもシンプルですね。この問題も、古典的に解く場合は総当たりで確認する以外に効率的に解くのが難しそうだなーと感じるのではないかと思います。早速回答の回路図を記載します。今から私達は、以下を実装します。
回路としてもいままで実装したアルゴリズムと大差ないように見えますが、複数回繰り返すという点が異なります。要は、オラクルの処理を複数回実施しなければ行けない (質問計算量が増える) ということを意味します。しかしながら、この反復回数も $\omicron (\sqrt N)$ で抑えられるため、古典アルゴリズムより高速な処理が可能となります。
グローバーのアルゴリズムの数理
流石に量子コンピュータの有用性を示した著名なアルゴリズムだけあって、巷にも解説がたくさんあります。いずれも素晴らしい解説ですが、個人的には最初の慶応大学の Youtube 動画がおすすめです。(余談ですが、この動画シリーズはグローバーに限らず全部素晴らしいです。)
量子コンピュータ授業 #4 グローバーのアルゴリズム - YouTube
sympy でグローバーアルゴリズム(量子ゲート計算) - Qiita
Grover の検索アルゴリズムとQuantum Amplitude Amplification/Estimation - 物理とか
アルゴリズムの解説は上記の参考サイトで超十分だと思うのですが、せっかくなので私の勉強ログもいかにまとめます。個人的に躓いたのは以下のような点でした。
- ほんとにこの回路で $\omega$ って取り出せんの?
- 平均に対する折り返しって何よ?
- ぐちゃぐちゃ言われてもよくわからん
- 結局どのくらいの性能が得られるの?
順番に進めます。
1. ほんとにこの回路で $\omega$ って取り出せんの?
まず、上記の回路で本当に $\omega$ が取り出せそうかを確認するため、最初の一回を処理してみましょう。まずは (1) と (2) を計算します。
\begin{aligned}
|0^n\rangle|1\rangle
\xrightarrow{(1)}& \frac{1}{\sqrt N}\sum_{x \in \{0, 1\}^n} |x\rangle \otimes \frac{1}{\sqrt 2}(|0\rangle - |1\rangle) \\
\xrightarrow{(2)}& \frac{1}{\sqrt N}\sum_{x \in \{0, 1\}^n} |x\rangle \otimes \frac{1}{\sqrt 2}(|0 \oplus f(x)\rangle - |1 \oplus f(x)\rangle) \\
&= \frac{1}{\sqrt N}\sum_{x \in \{0, 1\}^n} (-1)^{f(x)}|x\rangle \otimes \frac{1}{\sqrt 2}(|0\rangle - |1 \rangle) \\
&= \frac{1}{\sqrt N}\Big(-|\omega\rangle + \sum_{x \ne \omega} |x\rangle \Big) \otimes \frac{1}{\sqrt 2}(|0\rangle - |1 \rangle)
\end{aligned}
回答である $|\omega\rangle$ だけ位相が反転して出てくる点に注意すれば、$f(x)$ をアンシラから取ってくるあたりはもう何度もやった通りですね。続いて (3) 以降の処理については、まずは (3) ~ (5) をまとめて計算しておきます。また、ここでは $D := H^{\otimes n}(2|0^n\rangle\langle0^n| - I)H^{\otimes n}$と定義します。
\begin{aligned}
D=H^{\otimes n}(2|0^n\rangle\langle0^n| - I)H^{\otimes n} &= H^{\otimes n}2|0^n\rangle\langle0^n|H^{\otimes n} - H^{\otimes n}H^{\otimes n} \\
&= 2|\phi_0\rangle\langle\phi_0| - I \\
&=
\begin{pmatrix}
\frac{2}{N}-1 & \frac{2}{N} & \frac{2}{N} & \cdots & \frac{2}{N} \\
\frac{2}{N} & \frac{2}{N}-1 & \frac{2}{N} & \cdots & \frac{2}{N} \\
\frac{2}{N} & \frac{2}{N} & \frac{2}{N}-1 & \cdots & \frac{2}{N} \\
\frac{2}{N} & \frac{2}{N} & \frac{2}{N} & \ddots & \vdots \\
\frac{2}{N} & \frac{2}{N} & \frac{2}{N} & \cdots & \frac{2}{N} - 1
\end{pmatrix}
\end{aligned}
ただし $|\phi_0\rangle=\frac{1}{\sqrt N}\sum_{x \in {0, 1}^n} |x\rangle$ です。以外とスッキリした形になります。(2) の適用までで目標とする$|\omega\rangle$ とそれ以外に分離ができているので、上記の行列の計算も分けて考えましょう。
$x\ne\omega$ のときは $\omega$ とその他のどこかが打ち消し合うので
$$
\frac{1}{\sqrt N}\Big(\frac{2}{N}-1\Big)+\frac{2(N-3)}{N\sqrt N} = \frac{N-4}{N\sqrt N}
$$
となります。一方 $x =\omega$ のときは打ち消し合う所がないため、
$$
-\frac{1}{\sqrt N}\Big(\frac{2}{N}-1\Big)+\frac{2(N-3)}{N\sqrt N} = \frac{3N-4}{N\sqrt N}
$$
となります。本論だった計算を続けると、
\begin{aligned}
\xrightarrow{(3) - (5)}& \Big(\frac{3N-1}{N\sqrt N}|\omega\rangle + \frac{N-4}{N\sqrt N}\sum_{x \ne \omega} |x\rangle \Big) \otimes \frac{1}{\sqrt 2}(|0\rangle - |1 \rangle)
\end{aligned}
となることがわかります。$N >> 4$ なら上記の確率振幅は $\frac{3}{\sqrt N}$ と $\frac{1}{\sqrt N}$ であり、3 倍(確率で言えば 9 倍)に増幅されます。(1) で処理を行った直後はすべての状態が同じ確率だったので、先に示した回路で目標状態を取り出す確率が上げられそうだということが確認できました。
2. 平均に対する折り返しって何よ?
続いて、Grover のアルゴリズムの解説でも必ず見かける "平均に対する折り返し" という所についての説明です。回路図にも記載しましたが、この平均に対する折り返しってどういう意味でしょうか?巷の参考書ではブラケットでクロネッカーのデルタを考慮して…みたいな議論が多いのですが、量子情報の初心者にとってブラケット記法による議論は若干ハードルが高い気がします。行列で書き下してみると、割と簡単に確認できます。
行列 $D$ は先に記した通りです。今回は、任意の量子状態 $|\psi\rangle = \sum_x \alpha_x|x\rangle = (\alpha_1 \alpha_2 \dots \alpha_N)^T$ を変換してみましょう。
\begin{aligned}
D|\psi\rangle&=
\begin{pmatrix}
\frac{2}{N}-1 & \frac{2}{N} & \frac{2}{N} & \cdots & \frac{2}{N} \\
\frac{2}{N} & \frac{2}{N}-1 & \frac{2}{N} & \cdots & \frac{2}{N} \\
\frac{2}{N} & \frac{2}{N} & \frac{2}{N}-1 & \cdots & \frac{2}{N} \\
\frac{2}{N} & \frac{2}{N} & \frac{2}{N} & \ddots & \vdots \\
\frac{2}{N} & \frac{2}{N} & \frac{2}{N} & \cdots & \frac{2}{N} - 1
\end{pmatrix}
\begin{pmatrix}
\alpha_1 \\
\alpha_2 \\
\alpha_3 \\
\vdots \\
\alpha_N
\end{pmatrix} \\
&=
\begin{pmatrix}
\frac{2}{N}\sum_i \alpha_i - \alpha_1 \\
\frac{2}{N}\sum_i \alpha_i - \alpha_2 \\
\frac{2}{N}\sum_i \alpha_i - \alpha_3 \\
\vdots \\
\frac{2}{N}\sum_i \alpha_i - \alpha_N
\end{pmatrix}
=
\begin{pmatrix}
2\bar\alpha - \alpha_1 \\
2\bar\alpha - \alpha_2 \\
2\bar\alpha - \alpha_3 \\
\vdots \\
2\bar\alpha - \alpha_N
\end{pmatrix}
\end{aligned}
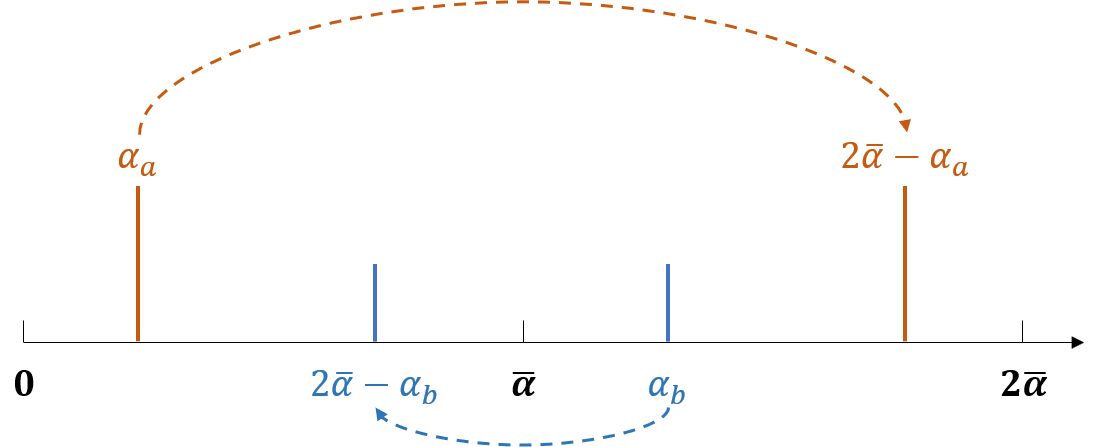
ここで、$\bar\alpha = \frac{1}{N}\sum_i \alpha_i$ としています。全部の確率振幅を足し合わせて要素数で割っているので、確率振幅の平均になっています。平均値の 2 倍から各値を引いた値というのは、数直線を書いてみると平均に対する折り返しとなっていることが確認できます。(もちろんこれは複素数なのですが)
図2 平均に対する折り返し
3. ぐちゃぐちゃ言われてもよくわからん
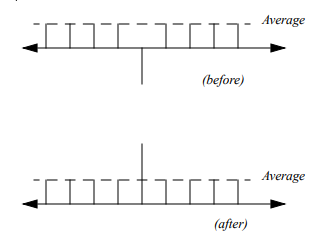
数式で上記の回路を通せば得たい回答 $\omega$ の確率が増幅されること、また、その処理は平均値に対する折り返しによって成り立つことがわかりましたが、結局直感的にはどう理解すればいいでしょうか?Grover の原著論文 にも、この処理の直感的な意味が記されています。
図3 グローバー オペレーターの直感的な理解
横軸は各状態 ($|x_i\rangle$) です。位相を反転して (図の上部) 平均に対して折り返す (図の下部) ことで目標状態だけを増幅させることが可能です。個人的にはこの図をみてなるほどそういうものかなと思えるようになりました。
4. 4. 結局どのくらいの性能が得られるの?
ここまででなんとなく Grover の有効性が理解できた気がしますが、まだ以下の疑問が残ります。
- 確率 1 で解を得られるようには到底思えない。どのくらいの確率で正しい回答が得られるんだろう?
- 繰り返し回数はどのくらいにすればいいんだろう?
この疑問に答えるために、Grover のアルゴリズムの多くの解説では、回答 $|\omega\rangle$ 以外の状態を示す $|\omega^\perp\rangle$ を導入し、2 次元での解析が進められます。いきなり何言ってんだと思われるかもしれませんが、$|\omega^\perp\rangle = \frac{1}{\sqrt N-1}\sum_{x \ne \omega}|x\rangle$ と定義すると例えば $|\phi_0\rangle=\frac{1}{\sqrt N}\sum_{x \in {0, 1}^n} |x\rangle$ だったので、
$$
|\phi_0\rangle=\frac{1}{\sqrt N}\sum_{x \in {0, 1}^n} |x\rangle
= \frac{1}{\sqrt N}\Big(|\omega\rangle + \sum_{x \ne \omega} |x\rangle \Big)
= \frac{1}{\sqrt N}|\omega\rangle + \sqrt{\frac{N-1}{N}}|\omega^\perp\rangle
$$
と書き直す事ができます。Grover の処理からも分かる通り、"目標ビット以外の処理はすべて同様に行われるため、個別の状態を考えなくともまとめて考えてしまえばよい" というのが上記の変形の直感的な理由です。個人的にはここが当たり前に出てくる所が理解に苦しむ点でした。
ここさえ乗り切れば、あとは式変形はめんどくさいものの、恐れるにたるようなものではありません。$|\phi_0\rangle$ を $|\omega\rangle$ - $|\omega^\perp\rangle$ 平面に表示すると以下のようになります。
図 4 $|\phi_0\rangle$ の様子
先の式そのままですが、目標とする $\omega$ の確率振幅は $\frac{1}{\sqrt N}$、それ以外の状態の合計の確率振幅が $\sqrt{\frac{N-1}{N}}$ となっています。このときの$|\phi_0\rangle$の角度を $\theta$ と置きます。すると、以下の定理が成り立ちます。
定理 1
グローバー オペレーターを $n$ 回適用したあとの量子ビットの状態 $|\phi_n\rangle$ は以下の式で表される。
$$|\phi_n\rangle = \alpha_n|\omega\rangle + \beta_n|\omega^\perp\rangle$$
ただし
$$\alpha_n = \sin{((2n+1)\theta)}, \beta_n = \cos{((2n+1)\theta)}$$
である。
急に定理とか出してしまいましたが、これが成り立つことさえわかってしまえばグローバーの数理は終わったも同然です。証明にはなりますが、堅苦しくないように進めましょう。
まず、$|\phi_0\rangle$ のときに上記が成り立つか考えます。考えますとか言っていますが、これは$\theta$ の定義を記した 図 4 からも明らかですね。$|\phi_0\rangle = \frac{1}{\sqrt N}\sin \theta + \sqrt{\frac{N-1}{N}} \cos \theta$ となっていることが確認できます。
続いて、ある $k$ に対して上記の式が成り立つとしましょう。さて、$k+1$ 回目の反復時はどうなるでしょうか。
\begin{aligned}
|\phi_{k+1}\rangle
&= DU_\omega|\phi_k\rangle \\
&= DU_\omega
\begin{pmatrix}
\alpha_k \\
\beta_k
\end{pmatrix} \\
&= (2|\phi_0\rangle\langle\phi_0| - I )
\begin{pmatrix}
-\alpha_k \\
\beta_k
\end{pmatrix} \\
&=
\begin{pmatrix}
2\alpha_0^2 - 1 & 2\alpha_0\beta_0 \\
2\alpha_0\beta_0 & 2\beta_0^2 - 1
\end{pmatrix}
\begin{pmatrix}
-\alpha_k \\
\beta_k
\end{pmatrix} \\
&=
\begin{pmatrix}
\alpha_k(1- 2\alpha_0^2) + 2\beta_k\alpha_0\beta_0 \\
-2\alpha_k\alpha_0\beta_0 + \beta_k(2\beta_0^2 - 1)
\end{pmatrix} \\
&=
\begin{pmatrix}
\sin{((2k+1)\theta)}(1-2\sin^2{\theta}) + 2\cos{((2k+1)\theta)}\sin{\theta}\cos{\theta} \\
-2\sin{((2k+1)\theta)}\sin{\theta}\cos{\theta} + \cos{((2k+1)\theta)}(2\cos^2{\theta} - 1)
\end{pmatrix} \\
&=
\begin{pmatrix}
\sin{((2k+1)\theta)}\cos 2\theta + 2\cos{((2k+1)\theta)}\sin 2\theta \\
-\sin{((2k+1)\theta)}\sin{2\theta} + \cos{((2k+1)\theta)}\cos{2\theta}
\end{pmatrix} \\
&=
\begin{pmatrix}
\sin{((2k+3)\theta)}\\
\cos{((2k+3)\theta)}
\end{pmatrix} \\
&=
\begin{pmatrix}
\alpha_{k+1}\\
\beta_{k+1}
\end{pmatrix}
\end{aligned}
上記から、$|\phi_k\rangle$ で成り立つなら $|\phi_{k+1}\rangle$ でも成り立つことが確認できました。0 のときも成り立つことを確認済みなので、これはすべての $n$ に対して成り立つと言えそうです。上記では、三角関数の加法定理 (あとは加法定理から導ける倍角の公式) を利用しています。この補題から、今回取得したい状態 $|\omega\rangle$ の確率振幅は反復回数 $n$ を利用して $\sin{((2n+1)\theta)}$ と書けることがわかりました。要は、グローバー オペレーターを反復して適用すると、確率振幅は $\sin$ 波で振動するということがわかりました。ここからも、振動する最大値の近辺で止めればいい感じの結果が得られそうなことと、やりすぎても結局振動が続くのでうまくいかないことがわかりますね。$\sin$ 波は $\frac \pi 2$ で最大値を取るので、
$$
(2n+1)\theta = \frac \pi 2 \Leftrightarrow n = \frac{\pi}{4\theta} - \frac 1 2
$$
が実数になればそこで止めれば確率 1 で解が得られますし、そうでないなら付近で繰り返しをやめれば解が高確率で得られます。だいぶいい感じになってきましたが、まだ$\theta$ が邪魔ですね。これ自体は、最初の $\phi_0$ から定義された値で、$N$ に依存する値なのでした。$\sin\theta < \theta$ を使って変形してやると
$$
n = \frac{\pi}{4\theta} - \frac 1 2 < \frac{\pi}{4\theta} < \frac{\pi}{4\sin \theta} = \frac{\pi \sqrt N}{4}
$$
が導かれます。ここから、繰り返し回数$\frac{\pi}{4\theta}$ が $\omicron (\sqrt N)$ で抑えられることが確認できました。繰り返し回数 $\frac{\pi}{4\theta}$ はもちろん整数値である必要があるので、適当な小数 $c$ を用いて $\lfloor\frac{\pi}{4\theta}\rfloor := \frac{\pi}{4\theta} + c$ として確率振幅を計算すると、
$$
\sin{((2n+1)\theta)} = \sin\Big(\Big(2\Big(\frac{\pi}{4\theta} + c\Big) + 1\Big)\theta \Big) = \sin\Big(\frac{\pi}{2} + \theta - 2c\theta \Big) = \cos((1-2c)\theta)
$$
確率は
$$
\cos^2((1-2c)\theta) = 1- \sin^2((1-2c)\theta) > 1- \sin^2 \theta = 1 - \frac{1}{N}
$$
となります。ようやく結論となりますが、Grover のアルゴリズムでは、$\lfloor\frac{\pi}{4\theta}\rfloor$ 回グローバー オペレーターを反復することで、$1 - \frac{1}{N}$ 以上の確率で探したい回答が得られるということがわかります。長かったですが、やっと正しさが確かめられましたね。
さあ、Grover が提案した内容も正しそうだということが確かめられたので、あとは心置きなく実装を進めるだけです。Task の解説に戻りましょう。
Task 2.1. The Hadamard transform
問題
入力: 任意の状態にある N 量子ビット
ゴール: すべての量子ビットにアダマール変換を適用せよ。
解説
先に示した回路図にもあったとおり、グローバーのアルゴリズムでも全量子ビットのアダマール変換が利用されます。これはもう何度も繰り返しやったとおりですね。
operation HadamardTransform (register : Qubit[]) : Unit {
body (...) {
for(i in 0..Length(register)-1) {
H(register[i]);
}
}
adjoint invert;
}
Task 2.2. Conditional phase flip
問題
入力: 任意の状態にある N 量子ビット
ゴール: 入力として与えられた量子ビットが $|0\dots0〉$ なら状態はそのままに、それ以外なら位相を反転せよ。
解説
これも特に難しい問題ではないかと思います。位相の反転は先のタスクでもやったとおり、アンシラビットを用意して、$|-⟩$ の状態で作用させれば良さそうです。また、今回は $|0\dots0⟩$ のときだけ状態を変更しないので、すべての量子ビットを反転させたあとで Controlled X を行えば良さそうです。
問題にもある通り、これは $2|00\dots\rangle\langle00\dots00| -I$ の計算に相当します。書くまでもないかもしれませんが、
2|00\dots\rangle\langle00\dots00| -I =
2\begin{pmatrix}
1 \\ 0 \\ 0\\ \vdots \\ 0
\end{pmatrix}
\begin{pmatrix}
1 & 0 & 0 & \cdots & 0
\end{pmatrix}
- I =
\begin{pmatrix}
1 & 0 & 0 & \cdots & 0 \\
0 & -1 & 0 & \cdots & 0 \\
0 & 0 & -1 & \cdots & 0 \\
0 & 0 & 0 & \ddots & \vdots \\
0 & 0 & 0 & \cdots & -1
\end{pmatrix}
となるためです。回答は以下です。
operation MyPahseFlip(register : Qubit[]) : Unit {
body(...) {
using(q = Qubit[1]) {
X(q[0]);
H(q[0]);
for(i in 0..Length(register) -1) {
X(register[i]);
}
(Controlled X)(register, q[0]);
for(i in 0..Length(register) -1) {
X(register[i]);
}
Reset(q[0]);
}
}
adjoint self;
}
operation ConditionalPhaseFlip (register : Qubit[]) : Unit {
body (...) {
MyPahseFlip(register);
}
adjoint invert;
}
Task 2.3. The Grover iteration
問題
入力: N 量子ビット $|x\rangle$ (入力レジスタ) と位相を反転するオラクル
ゴール: Grover iteration を実装せよ。
解説
これまでに作成したオペレーションをつなぎ合わせれば終了です。
operation GroverIteration (register : Qubit[], oracle : (Qubit[] => Unit : Adjoint)) : Unit {
body (...) {
// オラクル自体は与えられる
oracle(register);
// アダマール変換
HadamardTransform(register);
// 位相の反転
ConditionalPhaseFlip(register);
// アダマール変換
HadamardTransform(register);
}
adjoint invert;
}
Task 3.1. Grover's search
問題
入力: 状態 $|00\dots00\rangle$ の N 量子ビット、オラクル、および反復回数
ゴール: グローバーのアルゴリズムで検索を行う。
解説
先のタスクで Grover operator は作成したので、あとは繰り返し呼び出すだけです。繰り返し回数も外部から与えられるため、本当に for 文を書くだけで終了です。
operation GroversSearch (register : Qubit[], oracle : ((Qubit[], Qubit) => Unit : Adjoint), iterations : Int) : Unit {
body(...) {
HadamardTransform(register);
for(i in 0..iterations - 1) {
GroverIteration(register, OracleConverter(oracle));
}
}
}
Task 3.2 Using Grover's search
問題
ゴール: 実装した Grover search とオラクルを使って、Grover のアルゴリズムの動作を確認せよ。
解説
この問題はテストを作成するタスクなので、回答しなくてもテストは通ります。
$\sin \theta = \frac{1}{\sqrt N}$ なので、$\theta = \sin^{-1}\frac{1}{\sqrt N}$ となります。また、$N = 2^6 =64$ です。
operation E2E_GroversSearch_Test () : Unit {
// 今回の目標状態
let pattern = [true, true, true, true, false, true];
// Task 1.3 で作成した任意パターンに対するオラクルを利用
let oracle = Oracle_ArbitraryPattern (_, _, pattern);
// 繰り返し回数計算
let theta = ArcSin(1.0 / Sqrt(64.0));
let num = Floor(PI() / (4.0 * theta));
using (qs = Qubit[6]) {
GroversSearch(qs, oracle, num);
}
}
上記実行後、各量子ビットが 1 となる確率は
0.99826574262186674
0.99826574262186674
0.99826574262186674
0.99826574262186674
0.00173425737813382
0.99826574262186674
となりました。上記をもとに、いろいろと遊べそうですね。
まとめ
この記事では、Grover algorithm と Q# での実装方法について学んできました。Shor のアルゴリズムと並んで著名な量子アルゴリズムですが、アイデアも性能評価も思ったよりシンプルだった (とはいえめっちゃ難しいですが) 気がします。この記事が Grover のアルゴリズムや Q# を学ぶ方の参考になれば幸いです。