前書き
本記事では、Quantum Katas の Solve SAT with Grover について解説します。Q# や Quantum Katas って何よという方は Quantum Katas で始める量子コンピュータ入門 |0⟩ をご参照ください。また、まだ Grover のアルゴリズムを解いていない方は QuantumKatas/GroversAlgorithm や Quantum Katas で始める量子コンピュータ入門 |10⟩: Grover's algorithm を参照してください。
今回は充足可能性問題 (Satisfiability problem; 以下 SAT) を Grover のアルゴリズムで解くという内容を学んでいきます。また、前回の Kata では探索対象の空間にただ一つ解が存在するという前提を置いていましたが、今回はその前提も取っ払い、解の個数が未知である場合に Grover のアルゴリズムを適用する方法についても学んでいきます。
SAT とは
SAT とは一つの命題論理式が与えられたとき、それに含まれる変数の値を偽 (False) あるいは真 (True) にうまく定めることによって全体の値を'真'にできるか、という問題のことを言います。
例題
$(x_1 \lor x_2) \land (\bar x_1 \lor x_2) \land (\bar x_1 \lor \bar x_2)$
例えば上記なら、$x_1 = \text{False}, x_2 = \text{True}$ とすると全体を $\text{True}$ にできることがわかります。問題自体はただの論理演算なので、理解するのは難しくないですね。古典コンピューターでも、上記の SAT を解く SAT ソルバーというソフトウェアが数多く存在します。
なんの役に立つんだろう??と思った方は、SAT や SAT ソルバーでググってみてください。(一見ときにくいものを含めた) 様々な問題が、上記の SAT 形式に変換でき、SAT ソルバーで解を求めることでもとの問題を解く、ということが行われてきました。例えば以下の資料にまとまっています。
SAT と Grover ?
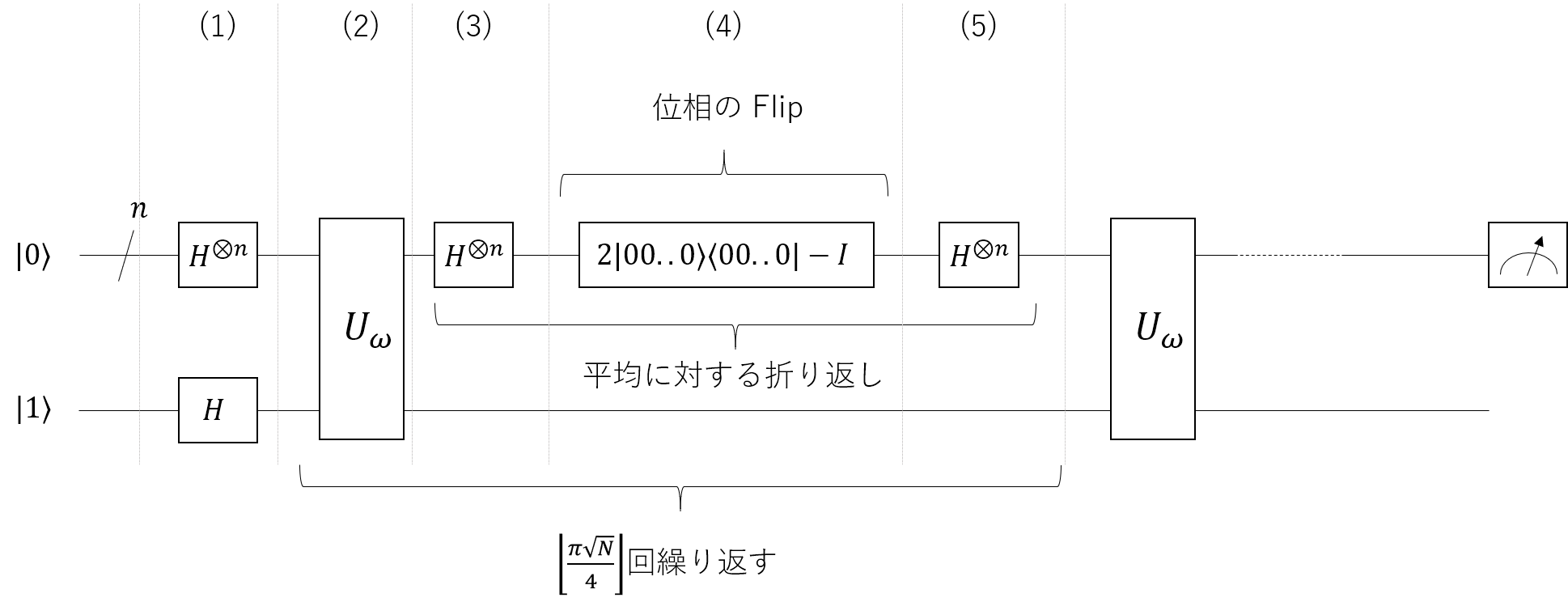
突然 SAT という問題が出てきましたが、さてこれが Grover のアルゴリズムとどう関係するのでしょうか。ちょっと Grover の復習になりますが、Grover 探索問題とアルゴリズムを実装した量子回路は以下のようなものでした。
グローバーの探索問題
関数 $f: \{0, 1\}^n \rightarrow \{0, 1\}$ が与えられたとする。$f(\omega) = 1$ を満たす解 $\omega \in \{0, 1\}^n$ がただ一つ存在する場合に、解 $\omega$ を求めよ。
ただし、関数 $f$ はオラクル $U_\omega$ を用いて以下の形式で与えらえる。
$$U_\omega|x⟩|y⟩ = |x⟩|y \oplus f(x)⟩$$
上記からも思い出せるように、Grover のアルゴリズムは $f(\omega) = 1$ を満たす解を求めることができるのでした。なので、オラクル $U_\omega$ を解きたい SAT に従って量子回路で実装できれば、Grover のアルゴリズムで SAT が解けるのです。Grover のアルゴリズムは $\omega$ 自体が求められるので、与えられた論理多項式が解を持つかどうかだけでなく、存在する場合は解自体を求めることができます。
さて、ここで本論に入る前に、ちょっと Grover の問題を緩和しておきましょう。2 段階で行きます。
- 解が複数ある場合
- 解の個数が未知の場合
緩和1 解の個数が 1 つじゃなかったら?
Grover の探索問題は、元々解がただ一つ存在することを仮定していました。SAT が解けるとか言っているくせにそんな制限あったら現実的じゃないですよね。解が $t$ 個あったらどうなるのでしょうか。
実は、解の個数が増えた場合も Grover のアルゴリズムには大した影響がありません。解が一つの場合の数理は 第 |10⟩ 段 で紹介していますが、Grover のアルゴリズムでは目標状態 $|\omega⟩$ と $|\omega^\perp\rangle$ に分離することができ、
$$
|\phi_0\rangle=\frac{1}{\sqrt N}\sum_{x \in {0, 1}^n} |x\rangle
= \frac{1}{\sqrt N}\Big(|\omega\rangle + \sum_{x \ne \omega} |x\rangle \Big)
= \frac{1}{\sqrt N}|\omega\rangle + \sqrt{\frac{N-1}{N}}|\omega^\perp\rangle
$$
と書くことができたのでした。解の個数が $t$ 個と決まっている場合は全く同様に考えれば、
$$
|\phi_0\rangle=\frac{1}{\sqrt N}\sum_{x \in {0, 1}^n} |x\rangle
= \frac{1}{\sqrt N}\Big(\sum_{x = \omega}|x\rangle + \sum_{x \ne \omega} |x\rangle \Big)
= \sqrt{\frac{t}{N}}|\omega\rangle + \sqrt{\frac{N-t}{N}}|\omega^\perp\rangle
$$
と書くことができます。式の形は全く一緒で、$|\phi_0\rangle$ を $|\omega\rangle$ - $|\omega^\perp\rangle$ 平面に表示した際の角度 $\theta$ だけが異なる状況となります。今回の角度を $\theta_t$ とすると、
$$
\begin{aligned}
&\sin \theta_t = \sqrt{\frac{t}{N}}\
&\cos \theta_t = \sqrt{\frac{N-t}{N}}
\end{aligned}
$$
です。あとの証明は解が一つのときと全く同じになります。結論として、解が $t$ 個あるようなオラクル $U_\omega$ を用いて Grover のアルゴリズムを実行した場合、$\lfloor\frac{\pi}{4\theta_t}\rfloor$ 回グローバー オペレーターを反復することで、$\sin^2{((2n+1)\theta_t)}$の確率で解が得られること、およびこの確率は$1 - \frac{t}{N}$ 以上となることがわかります。解の個数 $t$ に依存する $\theta_t$ が繰り返し回数に含まれているという点に注意してください。要は、いい感じの繰り返し回数を知るには解の個数が必要だ、ということになります。
余談ですが、個人的には最低確率が $t$ で制限されてしまうという点がちょっと気持ち悪いなと思いますが、皆さんはどうでしょうか。解が多すぎる場合は、下限が悪くなってしまうことになります。まあこれは $N$ が大きくなるほど誤差の下限がよくなるという点の裏返しなのでしょうがないのかなとも思いますし、解がたくさんあるような自明な問題は実行しないと思えば、対した問題ではないかもしれませんが。。。
緩和2 解の個数が未知だったら?
Grover のアルゴリズムは解が複数 1 つだけではなく、$t$ 個ある場合も有効であることが確認できました。では続いて、解の個数がわからない場合はどうでしょうか?SAT に置き換えて考えるのであれば、ある論理多項式を満たす解の個数がわかっているということも現実的ではない制約となります。次はこれを緩和しましょう。
この場合はいい感じの反復回数を知るすべがなくなるため、グローバー オペレーターの反復回数を増やしながらアルゴリズムを実行していくことで解を探索する必要があります。一番愚直に考えれば、繰り返し回数を 1 から 1 つずつ増やしていけば、いつかはいい感じの繰り返し回数となって解にたどり着くことが期待できます。しかしながらこの方法を使うと質問計算量が探索空間の増加に従って増えてしまい($U_\omega$ の使用回数は $\sum_{k=1}^{n} k = n(n+1)/2$ となってしまいます)、これもまた現実的ではありません。
そこで以下のように、$2^x$ 回の繰り返しのみ探索する方法が考案されました。
- 繰り返し回数 $n = 1$ とする
- 繰り返し回数 $n$ 回のグローバーのアルゴリズムを実行する
- 解が得られればアルゴリズムを終了する、解が得られなければ $n = 2n$ として 2. に戻る
これだけです。かなり探索をサボることになりますし、効率が落ちてしまいそうな気がします。そもそも最適な繰り返し回数に近づく気もしませんし、本当に正しい解が得られるのか不安ですよね。。。どれくらいのパフォーマンスが得られるか確かめてみましょう。
まず、繰り返し回数 $2^\tau$ を何度か試行を重ねて、最適な繰り返し回数 $\lfloor\frac{\pi}{4\theta_t}\rfloor$ に近い値を取り、以下の不等式を満たすことを考えます。
$$
2^\tau \le \frac{\pi}{4\theta_t}
$$
ただし、$n$ は上記を満たす最大の整数値であると仮定します。(最大でないとすれば、まだ次の施行で確率を上げられることになってしまいますからね。)このとき、左辺の値を 2 で割った値は繰り返し回数以下になるので、
$$
\frac{\pi}{8\theta_t} \le 2^\tau \le \frac{\pi}{4\theta_t}
$$
が成り立つ事もわかります。上記を少し変形すると、
$$
\frac{\pi}{4} \le 2^{\tau+1}\theta_t \le \frac{\pi}{2}
$$
となります。一方、求めたい解 $|\omega⟩$ が得られる確率振幅は
$$
\sin{((2n+1)\theta_t)} = \sin{((2\cdot 2^{\tau})\theta_t)} = \sin{(2^{\tau+1}\theta_t + \theta_t)}
$$
です。sin は $\frac{\pi}{2}$ で最大値をとるので、$\theta_t$ が十分に小さいとすると、先の不等式を使うことで少なくとも確率振幅は
$$
\sin{(2^{\tau+1}\theta_t + \theta_t)} \ge \sin{\Big(\frac{\pi}{4} + \theta_t\Big)} = \frac{1}{\sqrt 2}(\sin \theta_t + \cos \theta_t)
$$
となることがわかります。なので確率は
$$
\Big(\frac{1}{\sqrt 2}(\sin \theta_t + \cos \theta_t) \Big)^2 = \frac{1}{2}(1 + 2\sin \theta_t \cos \theta_t) = \frac{1}{2}\left(1 + 2 \sqrt{\frac{t}{N}}\sqrt{\frac{N-t}{N}}\right) = \frac{1}{2}\left(1 + 2 \frac{\sqrt{(N-t)t}}{N}\right)
$$
となることがわかりました。第二項目は定数項なので少なくとも $\frac{1}{2}$ 以上の確率で正しい解を得られる、ということがわかりました。
続いて上記の質問計算量を確かめてみましょう。数列を計算すれば
$$
\sum_{k=0}^{\tau} 2^k = 2^{\tau+1} -1 \le \frac{\pi}{2\theta_t} -1 \le \frac{\pi}{2\sin\theta_t} -1 = \frac{\pi}{2}\sqrt{\frac N t} -1
$$
となることがわかります。愚直に全部の繰り返し回数を計算するときは $\omicron (N^2)$ でしたが、この方法だと $\omicron (\sqrt N)$ で抑えられている事もわかります。
さて、長々と書いてきましたが、要は解の個数が不明なオラクルに対して Grover で探索を行う場合、探索の繰り返し回数を $2^k$ で繰り返して行けば最低でも確率 0.5 で正しい解が探索でき、その時の計算量は $\omicron (\sqrt N)$ で抑えられるということがわかりました。正解の確率は以外と低いなと思うかもしれませんが、まあそんなもんだということで、、、
かなり前置きが長くなりましたが、それでは Task の解説に入ります。
各 Task の解説
Task 1.1. The AND oracle: f(x) = x₀ ∧ x₁
問題
入力: $n$ 個の量子ビット $|x⟩$ と 1 量子ビット $|y⟩$
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$に変換せよ。ただし、$f(x) = \bigwedge_{i=0}^{n-1} x_i$ である。
解説
まずは任意の SAT をオラクルとして実装する練習として、AND を実装していきます。まあこれは簡単ですね。Controlled ファンクタを使って処理すればそれだけで終了です。
operation Oracle_And (queryRegister : Qubit[], target : Qubit) : Unit {
body (...) {
Controlled X(queryRegister, target);
}
adjoint auto;
}
Task 1.2. The OR oracle: f(x) = x₀ ∨ x₁
問題
入力: $n$個の量子ビット $|x⟩$ と 1 量子ビット $|y⟩$
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$に変換せよ。ただし、$f(x) = \bigvee_{i=0}^{n-1} x_i$ である。
解説
さっきは AND でしたが、今度は OR です。こちらもさっきと同様に楽勝と言いたい所ですが、単純に Controlled ファンクタだけ適用すれば OK だった先ほどの問題よりは工夫が必要となります。Contorlled ファンクタでは全部同じ (要は AND) の状態で処理を分岐させることしかできないので、OR も AND に変化して処理すれば良さそうです。ド・モルガンの法則から、
$$
\bigvee_{i=0}^{n-1} x_i = \overline{\bigwedge_{i=0}^{n-1} \overline x_i}
$$
であるので、全部をひっくり返して AND を計算した結果をさらにひっくり返せば良さそうです。回答は以下となります。
operation Oracle_Or (queryRegister : Qubit[], target : Qubit) : Unit {
body (...) {
ApplyToEachA(X, queryRegister);
(Controlled X)(queryRegister, target);
ApplyToEachA(X, queryRegister);
X(target);
}
adjoint auto;
}
Task 1.3. The XOR oracle: f(x) = x₀ ⊕ x₁
問題
入力: $n$個の量子ビット $|x⟩$ と 1 量子ビット $|y⟩$
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$に変換せよ。ただし、$f(x) = \sum_{i=0}^{n-1} x_i$ である。
解説
XOR といえば飽きるほどやってきた CNOT ですね。この問題のほうが簡単です。
operation Oracle_Xor (queryRegister : Qubit[], target : Qubit) : Unit {
body (...) {
for(i in 0..Length(queryRegister)-1) {
CNOT(queryRegister[i], target);
}
}
adjoint auto;
}
Task 1.4. Alternating bits oracle: f(x) = (x₀ ⊕ x₁) ∧ (x₁ ⊕ x₂) ∧ ... ∧ (xₙ₋₂ ⊕ xₙ₋₁)
問題
入力: $n$個の量子ビット $|x⟩$ と 1 量子ビット $|y⟩$
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$に変換せよ。ただし、$f(x) = (x_0 \oplus x_1) \land (x_1 \oplus x_2) \land \cdots \land (x_{n-2} \oplus x_{n-1})$ である。
解説
ヒントにもありますが、このオラクル $f(x)$ が 1 となるのは $(x_{i-1} \oplus x_{i})$ が全て 1 となるときなので、$1010\dots$ か、$0101\dots$ のどちらかに限られます。ので、偶数ビットだけ使って Controlled ファンクタを使うとかすれば解けるのですが、これまたヒントにあるとおりオラクルを作る練習なので真面目にやりましょう。
XOR は CNOT で実現できるので、各結果をアンシラビットに突っ込んで、最後に AND を撮ってやれば終了です。
operation Oracle_AlternatingBits (queryRegister : Qubit[], target : Qubit) : Unit {
body (...) {
let N = Length(queryRegister);
using(qs = Qubit[N-1]) {
for(i in 0..N-2) {
// x_{i} \oplus x_{i+1} を qs[i] に保存
CNOT(queryRegister[i], qs[i]);
CNOT(queryRegister[i+1], qs[i]);
}
// qs[] の AND を計算
(Controlled X)(qs, target);
// 以下はアンシラビットを開放前に 0 に戻すために実施
for(i in 0..N-2) {
CNOT(queryRegister[i], qs[i]);
CNOT(queryRegister[i+1], qs[i]);
}
}
}
adjoint auto;
}
Task 1.5. 2-SAT problem oracle
問題
入力: $n$個の量子ビット $|x⟩$ と 1 量子ビット $|y⟩$、および SAT を記述するタプル (Int, Bool) の 2 次元配列。
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$に変換せよ。ただし、$f(x) = \bigwedge_{i}{(a_{k} \lor a_{j})}$ であり、$a_*$ は $x_i$ または $\overline x_i$ を示す。
また、タプルの Int 要素は $x$ の要素のインデックスを、Bool は否定を取るか否かを示す。例えば[[(0, true), (1, true)], [(0, false), (1, false)]]は $f(x) = (x_0 \lor x_1) \land (\overline x_0 \lor \overline x_1)$ となる。
解説
ようやくタイトルにもある SAT という単語が登場しました。まずは 2-SAT という、一つの OR の項数が高々 2 であるような問題のオラクルを作成していきます。2 次元配列で受け取った Problem を分解して処理する所にだけ気をつければ、あとは既に作った OR や AND と同じようなものなので、そこまで難しくはありません。
もうちょっとスッキリかける気もしますが、回答は以下となります。
operation Oracle_2SAT (queryRegister : Qubit[],
target : Qubit,
problem : (Int, Bool)[][]) : Unit {
body (...) {
using(anc = Qubit[Length(problem)]) {
for(i in 0..Length(problem) - 1){
// 定義に従って位置と論理をタプルを分解して保存する
let (n1, isPositive1) = (problem[i][0]);
let (n2, isPositive2) = (problem[i][1]);
// 負論理の場合は反転
if(not isPositive1) {
X(queryRegister[n1]);
}
if(not isPositive2) {
X(queryRegister[n2]);
}
// Task の実装を使って OR を実行
Oracle_Or([queryRegister[n1],queryRegister[n2]], anc[i]);
// 負論理の場合はもとに戻す
if(not isPositive1) {
X(queryRegister[n1]);
}
if(not isPositive2) {
X(queryRegister[n2]);
}
}
// AND の計算
Controlled X(anc, target);
// 同じ処理を再実行してアンシラを 0 に戻す
for(i in 0..Length(problem) - 1){
let (n1, isPositive1) = (problem[i][0]);
let (n2, isPositive2) = (problem[i][1]);
if(not isPositive1) {
X(queryRegister[n1]);
}
if(not isPositive2) {
X(queryRegister[n2]);
}
Oracle_Or([queryRegister[n1],queryRegister[n2]], anc[i]);
if(not isPositive1) {
X(queryRegister[n1]);
}
if(not isPositive2) {
X(queryRegister[n2]);
}
}
}
}
adjoint auto;
}
Task 1.6. k-SAT problem oracle
問題
入力: $n$個の量子ビット $|x⟩$ と 1 量子ビット $|y⟩$、および SAT を記述するタプル (Int, Bool) の 2 次元配列。
ゴール: $|x, y⟩$ を $|x, y \oplus f(x)⟩$に変換せよ。ただし、$f(x) = \bigwedge_{i}\big(\bigvee_k a_{j}\big)$ であり、$a_*$ は $x_i$ または $\overline x_i$ を示す。
また、タプルの Int 要素は $x$ の要素のインデックスを、Bool は否定を取るか否かを示す。例えば[[(0, true), (1, true), (2, true)], [(0, false), (3, true), (4, true)]]は $f(x) = (x_0 \lor x_1 \lor x_2) \land (\overline x_0 \lor x_3 \lor x_4)$ となる。
解説
さっきの問題の一般化です。が、結構実装はめんどくさいなと思いました。面倒なポイントは、OR の計算です。OR の計算は AND の否定で行っていたのですが、与えられる個数がわからないと、Controlled ファンクタにまとめて突っ込むことができません。そのため、一旦配列に対象の量子ビットのインデックスをまとめて突っ込んでおいて、そのインデックスだけを抽出した配列を作ってから OR で処理する、ということが必要となります。解答は以下です。
operation OrOperation(queryRegister: Qubit[],
problem: (Int, Bool)[][],
anc: Qubit[]) : Unit {
body(...) {
// AND 節に対するループ
for(i in 0..Length(problem) - 1){
mutable elements = new Int[Length(problem[i])];
// OR 節に対するループ
for(j in 0..Length(problem[i]) - 1) {
let (n, isPositive) = (problem[i][j]);
// 負論理 なら反転
if(not isPositive) {
X(queryRegister[n]);
}
// 対象抽出用のインデックス
set elements[j] = n;
}
// 計算対象の配列
let sub = Subarray(elements, queryRegister);
// 先の Task で作成した OR を利用
Oracle_Or(sub, anc[i]);
// 負論理の反転をもとに戻す
for(j in 0..Length(problem[i]) - 1) {
let (n, isPositive) = (problem[i][j]);
if(not isPositive) {
X(queryRegister[n]);
}
}
}
}
adjoint self;
}
// 用意されていたオペレーション
operation Oracle_SAT (queryRegister : Qubit[],
target : Qubit,
problem : (Int, Bool)[][]) : Unit {
body (...) {
using(anc = Qubit[Length(problem)]) {
// OR の計算
OrOperation(queryRegister, problem, anc);
// AND の計算
Controlled X(anc, target);
// 再度 OR の処理を行ってアンシラビットをもとに戻す
OrOperation(queryRegister, problem, anc);
}
}
adjoint auto;
}
Task 2.2
問題
入力: 量子ビット数 $N$ 解答をマークするオラクル。
出力: オラクルが 1 となるような出力を得ることができる
Bool配列を求めよ。
解説
今回の Kata の最後の問題です。SAT で記述されるオラクルが与えられたときに、解を満たす Bool 配列を出力せよという問題で、要は SAT を解けという問題となります。原理は既にこの記事の冒頭で述べたように、$2^n$ 回の繰り返しを試行すれば、最低でも確率 $1/2$ で解が得られるという内容となります。
これまでの Kata ではループといえば for (i in 0..n) ばかりでしたが、今回は公比 2 の等比数列に対するループなので、まったく同様には書けません。(いや、もちろん事前に配列用意すればいいんでしょうけど。。。)repeat-until-success-loop を使ってみました。また、肝心のグローバーの検索自体は Grover's algorithm の Kata の回答をそのまま持ってきていますが以下では省略しています。
operation GroversAlgorithm (N : Int, oracle : ((Qubit[], Qubit) => Unit : Adjoint)) : Bool[] {
body(...) {
//答えを格納する配列
mutable ans = new Bool[N];
// 結果を格納する配列
mutable result = new Result[N];
//グローバーオペレーターの繰り返し回数
mutable num = 1;
let num_max = Floor(PI() * Sqrt(ToDouble(N)) / 4.0);
//解の探索の繰り返し回数
mutable i = 0;
let i_max = 10;
using( qs = Qubit[N+1] ) {
let register = qs[0..N-1];
let anc = qs[N];
repeat {
repeat {
Reset(anc);
// 検索の実行 (Grover's algorithm の Kata で作成したオペレーションをそのまま利用しています)
GroversSearch(register, oracle, num);
// 検索結果を観測
set result = MultiM(register);
// オラクルを使って現在の検索結果が回答となるかをチェック
oracle(register, anc);
} until (M(anc) == One || num > num_max) // 回答が見つかるか最大回数を超えたらループ停止
fixup {
set num = num *2;
}
} until (i > i_max || M(anc) == One)
fixup {
set i = i + 1;
}
set ans = BoolArrFromResultArr(result);
ResetAll(qs);
}
return ans;
}
}
まとめ
現実的な質問計算量に抑えつつ効率的に解を探索できる Grover のアルゴリズムを使うと、SAT のような具体的に意味のある問題も効率的に解決できるということを学ぶ Kata でした。個人的にはとっても楽しい Kata だなと思いましたが、いかがでしょうか。Grover’s algorithm の Kata では、明らかに答えがわかっているオラクルの探索を行うような意味が見えにくい問題を解いていましたが、今回のように具体的な意味のある SAT を解くという問題を行うことで、さらに量子コンピューターや Grover アルゴリズムの意味・意義が理解できたように感じます。次の Kata も楽しみです。