グローバーのアルゴリズムの一般化 Quantum Amplitude Amplification の論文解説

Quantum Amplitude Amplificationはグローバーのアルゴリズムを一般化した量子アルゴリズムで、他の量子アルゴリズムのサブルーチンとして用いられることも多い。そこでQuantum Amplitude Amplification を提案した論文 Quantum Amplitude Amplification and Estimationの解説を行う。必要な事柄は本記事内に記したつもりであるが、詳細が気になる人は原論文へ。

$$
\def\bra#1{\mathinner{\left \langle{#1}\right|}}
\def\ket#1{\mathinner{\left|{#1}\right\rangle}}
\def\braket#1#2{\mathinner{\left\langle{#1}\middle|#2\right\rangle}}
$$

目次

• Quantum Amplitude Amplificationのざっくりとしたイメージ(量子コンピュータを知らない人も理解できるように書いた。)
• 論文解説
  • Lemma1の証明
  • グローバーのアルゴリズム
  • Theorem3の確認(量子コンピュータの知識は必要ない。)

Quantum Amplitude Amplificationのざっくりとしたイメージ

1万分の1の確率で当たりが出るガチャをするとき、普通は(古典的には)、当たりを引くまでに、およそ数万回ガチャを回す必要がある¹。このガチャにQuantum Amplitude Amplification(以下、量子振幅増幅と言ったり、単に振幅増幅と言ったりする。)を行うと、数百回ガチャを回すだけで当たりが出る！

当たりが出る確率を$a$としよう。ガチャという操作$\mathcal{A}$を行うと状態は次のようになる。
$$
\mathcal{A}\ket{0} = \sqrt{a}\ket{当たり}+\sqrt{1-a}\ket{はずれ}
$$
ここで係数の絶対値の2乗が、当たり・外れが出る確率を表す。²
ここで$\mathcal{Q}\equiv -\mathcal{A}S_0\mathcal{A}^{-1}S_\chi$で定義される操作（つまりガチャを2回する）を状態$\mathcal{A}\ket{0} \equiv \ket{\Psi}$に $j$ 回施すと
$$
Q^{j}\ket{\Psi}=\sin{(2j+1)\theta_a}\ket{当たり} + \cos{(2j+1)\theta_a}\ket{はずれ}
$$
となり、当たりを得られる確率は$\sin^{2}{((2j+1)\theta_a)}$となる。ここで$\sin^{2}{\theta_a}=a$である。$a\approx 0$とすれば$\theta_a \approx \sqrt{a}$であり、当たりが出る確率を大きくしたければ、サインの中身が$\pi/2$に近ければよい。従って$(2j+1)\theta_a \approx (2j+1)\sqrt{a} \approx \pi/2$つまり$j \approx \frac{\pi}{4\sqrt{a}}$となるような回数だけ$\mathcal{Q}$をおこなえばよい。確率$a$のガチャから当たりを引くのに、$\mathcal{O}(1/\sqrt{a})$回の試行で済む。つまり$\mathcal{O}(\sqrt{N})$の試行回数で確率$1/N$のガチャの当たりを引くことができる。

グローバーのアルゴリズムは$a$の値が既知のときのさらに特殊な状況下のアルゴリズムである。$a$の値が分からなくても振幅増幅でQuadratic($\mathcal{O}(N) \to \mathcal{O}(\sqrt{N})$)なスピードアップが可能である。

論文解説

Lemma1の確認

Lemma1
$\mathcal{Q}\ket{\Psi_1} =(1-2a)\ket{\Psi_1} - 2a\ket{\Psi_0}$
$\mathcal{Q}\ket{\Psi_0} =2(1-a)\ket{\Psi_1} + (1-2a)\ket{\Psi_0}$

論文中でLemma1の証明が与えられていないが、決して自明なことではないように思える。(私は目で追うだけでは計算できなかった。）制御ゲートの計算でも似たようなテクニックを使うので、ここでLemma1の計算の確認をする。

任意のユニタリ変換$\mathcal{A}$をzero stateに行って得られる状態$\mathcal{A}\ket{0}$は
$$
\ket{\Psi}= \ket{\Psi_1} + \ket{\Psi_0}
$$
となる。ここで$\ket{\Psi_1}$はgood state、$\ket{\Psi_0}$はbad stateである。（前項でいうところの当たり・外れ）また、$a>0, \braket{\Psi_1}{\Psi_1}=a, \braket{\Psi_0}{\Psi_0}=1-a$である。good stateとbad stateは直交している。
$S_0$はzero stateにのみ、$S_\chi$は$\ket{\Psi_1}$にのみ作用し(それ以外の状態にはIdentity Operatorとして働く)振幅の符号を反転させる。
$\mathcal{Q} \equiv -\mathcal{A}S_0\mathcal{A}^{-1}S_\chi$と定義する。

次の計算で

\begin{align}
\mathcal{A}^{-1}\mathcal{A}\ket{0} &= \ket{0}\\
\mathcal{A}^{-1}\ket{\Psi} &= \ket{0}\\
\mathcal{A}^{-1}(\ket{\Psi_1} + \ket{\Psi_0}) &= \ket{0}\\
\mathcal{A}^{-1}\ket{\Psi_1} &= \ket{0} - \mathcal{A}^{-1}\ket{\Psi_0}\\
\end{align}

を得る。$S_0, S_\chi$は次のように表せる。

\begin{align}
S_0 &= I - 2\ket{0} \bra{0} \\
S_\chi &= I - \frac{2}{a}\ket{\Psi_1}\bra{\Psi_1}
\end{align}

これらを用い、Lemma1の第1式は

\begin{align}
\mathcal{Q}\ket{\Psi_1} &= -\mathcal{A}S_0\mathcal{A}^{-1}(I - \frac{2}{a}\ket{\Psi_1}\bra{\Psi_1})\ket{\Psi_1} \\
&= \mathcal{A}S_0\mathcal{A}^{-1}\ket{\Psi_1} \\
&= \mathcal{A}S_0(\ket{0} - \mathcal{A}^{-1}\ket{\Psi_0}) \\
&= \mathcal{A}(I - 2\ket{0} \bra{0})(\ket{0} - \mathcal{A}^{-1}\ket{\Psi_0}) \\
&= -\mathcal{A}\ket{0}-\ket{\Psi_0} + 2\mathcal{A}\ket{0}\bra{0}\mathcal{A}^{-1}\ket{\Psi_0} \\
\end{align} 

さらに$(\mathcal{A}\ket{0})^{\dagger}=\bra{0}\mathcal{A}^{-1}$だから、$\mathcal{A}\ket{0}\bra{0}\mathcal{A}^{-1}=\ket{\Psi}\bra{\Psi}$
である。従って

\begin{align}
\mathcal{Q}\ket{\Psi_1} &= -\ket{\Psi}-\ket{\Psi_0}+2(1-a)\ket{\Psi}\\
&=(1-2a)\ket{\Psi_1} - 2a\ket{\Psi_0}
\end{align} 

となり、Lemma1 第1式が成り立つことが確認できた。
第2式も第1式の導出過程をなぞれば成り立つことが確認できる。論文(3)~(7)式は三角関数の公式を用いて慎重に計算すれば追うことができ、この論文の重要な式(8)の導出も確認できる。³

グローバーのアルゴリズム

(書きかけ)⁴
グローバーのアルゴリズムはショアのアルゴリズムと並んで有名な量子アルゴリズムであるが、振幅増幅の視点から眺めると、探索アルゴリズムという言葉はあまり適切でないのかもしれない。

グローバーのアルゴリズムの流れは以下のようであった。詳細は@kyamazさんの記事等を参照のこと。@kyamazさんの記事
1. 重ね合わせ状態を作る
2. マーキング
3.　平均値周りの反転（拡散変換ともいう）
4. 2.3.を適当に繰り返す

n量子ビットの重ね合わせ状態は各量子ビットにアダマール変換を施せばよい。ここで$N \equiv 2^n$である。

$$
H^{\otimes n}\ket{0} = \frac{1}{\sqrt{N}} \Sigma_{k=0}^{N-1} \ket{k}
$$

マーキングする状態を$\ket{m}$とすれば
$$
H^{\otimes n}\ket{0} = \frac{1}{\sqrt{N}}\ket{m} + \frac{1}{\sqrt{N}} \Sigma_{k\neq m} \ket{k} \equiv \ket{good} + \ket{bad}

$$
ここで$\braket{good}{good}=\frac{1}{N}, \braket{bad}{bad}=\frac{N-1}{N}, \braket{bad}{good}=0$である。
$\mathcal{A}$として任意のユニタリ変換を取ってくることができるため、$H^{\otimes n}\equiv \mathcal{H}$をユニタリ変換$\mathcal{A}$として用いる。

ここで
$$
S_\chi = I - 2\ket{m}\bra{m} = I - 2\ket{good}\bra{good}
$$
は確かにマーキングを表している。
$\mathcal{Q} \equiv -\mathcal{A}S_0\mathcal{A}^{-1}S_\chi$であったので、$-\mathcal{A}S_0\mathcal{A}^{-1}$の計算をしよう。

$$
\begin{align}
-\mathcal{H}S_0\mathcal{H}^{-1} &= \mathcal{H}(2\ket{0}\bra{0} - I)\mathcal{H}^{-1} \
&=2\mathcal{H}\ket{0}\bra{0}\mathcal{H}^{-1} - I
&=2\ket{\psi}\bra{\psi}-I
\end{align}
$$
ここで$\ket{\psi}=H^{\otimes n}\ket{0} = \frac{1}{\sqrt{N}} \Sigma_{k=0}^{N-1} \ket{k}$
これは@kyamazさんの記事のオペレーター$D$にほかならない。

このようにしてグローバーのアルゴリズムは振幅増幅の一種とみなすことができる。

Theorem3の確認

ざっくりとしたイメージのところで書いたように、当たりが出る確率$a$がわかっていれば、適切な$\mathcal{Q}$の回数がわかり、Quadraticなスピードアップがはかれる。驚くことに、$a$の値が未知のときでさえ次のステップ(QSearch)を踏むことで、good stateを$\mathcal{O}(1/\sqrt{a})$回のみの$\mathcal{A}, \mathcal{A}^{-1}$の使用で得ることができる。
ここでは乱数シミュレーションで実際に確認してみる。証明は原論文参照。

前提

以下の事項を認めてしまえば量子コンピュータの知識がなくても、この先でやっていることは理解できる。

1. まず$\mathcal{A}$を一度使う
2. $\mathcal{Q}$をj回施すと確率$\sin^{2}{((2j+1)\theta_a)}$でgood stateを得る
3. $\sin^{2}{\theta_a}=a$
4. $\mathcal{Q}$一回につき$\mathcal{A},\mathcal{A}^{-1}$をそれぞれ一回ずつ使う

Qsearch

疑似コード

1 　$c$ = 1.5 //1<c<2の定数
2 　$l$ = 0
3 　while True:
4　　　　　Mを$c^{l}$以上の最小の整数にする
5　　　　　$\mathcal{A}$を一回使う ($\mathcal{A}\ket{0}$を作る)
6　　　　　ガチャを引く(当たる確率$a$) ($\mathcal{A}$の測定)
7　　　　　if 当たり: break
8　　　　　$\mathcal{A}$をもう一回使う ($\mathcal{A}\ket{0}$を作る)
9　　　　　jを1~Mの整数からランダムに選ぶ
10　　　　　$\mathcal{Q}$をj回使う ($\mathcal{Q}^{j}\ket{\Psi}$)
11　　　　　ガチャを引く(当たる確率$\sin^{2}{((2j+1)\theta_a)}$) ($\mathcal{Q}^{j}\ket{\Psi}$の測定)
12　　　　　if 当たり: break
13　　　　　$l$++

Qsearchを実際に乱数シミュレーションすると次のようになる。全体のコードはここから github

import numpy as np
import math
import matplotlib.pyplot as plt

def one_step(M,a,theta):
    if np.random.rand()<a:
        return True,1
    j = np.random.randint(1,M+1) 
    prob = (np.sin((2*j+1)*theta))**2
    if np.random.rand()<prob:
        return True, 2+2*j
    return False,2+2*j

疑似コード5行から12行目までを関数one_stepで実装する。当たり外れをTrue/Falseで返し、同時にone_stepに要した$\mathcal{A},\mathcal{A}^{-1}$の使用回数を返す。

def trial(a,theta):
    c = 1.5
    total_num = 0
    for i in range(1000):
        M = math.ceil(c**i)
        f,num = one_step(M,a,theta)
        total_num += num
        if f:
            return total_num,True
    return total_num,False

疑似コード全体はtrialで実装する。当たりがいっこうに出ず∞ループになることを防ぐためfor文で1000回までの繰り返しとした。当たりが出るまでに要した$\mathcal{A},\mathcal{A}^{-1}$の使用回数がtota_numに記録される。当たりが出ずに1000回のone stepが終了した場合にはFalseを返す。

a_list = [0.1**(i+1) for i in range(10)]
a_list = np.array(a_list)
query_classic = 1/a_list
query_quantum = np.empty(0)
for a in a_list:
    sum_query = 0
    theta = np.arcsin(np.sqrt(a))
    for i in range(1000):
        num,f = trial(a,theta)
        sum_query += num
        if f is False:
            print('Fail')
    ave = sum_query/1000
    print(f'a:{a} query:{ave}')
    query_quantum = np.append(query_quantum,ave)
plt.plot(np.log10(query_classic),np.log10(query_quantum))

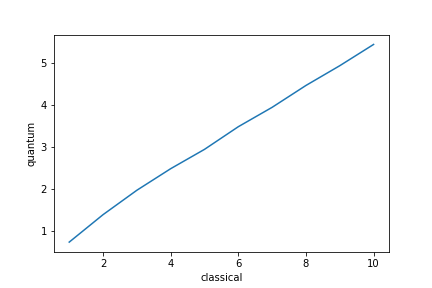
$a = 10^{-1},10^{-2},,,10^{-10}$についてそれぞれtrialを行い$\mathcal{A},\mathcal{A}^{-1}$の使用回数を記録する。統計値を取るためそれぞれの$a$で1000回trialを行った。使用回数の平均がquery quantumである。

実行結果

a:0.1 query:5.417
a:0.010000000000000002 query:24.43
a:0.0010000000000000002 query:93.222
a:0.00010000000000000002 query:304.467
a:1.0000000000000003e-05 query:879.014
a:1.0000000000000004e-06 query:3047.474
a:1.0000000000000004e-07 query:8827.552
a:1.0000000000000005e-08 query:29296.376
a:1.0000000000000005e-09 query:86620.926
a:1.0000000000000006e-10 query:278123.182

確率の逆数をquery classicalとして、query classicalとquery quantumを常用対数でプロットすると次のようになる。

傾きがおよそ$1/2$となっていることが読み取れ確かにQuadraticSpeedupが見られる。

---

1. ざっと$(0.9999)^{10000}\approx 0.37$である。cf. ネイピア数の逆数 ↩

2. 今は$\braket{当たり}{当たり}=1$である。ブラケット表記された状態は規格化していることが多いのだが、この論文中では必ずしもそうではないので注意。 ↩

3. (3),(4)式は$\mathcal{Q}\ket{\Psi_\pm}$が$(定数)\times \ket{\Psi_\pm}$になるように頑張る。(6)式も意地で頑張る。(7)式はQを固有値に置き換えれば良い ↩

4. 多くの人が解説記事を書いているので次項を書くことを優先した。 ↩