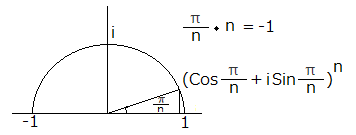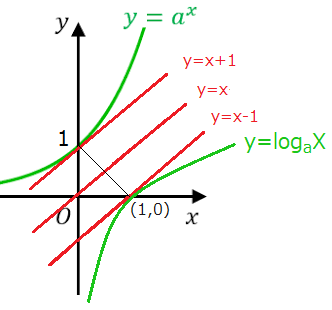はじめに
機械学習を学ぶ上で出てくる自然対数の底(ネイピア数 $e$)を理解していきたい。
シグモイド関数、ソフトマックス関数、交差エントロピー誤差、ガウス関数、ロジスティクス回帰の対数尤度関数にも自然対数という形で出てきます。
式としては、$e$ のように書かれてなく、$\exp$ や $\ln$ や $\log$ で表記されています。
あと、こんな話もできるとかっこいいよね。
まったく出会いが起こらない確率である37%は、スイスの数学者レオンハルト・オイラーが発見したネイピア数(e=約2.718)で1を割った数。
なぜ幸運の確率は5分5分でなく、63%か
数式が崩れる場合
2023年1月現在、ブラウザによって数式が崩れるとのこと。
対応として、数式部分で右クリック > Math Settings > Math Renderer > HTML-CSSにチェックが入っている部分を「Common HTML」に変更してください。

ネイピア数とは
ネイピア数 $e=2.71828182845904 \cdots$(鮒一羽二羽一羽二羽しごく惜しい)
$e$ は自然数の階乗の逆数を合計したものでもあります。どうしてこの式になるかは微分・積分の項目で説明
$e=\displaystyle 1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\cdots$
e = 0.0
x = 1.0
for i in range(1, 100):
e = e + x
x = x / i # 前の項の分母に1だけ大きい数を掛けた(x = x * 1/i)
print(e)
#2.7182818284590455
値が $2$ 以上 $3$ 未満なのは、$1$ と $\displaystyle \frac{1}{1!}=1$ を足すと $2$ となり、残り以降を足しても $1$ を超えないからです。
これから数Ⅲを学ぶ人に贈る「eってなんだよ?」 - Youtube 鈴木貫太郎
また、この後に出てくる $e^x$ は指数 $x$ を累乗して合計したものでもあります。
$e^x=\displaystyle 1 + \frac{1}{1!}x^1 + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + \frac{1}{4!}x^4 + \cdots$
先頭の $1$ も $\displaystyle \frac{1}{0!}$ と考えればより綺麗な式となると思い記載していましたが $e^0=1$ からなので訂正しました。
$e$ は「ネイピア数」あるいは「自然対数の底」と呼ばれる定数です。間違える人が結構多いですが、$e$ は「自然対数」ではありません。あくまで底となります。$e$ を使った対数が自然対数となり、10進の底が常用対数となります。
数学史上最も美しい等式としてよく取り上げられるオイラーの等式には、ネイピア数が含まれています。
オイラーの等式は、解析学・代数学・幾何学という異なる分野において定義された全く起源の異なる3つの数「e,i,π」が、「1」と「0」という数学の基礎となる数とシンプルな1つの式で結び付けられている。
オイラーの等式はなぜ美しいのか? - Youtube 予備校のノリで学ぶ「大学の数学・物理」
$e^{\pi i}+1=0$
- e ネイピア数
- π 円周率
- i 虚数単位
- 1 乗法の単位元、「存在を表し、また、存在を映す数」で、「ピッタリな自然数」
- 0 加法の単位元、「無を表す数」で、「宇宙」や「調和」を象徴する数
自然
自然対数 $\log_e x$ が「自然」であるというのは、数学において自然に生じ、よく見かけるということを根拠とするものである。
自然界の化学反応の速度や物質濃度の半減期を求める際等に現れます。
起源
まず、いつ、誰によって作られたのか、という点ですが、これがはっきりしません。
最古の痕跡としては、メソポタミア文明のころにはその存在は知られていたそうです。
しかし、その真の価値については微分が誕生してから再認識されたようです。
ネイピア数に初めて言及したのはイギリスの数学者ウィリアム・オートレッド(1575-1660)です。オートレッドは計算尺を発明した人で、これは対数の原理で機能する道具でした。しかし、オートレッドは実際には名前を付けたりネイピア数の値を計算したりしませんでしたが、最初の自然対数表を書きました。ちなみに乗法の記号である $\times$ や、三角関数を $\sin$ や $\cos$ と表記する方法もオートレッドの考案です。
初めてネイピア数そのものを計算したのはスイスの数学者ヤコブ・ベルヌーイ(1654-1705)だとされ金利計算の複利を調べて発見しました。
この定数に初めて記号を与えたのは、ドイツの数学者ゴットフリート・ライプニッツ(1646-1716)で、1690年、書簡の中で $b$ を使いました。ライプニッツはヤコブ・ベルヌーイと交流していて微積分を教えていました。ライプニッツの微積分学が発表されるころにはネイピア数はその地位がしっかり固まっていて、それ以降は避けて通れないものになりました。
$e$ という文字を初めて使ったのはスイスの数学者レインハルト・オイラー(1707-1783)で、1727年ごろ使い始めたようです。出版物では、1736年の『力学 (Mechanica)』が初出です。
「$e$」としてアルファベット $e$ を用いた理由については、2つの説が広く流布されています。
- オイラーの名前の頭文字から取った
- 指数 = exponential の先頭の文字
オイラーは謙虚な人柄でオイラー本人が自分の名にちなむようなことは不自然、オイラーは数式の書き方において、一般的な定数名には a,b,c,. . . を使い、変数名には x,y,z,. . . を使うべきと言っていることから後者が有力と思っている。
自然対数の底eの呼び名「ネイピア数」の由来はジョン・ネイピア(John Napier)。対数の発見者として知られる。
ネイピア数 〜美しきムダな数〜 - 野中文雄
ジョン・ネイピア(John Napier)については以前に記事を書きました。
定義
ネイピア数の定義は下記2通りある。
$\displaystyle e = \lim_{n \to \infty} \left(1 + \frac{1}{n} \right )^n$
もしくは
$\displaystyle e = \lim_{h \to 0} \left(1 + h \right )^\frac{1}{h}$
逆数
括弧の中をマイナスに変更しただけで、逆数になってしまう。
$\displaystyle \frac{1}{e} = \lim_{n\to \infty} \left(1 - \frac{1}{n} \right )^n$
以前、書いた記事の「ジョン・ネイピアが20年かけた対数表について」で
ジョン・ネイピアが求めた式があります。
$\displaystyle x=10^{7}\left(1-\frac{1}{10^{7}}\right)^y$
式を書き換えると次のようになり、実は $\displaystyle \frac{1}{e}$ を求めていたのです。
$\displaystyle \left(1-\frac{1}{10^{7}}\right)^{10^{7}} \fallingdotseq \left(1-\frac{1}{\infty}\right)^{\infty} = \frac{1}{e}$
連続複利
数式だけ見ると何の話をしているのかピンと来にくいと思うので、具体例を通じてネイピア数を理解していきましょう。
$\displaystyle \left (1 + \frac{1}{n} \right)^n$ は複利計算に関係している。金利計算で複利の計算をするとき、元本を表す「1」とのセットで行うのがふつうです。例えば 3% の金利であれば、「1+0.03」というのが基本のセットになります。
1年間の合計金利が100%になるように複利運用をしたら運用額はどうなるか?(中略)
実用上は現実性が薄くなりますが、同じ計算で分割回数をもっともっと細かくしていって、1日複利(÷365)、1時間複利(÷[365×24])、1秒複利(÷[365×24×360])のような極端な状態を考えることも理論上は可能です。
出展:【数列】連続複利とネイピア数 ”e” - 大人が学び直す数学
| 分割回数 | 計 算 式 | 増加率 | 受取額 | |
|---|---|---|---|---|
| 1年複利 | 1 | $\displaystyle \left (1 + \frac{1}{1} \right)^1$ | 2.000000 | 2,000,000 |
| 半年複利 | 2 | $\displaystyle \left (1 + \frac{1}{2} \right)^2$ | 2.25000 | 2,250,000 |
| 3ヶ月複利 | 4 | $\displaystyle \left (1 + \frac{1}{4} \right)^4$ | 2.44140 | 2,441,406 |
| 1ヶ月複利 | 12 | $\displaystyle \left (1 + \frac{1}{12} \right)^{12}$ | 2.61303 | 2,613,035 |
| 1日複利 | 365 | $\displaystyle \left (1 + \frac{1}{365} \right)^{365}$ | 2.71456 | 2,714,567 |
| 1秒複利 | 3,153,600 | $\displaystyle \left (1 + \frac{1}{3153600} \right)^{3153600}$ | 2.71828 | 2,718,281 |
最後の1秒複利では、ネイピア数 $e=2.7182818$ が現れてきましたね。
この $e$ を初めて計算したのは、スイスの数学者ヤコブ・ベルヌーイ(1654~1705)だと言われています。当時の西洋は大航海時代を経て商業と経済活動が活発化し、その分野への数学の応用も盛んで金融業で重要な利息に関する計算に注目されていたのでしょう。
人類最大の発明と言われる金利の研究。神の支配から解放され、ネイピア数は生まれた- YouTube
重要な性質
ネイピア数「$e$」を底とする指数関数 $y=e^x$ は重要で、$e^x$ は微分しても積分しても $e^x$ となり、何回微積分しても変わらない唯一の関数としても知られる。どちらかというと、そうなるような値を求めて $e$ としたと考えた方がいい。
「何回微積分しても変わらない」というのは、意味合い的には加法(足し算)においては $0$ 、乗法(掛け算)においては $1$ で、どちらも相手を変化させないですよね。数学ではこういう値が重要なのです。
定数 e そのものには、たいした意味はありません。重要なのは、指数関数 e^x です。この関数は、最も基本的な微分方程式 dy/dx = y の解です。
そのため、この関数を使って、様々な微分方程式の解が構成できるのです。
近代以降の物理では、自然現象の多くが、微分方程式によって記述されます。
e^x などと書くと、初めに e ありきのような印象なので、微分方程式 dy/dx = y, y(0) = 1 で定義される関数を y = exp(x) と書きましょう。e は、exp(1) の略記だと思えばよいです。
自然対数eは何に使えるのですか?- 教えてgoo
性質
- $e$ には、指数関数 $e^x$ を微分した結果は、$e^x$ となる。
$\displaystyle \frac{d}{dx}e^x = e^x$ - 底を $e$ とする対数関数 $\log(x)$ の微分は $\displaystyle \frac{1}{x}$ となる。
$\displaystyle \frac{d}{dx}\log_e x = \frac{1}{x}$
性質の確認
Googleが公開したブラウザ上で使えるプログラム実行環境「Colaboratory」はChromeのデスクトップ版で動作します。Python3を使用して性質を確認してみます。
参考:不思議な数「e」と自然対数
性質 ①
性質「$e$ には、指数関数 $e^x$ を微分した結果は、$e^x$ となる。」を確認する
微分の(f(x + h) - f(x - h)) / (2 * h)は平均値の定理により誤差が小さくなる。
参考:導関数の計算が面倒な場合の数値近似法
import numpy as np
import matplotlib.pyplot as plt
# 底
def get_base():
return 2 # 10 , 2.718
# 指数
def exp_func(x):
b = get_base()
return np.power(b, x)
# 微分
def numerical_diff(f, x):
h = 1e-2 # 0.001
return (f(x + h) - f(x - h)) / (2 * h)
def main():
x_values = np.arange(-1, 1, 0.1)
exp_values = exp_func(x_values)
diff_values = numerical_diff(exp_func, x_values)
# draw graph
plt.plot(x_values, exp_values, "-") # blue
plt.plot(x_values, diff_values, "-", color="red") # red
plt.grid()
plt.show()
if __name__ == '__main__':
main()
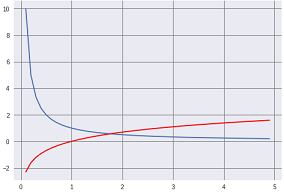
底2の指数関数(青)と傾きの微分関数(赤)をグラフにすると微分関数が下になります。
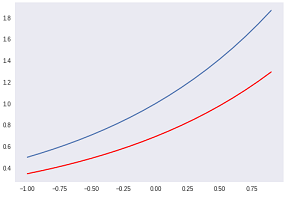
底10の指数関数(青)と傾きの微分関数(赤)をグラフにすると微分関数が上になります。
底2の時は微分関数が下に、底10の時に微分関数が上に来るとすると、2と10の間のある数では上でも下でもないという現象が起こりそう。早速底にいろんな数字を入れてみると、3ならば上、2.5なら下。こうやってどんどん一致する数に近づけていき 2.718 と入れるとほぼ一致するのです。(本当は、一致する値は最初から知ってました)
性質 ②
性質「底を $e$ とする対数関数 $\log(x)$ の微分は $\displaystyle \frac{1}{x}$ となる」を確認します。
import numpy as np
import matplotlib.pyplot as plt
# 逆数
def inverse_func(x):
return 1 / x
# 指数
def exp_func(x):
return np.exp(x)
# 対数
def log_func(x):
return np.log(x)
# 微分
def numerical_diff(f, x):
h = 1e-4 # 0.0001
return (f(x + h) - f(x - h)) / (2 * h)
def main():
x_values = np.arange(0.1, 5, 0.1)
exp_values = exp_func(x_values)
inverse_values = inverse_func(x_values)
log_values = log_func(x_values)
diff_values = numerical_diff(log_func, x_values)
# draw graph
plt.plot(x_values, inverse_values, "-") # blue
plt.plot(x_values, log_values , "-", color="red") # red
#plt.plot(x_values, diff_values , "-", color="red") # red
plt.grid(color='gray')
plt.show()
if __name__ == '__main__':
main()
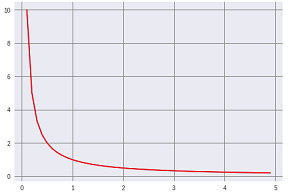
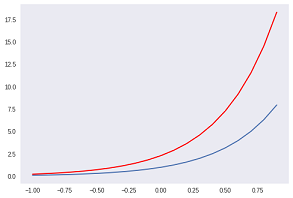
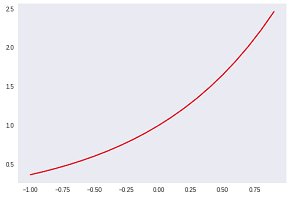
青線の傾きの関数 $\displaystyle \frac{1}{x}$の値は、$x = 0.5$ で $2$ に、$x = 1$ で $1$ に、 $x = 2$ で $0.5$ になります。
赤線は自然対数の関数 $\log(x)$ となり、反比例の関係が見て取れます。
#plt.plot(x_values, log_values , "-", color="red") # red
plt.plot(x_values, diff_values , "-", color="red") # red
コメントアウトを入れ替えます。
赤線が自然対数の関数 $\log(x)$ の微分となり、青線の傾きの関数 $\displaystyle \frac{1}{x}$ と一致します。
正の単調増加性
数学での単調とは「上がったり下がったりがない」という意味です。
放物線は、単調減少と単調増加があります。
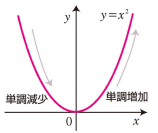
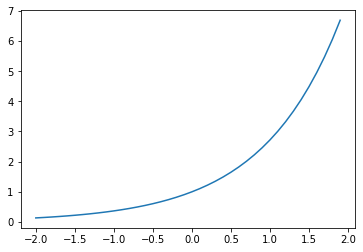
自然対数の底(ネイピア数) e は、負の値でも $e^x$ を通すと正の値になる。
また、右肩上がりの単調増加性をもつ。この性質は後述するソフトマックス関数で応用される。
import matplotlib.pyplot as plt
import numpy as np
x = np.arange(-2, 2, 0.1)
y = np.exp(x)
plt.plot(x, y)
plt.show()
使い道
ニッセイ基礎研究所がいいコラム「ネイピア数eについて」を掲載していたのでリンクしておきます。
対数・指数
数学・統計学では自然対数 $\log_ex$
生物・化学・工学では常用対数 $\log_{10}x$
欧米や関数電卓でも常用対数 $\log_{10}x$
情報理論では二進対数 $\log_2x$
自然対数・常用対数・二進対数の使い分け。log,ln,lg,expはどういう意味?
対数関数は指数関数の逆関数の関係にある。
C# 数学10 「常用対数、ネイピア数e-基本1、自然対数-基本1」e log ln exp
自然対数 $\log_e x$ の底 e を省略して単に $\log x$ と書くことも多いです。またたまに「ln x」と書かれることもある('ln'(エルエヌ) = 'natural logarithm':「自然対数(ログナチュラル)」)「ln4」、「ln8」などという書き方をします。
指数関数 $e^x$ のことを $\exp x$ と表記することがあります。exponential (「指数の」という形容詞)という英単語から来ています。単に「イーのエックス乗」、または「エクスポネンシャルエックス」と読む人が多いです。exp(1) は自然対数 ln(1) の底です
いくつかのプログラミング言語(のライブラリ)について、対数をどのように指定するか調べた結果が次の表だ。Delphi 以外は全て ln ではなく log だ。
出典:ln, log, log10 - まじかんと雑記
| 名称 | 自然対数 | 常用対数 | 一般の対数 |
|---|---|---|---|
| Mathematica | Log[N] | - | Log[b,N] |
| C/C++ | log(N) | log10(N) | - |
| Java | log(N) | log10(N) | - |
| ECMAScript | log(N) | - | - |
| .NET Framework | Log(N) | Log10(N) | Log(N,b) |
| ActiveBasic | Log(N) | - | - |
| Delphi | Ln(N) | - | LogN(b,N) |
| FORTRAN | log(N) | log10(N) | - |
| Octave | log(N) | log10(N) | - |
| Perl | log N | - | - |
| Prolog | log(N) | - | log(b,N) |
| Python | log(N) | log10(N) | log(N,b) |
| Ruby | log(N) | log10(N) | - |
底の変換公式
自然対数から常用対数への変換
$\displaystyle \log_{a}b = \frac{(\log_{c}b)}{(\log_{c}a)} = 対数$
$\displaystyle \log_{10}2 = \frac{(\log_{e}2)}{(\log_{e}10)}$
$\displaystyle = \frac{0.69314}{2.30258} = 0.301027$
対数の用途
- かけ算を足し算または割り算を引き算にすることで計算を楽にさせる。
$\displaystyle \log \left( \prod_{n=1}^{N} f(n) \right) = \sum_{n=1}^{N}\log f(n)$ ※$\prod$は、かけ算を繰り返す記号 - 機械学習では非常に大きな数を扱います。プログラムでこのような数を扱うと、オーバーフローを起こしてしまうときがあります。そのような数は、対数 をとって扱うことで、オーバーフローを防ぐことができます。例えば、$100000000 = 10^{8}$、$0.000000001 = 10^{-8}$ となります。
- 機械学習では確率を使いますが、同時確率の場合には 1 以下の数の掛け算の連続になります。多い場合にはアンダーフローを起こしてしまうときがあります。そのような数は、対数 をとって扱うことで、アンダーフローを防ぐことができます。
例としてサイコロを2回投げた場合、1回目に1の目が出て2回目に2の目が出る同時確率は、下記の計算となる。10回投げた場合はどうなるか想像つくでしょう。
$\displaystyle \frac{1}{6} \times \frac{1}{6} = \frac{1}{36}$ - 対数は単調増加関数であるため、ある関数 $f(x)$ があって $f(x)$ を最小にする値を求めた場合、対数をとった $\log f(x)$ でも最小の値は同じになります。また、最大値を求める場合でも同じです。
$f(x)=(x-1)^{2}+2$は、$x=1$の時、最小値をとる
$\log f(x)=\log ((x-1)^{2}+2)$ も、$x=1$の時、最小値をとる
微分・積分
$\log_{e}x$ の使い道として、対数変換してから微分する考え方の「対数微分法」がデータ分析や機械学習でよく使われます。
対数や合成関数の微分はぜひおさえておきたいところ。
- 対数微分法のやり方。4つのステップで分かる「急がば回れ」の微分法
- 積の微分、合成関数の微分、商の微分の導出- Youtube 鈴木貫太郎
- 世にも美しい微分の規則
- 微分の公式一覧 - Sci-pursuit
e を求める式
冒頭で $e$ は自然数の階乗の逆数を合計したものと記載しました。
$e=\displaystyle 1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\cdots$
では、どうしてこういう式になるのでしょうか?
それは微分と積分のべき乗の公式を理解すると見えてきます。
微分は、$(x^n)'=\displaystyle nx^{n-1}$
積分は、$\displaystyle \int x^ndx=\frac{1}{n+1}x^{n+1}$
$y=x$ という関数の積分は、$\displaystyle \frac{1}{2}x^{2}$ でした。これを微分すると $\displaystyle 2 \cdot \frac{1}{2}x^{2-1}=x$ となり元に戻ります。
この積分した式をもう一度積分すると、次のようになります。
$\displaystyle \int \frac{1}{2}x^{2}dx=\frac{1}{2} \cdot \frac{1}{3}x^{3}$
この式をさらにもう一度積分すると、このようになります。
$\displaystyle \int \frac{1}{2} \cdot \frac{1}{3}x^{3}dx=\frac{1}{2} \cdot \frac{1}{3}x^{3} \cdot \frac{1}{4}x^{4}$
この後も同じ規則になります。
$\displaystyle \frac{1}{2} \cdot \frac{1}{3} \cdot \frac{1}{4}\cdot \cdots \cdot \frac{1}{n}x^{n}$
順番に積分した結果を書き出してみましょう。
$x, \frac{1}{2}x^2, \frac{1}{2} \cdot \frac{1}{3}x^{3}, \frac{1}{2} \cdot \frac{1}{3} \cdot \frac{1}{4}x^{4} \cdots$
これを階上(!)の記号で表して見ると
$\displaystyle \left(\frac{1}{1!}\right)x,\left(\frac{1}{2!}\right)x^2,\left(\frac{1}{3!}\right)x^3,\left(\frac{1}{4!}\right)x^4 \cdots$
さらに列の先頭に$0$と$1$を加えます。というのは、$x$を微分すれば$1$となり、$1$を微分すると$0$になります。
$\displaystyle 0,1,\left(\frac{1}{1!}\right)x,\left(\frac{1}{2!}\right)x^2,\left(\frac{1}{3!}\right)x^3,\left(\frac{1}{4!}\right)x^4 \cdots$
この無限に続く列を積分とは逆に一斉に微分しても、列の作りからすれば1つ前に戻るだけで列全体の姿は変わりません。
※微分しても積分しても姿が変わらないという特殊な性質が今後$e$を使う上で重要ポイントになります。
さらにこの無限に続く列を全部足し合わせて見ると、
$\displaystyle 0 + 1 + \frac{1}{1!}x^1 + \frac{1}{2!}x^2 + \frac{1}{3!}x^3 + \frac{1}{4!}x^4 \cdots$
この式に$x=1$を代入したのが求める式になるわけです。$0$は省略
$e=\displaystyle 1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+\frac{1}{4!}+\cdots$
e を使う意図
自然現象には指数関数が非常によく出てきます。指数関数は $a^x$、ある数の $x$乗です。
この時ある数 $a$ はいろいろ変わるんですが、これを $e^{kx}$ と書き換えて $a$ の違いを $k$ に押し付けることで、ある数は全部 $e$ で統一できます。
説明すると、底を $a$ とする指数関数は以下のように表現できます。
$a^{x}=e^{x \cdot \ln{a}}$
$2^{3}=8$ と $10^{2}=100$ を例にしてみます。
$2^{3}=e^{3 \cdot \ln{2}}$ 、$10^{2}=e^{2 \cdot \ln{10}}$ と $e$ で統一できます。
import numpy as np
print(np.exp(3*np.log(2)))
print(np.exp(2*np.log(10)))
# 7.999999999999998
# 100.00000000000004
でも、なんで $e$ にするのかというと、$e$ にしておくと微分や積分が簡単になるからなんです。なにしろ $e^x$ は微分しても積分しても $e^x$ なんですから。
微分の計算の中で、指数・対数の計算が出てきたときに、底をネイピア数に揃えると計算がすっきりしてすこぶる簡単になるので、それが常に意識され、当然視されます。微分においては、このネイピア数が、算数の四則演算における「1」のように、基点になる数なのです。
【微分】指数関数を微分するⅡ~微分しても変わらない関数 - 大人が学び直す数学
式の簡略化例
性質「底を $e$ とする対数関数 $\log(x)$ の微分は $\displaystyle \frac{1}{x}$ となる」を使用します。
尤度関数の微分の一部分
$\displaystyle \frac{\partial u}{\partial v} = \frac{\partial u}{\partial v} \sum _{n=1}^{n} \left (y^{(i)} \log(v) + (1 - y^{(i)}) \log (1-v) \right)$
$u$ を $v$ で微分する。$\log(v)$ の微分は $\displaystyle \frac{1}{v}$ となる。
$\log (1-v)$ は合成関数にして微分、$\displaystyle -\frac{1}{1-v}$ となる。
すると、式が簡略化できる。
$\displaystyle \frac{\partial u}{\partial v} = \sum _{n=1}^{n} \left (\frac {y^{(i)}}{v} - \frac{1-y^{(i)}}{1-v} \right)$
オイラーの公式
性質 ① の「$e$ には、指数関数 $e^x$ を微分した結果は、$e^x$ となる。」がいまいち分からなくて、だから何なんだと思ってたんですが、オイラーの公式を知ることで重要性を理解しました。
Euler's formula 中学生の知識でオイラーの公式を理解しよう 最終回 - Youtube
$e^{\pi i}+1=0$ は、式変形すると、$e^{\pi i}=-1$ となります。
これが何故そうなるのか。
下図で半径1の円で角度 $\displaystyle \theta = \frac{\pi}{n}$ の位置は $\displaystyle \left(\cos \frac{\pi}{n} + i \sin\frac{\pi}{n} \right)^n$ となります。
角度をどんどん小さくしていって 0 に近づけます(無限)。
その時に接線(傾き)を求めるということは、$e^\theta$ を微分することになり、性質 ① の通り結果 $e^\theta$ のままとなります。
$\displaystyle \theta = \frac{\pi}{n}$ なので、半周させる(接線を反対側へ)と$n$倍することになり、$\displaystyle \frac{\pi}{n} \cdot n = \pi$ となります。
よって、$e^{\pi}=-1$ が求まります。(虚数 $i$ は 1 扱いで省略)
確率
100分の1を100回やってみる
「100回試したら一度は起こって欲しい事象に1/100の確率を使う馬鹿多過ぎwこれを100人で試したら、36人は統計的に100回では起きない概算になる。」(遠藤雅伸@evezoo)
参考: ゲームの神様「100分の1を100回やってみる」たとえば、100個にひとつ当たりが入っているチョコレートを箱買いした場合と、100個に1個の割合で当たり玉の入った福引の場合の違い。
1/nの確率でn回試しても事象が起きない確率を計算してみた。
ネイピア数 〜美しきムダな数〜
$\displaystyle \frac{1}{100}$ が起こらない確率は、$\displaystyle 1 - \frac{1}{100}$ になります。
$\displaystyle \frac{1}{100}$ を100回やっても起こらない確率、$\displaystyle \left (1 - \frac{1}{100} \right)^{100}$ になります。
数学なので式を一般化すると、$\displaystyle \left (1 - \frac{1}{n} \right)^{n}$ になります。
ネイピア数の定義と似ていますが、中の $+$ と $-$ が違います。
括弧の中を変形します。
$\displaystyle 1 - \frac{1}{n} = \frac{n}{n} - \frac{1}{n} = \frac{n-1}{n}$
さらに変形します。$m = n-1$ にして置き換えます。
$\displaystyle = \frac{n-1}{(n-1)+1} = \frac{m}{m+1}$
分子と分母を入れ替えて逆数をとる
$\displaystyle = \frac{1}{\left (\frac{m+1}{m} \right)} = \frac{1}{\left (\frac{m}{m} + \frac{1}{m} \right)}$
分母を調整すると、分母にネイピア数の定義が見えてくる。
$\displaystyle = \frac{1}{\left (1 + \frac{1}{m} \right)}$
$n$ 回掛け合わせて $n$ を無限大に
$\displaystyle = \frac{1}{\left (1 + \frac{1}{m} \right)} → \frac{1}{e} = 0.3678\dots$
まったく起こらない確率は $37%$ となる。
なぜ幸運の確率は5分5分でなく、63%か につながる。
標準シグモイド関数
$\displaystyle \mathrm{sig}(a) = \frac{1}{1 + \exp(-a)}\Bigl(=\frac {\exp(a)}{1+\exp(a)}\Bigr)$
オッズ(odds)は、確率論で確率を示す数値。ギャンブルなどで見込みを示す方法として古くから使われています。
オッズ $Odds$と確率 $p$ には以下の関係式が成り立つ。
$\displaystyle Odds=\frac{p}{1−p}$
$\displaystyle p=\frac{Odds}{1+Odds}$
オッズと標準シグモイド関数の定義は似ていることに気が付いたでしょうか。
ソフトマックス関数
ソフトマックス関数は、複数の出力の合計が1.0になるように正規化された関数で主に分類問題における出力層の活性化関数として使用されます。
$y_k=\dfrac {e^{s_k}}{\sum ^n_{i=1}e^s_i}$
大事なのは $e^x$ は正の値を返す単調増加関数であることだ。
スコアの値に正の値と負の値が混在している場合、絶対値を取るとスコアの大小関係がごちゃごちゃになってしまう。例えば[5, -3, 2]というスコア>が得られた場合、大小関係は5>2>−3である。しかし絶対値を取ると5>3>2という順序に大小関係が変わってしまう。これを解決してくれるのが単調増加関数である。 $e^x$ は非線形関数であるため、大小の比率を保つことはできないが、大小関係は維持されるのである。
統計
非線形の回帰分析をする際に、両辺の対数をとった式にすることで線形の単純回帰モデルとして表現し直すことができる。
経済学や自然科学の世界では「所得が1%増えるたびに需要は〇%増える」といったように弾力性が一定と考えられるものが多く存在することから、対数変換をしてから最小二乗法を使う方法がよく使われているんです。
対数変換を行う意味について。回帰分析において対数変換する背景にある前提とは?
- 弾力性と回帰係数
- 経済情報処理 講義ノート 第 10 回 回帰分析 Part-2 PDF
- 「過去、現在、未来の時間のレール」を走りぬけていく経済というイメージ pdf
- 回帰分析の時に対数をとる意味は? - 教えてgoo
正規分布
| イメージ | 正規分布(ガウス分布) | 標準正規分布 |
|---|---|---|
 |
$\displaystyle f(x)=\frac{1}{\sqrt{2\pi}\sigma}\exp\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$ | $\displaystyle f(x)=\frac{1}{\sqrt{2\pi}}\exp\left(-\frac{x^{2}}{2}\right)$ |
マイナスが付いた exp( - x ) っていうのは、逆に半分の1/2、そのまた半分の1/4、そのまた半分の1/8、そのまた半分の1/16、ってだんだん減ってく形なの。正規分布の山の裾野が、富士山みたいにダラーッて減ってくのは、この exp( - x ) の形だね。
でも、ただ exp( - x ) だけだと、片っ方だけ、右側だけしか減らないよ。そこで、左右両側が同じように減りますようにって、出てきたのが x^2 。二乗ってすると、マイナスxマイナス=プラスだから、左右の形がはねっ返りで同じになるんだ。
正規分布は指数減衰と二乗からできている
曲線 $\displaystyle y=exp(-\frac{x^2}{2})$ が山なりの形で誤差分布に似ているので採用された。あとは倍率を合わせたり平行移動させたりするのがくっついている。
正規分布の中でも平均が $μ=0$、分散が $σ^2=1$ であるのが標準正規分布となり式が簡単になる。
正規分布の基礎的な知識まとめ
係数に円周率 $\pi$ の平方根が使われているのは、「全確率が $1$ となる」ように調整するためにすぎないです。
例 標準正規分布の下表の合計値は $1$ になります。
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|---|
| y | 0.0045 | 0.0546 | 0.242 | 0.398 | 0.242 | 0.0546 | 0.0045 |
円周率の平方根について下記の動画が参考になる。
- 積分の二乗について。[ガウス積分] - Youtube ようつべ先生の数学教室
- バウムクーヘン積分からヤコビアンを理解する[重積分,変数変換,2変数関数] - Youtube ようつべ先生の数学教室
- ガウス積分の証明【あえて2乗する驚き】 - Youtube 予備校のノリで学ぶ「大学の数学・物理」
性質の証明
式の展開する上では、前提知識として組み合わせと二項定理を先に理解する。
展開式では、かけ算を「$\times$」ではなく「$\cdot$」で表現している。
ネイピア数 自然対数の底e とは - Youtube 鈴木貫太郎
組み合わせ(combination)
$\displaystyle _n C _r = \frac{_n P _r}{r!}$
$\displaystyle _n C _2 = \frac{n(n-1)}{2!}$
$\displaystyle _n C _3 = \frac{n(n-1) \cdot n(n-2)}{3!}$
二項定理
$(a+b)^n=\displaystyle\sum_{k=0}^n{}_n\mathrm{C}_ka^kb^{n-k}$
$=(a + b)(a + b)(a + b) \cdots (a + b)$
$=a^n + n \cdot a^{n-1}b + {}_n C _2 \cdot a^{n-2}b^2+ {}_n C _3 \cdot a^{n-3}b^3 \cdots \cdots b^n$
分母の無限は0
極限の考え方で、分母の無限は$0$として扱う。
$\displaystyle \lim_{n \to \infty} \frac{n-1}{2!n}$
展開する
$=\displaystyle \frac{n}{2!n} - \frac{1}{2!n}$
左側の$n$は約分で消せる。右側の$n$は分母が無限で扱っている場合、$0$ 扱いで消す。
$=\displaystyle \frac{1}{2!}$
実際に展開
二項定理を使って展開、組み合わせを更に展開、分母の無限は$0$として扱って展開する。
$\left(1 + \frac{1}{n} \right )^n$ は、$\left(a + b \right )^n$ と置き換えることが出来るので、二項定理が使える。
\begin{align}
e &= \lim_{n \to \infty} \left(1 + \frac{1}{n} \right )^n\\
&= 1 + {}_n C _1 \cdot 1 \cdot \frac{1}{n} + {}_n C _2 \cdot 1 \cdot \frac{1^2}{n^2} \cdot {}_n C _3 \cdot 1 \cdot \frac{1^3}{n^3} \cdots \cdots\\
&= 1 + \frac{n}{1!} \cdot 1 \cdot \frac{1}{n} + \frac{n(n-1)}{2!} \cdot 1 \frac{1}{n^2} \cdot \frac{n(n-1)(n-2)}{3!} \cdot 1 \cdot \frac{1}{n^3} \cdots \cdots\\
&= 1 + \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \frac{1}{4!} + \frac{1}{5!} \cdots \cdots \frac{1}{n!}\\
& \frac{1}{2!}以降は、幾ら足しても1より大きくなることはない。式全体は3より小さくなる\\
&= 1 + 1 + 0.7182818284590 \cdots\\
&= 2.7182818284590 \cdots\\
\end{align}
※先頭の $1$ も $\displaystyle \frac{1}{0!}$ と考えればより綺麗な式となる。
性質 ①
$e$ には、指数関数 $e^x$ を微分した結果は、$e^x$ となる。
「ネイピア数 e を底とする指数関数は、微分しても形が変わらない」という特殊な性質がある。
【微分】指数関数を微分するⅡ~微分しても変わらない関数 - 大人が学び直す数学
指数関数
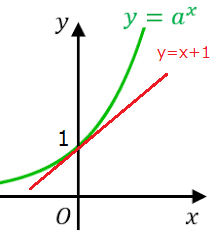
$e=2.7182818284590 \cdots$ であるということは分かったが、どうしてこんな値を定義したのか指数関数のグラフで考えてみる。
どんな指数関数も、必ず $1$ を通る。なぜなら、$a^0=1$ となっているから。
$x=0$ の時 $1$ を通る接線は、$y=x+1$ となる。
指数関数のグラフを描いた時に
$y=2^x$ の接線は、$0$ の時 $1$ を通る接線の傾きより小さいから、$a$ は $2$ ではない。
$y=3^x$ の接線は、$0$ の時 $1$ を通る接線の傾きより大きいから、$a$ は $3$ ではない。
$a$ の値は、$2 < a < 3$ の範囲内に存在する。この辺りで $a$ が $e$ だろうと匂わせてる。
微分してみる
ネイピア数とは、$y=a^x$ のグラフで $x=0$ での接線の傾きが $1$ となる $a$ の値である。
$a=e$ のとき $y$ 切片での接線の傾きが $1$ となるのである。
| a | y切片 | y切片での接線の傾き |
|---|---|---|
| 2 | 1 | 0.69314718056 |
| e | 1 | 1 |
| 3 | 1 | 1.09861228867 |
$y=e^x$ のグラフで $x=0$ での接線の傾きが $1$ となることが分かった。
ここから式の定義を導出してみる。
$x=0$ の時 $1$ を通る接線の傾きが、$1$ である特別な $a$ の値を考えてみる。
接線の傾きを求めるために、微分($y^\prime$)する。
\begin{align}
\displaystyle
y&=a^x\\
y^\prime &= \lim_{h \to 0} \frac{a^{x+h}-a^x}{h}\\
&=\lim_{h \to 0} \frac{a^x(a^h-1)}{h}
\end{align}
$X = 0$ の場合
$\displaystyle \lim_{h \to 0} \frac{a^{0+h}-a^0}{h} = \frac{a^{h}-1}{h} = 1$ である。
なぜ、$1$ なのか?
$X = 0$ の時に接線の傾き $1$ になるような定義の式を求めたから。
これを先程の式に代入してみる。
$\displaystyle y^\prime = \lim_{h \to 0} \frac{a^x(a^h-1)}{h} = a^x \cdot 1 = a^x$
$y^\prime=a^x$
つまり、微分しても微分する元の式 $y=a^x$ と同じになる。
性質 ②
底を $e$ とする対数関数 $\log(x)$ の微分は $\displaystyle \frac{1}{x}$となる。
逆関数
先に、$a=e$ であることを確認する。
逆関数の微分公式を例題と図で理解する - 高校数学の美しい物語
$y=a^x$
$x=\log_ay$
$y=\log_ax$
指数関数 $y=a^x$ に対して線対称となるのが逆関数となる対数関数 $y=\log_ax$
\begin{align}
\displaystyle
y&=\log_ax\\
y^\prime &= \lim_{h \to 0} \frac{\log_a(x+h)-\log_ax}{h}\\
&\frac{1}{h} を前にだし、対数関数の性質より引き算は割り算に直せる。\\
&=\lim_{h \to 0} \frac{1}{h}\log_a \frac{x+h}{x}\\
&=\lim_{h \to 0} \frac{1}{h}\log_a \left (1+\frac{h}{x} \right)
\end{align}
$X = 1$ の場合
$\displaystyle \lim_{h \to 0} \frac{1}{h}\log_a \left (1+\frac{h}{1} \right) = \frac{1}{h}\log_a (1+h) = 1$ である。
$\displaystyle \frac{1}{h}$ は対数関数の性質より、$α\log(x)=\log(x)α$ とできて指数に入れられるので
$\displaystyle \lim_{h \to 0} \log_a (1+h)^\frac{1}{h} = 1$ となる。
対数の底と真数部分が同じなら、その値は $1$ になります。
ネイピア数の定義 $\displaystyle e = \lim_{h \to 0} \left(1 + h \right )^\frac{1}{h}$ と
逆関数で求まった式 $\displaystyle \lim_{h \to 0} \log_a (1+h)^\frac{1}{h}$ は $\log_a$ を除けば同じ式である。
よって、$a=e$ である。
逆関数2
先程の微分の式を使う。
$\displaystyle y^\prime = \lim_{h \to 0} \frac{1}{h} , \log_a \left (1+\frac{h}{x} \right)$
$\displaystyle \frac{1}{h}$ は対数関数の性質より、$α\log(x)=\log(x)α$ とできて指数に入れられるので
$\displaystyle y^\prime = \lim_{h \to 0} \log_a \left (1+\frac{h}{x} \right)^\frac{1}{h}$
$\log$ の中の分数を $\displaystyle \frac{h}{x}$ を変数 $t$ に置き換える。
すると、$h=xt$ になります。
$\displaystyle = \lim_{t \to 0} \log_a (1+t)^\frac{1}{xt}$
$\displaystyle = \lim_{t \to 0} \log_a (1+t)^{\frac{1}{x}\frac{1}{t}}$
$\displaystyle \frac{1}{x}$ を対数の前に出し、さらに $t$ に関係ないので $\lim$ の前に出します。
$\displaystyle = \frac{1}{x}\lim_{t \to 0} \log_a (1+t)^\frac{1}{t}$
対数の底と真数部分が同じなら、その値は $1$ になります。
$\displaystyle \frac{1}{x}\lim_{t \to 0} \log_a (1+t)^\frac{1}{t}$ は $\displaystyle \frac{1}{x}$ と $\log_a$ を除けばネイピア数の定義と同じ式になります。
よって、$\displaystyle y^\prime = \frac{1}{x}$
底 $a$ の対数関数 $log_a(x)$ は、$\displaystyle \frac{1}{x}$ となる。
証明まとめ
指数関数の $y=a^x$ の $0$ の時 $1$ を通る接線は、微分($y^\prime=a^x$)しても元の指数関数と同じで、逆関数を求めたら $a=e$ であることが分かりました。
$a=e$ なので、$y=a^x$ は $y=e^x$ と表せる。
- $e$ には、指数関数 $e^x$ を微分した結果は、$e^x$ となる。
- 底を $e$ とする対数関数 $log(x)$ の微分は $\displaystyle \frac{1}{x}$ となる。
最後に
三角関数における度数法(360度で一周)と弧度法(2πで一周)の関係は、ある意味で、対数における常用対数(底が10)と自然対数(底がe)の関係に対応します。
前者は人間のしきたりに合わせたもので、それなりに便利ですが、これだと問題があります。
それは、微積分の理論を推し進めていくと、やがて三角関数の世界と指数関数の世界が相互に乗り入れるようになるのですが、度数法や常用対数だとこれがきれいにいかないのです。
他方、弧度法や自然対数は、数学自体にフィットするように作られていて、端的に言うと sin や log や exp のグラフが軸と交わるところで傾きが 1 になるようにうまく定義されています。
この統一的な仕様のおかげで、いろんな関数が「相互乗り入れ」したときに、うまい具合に式がひとつにつながる仕組みになっているのです。