0. はじめに
こんにちは、大学 1 年生になったばかりの E869120 です。本記事は、
からの続きです!!!
中編から読む方へ
21 世紀も中盤に入り、情報化社会が急激に進行していく中、プログラミング的思考やアルゴリズムの知識、そしてアルゴリズムを用いた問題解決力が日々重要になっています。
しかし、アルゴリズム構築能力・競プロの実力は、単純にプログラミングの知識を学ぶだけではあまり身につきません。問題解決にはもちろん、場合によっては問題文読解にすら数学的な面が重要になりつつあるのではないかと考えています。実際、私はこれまでの経験で「数学の壁でつまづいた競プロ参加者」をたくさん見てきました。
そこで本記事では、AtCoder のコンテストで戦ったり、様々なアルゴリズムを習得していくために必要な数学的知識や数学的考察テクニックを習得し、アルゴリズムと数学の密接さに気づいてもらうことを最大の目標とします。前編では、
を紹介しましたが、中編ではやや発展的なトピックについて、必要な数学知識をまとめます。
また、記事の後半では、前編・中編で扱った数学的知識に慣れるための**演習問題を用意しました**ので、5 章から先に見ても構いません。皆さん是非お読みください!
目次
前編
| 章 | タイトル | 備考 |
|---|---|---|
| 1. | はじめに | |
| 2. | これが分からないと問題が理解できない! ~最重要ポイント 12 選~ | ここからサポートします |
| 3. | アルゴリズムと密接に関わる数学<初級編> | 本記事のメインです(1 ~ 11 個目のトピックを扱います) |
中編
| 章 | タイトル | 備考 |
|---|---|---|
| 4. | アルゴリズムと密接に関わる数学<中級編> | 本記事のメインです(12 ~ 19 個目のトピックを扱います) |
| 5. | これだけ解けば理解が深まる! ~演習問題 32 問~ | 2 章から 4 章の内容をサポートします |
後編
| 章 | タイトル | 備考 |
|---|---|---|
| 6. | なぜ数学的考察が重要か? | 後編では数学的考察を扱います |
| 7. | 競プロで頻出! ~汎用的な数学的考察 7 選~ | |
| 8. | 問題特有の数学的考察テクニック 14 選 | 後編のメインです |
| 9. | おわりに | |
| 10. | 参考文献 |
4. アルゴリズムと密接に関わる数学<中級編>
2 章では問題文を読むために必要なテクニックを 12 個のポイントに絞ってまとめました。しかし、競プロに出題されるようなアルゴリズムだけを考えても、数学と結びつく場面はまだまだたくさんあります。例えば、
- 3-2. 節では、二分探索の計算量 $O(\log N)$ と対数関数の関係
- 3-6. 節・3-7. 節では、幾何計算と三角関数・ベクトルの関係
- 3-11. 節では、経路の数の計算とフェルマーの小定理の関係
について紹介してきました。4 章ではさらに追加で 8 個のトピックを紹介し、アルゴリズムを数学的側面から捉えていきたいと思います。皆さんにアルゴリズムと数学が如何に密接に関わっているかを体感してもらうことが最大の目標です。
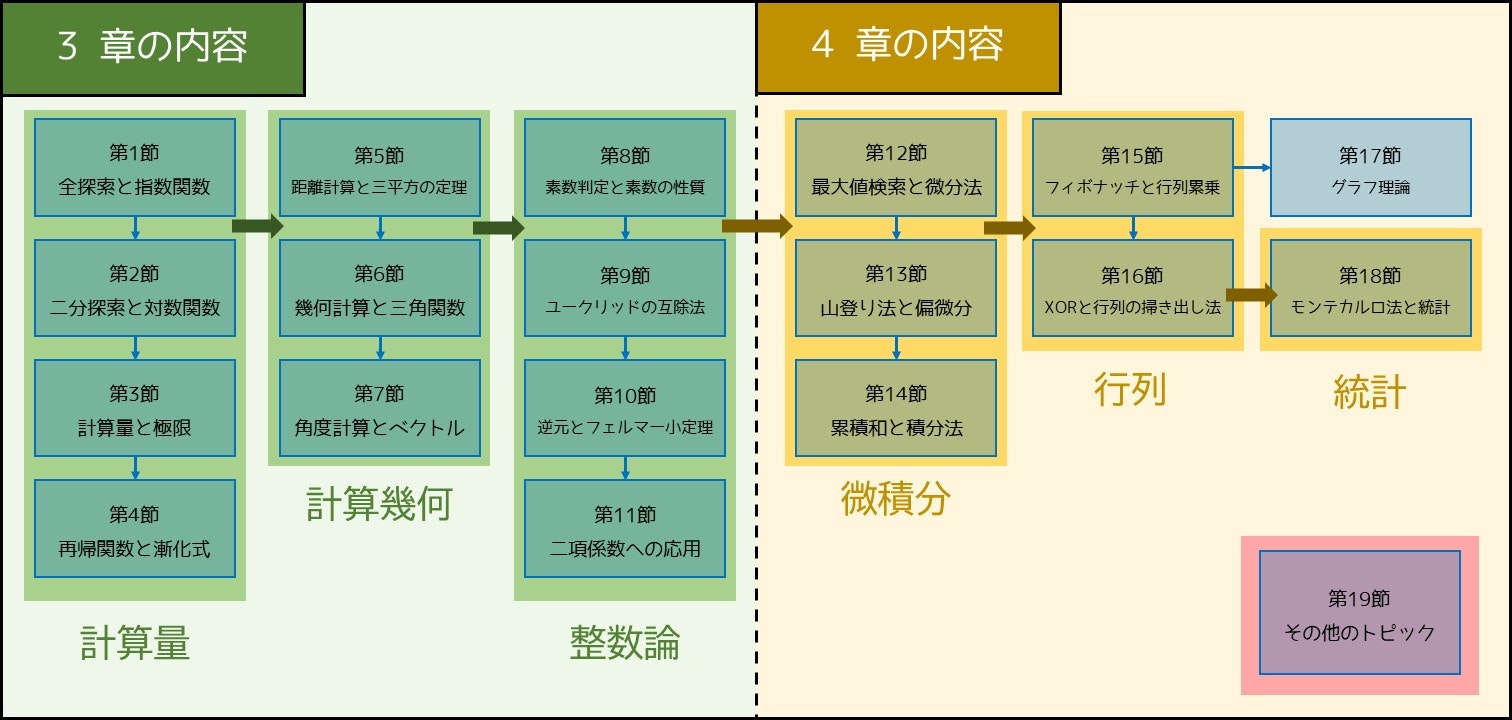
4-12. 最大値検索に学ぶ、微分法(レベル: 3)
3)
まず、次の問題を考えてみましょう。
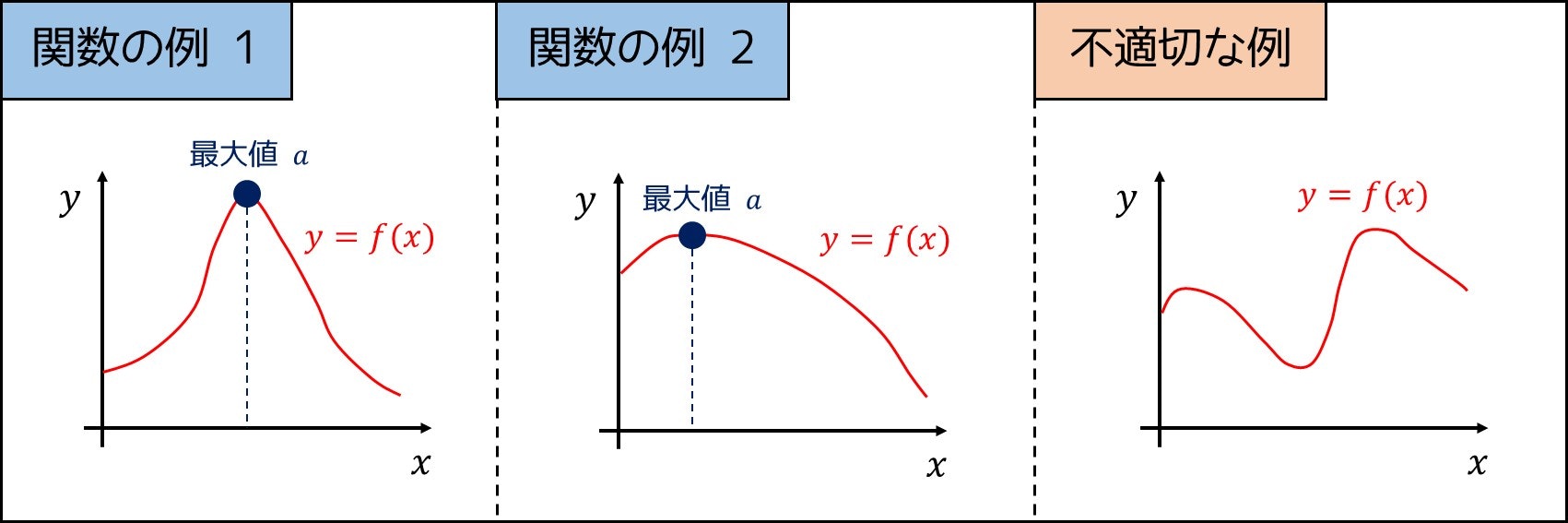
連続な関数 $f(x)$ がある。この関数には次のような性質がある。
- 以下の条件を満たす場所 $M$ $(0 \leq M \leq 3)$ が存在する。
- $x < M$ では $y = f(x)$ が単調増加である。
- $x > M$ では $y = f(x)$ が単調減少である。
あなたは $30$ 回まで、「実数 $x$ を選び、それに対する $f(x)$ の値をコンピューターに聞く」という形式の質問ができる。$f(x)$ の最大値を、できるだけ小さい誤差で求めよ。
例えば、以下のような関数が例として挙げられます。
では、どうやってこの問題を解けば良いのでしょうか。一つのアプローチとして、微分法が挙げられます。まず、「微分とは何か」から確認していきましょう。
微分とは何か?
おおまかなイメージとしては、
- 関数のグラフ $y = f(x)$ を考える
- グラフ上の点 $(a, f(a))$ に付近における関数の傾き(=接線の傾き)を求める操作が微分
だと思って良いです。例えば、下のような関数 $y = x^2$ を考えます。そこで、$a = 1$ とするとき、グラフ上の点 $(1, 1)$ を拡大していくと、傾きが $2$ に近づいていることが分かります。この傾きの値(微分係数)を求めるのが微分なのです。
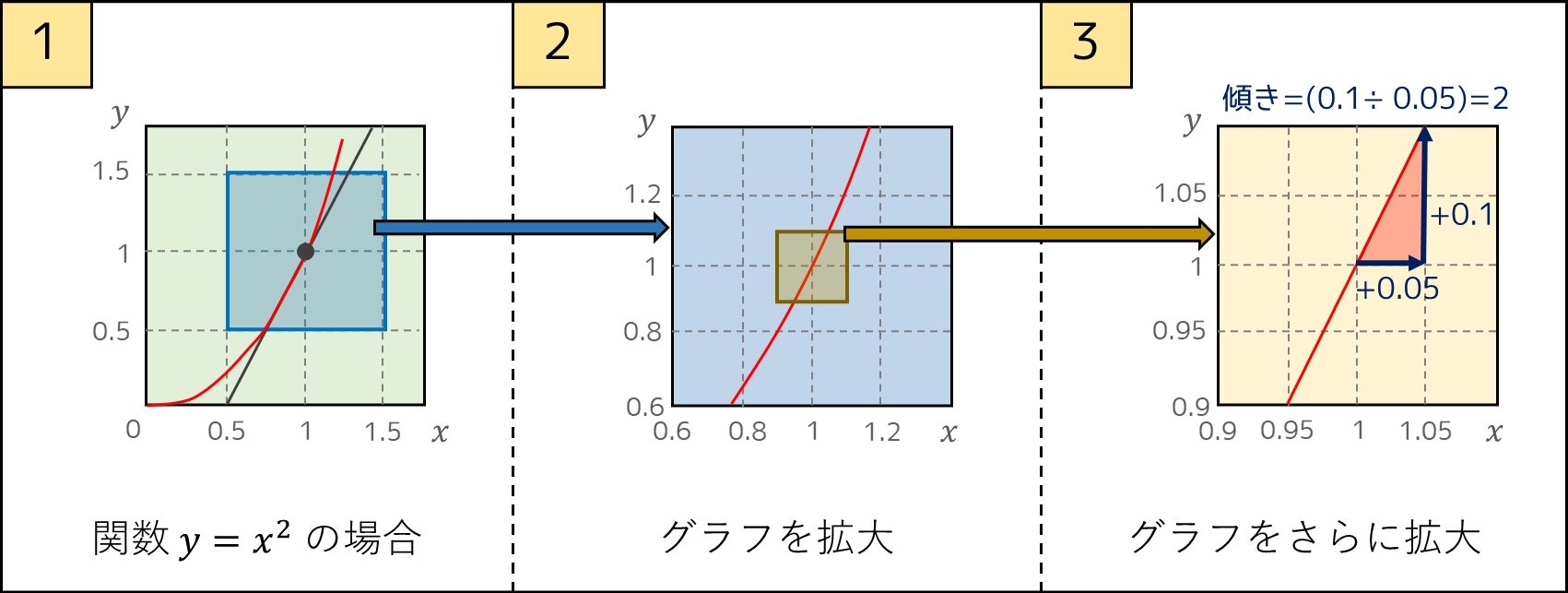
厳密な式で表すと、微分係数を $f'(a)$ とするとき次のようになります。
$$
f'(a) = \lim_{h \to 0} \frac{f(a + h) - f(a)}{h}
$$
例えば、$h = 1$ では $f'(a) = \frac{4-1}{1} = 3$ と計算できてしまいますが、
- $h = 0.5$ では $\frac{2.25-1}{0.5} = 2.5$
- $h = 0.1$ では $\frac{1.21-1}{0.1} = 2.1$
といった感じで、段々と $2$ に近づいていくのが分かると思います。なお、極限については 3-3. 節で解説しています。
どうやって微分係数を求めるか?(数学編)
(i) まず、関数 $f(x) = x^n$ の形で表されるとき、$f'(a)$ の値は次のように求められます。
$f'(a) = n \cdot a^{n-1}$
例えば $y = x^2$ のとき、$f'(1) = 2, f'(5) = 10$
(ii) 次に、関数 $g'(x) = px^n$ の形で表されるとき、$g(x)$ は $y = x^n$ を $y$ 軸方向に $p$ 倍に伸ばしたグラフであることから、$g'(a) = p \cdot f'(a)$ であることが分かります。したがって、$g'(a)$ の値は次のように求められます。
$g'(a) = p \cdot n \cdot a^{n-1}$
(iii) 最後に、関数 $h(x)$ が一般の多項式の場合、$h'(a)$ の値は次のように求められます。例えば $x^2 + 2x + 1$ の場合、$h(x)$ を $x^2$ と $2x$ と $1$ に分解して (ii) の場合に帰着し、その後全部足し合わせるイメージだと、理解しやすいと思います。
$f(x) = p_nx^n + p_{n-1}x^{n-1} + ... + p_1x_1 + p_0$ とする
そのとき、$f'(a) = np_na^{n-1} + (n-1)p_{n-1}a^{n-2} + ... + 2p_2a + p_1$
例えば $f(x) = x^6$ のとき、$f'(1) = 6, f'(10) = 600000$
しかし、より複雑な関数や、連続ではない関数を扱う場合、このような方法が通用しません。コンピュータでは、どのように計算すれば良いのでしょうか。
どうやって微分係数を求めるか?(コンピュータ編)
そこで、微分係数の近似値を求めるにあたって、微分の定義を振り返ってみましょう。
$$
f'(a) = \lim_{h \to 0} \frac{f'(a + h) - f'(a)}{h}
$$
このとき、$h = 0$ で求めるのは無理があるとしても、$h = 10^{-5}$ などにして計算をすることで、十分近似された値が計算できるのです。例えば $y = x^3$ の場合でも、
$$
f'(1) = \frac{1.00001^3 - 1^3}{0.00001} = 3.00003000011...
$$
となり、ほとんど正しい値が計算できました。したがって、たった 2 回の質問で $f'(a)$ の近似値が分かるのです。
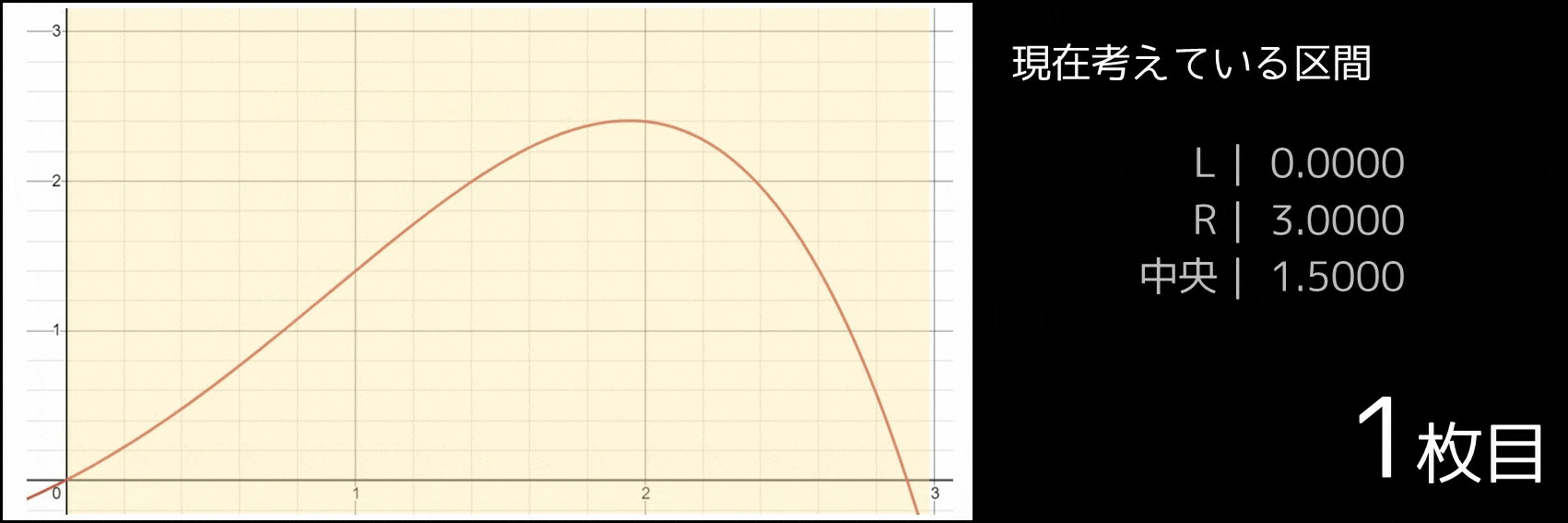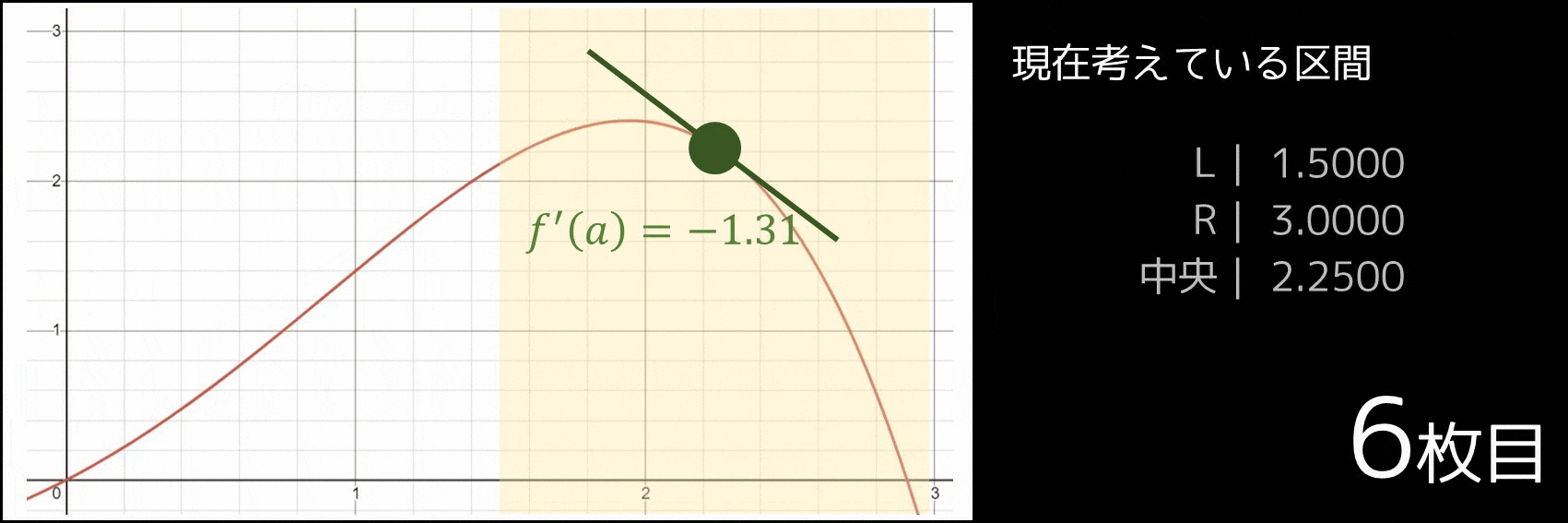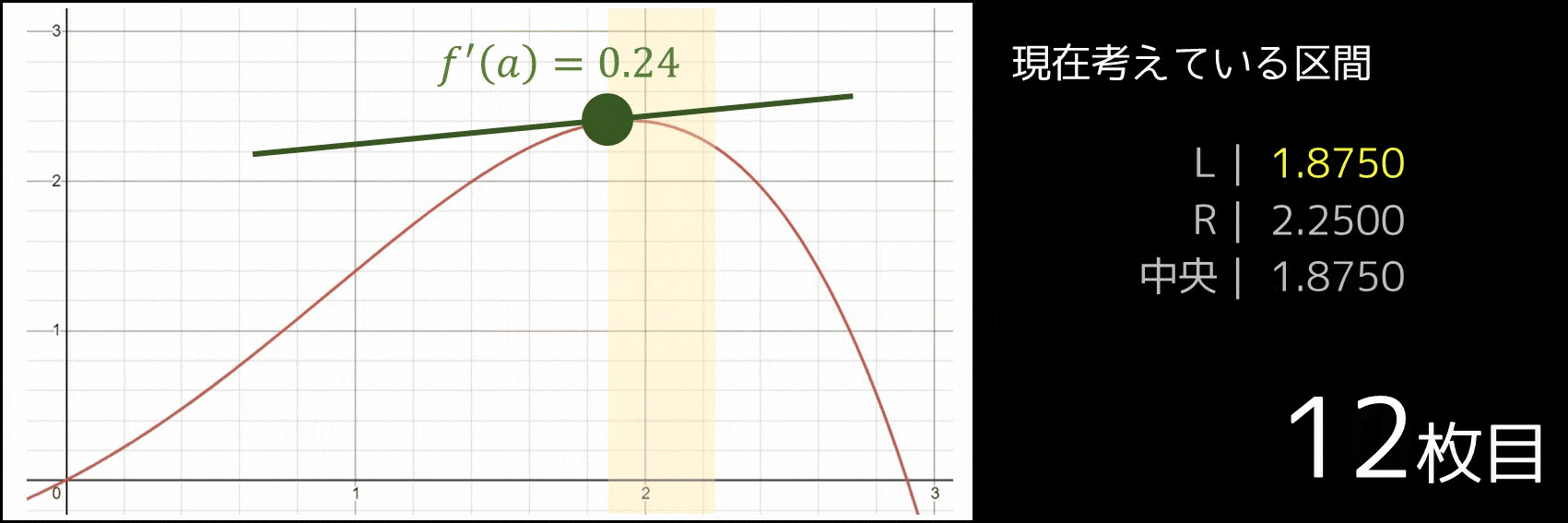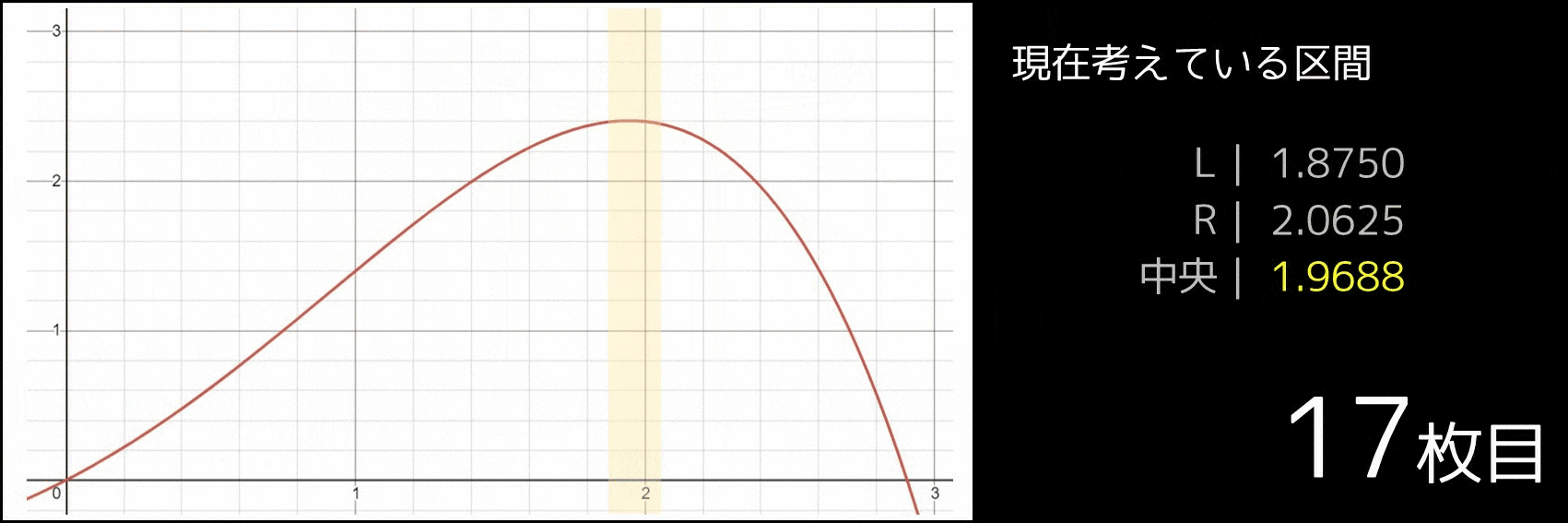
最初の問題の答え
あとは、$x < M$ では $f'(x) > 0$、$x > M$ では $f'(x) < 0$ となるため、次表のように二分探索をしていけば良いです。($y = -0.1x^4 + 0.5x^2 + x$ の場合の例です。最初から最大値を取る $x$ の位置が $0$ 以上 $3$ 以下であることが分かっているものとします)
補足(関連する解法)
微分と直接関係はしませんが、似た解法として三分探索が挙げられます。詳しくは
をご覧ください。ただし、質問回数が $30$ 回の場合の精度については、
- 三分探索による解法が、絶対誤差 $3 \div \left( 1.5^{30 \div 2} \right) = 0.00685...$
- 微分法 + 二分探索による解法が、絶対誤差 $3 \div \left( 2^{30 \div 2} \right) = 0.00009...$
となり、後者の方がアルゴリズムの効率が良いです。なお、今回紹介した問題は $f(x)$ が一般の多項式の場合にも解くことができます。これについては 5 章の演習問題に載っていますので、是非ご覧ください。
4-13. 勾配降下法に学ぶ、偏微分(レベル: 4)
4)
まず、以下の問題を考えてみましょう。
パラメータ $x_1, x_2, ..., x_n$ に対して、評価関数 $f(x_1, x_2, ..., x_n)$ が決まっています。
評価関数ができるだけ小さくなるようなパラメータ $x_1, x_2, ..., x_n$ を求めて下さい。
さて、どのように解けるのでしょうか。
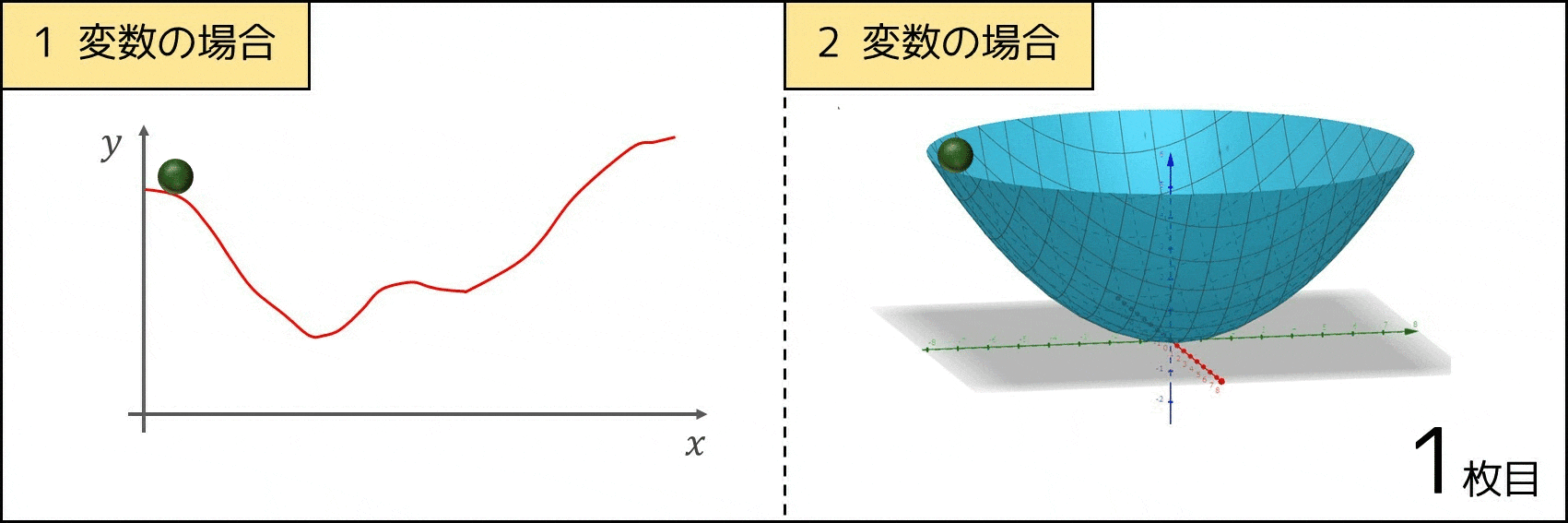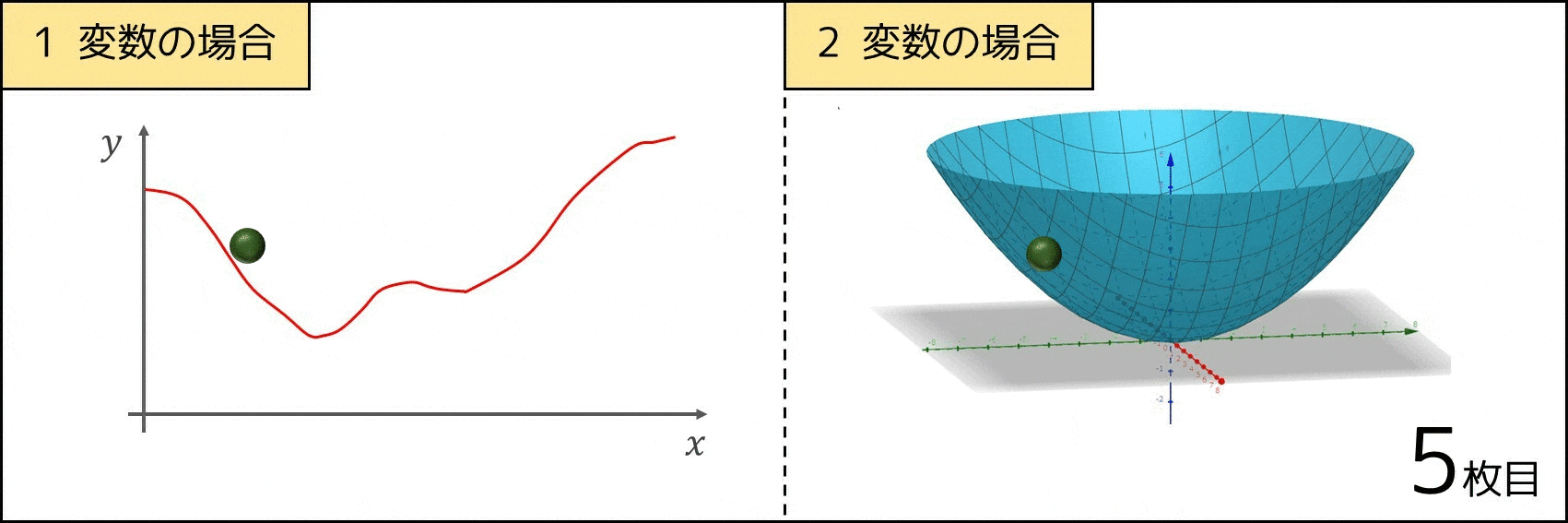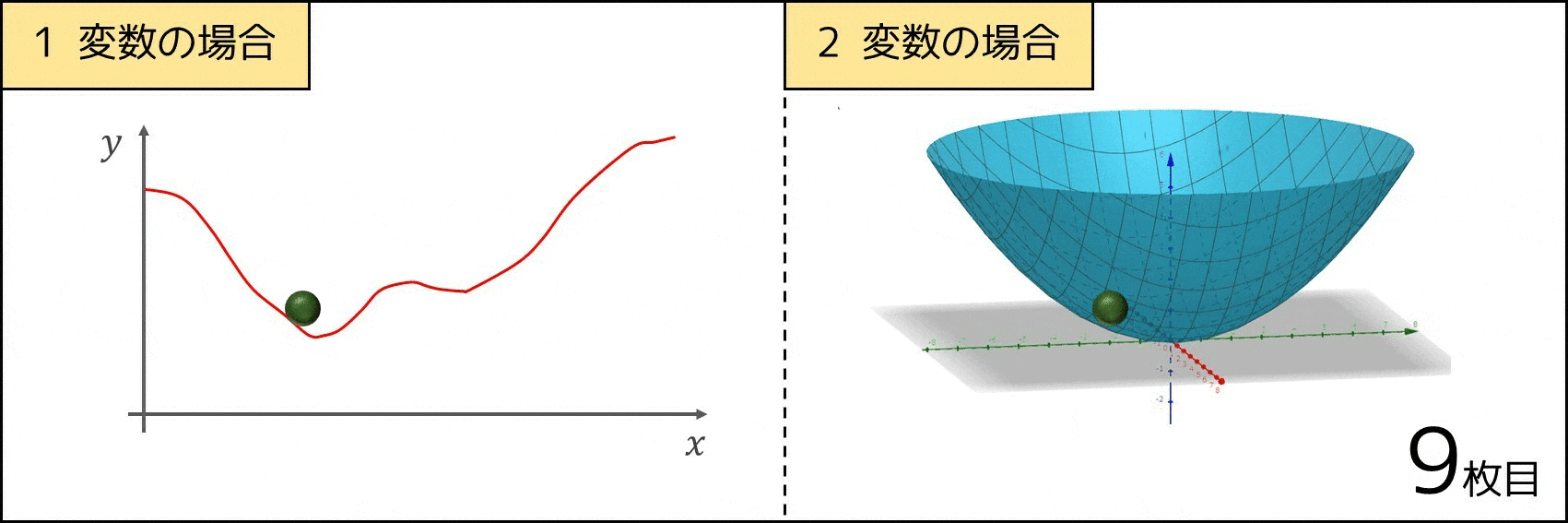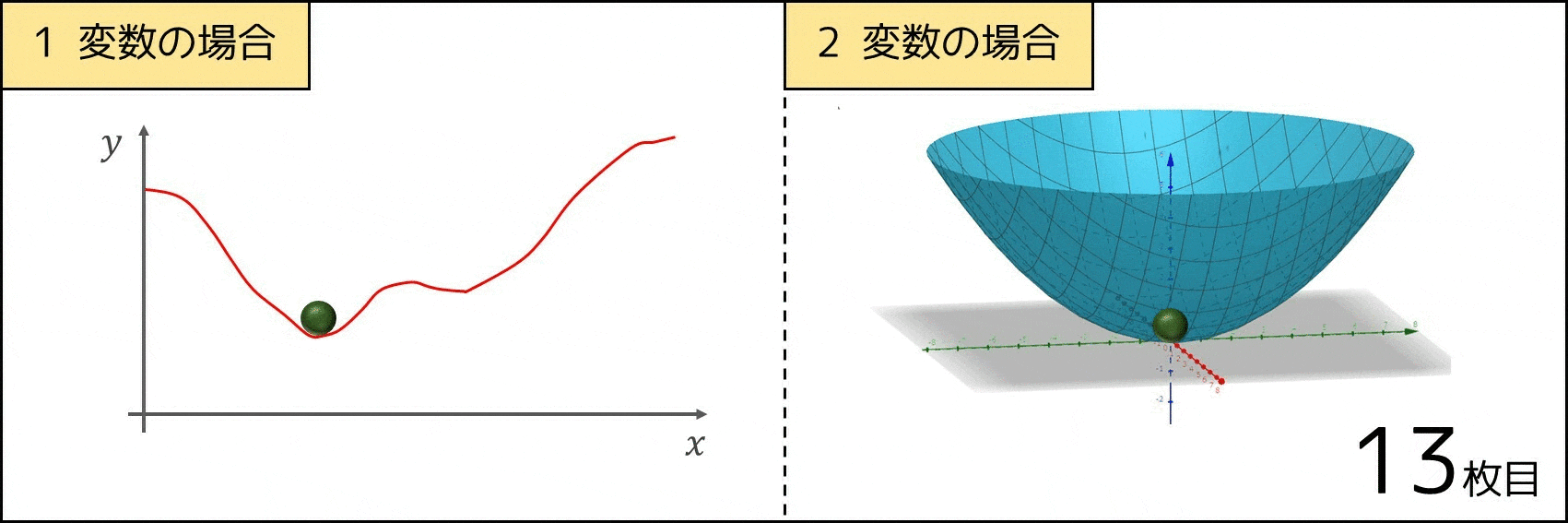
1 つのアイデアとしては、「球をある場所に置くと物理現象的に高さの低いところに移動するので、それをシミュレーションして最終的に止まった場所を求める」といった方法が挙げられます。これを数式に表した上で実装したのが勾配降下法なのです。
偏微分とは何か
では、次に移動する方向はどのようにして求めるのか。これは偏微分によって計算できます。偏微分は「微分を 2 変数関数以上に拡張させたもの」であり、次の通りのイメージです。
$x_1, x_2, ..., x_n$ のうち、ある $1$ つの変数 $x_i$ を $h$($0$ に近い正の実数)増やし、他の変数 $x_1, ..., x_{i-1}, x_{i+1}, ..., x_n$ を固定したとき、評価関数 $f(x_1, x_2, ..., x_n)$ の値が $h$ の何倍くらいずれるかを求める。これを「関数 $f$ を $x_i$ について偏微分する」という。
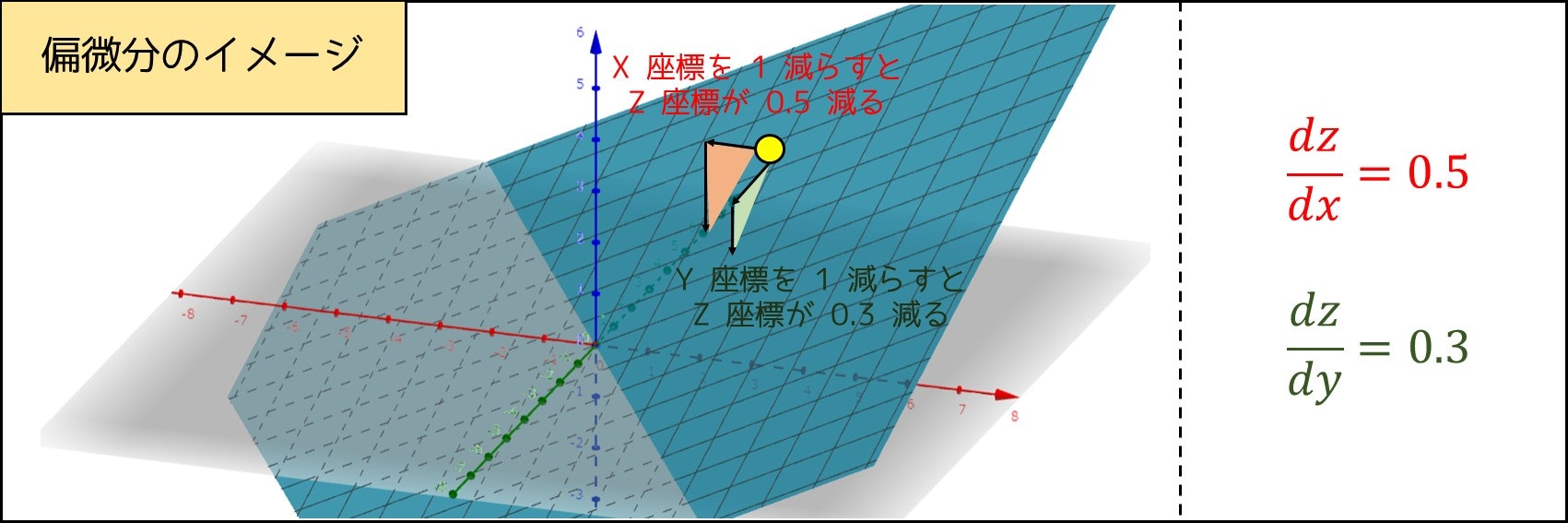
図で表すと、こんな感じのイメージです。
なお、関数 $f$ の $x_i$ についての偏微分を $\frac{df}{dx_i}$ のように表します。
偏微分の例
上の説明だけでは分かりにくいと思うので例を挙げます。関数 $f(x, y) = x^2 + xy + y^2$ を考えてみましょう。そこで $x$ の値を $h=0.01$ だけ増やした場合、
$$
f(x + 0.01, y) - f(x, y) = (0.02x + 0.0001) + 0.01y
$$
となり、評価値が $(2x + y + 0.01) \times h$ だけ変わっていることが分かります。また $h$ をさらに小さくすると、変化量が $(2x + y) \times h$ に近づきます。このように、求める偏微分の値は、
$$
\frac{df}{dx} = 2x + y
$$
と書き表すことができるのです。この式に従って計算すると、$f(3, 2)$ の $x$ についての偏微分係数が $2 \times 3 + 2 = 8$ であることが分かります。同様に、$y$ 方向の偏微分は次の通りです。
$$
\frac{df}{dy} = x + 2y
$$
偏微分を使って、どのように次に動く方向を計算できるか
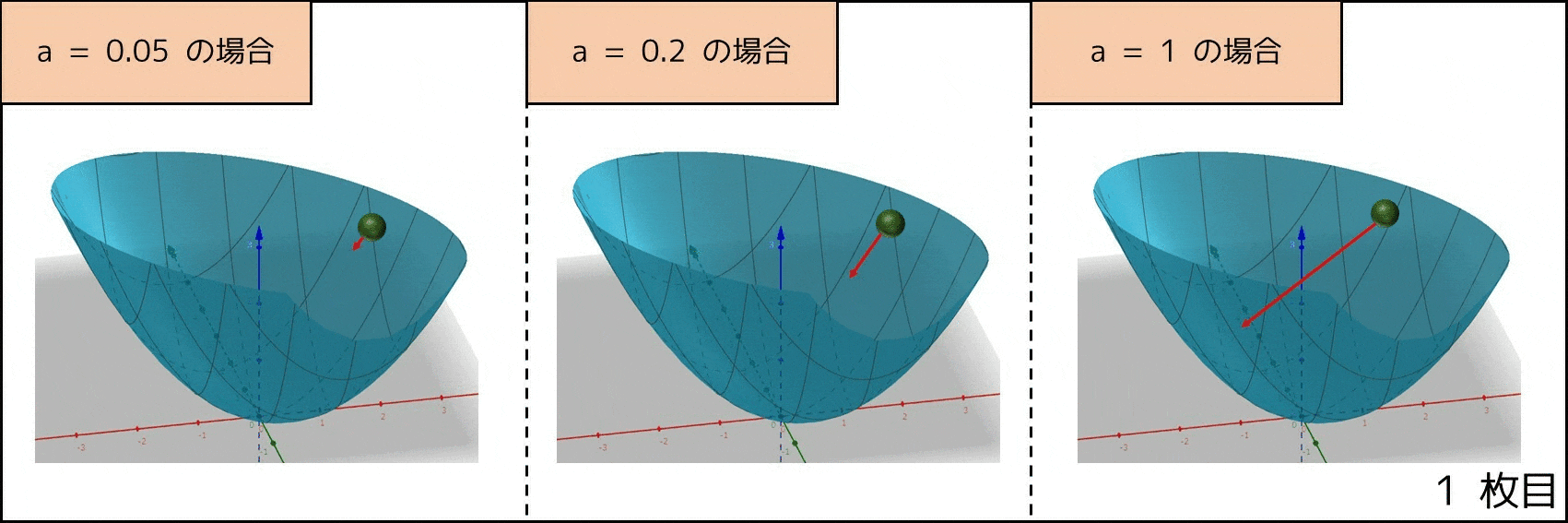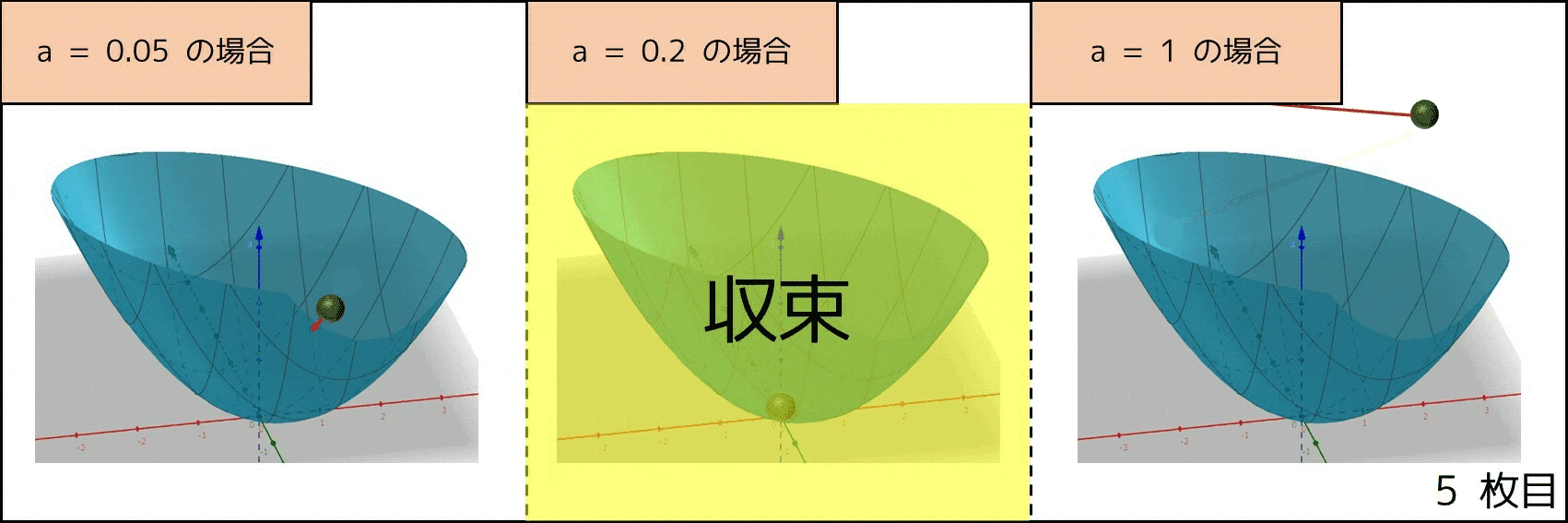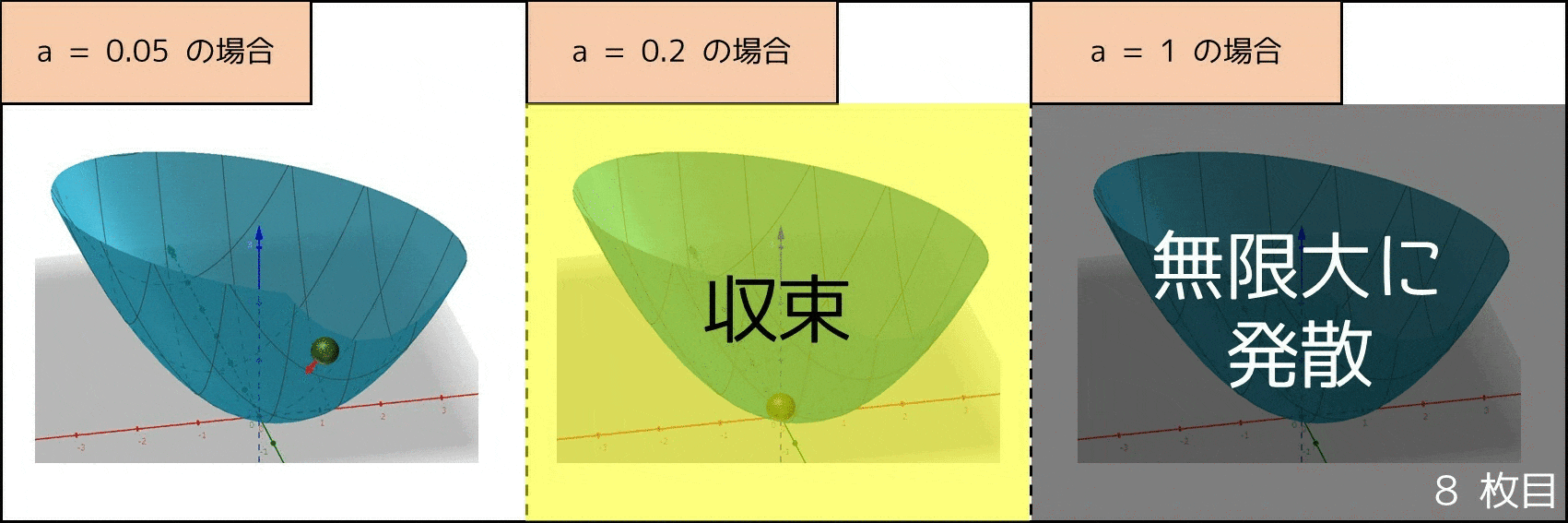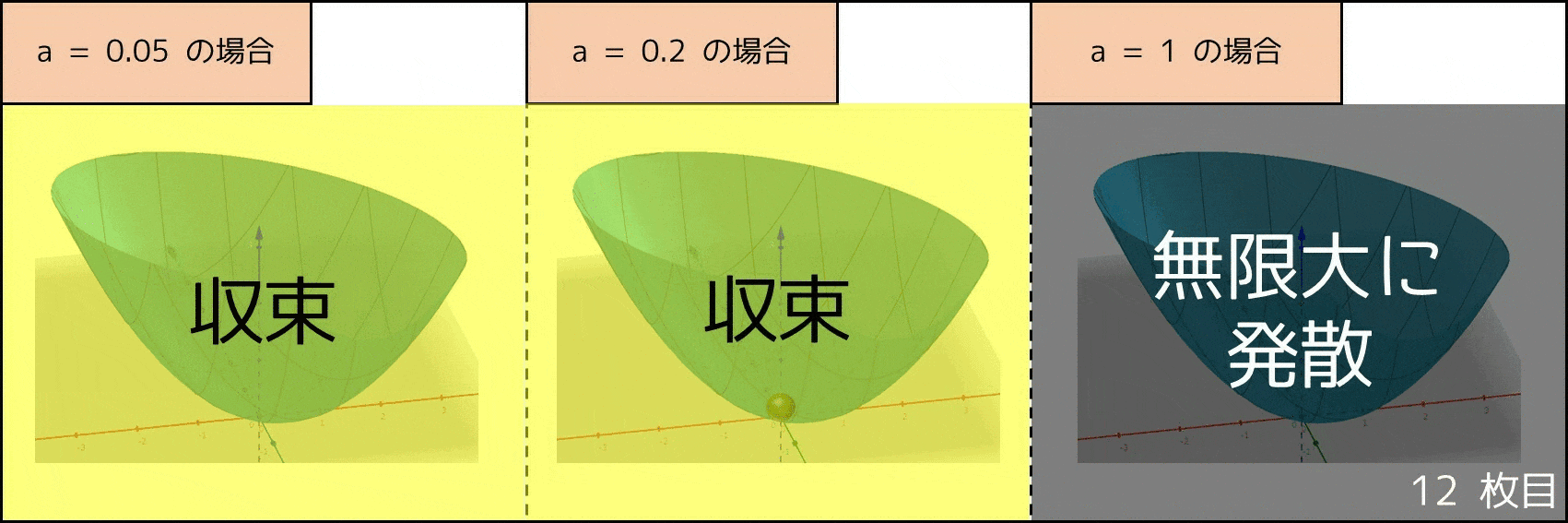
基本的に、物体は傾きが大きい方向に動くので、各変数に対する偏微分の値が $d_1, d_2, ..., d_n$ の場合、各変数をそれぞれ $(-ad_1, -ad_2, ..., -ad_n)$ だけ動かせば良いです($a$ は定数)。そこで、関数 $f(x) = x^2 + xy + y^2$ に対して $a = 0.2$ の場合、次のようにプログラムが動きます。評価値が段々と減っていくのが分かると思います。
| (x, y) の値 | 関数 f(評価値) | x の偏微分 | y の偏微分 | 次に動く方向 |
|---|---|---|---|---|
| (2.0000, 1.0000) | 7.0000 | 5.0000 | 4.0000 | (-1.0000, -0.8000) |
| (1.0000, 0.2000) | 1.2400 | 2.2000 | 1.4000 | (-0.4400, -0.2800) |
| (0.5600, -0.0800) | 0.2752 | 1.0400 | 0.4000 | (-0.2080, -0.0800) |
| (0.3520, -0.1600) | 0.0932 | 0.5440 | 0.0320 | (-0.1088, -0.0064) |
| (0.2432, -0.1664) | 0.0464 | 0.3200 | -0.0896 | (-0.0640, 0.0179) |
なお、$a$ の値が大きい方が早く収束しますが、$a$ の値があまりにも大きいと $x, y$ の値が無限に大きくなる(発散する)リスクがあります。したがって、勾配降下法では適切に $a$ の値を調整するのは重要です。また、すべての評価関数でこの手法が上手くいくとは限らず、例えば評価値が周りより小さい地点が 2 箇所以上あった場合、局所的最適解に陥る可能性があります。
4-14. 累積和に学ぶ、積分法
まず、以下の問題を考えてみてください。
長さ $N$ の整数列 $A = (A_1, A_2, ..., A_N)$ がある。
以下の $Q$ 個の質問に全部答えてください。
$i$ 個目の質問:$A_{L_i} + A_{L_i + 1} + ... + A_{R_i}$ の値を出力する。
この問題は、二重ループを用いて単純に足し算をすると、$O(NQ)$ かかってしまい、例えば $N, Q = 10^6$ のデータでは、実行が終わるまでに 1 分以上かかってしまいます。
for (int i = 1; i <= Q; i++) {
int sum = 0;
for (int j = L[i]; j <= R[i]; j++) {
sum += A[j];
}
}
アルゴリズムの改善
そこで、次のような方法によって、計算量を改善することができます。
- $B_i = A_1 + A_2 + ... + A_i$ とする。
- そこで、$B_0, B_1, B_2, ..., B_N$ の値を前もって記録しておく。
- これは、$B_i = B_{i-1} + A_i$ とすると、累積的に計算できる。
そのとき、$(A_L + A_{L+1} + ... + A_R) = B_R - B_{L-1}$ と計算できるため、計算量が $O(N+Q)$ となり、$N, Q = 10^6$ 程度でも 1 秒以内で実行を終わらせることができます。例えば $A = (3, 1, 4, 1, 5, 9, 2, 6)$ の場合次図のようになります。
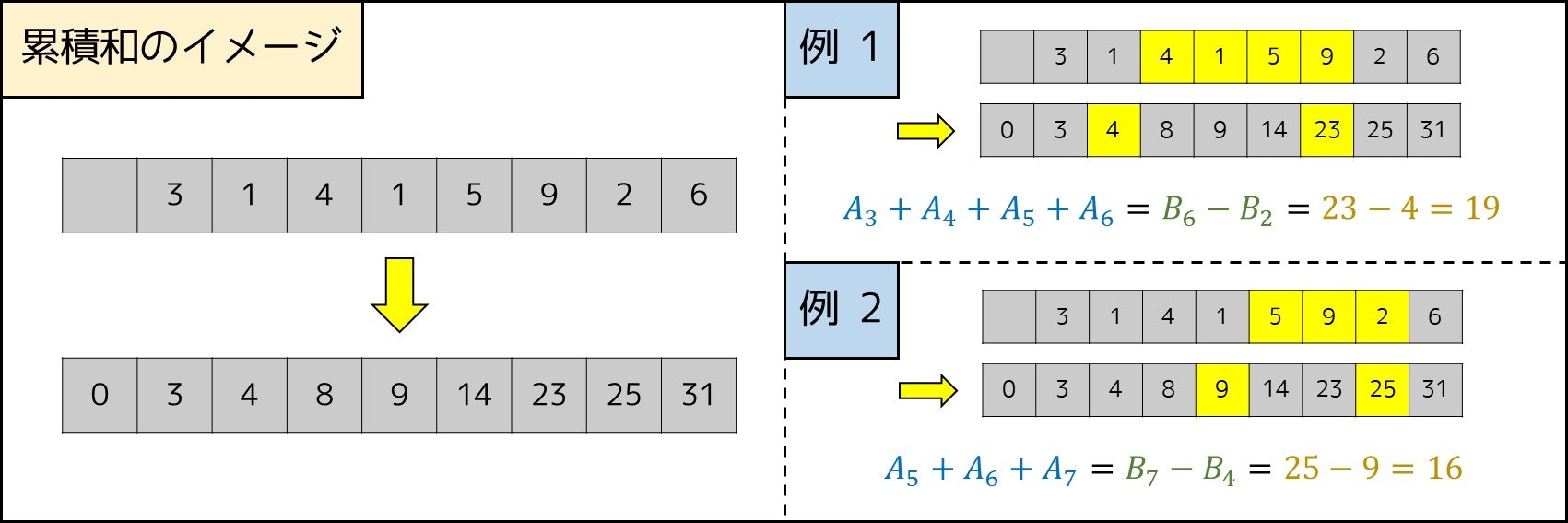
このような手法を累積和といいます。詳しくは、
をご覧ください。
さて、ここまでアルゴリズムの説明ばかり書きましたが、どのような点で積分法と関係があるのでしょうか。まず、「積分とはどういうものか」について紹介します。
積分とは何か
分かりやすく説明すると、積分は基本的に面積のイメージです。
車の速度を例にとると、「時刻 $x$ には車が $f(x)$ メートル毎秒で前に向かって走っているとき、時刻 $a$ から時刻 $b$ までに何メートル進みましたか」といったものを計算するのが定積分です。一般に、関数 $f(x)$ に対する区間 $[a, b]$ における定積分の値は、
$$
\int_{a}^{b} f(x) \ dx
$$
と表され、下図の黄色部分の面積から青色部分の面積を差し引いた値となっています。
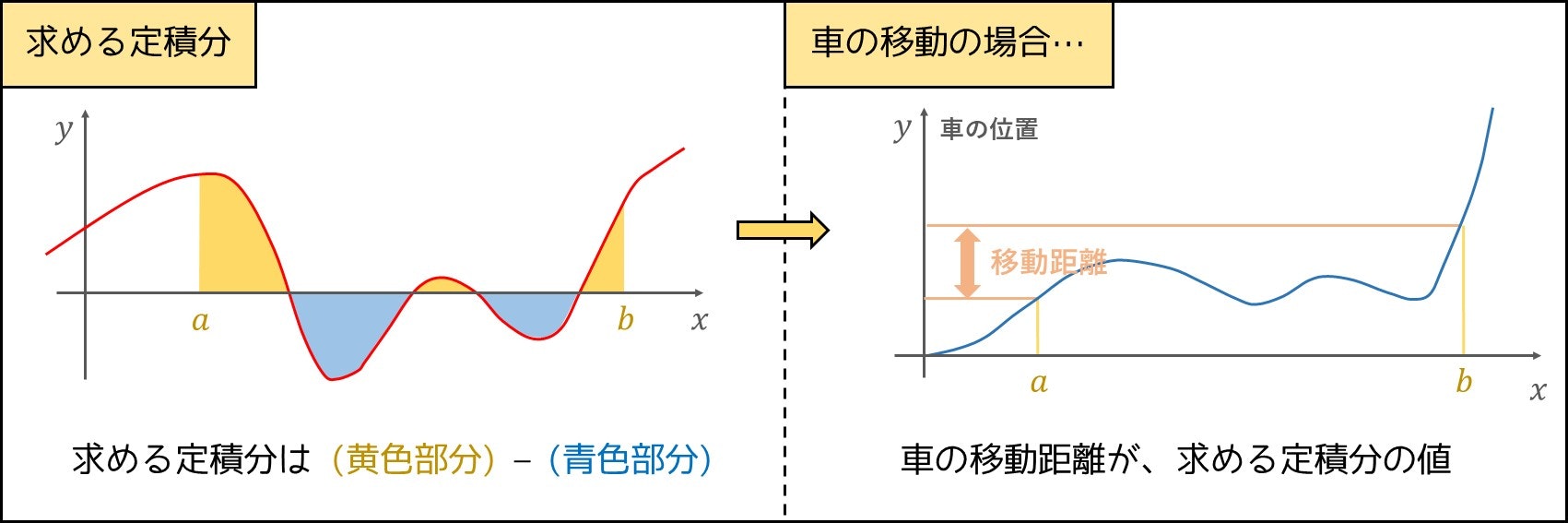
累積和との関係
図を見た感じ、累積和と似ているように感じませんでしたか?
実は非常によく似ています。$A_i$ の値が「車の速度」、$B_i$ の値が「車の位置」といった関係になっているのです。もう少し厳密に関数を用いて表すと、
f(x) = 0 \ (x < 0, N \leq x) \\
f(x) = A_i \ (i-1 \leq x < i, 1 \leq i \leq N)
とするとき、
B_i = \int_{0}^{i} f(x) \ dx \\
A_L + A_{L+1} + ... + A_R = \int_{L-1}^{R} f(x) dx = \int_{0}^{R} f(x) dx - \int_{0}^{L-1} f(x) dx = \left(B_R - B_{L-1}\right)
となるのです。これは、微分と積分が一対一関係となっているように、数列 $A_i$ と累積和 $B_i$ が一対一関係になっているということを意味します。積分法と累積和は非常によく似ていたのです。
4-15. フィボナッチ数の計算に学ぶ、行列累乗(レベル: 3)
3)
まず、以下の問題を考えてみましょう。3-4. 節でも取り上げた問題です。
- $a_1 = 1, a_2 = 1$
- $a_N = a_{N-1} + a_{N-2} \ (N \geq 3)$
とします。そのとき、$T$ が与えられるので $a_T$ を $10^9+7$ で割った余りを求めてください。
つまり、フィボナッチ数の第 $T$ 項を求めてください。
この問題は、再帰関数を使って解くこともできますが、漸化式を $a_3, a_4, a_5, ...$ と順番に、問題文に書かれた通りに計算していく手法でも解けます。計算量は $O(N)$ です。
int a[1009], N;
cin >> N;
for (int i = 3; i <= N; i++) {
if (i == 1) a[i] = 1;
if (i == 2) a[i] = 1;
if (i >= 3) a[i] = a[i - 1] + a[i - 2];
}
cout << a[N] << endl;
しかし、この形のままだと高速化しにくいので、次のように漸化式を変えてみましょう。
$a_{2, 1} = 1, a_{2, 2} = 1$
$a_{N, 1} = a_{N - 1, 1} + a_{N - 1, 2} \ (N \geq 3)$
$a_{N, 2} = a_{N - 1, 1} \ (N \geq 3)$
1 項前の値しか見ずに計算できるので便利です。実際、これを経路図のような形に表してみると、次のような感じになります。矢印が入っているところを足し算すると計算できます。
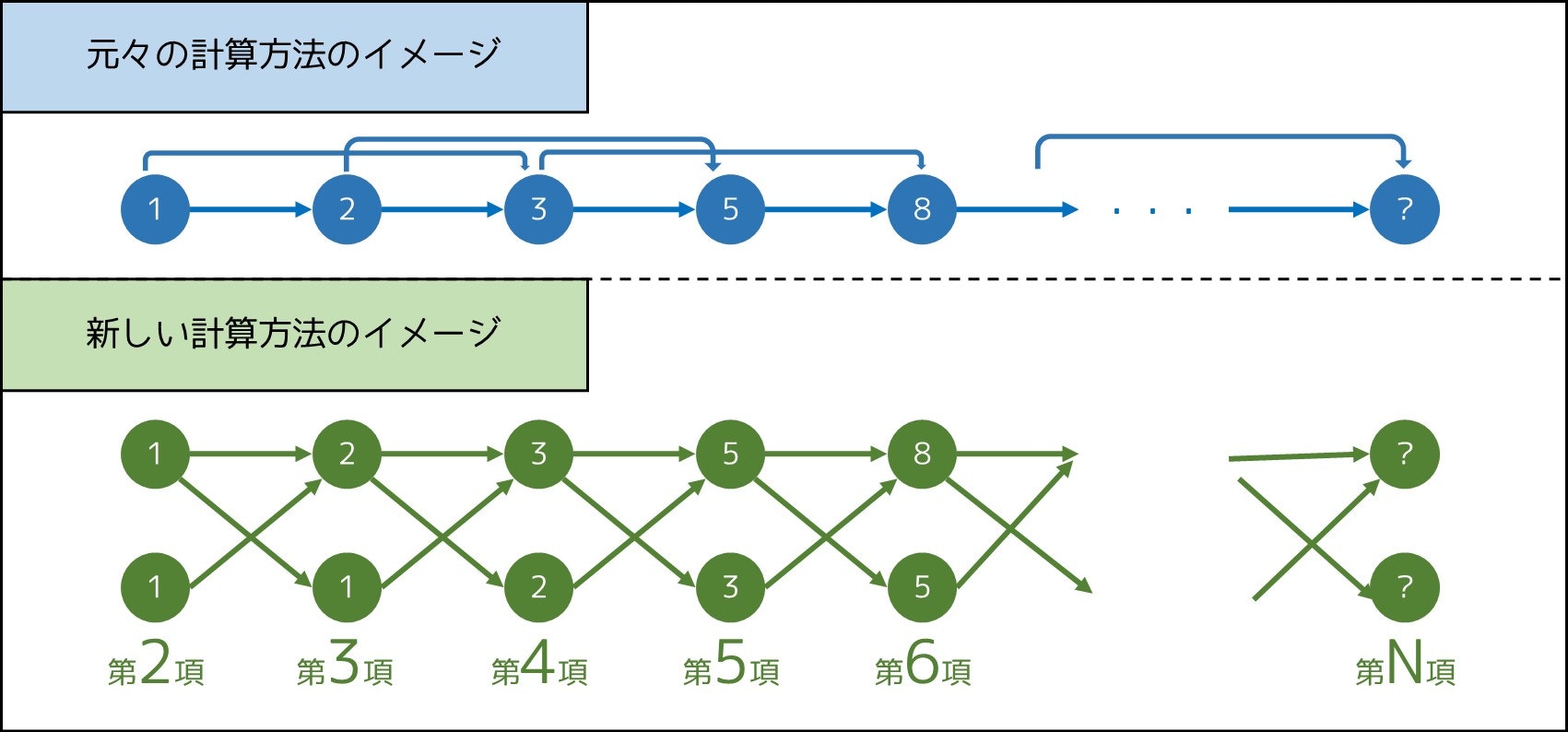
しかし、それでも計算量は $O(N)$ と変わりません。どうやって計算を効率化することができるのでしょうか。そこで、2-12. 節で紹介した行列を導入します。
知識:行列の掛け算
一般に、行列 $P$($A \times B$ 行列1)、行列 $Q$($B \times C$ 行列)の積 $R=PQ$ は $A \times C$ 行列となり、その各成分 $(i, j)$ の値は以下のように表せます。
$$
R_{i, j} = \sum_{k=1}^{B} \left( P_{i, k} \times Q_{k, j} \right)
$$
例えば、次の式が成り立ちます。
\begin{pmatrix}
8 & 6 & 9 \\
1 & 2 & 0
\end{pmatrix}
\begin{pmatrix}
10 \\
0 \\
1
\end{pmatrix}
=
\begin{pmatrix}
8 \times 10 + 6 \times 0 + 9 \times 1 \\
1 \times 10 + 2 \times 0 + 0 \times 1
\end{pmatrix}
=
\begin{pmatrix}
89 \\
10
\end{pmatrix}
行列の計算に落とし込む
まず、第 $4$ 項と第 $5$ 項の関係を観察してみましょう。行列を使って次のように表せます。
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
3 \\
2
\end{pmatrix}
=
\begin{pmatrix}
5 \\
3
\end{pmatrix}
次に、第 $3$ 項と第 $4$ 項の関係を観察してみましょう。
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
2 \\
1
\end{pmatrix}
=
\begin{pmatrix}
3 \\
2
\end{pmatrix}
次に、第 $2$ 項と第 $3$ 項の関係を観察してみましょう。
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
1 \\
1
\end{pmatrix}
=
\begin{pmatrix}
2 \\
1
\end{pmatrix}
それら $3$ つの情報から何が分かるのでしょうか。次のようになります。なお、行列の積は結合的であるため、どのような計算順序で計算を行っても答えは変わりません。(行列 $A, B, C$ について、$A \times (B \times C) = (A \times B) \times C$ が成り立ちます)
\begin{pmatrix}
5 \\
3
\end{pmatrix}
=
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
3 \\
2
\end{pmatrix}
=
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
2 \\
1
\end{pmatrix}
=
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}
\begin{pmatrix}
1 \\
1
\end{pmatrix}
=
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}^{3}
\begin{pmatrix}
1 \\
1
\end{pmatrix}
このように考えていくと、一般にフィボナッチ数の第 $N$ 項は、次の計算によって求められる行列の $(1, 1)$ 成分であることが分かります。
\begin{pmatrix}
1 & 1 \\
1 & 0
\end{pmatrix}^{N-2}
\begin{pmatrix}
1 \\
1
\end{pmatrix}
あとは行列累乗を求められればよい
では行列 $A$ の $N-2$ 乗はどうやって計算できるのでしょうか。これは繰り返し二乗法(3-10. 節で紹介済)を応用できます。$A^1, A^2, A^4, A^8, A^{16}, ...$ を前もって計算しておくことで、$A^N$ の値も高速に求められるのです。例えば、
$$
A^{47} = A^{32} \times A^{8} \times A^{4} \times A^{2} \times A^{1}
$$
という式になります。つまり、$2 \times 2$ 行列同士の掛け算にかかる計算量を $O(1)$ とすると、僅か $O(\log N)$ でフィボナッチ数の第 $N$ 項を $10^{9} + 7$ で割った余りが分かるのです。このように、行列の演算を使うと、$N = 10^{18}$ 程度の場合でも一瞬でこの問題を解けます。
4-16. XOR 部分和問題と行列の掃き出し法(レベル: 4)
4)
まず、以下の問題を考えてみましょう。(XOR については 2-5. 節参照)
$N$ 枚のカードが一列に並べられており、左から $i$ 番目のカード(以降カード $i$ とする)には整数 $A_i$ が書かれている。$N$ 枚のうちいくつかを選ぶ方法の中で、選んだカードに書かれた整数を全部 XOR した値がちょうど $T$ となるようなものは存在するか、判定せよ。
カードの選び方を $2^N$ 通り全探索する方法が考えられますが、これは $N = 100$ の時点で $10^{30}$ 通り以上の探索が必要となり、効率が悪いです。これ以上高速化することはできないのでしょうか。
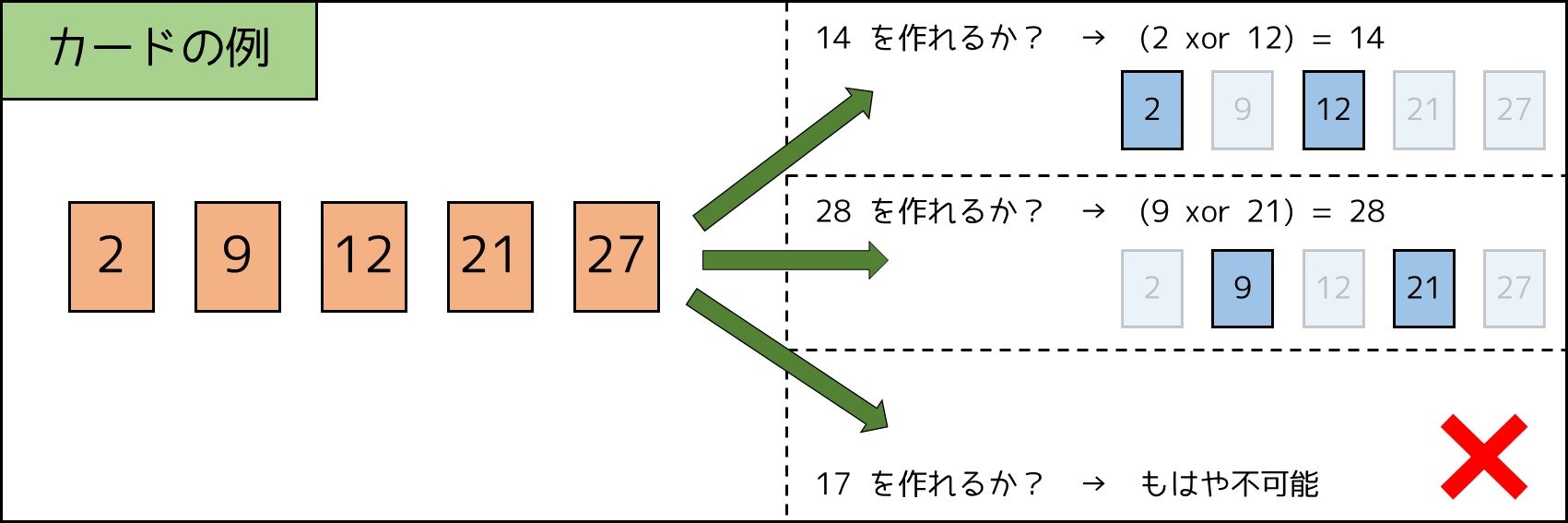
ステップ 1. 重要な性質を使う
そこで、以下のような性質が成り立ちます。これは行基本変形と似た性質です。
整数 $i, j$ を選び、$A_i$ の値を $A_i \ xor \ A_j$ に変更する操作を行っても、作れる数の集合は変わらない。どのような $i, j$ を選んでも、この性質が成り立つ。
例えば $A = (3, 5, 6)$ の場合を考えましょう。このとき、作れる数の集合は $S = \{0, 3, 5, 6\}$ であり、どのように整数を選んでも $1$ などを作ることはできません。その後、$i = 1, j = 2$ を選んで操作すると $A' = (3 \ xor \ 5, 5, 6) = (6, 5, 6)$ となりますが、作れる数の集合は $\{0, 3, 5, 6\}$ のままです。
操作前と操作後で、できる数が同じになるようなカードの選び方が、次表のように一対一対応することから証明できます。例えば、$i = 1, j = 2$ の操作を行った場合、
- 操作前に番号 $\{1, 3\}$ のカードを選んだときにできる数
- 上の例だと $3 \ xor \ 6 = 5$
- 操作後に番号 $\{1, 2, 3\}$ のカードを選んだときにできる数
- 上の例だと $6 \ xor \ 5 \ xor \ 6 = 5$
が同じです。
| 元々の選び方 | 操作後の選び方 | XOR した値(操作前の値) |
|---|---|---|
| カード $i, j$ 両方選ばない場合 | カード $i, j$ 両方選ばない | $0$ |
| カード $i$ のみ選ぶ場合 | カード $i, j$ 両方選ぶ | $A_i$ |
| カード $j$ のみ選ぶ場合 | カード $j$ のみ選ぶ | $A_j$ |
| カード $i, j$ 両方選ぶ場合 | カード $i$ のみ選ぶ | $A_i \ xor \ A_j$ |
ステップ 2. 行列に変形すると上手くいくのでは?
次に、行う操作が行列の行基本変形(大学の線形代数という分野で習います)と似ているため、行列の形にしてみましょう。
XOR などの論理演算を扱う際は、ビットごとに分ければ便利なので、$N \times B$ 行列 $F$ を用意し、$(i, j)$ 成分を「$A_i$ を 2 進数で表したときの $j$ 桁目」とします、例えば、$A = (27, 21, 12, 9, 2), B = 7$ の場合、行列 $F$ は次のようになります。
F =
\begin{pmatrix}
0 & 0 & 1 & 1 & 0 & 1 & 1 \\
0 & 0 & 1 & 0 & 1 & 0 & 1 \\
0 & 0 & 0 & 1 & 1 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 & 1 \\
0 & 0 & 0 & 0 & 0 & 1 & 0
\end{pmatrix}
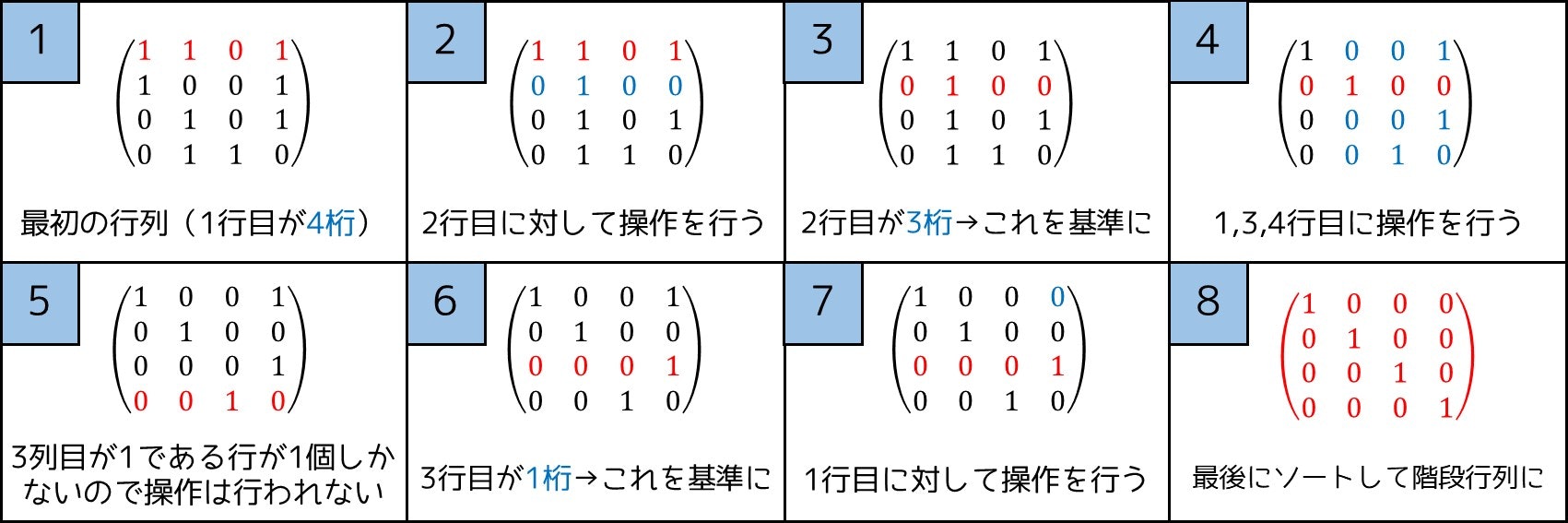
ステップ 3. 行基本変形を繰り返して「階段行列」にする
そこで、以下の性質が成り立つのです。これは、任意の行列が「行基本変形」を繰り返すことで階段行列(こちらのリンクで調べてください)になる性質と非常に良く似ています。
操作(整数 $i, j$ を選び、$i$ 行目の値に $j$ 行目の値を $xor$ するもの)を適切に行うことで、$F$ を階段行列にすることができる。
これは、次のようなアルゴリズムを使うことで実現できます。全体計算量は $O(NB)$ です。
ただし本節での「$u$ 桁となっている行」は、$1, 2, ..., B-u$ 列目が全部 $0$ であり、$B-u+1$ 列目が $1$ であるような行のことを指します。
- $r = 1, 2, 3, ..., B$ の順に、次の操作を行う。
- $B-r+1$ 桁の行が存在しなければ、何も行わない。
- $B-r+1$ 桁の行が存在するとき、その中で行番号が最小のものを $t$ 行目とする。
- そこで、$(p, r)$ 成分が $1$ であるような $p \ (p \neq t)$ について、$i = p, j = r$ として操作を行う。
- それによって、$B-r+1$ 桁の行はただ $1$ つしか存在しなくなる。
なお、このアルゴリズムは「行列の掃き出し法」の 1 つです。詳しくは
ステップ 4. 最後に判定問題を解く
では、$A_1, A_2, ..., A_N$ に「2 進数で同じ桁数のもの」が存在しない場合、どのようにして解くのでしょうか。これは一番上の行($A_i$ が最も大きいもの)から貪欲に取っていけばよいです。例えば、$T = 8$ を作れるかどうか判定する問題は、次のような感じで解けます。
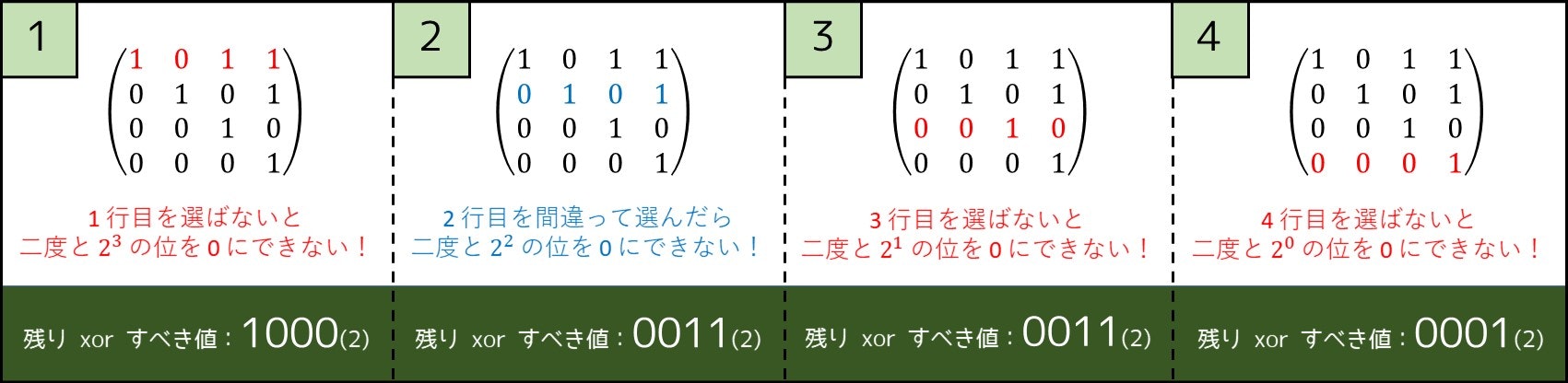
4-17. 離散数学に学ぶ、グラフ理論(レベル: 2)
2)
いよいよ 3・4 章で紹介する「アルゴリズムと密接に関わる数学」も、残り少なくなってきました。本節では、最短経路問題・最小全域木問題などを解くにあたって必要なグラフ理論についてまとめます。
グラフを使ったアルゴリズム(深さ優先探索(DFS)・幅優先探索(BFS)・ダイクストラ法・ワーシャルフロイド法・クラスカル法など)まで説明したらキリがなく、数学と少し離れてしまうので、本節では重要な用語の説明にとどめておきます。
グラフとは何か?
アルゴリズムにおける文脈でのグラフ(Graph)とは、頂点と辺で構成されるデータ型のことを指します。Excel で書くような、関数 $y = f(x)$ のグラフとは少し違うのでご注意ください。
下図において、円のようなものが頂点、直線のようなものが辺だと思ってよいです。電車の路線図や道路網を想像してみれば分かりやすいと思います。
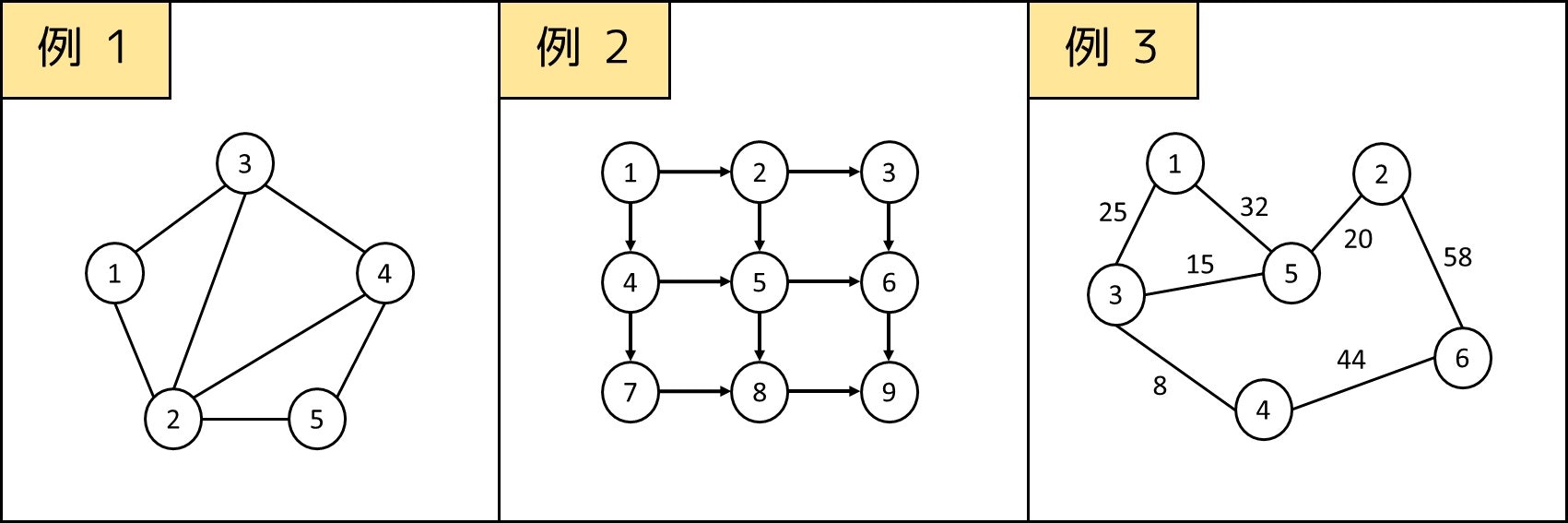
グラフは辺の向きが存在するかどうかに応じて「有向グラフ」「無向グラフ」に大別されます。例 1・例 3 は無向グラフで、例 2 は有向グラフです。用途に応じて使い分けることが重要で、例えば、
- 一方通行の道路が存在する
といった場合、有向グラフの方が管理しやすいですね。
また、辺の重みが存在するかどうかに応じて「重みなしグラフ」「重み付きグラフ」に大別されます。例 1・例 2 は重みなしグラフで、例 3 は重み付きグラフです。これも使い分けが重要で、例えば、
- 通る駅の数の最小値を求めたい場合、重みなしグラフ
- 移動距離の最小値を求めたい場合、重み付きグラフ(道路によって長さが異なるため)
の方が都合よいですね。
どのような問題でグラフ理論が使えるか?
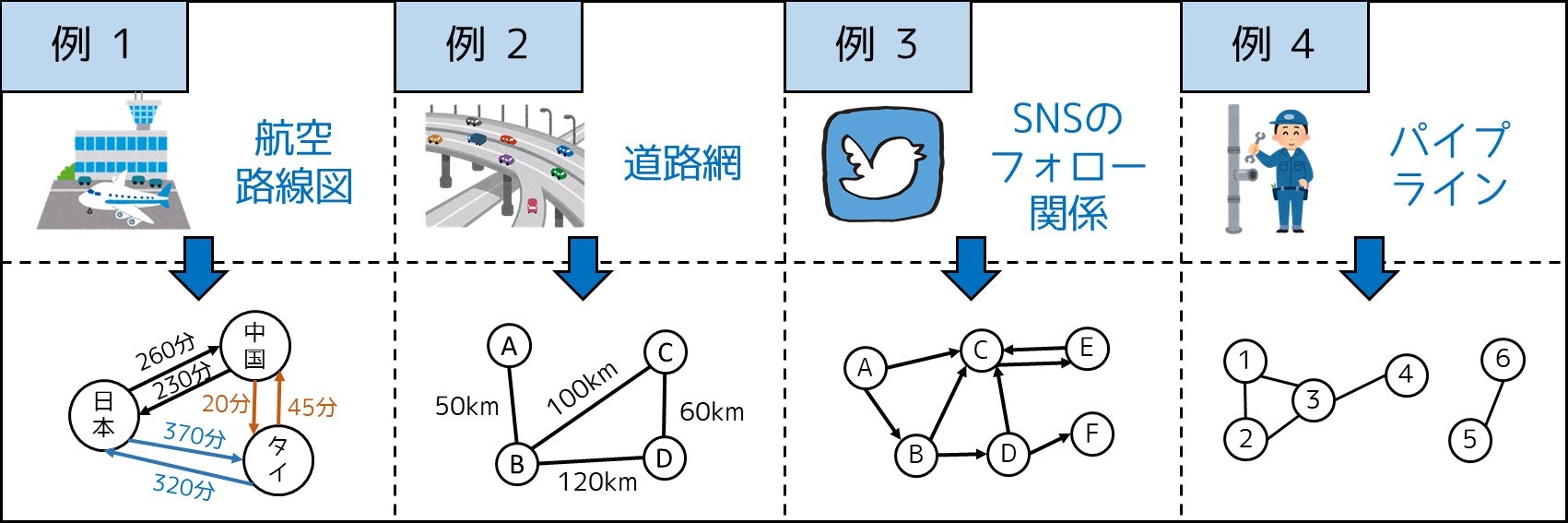
さて、グラフ理論というデータ型を使うことには、どのようなメリットがあるのでしょうか。実は、グラフは万能と言って良いほど、様々なものがグラフで表すことができます。例えば、
- 航空路線図を重み付き有向グラフで表す
- 道路網を重み付き無向グラフで表す
- SNS のフォロー関係を重みなし有向グラフで表す2
- パイプラインを重みなし無向グラフで表す
といった例が挙げられます。
したがって、グラフ理論を学ぶと、解ける問題の範囲が相当広がります。
グラフの表記方法について
次に、グラフの表記方法について解説します。
- 頂点の集合を $V$、頂点の数を $|V|$ と表記することが多いです。
- 辺の集合を $E$、辺の数を $|E|$ と表記することが多いです。
- グラフ全体を $G$ と表し、頂点の集合が $V$、辺の集合が $E$ であるようなグラフを $G(V, E)$ と表記することが多いです。
例えば、本節最初の図における例 1 の場合、
- $V = \{1, 2, 3, 4, 5\}$
- $E = \{(1, 2), (1, 3), (2, 3), (2, 4), (2, 5), (3, 4), (4, 5)\}$
- $|V| = 5, |E| = 7$
といった感じになります。
頂点の次数
頂点の次数は、この頂点から何本の辺が出ているかという値です。例えば、本節最初の図における例 1 の場合、次数は次表のようになります。
| 頂点 1 | 頂点 2 | 頂点 3 | 頂点 4 | 頂点 5 |
|---|---|---|---|---|
| 次数 2 | 次数 4 | 次数 3 | 次数 3 | 次数 2 |
また、有向グラフの場合入次数と出次数を分けて考えることも多いです。
- 頂点 $i$ の入次数:頂点 $i$ に向けて何本の辺が入っているか
- 頂点 $i$ の出次数:頂点 $i$ から何本の辺が出ているか
となっています。Twitter のフォロー関係の例であれば、フォローする人からフォローされる人に向かった辺を追加するとき、フォロー数が出次数、フォロワー数が入次数となります。
グラフの連結成分数(無向グラフ)
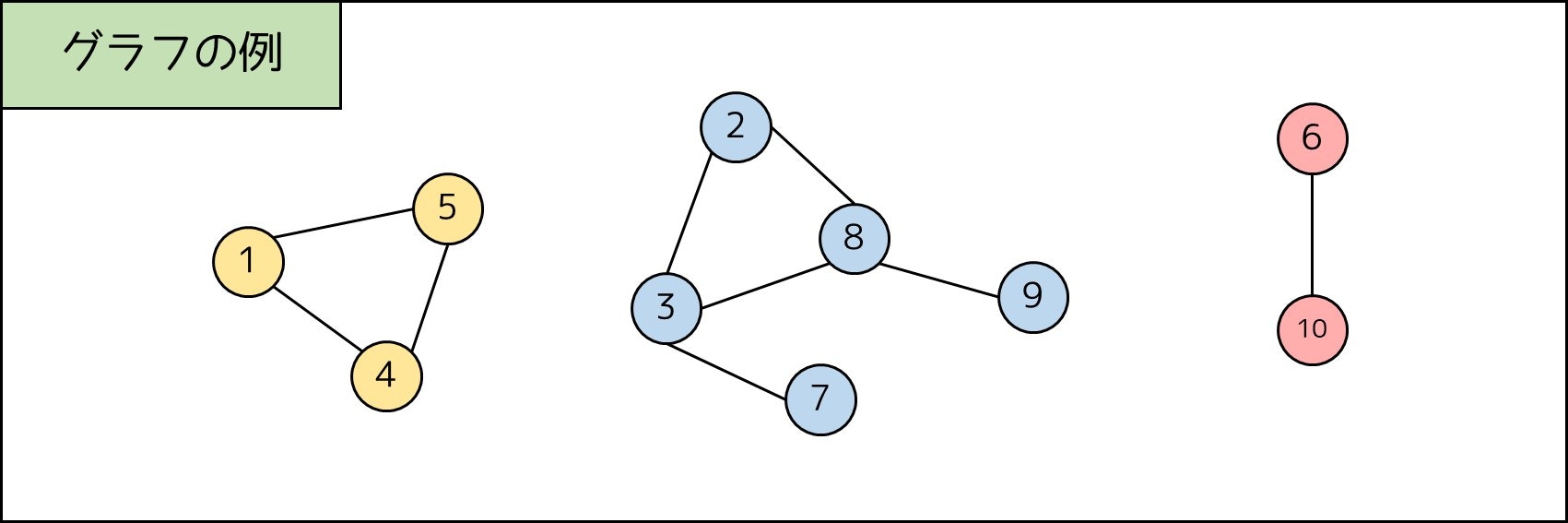
グラフの連結成分数は、特に無向グラフの場合、次のように定義されます。
いくつかの辺をたどって行くことができる頂点同士を同じグループとし、そうでない頂点同士を違うグループとするとき、いくつのグループに分かれるか
例えば、下図の場合 $\{1, 4, 5\}, \{2, 3, 7, 8, 9\}, \{6, 10\}$ の 3 つのグループに分かれるため、連結成分数は 3 です。特に連結成分数が 1 であるとき、グラフは連結であるといいます。
グラフの強連結性(有向グラフ)
有向グラフについても連結性を定義することができます。
- 頂点 $u$ から $v$ まで、いくつかの有向辺を規定された向きの通りにたどることで行ける
- 頂点 $v$ から $u$ まで、いくつかの有向辺を規定された向きの通りにたどることで行ける
- そのとき、頂点 $u, v$ は強連結である
本節の最後に名前だけ紹介する強連結成分分解などと深く結びつきます。
多重辺・自己ループ
多重辺は、グラフの辺のうち同じ 2 頂点間を結ぶ辺が複数存在するものを指します。例えば、
- $V = \{1, 2, 3, 4\}$
- $E = \{(1, 2), (1, 3), (2, 3), (2, 3), (2, 4), (4, 4)\}$
のとき、グラフ $G(V, E)$ には多重辺 $(2, 3)$ が存在します。
また、自己ループは辺の $2$ つの端点が同じような辺のことを指します。直前の例の場合、辺 $(4, 4)$ が自己ループです。
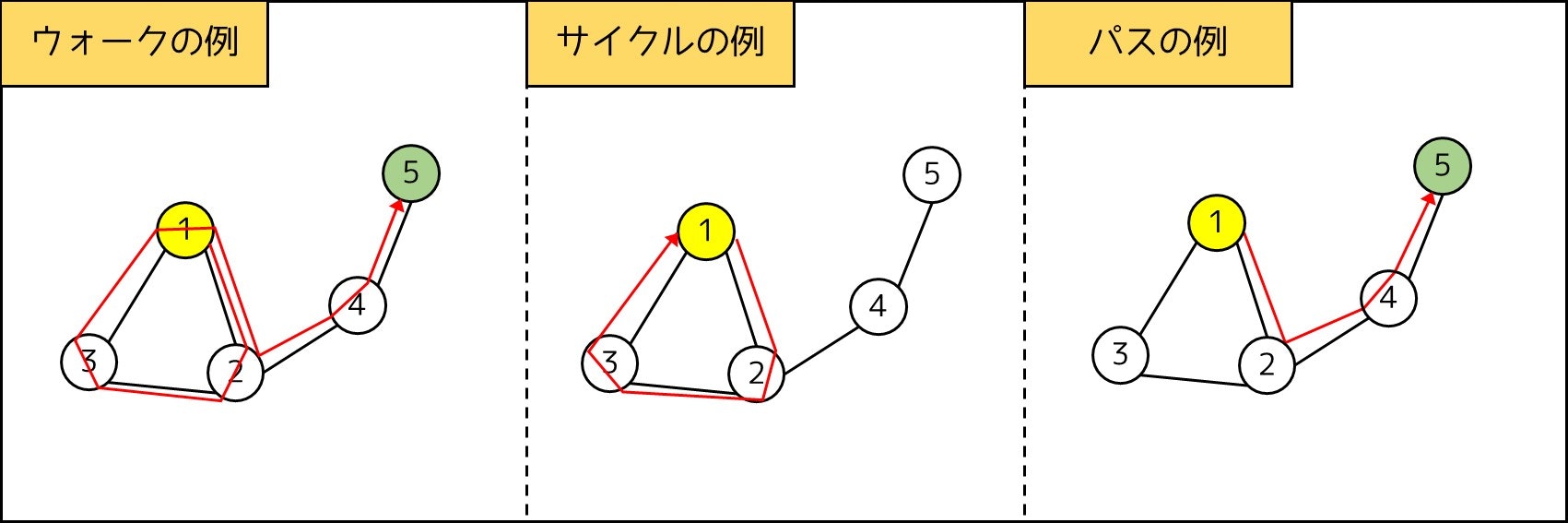
ウォーク・パス・サイクル
これもグラフ理論で頻出の用語です。
- **ウォーク:**頂点 $s$ から頂点 $t$ まで行くようなルートのこと。下図の例だと
1 -> 2 -> 3 -> 1 -> 2 -> 4 -> 5はウォークである。$s-t$ 路ともいわれる。 - **サイクル:**始点と終点が等しいルートのこと。下図の例だと
1 -> 2 -> 3 -> 1はサイクル閉路ともいわれる。 - **パス:**頂点 $s$ から頂点 $t$ まで行くようなルートのうち、同じ頂点を二度通らないもの。下図の例だと
1 -> 2 -> 4 -> 5はパスであるが、1 -> 2 -> 3 -> 1 -> 2 -> 4 -> 5はパスではない。
彩色数
隣接する頂点(直接辺で結ばれている頂点)同士が同じ色にならない塗り方の中で、最も使う色の数が少ない塗り方における、使った色の種類数です。特に彩色数が 2 であるグラフは二部グラフと呼ばれ、特殊な性質を持ちます。3
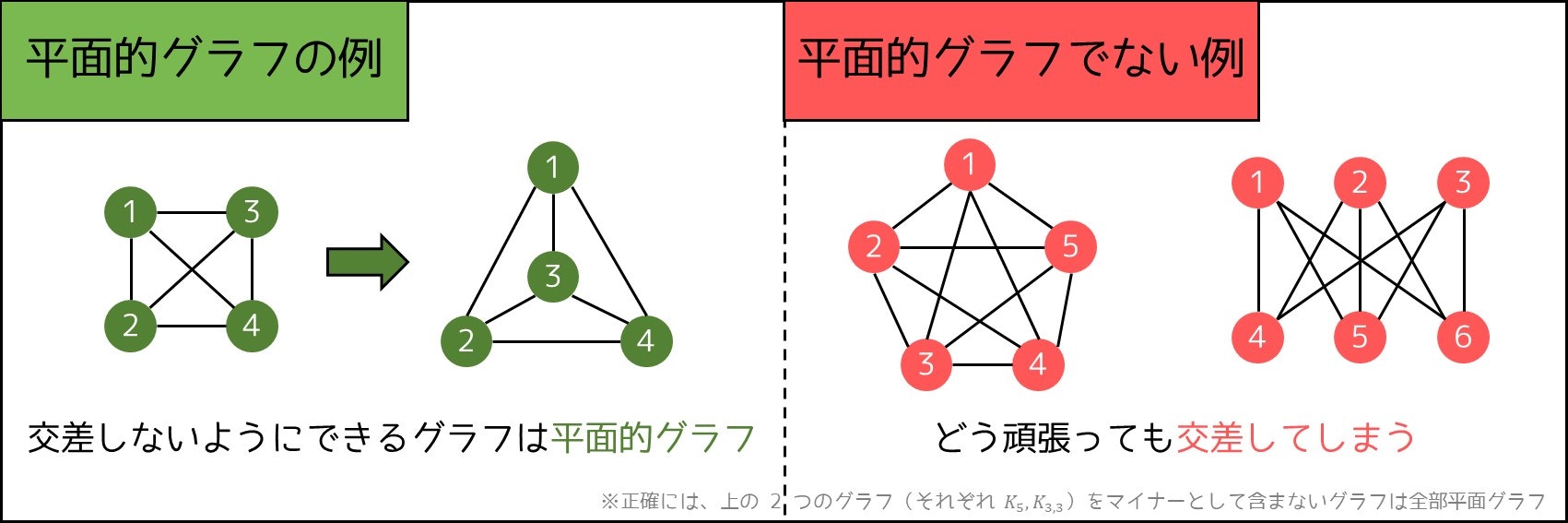
平面的グラフ
平面的グラフとは、頂点を上手く動かしたとき、どの辺も端点以外で交差しないようにできるグラフのことを指します。例えば、
- 彩色数が 4 以下である(四色定理)
最大安定集合
$|V|$ 頂点からいくつかを選ぶ方法は $2^{|V|}$ 通りありますが、その中で「隣接する頂点が両方選ばれる」ことがないもののうち、選んだ頂点数が最大となるような選び方を指します。
なお、最大安定集合を求める問題は、多項式時間アルゴリズムで解くことが絶望的とされている NP 完全問題という部類に属し、とても難しい問題として知られています。
木構造について
$N$ 頂点 $N-1$ 辺の連結なグラフを木構造といいます。
- 閉路が存在しない
- パスが 1 通りに定まる
といった特殊な性質を持ちます。詳しく知りたい方は、
をご覧ください。
では、ここまでグラフ理論について色々説明してきましたが、本節のタイトルにあった「離散数学」とは一体どういうものなのでしょうか。これは微積分や極限のように連続的な概念を扱わず、整数やグラフといった「とびとびの対象」を扱う学問領域のことを指します。組合せ論・グラフ理論の分野があり、アルゴリズムと非常に密接に関わる部分です。
4-18. モンテカルロ法に学ぶ、確率分布と統計的な推測(レベル: 3)
3)
まず、次の問題を考えてみましょう。
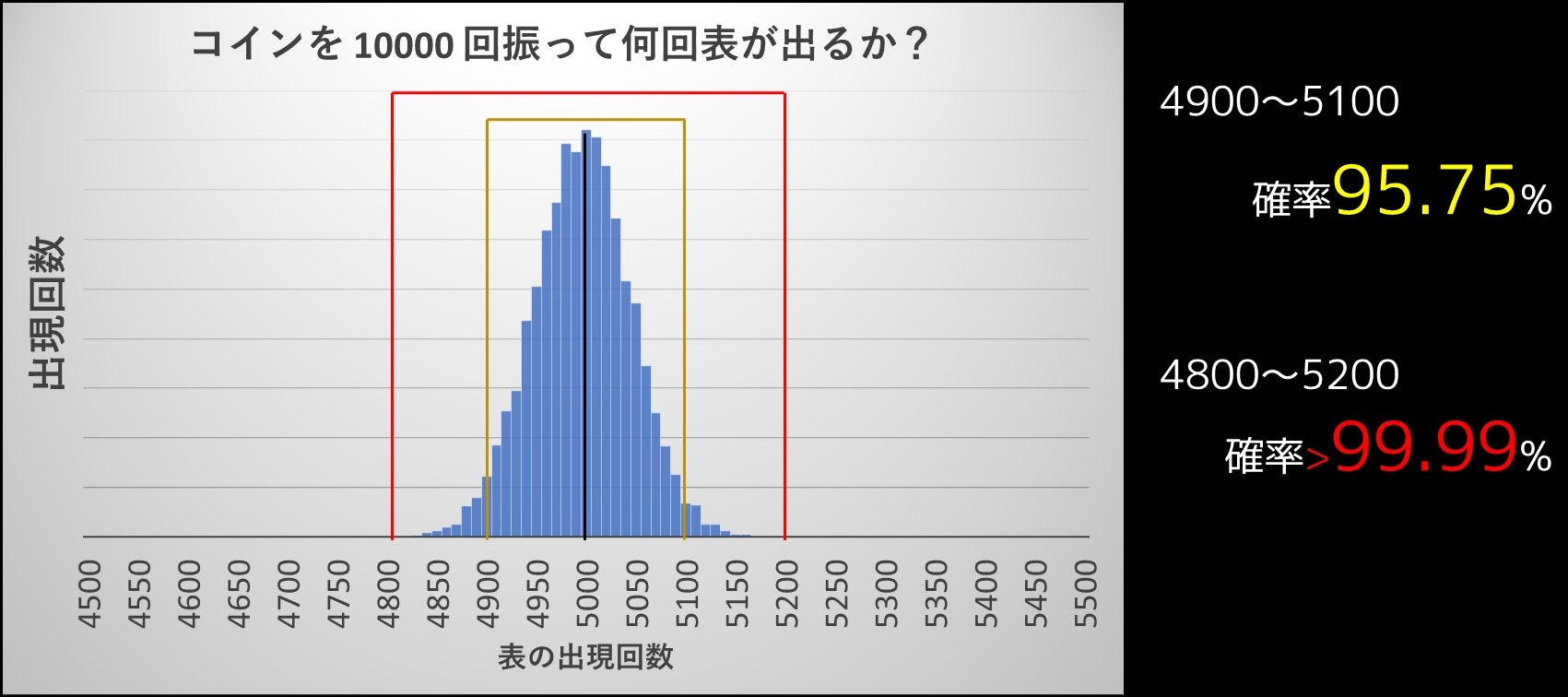
あなたは表裏が等確率で出るコインを 10000 枚投げます。
表が出た回数を $x$ とするとき、$x$ の確率分布はどのようになっているのでしょうか。
人によっては、「6000/10000 枚くらい表が出ることがあるかもしれない」と思うかもしれませんが、シミュレーションをした結果は下図の通りであり、ほとんどが 49% ~ 51% に収まっていることが分かります。
本節で扱う問題
何回も試行をすると「想定された確率」に非常に近い値が得られることが分かったところで、別の問題を考えてみましょう。
座標 (0, 0)、(0, 1)、(1, 1)、(1, 0) を頂点とする正方形の紙がある。
紙の中には $N$ $(\leq 100)$ 個の円が描かれており、$i$ 個目の円は中心座標 $(x_i, y_i)$、半径 $r_i$ である。1 つ以上の円の内部に入っている領域は赤い。
赤い領域の面積を、絶対誤差 0.01 以内で求めよ。
これは一見難しい幾何計算をする必要があると思うかもしれませんが、そんなことはありません。絶対誤差が 0.01 以内 という制約に注目してみましょう。
ランダムサンプリングできないか?
そこで、次のような方法を考えます。
- 点を正方形内のランダムな位置に $B$ 個打つ
- 各点について、1 つ以上の円の内部に入っているか、距離計算を用いて $O(N)$ で判定する
- 1 つ以上の円の内部に入っている点の割合が、求める面積である
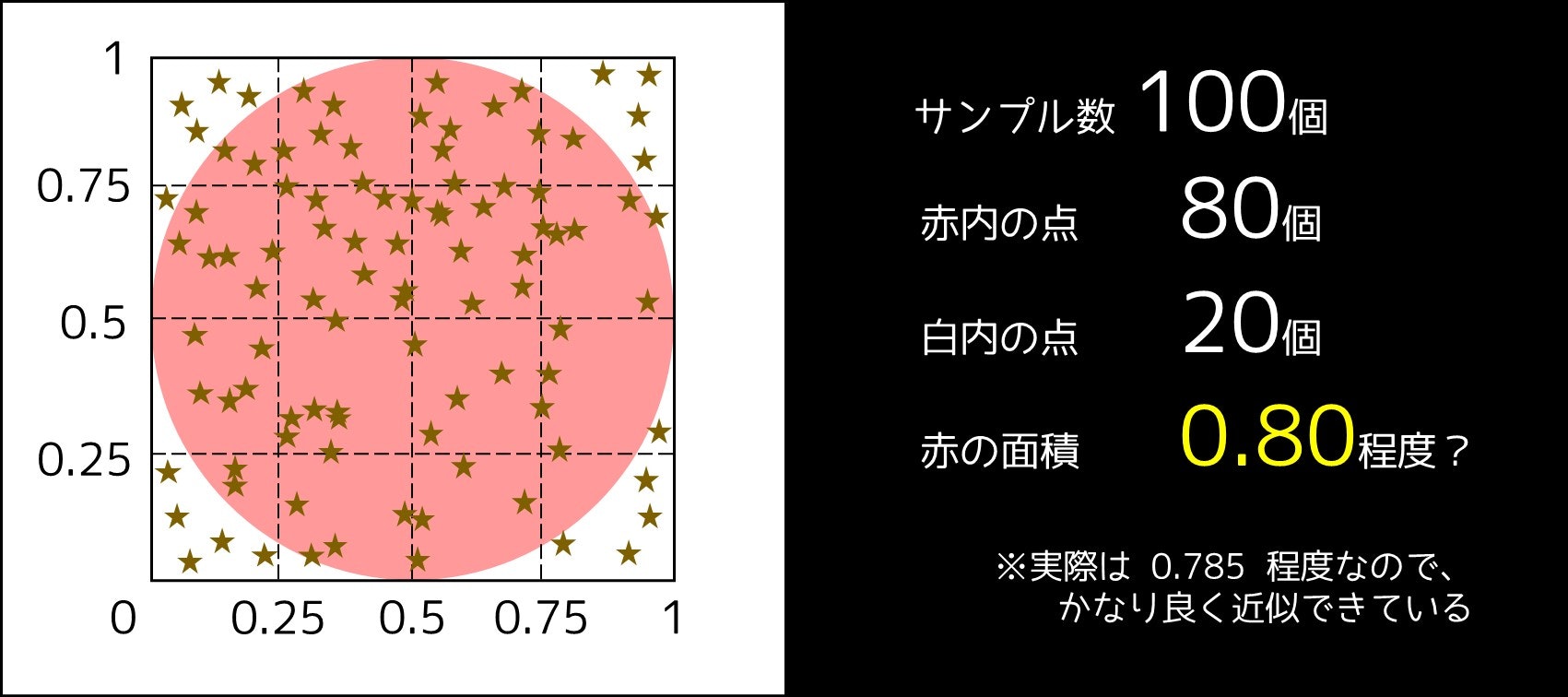
下図を見ると、どんな感じか分かると思います。では実際には、どの程度のサンプル数 $B$ が必要なのでしょうか。そこで「母平均の推定」を使います。
理論面 1. どうやって母平均を推定するか?
一般に、$N$ 回の試行を行い、そのうち確率 $p$ で成功した場合、実際の成功確率 $p'$ として考えられる確率分布は以下の公式によって表されます。
- $p'$ の期待値(平均してどのくらいの確率になるか): $p$
- $p'$ の標準偏差(どの程度ばらけるか): $\sqrt{p \times (1-p) \div n}$
例えば、偏りのあるコインを $10000$ 回振って $8000$ 回表が出た場合について考えましょう。そのとき、
- $p'$ の期待値: $8000 \div 10000 = 0.8$
- $p'$ の標準偏差: $\sigma = \sqrt{0.8 \times (1 - 0.8) \div 10000} = 0.004$
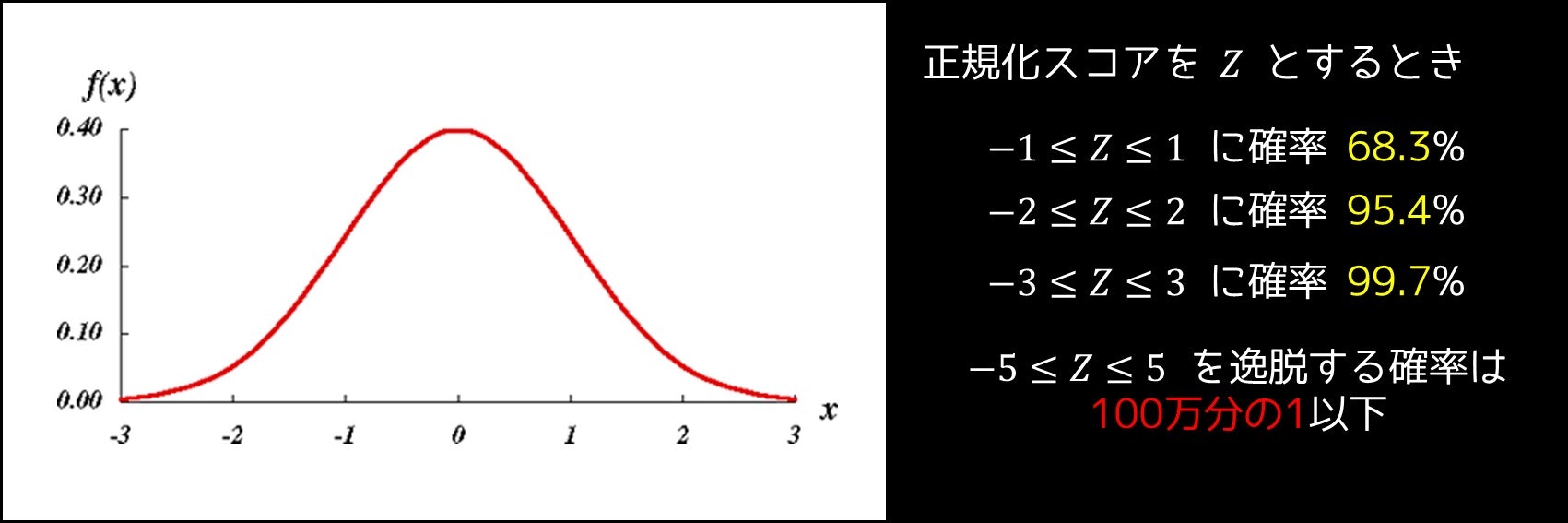
と計算することができます。ちなみに、このような問題においては、$p'$ の確率分布は正規分布(下図参照)に近似することができます。ただし、実際の確率 $x = p'$ の正規化スコアは $Z = \frac{x-m}{\sigma}$ として表されます。4
例えばコインを $10000$ 回振って $8000$ 回表が出た場合、約 95.4% の確率で $-2 \leq Z \leq 2$ となる、つまり $0.792 \leq p' \leq 0.808$ になることを意味します。
理論面 2. ほぼ確実に誤差が 0.01 以下となる B の値
そこで正規分布において、$-5 \leq Z \leq 5$ となる確率は 99.9999% 以上なので、そうでない可能性はほぼ無視することができます。そこで絶対誤差を $0.01$ 以下にするためには、
$$
5 \times \sigma \leq 0.01 \ (\Leftrightarrow) \ \sigma \leq 0.002 \ (\Leftrightarrow) \ \sqrt{\frac{p(1-p)}{B}} \leq 0.002 \ (\Leftrightarrow) \ \frac{p(1-p)}{B} \leq 4 \times 10^{-6}
$$
が成り立つ必要があります。そこで、$p(1-p)$ の値は $p=0.5$ で最大値 $0.25$ を取るので、
$$
\frac{0.25}{B} \leq 4 \times 10^{-6} \ (\Leftrightarrow) \ B \geq 6.25 \times 10^{4}
$$
であれば良い、ということが分かります。
本節のまとめ
このように、乱数を用いて何回か試行を行うことで近似解を求めるアルゴリズムをモンテカルロ法といいます。今回扱った問題では、僅か 62500 回の試行でほぼ 100% 正解を出せることが分かりましたが、他にも
などの問題で使われることがあります。モンテカルロ法や乱択アルゴリズムのように、場合によっては競プロ・アルゴリズムと統計が絡んでくる場合もあるのです。
# include <iostream>
using namespace std;
int N;
double X[109], Y[109], R[109];
bool solve(double px, double py) {
for (int i = 1; i <= N; i++) {
if ((px - X[i]) * (px - X[i]) + (py - Y[i]) * (py - Y[i]) <= R[i] * R[i]) {
return true;
}
}
return false;
}
int main() {
// Step #1. Input
cin >> N;
for (int i = 1; i <= N; i++) cin >> X[i] >> Y[i] >> R[i];
// Step #2. Randomize [Rand(l, r) は l 以上 r 以下の一様な実数の乱数を返すものとする]
int Loops = 62500;
int Cnts = 0;
for (int i = 1; i <= Loops; i++) {
double px = Rand(0, 1);
double py = Rand(0, 1);
bool ret = solve(px, py);
if (ret == true) Cnts += 1;
}
printf("%.12lf\n", 1.0 * Cnts / Loops);
return 0;
}
4-19. その他のトピックと、さらなる発展(レベル: 4)
4)
3・4 章では、アルゴリズムと数学が密接に関わる点について、全部で 18 個のトピックを取り上げてきました。例えば、
について紹介しました。しかし、紙面の都合上、入れようと思ったアルゴリズムも載せることができず、削らざるを得なかったものも存在します。このような理由で、黄色コーダーになるための数学的知識はまだ全部カバーできていないと考えます。そこで 4 章の最後に、
- ここまでで紹介できなかった、アルゴリズムや競プロで問われる数学的知識
- 今後、アルゴリズムや競プロ関連の書籍・記事等を読む際に必要となり得る数学的知識
について、少しだけ解説したいと思います。なお、この章は難易度が高く、大学数学の範囲が中心となっておりますので、読み飛ばして 5 章の演習問題に行ってもかまいません。
調和級数
まず、以下の式が成り立ちます。
$$
N + \frac{N}{2} + \frac{N}{3} + ... + \frac{N}{N} = O(N \log N)
$$
この性質を使うことで、例えば $1$ から $N$ までの約数列挙が $O(N \log N)$ でできたりします。また、クイックソートの平均計算量が $O(N \log N)$ であることも、調和級数の性質を使うと証明できます。
// 1 から N までの約数を列挙(vec[i]: i の約数が全部入っているリスト)
vector<int> vec[1000009];
for (int i = 1; i <= N; i++) {
for (int j = i; j <= N; j += i) vec[j].push_back(i);
}
形式的べき級数
多項式を無限に続けていった式
$$
f(x) = a_0x^0 + a_1x^1 + a_2x^2 + a_3x^3 + \cdots
$$
を形式的べき級数(Formal Power Series)といいます。かなり汎用性がありますが、競プロでは数え上げ問題を解く際によく使われます。詳しくは
をご覧ください。
モノイドとセグメント木
競プロの問題に出題される典型的なデータ構造として、セグメント木(Segment Tree)が挙げられます。このうち、
など比較的単純な問題は、セグメント木の中身に整数を格納するだけで解けます。
しかし、場合によっては行列などのデータをセグメント木に格納することもあります。そこで重要になってくるのはモノイドです。モノイドとは、次の条件を満たす型のことを指します。
- 結合法則を満たす。つまり、どんな $a, b, c$ でも、$(a \cdot b) \cdot c = a \cdot (b \cdot c)$ を満たす。
- 単位元が存在する。つまり、どんな $a$ でも $(a \cdot e) = (e \cdot a) = a$ となる $e$ がある。
- 例えば、実数の掛け算では単位元が $1$
- 例えば、行列の掛け算では単位元が単位行列
基本的に、モノイドであれば、セグメント木にデータを入れることができます。
高速フーリエ変換(FFT)
次の問題を考えてみましょう。(なお、このような形式の問題を畳み込みといいます)
$N$ 次多項式 $A, B$ がある。$A = a_Nx^N + a_{N-1}x^{N-1} + ... + a_1x^1 + a_0x^0$、$B = b_Nx^N + b_{N-1}x^{N-1} + ... + b_1x_1 + b_0x^0$ である。
$A \times B$ は $2N$ 次の多項式になるが、各項の係数をそれぞれ求めよ。
この種の問題は、単純に式を展開して計算すると $O(N^2)$ かかってしまいますが、高速フーリエ変換(FFT)を使うと $O(N \log N)$ で解くことができます。難しい数学的知識を使うアルゴリズムなので本記事では説明を省略しますが、詳しく知りたい方は
をご覧ください。なお、競プロでも畳み込みの問題は頻出ですが、このうち多くは FFT の原理を完全に理解しなくても AtCoder Contest Library (ACL) を使うだけで解けるので、まずは「FFT を使うとこういう問題が $O(N \log N)$ で解ける」という事実に慣れることが重要です。
直積の定義と用語
$2$ つの集合 $X, Y$ について、直積集合 $Z = X \times Y$ は次のように定義されます。
$$
Z = \{(x, y) | x \in X, y \in Y\}
$$
例えば、$X = \{1, 3, 6\}, Y = \{25, 50\}$ の場合、
$$
X \times Y = \{(1, 25), (1, 50), (3, 25), (3, 50), (6, 25), (6, 50)\}
$$
となります。$3$ つ以上の集合についても直積を定義することができ、例えば集合 $A, B, C$ について、直積 $Z = A \times B \times C$ は次のようになります。サイズは $|A| \times |B| \times |C|$ です。
$$
Z = \{(a, b, c) | a \in A, b \in B, c \in C\}
$$
また、集合 $X$ に対して、直積 $X \times X$ を $X^2$、$X \times X \times X$ を $X^3$ と書き表すことがあります。特に $X$ が実数全体の集合($X = \mathbb{R}$)の場合、
- 直積 $X \times X$ を $\mathbb{R}^2$
- 直積 $X \times X \times X$ を $\mathbb{R}^3$
- 直積 $X \times X \times ... \times X$($N$ 回掛け算する)を $\mathbb{R}^N$
と表記します。座標平面が $\mathbb{R}^2$、$N$ 次元ベクトルが $\mathbb{R}^N$ と書かれることが多いのは、そういった理由があるためです。
写像
写像は関数を拡張させたものですが、相違点があります。
| 名前 | 特徴 |
|---|---|
| 関数 | 実数から実数に対応する |
| 写像 | 集合 $X$ の要素から集合 $Y$ の要素に対応する |
一体どのようなことなのでしょうか。例えば、次のようなコードを考えましょう。
int func(int N) {
if (N == 1001) return 2553;
if (N == 869120) return 2935;
}
この「関数」は、高校数学までに扱った $f(x) = x^2$ などの連続的なものとはイメージが全然違うかもしれません。しかし、これは集合 $X = \{1001, 869120\}$、$Y = \{2553, 2935\}$ とすると、func(int N) は集合 $X$ の各要素(元)が集合 $Y$ の要素の 1 つに対応しています。
このような性質を満たす「関数」を「$X$ から $Y$ への写像」といい、$func: X \to Y$ といった形で表します。(なお、これは大学数学の範囲なので 2-2. 節 では写像という言葉を用いずに関数として説明していましたが、多くのプログラミング言語では、写像のようなものも関数といわれています。)
特殊な写像、全射・単射など
写像の中で、以下の性質を満たすものをそれぞれ全射・単射・全単射といいます。
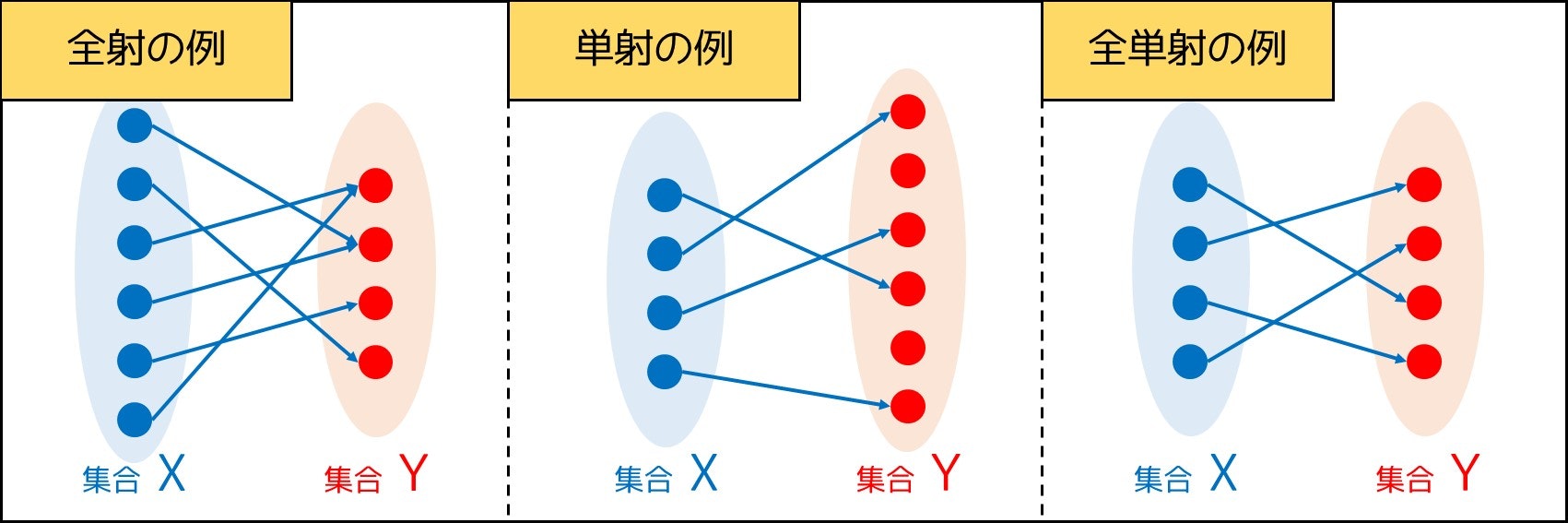
- **全射:**すべての $Y$ の要素 $y$ について、$f(x) = y$ となる $X$ の要素 $x$ が最小でも 1 つある
- **単射:**すべての $Y$ の要素 $y$ について、$f(x) = y$ となる $X$ の要素 $x$ が高々 1 つしかない
- **全単射:**すべての $Y$ の要素 $y$ について、$f(x) = y$ となる $X$ の要素 $x$ が丁度 1 つある
イメージとしては、下図のような感じです!
なお、これを知っておくと、$\bmod 1000000007$ 系数え上げ問題の頻出パターンである写像 12 相などが理解しやすくなると思います!
特殊なシグマ記号
2-9. 節で紹介したように、シグマ記号は基本的に次のような形で使われます。
$$
\sum_{i=1}^{4} i^3 = 1 + 8 + 27 + 64 = 100
$$
しかし、特に 4-17. 節で紹介したグラフ理論では、シグマ記号は $i = L, L+1, ..., R$ における総和以外の文脈でも使われることがあります。例えば無向グラフ $G(V, E)$ に対し、
$$
\sum_{v \in V} \deg(v) = 2 \times |E|
$$
が成り立つのですが、「これは $V$ の要素すべて(つまり全部の頂点)に関する次数 $\deg(v)$ の総和」という意味です。このように、集合内の要素すべてに対する総和の意味で、シグマ記号が使われることもあります。
述語論理の基本
皆さん、次のような表記を見たことがありますでしょうか。
∀$x \in \mathbb{R}$ $(x \leq 2 \Rightarrow x^2 \leq 4)$
∃$x \in \mathbb{R}$ $(2^{-x}=8 \Rightarrow x^2 = 9)$
このような書き方のことを述語論理というのですが、特に以下の $3$ つの書き方は、競プロの解説記事などでよく目にするので、確認しておきましょう。
- ∃$x \in \mathbb{R}$ (条件A):条件 A を満たすような実数 $x$ が存在する。
- ∀$x \in \mathbb{R}$ (条件A):どのような実数 $x$ でも条件 A を満たす。
- ∀$x \in \mathbb{R}$ (条件A ⇒ 条件 B):どのような実数 $x$ でも条件 A を満たすものは条件 B も満たす。
ここまでの章では、アルゴリズムを学ぶ、そしてプログラミングコンテストでで戦うにあたって必要な数学的知識を、合計 12+19=31 個のポイントに分けてまとめました。記事が長く、読むのに時間がかかったかと思いますが、とりあえずお疲れ様でした。
「数学的知識編」の最後に、5 章では 2・3・4 章の内容に関する理解を深めるため、演習問題を 30 問用意します。皆さん是非お読みください。
5. これだけ解けば理解が深まる! ~演習問題 32 問~
いよいよ数学的知識編のラスト、演習問題です!!!
ここまで非常に多くのポイントについて記してきたので、理解が追いつかなかった方も多いと思います。そこで、アルゴリズムで使う数学的知識の理解をさらに深めてもらうため、章別に問題を用意しました!!!
構成は次表のようになっています。
| 節 | 内容 | 問題数 | 問題番号 |
|---|---|---|---|
| 5-1. 節 | 2 章で紹介した、問題文理解に必要な知識 | 14 問 | 1 ~ 14 |
| 5-2. 節 | 3 章で紹介した、基本的なアルゴリズムに必要な知識 | 9 問 | 15 ~ 23 |
| 5-3. 節 | 4 章で紹介した、発展的なアルゴリズムに必要な知識 | 9 問 | 24 ~ 32 |
5-1. 問題文の理解に必要な、2 章の演習問題 14 問
本節では、2 章の内容から 14 題出題されます。
また、各問題の解説はこちらのページで閲覧できます。現在 10 問目までしか載っていませんが、順次更新される予定です。
問題 1( )
)
$\{-5, -4.5, -2, 0, 4, 6\}$ の中から整数をすべて選んでください。
また、非負整数のもの、自然数のものを、それぞれすべて選んでください。
問題 2( )
)
$N! \mod 1000000007$ の値を求めるプログラムを書いてください。
ただし、時間計算量 $O(N)$ で実行できればよいものとします。
問題 3( )
)
整数 $N$ を引数として、$N$ が素数なら true、$N$ が素数ではない(合成数である)なら false を返す関数 func を含むプログラムを書いてください。
問題 4(
 )
)
ある有名人がツイートすると、すぐ 1 人のユーザーがそのツイートを Retweet します。
また、あるユーザーが Retweet すると、1 分後に 2 人のユーザーが Retweet します。
例えば、ツイート直後(0 分後)には 1 人が、1 分後には 2 人が、2 分後には 4 人が、3 分後には 8 人がリツイートするため、3 分後の時点での合計 Retweet 数は 15 となります。
$N$ 分後における Retweet 数を $N$ の式で表してください。また、Retweet 数が $10^{8}$ を超えるのは何分後でしょうか。
問題 5(
 )
)
$21$ を $2$ 進数で表してください。
また、$2$ 進数で $11010100001100000000$ となるような整数は、$10$ 進数表記で何でしょうか。ただし、プログラムを書いて解答してもよいです。
問題 6(
 )
)
$1 \ xor \ 2 \ xor \ 3 \ xor \ ... \ xor \ N$ を求めるプログラムを書いてください。
ただし、時間計算量 $O(N)$ かけても良いですが、$O(1)$ で解けるアルゴリズムも存在します。
問題 7(
 )
)
以下の値を計算するプログラムを書いてください。
$$
\sum_{a=1}^{N} \sum_{b=1}^{N} \sum_{c=1}^{N} abc
$$
ただし、時間計算量 $O(N^3)$ かけても良いですが、$O(N)$ や $O(1)$ で解けるアルゴリズムも存在します。
問題 8( )
)
$\{8, 10, 12, 15, 20\}$ の中から $2$ つを選ぶ方法は $10$ 通りありますが、その中で選んだ $2$ つの整数が互いに素になる方法が $1$ 通りだけ存在します。これはどのような方法でしょうか。
問題 9(

 )
)
文字列 $S$ が与えられます。
qiita は文字列 $S$ の部分文字列でしょうか。Yes か No で出力してください。
問題 10(
 )
)
$A = \{1, 2, 9, 14\}$、$B = \{1, 3, 8, 9, 12\}$ のとき、$A \cup B$、$A \cap B$、$A \setminus B$ をそれぞれ求めてください。ただし $A \setminus B$ については 2 章で触れていないですが、差集合といわれるものです。
問題 11(
 )
)
集合 $S = \{1, 2, 3, ..., N\}$ の空でない部分集合はいくつ存在しますか。
$N$ を使った式で表してください。
問題 12(

 )
)
整数 $N$ $(\leq 10^{18})$ が与えられます。
$\lfloor \sqrt{N} \rfloor$ の値と $\lceil \sqrt{N} \rceil$ の値を出力するプログラムを書いてください。
問題 13(
 )
)
数列 $A = (A_1, A_2, ..., A_N)$ が与えられます。
以下の形式の質問が $Q$ 個与えられるとき、各質問に答えるプログラムを書いてください。
- $i$ 個目の質問について:
- 整数 $L_i, R_i$ $(1 \leq L_i < R_i \leq N + 1)$ が与えられる。
- そのとき、数列 $A$ の区間 $[L_i, R_i)$ の和を計算し、出力する。
ただし、時間計算量 $O(NQ)$ かけても良いですが、$O(N + Q)$ で解くアルゴリズムも存在します。
問題 14(
 )
)
$3 \times 3$ 行列
A =
\begin{bmatrix}
A_{1, 1} & A_{1, 2} & A_{1, 3} \\
A_{2, 1} & A_{2, 2} & A_{2, 3} \\
A_{3, 1} & A_{3, 2} & A_{3, 3} \\
\end{bmatrix}
が与えられるとき、行列式を求めるプログラムを書いてください。
※競プロの問題ではよく知られていない用語の定義が出てきた場合、説明文が付いたり、リンクが付いたりする場合もありますが、そうでない場合もあります。例えば AtCoder では検索が使えるので、知らないキーワードが出た場合は Google 検索などを使うのも重要です。
どれくらい解けましたでしょうか。もし分からないことがあった場合、
に戻って、再確認してみましょう。
5-2. 基本的なトピック、3 章の演習問題 9 問
本節では、3 章の内容から 9 題出題されます。
また、各問題の解説はこちらのページで閲覧できます。現在 10 問目までしか載っていませんが、順次更新される予定です。
問題 15(
 )
)
$N$ 個の 6 面体サイコロがあり、$i$ 個目のサイコロは、各面に整数 $A_{i, 1}, A_{i, 2}, A_{i, 3}, A_{i, 4}, A_{i, 5}, A_{i, 6}$ が書かれています。
そのとき、サイコロの出目の和が $T$ となる可能性があるかどうか判定する問題を、全探索によって解くこと考えます。何通りのパターンを考える必要があるか $N$ の式で表した上で、$N$ がどの程度までなら現実的な時間(数秒以内)で実行が終わるか、考えてみてください。
問題 16(

 )
)
以下の 2 つのアルゴリズムを考えます。
- 計算回数(質問回数)が $\log_{2} N$ 回の二分探索
- 計算回数(質問回数)が $\log_{1.5} N$ 回の三分探索
このアルゴリズムのオーダーが両方 $\Theta (\log N)$ であることを示してください。また、質問回数の差が何倍になっているか、考えてみてください。
問題 17(

 )
)
次のアルゴリズムの計算量を見積もってください。
// func(N) を呼び出す
int func(int N) {
if (N == 0) return 1;
if (N == 1) return 2;
return func(N - 1) + func(N - 2) + func(N - 2);
}
問題 18(
 )
)
$N$ 個の点が与えられます。番号 $i$ の点は整数座標 $(x_i, y_i)$ にあります。
$2$ つの点の間の距離がちょうど整数 $K$ となるような組は、いくつ存在するでしょうか。
ただし、計算量が $O(N^2)$ であればよいものとします。
問題 19(

 )
)
$2$ 点 $A(x_1, y_1), B(x_2, y_2)$ が与えられます。三角形 $ABC$ が正三角形となるような、点 $C$ の座標として考えられるものを 1 つ出力するプログラムを書いてください。
問題 20(
 )
)
整数 $A_1, A_2, ..., A_N$ の中に素数がいくつ存在するか出力するプログラムを書いてください。
ただし、$A_i \leq 10^9, N \leq 1000$ の制約下で、数秒以内で実行が終われば良いものとします。
問題 21(

 )
)
以下のような道路網を考えます。
- $N$ 個の都市がある。
- $i = 2, 3, ..., N$ それぞれについて、都市 $i$ と都市 $\lfloor i \div 2 \rfloor$ を双方向に結ぶ道路がある。
- 各道路は、2 つの都市間を 1 分で移動できる。
そこで、「どの都市 $u$ $(1 \leq u \leq N)$ を選んでも、都市 $1$ から $T$ 分以内で移動できる」ような $T$ として考えられる最小の値を $N$ の式で表してください。
※なお、このような構造を持つグラフのことを二分木といいます。調べてみましょう。
問題 22(

 )
)
集合 $S = \{1, 2, 3, ..., N\}$ があります。$N$ が与えられるとき、集合 $S$ の空でない部分集合の個数を $10^9 + 7$ で割った余りを求めるプログラムを書いてください。ただし、計算量 $O(\log N)$ のアルゴリズムが要求されます。
問題 23(

 )
)
次の形式の質問が $Q$ 個与えられたとき、各質問に答えるプログラムを書いてください。
- $i$ 個目の質問について:
- 整数 $a_i, b_i$ が与えられる。
- そのとき、$\left( a_i \times (a_i+1) \times ... \times b_i \right)$ の値を $10^9 + 7$ で割った余りを出力する。
ただし、$1 \leq a_i, b_i, Q \leq 200000$ の制約下で、数秒以内で実行が終わる必要があります。
どれくらい解けましたでしょうか。もし分からないことがあった場合、
に戻って、再確認してみましょう。
5-3. 発展的なトピック、4 章の演習問題 9 問
本節では、4 章の内容から 9 題出題されます。
また、各問題の解説はこちらのページで閲覧できます。現在 10 問目までしか載っていませんが、順次更新される予定です。
問題 24(
 )
)
$f(x) = x^3$ とするとき、$f'(2), f'(5)$ の値を求めてください。
問題 25(

 )
)
2 変数関数 $f(x, y) = x^3 + xy + y^3$ を考えます。
- $x$ についての偏微分
- $y$ についての偏微分
をそれぞれ計算してください。
問題 26(


 )
)
トリボナッチ数列
- $A_1 = A_2 = A_3 = 1$
- $A_N = A_{N-1} + A_{N-2} + A_{N-3} \ (N \geq 4)$
の第 $N$ 項を $O(\log N)$ で計算するアルゴリズムを考えてみてください。
問題 27(
 )
)
次のようなグラフ $G(V, E)$ を図に表してみてください。また、彩色数を求めてください。
- $V = \{1, 2, 3, 4, 5\}$
- $E = \{(1, 4), (2, 4), (3, 4), (1, 5), (2, 5), (3, 5)\}$
問題 28(

 )
)
$N$ 頂点 $M$ 辺のグラフの連結成分数として考えられる最小値を、$N, M$ を使った式で表してください。
問題 29(

 )
)
次の問題を解くプログラムを書いてみてください。
$N$ $(\leq 30)$ 個の椅子がある。最初、椅子 $i$ には番号 $i$ の生徒が座っている。
あなたは以下の操作を $Q$ $(\leq 30)$ 回行う。
- 整数 $x, y$ $(1 \leq x, y \leq N)$ を一様な確率で選ぶ。
- そして、椅子 $x, y$ に座っている生徒を交換する。ただし $x=y$ の場合は何もしない。
「生徒の番号と座っている椅子の番号が同じ位置」が存在しない確率を求めなさい。ただし、絶対誤差が $0.02$ 以内であれば正解となる。
問題 30(


 )
)
まず、$N + \frac{N}{2} + \frac{N}{3} + ... + \frac{N}{N} = O(N \log N)$ であることを証明してください。
次に、エラトステネスの篩の計算量が $O(N \log N)$ であることを証明してください。(実際の計算量は $O(N \log \log N)$ ですが、そこまでタイトに証明する必要はありません)
問題 31(



 )
)
クイックソートの平均計算量が $O(N \log N)$ であることを証明してください。
問題 32(



 )
)
実数 $L, R, a_0, a_1, a_2, ..., a_n$ が与えられます。
$N$ $(\leq 50)$ 次関数 $f(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_1x^1 + a_0x^0$ があります。
定義域が $L \leq x \leq R$ のとき、関数 $f(x)$ の最大値を、できるだけ小さい誤差で求めるプログラムを書いてください。ただし、概ね 0.01 秒以内で実行が終わる必要があります。
どれくらい解けましたでしょうか。もし分からないことがあった場合、
に戻って、再確認してみましょう。
5-XX. 本記事を終えた次は?
本記事の内容をマスターすれば、黄色コーダーになるために必要な数学的知識はほとんどカバーできたと言って良いと思います。しかし、
- 数学的知識だけでは、プログラミングコンテストでは戦えない
- 数学的考察も重要である
という現状があるので、後編では初心者レベルから水色コーダーレベルまでに要求される数学的考察について解説したいと思います。独立したトピックですので、初心者から競プロ経験者まで楽しめる構成となっております。興味があれば是非お読みください。
後編
-1. つづく
後編に続きます。
-
$A \times B$ 行列は、縦 $A$ 行、横 $B$ 列の行列の事を指します。 ↩
-
フォロー関係を表したグラフでは、スモールワールド性という面白い性質があって、$2$ 人のユーザーをランダムに取ってきたときに、おおよそ $5~6$ 回程度フォロワーに遷移することで、一方からもう一方まで行くことができるようです。(例えば $1$ 回の遷移だとフォロワー、$2$ 回の遷移だとフォロワーのフォロワー、といった感じになります。 ↩
-
偏差値に換算すると分かりやすいかもしれません。$Z = 0$ だと偏差値 50、$Z = 1$ だと偏差値 60、$Z = 2$ だと偏差値 70、… といったイメージです。 ↩