こんにちは、高校 3 年生の E869120 です。
私は競技プログラミングが趣味で、AtCoder や日本情報オリンピックなどに出場しています。ちなみに、2020 年 7 月 26 日現在、AtCoder では赤(レッドコーダー)です。
本記事では、前編で「全探索」「二分探索」「半分全列挙」などの探索アルゴリズムを図を用いて解説し、後編でそれらが使える事例を紹介していきたいと思います。一部の章では C++ での実装例を紹介していますが、読者が使うプログラミング言語に関係なく読める内容になっているでしょう。
【シリーズ】
- たのしい探索アルゴリズムの世界【前編:全探索、bit全探索から半分全列挙まで】 ←本記事
- たのしい探索アルゴリズムの世界【後編:探索手法で実社会の様々な問題を斬る!】
0. はじめに
日々コードを書いていく中で、様々なアルゴリズムを学習する人も多いと思います。特に競技プログラミングの分野ではアルゴリズムの勉強が欠かせません。競技プログラミングをやっていない方であっても、コーディング試験や業務でアルゴリズムを使う機会は少なくないと思います。
そんな中で、忘れられがちなのが全探索などの「探索アルゴリズム」です。実際にコードを書くとき、以下のような場面に遭遇することも多いと思います。
- そもそもどうやって全探索すれば良いのか分からない
- 単純な for ループの全探索は書けるが、複雑な構造やその工夫になると書けない
- 問題を解く時に「法則を見つけよう」という方向に走りがちで、「探索で解ける」という視点を捨ててしまう
実際に「探索」視点を持てている人は少ない
分かりやすいように、AtCoder に出題された問題の正答率で比較しますが、実際に、「探索」で解ける問題の方が、他の同難易度の問題より正解率が低くなっているという現状があります。
| 分野 | 問題 | 正解率 |
|---|---|---|
| 探索 | ABC165 C - Many Requirements | 2514/11731 (21%) |
| 探索 | ABC167 C - Skill Up | 5652/11940 (47%) |
| 探索以外 | ABC163 C - management | 8976/11551 (78%) |
| 探索以外 | ABC164 C - gacha | 9553/11302 (85%) |
| 探索以外 | ABC166 C - Peaks | 7970/11690 (68%) |
本記事のゴール
前述したように、探索アルゴリズムは基本的であるがために忘れられがちです。しかし、探索アルゴリズムは応用範囲が幅広く、例えば「15パズル」や「オセロのAI作成」にも探索の視点が使われています。(詳しくは後編で述べます)このように、探索アルゴリズムはとても奥深いです。
そこで、本記事では、
皆さんに、様々な探索アルゴリズムを知ってもらい、「探索」視点で考える事の重要性と、探索アルゴリズムの応用範囲の幅広さや奥深さを知ってもらう
ことを最大の目標にします。競技プログラミングやアルゴリズムを知らない方でも理解できるように、分かりやすく説明するよう努力しましたので、是非お読みください!
目次
前編
| 章 | タイトル | 備考 |
|---|---|---|
| 0. | はじめに | |
| 1. | 探索アルゴリズムとは | ここからサポートしていきます |
| 2. | すべての基本、全探索 | |
| 3. | 種々の全探索 ~bit全探索、順列全探索など~ | 2 章より複雑な構造を扱います |
| 4. | 効率的な探索手法 ~二分探索と三分探索~ | |
| 5. | はやい探索法 ~半分全列挙~ | |
| 6. | 意外と強い、枝刈り全探索 |
後編
| 章 | タイトル | 備考 |
|---|---|---|
| 7. | 「おねえさん問題」で役立つ、全探索 | 後編では探索が役立つ事例を紹介します |
| 8. | 「高次方程式の解の発見」で役立つ、二分法 | |
| 9. | 「15パズル」で役立つ、半分全列挙と枝刈り全探索 | |
| 10. | 更なる探索アルゴリズムの奥深さ | |
| 11. | おわりに |
1. 探索アルゴリズムとは
探索アルゴリズムとは、以下のような手法のことを指します。
探索アルゴリズムとは、大まかに言えば、問題を入力として、考えられるいくつもの解を評価した後、解を返すアルゴリズムである。(Wikipediaより)
もう少し具体的に書くと、「あり得るパターンを全部列挙する」という手法のことを全探索といい、これが探索アルゴリズムの基本です。また、4 章で後述する二分探索などを用いて探索回数を減らすアルゴリズムも探索アルゴリズムの仲間です。
分かりやすいように、一個例を説明しましょう。
「おねえさん問題」に学ぶ、探索アルゴリズム
ところで、以下の問題をご存知でしょうか。
$N \times N$ の碁盤目状道路がある。左上座標を $(0, 0)$、右下座標を $(N, N)$ とするとき、左上の座標から右下の座標まで、同じ交差点を通らずに行くような方法は何通りあるか。
例えば、$N = 2$ の場合は、以下の $12$ 通りの行き方が存在します。(出典:「フカシギの数え方」おねえさんといっしょ!みんなで数えてみよう!)
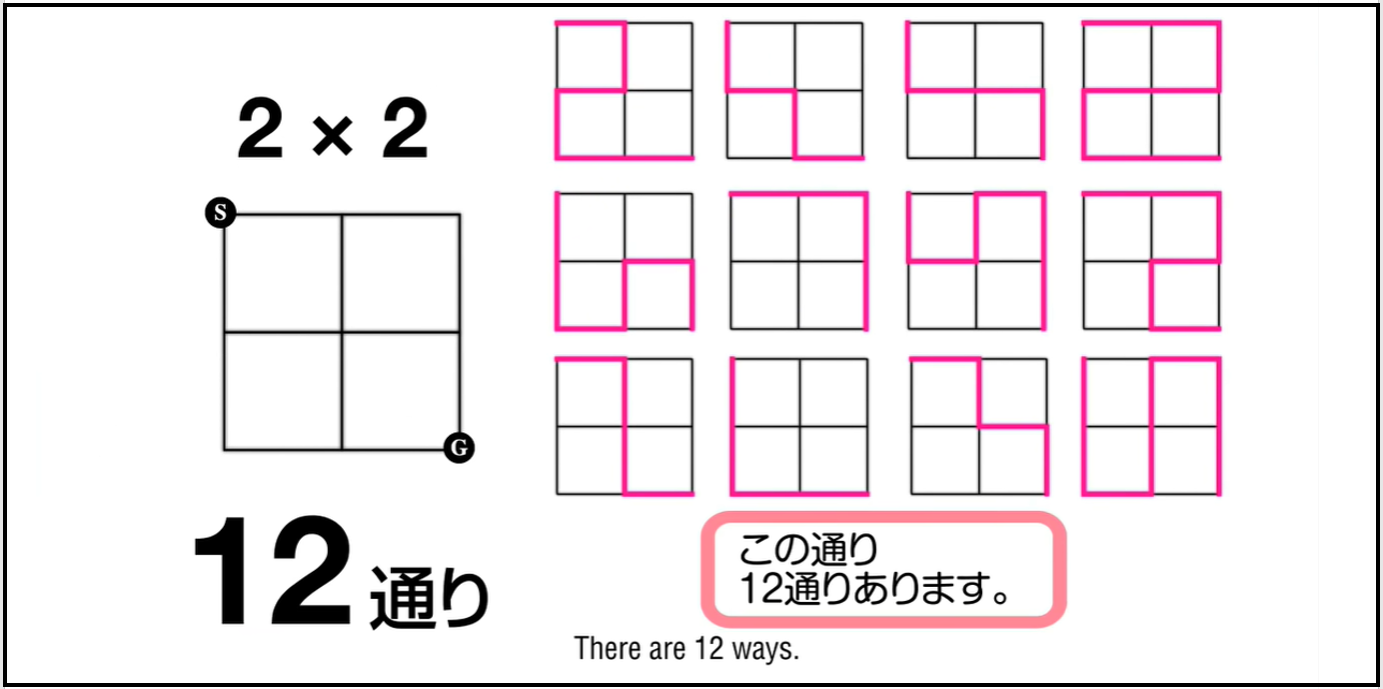
もっと詳しく知りたい方は、上の出典の動画を見てください。(約 8 分です)
このように、全ての行き方(パターン)を列挙することによって通り数などを求めるアルゴリズムを全探索といいます。また、全探索以外にも様々な探索アルゴリズムが存在します。ちなみに補足ですが、$N = 3$ の場合 $184$ 通り、$N = 4$ の場合 $8512$ 通り… という感じで通り数が指数関数的に増えていきます。$N = 6$ くらいになると全探索でも数秒で実行できなくなるので、工夫が必要です。
探索アルゴリズムの奥深さ
前述の「おねえさん問題」について、以下の疑問を持った読者も多いのではないでしょうか。
- 単純な for ループを回すだけでは書けない。どうやって全探索を実装するのか
- 更に効率の良い探索アルゴリズムが存在するのか
「おねえさん問題ソルバー」の実装
多くの全探索問題は、2 章で解説するように、単純な for 文ループを回すだけで実装することができます。一方、この問題は複雑な構造を扱うので、一筋縄ではいきません。3-3. 節で紹介する「再帰関数」を用いてやっと解くことができるのです。
探索通り数を減らせないか?
実は比較的簡単に改善できる方法が一つあります。$N \times N$ の碁盤目状道路は対角線を軸に線対称なので、全体の通り数を $S$、初手で下向きに進む通り数を $T$ とするとき、必ず $S = 2T$ となります。したがって、全通り探索する必要はなく、最初に下向きに進むものの通り数だけを計算すれば、計算時間が $\frac{1}{2}$ に削減できます。それ以外にも様々な改善方法が存在します。
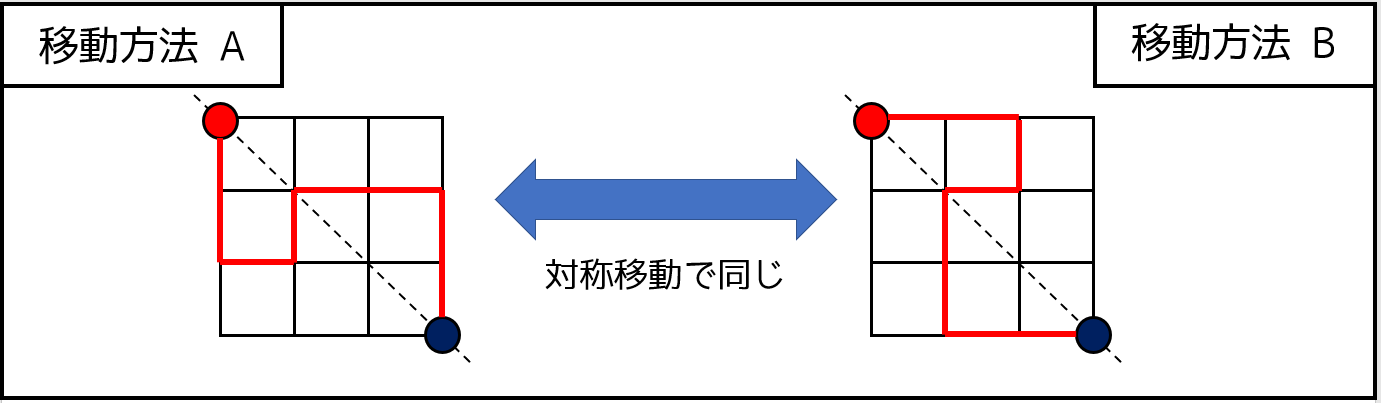
このように、
- 「探索視点」という新たな視点でアルゴリズムを考えられる
- 全探索を実装するだけでも、実は単純とは限らない
- 工夫をすると計算時間が減るような、様々な探索アルゴリズムが存在する
といった点で、探索アルゴリズムは奥深く面白いのです。
2 章以降では、様々な探索アルゴリズムとそのテクニック、そしてその面白さについて紹介していきます。続きも是非お読みください。
2. すべての基本、全探索
まず、探索アルゴリズムのうち「すべての基本」である全探索について解説していきたいと思います。この章は比較的簡単で、初心者あるいは中級者向けなので、「既に競技プログラミングで上達している!」という方は読み飛ばしていただいても構いません。
2-1. 全探索とは
1 章で説明した通り、全探索は「全てのあり得る通り数を探索する」ということです。例えば、下のような問題を考えましょう。
$N$ 個のカードが一列に並んでおり、左から $i$ 番目のカードに書かれた数は $A_i$ です。$N$ 個の中から $3$ つのカードを選び、和を $K$ にするような方法は何通りあるでしょう?
制約:$1 \leq N \leq 50$、$1 \leq A_i, K \leq 10^8$
これは、三重ループを用いて以下のように綺麗に実装できます。
# include <iostream>
using namespace std;
int N, K, A[59];
int cnt = 0;
int main() {
cin >> N >> K;
for (int i = 1; i <= N; i++) cin >> A[i];
for (int i = 1; i <= N; i++) {
for (int j = i + 1; j <= N; j++) {
for (int k = j + 1; k <= N; k++) {
if (A[i] + A[j] + A[k] == K) cnt += 1;
}
}
}
cout << cnt << endl;
return 0;
}
このように、ループを用いてあり得る状態を全通り探索するのが全探索の基本です。
2-2. 全探索では、通り数を見積もることが重要
全探索で最も重要なことは、「通り数をしっかり見積もること」です。一般に、コンピューターでは、$1$ 秒間に $10^8$ ~ $10^9$ 回程度計算できるといわれています。例えば競技プログラミングだと $1$ ~ $2$ 秒以内で答えを出さなければならないので、およそ $2$ 億 ~ $10$ 億通り程度しか探索できないことが多いです。
例えば、前述の問題の場合、$3$ 枚のカードの選び方は高々 $\frac{50 \times 49 \times 48}{6} = 19600$ 通りしか存在せず、十分余裕を持って間に合います。しかし、カードが $10000$ 枚になったらどうでしょうか。この場合は $\frac{10000 \times 9999 \times 9998}{6} \fallingdotseq 1.67 \times 10^{11}$ 通りとなり間に合いません。
したがって、探索視点でアルゴリズムを書くときは、
- 「全部で何通りになるか」を考えること
- 全体の計算回数がどれくらいになるかを考えること
がとても重要になってきます。一方で、たとえ AtCoder やコーディング試験の問題であっても、全探索で解ける問題は多いです。次の節で、全探索の問題パターンを整理していきたいと思います。

2-3. 全探索で問われる基本パターン 3 個
競技プログラミングやコーディング試験において、問われる全探索は基本的に以下の 3 パターンから成ります。
1. 問題文の通りに全探索すると解ける問題
2. あり得る通り数を全部試すと解ける問題
3. 答えを全探索する問題
パターン 1. 問題文の通りに全探索する
以下の問題を考えましょう。
$105$ は奇数であり正の約数を $8$ 個持ちます。さて、$1$ 以上 $N$ 以下の奇数のうち、正の約数をちょうど $8$ 個持つ数の個数はいくつでしょうか?
制約:$1 \leq N \leq 200$
出典:ABC106 B - 105
この問題は、問題文の通りに $1$ 以上 $N$ 以下の数それぞれについて、条件を満たすかどうか試せば良いだけです。これが全探索の 1 つ目の考え方です。このような問題では、
- 関数を用いて実装すると、実装とデバッグが楽になることがある
- $N$ が $10^9$ 以下などと大きい場合、この手法では間に合わないことがあるので、通り数の見積もりに気を遣う
ことが大切です。実装例(C++)は以下のようになります。
# include <iostream>
using namespace std;
bool solve(int n) {
int cnt = 0;
for (int i = 1; i <= n; i++) {
if (n % i == 0) cnt += 1;
}
if (cnt == 8 && n % 2 == 1) return true;
return false;
}
int main() {
int N, ans = 0;
cin >> N;
for (int i = 1; i <= N; i++) {
if (solve(i) == true) ans += 1;
}
cout << ans << endl;
return 0;
}
類題
類題としては以下の問題があります。
- AtCoder Beginner Contest 136 B - Uneven Numbers
- AtCoder Beginner Contest 068 B - Break Numbers
- AtCoder Beginner Contest 133 B - Good Distance ※問題文の通りに $N^2$ 個の組で試します
パターン 2. あり得るものを全通り試す
以下の問題を考えましょう。
$1$ から $N$ までの数の中から、重複無しで $3$ つの数を選び、合計が $x$ となるような通り数を求めてください。例えば $(N, x) = (5, 9)$ の場合、$2+3+4=9$ と $1+3+5=9$ の $2$ 通りがあります。
制約:$3 \leq N \leq 100$, $0 \leq x \leq 300$
出典:AOJ ITP1-7B How Many Ways?
この問題は、あり得る通り数を全通り調べ上げることで解くことができます。パターン 1 のように、問題文に直接「$1$ 以上 $N$ 以下について調べてください」といったようなことが書かれていなくても、あり得る状態が何通りあるか考えるのは重要です。選ぶ $3$ つの数を小さい順に $i, j, k$ とするとき、$1 \leq i < j < k \leq N$ と仮定することができるので、このような $(i, j, k)$ の組は高々 $\frac{100 \times 99 \times 98}{6} = 161700$ 通りとなり、全通り試しても十分間に合います。これが全探索の 2 つ目の考え方です。このような問題では、
- 全体の通り数に気を遣う(大体 $10^8$ 通り以下だと $1$ 秒以内で実行できる)
- for 文を用いた多重ループで実装することができる問題か確認する
- 詳しくは 3 章で述べるが、例えば以下のような問題は、単純な for 文で実装できない。
- $N$ 個のものの選び方を $2^N$ 通り全探索する問題
- 順列を $N!$ 通り全探索する問題
- 上の 2 つより複雑な構造を全探索する問題
- 詳しくは 3 章で述べるが、例えば以下のような問題は、単純な for 文で実装できない。
ことが大切です。以下のように三重ループを用いれば、実装できます。(C++ での実装例)
# include <iostream>
using namespace std;
int main() {
int N, X, ans = 0;
cin >> N >> X;
for (int i = 1; i <= N; i++) {
for (int j = i + 1; j <= N; j++) {
for (int k = j + 1; k <= N; k++) {
if (i + j + k == X) ans += 1;
}
}
}
cout << ans << endl;
return 0;
}
類題
類題としては以下の問題があります。
- 三井住友信託銀行プログラミングコンテスト2019 B - Tax Rate
- M-SOLUTIONSプロコンオープン2020 B - Magic 2
- AtCoder Beginner Contest 105 B - Cakes and Donuts
- AtCoder Beginner Contest 157 C - Guess the Number
パターン 3. 「答え」を全探索する
以下の問題を考えましょう。
$N$ 日間の気温のデータがあり、$i$ 日目の気温は $A_i$ 度でした。Qiita 君にとって、ある一定の「適温」を超えると暑いと感じます。$P$ 日連続で暑いと感じた場合、熱中症になってしまいます。熱中症にならなかったとき、Qiita 君の適温としてあり得る値のうち最小のものを求めてください。
制約:$1 \leq P \leq N \leq 1000, 0 \leq A_i \leq 40$, $A_i$ は整数
出典:オリジナル問題
これは、答えを全探索することで解けます。最小適温は必ず整数になるので、答えは $0, 1, 2, 3, ..., 40$ のいずれかであることが分かります。したがって、$41$ 通りそれぞれについて「熱中症にならないか」試せば良いです。これが全探索の 3 つ目の考え方で、4-2. 節で述べる「答えを二分探索するテクニック」にも繋がります。このような問題では、
- 判定する部分に関数を用いると、実装とデバッグが楽になることがある
- 答えの通り数が現実的な数になるのか見積もる
- 例えば、この問題で制約が $0 \leq A_i \leq 10^9$ の場合は、単純に $0, 1, ..., 10^9$ を全探索することはできない
ことが大切です。実装例(C++)は以下のようになります。
# include <iostream>
using namespace std;
int N, P, A[1009];
bool solve(int border) {
int CurrentLength = 0;
for (int i = 1; i <= N; i++) {
if (A[i] > border) CurrentLength += 1;
else CurrentLength = 0;
if (CurrentLength >= P) return false;
}
return true;
}
int main() {
cin >> N >> P;
for (int i = 1; i <= N; i++) cin >> A[i];
for (int i = 0; i <= 40; i++) {
if (solve(i) == true) { cout << i << endl; break; }
}
return 0;
}
2-4. 全探索の工夫パターン 3 個
2-3. 節で、全探索の基本 3 パターンについて紹介しました。しかし、それだけでは解けない全探索の問題もあります。そこで使えるのが、以下の 3 つの工夫テクニックです。
A. 既に分かっているものは探索しない
B. 探索の通り数を絞り込む
C. 別の視点から全探索する
パターン A. 既に分かっているものは探索しない
2-3. 節のパターン 2 で紹介した問題のアップグレードを考えましょう。
$1$ から $N$ までの数の中から、重複無しで $3$ つの数を選び、合計が $x$ となるような通り数を求めてください。例えば $(N, x) = (5, 9)$ の場合、$2+3+4=9$ と $1+3+5=9$ の $2$ 通りがあります。
制約:$3 \leq N \leq 8000$, $0 \leq x \leq 24000$
制約が大幅に上がって、$N \leq 100$ だったものが $N \leq 8000$ になってしまいました。したがって、$3$ つの数を選ぶ通り数は最大で $\frac{8000 \times 7999 \times 7998}{6} \fallingdotseq 8.5 \times 10^{10}$ 通りとなり、2-3. 節のパターン 2 の解法を用いると、実行に $2$ 分くらいかかってしまいます。そこで、以下の性質を考えます。
$3$ つの数を小さい順に $i, j, k$ として、$i, j$ の値が決まれば、$k$ の値が一意に定まる(必ず $X-i-j$ になる)
つまり、$i$ と $j$ しか探索しなくて良いので、探索する通り数は高々 $\frac{8000 \times 7999}{2} \fallingdotseq 3.2 \times 10^7$ 通りとなり、$1$ 秒以内で計算できます。
このように、「一部探索しただけで他が一意に定まる」性質を用いた全探索もできます。
実装例(C++)は以下のようになります。
# include <iostream>
using namespace std;
int main() {
int N, X, ans = 0;
cin >> N >> X;
for (int i = 1; i <= N; i++) {
for (int j = i + 1; j <= N; j++) {
int k = X - i - j;
if (j < k && k <= N) ans += 1;
}
}
cout << ans << endl;
return 0;
}
類題
類題としては以下の問題があります。
パターン B. 探索の通り数を絞り込む
2-3. 節のパターン 3 で紹介した問題のアップグレードを考えてみましょう。
$N$ 日間の気温のデータがあり、$i$ 日目の気温は $A_i$ 度でした。Qiita 君にとって、ある一定の「適温」を超えると暑いと感じます。$P$ 日連続で暑いと感じた場合、熱中症になってしまいます。熱中症にならなかったとき、Qiita 君の適温としてあり得る値のうち最小のものを求めてください。
制約:$1 \leq P \leq N \leq 1000, 0 \leq A_i \leq 10^9$, $A_i$ は整数
制約が大幅に上がって、$A_i \leq 40$ だったものが $A_i \leq 10^9$ になっています。単純に適温を全探索すると、$0, 1, 2, ..., 10^9$ 度全部調べ上げることになり、現実的な時間で計算が終わりません。そこで、以下の性質を考えます。
適温の最小値は、必ず $A_1, A_2, ..., A_N$ のいずれかになる。
その場合、$N$ 通りしか適温を探索する必要がないため、$N \leq 1000$ であっても高々 $1000 \times 1000 = 10^6$ 回程度の計算で済みます。
このように、探索するパターン(通り数)を絞り込むことができます。
実装例(C++)は以下のようになります。
# include <iostream>
using namespace std;
int N, P, A[1009];
int ans = 1000000007;
bool solve(int border) {
int CurrentLength = 0;
for (int i = 1; i <= N; i++) {
if (A[i] > border) CurrentLength += 1;
else CurrentLength = 0;
if (CurrentLength >= P) return false;
}
return true;
}
int main() {
cin >> N >> P;
for (int i = 1; i <= N; i++) cin >> A[i];
for (int i = 1; i <= N; i++) {
if (solve(A[i]) == true) ans = min(ans, A[i]);
}
cout << ans << endl;
return 0;
}
類題
類題としては以下の問題があります。
パターン C. 別の視点から全探索する
以下の問題を考えましょう。
$N$ 桁のラッキーナンバー $S$ があります。高橋君は、$S$ から $N-3$ 桁を消して残りの $3$ 桁を左から順に読んだものを暗証番号として設定することにしました。このとき、設定され得る暗証番号は何通りあるでしょうか。ただし暗証番号は $0$ から始まっても良いものとします。
制約: $1 \leq N \leq 30000$、ラッキーナンバーは '0' ~ '9' までの数字から成る
出典: 三井住友信託銀行プログラミングコンテスト2019 D - Lucky PIN
これは、単純に消す番号を全探索すると、$\frac{30000 \times 29999 \times 29998}{6} = 4.5 \times 10^{12}$ 通りとなり、間に合いません。(通り数を見積もるのが重要です)
しかし、暗証番号は高々 $10^3 = 1000$ 通りしかありません。また、ある特定の暗証番号については、左から順に貪欲にあてはめていくことで $O(N)$ で「暗証番号が作れるかどうか」判定できます。(紙面の都合上詳細な説明は省略しますが、詳しくは 公式解説 p.4 をご覧ください)
したがって、暗証番号を全探索すると $1000 \times 30000 = 3 \times 10^7$ 回程度の計算しか必要なくなり、$1$ 秒以内に計算することができます。
このように、別の視点から全探索をすることによって解くこともできます。
実装例(C++)は以下の通りです。
# include <iostream>
# include <string>
using namespace std;
int N, cnt; string S;
int main() {
cin >> N >> S;
for (int i = 0; i < 1000; i++) {
int a[3] = { i / 100, (i / 10) % 10, i % 10}, process = 0;
for (int j = 0; j < N; j++) {
if (process <= 2 && a[process] == (int)(S[j] - '0')) process++;
}
if (process == 3) cnt += 1;
}
cout << cnt << endl;
return 0;
}
類題
類題としては以下の問題があります。
3. 種々の全探索 ~bit全探索、順列全探索など~
全探索は、for 文ループを回すだけに尽きません。実際には、
- $1$ から $N$ までの長さ $N$ の順列を $N!$ 通り試す
- $N$ 個のものの選び方 $2^N$ 通り全部試す
- 1 章で紹介したお姉さん問題のような、更に複雑な構造
を扱わなければならない場合もあります。3 章では、それについて紹介していきたいと思います。今回紹介するのは以下の 4 つのアルゴリズムです。
3-1. bit 全探索
以下の問題を考えましょう。
$N$ 個の硬貨があります。番号 $i$ の硬貨は $A_i$ 円です。硬貨の選び方は $2^N$ 通りありますが、その中で合計価格が丁度 $X$ 円となる選び方は存在するでしょうか。
制約:$1 \leq N \leq 20, 1 \leq X, A_i \leq 10^8$
2 章で述べたように普通に for 文で全探索を書くと、ソースコードは以下のようになります。($k_i = 1$ のとき番号 $i$ の硬貨を選び、$k_i = 0$ のとき選ばないことを意味します。)
bool flag = true;
if (N == 1) {
for (int k1 = 0; k1 <= 1; k1++) {
int sum = 0;
if (k1 == 1) sum += A[1];
if (sum == X) flag = true;
}
}
if (N == 2) {
for (int k1 = 0; k1 <= 1; k1++) {
for (int k2 = 0; k2 <= 1; k2++) {
int sum = 0;
if (k1 == 1) sum += A[1];
if (k2 == 1) sum += A[2];
if (sum == X) flag = true;
}
}
}
:
if (N == 20) {
// とても長くなるので省略
}
if (flag == true) cout << "Yes" << endl;
else cout << "No" << endl;
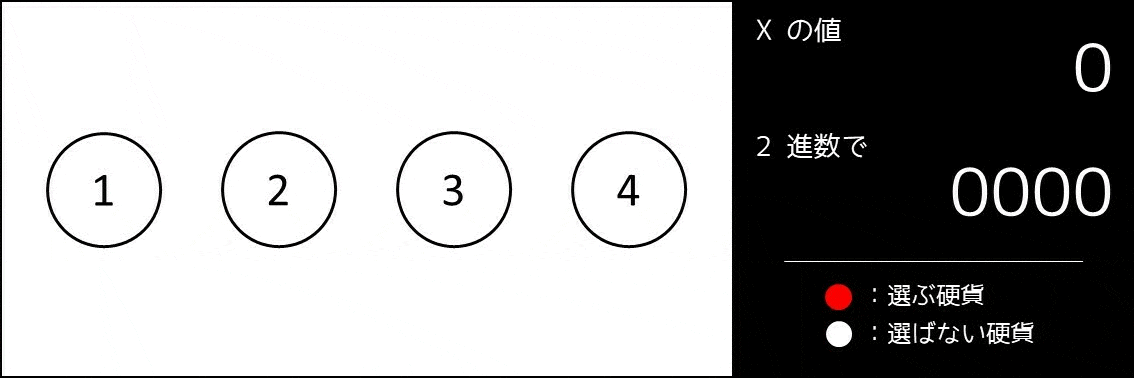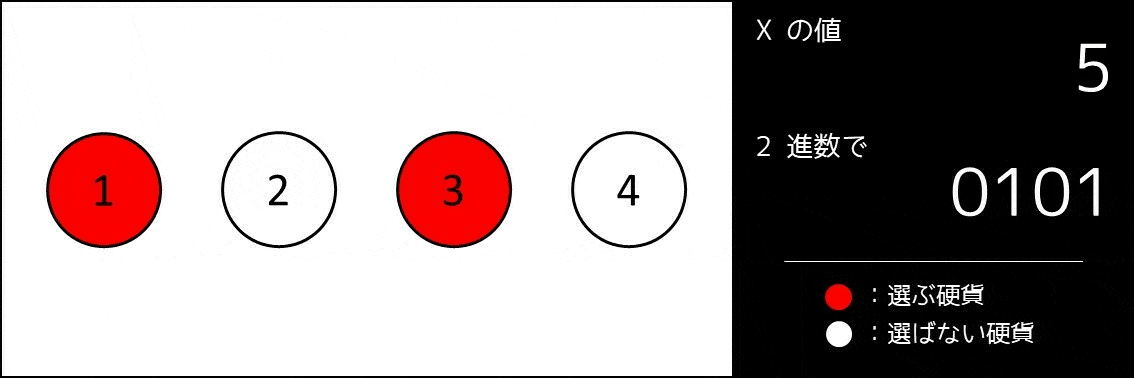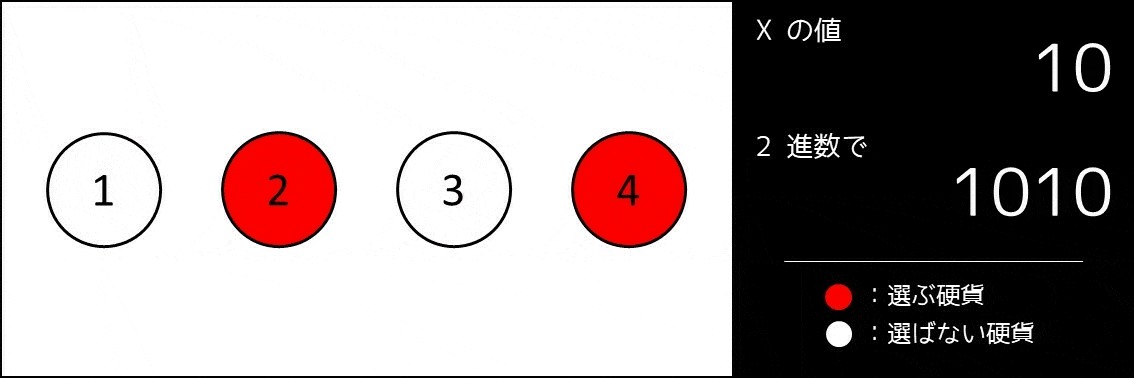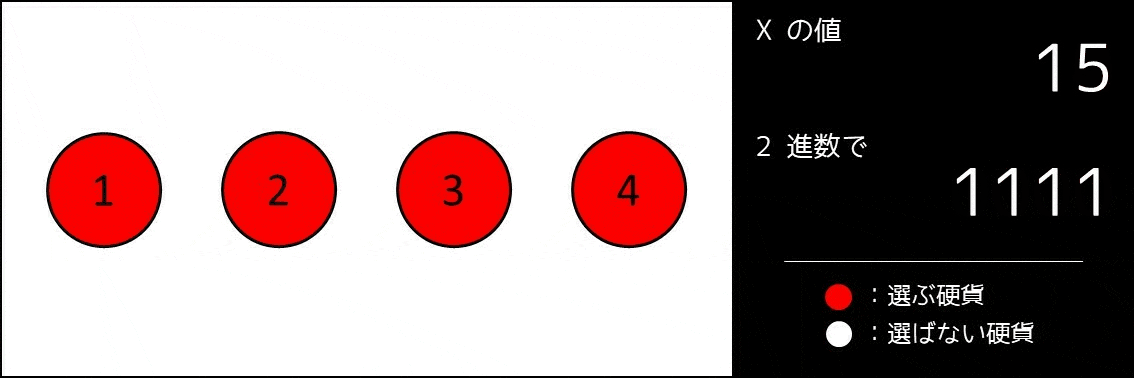
こんな実装をしてしまっては、コードがとても長くなり、読みにくくなってしまいます。そこで、実装量が減るすごい方法があります。これは**2進数を使うことです。**まず、bit 全探索のアイデアを説明した以下の GIF 画像をご覧ください。
つまりどういうことか
$x$ を二進数展開したときに、右から $i$ 桁目($2^{i-1}$ の位)の数を $A_{x, i}$ とします。そのとき、$0 \leq x \leq 2^{N}-1$ を満たす各 $x$ について、「$A_{x, i} = 1$ のとき番号 $i$ の硬貨を選び、そうでないとき選ばない」とすると、なんと $2^N$ 通り全ての選び方が $1$ 度ずつ探索できているのです。例えば $N = 3$ の場合、以下の通りになります。
- $x = 0: A_0 = (0, 0, 0)$ [どの硬貨も選ばない]
- $x = 1: A_1 = (1, 0, 0)$ [番号 $1$ の硬貨のみを選ぶ]
- $x = 2: A_2 = (0, 1, 0)$ [番号 $2$ の硬貨のみを選ぶ]
- $x = 3: A_3 = (1, 1, 0)$ [番号 $1, 2$ の硬貨を選ぶ]
- $x = 4: A_4 = (0, 0, 1)$ [番号 $3$ の硬貨のみを選ぶ]
- $x = 5: A_5 = (1, 0, 1)$ [番号 $1, 3$ の硬貨を選ぶ]
- $x = 6: A_6 = (0, 1, 1)$ [番号 $2, 3$ の硬貨を選ぶ]
- $x = 7: A_7 = (1, 1, 1)$ [すべての硬貨を選ぶ]
そうすると、最初の実装のような $20$ 重ループなど書く必要なく、$x$ を全探索して 2 進数表示をするだけで簡単に実装ができてしまうのです。
補足:二進数変換をするアルゴリズム
$x$ の二進数表示は、以下のようにして求めることができます。ただし、$bit_i$ は $x$ を二進数で表した数の右から $i$ 桁目($2^{i-1}$ の位)とします。
void Binary(int x) {
int bit[30];
for (int i = 0; i < 30; i++) {
int Div = (1 << i);
bit[i] = (x / Div) % 2;
}
}
したがって、以下のように実装すれば、3-1. 節冒頭の問題が解けます。
# include <iostream>
using namespace std;
int N, X, A[22];
bool flag = false;
int main() {
cin >> N >> X;
for (int i = 1; i <= N; i++) cin >> A[i];
for (int i = 0; i < (1 << N); i++) {
int bit[30], sum = 0;
for (int j = 0; j < N; j++) {
int Div = (1 << j);
bit[j] = (i / Div) % 2;
}
for (int j = 0; j < N; j++) sum += A[j] * bit[j];
if (sum == X) flag = true;
}
if (flag == true) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}
類題
類題としては以下の問題があります。
- AtCoder Beginner Contest 128 C - Swiches
- AtCoder Beginner Contest 147 C - HonestOrUnkind2
- AtCoder Beginner Contest 167 C - Skill Up
- Square869120Contest #4 B - Buildings are Colorful! ※難しいです
3-2. 順列全探索
以下の問題を考えましょう。
$N$ 個の都市があります。飛行機を使って、都市 $i$ から $j$ へ直接移動するのに $A_{i, j}$ 円かかります。Qiita 君は好きな都市から出発し、全ての都市を飛行機で一度ずつ巡りたいです。最小で何円必要ですか。
制約:$1 \leq N \leq 10, 1 \leq A_{i, j} \leq 1000$
この問題では、都市を巡る順番 $N!$ 通りを全探索することが要求されます。もし、2 章で述べたように for 文でループを書くと、$10$ 重以上のループを書く必要があり大変です。そこで、C++ の標準ライブラリである**「next_permutation」**という関数を用いて順列全探索を行うこと、楽に全探索ができます。なお、その他の多くの言語ではそのような関数がサポートされていないので、3-3. 節で紹介する「再帰関数を用いた全探索」やその他の手法を用いてこの問題を解かなければなりません。
next_permutation とは
順列を自動で全探索してくれる C++ の標準ライブラリです。基本的には以下のように書きます。
do {
// ここに処理を書く
} while(next_permutation(P, P + N));
なお、$P$ は最初昇順にソートされている必要があります。例えば $N = 3, P = (1, 2, 3)$ の場合
- $1$ 回目のループでは $P = (1, 2, 3)$ として処理が行われる
- $2$ 回目のループでは $P = (1, 3, 2)$ として処理が行われる
- $3$ 回目のループでは $P = (2, 1, 3)$ として処理が行われる
- $4$ 回目のループでは $P = (2, 3, 1)$ として処理が行われる
- $5$ 回目のループでは $P = (3, 1, 2)$ として処理が行われる
- $6$ 回目のループでは $P = (3, 2, 1)$ として処理が行われる
- $6$ 回目のループが終わり次第、ループから抜ける
という感じで、全ての順列を更新してくれる便利な関数です。詳しくは、
をお読みください。
順列全探索の実装例
以下のように実装することができます。計算量は $O(N! \times N)$ です。
# include <iostream>
# include <algorithm>
using namespace std;
int N, A[11][11], ans = 1000000000;
int P[11] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11};
int main() {
cin >> N;
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) cin >> A[i][j];
}
do {
int ret = 0;
for (int i = 0; i < N - 1; i++) ret += A[P[i]][P[i + 1]];
ans = min(ans, ret);
} while(next_permutation(P, P + N));
cout << ans << endl;
return 0;
}
類題
類題としては以下の問題があります。
- AtCoder Beginner Contest 145 C - Average Length
- AtCoder Beginner Contest 150 C - Count Order
- AtCoder Beginner Contest 054 C - One-stroke Path
3-3. 再帰関数を用いた全探索
以下の問題を考えましょう。
すべての桁が $1$ 以上 $M$ 以下であるような、増加的な $N$ 桁の整数をすべて出力してください。(増加的な整数とは、$112$ や $1355679$ のような数のことを指します。)
制約: $1 \leq N \leq 10, 1 \leq M \leq 9$
ヒント:条件を満たす整数の個数は、どんな入力でも $100000$ 通り以下
この問題も 2 章で示したように for 文を書くと $10$ 重以上のループが必要となり、非常に複雑になってしまいます。ここで便利なのが再帰関数です。
再帰関数とは
再帰関数とは、自分自身の関数を呼び出す関数のことを指します。例えば func(int a) という関数があったとして、その関数の中で func を呼び出すのは再帰関数です。例えば、以下のようなコードを書いたとしましょう。
int func(int a) {
if (a == 0) return 1;
int z1 = 0; if (a >= 1) z1 = func(a - 1);
int z2 = 0; if (a >= 2) z2 = func(a - 2);
return z1 + z2;
}
そこで func(4) を呼び出すと、以下の GIF 画像のように遷移が行われ、$5$ が返ってきます。
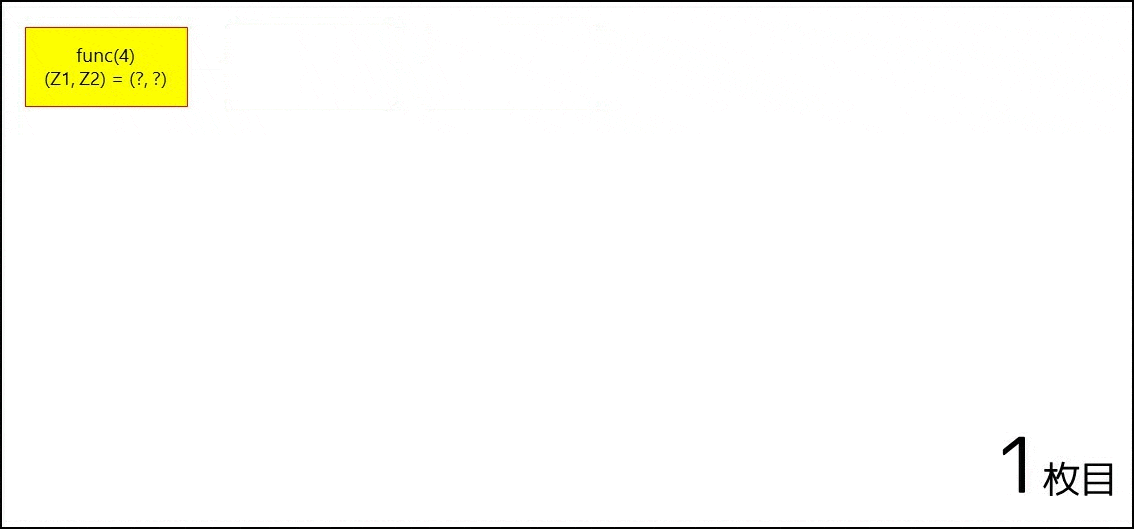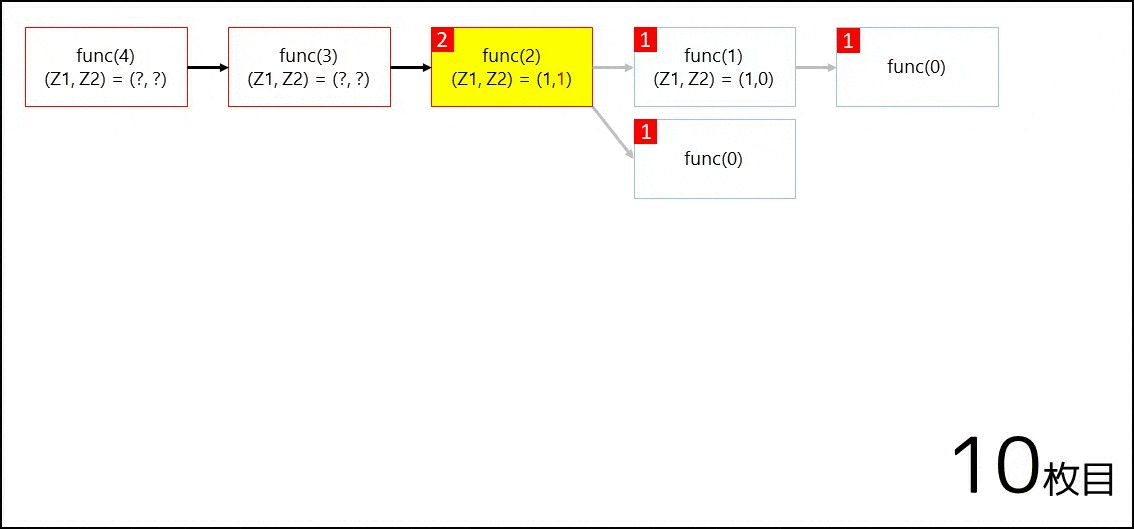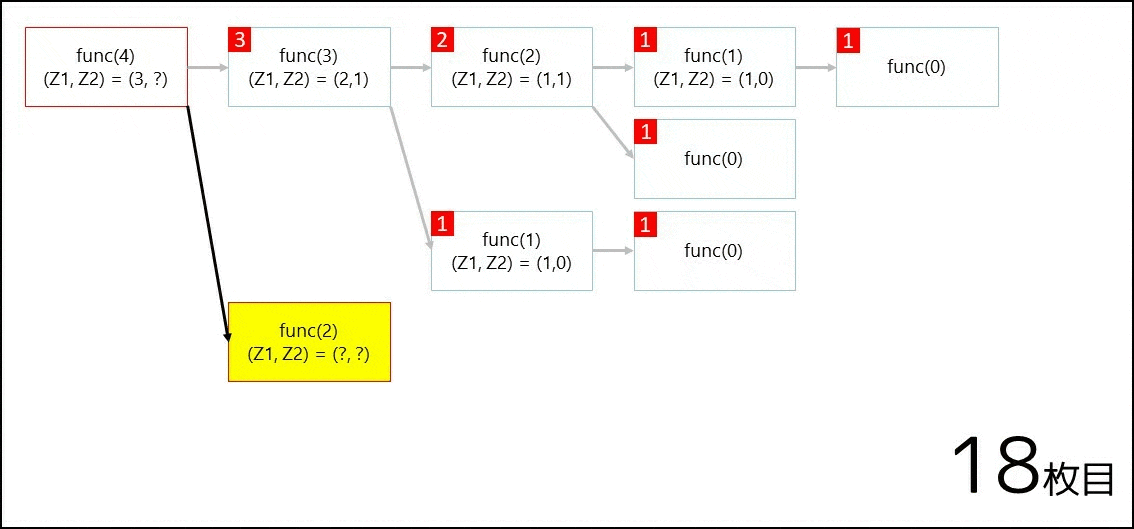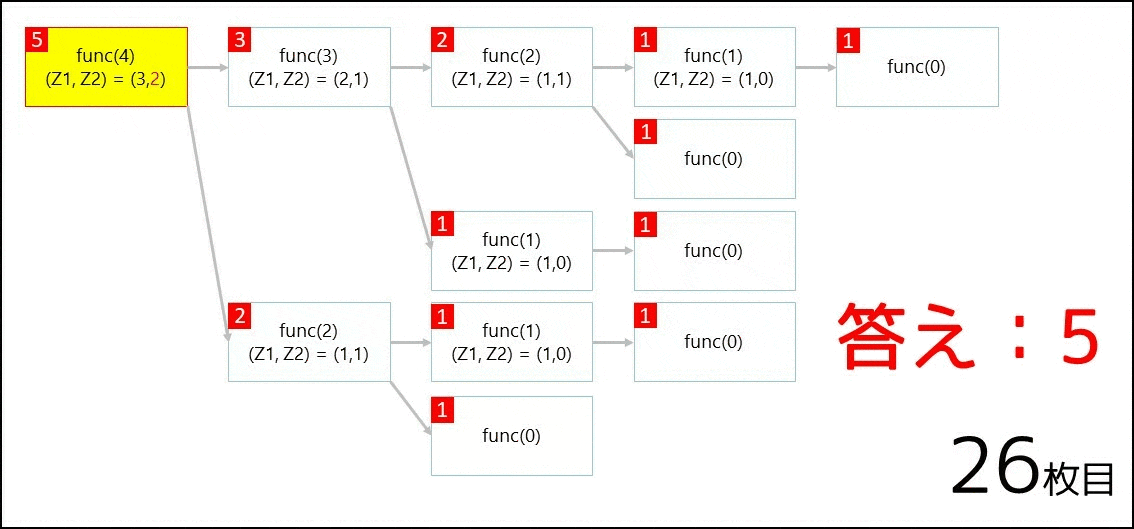
より詳しい話は、
をご覧ください。
全探索の具体的な実装
基本的には、「左の桁から $1$ 桁ずつ順番に書いていく」という考え方を利用します。
そこで、現在書かれている数を表す文字列 $cur$ を用いた再帰関数 func(string cur) を実装することを考えます。文字列 $cur$ の最後の桁を $last$($cur$ が空文字列の場合は $1$)とするとき、次の桁は $last, last+1, ..., M$ のいずれかになります。例えば $N = 5, M = 5, cur = $"$122$" の場合、次の遷移は以下の $4$ 通りになります。
-
func("1222")を呼び出す -
func("1223")を呼び出す -
func("1224")を呼び出す -
func("1225")を呼び出す
したがって、以下のように実装すれば良いです。なお、このように再帰関数を用いて全通り調べ上げる手法を**深さ優先探索(DFS)**ということがあります。
void func(string cur) {
if (cur.size() == N) { cout << cur << endl; return; }
int last = 1;
if (cur.size() >= 1) last = cur[cur.size() - 1];
for (int i = last; i <= M; i++) {
string nex = cur; nex += ('0' + i);
func(nex);
}
}
実際に $M = 3, N = 3$ の場合、再帰関数は以下の GIF 画像のように動いています。(最初は func("") を呼び出します)

類題
類題としては以下の問題があります。
- AtCoder Beginner Contest 165 C - Many Requirements
- CPSCO2019 Day1 C - Coins
- パナソニックプログラミングコンテスト 2020 D - String Equivalence
3-4. 幅優先探索
ここまでで、以下の 4 パターンの全探索について紹介していきました。
- for 文を用いた全探索 (2 章)
- bit 全探索 (3-1. 節)
- 順列全探索 (3-2. 節)
- 再帰関数を用いた深さ優先探索 (3-3. 節)
基本的に、状態を全部数え上げるために使われる全探索で必要なものはここまでです。しかし、「探索」という名前が付いた全探索アルゴリズムは他にもあります。この一つが幅優先探索です。
幅優先探索 (BFS) は、キューというデータ構造を用いた探索アルゴリズムの一つです。このアルゴリズムを使うと、基本的に以下のような問題を解くことができます。
$N$ 個の都市と $M$ 個の道路があります。番号 $i$ の道路は都市 $A_i$ と $B_i$ を双方向に繋いでいます。都市 $1$ から都市 $N$ まで行くためには、最小で何本の道路を通る必要があるでしょうか?
※このような問題を「最短経路問題」といいます
これは、以下のようなアルゴリズムを利用することで計算できます。
- キューというデータ構造を用意する。これを $Q$ とする。
- $1 \leq i \leq N$ に対し、$dist_i = \infty$ とする。
- $Q$ にスタート地点である $1$ を push し、$dist_1 = 0$ とする。
- キューが空になるまで、以下の操作を繰り返す。
- キューの先頭要素を取り出す。これを $pos$ とする。
- $pos$ から隣接している頂点の中でまだ訪れていない頂点 $v$(つまり、$dist_v = \infty$ である頂点)それぞれについて、$dist_v = dist_{pos} + 1$ とし、キュー $Q$ に $v$ を push する。
このアルゴリズムは、例えば以下の GIF 画像の通りに動きます。
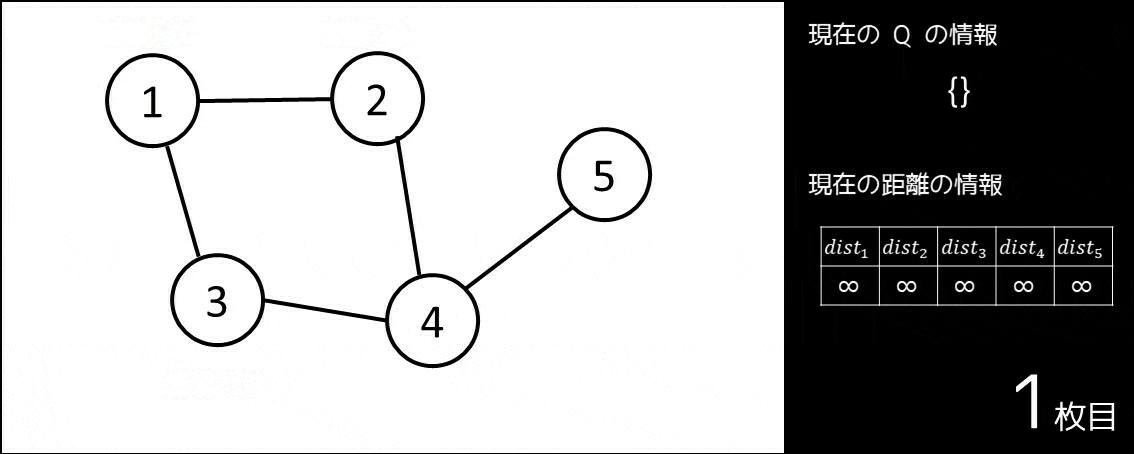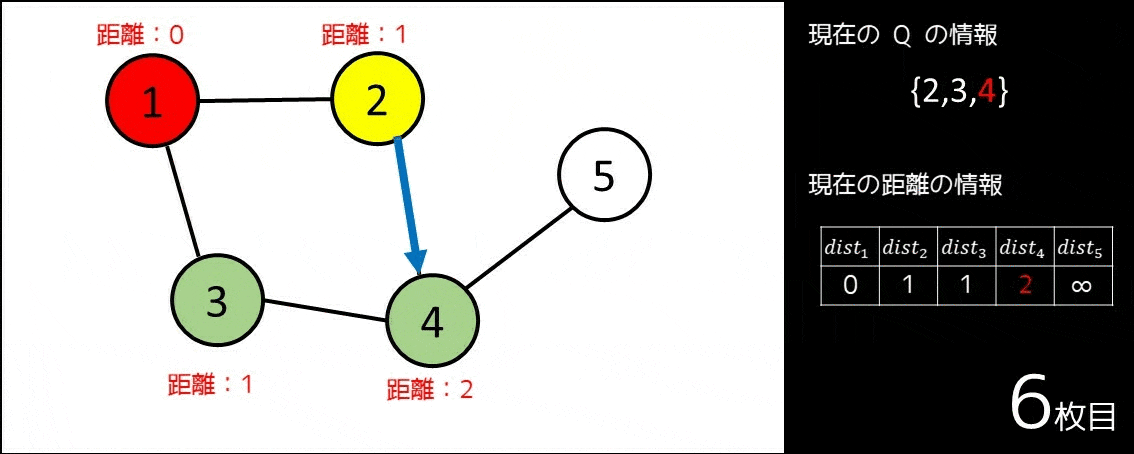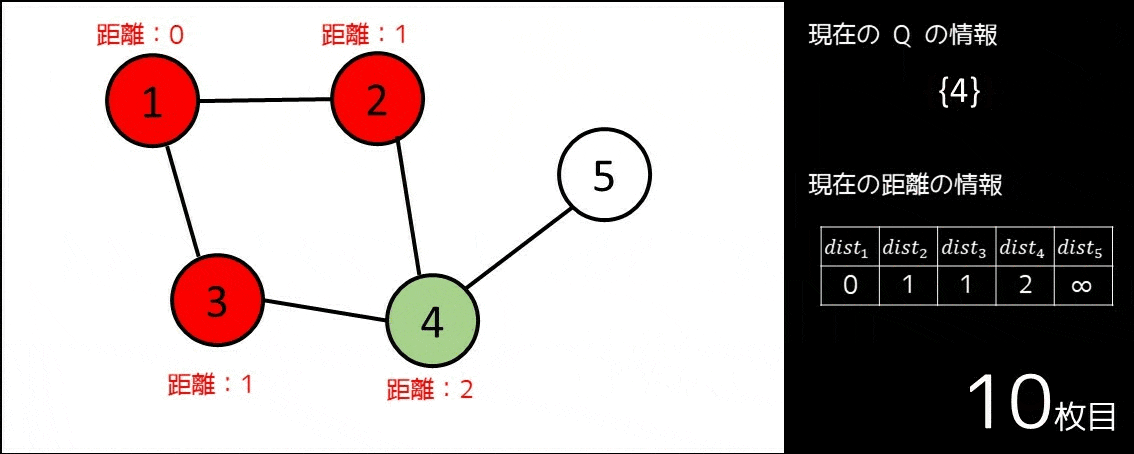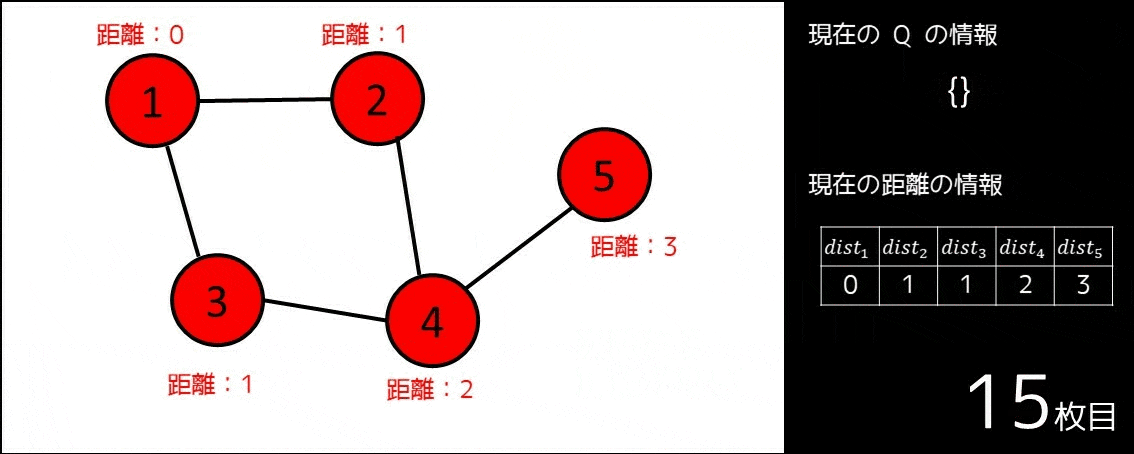
このように、幅優先探索は最短経路問題を解くにあたって使われることが多く、これまでの全探索で扱ったような「全通り数え上げる」系の問題にはあまり使われません。幅優先探索、最短経路問題についてより詳しく知りたい方は、以下の記事をお読みください。
類題
類題としては以下の問題があります。
3-5. bit 全探索の拡張
3-1. 節で bit 全探索を扱いました。この手法では、2 進数を用いることによって $2^N$ 通りの選び方を探索しました。そこで、3 進数 以上でもできないのかと考えるのは自然な発想だと思いますが、実はできます。例えば以下の問題を考えましょう。
$N$ 個のライトがあります。番号 $i$ のライトを赤色に灯せば $R_i$、緑色に灯せば $G_i$、青色に灯せば $B_i$ のスコアが得られます。スコアを丁度 $K$ にすることができるか判定してください。
制約:$1 \leq N \leq 13$
この問題は、実は bit 全探索を少し変えるだけで解けます。例えば、今まで $2$ 進数変換でやっていた部分を $3$ 進数変換してしまい、「$0$: 赤色、$1$: 緑色、$2$: 青色」というように対応させれば、全通り探索することができます。ちなみに、$3$ 進数変換は以下のように実装することができます。(ここでは $B_i$ が $3$ 進数表示での右から $i$ 桁目、つまり $3^{i-1}$ の位である)
void solve(int x) {
int B[18], power3 = 1;
for (int i = 0; i < 18; i++) {
B[i] = (x / power3) % 3;
power3 *= 3;
}
}
類題
類題としては以下の問題があります。
3-6. <発展>再帰関数を用いた全探索の応用~メモ化再帰~
3-3. 節の再帰関数の導入部分で、以下の関数を定義しました。
int func(int a) {
if (a == 0) return 1;
int z1 = 0; if (a >= 1) z1 = func(a - 1);
int z2 = 0; if (a >= 2) z2 = func(a - 2);
return z1 + z2;
}
例えば func(4) を呼び出したとしましょう。そのとき、同じ $a$ の値の関数が何回も呼び出されてしまいます。以下の GIF 画像のように、func(0) は $5$ 回、func(1) は $3$ 回、func(2) は $2$ 回呼び出され、それぞれについて同じ結果がでています。したがって、何度も同じ $a$ の値について探索するのは時間の無駄です。
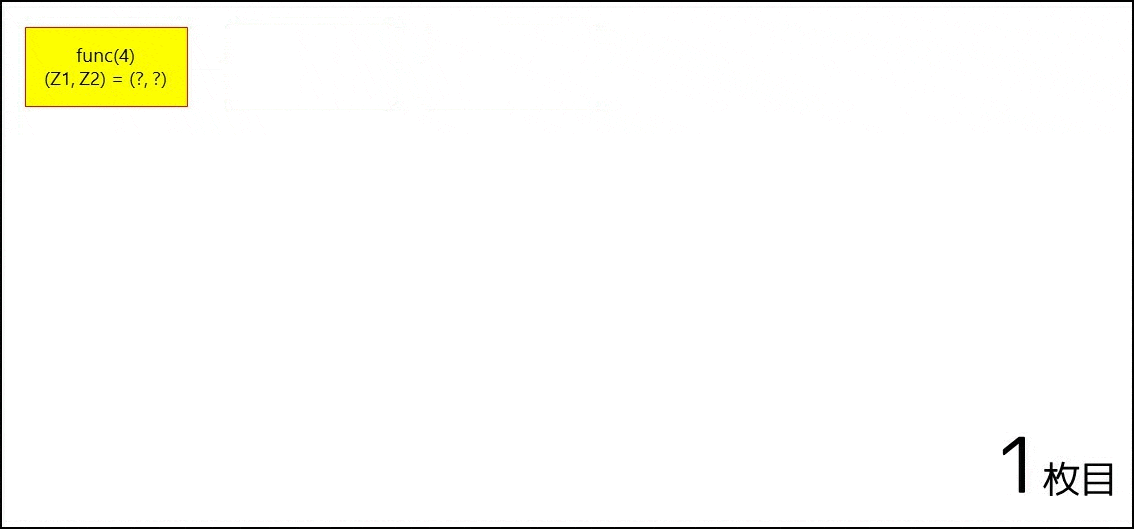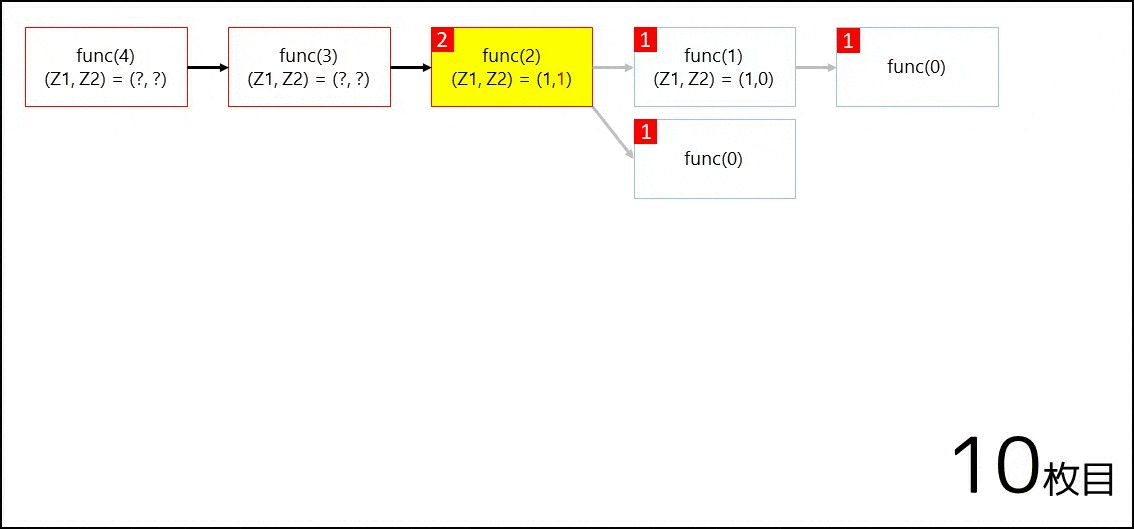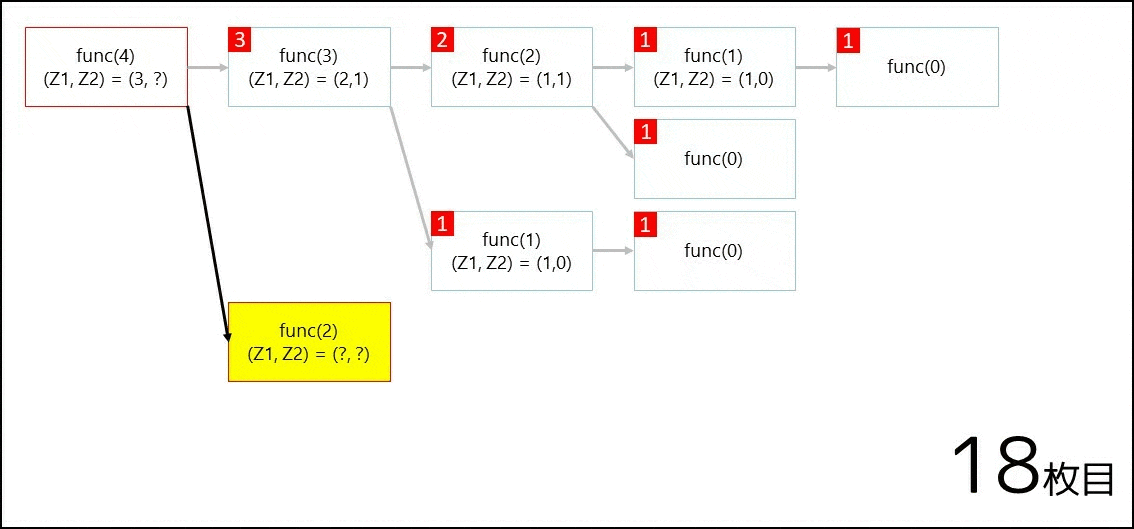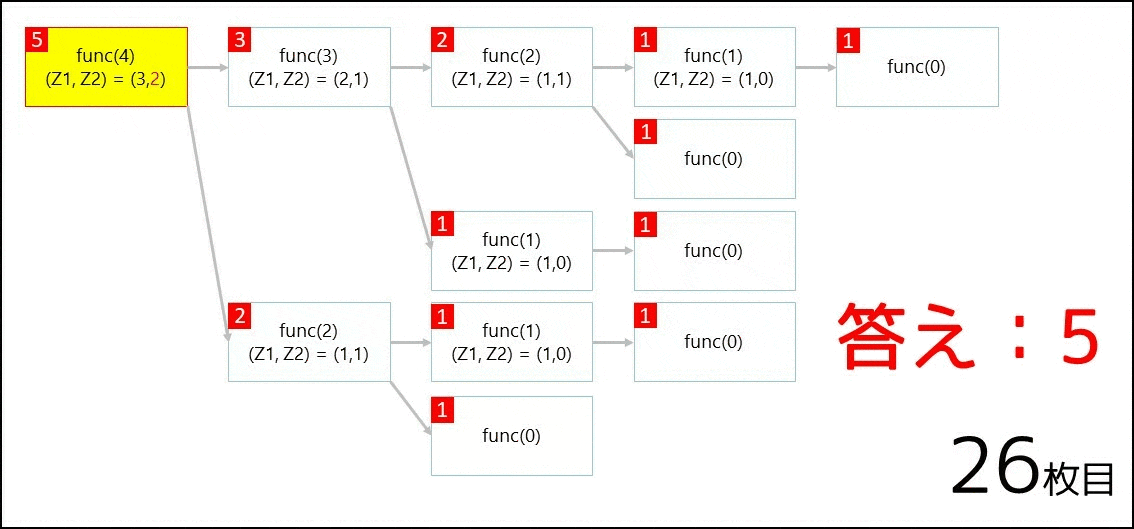
そこで、一度求まった値は記録しておくことを考えます。つまり、例えば一度 func(2) の
値が $2$ であると分かったら、今後 func(2) が呼び出されたときに func(1) と func(0) を呼び出さず、そのまま $2$ を返すということです。ソースコードで書くと以下の通りになります。
int Memo[1009];
int func(int a) {
if (a == 0) return 1;
if (Memo[a] >= 1) return Memo[a];
int z1 = 0; if (a >= 1) z1 = func(a - 1);
int z2 = 0; if (a >= 2) z2 = func(a - 2);
Memo[a] = z1 + z2;
return z1 + z2;
}
それを実行してみると、以下の GIF 画像のようになり、ステップ数が 26ステップから 16ステップまで大幅に減ります。このようなテクニックをメモ化再帰といい、これは全探索ではなく動的計画法の仲間です。このように、再帰関数による深さ優先探索のアイデアは、少し変えただけで動的計画法という全く別のアルゴリズムになるのです。

3-7. ここまでのまとめ
2 章と 3 章では、以下の全探索を扱ってきました。
| 章/節 | アルゴリズム | 計算量 |
|---|---|---|
| 2. | for 文ループで書ける全探索 | いろいろ |
| 3-1. | bit 全探索 | $O(2^N \times N)$ |
| 3-2. | 順列全探索 | $O(N! \times N)$ |
| 3-3. | 再帰関数を用いた全探索 | いろいろ |
| 3-4. | 幅優先探索 | $O(グラフの辺の数)$ |
| 3-5. | 3 進数での bit 全探索 | $O(3^N \times N)$ |
ちなみに、計算量とは「大まかににどれくらいの計算時間がかかるか」だと思って良いです。例えば $O(2^N)$ のアルゴリズムでは大体 $2^N$ 回の計算時間がかかります。詳しく知りたい方は、以下の記事をご覧ください。
ここまでの章で扱ったアルゴリズムは、すべて全通り探索するというものがベースでした。簡単な構造から複雑な構造まで、様々なものを全探索していきました。しかし、4 章以降で紹介するアルゴリズムは、
全通り探索しなくても、実は正しい答えが求められる効率的な探索アルゴリズム
が中心となっています。実は「探索アルゴリズム」は全探索だけではなく、もっと効率的ですごいアルゴリズムもたくさんあるのです。この素晴らしさを 4 章以降で紹介していきたいと思います。
4. 効率的な探索手法 ~二分探索と三分探索~
探索アルゴリズムは、ただ「全通り探索すること」に限ったものではありません。効率よく探索を行い、時間を削減する方法が実は存在するのです。そこで本章では、
を解説していきます。
4-1. 二分探索アルゴリズム
以下の問題を考えましょう。
$N$ 人の生徒が背の順に整列しています。前から $i$ 番目の生徒は $A_i$ センチメートルです。そのとき、「身長が $V$ センチより低い人は何人か?」という質問をできるだけ短い時間で答えてください。
制約:$1 \leq N \leq 1000000, 1 \leq A_i \leq 10^9, A_1 \leq A_2 \leq ... \leq A_N$
たとえば「前から $1$ 番目より低いか」「前から $2$ 番目より低いか」…「前から $N$ 番目より低いか」とすべて調べ上げ、2 章で説明した通りに for 文ループで全探索(線形探索)をすると、ソースコードは以下のようになります。
int query(int V) {
// N と A[i] は既に入力で与えられているものとする
int Answer = 0;
for (int i = 1; i <= N; i++) {
if (A[i] < V) Answer += 1;
}
return Answer;
}
しかし、この方法だと $1$ 回の質問につき $N$ 回の計算がかかってしまいます。もっと効率的な手法があるのでしょうか。そこで、一つ例を挙げて考えてみましょう。

たとえば、生徒が上のような身長であるとします。そこで、身長 $V=169$ センチより低い生徒が何人いるか考えてみましょう。
ステップ 1
現時点で、答えは $0$ 人以上 $16$ 人以下であることが分かっています。そこで、Yes と No になる確率が半分になるように、「答えが $7$ 人以下か」という質問を考えます。前から $8$ 番目の生徒の身長は $173$cm で、$V=169$cm を超えるので、答えが $7$ 人以下であることが分かります。

ステップ 2
現時点で、答えは $0$ 人以上 $7$ 人以下であることが分かっています。そこで、Yes と No になる確率が半分になるように、「答えが $3$ 人以下か」という質問を考えます。前から $4$ 番目の生徒の身長は $166$cm で、$V=169$cm 以下なので、答えが $4$ 人以上であることが分かります。

ステップ 3
現時点で、答えは $4$ 人以上 $7$ 人以下であることが分かっています。そこで、Yes と No になる確率が半分になるように、「答えが $5$ 人以下か」という質問を考えます。前から $6$ 番目の生徒の身長は $167$cm で、$V=169$cm 以下なので、答えが $6$ 人以上であることがわかります。

ステップ 4
現時点で、答えは $6$ 人以上 $7$ 人以下であることが分かっています。そこで、Yes と No になる確率が半分になるように、「答えが $6$ 人以下か」という質問を考えます。前から $7$ 番目の生徒の身長は $170$cm で、$V=169$cm 以下なので、答えが $6$ 人以下であることが分かります。

このように、半分ずつ区間を縮小していくことで探索回数を減らすアルゴリズムを二分探索といいます。この場合、探索回数は $O(\log_2 N)$ となります。具体的には以下の通りです。
| $N$ | 10 | 100 | 1000 | 10000 | 100000 | 1000000 |
|---|---|---|---|---|---|---|
| $\log_2 N$ | 4 | 7 | 10 | 14 | 17 | 20 |
また、前述したステップのような処理を実装すると、以下のようになります。(このような実装手法のことを「めぐる式二分探索」といいます)
int query(int V){
int ng = 0, ok = N + 1;
while(ok - ng > 1){
int m = (ng + ok) / 2;
if(A[m] >= V) ok = m;
else ng = m;
}
return ok;
}
便利な関数「lower_bound」
しかし、このような実装をしなくても、今回紹介した問題は解けます。これは C++ の標準ライブラリにサポートされている lower_bound という関数です。例えば以下のように使うと、$A_1, A_2, ..., A_N$ の中で $V$ より低い値が何個あるかを $O(\log_2 N)$ で求めてくれます。
int query(int V){
return (lower_bound(A + 1, A + N + 1, V) - A) - 1;
}
詳しくは、
をご覧ください。また、めぐる式二分探索について詳しく知りたい方は、
をお読みください。
4-2. 二分法アルゴリズム
二分探索が分かったところで、次に「二分法」という二分探索に似た手法を紹介します。例えば、以下の問題を考えましょう。
$\sqrt{2}$ を小数第 9 位まで求めなさい。ただし、sqrt 関数と pow 関数は使ってはならない。
そこで、単純な探索手法を用いると、答えが $1$ 以上 $2$ 以下であることを仮定しても、
- $1.000000000^2 \leq 2$ か?
- $1.000000001^2 \leq 2$ か?
- $1.000000002^2 \leq 2$ か?
:
- $1.999999999^2 \leq 2$ か?
- $2.000000000^2 \leq 2$ か?
という計算をすることになってしまい、計算回数が爆発してしまいます。そこで、二分探索のアイデアを用いて、以下のような計算を行うことを考えます。
| 現在分かっている $x$ の範囲 | 行う計算 | 計算結果 |
|---|---|---|
| $1.0000 \leq x \leq 2.0000$ | $1.5000^2 \leq 2$ か? | 間違い($\sqrt{2} < 1.5000$) |
| $1.0000 \leq x \leq 1.5000$ | $1.2500^2 \leq 2$ か? | 正しい($\sqrt{2} \geq 1.5000$) |
| $1.2500 \leq x \leq 1.5000$ | $1.3750^2 \leq 2$ か? | 正しい($\sqrt{2} \geq 1.5000$) |
| $1.3750 \leq x \leq 1.5000$ | $1.4375^2 \leq 2$ か? | 間違い($\sqrt{2} < 1.5000$) |
| $1.3750 \leq x \leq 1.4375$ | $1.4063^2 \leq 2$ か? | 正しい($\sqrt{2} \geq 1.4063$) |
| $1.4063 \leq x \leq 1.4375$ | $1.4219^2 \leq 2$ か? | 間違い($\sqrt{2} < 1.4219$) |
| $1.4063 \leq x \leq 1.4219$ | $1.4141^2 \leq 2$ か? | 正しい($\sqrt{2} \geq 1.4141$) |
このように計算を行うと、$35$ 回程度の計算で $\sqrt{2}$ のほぼ正確な値が求まります。このように、方程式 $f(x) = 0$ の解を二分探索のような手法を用いて求めることを二分法といいます。
# include <iostream>
using namespace std;
int main() {
double l = 1.0, r = 2.0;
for (int i = 1; i <= 35; i++) {
double m = (l + r) / 2;
if (m * m <= 2.0) { l = m; }
else { r = m; }
}
printf("%.9lf\n", l);
return 0;
}
補足:答えで二分探索するテクニック
二分法のアイデアは、方程式 $f(x) = 0$ の解を求めるだけでなく、答えを二分探索したいときにも使われます。例えば以下のような問題を考えましょう。
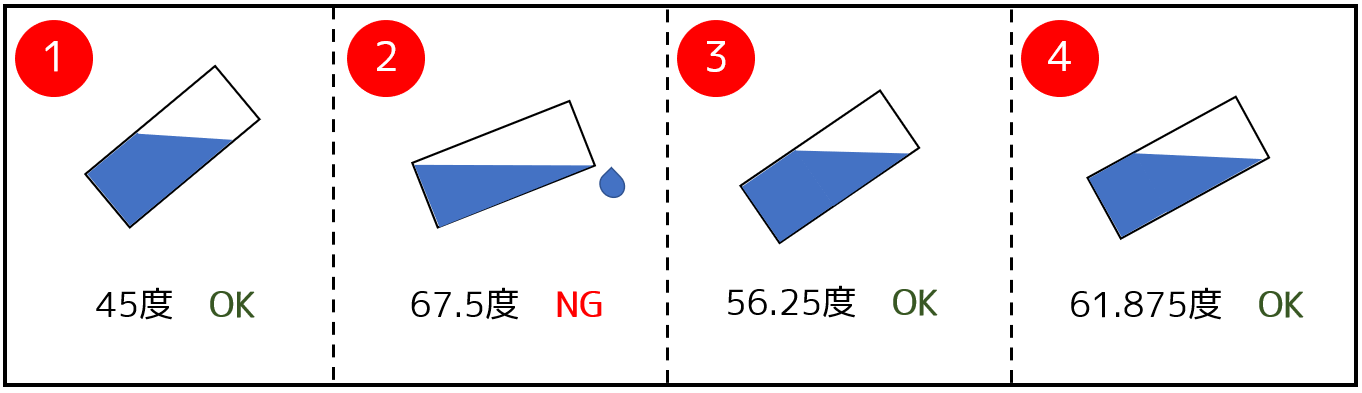
高橋君は、底面が 1 辺 $a$cm の正方形であり、高さが $b$cm であるような直方体型の水筒を持っています。この水筒の中に体積 $x$cm3 の水を入れ、底面の長方形の $1$ 辺を軸にして、この水筒を徐々に傾けます。水を溢れさせずに何度まで傾けられるでしょうか。
出典:ABC144 D - Water Bottle
この場合は、以下の図のように二分法が使えます。基本的には、指定した区間において、$x$ に対して答え $f(x)$ が単調増加あるいは単調減少である場合、二分法が通用します。
4-3. 三分探索
次に紹介するのは三分探索です。例えば以下の問題を考えてみましょう。
関数 $f(x) = 2^x - x$ の最小値を求めよ。
この問題は微分法を使っても解けるのですが、もう少し直感的な方法があります。これは二分探索と似たアイデアの一つである三分探索です。例えば、以下のように計算を行ってみることを考えましょう。
| 現在分かっている $x$ の範囲 | 行う計算 | 計算結果 |
|---|---|---|
| $0.0000 \leq x \leq 0.9000$ | $f(0.3000) \leq f(0.6000)$ か? | いいえ |
| $0.3000 \leq x \leq 0.9000$ | $f(0.5000) \leq f(0.7000)$ か? | はい |
| $0.3000 \leq x \leq 0.7000$ | $f(0.4333) \leq f(0.5667)$ か? | いいえ |
| $0.4333 \leq x \leq 0.7000$ | $f(0.5222) \leq f(0.6111)$ か? | はい |
| $0.4333 \leq x \leq 0.6111$ | $f(0.4889) \leq f(0.5555)$ か? | いいえ |
さて、上の表は何をやっているのでしょうか。
実は、以下のようなアルゴリズムを実行しているのです。
- $f(x)$ が最小となる $x$($x_{min}$ とする)は $0$ 以上 $0.9$ 以下なので、$l = 0, r = 0.9$ とおく。
- 以下の操作を繰り返す。
- $c_1 = \frac{l+l+r}{3}$ とする。
- $c_2 = \frac{l+r+r}{3}$ とする。
- $f(c_1) \leq f(c_2)$ であれば絶対 $l \leq x \leq c_2$ なので、$r = c_2$ とする。
- $f(c_1) > f(c_2)$ であれば絶対 $c_1 \leq x \leq r$ なので、$l = c_1$ とする。
図で表すと以下のようになります。確かに区間が $x_{min}$ に近づいているのが分かります。
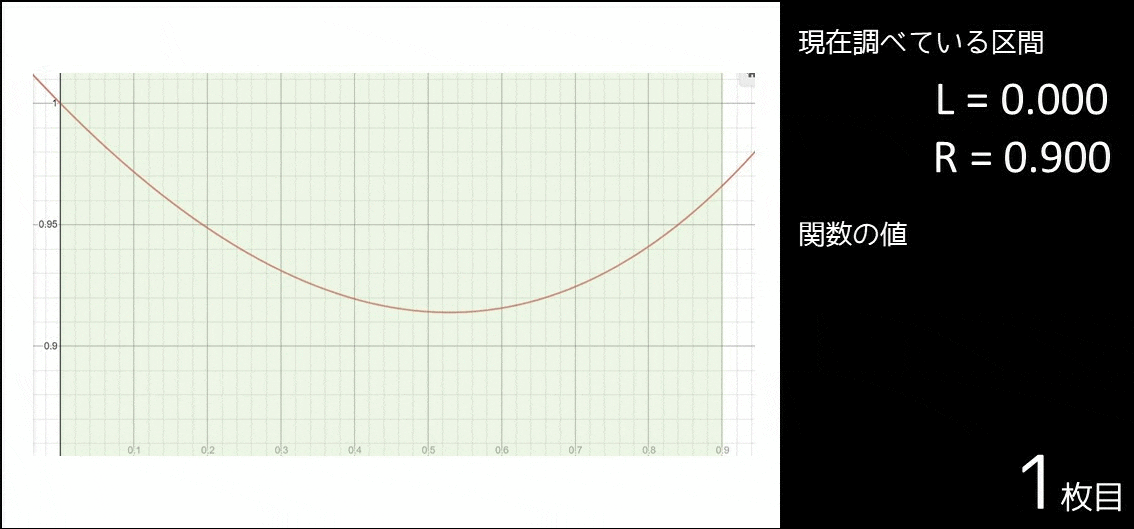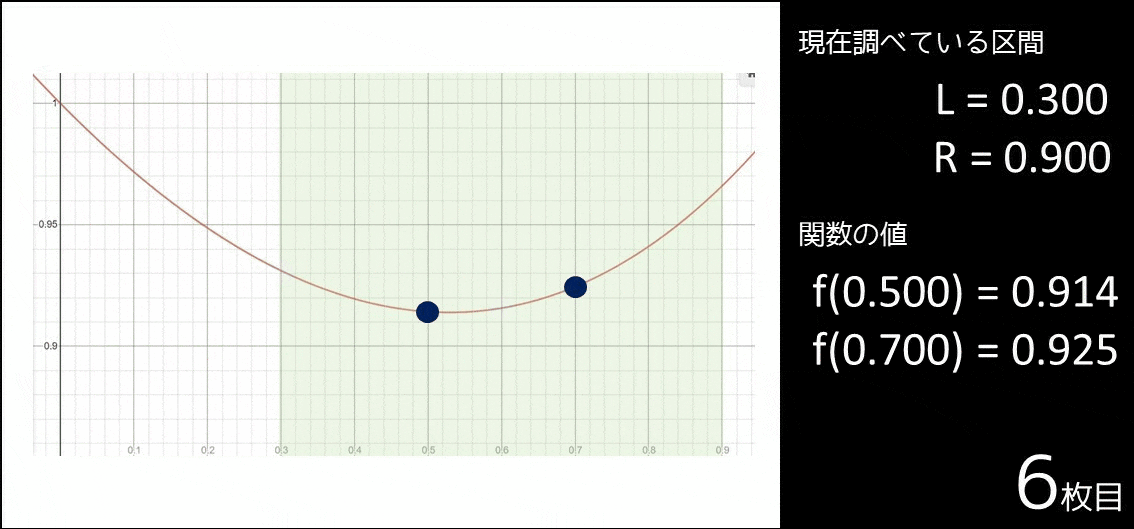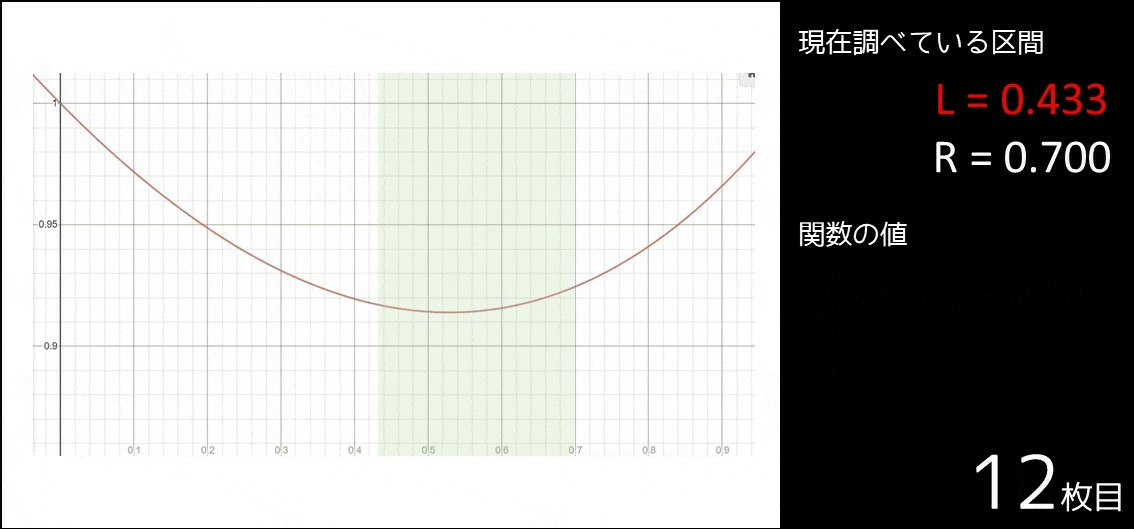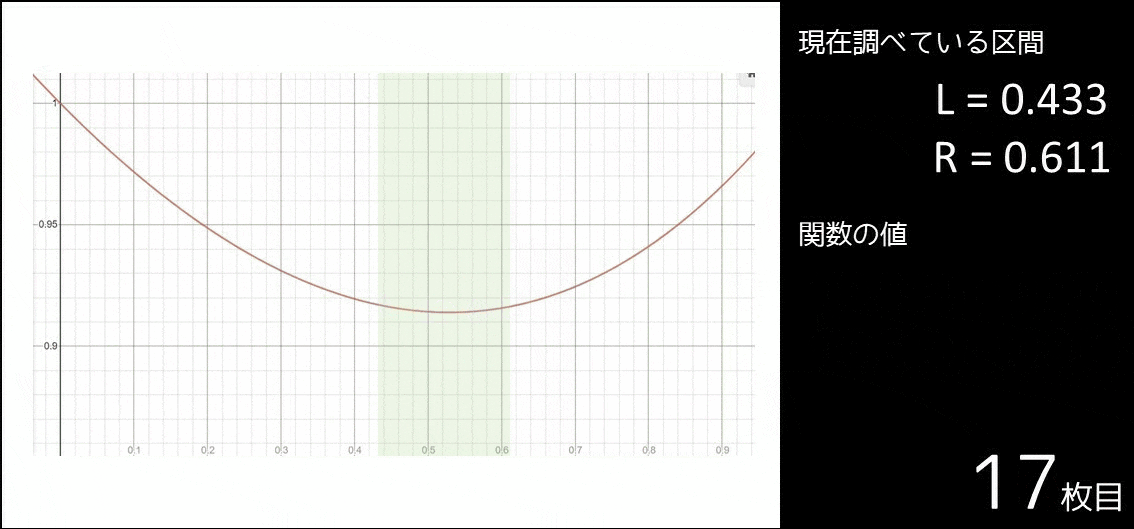
一般に、関数 $f(x)$ が以下のような条件を満たす場合、三分探索をすることが可能です。
- $f(x)$ が $x = x_{min}$ で最小値をとるとする。また、$l \leq x_{min} \leq r$ であることが最初から分かっているとする。そのとき、以下の条件を同時に満たせば良い。
- $l \leq a \leq x_{min}$ について、関数 $f(a)$ は単調減少(または単調増加)である。
- $x_{min} \leq a \leq r$ について、関数 $f(a)$ は単調増加(または単調減少)である。
もう少し詳しく三分探索について知りたい方は、以下の記事をお読みください。
4-4. 4 章のまとめ
4 章では、以下のアルゴリズムを扱ってきました。
| 章/節 | アルゴリズム | 計算量 |
|---|---|---|
| 4-1. | 二分探索 | $O(\log_2 N)$ |
| 4-2. | 二分法 | $O(\log_2 精度の逆数)$ |
| 4-3. | 三分探索 | $O(\log_{1.5} 精度の逆数)$ |
この章で扱ってきたアルゴリズムは、すべて区間を半分や 3 分の 2 ずつ縮めていくことで探索を効率化する手法でした。さて、5 章では 4 章で扱った二分探索のアイデアを用いて、$N$ 通りの全列挙を $\sqrt{N}$ に近い計算回数で求める「半分全列挙」というアルゴリズムを紹介していきます。
5. はやい探索法 ~半分全列挙~
2 章と 3 章では「全探索」を扱ってきました。全探索では全通り直接的に探索を行うので、$N$ 通りを調べるために $N$ 回以上の計算がかかってしまいます。しかし、4 章で扱った「二分探索」を上手く利用すれば、この計算を素早く行うことができる場合があるのです。
本章では、半分全列挙のアイデアにできるだけ近づいていけるように、「ルーレット問題」を紹介したうえで、最初の全探索アルゴリズムを段々と改善していく形式で解説します。アルゴリズムから知りたい方は、 5-3. 節から読んでも構いません。
5-1. 今回扱う問題
以下の問題を考えましょう。2 章の復習です。
あなたはルーレットを $4$ 回まわします。ルーレットの出目は $N$ 個あり、$A_1, A_2, ..., A_N$ が等確率で出ます。あなたの得点は、$4$ 回のルーレットで出た目の合計です。合計スコアが $K$ 点になる可能性がありますか。
制約:$1 \leq N \leq 100, 1 \leq A_i, K \leq 10^{12}$
この制約の場合は、全探索をすることで解けます。$4$ 回の出目の通り数は高々
$$100 \times 100 \times 100 \times 100 = 10^8$$
通りになるので、四重ループを用いて全探索を書いても $1$ 秒以内で実行できます。
5-2. アップグレードした問題
しかし、$N \leq 100$ だと簡単なので、更にアップグレードしたものを考えてみましょう。
あなたはルーレットを $4$ 回まわします。ルーレットの出目は $N$ 個あり、$A_1, A_2, ..., A_N$ が等確率で出ます。あなたの得点は、$4$ 回のルーレットで出た目の合計です。合計スコアが $K$ 点になる可能性がありますか。
制約:$1 \leq N \leq 300, 1 \leq A_i, K \leq 10^{12}$
制約が $N \leq 300$ になりました。この場合は、5-1. 節で紹介した全探索解法を用いる場合、
$$300 \times 300 \times 300 \times 300 \fallingdotseq 8.1 \times 10^{9}$$
通りを探索する必要があるため、数秒の実行では終わりません。(通り数を見積もることが重要です)そこで、4 章で扱った二分探索のアイデアを使います。
より簡単な問題
そこで、以下の問題を考えましょう。
$A_1, A_2, ..., A_N$ の中で、値が $X$ と同じものが存在するか。
この問題は 4-1. 節の復習です。最初に $A_1, A_2, ..., A_N$ をソートした後、二分探索を使うことによって、各質問に対し $O(\log_2 N)$ で答えることができます。(map などのデータ構造を用いても解けますが、本記事では探索を扱っているので二分探索を想定解法とします。)なお、ソートを知らない方は以下の記事をお読みください。
重要な考察
さて、最初の $3$ 回のルーレットの出目を全探索することを考えましょう。$3$ 回の出目をそれぞれ $A_i, A_j, A_k$ とします。そうすると、合計を $K$ 点にするためには、残りの $1$ 回の出目は必ず $K-(A_i+A_j+A_k)$ にならなければなりません。
残りの $1$ 回の出目を $K-(A_i+A_j+A_k)$ にすることができるかは、「より簡単な問題」の項で扱った、二分探索を用いた手法で $O(\log_2 N)$ で判定できます。したがって、計算回数は $O(N^3 \times \log_{2} N)$ となり、何とか間に合います。
実装例
# include <iostream>
# include <algorithm>
using namespace std;
long long N, K, A[309];
bool flag = false;
int main() {
cin >> N >> K;
for (int i = 1; i <= N; i++) cin >> A[i];
sort(A + 1, A + N + 1);
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
for (int k = 1; k <= N; k++) {
long long rem = K - (A[i] + A[j] + A[k]);
int pos1 = lower_bound(A + 1, A + N + 1, rem) - A;
if (A[pos1] == rem) flag = true;
}
}
}
if (flag == true) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}
5-3. さらにアップグレードした問題(半分全列挙の本質)
5-1. 節、5-2. 節で扱った問題を、さらにアップグレードしたものを考えてみましょう。
あなたはルーレットを $4$ 回まわします。ルーレットの出目は $N$ 個あり、$A_1, A_2, ..., A_N$ が等確率で出ます。あなたの得点は、$4$ 回のルーレットで出た目の合計です。合計スコアが $K$ 点になる可能性がありますか。
制約:$1 \leq N \leq 1200, 1 \leq A_i, K \leq 10^{12}$
$N \leq 300$ だった制約が $N \leq 1200$ になりました。5-2. 節で紹介した二分探索を用いた解法を使っても、3 個の出目を全探索する時点で、
$$1200 \times 1200 \times 1200 \fallingdotseq 1.7 \times 10^9$$
通りを探索することになり、すなわちこの回数だけ二分探索をしなければならないということになります。数秒ではまず実行できません。そこで、5-2. 節の方法を半分全列挙のアイデアを用いて改善します。
重要な考察
5-2. 節では、「3個」と「残りの1個」に分けましたが、「2個」と「残りの2個」に分けることを考えます。まず以下のように、長さ $N \times N$ の配列を定義することを考えます。
$$W = (A_1+A_1, A_1+A_2, A_1+A_3, ..., A_i+A_j, ..., A_N+A_N)$$
このように、$W$ には $2$ 回ルーレットを回したときのスコアとして考えられる値すべてが入っています。したがって、$4$ 回ルーレットを回したときのスコアとして考えられる値は、必ず整数 $i, j$ を用いて $W_i + W_j$ で表すことができます。
例えば、$A = (1, 3, 10)$ としましょう。そのとき、
$$W = (2, 4, 11, 4, 6, 13, 11, 13, 20)$$
となります。そこで、$4$ 回ルーレットを回したときのスコアが $24$ となるときを考えます。
$$W_3 + W_6 = (A_1 + A_3) + (A_2 + A_3) = 24$$
となり、スコアが $24$ になり得ることが分かります。一方、スコアが $34$ のときを考えると、$W_i + W_j = 34$ となるような組 $(i, j)$ は存在せず、かつスコア $34$ となるようなルーレットの出方は存在しないことが分かります。
最後に部分問題を解く
そこで、$W_i + W_j = K$ となるような $(i, j)$ が存在するかどうかを判定しなければなりません。数列 $W$ は $N^2$ 要素であり、最大で $1440000$ 要素となってしまうため、全探索では間に合いません。そこで使うのが二分探索です。
$W_i$ を決めると、$W_j = K - W_i$ となります。最初に $W$ をソートしておくと、あとは二分探索で $W_j = K - W_i$ となる $j$ が存在するかどうかが $O(\log_{2} N)$ で判定できるので、全体で $O(N^2 \times \log_{2} N)$ で判定することができます。したがって、$N \leq 1200$ の場合のルーレット問題を解くことができました。
実装例
# include <iostream>
# include <algorithm>
using namespace std;
long long N, K, A[1209];
long long Lens, W[1440009];
bool flag = false;
int main() {
cin >> N >> K;
for (int i = 1; i <= N; i++) cin >> A[i];
for (int i = 1; i <= N; i++) {
for (int j = 1; j <= N; j++) {
Lens += 1;
W[Lens] = A[i] + A[j];
}
}
sort(W + 1, W + Lens + 1);
for (int i = 1; i <= Lens; i++) {
long long rem = K - W[i];
int pos1 = lower_bound(W + 1, W + Lens + 1, rem) - W;
if (W[pos1] == rem) flag = true;
}
if (flag == true) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}
5-4. 別の視点からの半分全列挙
半分全列挙が対応できるのは for 文全探索で解ける「ルーレット問題」などの高速化だけではありません。実は bit 全探索にも対応することができるのです。例えば以下の問題を考えましょう。(3-1. 節で扱った問題をアップグレードしたものです)
$N$ 個の硬貨があります。番号 $i$ の硬貨は $A_i$ 円です。硬貨の選び方は $2^N$ 通りありますが、その中で合計価格が丁度 $X$ 円となる選び方は存在するでしょうか。
制約:$1 \leq N \leq 40, 1 \leq X, A_i \leq 10^8$
制約が $N \leq 20$ であれば bit 全探索で解けるのですが、$N \leq 40$ だと $2^{40} \fallingdotseq 1.1 \times 10^{12}$ 通りを調べる必要があるため、数秒で実行することができません。そこで半分全列挙を使います。
重要な考察
$40$ 個まとめて全探索するのではなく、$20$ 個と $20$ 個に分けて全探索することを考えましょう。長さ $2^{20}$ の数列 $W_1, W_2$ を定義して、
- $W_1$ には前半 $20$ 個の硬貨の選び方 $2^{20}$ 通りそれぞれの合計価格
- $W_2$ には後半 $20$ 個の硬貨の選び方 $2^{20}$ 通りそれぞれの合計価格
を記録します。そこで、$W_{1, i} + W_{2, j} = X$ となるような $(i, j)$ の組が存在すれば、合計価格が丁度 $X$ 円となる硬貨の選び方が存在することがわかります。
さて、どうすれば $W_{1, i} + W_{2, j} = X$ となるような $(i, j)$ の組が存在するかどうか判定できるのでしょうか。最初に $W_1, W_2$ を昇順にソートしておいて、$i$ を全探索したうえで $W_{2, j} = K - W_{1, i}$ となるような $j$ が存在するかどうかを二分探索によって求めると、$O(|W_1| \times \log |W_2|)$ で解くことができます。
$N = 40$ のとき、$|W_1| = 2^{20}$、$|W_2| = 2^{20}$ となり、$1$ 秒以内で実行できます。
実装例
# include <iostream>
# include <algorithm>
using namespace std;
long long N, X, A[40];
long long W1[1 << 20], W2[1 << 20];
bool flag = false;
int main() {
cin >> N >> X;
for (int i = 0; i < N; i++) cin >> A[i];
// 前半 N/2 個を bit 全探索で全列挙する
for (int i = 0; i < (1 << (N / 2)); i++) {
long long sum = 0;
for (int j = 0; j < (N / 2); j++) {
if ((i / (1 << j)) % 2 == 0) sum += A[j];
}
W1[i] = sum;
}
// 後半 N - N/2 個を bit 全探索で全列挙する
for (int i = 0; i < (1 << (N - (N / 2))); i++) {
long long sum = 0;
for (int j = 0; j < N - (N / 2); j++) {
if ((i / (1 << j)) % 2 == 0) sum += A[j + (N / 2)];
}
W2[i] = sum;
}
// ソートしたうえで半分全列挙をする
sort(W1, W1 + (1 << (N / 2)));
sort(W2, W2 + (1 << (N - (N / 2))));
for (int i = 0; i < (1 << (N / 2)); i++) {
long long rem = X - W1[i];
int pos1 = lower_bound(W2, W2 + (1 << (N - (N / 2))), rem) - W2;
if (W2[pos1] == rem) flag = true;
}
if (flag == true) cout << "Yes" << endl;
else cout << "No" << endl;
return 0;
}
5-5. <発展>さらにさらにアップグレードした問題
これは上級者用ですので、読み飛ばしても構いませんが、解きたい人は是非挑戦してみてください。読者への課題とします。5-1. 節、5-2. 節、5-3. 節で扱った問題をさらにアップグレードしたものです。
あなたはルーレットを $4$ 回まわします。ルーレットの出目は $N$ 個あり、$A_1, A_2, ..., A_N$ が等確率で出ます。あなたの得点は、$4$ 回のルーレットで出た目の合計です。合計スコアが $K$ 点になる可能性がありますか。
制約:$1 \leq N \leq 9000, 1 \leq A_i, K \leq 10^{12}$
この問題は非常に難しく、5-3. 節 で扱った半分全列挙を用いた $O(N^2 \log N)$ のアルゴリズムも通用しません。したがって、$O(N^2)$ で解かなければ数秒で実行できません。1
5-6. 5 章のまとめ~半分全列挙とは一体何だったのか~
半分全列挙とは、いくつかのパーツを半分ずつのグループに分け、全探索(全列挙)を高速化するテクニックのことを指します。$N$ 通りの全探索を半分全列挙を用いて高速化する場合、$O(\sqrt{N} \times \log \sqrt{N})$ といった計算量になります。
しかし、すべての問題に半分全列挙が使えるわけではありません。本章では
- for 文ループの半分全列挙による改善
- bit 全探索の半分全列挙による改善
を扱いましたが、例えば
- 順列全探索(3-2. 節で扱った、$N!$ 通りを全探索するテクニック)
は半分全列挙による高速化が通用しません。その点について、注意が必要です。
6. 意外と強い、枝刈り全探索
前編の最後に、全探索の工夫に関して扱います。
「枝刈り全探索」という手法を用いると、普通に全探索をすると数秒で実行が終わらないような問題でも、高速に計算できる場合があるのです。
6-1. 枝刈り全探索とは
例として「最適解を、再帰関数を用いた全探索で求める問題」を考えましょう。そのとき、状態遷移は例えば下図のようになります。
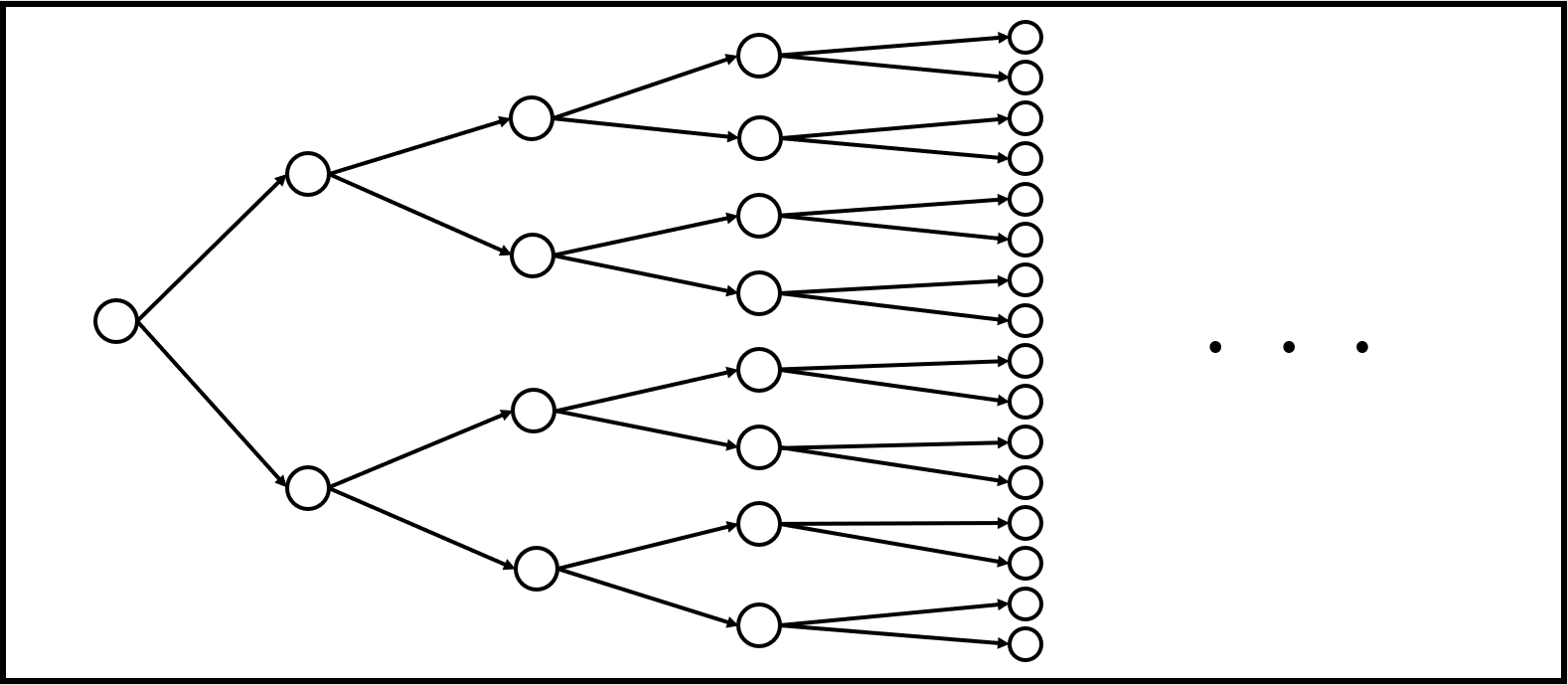
これを、途中で「絶対最適ではない」と明らかに判断できる状態になる場合に遷移を中断させ、遷移数を減らすことを枝刈り全探索といいます。その場合、状態遷移は下図のようになります。

6-2. 枝刈り全探索が通用する例
以下の問題を考えましょう。3-1. 節で扱った問題です。
$N$ 個の硬貨があります。番号 $i$ の硬貨は $A_i$ 円です。硬貨の選び方は $2^N$ 通りありますが、その中で合計価格が丁度 $X$ 円となる選び方は存在するでしょうか。
制約:$1 \leq N \leq 20, 1 \leq X, A_i \leq 10^8$
この問題は bit 全探索でも解くことができますが、ここでは 3-3. 節で紹介した「再帰関数を用いた全探索」を利用して解くことを考えます。たとえば以下のように実装できます。
bool dfs(int pos, int sum) {
if (pos == N) {
if (sum == X) return true;
else return false;
}
// 遷移
bool I1 = dfs(pos + 1, sum);
bool I2 = dfs(pos + 1, sum + A[pos + 1]);
if (I1 == true || I2 == true) return true;
return false;
}
このプログラムで dfs(0, 0) が true だった場合、合計価格が $X$ 円となるよう硬貨の選び方が存在することになります。しかし、dfs(pos, sum)という状態からは、$sum$ 円未満の最終金額、$sum + (A_{pos+1} + ... + A_N)$ 円を超える最終金額は実現することができません。そこで、
$$sum \leq X \leq sum + (A_{pos + 1} + A_{pos + 2} + ... + A_N)$$
が満たされない限り、遷移を中断する(return する)ことを考えると、以下のような実装になります。ただし、以下のプログラム内の $B_i$ は、$B_i = A_i + A_{i+1} + ... + A_N$ を満たすものとします。
bool dfs(int pos, int sum) {
if (pos == N) {
if (sum == X) return true;
else return false;
}
// 枝刈り
if (X < sum || sum + B[pos + 1] < X) return false;
// 遷移
bool I1 = dfs(pos + 1, sum);
bool I2 = dfs(pos + 1, sum + A[pos + 1]);
if (I1 == true || I2 == true) return true;
return false;
}
そこで、2 つのコードを見比べてみましょう。例えば、
N = 20, X = 869
A = {31, 41, 59, 26, 53, 58, 97, 93, 23, 84, 62, 64, 33, 83, 27, 95, 2, 88, 41, 97}
というテストケースの場合、計算回数は以下のようになりました。
実際に、枝刈りをした方が 8倍以上高速であることがわかります。
| 方法 | 再帰の呼び出し回数 | 計算時間 |
|---|---|---|
| 普通の全探索 | 2097151 回 | 3.942 ミリ秒 |
| 枝刈り全探索 | 116613 回 | 0.449 ミリ秒 |
6-3. 枝刈り全探索のアルゴリズム~IDA* と A*~
今回紹介した硬貨の問題とは少し方向が異なりますが、最適解(パズルの最短手数など)を求めるにあたって、名前が付いている枝刈り全探索アルゴリズムがあります。2 これについて、6 章の最後に紹介したいと思います。
前提知識:反復深化
例えば、パズルの最短手数を求める問題を考えましょう。状態数は多い一方で、短い手数で解けそうなパズルがあった時に、最初から深さ優先探索(再帰関数を用いた全探索)をせず、以下のように考えます。
- 1 手だとできるのか?
- 2 手だとできるのか?
- 3 手だとできるのか?
- 4 手だとできるのか?(以下省略)
そうすると、最短手数が短いときに早く解を出すことができます。そのようなアルゴリズムを反復深化といいます。図でイメージすると、以下のような感じになります。
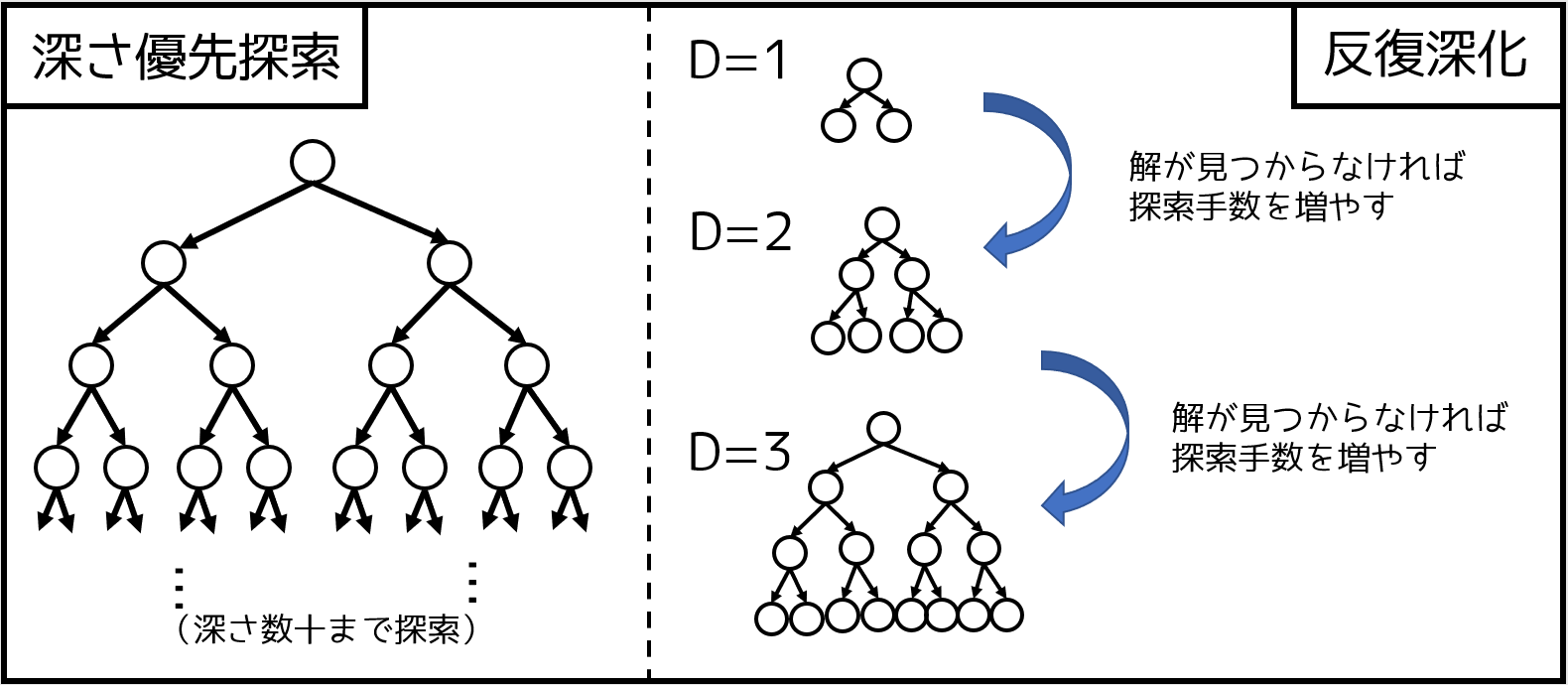
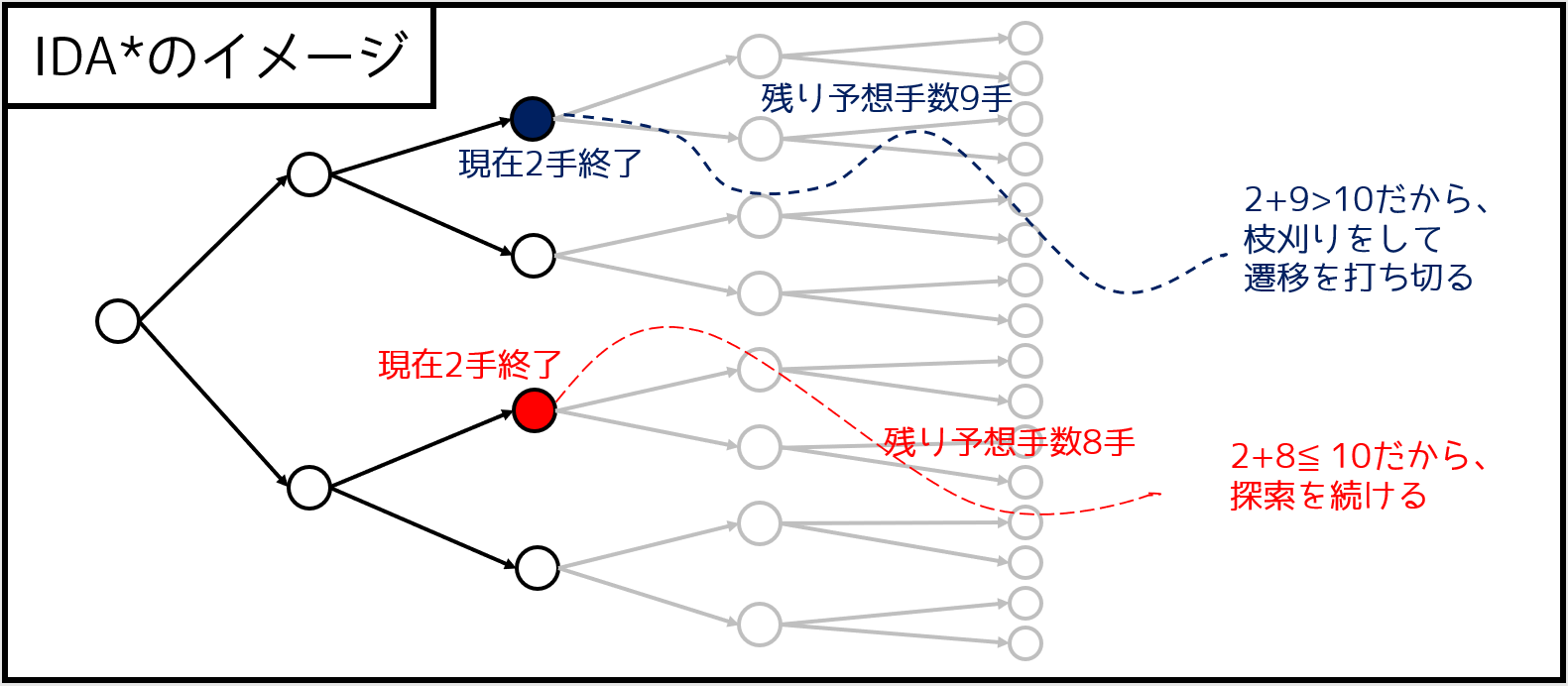
IDA* アルゴリズム
IDA* というアルゴリズムは、反復深化に枝刈りを加えたものです。例えば「$10$ 手以内に解けるか」という、反復深化アルゴリズムの途中で出てくる問題を考えるとします。
既に $g$ 手だけ操作しているという状態があって、「ここからあと何手は必要だろう」という目標状態までの最短手数の推定値を $h$ とするとき、$g + h > 10$ であれば遷移をやめて枝刈りする、といった手法を IDA* といいます。なお、推定値を求めるにあたっては、$h$ が大きいと高速に動きますが、大きすぎると正しい解を見逃してしまう可能性があるので注意が必要です。($h$ は見積もり値であり、正確な値でなくても構いません)
<発展>A* アルゴリズム
A* アルゴリズムは、IDA* で扱った「反復深化」(深さ優先探索をベースにしたアルゴリズム)とは違い、最短経路問題を解くようにして効率よく最適解を求めるアルゴリズムです。
最短経路問題を解くにあたっての一つの手法として「ダイクストラ法」というアルゴリズムがありますが、A* アルゴリズムはこれに似ています。普通のダイクストラ法では、優先度付きキューに「現時点での距離(手数)」を入れるのに対し、A* アルゴリズムでは優先度付きキューに「現時点での手数 $g$ + 残り手数の推定値 $h$」を入れます。
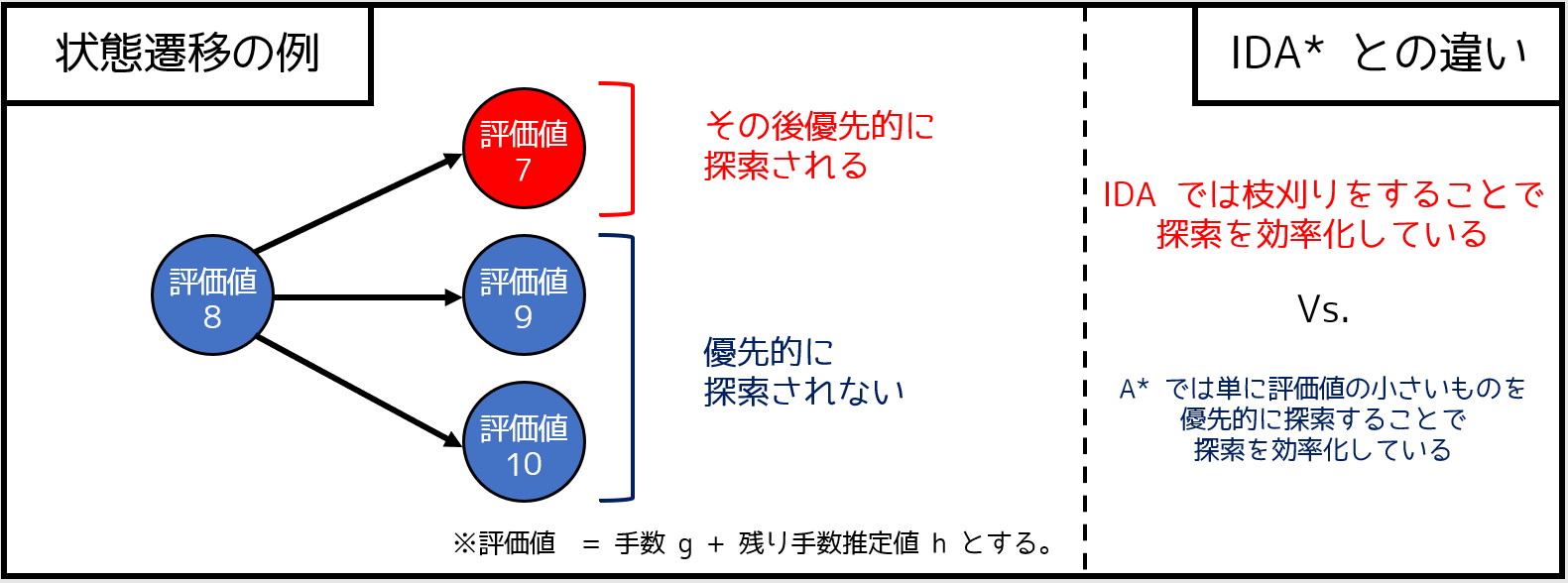
具体的には以下のようなアルゴリズムです。
ただし、ある状態 $S$ における「残り手数推定値」を $h(S)$ とし、最初の状態を $S_{init}$ とします。
-
優先度付きキュー $Q$ を用意する。ただし、$Q$ には tuple 型の要素を入れるとする。
- 第一引数には、評価値が入る。小さい方が良い。
- 第二引数には、状態が入る。
- 第三引数には、既に操作した手数が入る。
- $Q$ に $(h(S_{init}), S, 0)$ を push する。
- $Q$ が空になるまで、以下の操作を繰り返す。
- $Q$ の先頭(最も評価値が小さいもの)の状態を $T$ とする。
- また、状態 $T$ にたどり着くまでに、既に $g$ 手操作されているものととする。
- まず、$Q$ から先頭要素である $T$ を pop する。
- 次に、$T$ から次の一手で動かせかつ未探索である状態を $T_1, ..., T_P$ とする。そのとき、
- $Q$ に $((g + 1) + h_{T_1}, T_1, g+1)$ を push する。
- $Q$ に $((g + 1) + h_{T_2}, T_2, g+1)$ を push する。
- :
- $Q$ に $((g + 1) + h_{T_P}, T_P, g+1)$ を push する。
そうすると、「現在手数 + 残り手数推定値」が小さいもの、つまり答えに近そうなものを優先的に探索、そして優先的に状態遷移することができるので、より速く解を見つけることができます。
前編のまとめ
前編では、以下のアルゴリズムを扱いました。
| 章/節 | アルゴリズム | 計算量 |
|---|---|---|
| 2. | for 文で書ける全探索 | いろいろ |
| 3-1. | bit 全探索 | $O(2^N \times N)$ |
| 3-2. | 順列全探索 | $O(N! \times N)$ |
| 3-3. | 再帰関数を用いた全探索 | いろいろ |
| 3-4. | 幅優先探索 | O($グラフの辺の数$) |
| 4-1. | 二分探索 | $O(\log N)$ |
| 4-2. | 二分法 | $O(\log N)$ |
| 4-3. | 二分法 | $O(\log N)$ |
| 5. | 半分全列挙 | 通り数の $0.5$ 乗くらい |
| 6. | 枝刈り全探索(IDA*, A* など) | いろいろ |
後編では、今回紹介した「探索アルゴリズム」たちがどのような場面で使えるのか、そしてどのような場面で役に立つのかについて紹介していきたいと思います。例えば、
- 1 章で紹介した、「おねえさん問題」の実装
- $100$ 次方程式の解を求める
- オセロの "強い" AI の実装
などの問題は、探索アルゴリズムが全面的に役に立ちます。
とても楽しい内容となっているので、前編の内容を完璧に理解していなくても面白いと思います。是非後編にも目を通していただけると嬉しいです。
つづく
に続きます。是非お読みください!