【図解】二分探索はもう間違えない！スリーステップ実装法＆記憶に残るアニメーション

この記事では**「二分探索 (にぶんたんさく，binary search)」**について紹介します．とても有名なアルゴリズムなので多くの人が知っていると思いますが，基礎から丁寧に説明します．また，考察のポイントから，絶対に間違えない実装の考え方まで，アニメーションを用いて説明します．

1. 二分探索でできること

二分探索で解くことができる問題を 2 つ紹介します．いずれもオリジナルなので，ネタバレ要素はありません．

誕生日当てクイズ

出典：幼少期の思い出

• きたむーはお友達の誕生日を当てたい．
• お友達に「あなたの誕生日は〇月△日よりも後ですか？」という質問を $9$ 回までできる．
• 誕生日を特定しよう．

細胞分裂

出典：勝手に JOI 春プラクティス (ジャッジは存在しません)
考えやすいように少し改変してあります．

• 細胞分裂の実験を $1,000,000$ 秒間行った．細胞の数が実験中に減ることは無かった．
• 教授は各時刻の細胞の数のデータを持っているが，教えてくれない．
• 代わりに，「実験開始から〇秒後の細胞の数は何個でしたか？」という質問を $20$ 回までできる．
• 細胞の数が初めて $1,000$ 個以上になった時刻を求めたい．

この博士可愛くないですか？

2. 二分探索の発想

二分探索はその名の通り，「二分する」，つまり候補を半分にしながら探索していくアルゴリズムです．上の例題で考えてみましょう．

誕生日当てクイズ

今，お友達の誕生日の候補は 1 月 1 日 ～ 12 月 31 日です．
まずは，だいたい真ん中の 6 月 30 日を質問してみましょう．

きたむー「あなたの誕生日は 6 月 30 日よりも後ですか？」
お友達　「はい」

これで，お友達の誕生日は 7 月 1 日 ～ 12 月 31 日に絞られました．
次は，この更に真ん中ぐらいの，9 月 30 日で質問してみます．

きたむー「あなたの誕生日は 9 月 30 日よりも後ですか？」
お友達　「はい」

今度は誕生日の候補が 10 月 1 日 ～ 12 月 31 日に絞られました．
次は，11 月 15 日を質問してみます．

きたむー「あなたの誕生日は 11 月 15 日よりも後ですか？」
お友達　「いいえ」

これで誕生日は 10 月 1 日 ～ 11 月 15 日に絞られました．

続く・・・

誕生日当てクイズの考察

「誕生日は 1 月 1 日ですか？」
「誕生日は 1 月 2 日ですか？」
「誕生日は 1 月 3 日ですか？」
「誕生日は 1 月 4 日ですか？」

と聞いていくと，最大で 366 回も質問しなければなりません．でも，二分探索を用いれば，なんとなく高速に誕生日がわかりそうな気がしてきます．実際には何回で特定できるのか，きちんと計算してみましょう．

1. 最初，候補は 366 日あります．質問することで，候補を 183 日に絞れます．
2. 今，候補は 183 日あります．質問することで，候補を 92 日に絞れます．(183÷2 は 91.5 なので，範囲を 92 と 91 に分けることになりますが，ここでは運悪く誕生日が 92 日の方にあったと考えます．)
3. 今，候補は 92 日あります．質問することで，候補を 46 日に絞れます．
4. 今，候補は 46 日あります．質問することで，候補を 23 日に絞れます．
5. 今，候補は 23 日あります．質問することで，候補を 12 日に絞れます．
6. 今，候補は 12 日あります．質問することで，候補を 6 日に絞れます．
7. 今，候補は 6 日あります．質問することで，候補を 3 日に絞れます．
8. 今，候補は 3 日あります．質問することで，候補を 2 日に絞れます．
9. 今，候補は 2 日あります．質問することで，候補を 1 日に絞れます．
10. 候補は 1 日に絞られました．つまり，誕生日を特定できました．

というわけで，9 回の質問で誕生日を特定できることがわかりました．366 回も質問するのは大違いですね．

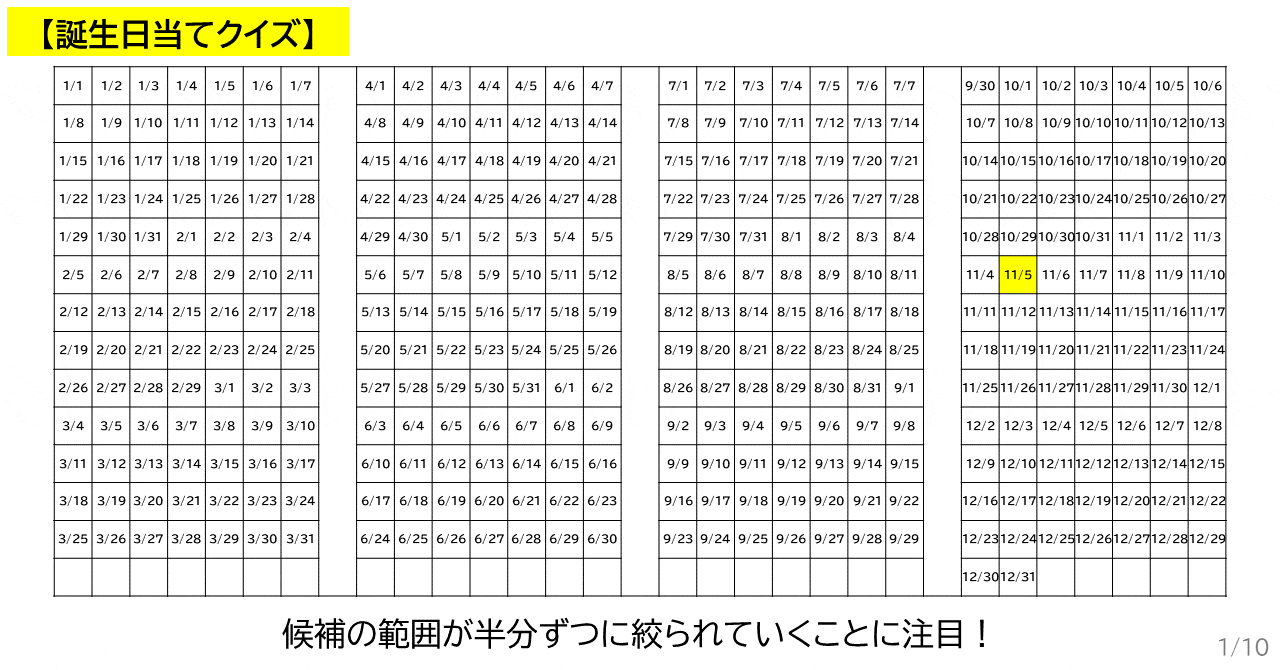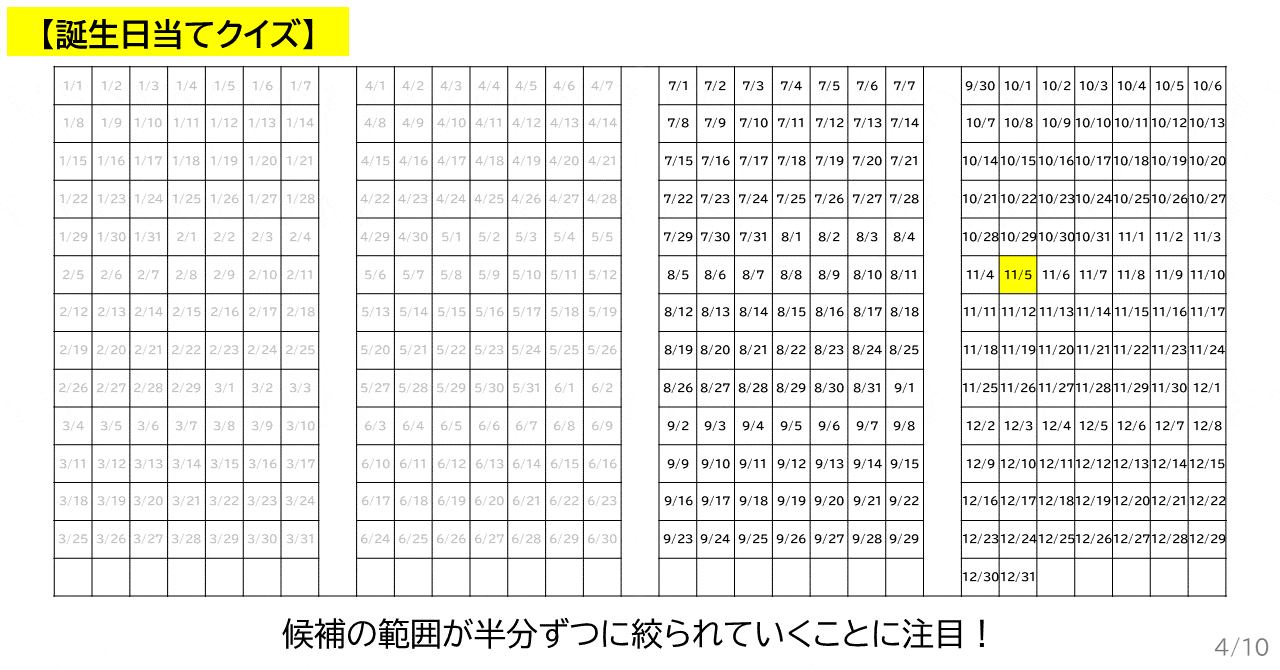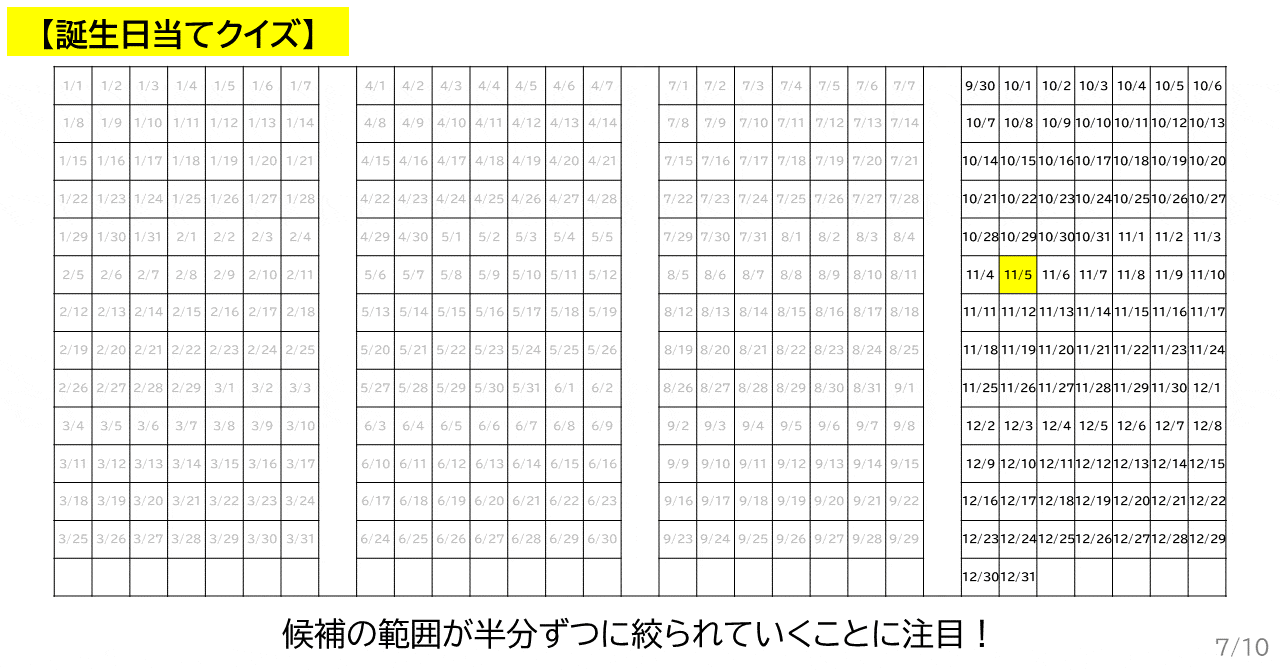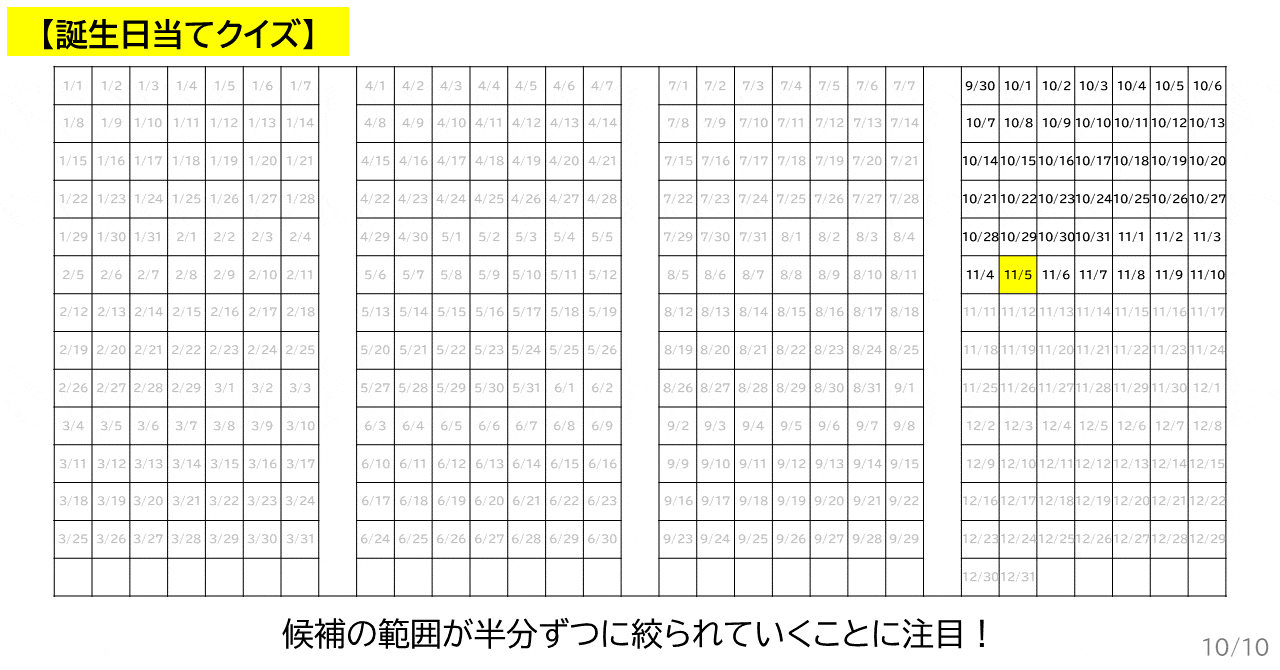
▲ 3 回目まで質問しているところのアニメーション．ただし，ざっくり二分しています．

ところで，この 9 回という数字はどこから出てきたのでしょうか．

対数

ここでは高校で履修する「数学Ⅱ」で学習する内容が出てきます．難しければ無理に読む必要はありません．

値 $x$ を半分にする操作を繰り返したとき，値が $1$ になるまでにかかる操作の回数を $\log_2 x$ と表現します．これは「ログ $2$ の $x$」などと読みます．

ただし，例えば $\log_2 366 = 8.51...$ と，$\log$ の値は小数になることもあり，$8.5$ 回質問することはできないので，誕生日当てクイズの場合は切り上げた $9$ 回の質問が必要です．

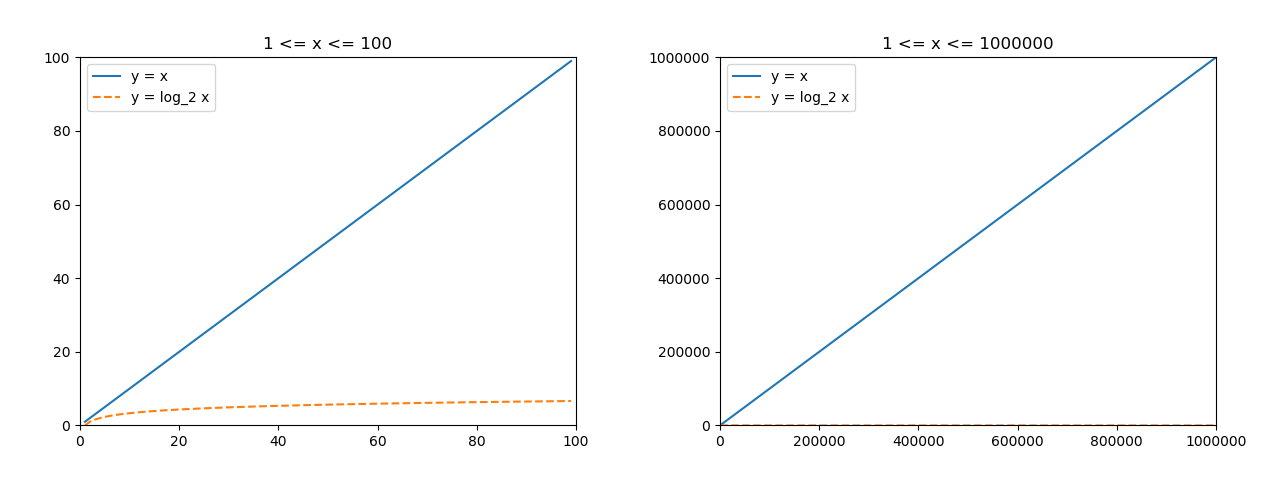
$y=x$ のグラフと $y=\log_2 x$ のグラフを比較すると一目瞭然，$\log_2 x$ はかなり小さい値を取ることがわかります．$x$ が $100$ 万までの右のグラフを見ると，もはや $y=\log_2 x$ はずっと $0$ なのか？という錯覚さえしてきます．(実際には $20$ ぐらいです．)

ここでは，「$\log$ っていうのが出てくると，速くていいんだなあ」ぐらいの理解でも大丈夫です．

3. 考察のポイント「この問題は二分探索で解けるの？」

二分探索を使いたいときに重要なのは**「質問」**です．次のような質問を見つけることが出来たら，二分探索が使えます．

• Yes / No で答えられる質問である．
• あるところを境界として，そこより小さいところではずっと Yes だし，そこより大きいところではずっと No である．
• または，あるところを境界として，そこより小さいところではずっと No だし，そこより大きいところではずっと Yes である．

誕生日当てクイズの考察

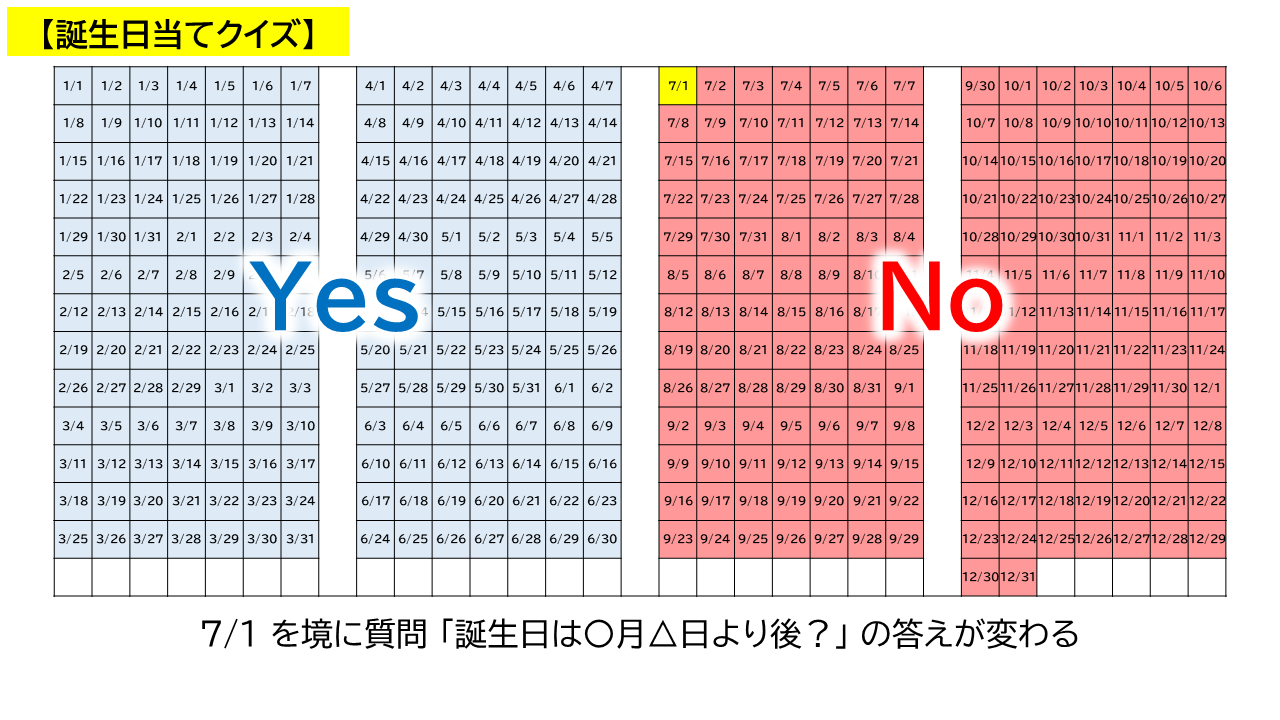
誕生日当てクイズでは二分探索が使えたので，何かしらの**「質問」があるはずです．それはもちろん，「誕生日は〇月△日よりも後か」**です．

誕生日が 7 月 1 日だとしたら，1 月 1 日 ～ 6 月 30 日の質問の答えはすべて Yes になるし，7 月 1 日 ～ 12 月 31 日では質問の答えはすべて No になります．7 月 1 日を境界として，Yes / No が変化しているのです．

細胞分裂の考察

細胞分裂の場合の**「質問」**は練習として自分で考えてみて下さい．Yes / No で答えられる質問でないとだめですよ．

答え

質問は**「実験開始から〇秒後の細胞の数は $1,000$ 個以上か」**です．問題では細胞の数を質問できますが，あれは必要以上の情報が手に入るだけで，実際にはこのような質問が本質になります．

この質問の場合，細胞が $1,000$ 個になるまでの時間はずっと No だし，細胞が $N$ 個になればずっと Yes です．$N$ 個になる瞬間を境に，Yes / No が変化しています．

このような，Yes / No がどこかを境に切り替わる質問であれば二分探索が使用できるし，逆にそのような質問を見つけられなければ，二分探索は使えません．

4. 二分探索の実装

ここまで説明してきた二分探索を実際に実装してみましょう．

例題

以下では，少し一般化した次の例題を考えます．

• 要素数 $N$ の広義単調増加な数列 $A = \{A_0, A_1, \cdots, A_{N-1}\}$ がある．
• $K \leqq A_i$ を満たす要素のうち，最小のものの $i$ をだいたい $\log_2 N$ 回の質問で求める．

広義単調増加な数列というのは，数が小さくなることがない数列のことです．

例えば，$A = \{1, 3, 5, 7, 9\}$，$K = 7$ の場合，$A_4 = 7$，つまり $i = 4$ が答えになります．

めぐる式二分探索・スリーステップ実装法

二分探索のわかりやすい実装方法として**「めぐる式二分探索」**というものがあります．めぐる式二分探索では慣習的に Yes を OK， No を NG と表記することが多いので，ここから先はそれに従います．

では，めぐる式二分探索をスリーステップで解説します．

1. 質問を考えて関数を作る．
2. 質問の答えが絶対に OK になる値と，質問の答えが絶対に NG になる値を考えて，変数 $ok$ と $ng$ に代入する．
3. $ok$ と $ng$ の中央値 $m$ の質問に対する答えを調べて，範囲を広げる．

二分探索は，たったこれだけのステップに従うだけで，実装ができます．でも，3 の「範囲を広げる」とか，どういうことなのでしょう．次のアニメーションを見てください．

▲ めぐる式二分探索のイメージ

上のアニメーション同様，$A = \{4, 6, 9, 9, 12, 15, 16, 17, 19, 19\}$，$K = 15$ の場合を考えます．

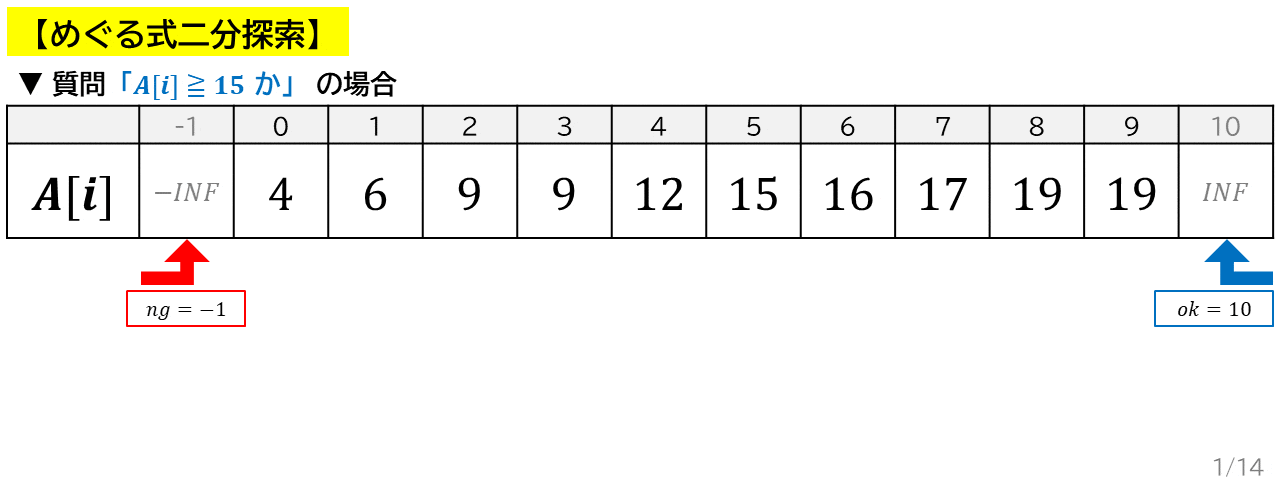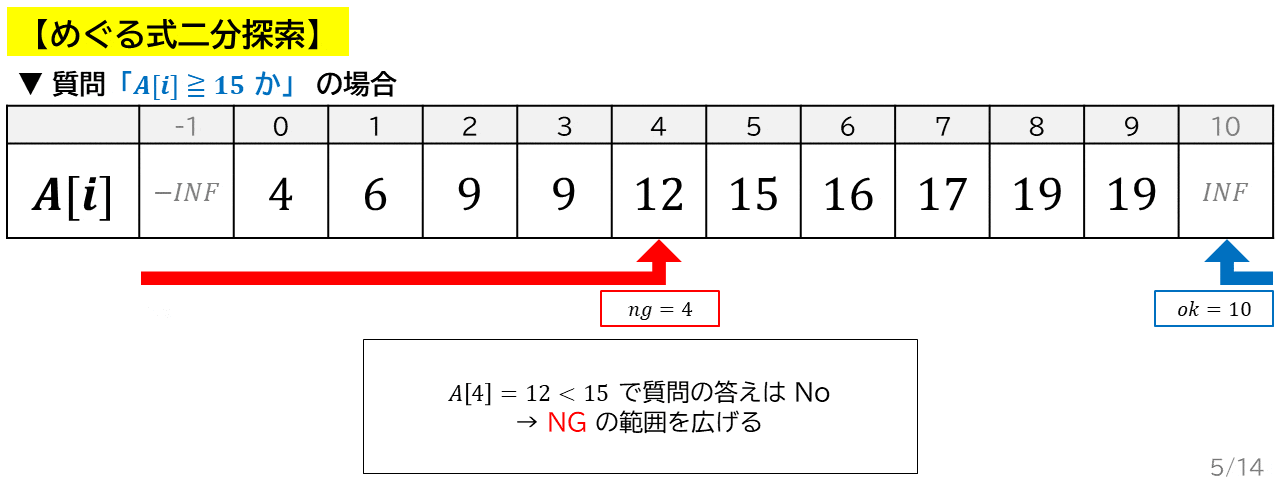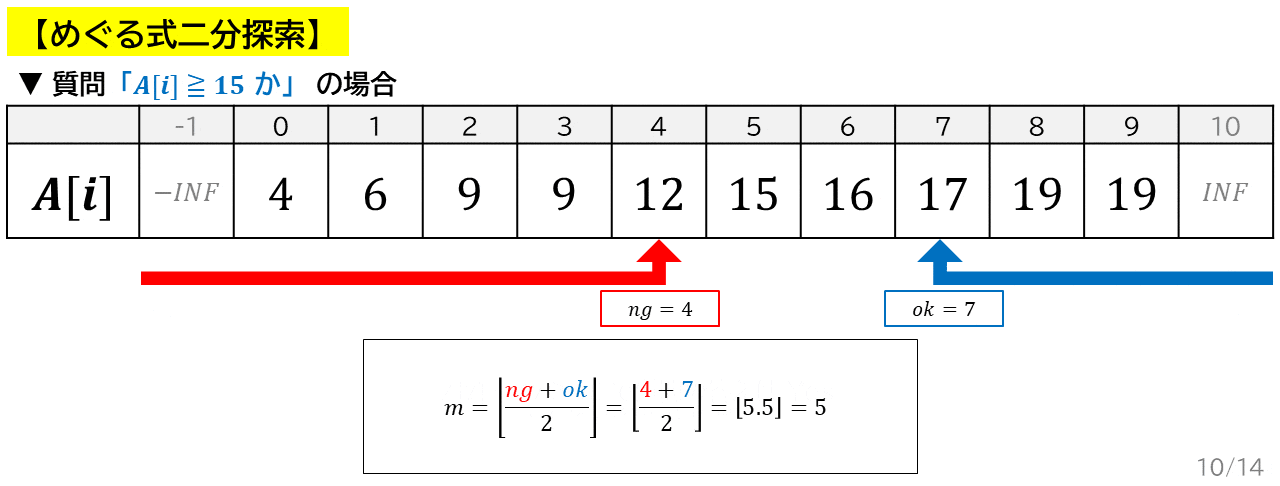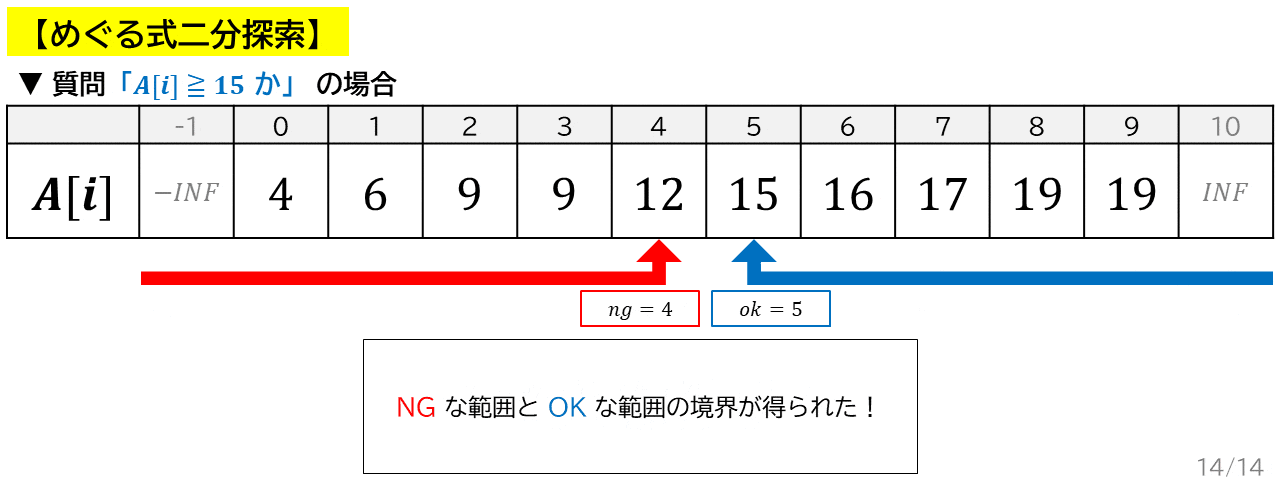
1. まず，質問を考えます．$K$ 以上の数のうち，最小のものを求めたいので，質問は「$A_i \geqq K$ か」にしました．この質問は Yes / No がぱたんと切り替わるので，質問の条件を満たしています．
2. 質問の答えが絶対に OK になる，つまり確実に $K$ 以上の値を考えます．しかし，残念ながらそんな値は存在しません．そこで，数列を左右に $1$ ずつ伸ばして，左端 $A_{-1}$ を $-\infty$，右端 $A_N$ を $\infty$ にしてしまいます．これで，$A_N$ は絶対に $K$ 以上なので，$ok = N = 10$ とすればよいです．同様に，$ng = -1$ とできます．
3. あとは OK 軍と NG 軍の陣取り合戦です．互いの前線の丁度真ん中を見て，そこが OK なら OK 軍が前進，NG なら NG 軍が前進します．変数 $ok$，$ng$ は各軍の前線の位置と言えます．(アニメーションを参照)

実装例 (C++)

この発想を実装すると，次のようになります．

Source.cpp

#include<bits/stdc++.h>
using namespace std;

int N, A[1000000];

bool question(int m, int K){
    return A[m] >= K;
}

int binarySearch(int K){
    int ng = -1;
    int ok = N;
    while(ok - ng > 1){
        int m = (ng + ok) / 2;
        if(question(m, K)) ok = m;
        else ng = m;
    }
    return ok;
}

int main(){
    cin >> N;
    for(int i=0; i<N; i++) cin >> A[i];

    int K;
    cin >> K;
    cout << binarySearch(K) << endl;
}

このソースコードに，次のような入力を与えると，確かに $5$ が出力されます．

input.txt

10
4 6 9 9 12 15 16 17 19 19
15

二分探索のポイントは**「質問」**です．これを強調するために，上のソースコードでは question() 関数を作りましたが，慣れてくれば次のように書いてももちろん構いません．

Source.cpp

#include<bits/stdc++.h>
using namespace std;

int N, A[1000000];

int binarySearch(int K){
    int ng = -1;
    int ok = N;
    while(ok - ng > 1){
        int m = (ng + ok) / 2;
        if(A[m] >= K) ok = m; // question() 関数を埋め込んだ
        else ng = m;
    }
    return ok;
}

int main(){
    cin >> N;
    for(int i=0; i<N; i++) cin >> A[i];

    int K;
    cin >> K;
    cout << binarySearch(K) << endl;
}

5. 二分探索のまとめ

1. どこかで Yes / No が切り替わる質問を考える．
2. 両端を決めて，$ok$ と $ng$ に代入する．
3. $ok$ と $ng$ の中央値 $m$ を見て，OK な範囲，NG な範囲を広げていく．

以上が二分探索の考え方・実装方法です．

6.【発展】二分探索からの判定問題

二分探索の最も重要な要素は**「質問」**を考えることです．しかし，質問を考えるのは難しいこともあります．そこで，少し難しい質問のパターンを見ていきます．

密度最大化

出典：なし (オリジナル)

• $N$ 個の粘土を持っている．それぞれ $1$ から $N$ の番号が振られている．
• 粘土 $i$ は質量 $M_i$ $\mathrm{[g]}$，体積 $V_i$ $\mathrm{[{cm}^3]}$ である．
• このうち $K$ 個の粘土を選んで練り合わせ，物体 X を作る．(粘土はちぎってはいけない．)
• 物体 X の密度 $\mathrm{[g/{cm}^3]}$ の最大値を $O(N \log N)$ で求めたい．

ヒント「質問は何？」

質問は「密度 $x$ 以上の物体を作れる？」です．

解法

質問は「密度 $x$ 以上の物体を作れる？」です．では，これはどのように判定すればいいのでしょうか．数学的に丁寧に考察してみましょう．

密度の定義は，$\frac{\sum M_i}{\sum V_i}$ です．これが $x$ 以上であればいいので，この質問の答えは次の式と同値です．

$\frac{\sum M_i}{\sum V_i} \geqq x$

これを更に変形すると，次のようになります．

$\sum M_i \geqq x \sum V_i$

$\sum(M_i - x V_i) \geqq 0$

よって，各 $i$ について $M_i - x V_i$ を求めて，ソートして，大きい方から $K$ 個選べばよいです．その和が $0$ 以上なら質問の答えは OK になるし，$0$ 未満なら NG になります．

これで質問の答えの求め方がわかったので，二分探索ができ，$ok$ が答えになります．

考察

二分探索を用いると，「ある条件を満たす数の最大値 (最小値) を求めよ」という問題を「ある条件を満たすか判定せよ」という問題に変形できることが多いです．

ただ，その変形したいわゆる**「判定問題」**が難しいことも多々あります・・・．

競技プログラミングにおいては，二分探索は他のアルゴリズムや発想とくっつけて，補助的に用いられることが多いように思います．いろいろなところでベースになる大切なアルゴリズムです．是非マスターしてください．

参考になったと思ったら，是非 いいね👍 を押してください．励みになります．ここまでお読みいただきありがとうございました．

7. 二分探索を使う問題たち

ネタバレ防止のため，畳んでいます．

• AtCoder Beginner Contest 077 C - Snuke Festival
• AtCoder Beginner Contest 013 C - 節制
• AtCoder Beginner Contest 034 D - 食塩水
• AtCoder Beginner Contest 023 D - 射撃王
• JOI2007/2008 春合宿 Day2-2 カンニング対策

AtCoder 上で他の簡単な問題を見かけたら適宜追加します．

難しい問題も解いてみたい場合は hamayanhamayan さんのページ を参照してください．

8. 参考文献など

• めぐるのアルゴリズム講座 (因幡めぐる@競技プログラミング さんのツイート)
• プログラミングコンテストチャレンジブック [第 2 版]
• 二分探索アルゴリズムを一般化 〜 めぐる式二分探索法のススメ 〜 (けんちょんさん)

この記事で使用している挿絵は いらすとや よりお借りしました．
アルゴリズムの説明で用いている図とアニメーションは自作です．無断転載は許可していません．