BFS (幅優先探索) 超入門！ 〜 キューを鮮やかに使いこなす 〜

0. はじめに

メジャーなグラフ探索手法には深さ優先探索 (depth-first search, DFS) と幅優先探索 (breadth-first search, BFS) とがあります¹。このうち DFS については

• DFS (深さ優先探索) 超入門！ 〜 グラフ理論の世界へ 〜 【前編】
• DFS (深さ優先探索) 超入門！ 〜 グラフ理論の世界へ 〜 【後編】

にて詳しく特集しました。これらの記事中で幅優先探索 (BFS) についても簡単に触れているのですが、今回改めて特集します。特に、後編で紹介した

• グラフの二点間の到達可能性
• グラフの連結成分の個数
• 二部グラフ判定
• トポロジカルソート
• サイクル検出

といった問題たちが BFS によっても解くことができることを示します。一つの問題を DFS・BFS と様々な探索手法で解くことで、グラフの様々な性質をより深く親しむことを狙います。なお本記事は、グラフについて知っていれば DFS 記事とは独立に読むことができるようにしました。

1. 幅優先探索 (BFS)

まずは BFS について整理します。

1-1. BFS の動作

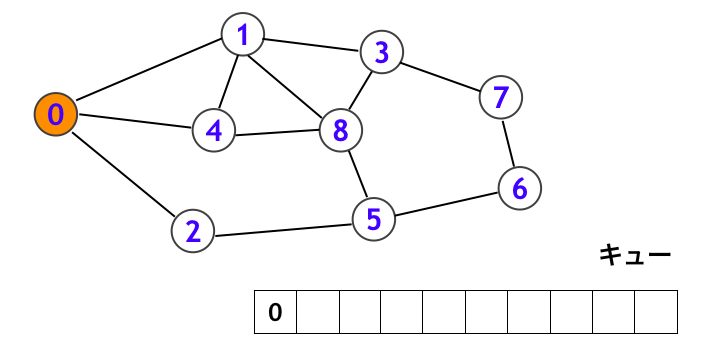
DFS の記事中でネットサーフィンを例にとりながら BFS の動きについても簡単な解説を行っていましたが、ここで今一度詳細に追ってみましょう。頂点 0 から探索を開始するとします。まず頂点 0 をキューに入れた状態からスタートします。

なお今後、各頂点の状態を以下の三色で表すことにします²。

色	状態
赤	その頂点がすでに訪問済みであることを表す (ネットサーフィンで言えば、ページを読了済みであること)
橙	その頂点がすでに発見されていて、これから訪問予定であることを表す
白	その頂点が未発見であることを表す。

そして、橙状態の頂点を格納するキューを用意します。

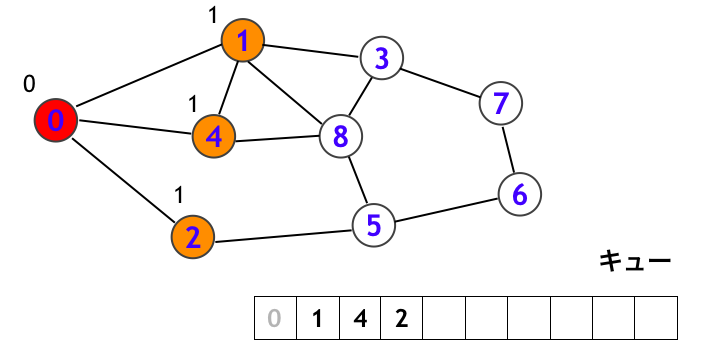
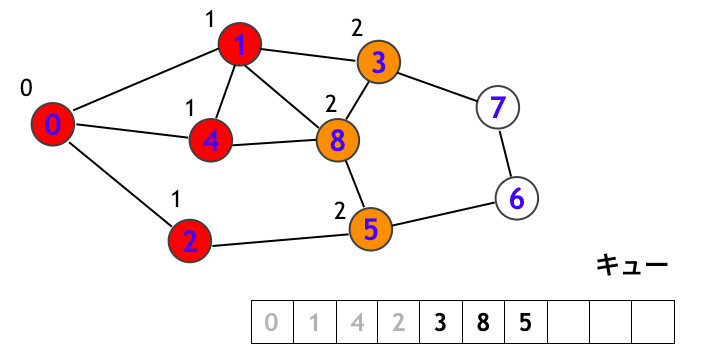
まずキューの先頭にある頂点 0 を取り出して、頂点 0 を訪問します。下図で訪問済みの頂点は赤く示しています。そして頂点 0 から辿れる頂点 (1, 2, 4) をキューに入れます。これらの訪問予定の頂点を橙色で示しています。また下図において、頂点 1, 4, 2 のところに「1」という数値を書いていますが、これは頂点 1, 4, 2 がいずれも頂点 0 から 1 step で到達できることを表しています (同様に頂点 0 は頂点 0 から 0 step で到達できます)。

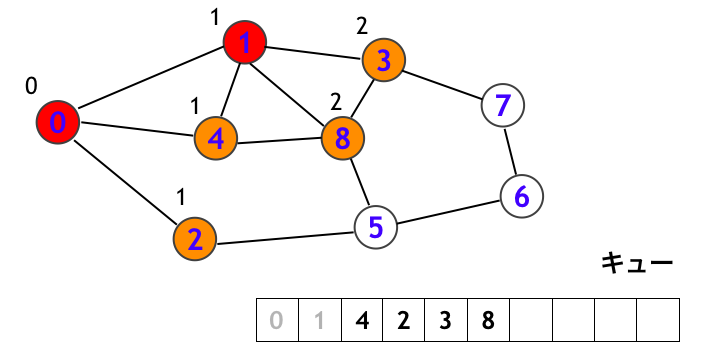
次にキューの先頭にある頂点 1 を取り出して、頂点 1 を訪問します。そして頂点 1 から辿れる頂点 (0, 3, 4, 8) のうち、白頂点 (3, 8) をキューに追加します。このとき下図において頂点 3, 8 のところには「2」を記入しています。これは頂点 3, 8 には頂点 0 から出発して 2 step で到達できることを意味しています。

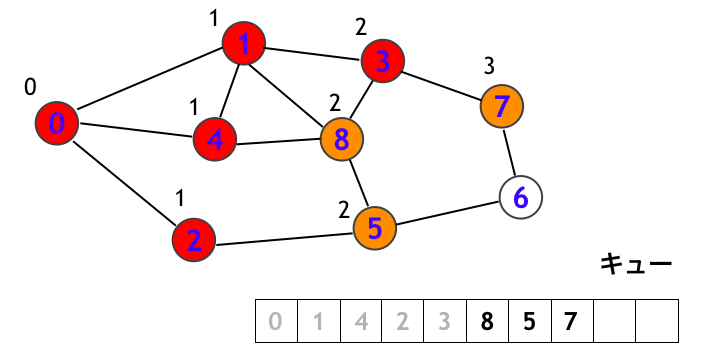
次にキューの先端にある頂点 4 を取り出して、頂点 4 を訪問します。そして頂点 4 から辿れる頂点 (0, 1, 8) の中に白頂点はないので、特に新たにキューに頂点を追加することなくステップを終えます。

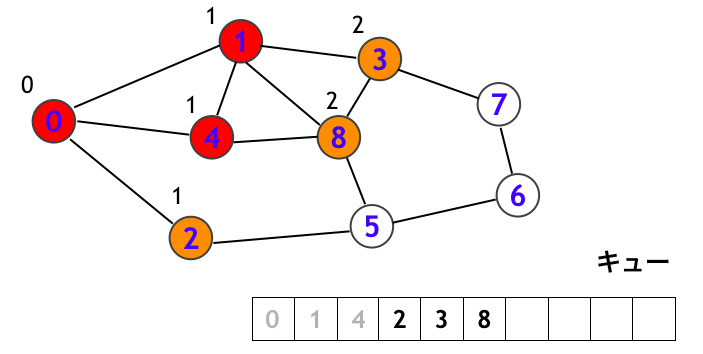
次にキューの先端にある頂点 2 を取り出して、頂点 2 を訪問します。そして頂点 2 から辿れる頂点 (0, 5) のうちの白頂点 (5) を新たにキューに追加します。

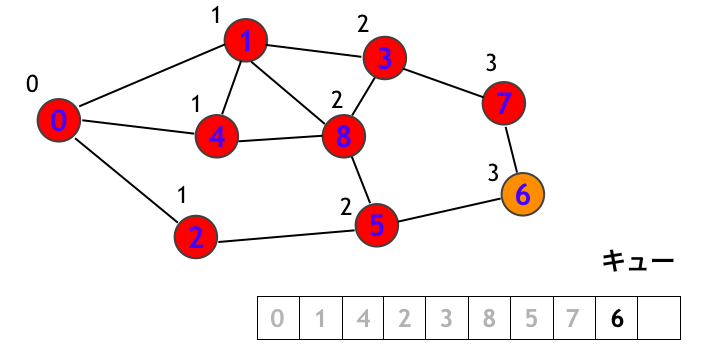
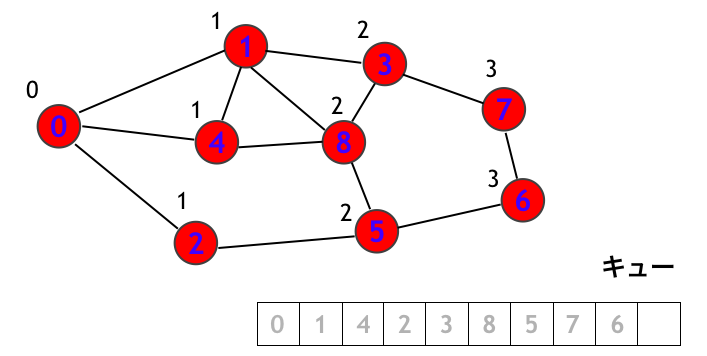
以後、順にステップを追うと、下図のように続きます。まず頂点 3 を訪問します。このとき頂点 7 にはついにラベル「3」がつきます。これは頂点 0 から 3 step で到達できることを意味します。

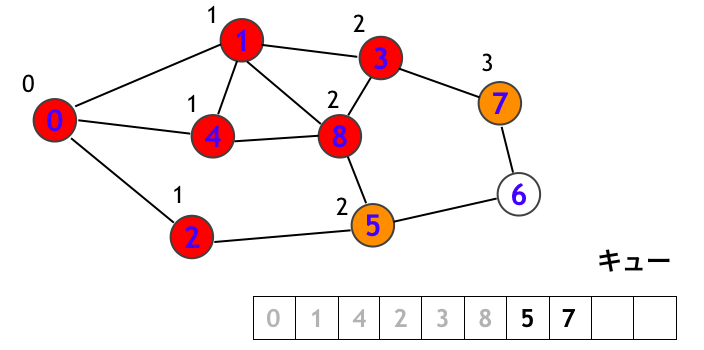
頂点 8 を訪問します。

頂点 5 を訪問します。

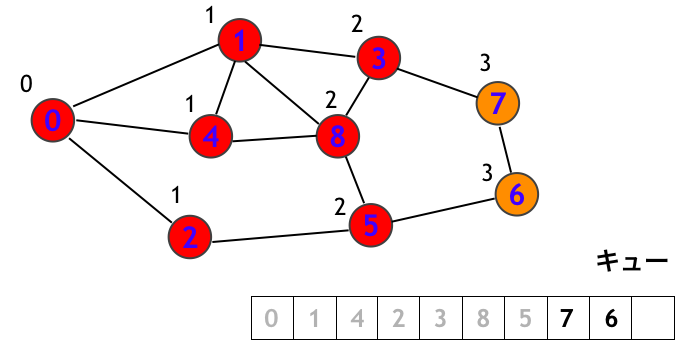
頂点 7 を訪問します。

最後に頂点 6 を訪問して終了です！！！

1-2. BFS の実装

以上の探索処理を実装してみましょう！！！！！
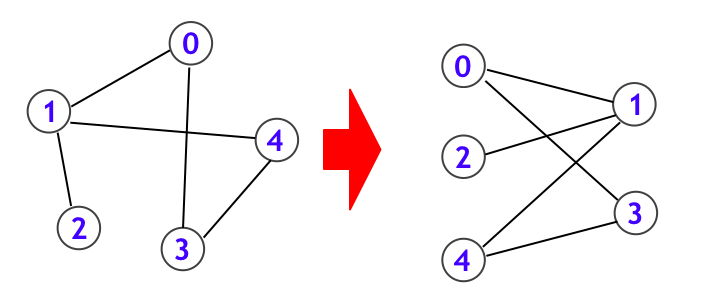
なお、グラフの計算機上での扱い方については

• DFS 記事の第 2 章

を読んでいただけたらと思います。ここでは

using Graph = vector<vector<int>>;

とします。グラフの入力データは以下の形式で表すことにします。$N$ はグラフの頂点数、$M$ は辺数を表します。また、各辺 $i = 0, 1, \dots, M-1$ は、頂点 $a_i$ と頂点 $b_i$ をつないでいることを表します。有向グラフの場合は $a_i$ から $b_i$ への辺があることを表し、無向グラフの場合は $a_i$ と $b_i$ とをつなぐ辺があることを表すものとします。

$N$ $M$
$a_0$ $b_0$
$a_1$ $b_1$
$\dots$
$a_{M-1}$ $b_{M-1}$

さて、上記の探索を実施するためのデータ構造として以下のものを用います:

データ構造		説明
vector	dist	dist[v] はスタート頂点から頂点 v まで何ステップで到達できるかを表す
queue	que	その時点での橙色頂点 (発見済みだが未訪問な頂点) を格納するキュー

配列 dist は初期状態として -1 に初期化しておくことで、「その頂点が発見済みかどうか」も同時に管理することができます。すなわち

• dist[v] == -1
• v は白色頂点である

が同値であるということになります。このデータ構造を用いて BFS は以下のように実装できます。

BFSの実装テンプレ

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
using Graph = vector<vector<int>>;

int main() {
    // 頂点数と辺数
    int N, M; cin >> N >> M;

    // グラフ入力受取 (ここでは無向グラフを想定)
    Graph G(N);
    for (int i = 0; i < M; ++i) {
        int a, b;
        cin >> a >> b;
        G[a].push_back(b);
        G[b].push_back(a);
    }

    // BFS のためのデータ構造
    vector<int> dist(N, -1); // 全頂点を「未訪問」に初期化
    queue<int> que;

    // 初期条件 (頂点 0 を初期ノードとする)
    dist[0] = 0;
    que.push(0); // 0 を橙色頂点にする

    // BFS 開始 (キューが空になるまで探索を行う)
    while (!que.empty()) {
        int v = que.front(); // キューから先頭頂点を取り出す
        que.pop();

        // v から辿れる頂点をすべて調べる
        for (int nv : G[v]) {
            if (dist[nv] != -1) continue; // すでに発見済みの頂点は探索しない

            // 新たな白色頂点 nv について距離情報を更新してキューに追加する
            dist[nv] = dist[v] + 1;
            que.push(nv);
        }
    }

    // 結果出力 (各頂点の頂点 0 からの距離を見る)
    for (int v = 0; v < N; ++v) cout << v << ": " << dist[v] << endl;
}

このコードに以下の入力 (上で動作例を示した図のグラフです) を与えてみます:

9 13
0 1
0 4
0 2
1 4
1 3
1 8
2 5
3 8
4 8
5 8
5 6
3 7
6 7

そうすると、以下の出力結果となりました。各頂点について、頂点 0 から何ステップで到達できるかを正しく求められていることがわかります。

1: 1
2: 1
3: 2
4: 1
5: 2
6: 3
7: 3
8: 2

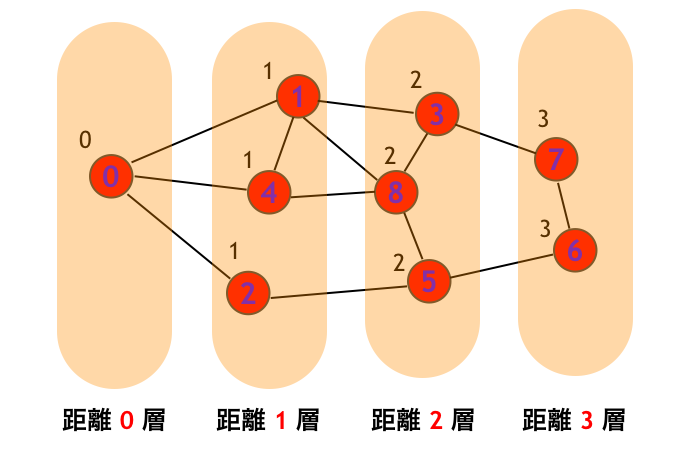
dist の面白い性質として、頂点 u と頂点 v が隣接しているならば、dist[u] と dist[v] との差は 1 以下であることが言えます。つまり BFS は

• 始点
• 始点から 1 ステップで行ける頂点のなす層
• 始点から 2 ステップで行ける頂点のなす層
• ...

とに分けていくアルゴリズムですが、このときすべての辺は

• 同じ層の頂点同士を結ぶ
• 隣り合う層の頂点同士を結ぶ

のいずれかになることがわかります。

1-3. BFS と最短経路

すでに多くの方が気付いている通り、BFS は

---

探索の始点となる頂点から、各頂点への最短経路を求めることのできるアルゴリズム
(dist[v] の値が、始点から v への最短経路の長さを表しています)

---

となっています。ただし条件として、今回のように各辺に重みのない重みなしグラフであること、言い換えれば各辺の重みがすべて等しいことが条件となっています。各辺に重みがある場合には Dijkstra 法など、より高度なアルゴリズムを用いて最短経路を求めることが多いです。

なお、BFS によって求められる dist[v] の値が、実際に始点から頂点 v への最短経路長を表すことについては、直感的には明らかですが、実際はきちんと証明すべきことです。念のため簡単に議論してみます。難しく感じたら飛ばしていただけたらと思います。

BFS が最短経路長を求めることの証明

直感的には

• 始点から 1 ステップで行ける頂点は最初にすべて探索され尽くされる
• 次に始点から 2 ステップで行ける頂点がすべて探索され尽くされる
• 次に始点から 3 ステップで行ける頂点がすべて探索され尽くされる
• ...

という流れが壊れることなく続いていくイメージになります。こういう場面で有効な証明方法は「壊れる箇所があるなら、その最初に壊れる場所を議論して、その直前も壊れてないとダメであることを示して矛盾を導く」というものです。一種の数学的帰納法ですね。

• dist[v] := BFS 中に求まる値
• shortest[v] := 始点から v までの最短経路長

としたとき、もし dist[v] > shortest[v] となるような頂点 v が存在すると仮定して矛盾を導きます。そのような v のうち、shortest[v] の値が最小となるものを考えます。このとき、始点から v への最短経路において v の直前の頂点を u とすると

shortest[v] = shortest[u] + 1

が成立しています。このとき帰納法の仮定より

dist[u] = shortest[u]

が成立しているはずです。よって

dist[v] > shortest[v] = shortest[u] + 1 = dist[u] + 1

となっていることがわかります。つまり、頂点 u と頂点 v との間で dist の値が 2 以上離れることになるわけですね。u と v は辺で結ばれているので、こんなことは絶対に起こりません。

1-4. BFS の計算量

BFS によって探索するグラフの頂点数を $N$、辺数を $M$ とします。

• 各頂点はキューに高々一回挿入され、高々一回取り出されるので、その分の計算量が $O(N)$
• 各辺は高々一回だけ探索されることになるので、その分の計算量が $O(M)$

となります。合わせて計算量は $O(N + M)$ となります。DFS と同じく線形時間であり、グラフを入力として受け取るのと同等の計算時間で探索も行えることを意味しています。

1-5. DFS と BFS との比較

ほとんどの問題に対しては、それをグラフ上の探索問題に帰着できたとき、DFS で解くことも BFS で解くこともできます。しかしながら問題によっては、DFS の方が適切であったり BFS の方が適切であったりします。そのあたりのことを簡単にまとめます。

DFS の方がよい場合

• 解がスタートから遠いところにあることがわかっていて、幅優先探索によってしらみつぶすことが現実的でない場合でも、DFS であれば適切な枝刈りや探索順序の工夫によって解が求められることがあります。

• グラフの頂点の順序に意味がある場合、例えば辞書順最小な経路から順番に探索したい場合などは、DFS によって自然に実装できることが多いです。

• キャッシュにメモしながら動的計画法を行う場合など、帰りがけ時に子ノードたちの結果をまとめるような処理が重要な場合には、再帰関数を用いた DFS が簡明です (メモ化再帰とよばれます)。

BFS の方がよい場合

• BFS は最短経路アルゴリズムとしても活用できることから、そのような用途に適しています。

• 探索空間 (グラフのサイズ) 自体はとても大きいが、解がスタートから十分近いところにあることがわかっている場合は、BFS によって解を発見できることがあります。

2. BFS の応用例

BFS でできることの割と多くは DFS でもできるのですが、BFS は最短経路を求めることができるアルゴリズムであるというのが大きな特徴となっています。この性質を活用する典型的な応用例としては

• パズルを解くための最小手数を求める
• Facebook の友達関係などにおいて、ある人からある人へ何ステップで行けるかを求める

といったものが挙げられます。また 3 章で見るように、DFS と同様グラフに関する様々な問題を BFS によっても解くことができます。さらに BFS で用いるキューの使い方を工夫することで、

• 3-5. サイクル検出
• 3-6. 後退解析

といった多彩な探索もできるようになります。ここではいくつかのパズルについて最小手数を解析する具体例を紹介してみます。

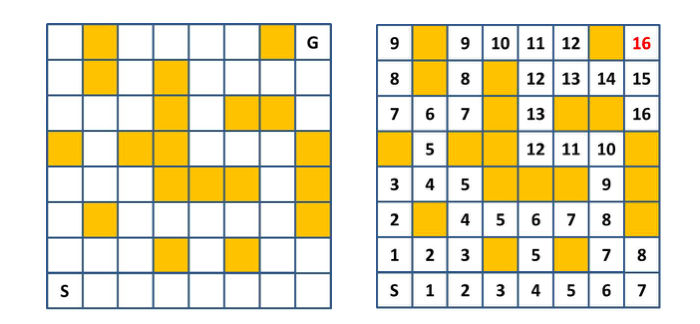
迷路の最短路

下図左のような迷路についてスタート (S マス) からゴール (G マス) まで辿り着くまでの最短路を考えます。毎ステップごとに上下左右のいずれかに進むことができますが、黄色マスには進むことができないものとします。

これに対して BFS を適用すると、各マスについての dist の値は下図右のようになります。スタートからゴールまで最短 16 手で到達できることがわかります。なお、この BFS、および実際の最短経路を復元する方法については下記記事を参考にしていただけたらと思います。

• スタックとキューを極める！ 〜 考え方と使い所を特集 〜
• 意外と解説がない！動的計画法で得た最適解を「復元」する一般的な方法

8パズルと15パズル

下図 (amazon サイトより) のようなスライドパズルは、誰もが一度は遊んだことがあるのではないでしょうか。

これを適当に崩した状態から出発して、上図の状態に復元するパズルです。それが可能かどうかを判定したり、復元するための最小手数を求める問題では、まさに幅優先探索 (BFS) が活躍します。

3×3 サイズの 8 パズルであれば、特に工夫なしの BFS でも十分解くことができます。4×4 サイズの 15 パズルに関しては、探索領域が広くなることもあって単純な BFS では厳しくなります。IDA* といった改良型の探索を行うことで 15 パズルも解くことができるようになります。

ルービックキューブ

ルービックキューブにおいて

• 任意の局面から $N$ 手以内で六面を揃えることができる
• どのような順番で回しても六面を揃えるのに $N$ 手以上を要する局面が存在する

という条件を満たす整数 $N$ は「神の数字」と呼ばれ、これを求めることは古くからの重要課題でした。これが解決したのは割と最近で 2010 年 8 月のことです。$N = 20$ であることが確定しました。

最終的に神の数字を求める証明に用いられた手法は BFS とは異なりますが、歴史的には BFS に改良を加えた IDA* は重要な役割を果たしてきました。神の数字を求める歴史については以下の記事が大変面白いです。

• ルービックキューブをアルゴリズムで解くということ

3. グラフの様々な例題

DFS 記事でも解いた問題やその他の問題たちを、今度は BFS によって解いてみます。

3-1. s から t へ辿り着けるか

グラフ $G$ の二頂点 $s, t \in V$ が与えられたとき、$s$ から辺をたどって $t$ に到達できるかどうかを判定する問題を考えてます。

これは単純に、$s$ を始点とした BFS を実施してあげればよいです。BFS 実施後において dist 配列を見ることで、各頂点が探索されたかどうかを判定することができます。dist[t] == -1 であれば t へ辿り着けないことを表し、dist[t] != -1 であれば t へ辿り着けることがわかります。

sからtへ辿り着けるか

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
using Graph = vector<vector<int>>;

int main() {
    // 頂点数と辺数、s と t
    int N, M, s, t; cin >> N >> M >> s >> t;

    // グラフ入力受取
    Graph G(N);
    for (int i = 0; i < M; ++i) {
        int a, b;
        cin >> a >> b;
        G[a].push_back(b);
    }

    // 頂点 s をスタートとした探索
    vector<int> dist(N, -1);
    queue<int> que;
    dist[s] = 0, que.push(s);
    while (!que.empty()) {
        int v = que.front(); que.pop();
        for (auto nv : G[v]) {
            if (dist[nv] == -1) {
                dist[nv] = dist[v] + 1;
                que.push(nv);
            }
        }
    }

    // t に辿り着けるかどうか
    if (dist[t] != -1) cout << "Yes" << endl;
    else cout << "No" << endl;
}

3-2. 連結成分の個数

次に連結とは限らない無向グラフが与えられたとき、それが何個の連結成分からなるのかを数える問題を考えます。BFS も DFS と同様、指定した頂点 $s$ から出発して辿れる頂点をすべて探索します。したがって DFS と同様、

• まだ探索済みでない頂点 $v$ を一つ選んで $v$ を始点とした BFS を行う

というのを、全頂点が探索済みの状態になるまで繰り返せばよいです。

無向グラフの連結成分の個数

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
using Graph = vector<vector<int>>;

int main() {
    // 頂点数と辺数
    int N, M; cin >> N >> M;

    // グラフ入力受取
    Graph G(N);
    for (int i = 0; i < M; ++i) {
        int a, b;
        cin >> a >> b;
        G[a].push_back(b);
        G[b].push_back(a);
    }

    // 頂点 s をスタートとした探索
    vector<int> dist(N, -1);
    queue<int> que;
    int count = 0;
    for (int v = 0; v < N; ++v) {
        if (dist[v] != -1) continue; // v が探索済みならスルー
        dist[v] = 0, que.push(v);
        while (!que.empty()) {
            int v = que.front(); que.pop();
            for (auto nv : G[v]) {
                if (dist[nv] == -1) {
                    dist[nv] = dist[v] + 1;
                    que.push(nv);
                }
            }
        }
        ++count;
    }
    cout << count << endl;
}

3-3. 二部グラフ判定

次は与えられた無向グラフが二部グラフ (bipartite graph) かどうかを判定する問題を考えます。二部グラフとは以下の条件を満たすように全頂点を白または黒に塗り分けられるグラフのことです:

• 白頂点同士が辺で結ばれることはなく、黒頂点同士が辺で結ばれることもない

言い換えれば、二部グラフとは下図のように、グラフを左右のカテゴリに分割して、すべての辺は異なるカテゴリ間を結んでいる状態にできることをいいます。

さて、BFS を用いた二部グラフ判定方法は極めて明快です。まずグラフ上の頂点 $s$ を一つ選びます。この頂点を白く塗るとしても一般性を失いません。そして

• 頂点 $s$ を一つ選んで白く塗る
• 頂点 $s$ から 1 ステップで到達できる頂点を黒く塗る
• 頂点 $s$ から 2 ステップで到達できる頂点を白く塗る
• ...

という風に塗っていくしかないことがわかります。なぜなら

• 白頂点に隣接した頂点は黒でなければならない
• 黒頂点に隣接した頂点は白でなければならない

という状況になっているからです。こうして各頂点を塗っていったときに整合しているかどうかを check すればよいです。整合性の確認方法ですが、

• 白頂点: dist[v] が偶数な頂点 v
• 黒頂点: dist[v] が奇数な頂点 v

となっていることから、v と nv とが隣接しているとき、dist[v] % 2 と dist[nv] % 2 とが異なっているかどうかを確認すればよいことになります。そして実際には dist[v] と dist[nv] との差は 1 以下であることに留意すると、dist[v] != dist[nv] が成立するかどうかのみを確認すればよいことになります。以上をまとめると結論は大変シンプルで

---

連結な無向グラフ $G$ で頂点 $s$ を一つ選んで $s$ を始点とした BFS を行ったとき

• $G$ は二部グラフである
• dist の値が等しい頂点同士が隣接することはない

とが同値になる

---

ということがわかりました。

二部グラフ判定

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
using Graph = vector<vector<int>>;

int main() {
    // 頂点数と辺数
    int N, M; cin >> N >> M;

    // グラフ入力受取
    Graph G(N);
    for (int i = 0; i < M; ++i) {
        int a, b;
        cin >> a >> b;
        G[a].push_back(b);
        G[b].push_back(a);
    }

    bool is_bipartite = true;
    vector<int> dist(N, -1);
    queue<int> que;
    for (int v = 0; v < N; ++v) {
        if (dist[v] != -1) continue; // v が探索済みならスルー
        dist[v] = 0, que.push(v);
        while (!que.empty()) {
            int v = que.front(); que.pop();
            for (auto nv : G[v]) {
                if (dist[nv] == -1) {
                    dist[nv] = dist[v] + 1;
                    que.push(nv);
                } else {
                    // 整合性を確認する
                    if (dist[v] == dist[nv]) is_bipartite = false;
                }
            }
        }
    }

    if (is_bipartite) cout << "Yes" << endl;
    else cout << "No" << endl;
}

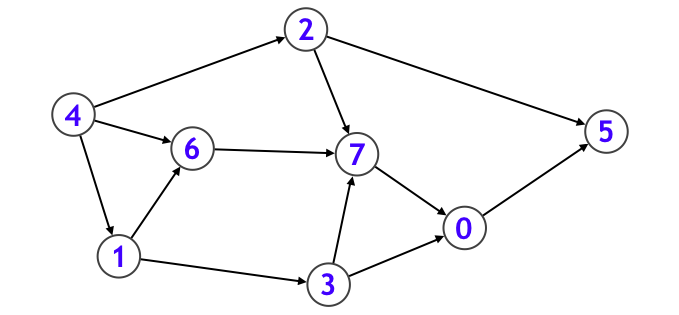
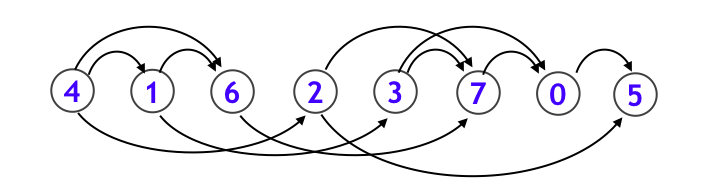
3-4. トポロジカルソート

この辺りから純粋な BFS を超えて、キューを鮮やかに使いこなすような探索になります。トポロジカルソートとは以下のような DAG (サイクルのない有向グラフ) に対し、

下図のように、各頂点を辺の向きに沿うように一列に並べることです。応用例として makefile などに見られるような、依存関係を解決する処理などは、まさにトポロジカルソートそのものです。なお、DAG であることと、トポロジカルソート可能であることは同値になります。

さて、トポロジカルソートは DFS を用いた方法と、キューを用いた方法の二つが代表的ですが、歴史的にはキューを用いた方法が先に登場しました。ここでまずグラフの用語をいくつか定義します:

• 出次数 deg[v]： 頂点 $v$ を始点とする辺の個数
• シンク： 出次数が 0 であるような頂点

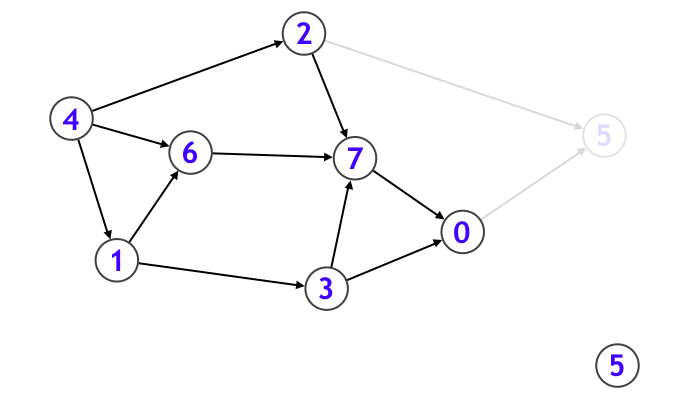
このときトポロジカルソートにおいて、まずシンクたちが最後尾集団になることがわかります。シンクは複数個存在することがありえますが、それらはトポロジカルソートの最後尾集団の中ではどの順序で並べてもよいです。そしてシンクたちと、シンクに向かって伸びている辺たちを、元のグラフから削除します。上図のグラフの場合、頂点 5 がシンクとなっています。

そうすることで新たに頂点 0 がシンクになりました。そこで今度は頂点 0 を取り出して、頂点 0 に向かって伸びている辺たちを、元のグラフから削除します。

そうすると今度は頂点 7 が新たにシンクになったので...と繰り返していきます。

この一連の手続きにおいて頂点を削除した順序の逆順に並べることで、トポロジカルソート順が選べます。なお実装上は

• グラフの頂点削除を扱うのは大変なので、頂点 v を削除するときは、頂点 v へと伸びている各頂点たちの出次数をデクリメントすることで代用する
• シンクであるかどうかは出次数が 0 かどうかで判定する

という風にします。また頂点 v へと伸びている各頂点たちを走査することが必要なため、予めグラフの辺の向きを逆にしておきます。

トポロジカルソート

#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
using Graph = vector<vector<int>>;

int main() {
    // 頂点数と辺数
    int N, M; cin >> N >> M;

    // グラフ入力受取
    Graph G(N);
    vector<int> deg(N, 0); // 各頂点の出次数
    for (int i = 0; i < M; ++i) {
        int a, b;
        cin >> a >> b;
        G[b].push_back(a); // 逆向きに辺を張る
        deg[a]++; // 出次数
    }

    // シンクたちをキューに挿入する
    queue<int> que;
    for (int i = 0; i < N; ++i) if (deg[i] == 0) que.push(i);

    // 探索開始
    vector<int> order;
    while (!que.empty()) {
        // キューから頂点を取り出す
        int v = que.front(); que.pop();
        order.push_back(v);

        // v へと伸びている頂点たちを探索する
        for (auto nv : G[v]) {
            // 辺 (nv, v) を削除する
            --deg[nv];

            // それによって nv が新たにシンクになったらキューに挿入
            if (deg[nv] == 0) que.push(nv); 
        }
    }

    // 答えをひっくり返す
    reverse(order.begin(), order.end());
    for (auto v : order) cout << v << endl;
}

3-5. サイクル検出

次にグラフにサイクルがあるかどうかを判定する問題に取り組みます。先ほどのトポロジカルソートとほとんど同じ手法になります。先ほどのようなキューを用いた探索を終えた状態で、

• サイクルに含まれる頂点は一度もシンクになることはありえないため、キューに挿入されることはない

ということが言えます。したがって各頂点についてキューに挿入されたかどうかを覚えておくことで、サイクルがあるかどうかを判定することができます。さてここでは「AOJ 2891 - な◯りカット」を解いてみます。これは

---

• サイクルをただ一つ含むことが保証された無向グラフにおいて
• 「二頂点 $a, b$ がともにそのサイクル上にあるときは 2 を出力して、そうでないときは 1 を出力する」というクエリを大量に答える

---

という問題です。

AOJ2891の解答例

#include <iostream>
#include <vector>
#include <queue>
using namespace std;
using Graph = vector<vector<int>>;

int main() {
    // 頂点数 (サイクルを一つ含むグラフなので辺数は N で確定)
    int N; cin >> N;

    // グラフ入力受取
    Graph G(N);
    vector<int> deg(N, 0); // 各頂点の出次数
    for (int i = 0; i < N; ++i) {
        int a, b; cin >> a >> b;
        --a, --b; // 0-indexed にする
        G[a].push_back(b);
        G[b].push_back(a);
        ++deg[a], ++deg[b];
    }

    // 葉たちをキューに挿入する
    // 今回は無向グラフなので、deg[v] == 1 が葉の条件になります
    queue<int> que;
    for (int v = 0; v < N; ++v) if (deg[v] == 1) que.push(v);

    // 探索
    vector<bool> ispushed(N, false);
    while (!que.empty()) {
        int v = que.front(); que.pop();
        ispushed[v] = true;
        for (auto nv : G[v]) {
            --deg[nv];
            if (deg[nv] == 1) que.push(nv);
        }
    }

    // クエリに答える
    int Q; cin >> Q;
    for (int _ = 0; _ < Q; ++_) {
        int a, b; cin >> a >> b; --a, --b;
        if (!ispushed[a] && !ispushed[b]) cout << 2 << endl;
        else cout << 1 << endl;
    }
}

3-6. 後退解析

3-5 で見たようなキューを用いた探索手法を、特に組合せゲーム理論の分野では後退解析とよぶことがあります。

一般に、「オセロ」「将棋」「囲碁」といったゲームに対して

• 先手と後手が双方最善を尽くしたとき、どちらが必勝かを求める
• その必勝手順を求める
• 考えられるすべての局面について、それが先手勝ちの局面か後手勝ちの局面かを判定する

といった営みを「ゲームを解く」といいます。ゲームを解く上で「ゲームの局面遷移を表すグラフにサイクルがあるかどうか」が比較的重要になります。サイクルがある場合はうかつにゲーム探索を行うと無限ループに陥ることがあり、注意が必要です。

このようなサイクルがあるゲームを解析する手法として、キューを用いた後退解析がよく用いられます。実際にどうぶつしょうぎなどは後退解析によって解かれました。後退解析の考え方について詳しくは

• ゲームを解く！Educational DP Contest K, L 問題の解説

を参考にしていただけたらと思います。

4. 参考文献

DFS 記事の参考文献と同様です。本記事を書くために参考にした書籍や、今後のさらなる勉強の役に立つ書籍たちです。

• DFS 記事第 7 章: 参考文献

5. おわりに

DFS や BFS はグラフ探索に限らず、あらゆるグラフ上のアルゴリズムの重要な基礎になります。また、一見してグラフに関する問題でなくても、グラフを用いて定式化することで見通しがよくなる問題は多数あります。その意味で、DFS/BFS はアルゴリズムの重要な登竜門といえるでしょう。本記事を通して、グラフと慣れ親しんでいただけたならば、とても嬉しく思います。

1. もちろんグラフ探索はこの二種類だけでなく、最良優先探索などをはじめとして、様々なな柔軟な探索アルゴリズムを組むことができます。DFS・BFS をすべてと思うのではなく、あくまでグラフ探索の基本形として理解するのが良さそうです。 ↩

2. 本記事で「赤・橙・白」で示したものは、「黒・灰・白」で示す書籍が多いかもしれません。 ↩