自分は孫弟子にあたるらしいRichard E. Korf 先生の論文紹介です。
会ったことないですがKorf先生→
https://www.youtube.com/watch?v=EnX8cQPiB1M
https://www.youtube.com/watch?v=TAjyI06Q1x8
IDAはAと同じく最適解を返すアルゴリズムですが、A*と異なり メモリ使用量が線形 であるという違いがあります。
Iterative Deepening Depth First Search
だれだ反復深化深さ優先探索なんて長ったらしい名前を付けたのは。
反復Xは長いのでIDDFSと呼びましょう。 IDDFSは、ダイクストラの深さ優先版です。
ダイクストラやA*などの最良優先探索系、もとい幅優先探索系に共通する問題は、OPENリストを全部メモリに確保しておかないといけないという点です。
しかし、実際のコンピュータに載っているメモリは、非分散環境では最大でも数テラバイトぐらい、信頼性が必要でかつ機器が2,3世代古い宇宙探査機、他にもスマートフォンなどでは、最大でも1Gぐらいでしょう。 昔は数キロ、数メガでした。
このような場合、Memory Greedyな探索アルゴリズムであるA*,Dijkstra法は使えません。なぜなら、A*やDijkstraは数メガのメモリならほぼ一瞬で、数ギガのメモリですら5分程度で消費し尽くしてしまうからです。
下は、STRIPSプランニング問題のState-of-the-ArtソルバであるFast Downwardを、International Planning Competition 2011 に用いられた問題の1つ Visitall に対して30秒ぐらい実行したログです。実行環境は私の古めのデスクトップ(AMD Phenom II X6 @ 2.8GHz)です。
INFO Running search.
INFO search input: output
INFO search arguments: ['--search', 'astar(blind())']
INFO search time_limit: None
INFO search memory limit: 2e+03 MB
reading input... [t=0.00s]
Simplifying transitions... done!
done reading input! [t=0.00s]
packing state variables...done! [t=0.00s]
Variables: 144
Facts: 430
Bytes per state: 20
Building successor generator...done! [t=0.00s]
done initalizing global data [t=0.00s]
Conducting best first search with reopening closed nodes, (real) bound = 2147483647
Initializing blind search heuristic...
New best heuristic value for blind: 1
[g=0, 1 evaluated, 0 expanded, t=0.00s, 3252 KB]
f = 1 [1 evaluated, 0 expanded, t=0.00s, 3252 KB]
f = 2 [5 evaluated, 1 expanded, t=0.00s, 3252 KB]
f = 3 [21 evaluated, 5 expanded, t=0.00s, 3252 KB]
f = 4 [81 evaluated, 21 expanded, t=0.00s, 3252 KB]
f = 5 [287 evaluated, 81 expanded, t=0.00s, 3388 KB]
f = 6 [991 evaluated, 287 expanded, t=0.00s, 3388 KB] <<< 探索空間が綺麗に指数爆発中。対数プロットいらず
f = 7 [3269 evaluated, 991 expanded, t=0.02s, 3512 KB]
f = 8 [10695 evaluated, 3269 expanded, t=0.04s, 4036 KB]
f = 9 [33876 evaluated, 10695 expanded, t=0.12s, 5440 KB]
f = 10 [106476 evaluated, 33876 expanded, t=0.36s, 9924 KB]
f = 11 [325609 evaluated, 106476 expanded, t=1.16s, 24100 KB]
f = 12 [985207 evaluated, 325609 expanded, t=3.54s, 64108 KB]
f = 13 [2909959 evaluated, 985207 expanded, t=10.96s, 187416 KB]
f = 14 [8497431 evaluated, 2909959 expanded, t=32.56s, 525844 KB]
$8\times 10^6$ ぐらいのノードを30秒で展開しているので、展開速度はざっと見積もって$2\times 10^5$ node/sec ぐらいでしょうか。このログからわかるのは、一部のグラフ探索問題では、探索設定によっては30秒で500MBのメモリを消費するということです。
注: もちろん、これは h の計算がどれだけ重い計算かに依存します。Blindは0を返すだけの軽いヒューリスティクスです。一方世の中には、STRIPSプランニング問題のLandmark-cut ヒューリスティック(Helmert 2008)や、一回計算するごとに線形計画問題を解くLPヒューリスティクスなど、より精度の高いヒューリスティクスがあります。それらの関数は一回あたりの計算も重いです。例えばLMcutでは、一つのノードのhの計算に1ms程度かかり($\approx 10^3$ node / sec)、二桁ぐらい展開速度が違います。重いヒューリスティクスを用いればメモリ使用スピードは遅くなりますが、大規模なグラフ探索問題を4,5時間かけて解く場合には、やはり指数的に大きなメモリ使用量が問題になります。
IDA* (Korf 1985)
そこでIDAの出番です。(IDDFSはIDAの $h=0$ 版です。) IDAは、答えとなる経路の深さ$d$, ノードの子の数の平均値$b$ (branching factor) に対して、最悪で$O(bd)$のメモリしか用いません。一方、A(およびDijkstra)は最悪で$O(b^d)$、すなわち指数的に大きなメモリ量を要する可能性があります。
IDA* は、用いるヒューリスティクスがconsistentであれば常に最適解を返します。Rubik's Cube, 15/24-Puzzleなど有名なパズル問題に用いられるパターンデータベース(PDB)ヒューリスティクスは、計算が早くかつconsistentなので、よくIDA*と共につかわれます。
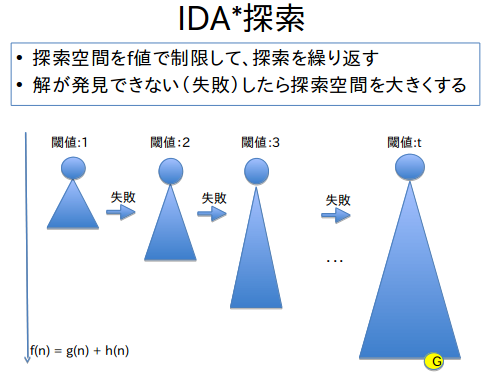
IDA*を一言で表すと、「最大深さを制限した深さ優先探索(DFS)を、深さを増やしながら繰り返す」です。それぞれのイテレーションでは、最大深さの限界値はグローバル変数として設定しておき、その深さ以上には探索しません。ここで、「深さ」は正しくはf値です。仮に$h=0,f=g$とすると、f値は深さと同義になり、このアルゴリズムはIDDFSと呼ばれます。
(やっぱりQiitaのバグでアップロードできませんので、またDropboxからアップロードしました。ただし、今回はリンクの方法を変えて、http://cantonbecker.com/work/musings/2014/how-to-directly-link-or-embed-dropbox-images/ に従いました。javascriptデバッガを呼び出してみると、XMLHttpRequestが行う通信にクロスオリジンリソースシェアリング(CORS)設定が記述されていなくて通信がブロックされている。時々通信できるのはナゼ?)
Algorithm IDA*:
- Let the depth threshold $F\leftarrow 0$
- Let $f_{max}$ be the largest $f$ in each iteration, initialized to $f_{max}\leftarrow 0$
- Let the start node $v_0$ be the DFS root
- Start DFS from $v_0$ :
- Let $Q$: a LIFO queue.
- Let $f_{next}\leftarrow \infty$
- Initialize: $push(v_0,Q)$
- Until $empty(Q)$
- Let $v \leftarrow pop(Q)$
- When $v = v_g$ then return $reverse(unfold(parent, v_g))$
- Else, for each $v' \in children(v)$ do
- If $f(v')\leq F$ ;; (new in IDA*)
- then $push(v',Q)$
- Else
- Backtrack. $F_{next} \leftarrow \min (F_{next}, f(v'))$
- If $f(v')\leq F$ ;; (new in IDA*)
- $F \leftarrow F_{next}$
キューの操作は別にただのスタックなので再帰で書いてもいいのですが、ここは手続き的に書きました。
IDAのからくりは、一度探索したノードを忘れることにあります。ノードを忘れてしまえば、メモリを解放できますよね。IDAは、一回のイテレーションが終わるたびに、今まで探索された最大のf値 $f_{next}$ のみ保存します。その他の情報、すなわちグラフやノード、そのf値など、A*ならば常に保存している全ての情報を忘れてしまいます。
この「忘れる」動作のおかげで、IDAを実行するのに必要なメモリ量は現在スタックに載っている量のメモリだけです。スタックの長さは解の長さに比例するので、IDAの線形メモリが示されます。
一方、$F$が更新されるたびにノードを忘れてしまうIDAは、同じノードを何度も展開することになります。従って、IDAに重いヒューリスティクスを組み合わせるのは得策とはいえないでしょう。重いヒューリスティクスを何度も計算することになってしまいますからね。
IDA*の改良 -- Transposition Table
IDAの「全ての情報を忘れることで線形メモリを保つ」という動作には、以上に述べたとおりいくらかの非効率さが存在します。そこで考え出されたのが IDA with Transposition Table (TT) です (Zobrist 1970, Slate & Atkin 1977)。自分ではあんまり知らないので、この知識についてはいい加減。DINDIN氏のほうが知ってるかも。
TTはいくつかのノードのh値,f値を固定サイズのハッシュテーブルに記録し、探索におけるキャッシュとして働きます。どのように保存するかにはいくつかのバリエーションがあるらしいので、深いところは読者の皆様ご自身でグーグルスカラってください。
まとめ
IDAを紹介しました。次は、IDA+inconsistent heuristicsにある問題点を解説し、続いてその解決策であるRBFSを解説します。