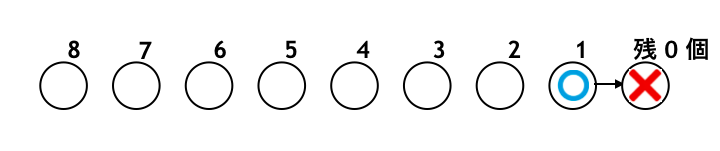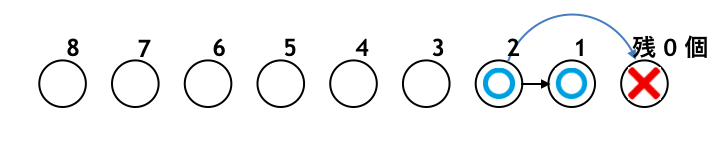0. ゲームを解くとは
世の中には将棋や、囲碁や、オセロのような複雑で難しいゲームから、マルバツゲームや、割りばしゲームや、立体三目並べのような比較的単純なゲームまで、たくさんの種類のゲームがあります。
この種の二人プレイのボードゲームにはある共通の特徴があります。それは
双方が最善を尽くした場合において、「先手必勝」か「後手必勝」か「引き分け」かが予め決まっている。
そして無限の計算時間と計算機資源さえあれば、それを容易に解析できる。
という点です。このように
- 「先手必勝」か「後手必勝」か「引き分け」なのかを解析する
- その必勝手順を求める
- できれば + α として初期盤面だけでなく、すべての局面について「先手勝ち」か「後手勝ち」か「引き分け」かも特定して最善手も求める
という営みが「ゲームを解く」ということであり1、それができたならばそのゲームを「完全に理解した」ということができます。本記事では探索領域がそれほど広くない簡単なゲームについて、ゲームを解くアルゴリズムを機械的に書けるようになることを目標にします。それができれば、宇宙が誕生してから現在までの経過時間を $5000$ 兆回繰り返しても終わらないほどの無尽蔵の計算時間と計算機資源が駆使できるならば、将棋のような複雑なゲームの必勝法を求めるアルゴリズムも容易に実装できることとなります。
すべての局面には答えがある
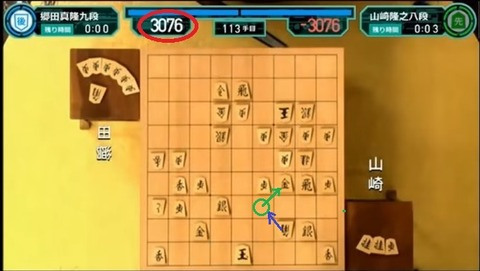
将棋の世界では近年コンピュータ将棋の発達が凄まじく、プロ棋士同士の対局放送においてもコンピュータ将棋によって局面の評価値が表示され、「どの手がよかった」「どの手が悪かった」が可視化される時代となりました (下図は「将棋 叡王戦決勝三番勝負第一局は大逆転で山崎隆之八段が先勝!」から引用)。
おおむね評価値が $1000$ を超えると優勢を表すようです。評価値を見て思うことは
理論上はすべての局面について、両者が最善を尽くした場合に「先手が勝つ」「後手が勝つ」「引き分けになる」のうちのどれになるかが決まっている2。
よって、究極の将棋の神とも云うべきソフトが存在したならば、評価値は$「+1」「0」「-1」$の三種類だけでいい。
ということです。しかし現実には、Ponanza 開発者の山本氏のブログ「コンピュータ将棋のよくある誤解(その2)」によると
- 将棋の完全解析のために調べる必要のある局面数: 約 142724769270595988105828596944949513638274662400000000000000000000000000000000000000000000000000
- Ponanza (2014) が 1 秒に読める局面数: 約 7000000
とのことであり、「将棋の完全解析」など、望むべくもない状態です。無尽蔵の計算時間が必要なだけでなく、無尽蔵の記憶容量も必要です。よって $「+1」「0」「-1」$ のみで評価値を表すのではなく、より勝ちやすいと思われる局面により高いスコアをつけることが重要になっています。
1. 二人零和有限確定完全情報ゲーム
将棋や、オセロや、マルバツゲームにおいて、双方が最善を尽くした場合の「先手必勝」か「後手必勝」か「引き分け」かが予め決まっているという話は、二人零和有限確定完全情報ゲームに一般化されます。理論上は全局面について、完全な先読みが可能です。このことは組合せゲームの基本定理とも呼ばれています3。
| 用語 | 意味 | 備考 |
|---|---|---|
| 二人 | 二人でするゲーム | |
| 零和 | どちらかが勝てばどちらかが負ける (その逆も) | |
| 有限 | 有限回の手順で必ず勝敗 (もしくは引き分け) が決まる | 将棋のような状態がループし得るゲームでは「同一局面が 4 回以上現れたら引き分け」といった規定を設けています |
| 確定 | 偶然的要素を含まない | サイコロを振るゲームは満たしません |
| 完全情報 | 隠された情報はない | 大富豪 (3 人以上) などのトランプゲームの多くは満たしません |
伝統的なボードゲームの多くが、この二人零和有限確定完全情報ゲームに分類されます。それらの代表的なゲームたちに対して、完全解析の進捗状況は以下の感じのようです。少しずつ進んで来ていますが、オセロ・将棋・囲碁が完全解析されるまでにはまだまだブレイクスルーが必要そうです。
| ゲーム | 結論 | 備考 |
|---|---|---|
| マルバツゲーム | 引き分け | 紙とペンでも簡単に示せます (このページなどを参照) |
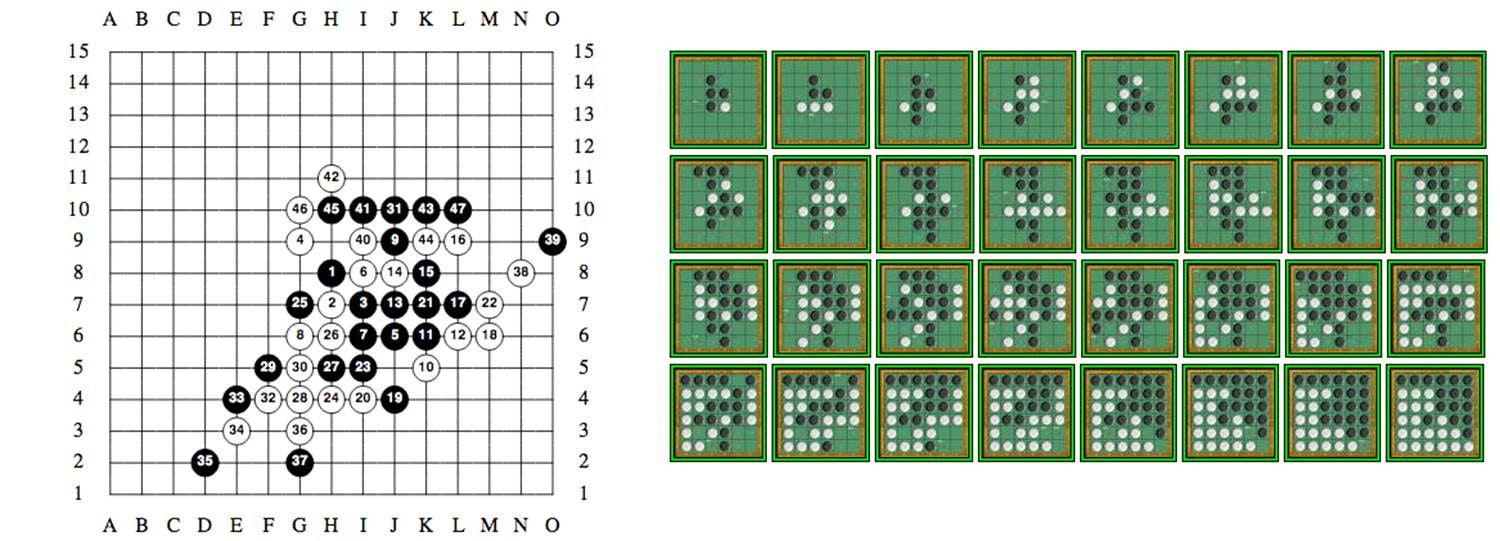
| 連珠 (五目並べの先手着手に制限) | 先手必勝 | [1] に 47 手の解が示されている (下図は論文中図より) |
| チェッカー | 引き分け | [2] 2007 年、シェッファーらにより |
| 6 × 6 リバーシ | 後手必勝 | [3] に 16-20 の解が示されている (下図はこのページより) |
| 4 × 4 囲碁 | 引き分け | [4] |
| 5 × 5 囲碁 | 先手必勝 | [5] 黒の 24 目勝ち |
| どうぶつしょうぎ | 後手必勝 | [6] 78 手 |
| アンパンマンしょうぎ | 引き分け | [7] |
2. ゲーム探索
ゲーム探索の考え方に馴染んで行きます。
2-1. ゲームのグラフ
二人零和有限確定完全情報ゲームでも、
- 盤面がループすることはない (オセロや石取りゲームなど)
- 盤面がループすることはあるが、なんらかのカウンタに基づく「引き分け」の規定がある (将棋の「千日手」など)
とで扱いやすさが多少変わって来ます。将棋は持将棋規定がなかったら、同一局面を何度も何度も繰り返すことが可能です。まずはそもそも盤面がループすることもないゲームの探索について考えます。
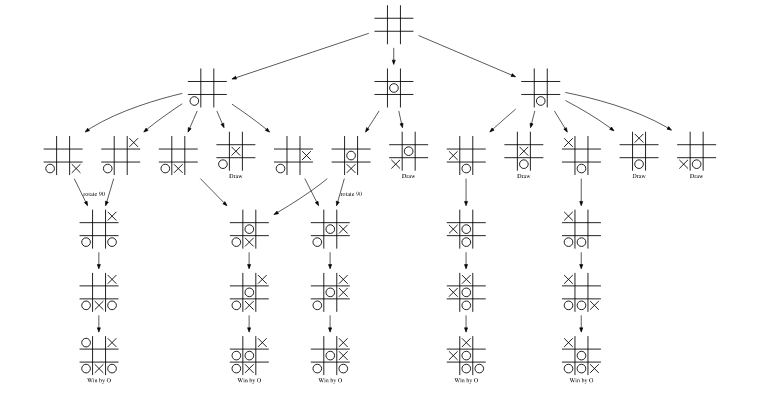
マルバツゲームのようなループのないゲームは、局面遷移をグラフに表すと上図のように DAG (Directed Acyclic Graph) になります (図はこの資料から引用)。すなわち、
- 局面遷移は有向グラフ (Directed Graph)
- 状態がループすることはない (Acyclic)
ということになります。注意点として、確かにサイクル (ループ) はないのですが、異なる盤面から同一盤面へと遷移する合流があるので「木」になるとは限らないです。ゆえに、
解析済みの局面については、その勝敗をメモしておく
という動的計画法・メモ化再帰の営みが必要になります。それをしないと同一局面を何度も何度も解析する羽目になります。しかしながらオセロ以上の複雑なゲームになると、地球上に存在する原子の数よりも多い局面数をもつこととなり、その完全解析はかなり厳しい現状があることがわかります。
一方、将棋や囲碁のような、サイクル (ループ) のあるゲームの解析は少しややこしいです。そのようなゲームに対しては後退解析と呼ばれる手法がよく知られています。これも、勝敗が自然に決まる局面以外は「引き分け」になることがわかるというシンプルな手法です。
2-2. ゲーム解析の例
まずはループのない非常に簡単なゲーム (石取りゲーム) を例にして、ゲーム探索の思想を体験してみます。
例題 1. 石取りゲーム
$K$ 個の石が山になっている。先手と後手が交互に
- 山から $1$ 個, $2$ 個, $3$ 個のいずれかの個数の石をとる
を繰り返します。ただし、山に残っている石の個数より多くの個数の石をとることはできません。先に山から石がとれなくなった方の負けです。先手と後手がお互いに最善を尽くしたとき、勝つのはどちらでしょう?

【解法】
この問題はとても有名で、必勝法も有名です。
- $K$ が $4$ の倍数のとき、後手必勝
- $K$ が $4$ の倍数でないとき、先手必勝
ということが知られています。具体的には、例えば最初に与えられた山に石が $22$ 個あったとします。
- 先手は $22$ 個の山から $2$ 個とって $20$ 個にする ($4$ の倍数にする)
- それ以降、以下を繰り返す:
- 後手が $1$ 個とったなら $3$ 個とる
- 後手が $2$ 個とったなら $2$ 個とる
- 後手が $3$ 個とったなら $1$ 個とる
とすればよいです。こうすることで先手が手番を終えたときの石の個数は、
$20$ 個 -> $16$ 個 -> $12$ 個 -> $8$ 個 -> $4$ 個
となり、残り $4$ 個の状態で後手が何個とったとしても、最後に残り全部の石をとって先手勝ちとなります。
反対に最初の石の個数が $4$ の倍数だった場合には、先手はどう足掻いても、毎回後手に $4$ の倍数にされてしまい、負けてしまいます。
石取りゲームのグラフの探索
上の議論では石取りゲームの必勝法を天下りに与えましたが、もう少しシステマティックに解析してみましょう。ゲーム解析の基本思想は
勝敗が決している局面から出発して、後ろから遡るようにして解析する
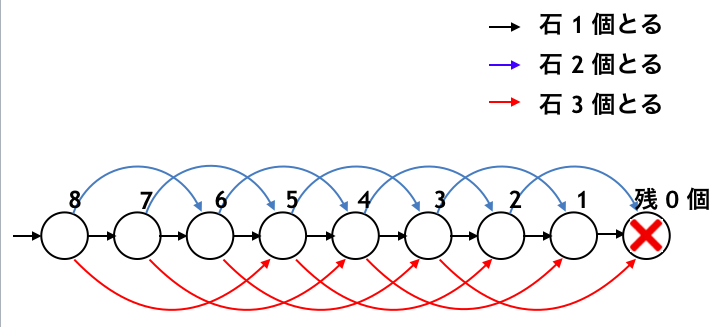
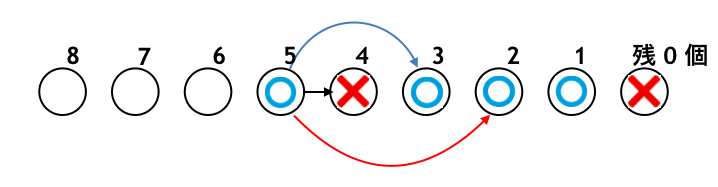
です。例えば石取りゲームの探索グラフは下図のようになっています。石残り $0$ 個の状態を「×」と書いていますが、石が $0$ の状態で手番が回っていたら何もできずに負けなので「×」と記しています4。注意点として、ここでは先手番か後手番かは区別していません。「×」は、先手番であれば先手負け・後手勝ち、後手番であれば後手負け・先手勝ちを表しています。
さて、石が残り $1$ の状態は、残り $0$ 個の状態にすることができて、そうすると「×」を相手に渡せて相手を負けさせることができます。よって石が $1$ 個の状態は「○」になります。ここでも同様に先手番か後手番かの区別をしていません。先手番であれば先手勝ち・後手負け、後手番であれば後手勝ち・先手負けを表しています。
石が残り $2$ 個の場合は「石を残り $1$ 個にする」「石を残り $0$ 個にする」という $2$ 通りの選択肢があります。前者を選んでしまうと相手に「○」を渡してしまい、こちらが負けてしまいます。しかしながら後者を選べば相手に「×」を渡すことができて、こちらが勝つことができます。よって石が $2$ 個の状態も「○」になります。
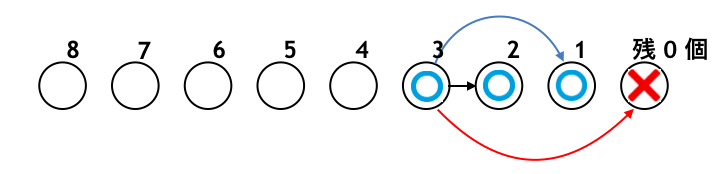
同様に石が $3$ 個の状態からも、石が $0$ 個の状態にすれば「×」を相手に渡せるので勝つことができます。よって「○」です。
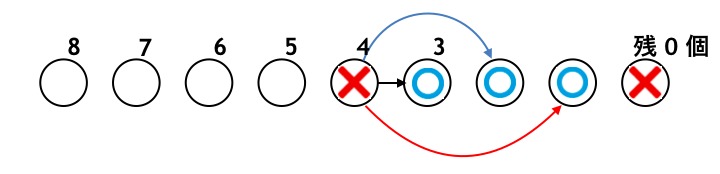
では、石が $4$ 個の場合はどうでしょう。石を「残り $3$ 個にする」「残り $2$ 個にする」「残り $1$ 個にする」という $3$ 通りの選択肢がありますが、いずれも相手に「○」を渡してしまいます。よってどんなに頑張っても相手が必ず勝つこととなり、こちらは負けてしまいます。よって「×」になります。
石が $5$ 個の場合は「石を 1 個とる」とすることで相手に「×」を渡して勝てるので「○」になります。
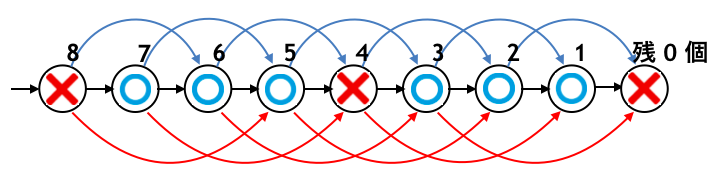
以後同様に解析を進めて行くと下図のようになり、結局
- 残り $4$ の倍数のとき: 「×」
- 残りがそれ以外のとき: 「○」
と求めることができました。
このように勝ち負けがすでに決まっている局面を元にして
- 遷移先に「×」が存在するならば、「○」
- 任意の遷移先が「○」ならば、「×」
という処理を繰り返して行くことで、すべての局面の勝敗を求めることができます。なお、この石取りゲームを例にとった解析では、基本的にどの局面においても先手と後手とで取りうる選択肢がまったく同一でした。このようなゲームを不偏ゲームと呼びます。オセロなどは非不偏ゲームの例です。非不偏の場合には局面の勝敗を決定する上で「先手と後手のどちらが手番か」という情報も必要になります。
次章にて、石取りゲームを一般化したゲームについて、実際に完全解析するプログラムを実装してみます。
3. 単純なゲーム探索の実装 〜 EDPC K, L 問題を題材に 〜
簡単なゲームについて、ゲームを実際に解くプログラムを書いてみましょう!
例題 2. EDPC K 問題 - Stones 〜 石取りゲームの一般化 〜
まずは石取りゲームを一般化した問題です。この問題は、AtCoder 上のジャッジサーバーにソースコードを提出すると、正しくプログラムが書けているかどうかをジャッジしてくれます。
問題概要
$N$ 個の正整数 $a_1, a_2, \dots, a_N$ が与えられます。
$K$ 個の石が山になっていて、先手と後手が交互に
- 山から $a_1, a_2, \dots, a_N$ のいずれかの個数の石をとる
を繰り返します。ただし、山に残っている石の個数より多くの個数の石をとることはできません。先に山から石がとれなくなった方の負け (最後の石をとった方が勝ち) です。先手と後手がお互いに最善を尽くしたとき、勝つのはどちらでしょう?
入力ケースの制約
- $1 \le N \le 100$
- $1 \le K \le 10^{5}$
- $1 \le a_1 < a_2 < \dots < a_N <= K$
解法
先ほどの石取りゲームは $a$ = {$1, 2, 3$} の場合に相当しますね。一般の場合になっても再帰関数を用いることで解析することができます。
このゲームの探索領域の広さを見積もってみましょう。山は初期状態は $K$ 個で、それより増えることはありません。したがって探索が必要な局面数は多くても $K+1$ 個 (石の個数が $0, 1, 2, \dots, K$ 個の場合) です。この程度なら全部探索し尽くせそうです。
「勝敗が決している局面を元にして、遡るように順々に新たな局面の勝敗を決定していく」という営みを実行してみます。以下のように局面の勝敗をメモする配列を用意しましょう。配列名 dp は動的計画法を表す Dynamic Programming の略です。
- ${\rm dp[i]}$ := 石の個数が残り $i$ 個の局面が勝ちか負けかを bool 値で表したもの
としてみます。まず明らかに勝敗が決している部分として
- ${\rm dp[0] = false}$
となります。残り $0$ 個では何も手を打てないので「負け」となります。ここから数学的帰納法的な発想をして、${\rm dp[0], dp[1], \dots, dp[i-1]}$ の値が確定しているという仮定のもとで、${\rm dp[i]}$ の値を考えてみます。すでに見た通り
-
石の個数が ${\rm i}$ 個の状態から遷移できる ${\rm dp[i} - a_1], {\rm dp[i} - a_2], \dots, {\rm dp[i} - a_N]$ のうち、負けの局面が存在したならば、それを相手に押し付けてこちらが勝ち
-
存在しなかったならば、どうやってもこちらの負け
となります。実装上は
- ${\rm dp}$ 配列全体を false で初期化しておく
- ${\rm i} = 1, 2, \dots, K$ の順に ${\rm dp[i]}$ |= ${\rm !dp[i} - a_j]$ ($j = 1, 2, \dots, N$) で表される更新を行う
とすればよいでしょう。以下のようにすごくシンプルに書けます。
#include <iostream>
#include <vector>
using namespace std;
// DP テーブル (配列全体が false に自然に初期化される)
bool dp[110000]; // 局面数は最大 100001 だが少し余裕もたせる
int main() {
// 入力受け取り
int N, K; cin >> N >> K;
vector<int> a(N);
for (int i = 0; i < N; ++i) cin >> a[i];
// DP
for (int i = 1; i <= K; ++i) {
for (int j = 0; j < N; ++j) {
if (i - a[j] >= 0) dp[i] |= !dp[i - a[j]];
}
}
// 答え
if (dp[K]) cout << "First" << endl;
else cout << "Second" << endl;
}
例題 3. EDPC L 問題 - Deque 〜 得点差も最大化したい 〜
次に、単に勝ち負けを決めるだけでなく、相手との得点差も最大化する問題を考えてみましょう。考え方はほんの少し修正するだけでよいです。
多くのゲームが、自分の総得点を $X$、相手の総得点を $Y$ としたとき
- 自分は、$X - Y$ を最大にしたい
- 相手は、$X - Y$ を最小にしたい
という構造を持っています5。自分を太郎君、相手を次郎君と呼ぶとき、
-
太郎君の手番では、次の一手のうち、「その後終局まで双方最善を尽くしたときの $X - Y$」 + 「その一手のスコア」が最大となるものを選ぶ
-
次郎君の手番では、次の一手のうち、「その後終局まで双方最善を尽くしたときの $X - Y$」 - 「その一手のスコア」が最小となるものを選ぶ
とすればよいだけです。このような探索手法は min-max 法と呼ばれることが多いです。ここで次郎君側の「その一手のスコア」は $Y$ の増加を意味していて、つまり $X - Y$ の値が減少することを意味するので「-」をつけています。
問題概要
$N$ 要素の数列 $a_1, a_2, \dots, a_N$ を使って勝負します!
数列が空になるまで
- 先頭要素を取り除いて、その要素の得点を得る
- 末尾要素を取り除いて、その要素の得点を得る
のいずれかを交互に繰り返します。ゲーム終了時の先手の総得点を $X$、後手の総得点を $Y$ としたとき、先手は $X-Y$ を最大化しようとしていて、後手は $X-Y$ を最小化しようとしています。双方最善を尽くしたときの、$X-Y$ の値を求めてください。
入力ケースの制約
- $1 \le N \le 3000$
- $1 \le a_i \le 10^9$
例
- $N = 4$
- $a = (10, 80, 90, 30)$
このとき、
- 先手: $(10, 80, 90, 30) → (10, 80, 90)$
- 後手: $(10, 80, 90) → (10, 80)$
- 先手: $(10, 80) → (10)$
- 後手: $(10) → ()$
とするのが最善で、$X=30+80=110, Y=90+10=100$ となります。よって答えは $10$ です。
解法
この手のゲームを力技探索で解く場合は、やることはルーチン化していています。問題に応じて考えるべきことは
- ありうる局面の列挙
- 局面間の遷移を列挙
だけです。今回のありうる局面は、常に「元の数列から連続した区間を抜き取ったもの」になることがわかります。このことを生かして、改めて DP テーブルを
- ${\rm dp[i][j]}$ := 元の数列から連続する区間 $a_i, a_{i+1}, \dots, a_{j-1}$ を抜き出した状態の局面から出発して、双方最善を尽くしたときの $X - Y$ の値
としてあげます。注意点として区間の取り方は「左側が閉区間で右側が開区間」という取り方をしています。つまり区間 $[i, j)$ であって $i$ は含むが $j$ は含まないようにしています。これは世の中のライブラリで一般的な取り方です。
また本来であれば、DP テーブルにおいて「手番が先手か後手か」の情報も持たせたいところです。なぜなら先手と後手とで $X-Y$ を最大にしたいのか最小にしたいのかが変わって来るからです。しかし今回は $j - i$ の値が「石の残り個数」を表していて、
- $N - (j - i) = 0, 2, 4, \dots$ のときは先手番
- $N - (j - i) = 1, 3, 5, \dots$ のときは後手番
ということが自然にわかるので大丈夫です。さて DP の初期条件は
- ${\rm dp[i][i] = 0}$ (数列が残っていなくて終局した状態です)
とすればよいでしょう。ありうる遷移としては
- 左側をとる: 区間 ${\rm [i+1, j)}$ に遷移
- 右側をとる: 区間 ${\rm [i, j-1)}$ に遷移
の二通りがあります。DP テーブルの数値が決まっていく順序に注意します。
- 区間幅 ${\rm len = j - i}$ が $0$ の場合が終局条件 (上の ${\rm dp[i][i] = 0}$)
- 区間幅 ${\rm len = j - i}$ が $1$ の場合が次に決まる (数列が残り $1$ 個)
- 区間幅 ${\rm len = j - i}$ が $2$ の場合が次に決まる (数列が残り $2$ 個)
- ...
という順番で DP 値が決まって行きます。ここまでわかると実装は結構シンプルになります。
#include <iostream>
#include <vector>
using namespace std;
// DP テーブル
long long dp[3100][3100];
int main() {
// 入力受け取り
int N; cin >> N;
vector<int> a(N);
for (int i = 0; i < N; ++i) cin >> a[i];
// 初期条件
for (int i = 0; i < N; ++i) dp[i][i] = 0;
// DP
for (int len = 1; len <= N; ++len) {
for (int i = 0; i + len <= N; ++i) {
int j = i + len;
// 先手番
if ((N - len) % 2 == 0)
dp[i][j] = max(dp[i + 1][j] + a[i], dp[i][j - 1] + a[j - 1]);
// 後手番
else
dp[i][j] = min(dp[i + 1][j] - a[i], dp[i][j - 1] - a[j - 1]);
}
}
// 答え
cout << dp[0][N] << endl;
}
4. 後退解析: サイクルによる引き分けのあるゲーム
4-1. 後退解析の考え方
ここまで、ゲームの局面がサイクルしないものだけを考えて来ました。そのようなゲームではすべての局面について「勝ち」か「負け」かが決まります (得点差を競うゲームでは「引き分け」もありえます)。
一方、将棋のようにサイクルすると話が少しややこしくなります。そのようなゲームでは無限に同じことを繰り返してしまうことがないように
- 同一局面が $k$ 回あらわれたら引き分け
という規定を設けていることが多いです。これによって二人零和有限確定完全情報ゲームでいうところの「有限性」が担保されることとなります。ゲームの局面に「勝ち」と「負け」だけでなく「引き分け」が新たに加わりました。このようなゲームでは後退解析と呼ばれる手法が有効です6。
アイディアはとてもシンプルで今までは
- 相手に「負け」の局面を渡せるような手を選べる局面は「勝ち」
- どの手を選んでも相手に「勝ち」の局面を渡してしまうような局面は「負け」
としていましたが、これに
- そのどちらでもない局面は「引き分け」
とするだけです!!!!!!!!
順を追って見てみます。以下のような局面遷移図をもつゲームを考えてみましょう。まず「次に遷移するところのない頂点」は「負け」が確定しているので「×」を描いています。
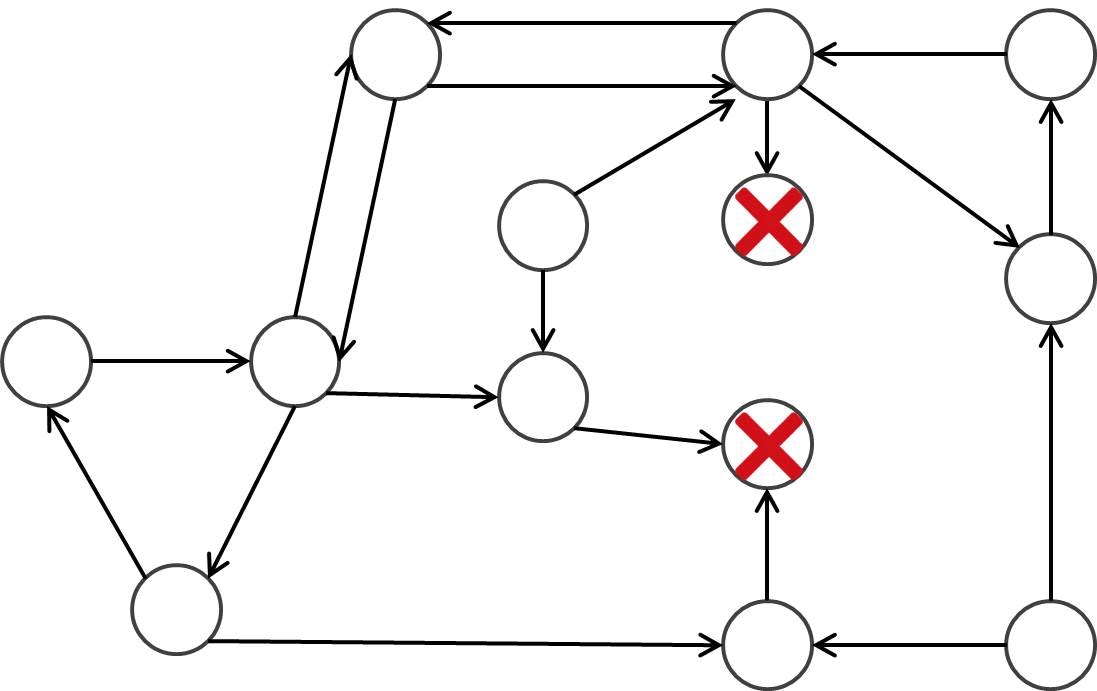
まず「×」へと進める局面は「○」が確定して...

行き先がすべて「○」になっている局面は「×」が確定して... (このとき、行き先の中に「○」か「×」かわからないようなものがある場合は放置します)

この調子で続けていくと、以下のようになります。

ここで残った頂点はいずれも
- そこから「×」には行けない
- 行き先の中に「残った頂点」がある
という性質をもっています。残った頂点は実は「引き分け」になります。なぜなら、「残った頂点」から移動できるのは「○」か「残った頂点」のどちらかですが、「○」に移動すると相手が勝ってしまうため「残った頂点」へと移動させることになります。
相手も同じことを行うため、「残った頂点」から「残った頂点」への移動を繰り返しているうちは負けることはありません。一方そうすると、「残った頂点」から「×」へ移動させるようなことは、永遠にできないことがわかります。
よって永遠に「残った頂点」から「残った頂点」への移動を繰り返すことになります。勝てないですが負けない戦略です。将棋の場合は同一局面が $4$ 回登場したら千日手 (引き分け) になります。

このような「残った頂点」の勝敗に関する取り扱いに関しては、ゲームによって様々でしょう。
4-2. 後退解析の実装
後退解析の実装には std::queue を使うと簡明です。ここで各頂点 $v$ から出ている辺の本数のことを、頂点 $v$ の出次数とよび、${\rm deg}[v]$ と表すこととします。また
- ${\rm dp}[v] = 1$ (勝ち)、$0$ (負け)、$-1$ (未確定)
とします。このとき、キューを用いて後退解析は以下のように実装できるでしょう。
Q をキューとする
dp テーブル全体を -1 に初期化する
for each 各ノード v do
if deg[v] == 0 then
dp[v] = 0
v を Q に push
while Q が空ではない do
Q からノード v を pop して取り出す
for each v を終点とする辺 e とその始点のノード nv do
if nv はすでに訪れたノード then
continue
辺 e をグラフから削除 (実装上は deg[nv] の値を減らせば OK)
if dp[v] = 0 then
dp[nv] = 1
nv を Q に push
else if dp[v] = 1 then
if deg[nv] = 0 then (辺を削除して行ったことで出次数が 0 になったら負けノード確定です)
dp[nv] = 0
nv を Q に push
グラフを葉から順番に削り落としていくイメージですね。葉を削ることでまた新たな葉が生まれ、それを削ることでまた新たな葉が生まれ...を繰り返していく感じです。実際にはグラフから辺を削除するのを愚直に実装するのではなく、各頂点 $v$ の出次数 ${\rm deg}[v]$ を減らしていけばいいです。
4-3. 後退解析の使い所
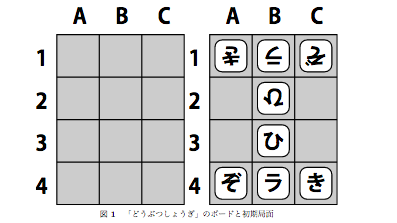
後退解析がゲーム解析に有効に用いられた例として、どうぶつしょうぎがあります。
小さな子供たちや初心者にも楽しめるようにしたにミニ将棋ですね。通常の将棋と同様、同一局面の繰り返しがあるので、後退解析的な処理が必要になります。具体的な解析の様子を記述した論文があります:
どうぶつしょうぎに関する有用の知見も含まれていて、とても面白いです (下図は論文より引用)。
また、後退解析的な queue の使い方はゲームの解析のみならず、様々な有向グラフの解析に有効なケースも多々あります。プログラミングコンテストにおいても以下のような出題例があります:
- キューを用いたトポロジカルソート
- AOJ 2891 な◯りカット (AUPC 2018 day3 C)
- AtCoder AGC 027 C - ABland Yard
- AtCoder ARC 038 D - 有向グラフと数
- Codeforces Manthan Codefest 18 E - Trips
次節で、このうちの「AtCoder ARC 038 D - 有向グラフと数」を解いてみます。
例題 4. AtCoder ARC 038 D - 有向グラフと数
後退解析を用いる例題を解いてみます。少し難しめです。
問題概要
$N$ 頂点 $M$ 辺の有向グラフが与えられる。各頂点 $v$ には値 $X_v$ が割り振られている。先手と後手とで以下の対戦を行う
- スタート時には駒を頂点 $1$ に置く
- 各プレイヤーは各ターンにおいて
- 駒をどこかに移動させる (グラフの辺に沿って)
- ゲームを終了宣言する
- 双方ともに終了宣言しないまま後手が $10^9$ 回目のプレイをしたならばその時点でゲームは強制終了する
ゲームを終了宣言された時点での駒の置いてあるノードの値 $X$ がこのゲームにおける得点となる。先手は得点を最大化したくて、後手は得点を最小化したい。双方最善を尽くしたときの得点を求めよ。
入力ケースの制約
- $1 \le N \le 10^5$
- $1 \le M \le 2 × 10^5$
解法
判定問題にして解くことを考えます。つまり
与えられた値 $D$ に対して、得点が $D$ 以上で終えることができるか
という問題を考えます。$D$ 以上にできるならば先手勝ち、できないならば後手勝ちということになります。そしてこの答えが Yes となるような $D$ の値の最大値を二分探索で求めます。それがこの問題の答えです。
さて、まずはこのゲームのグラフがどのようになるかですが、
- 駒がどのノードにあるか
- 先手番か後手番か
に応じて $2N$ 個の局面があることがわかります ($N$ 個として扱う方法もあるようです)。ここでは
- 先手がノード $i$ ($i = 0, 1, \dots, N-1$) にいる状態: $i$
- 後手がノード $i$ ($i = 0, 1, \dots, N-1$) にいる状態: $i + N$
で表すことにします。また $v = 0, 1, \dots, 2N-1$ に対して
- ${\rm dp}[v]$ = ノード $v$ の状態でその手番の人が勝つときは $1$、負けるときは $0$、未確定は $-1$
とします。まずゲームの勝敗が予め明らかな部分を列挙します。
- 値 $X_v$ が $D$ 以上で先手番: そのまま「先手勝ち」で ${\rm dp}[v] = 1$ です
- 値 $X_v$ が $D$ 未満で先手番で ${\rm deg}[v] = 0$: 「先手負け」で ${\rm dp}[v] = 0$ です
- 値 $X_v$ が $D$ 未満で後手番: そのまま「後手勝ち」で ${\rm dp}[v] = 1$ です
- 値 $X_v$ が $D$ 以上で後手番で ${\rm deg}[v] = 0$: 「後手負け」で ${\rm dp}[v] = 0$ です
そしてここから後退解析をして行きます。なお退解析を終えたとき、「引き分け」ノードの扱いについては、$10^9$ 回後の後手の移動の直後にゲーム強制終了となることから結果として後手勝ちになります。
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// グラフの頂点数、辺数、各ノードの重み
int N, M;
vector<int> X;
// ゲームグラフ (後退解析のために辺の向きを逆にする)
vector<vector<int> > G;
vector<int> deg; // ゲームグラフにおける出次数 (辺の向きを逆にした状態で入次数)
// 二分探索判定 (D 以上にできるかどうか)
bool judge(int D) {
vector<int> cdeg = deg;
queue<int> que; // キュー
vector<int> dp(N * 2, -1); // 最初は全体を -1 で初期化
// 初期条件
for (int i = 0; i < N; ++i) {
if (X[i] >= D) {
dp[i] = 1; // 先手勝ち
que.push(i);
if (cdeg[i] == 0) {
dp[i + N] = 0; // 後手負け
que.push(i + N);
}
}
else {
dp[i + N] = 1; // 後手勝ち
que.push(i + N);
if (cdeg[i] == 0) {
dp[i] = 0; // 先手負け
que.push(i);
}
}
}
// 後退解析 (ここは自動的に書ける)
while (!que.empty()) {
int v = que.front(); que.pop();
for (auto nv : G[v]) {
// すでに見た頂点はスルー
if (dp[nv] != -1) continue;
--cdeg[nv]; // 辺 (nv, v) を削除
if (dp[v] == 0) {
dp[nv] = 1;
que.push(nv);
}
else if (dp[v] == 1) {
if (cdeg[nv] == 0) {
dp[nv] = 0;
que.push(nv);
}
}
}
}
// ノード 0 が先手番で勝ちかどうか
return (dp[0] == 1);
}
int main() {
// 入力
cin >> N >> M;
X.resize(N*2);
for (int i = 0; i < N; ++i) cin >> X[i];
for (int i = 0; i < N; ++i) X[i+N] = X[i];
G.assign(N*2, vector<int>());
deg.assign(N*2, 0);
for (int i = 0; i < M; ++i) {
int a, b; cin >> a >> b; --a, --b;
G[b + N].push_back(a); // 後手番での後退遷移
G[b].push_back(a + N); // 先手番での後退遷移
deg[a]++; deg[a + N]++;
}
// 二分探索
int low = 0, high = 1000000007; // low: 絶対先手勝つ、high: 絶対先手負ける
while (high - low > 1) {
int mid = (low + high) / 2;
if (!judge(mid)) high = mid;
else low = mid;
}
cout << low << endl;
}
5. 発展的話題
今回の記事ではゲーム探索の考え方を紹介しましたが、組合せゲーム理論にはさらにずっと深淵な理論が続いています。その一端を簡単に紹介してみます。
5-1. α-β 探索法
例題 3. EDPC L 問題 - Deque にて、ゲーム探索の基本手法である min-max 法を紹介しましたが、これを高速化したものが α-β 探索法です。基本的には、min-max 法をベースにしていますが、
探索の必要がないことが確定した部分を枝刈りする
というアイディアを実現したものです。基本的には分枝限定法と同様の枝刈りを行っています。
5-2. Nim
石取りゲームの山が複数個になったバージョンを考えてみます。
- 山が $N$ 個あって、それぞれ初期状態で $a_1, a_2, \dots, a_N$ 個の石が積まれている
- 先手と後手は交互に、好きな山を一つ選んで、好きな個数の石を取り去る
先に石をとれなくなった方の負けです。先手と後手のどちらが勝つでしょうか?
これをゲーム探索のフレームワークで解こうとすると、ありうる局面数が
$(a_1 + 1)(a_2 + 1) \dots (a_N + 1)$
となって大変なことになってしまいます。しかし実はこのゲームは数学的に鮮やかに解かれていて
- $a_1 {\rm XOR} a_2 {\rm XOR} \dots {\rm XOR} a_N = 0$ のとき、後手必勝
- そうでないとき、先手必勝
であることが知られています。この答えさえ知っていれば、証明は意外と簡単なので是非チャレンジしてみてください。
5-3. Grundy 数
一見すると、Nim はすごく特殊なゲームに見えるかもしれません。複数山の石取りゲームという特殊な問題をたまたま鮮やかに解けただけに見えるかもしれません。しかし Nim の発想を多くのゲームに適用できるようにした理論があります。Grundy 数を学ぶと、Nim が組合せゲーム理論の基本をなす重要なゲームであることが実感できます。
興味のある方は是非「石取りゲームの数学」を読んでみてください。とても面白いです。
6. おわりに
ネットなどではしばしば「将棋に必勝法はあるのか」「将棋はいつか完全に解かれてしまうのではないか」といった議論を見かけます。実際は探索空間があまりにも膨大で、現在のところ完全解析の目処はまったく立っていない状態と言えます。しかし一方では「原理的には先手必勝か後手必勝か決まっているはず」と随所で言及されることについて、その原理を理解することは有益だと思います。
さて、基本的なゲーム探索手法の習得の後に続いていく世界としては、
- ゲームに限らず、探索法そのものを深く深く追求していく世界
- ゲームそのもののもつ構造を深く深く追求していく世界
とがあるでしょう。どちらもすごく面白そうです。
7. 参考資料
参考になる資料を挙げていきます。
各種ゲームの完全解析
各種ボードゲームを完全解析した旨の報告たちを挙げます:
[1] Janos Wagner and Istvan Virag: Solving renju, ICGA Journal, Vol.24, No.1, pp.30-35 (2001), http://www.sze.hu/~gtakacs/download/wagnervirag_2001.pdf
[2] Martin Muller, Robert Lake, Paul Lu, and Steve Suphen: Checkers is solved, Science Vol.317, No,5844, pp.1518-1522 (2007), http://www.sciencemag.org/content/317/5844/1518.full.pdf
[3] Joel Feinstein: Amenor Wins World 6x6 Championships!, Forty billion noted under the tree, pp.6-8, British OthelloFederation's newsletter., (1993), http://www.britishothello.org.uk/fbnall.pdf
[4] 清慎一, 川嶋俊: 探索プログラムによる四路盤囲碁の解, 研究報告ゲーム情報学(GI), Vol. 2000-GI-004, pp.69-76, 情報処理学会, (2000), http://id.nii.ac.jp/1001/00058633/
[5] Eric C.D. van der Welf, H.Jaap van den Herik, and Jos W.H.M.Uiterwijk: Solving Go on Small Boards, ICGA Journal, Vol.26, No.2, pp.92-107 (2003).
[6] 田中哲郎: 「どうぶつしょうぎ」の完全解析, 情報処理学会研究報告, Vol.2009-GI-22 No.3, pp.1-8, (2009), http://id.nii.ac.jp/1001/00062415/
[7] 塩田好, 石水隆, 山本博史: 「アンパンマンはじめてしょうぎ」の完全解析, 2013年度 情報処理学会関西支部 支部大会 講演論文集, (2013), http://id.nii.ac.jp/1001/00096792/
組合せゲーム理論の参考書
組合せゲーム理論を学ぶことのできる参考書たちです。
本格的な組合せゲーム理論の入門書です。
Nim や Grundy 数から始まる組合せゲーム理論の物語です。
-
初期盤面の勝敗のみがわかることを超弱解決、初期盤面の勝敗がわかっていてそれを証明するのに必要な各局面の最善手もわかることを弱解決、すべての局面について勝敗も最善手もわかることを強解決と呼んで区別することもあります。 ↩
-
厳密には将棋というゲームは現在「勝ちか負けか引き分けかがルール上曖昧な局面」が存在することがわかっており (「最後の審判」を参照)、それが曖昧なままだと初期盤面において先手必勝かどうかは判断できないかもしれません。 ↩
-
基本定理の主張には「引き分け」を含むゲームについては含めないことも多いです。 ↩
-
石を残り $0$ 個にして相手に手番を回せば勝ちという理由から、これを「○」にする考え方もあります。どちらの考え方をしているのかを混乱しないようにすることが肝要です。 ↩
-
言い換えると、自分は $X - Y$を最大にしたくて、相手は $Y - X$ を最大にしたいです。これらを合計すると $0$ になっています。これが二人零和有限確定完全情報ゲームで言うところの「零和」の意味です。 ↩
-
今までのも解析も後退解析の一種ではあるのですが、特に引き分け局面も含む場合に後退解析と呼ぶことが多いです。 ↩