目次
からの続きです!!
前編
後編 (いまここ)
4. グラフ上の様々な例題
いよいよ、深さ優先探索 (DFS) を用いて、グラフに関する様々な問題を解いてみましょう。グラフの連結性に関する問題の多くが、単純な探索によって解決できることがわかります。
そしてグラフ探索はとにかく「習うより慣れろ」の精神が重要なテーマでもあります。本記事では、グラフの連結性に関する諸概念に親しみながら、探索にも慣れるという一石二鳥を狙います。なお、ここで取り上げる問題のほとんどは DFS だけでなく BFS で解くこともできます。BFS を用いた解法については別途記事にしたいと思います。
4-1. s から t へ辿り着けるか
まずは手始めに有向グラフ $G$ の二頂点 $s, t \in V$ が与えられたとき、$s$ から辺をたどって $t$ に到達できるかどうかを判定する問題を考えてみましょう。
これは単純に、$s$ を始点とした DFS を実施してあげればよいです。DFS 実施後において seen 配列を見ることで、各頂点が探索されたかどうかを判定することができます。特に seen[t] を見ることで頂点 $t$ に到達できるかどうかを判定することができます。
# include <iostream>
# include <vector>
using namespace std;
using Graph = vector<vector<int>>;
// 深さ優先探索
vector<bool> seen;
void dfs(const Graph &G, int v) {
seen[v] = true; // v を訪問済にする
// v から行ける各頂点 next_v について
for (auto next_v : G[v]) {
if (seen[next_v]) continue; // next_v が探索済だったらスルー
dfs(G, next_v); // 再帰的に探索
}
}
int main() {
// 頂点数と辺数、s と t
int N, M, s, t; cin >> N >> M >> s >> t;
// グラフ入力受取
Graph G(N);
for (int i = 0; i < M; ++i) {
int a, b;
cin >> a >> b;
G[a].push_back(b);
}
// 頂点 s をスタートとした探索
seen.assign(N, false); // 全頂点を「未訪問」に初期化
dfs(G, s);
// t に辿り着けるかどうか
if (seen[t]) cout << "Yes" << endl;
else cout << "No" << endl;
}
グリッドグラフの場合
「頂点 $s$ から頂点 $t$ へ辿り着けるか問題」について、今後は下のような二次元グリッドについて解いてみましょう。入力形式としては
- 最初の一行目は盤面のサイズ
- '.' は通路を表す
- '#' は壁を表す (壁マスには進めない)
- 's' はスタート地点
- 'g' はゴール地点
とします。's' から出発して、上下左右に移動しながら通路マスのみを通って 'g' へ辿り着けるかどうかを判定します (下の例では "Yes" になります)。なおこの問題は以下のページでジャッジすることができます。
10 10
s.........
######### .
# .......#.
# ..####.#.
## ....#.#.
##### .#.#.
g.#.#.#.#.
# .#.#.#.#.
# .#.#.#.#.
# .....#...
グリッドグラフ形式になっても DFS の実装は大きくは変わりません。頂点 $v$ に対応するものとしては「$i$ 行目, $j$ 列目のマス」といった具合になります。またグリッド上の探索に特有なこととして、以下のような上下左右への移動を表す配列を予め用意しておくと楽です。
const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, 1, 0, -1};
# include <iostream>
# include <vector>
# include <string>
# include <cstring>
using namespace std;
// 四方向への移動ベクトル
const int dx[4] = {1, 0, -1, 0};
const int dy[4] = {0, 1, 0, -1};
// 入力
int H, W;
vector<string> field;
// 探索
bool seen[510][510]; // seen[h][w] := マス (h, w) が検知済みかどうか
void dfs(int h, int w) {
seen[h][w] = true;
// 四方向を探索
for (int dir = 0; dir < 4; ++dir) {
int nh = h + dx[dir];
int nw = w + dy[dir];
// 場外アウトしたり、移動先が壁の場合はスルー
if (nh < 0 || nh >= H || nw < 0 || nw >= W) continue;
if (field[nh][nw] == '#') continue;
// 移動先が探索済みの場合
if (seen[nh][nw]) continue;
// 再帰的に探索
dfs(nh, nw);
}
}
int main() {
// 入力受け取り
cin >> H >> W;
field.resize(H);
for (int h = 0; h < H; ++h) cin >> field[h];
// s と g のマスを特定する
int sh, sw, gh, gw;
for (int h = 0; h < H; ++h) {
for (int w = 0; w < W; ++w) {
if (field[h][w] == 's') sh = h, sw = w;
if (field[h][w] == 'g') gh = h, gw = w;
}
}
// 探索開始
memset(seen, 0, sizeof(seen)); // seen 配列全体を false に初期化
dfs(sh, sw);
// 結果
if (seen[gh][gw]) cout << "Yes" << endl;
else cout << "No" << endl;
}
4-2. 連結成分の個数
次に連結とは限らない無向グラフが与えられたとき、それが何個の連結成分からなるのかを数える問題を考えます1。これもやり方は単純で
- まだ探索済みでない頂点 $v$ を一つ選んで $v$ を始点とした DFS を行う
というのを、全頂点が探索済みの状態になるまで繰り返せばよいです。これは 「3-5. DFS の計算量」にて、DFS の計算量を解析したときの設定でもあります。実装上は
for (int v = 0; v < N; ++v) {
if (seen[v]) continue;
dfs(G, v); // v が未探索なら v を始点とした DFS を行う
}
という風にしてあげることで、最終的に全頂点が訪問済みの状態にすることができます。
# include <iostream>
# include <vector>
using namespace std;
using Graph = vector<vector<int>>;
// 深さ優先探索
vector<bool> seen;
void dfs(const Graph &G, int v) {
seen[v] = true;
for (auto next_v : G[v]) {
if (seen[next_v]) continue;
dfs(G, next_v); // 再帰的に探索
}
}
int main() {
// 頂点数と辺数
int N, M; cin >> N >> M;
// グラフ入力受取
Graph G(N);
for (int i = 0; i < M; ++i) {
int a, b;
cin >> a >> b;
G[a].push_back(b);
G[b].push_back(a);
}
// 全頂点が訪問済みになるまで探索
int count = 0;
seen.assign(N, false);
for (int v = 0; v < N; ++v) {
if (seen[v]) continue; // v が探索済みだったらスルー
dfs(G, v); // v が未探索なら v を始点とした DFS を行う
++count;
}
cout << count << endl;
}
グリッドグラフの場合の類題
この問題のグリッドグラフの場合については、蟻本 P.35 に載っている例題「POJ No.2386 - Lake Counting」が有名です。ただしこの例題では、グリッド上のマスの隣接関係は四近傍ではなく八近傍になっていることに注意します。
そしてほぼ全く同じ問題が AOJ にも収録されています。POJ よりはお手軽にジャッジできると思います。
また類題として、「一マスを埋めることが許されているとき、全体を連結にすることができるか」を問う問題が AtCoder で出題されています。
これらの問題は DFS の練習にとてもよいです。ここでは「AOJ 1160 - 島はいくつある?」についての実装例を示します。実装上の工夫として、探索済みのところは「1」を「0」に書き換えてしまうことによって seen 配列の代用としています (蟻本の例題に対する実装も同様の工夫によって seen 配列を不要としています)。
# include <iostream>
# include <vector>
using namespace std;
// 入力
int H, W;
vector<vector<int>> field;
// 探索
void dfs(int h, int w) {
field[h][w] = 0;
// 八方向を探索
for (int dh = -1; dh <= 1; ++dh) {
for (int dw = -1; dw <= 1; ++dw) {
int nh = h + dh, nw = w + dw;
// 場外アウトしたり、0 だったりはスルー
if (nh < 0 || nh >= H || nw < 0 || nw >= W) continue;
if (field[nh][nw] == 0) continue;
// 再帰的に探索
dfs(nh, nw);
}
}
}
int main() {
// 入力受け取り
while (cin >> W >> H) {
if (H == 0 || W == 0) break;
field.assign(H, vector<int>(W, 0));
for (int h = 0; h < H; ++h) for (int w = 0; w < W; ++w) cin >> field[h][w];
// 探索開始
int count = 0;
for (int h = 0; h < H; ++h) {
for (int w = 0; w < W; ++w) {
if (field[h][w] == 0) continue; // 残島じゃなかったらスルー
dfs(h, w);
++count;
}
}
cout << count << endl;
}
}
4-3. 二部グラフ判定
少しずつ面白い応用例に入っていきます。次は与えられた無向グラフが二部グラフ (bipartite graph) かどうかを判定する問題です。二部グラフとは以下の条件を満たすように全頂点を白または黒に塗り分けられるグラフのことです:
- 白頂点同士が辺で結ばれることはなく、黒頂点同士が辺で結ばれることもない
言い換えれば、二部グラフとは下図のように、グラフを左右のカテゴリに分割して、すべての辺は異なるカテゴリ間を結んでいる状態にできることをいいます。
では、与えられた無向グラフ $G$ が二部グラフであるかどうかを判定する問題を考えます。この問題も DFS だけでなく、BFS や Union-Find 木 (頂点倍加テクニックを用います) で解くこともできますが、ここでは DFS を用いた解法を示します。
まず、DFS の始点となる頂点 $v$ については白黒いずれに塗ってもよいです。ここでは白としてみます。そうすると
- 白頂点に隣接した頂点は黒でなければならない
- 黒頂点に隣接した頂点は白でなければならない
といった具合に、各頂点が何色でなければならないかが自動的に決まっていきます。このときもし「ある条件によって黒に決まった頂点が、他の黒頂点と隣接してしまった」といった状況が発生したら、二部グラフではないということになります。
なお以下の実装では、配列 color に各頂点の色を格納しますが、これを seen 配列の役割も同時に持たせることにします。すなわち
- color[v] = 1 (黒確定)、0 (白確定)、-1 (未訪問)
を表すようにします。
# include <iostream>
# include <vector>
using namespace std;
using Graph = vector<vector<int>>;
// 二部グラフ判定
vector<int> color;
bool dfs(const Graph &G, int v, int cur = 0) {
color[v] = cur;
for (auto next_v : G[v]) {
// 隣接頂点がすでに色確定していた場合
if (color[next_v] != -1) {
if (color[next_v] == cur) return false; // 同じ色が隣接したらダメ
continue;
}
// 隣接頂点の色を変えて、再帰的に探索 (一回でも false が返ってきたら false)
if (!dfs(G, next_v , 1 - cur)) return false;
}
return true;
}
int main() {
// 頂点数と辺数
int N, M; cin >> N >> M;
// グラフ入力受取
Graph G(N);
for (int i = 0; i < M; ++i) {
int a, b;
cin >> a >> b;
G[a].push_back(b);
G[b].push_back(a);
}
// 探索
color.assign(N, -1);
bool is_bipartite = true;
for (int v = 0; v < N; ++v) {
if (color[v] != -1) continue; // v が探索済みだったらスルー
if (!dfs(G, v)) is_bipartite = false;
}
if (is_bipartite) cout << "Yes" << endl;
else cout << "No" << endl;
}
類題
類題としては以下の問題があります。
- AtCoder ABC 126 D - Even Relation (二部グラフになるように白黒の塗り分けを行う問題です)
- CODE FESTIVAL 2017 qualB C - 3 Steps (よさげな問題です)
4-4. 根のない木の走査
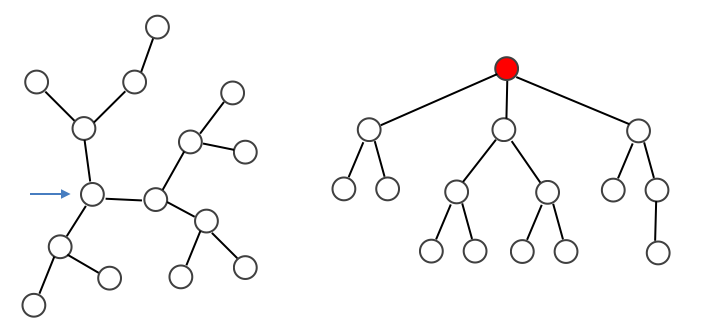
木というと多くの場合、根があって下へ下へと伸びていく根つき木を想起してしまいます。しかしながら木は一般には単に「閉路がない連結なグラフ」を意味するのみであり、特に根が指定されていない場面も多いです。
そこで今回は特に根の指定されていない木に対し、一つ頂点を決めて根にすることでどんな根つき木になるのかを求める問題を考えてみます (下図は左側の木に対して矢印で示した頂点を根とすると、右側に示したような根つき木になることを表しています)。
まず基本的には今まで通りの DFS と同じ実装でよいのですが、木であることを生かして seen 配列をなくすことができます。木上の DFS では
- 頂点 $v$ の隣接頂点 $v'$ を見ていったときに、$v'$ がすでに探索済みである場合というのは、$v'$ が $v$ の親である場合のみ
という特徴があります。すなわち元々 $v$ は $v'$ の子供として $v'$ から来たのに、それを逆流して $v'$ を探索しようとする場合です。

これを防ぐために、木上の DFS ではしばしば下記のような実装をします。木に根を指定してできる根つき木に関する種々の情報は、下記の実装にほんの少し手を加えるだけで求めることができます。
# include <iostream>
# include <vector>
using namespace std;
using Graph = vector<vector<int>>;
// 木上の探索
// v: 現在探索中の頂点、p: v の親 (v が根のときは -1)
void dfs(const Graph &G, int v, int p) {
for (auto nv : G[v]) {
if (nv == p) continue; // nv が親 p だったらダメ
dfs(G, nv, v); // v は新たに nv の親になります
}
}
int main() {
// 頂点数 (木なので辺数は N-1 で確定)
int N; cin >> N;
// グラフ入力受取
Graph G(N);
for (int i = 0; i < N-1; ++i) {
int a, b;
cin >> a >> b;
G[a].push_back(b);
G[b].push_back(a);
}
// 探索
int root = 0; // 仮に頂点 0 を根とする
dfs(G, root, -1);
}
ここでは一例として、与えられた木の頂点 0 を根として指定した根つき木において、
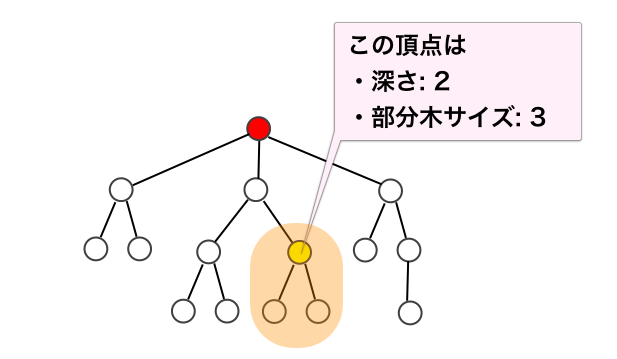
- 各頂点の根からの距離 (深さ (depth) といいます)
- 各頂点を根とした部分木のサイズ (部分木に含まれる頂点数)
をそれぞれ求めてみましょう。
まず深さについては再帰関数の引数に深さの情報を追加することで実現できます。
vector<int> depth;
// d: 頂点 v の深さ
void dfs(const Graph &G, int v, int p, int d) {
depth[v] = d;
for (auto nv : G[v]) {
if (nv == p) continue; // nv が親 p だったらダメ
dfs(G, nv, v, d+1); // d を 1 増やして子ノードへ
}
}
次に頂点 v を根とする部分木のサイズですが、これは以下の式によって求めることができます。最後の「+ 1」はノード v 自身を表しています。
- (v を根とする部分木のサイズ) = (v のそれぞれの子ノード c についての部分木のサイズの総和) + 1
この式は v についての情報を求めるのに、v の子頂点についての情報がすべて求まっている必要があることを意味します。したがってこの処理は帰りがけ時に行うようにするとよいです。詳しい実装は下を見ていただけたらと思います。
なお、このような「子ノードについての情報を用いて、親ノードについての情報を更新する」という処理はしばしば木 DP とよばれます。各頂点についての部分木のサイズを求める問題は、木 DP で解ける最も簡単な一例といえます。
# include <iostream>
# include <vector>
using namespace std;
using Graph = vector<vector<int>>;
// 木上の探索
vector<int> depth;
vector<int> subtree_size;
void dfs(const Graph &G, int v, int p, int d) {
depth[v] = d;
for (auto nv : G[v]) {
if (nv == p) continue; // nv が親 p だったらダメ
dfs(G, nv, v, d+1);
}
// 帰りがけ時に、部分木サイズを求める
subtree_size[v] = 1; // 自分自身
for (auto c : G[v]) {
if (c == p) continue;
subtree_size[v] += subtree_size[c]; // 子のサイズを加える
}
}
int main() {
// 頂点数 (木なので辺数は N-1 で確定)
int N; cin >> N;
// グラフ入力受取
Graph G(N);
for (int i = 0; i < N-1; ++i) {
int a, b;
cin >> a >> b;
G[a].push_back(b);
G[b].push_back(a);
}
// 探索
int root = 0; // 仮に頂点 0 を根とする
depth.assign(N, 0);
subtree_size.assign(N, 0);
dfs(G, root, -1, 0);
// 結果
for (int v = 0; v < N; ++v) {
cout << v << ": depth = " << depth[v] << ", subtree_size = " << subtree_size[v] << endl;
}
}
総じて、
- 各頂点の深さ: 行きがけ順に求めた
- 各頂点を根とした部分木のサイズ: 帰りがけ順に求めた
といえます。このように木上の DFS は、行きがけ順・帰りがけ順を自在に操ることで様々な処理を行うことができます。行きがけ順を意識した処理は「親ノードについての情報を子ノードへと配る」のに適していて、帰りがけ順を意識した処理は「子ノードの情報を集めて親ノードの情報を更新する」のに適しています。
4-5. トポロジカルソート
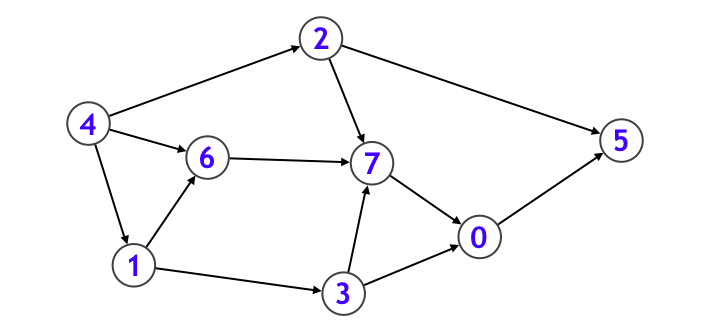
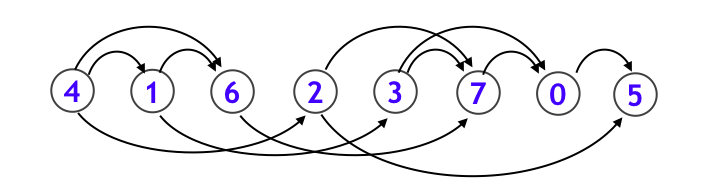
トポロジカルソートとは以下のような DAG (サイクルのない有向グラフ) に対し、
下図のように、各頂点を辺の向きに沿うように一列に並べることです。応用例として makefile などに見られるような、依存関係を解決する処理などは、まさにトポロジカルソートそのものです。
なお、DAG であることと、トポロジカルソート可能であることは同値になります。トポロジカルソートは DFS の帰りがけ順をうまく整理することで求めることができます。詳しくは
の「4-3. DAG のトポロジカルソート」のところを読んでいただけたらと思います。なおトポロジカルソートも DFS だけでなく BFS っぽく実現することもできます。
4-6. サイクル検出
少し難しい話になります。有向グラフまたは無向グラフにおいてサイクルがあるかどうかを判定し、サイクルがある場合は具体的に一つ出力する問題に取り組みます。
- 無向グラフではサイクルのないグラフは森 (木を集めたもの)
- 有向グラフではサイクルのないグラフは DAG (Directed Acyclic Graph)
となります。なお、有向グラフであってサイクルのないグラフのことを DAG とよびます。DAG はすなわち、どの頂点 $v$ から探索を開始しても、二度と $v$ に戻ってくることはないようなグラフであるといえます。下に DAG の一例を示します。
さて、与えられたグラフがサイクルを含むということは、ある頂点 $v$ に対して
- 頂点 $v$ から出発した探索が、$v$ から行くことのできる全頂点の探索を終えるよりも先に (すなわち帰りがけの状態になる前に)、$v$ に戻って来てしまう
という状況が発生すること同値です。これを検知するために seen 以外の新たなデータを用意します:
- seen[v] := 行きがけ順の意味で v が訪問済みであることを表す (帰りがけ順の意味で v が訪問済みかどうかは定かではない)
- finished[v] := 帰りがけ順の意味で v が訪問済みであることを表す
ここで「seen[v] = true && finished[v] = false」の状態で、頂点 v について再帰関数を呼び出したとき、「グラフはサイクルを含み、v はサイクル内の頂点である」ということが確定します。
あとはその v を含むサイクルを復元したいので基本的には v から探索した頂点たちの訪問履歴をもつことにします。しかしながら v から出発して v へと至る過程でサイクルから伸びているサイクル以外の枝葉を通っている可能性もあるため、それは除外したいです。訪問履歴として「行きがけ順訪問時に push して、帰りがけ時には pop するスタック」を用意することで上手くいきます。
複雑に混み入った話になってしまいましたが、実装を見るとなんとなくわかるかと思います。これは「AOJ 2891 - な◯りカット」を解くコードになっています。この問題は意訳すると
- サイクルをただ一つ含むことが保証された無向グラフにおいて
- 「二頂点 $a, b$ がともにそのサイクル上にあるときは 2 を出力して、そうでないときは 1 を出力する」というクエリを大量に答える
という問題です。なお、サイクル検出も DFS だけでなく、BFS っぽく方法で実現することがもできます。
# include <iostream>
# include <vector>
# include <set>
# include <stack>
using namespace std;
using Graph = vector<vector<int>>;
// 探索
vector<bool> seen, finished;
// サイクル復元のための情報
int pos = -1; // サイクル中に含まれる頂点 pos
stack<int> hist; // 訪問履歴
void dfs(const Graph &G, int v, int p) {
seen[v] = true;
hist.push(v);
for (auto nv : G[v]) {
if (nv == p) continue; // 逆流を禁止する
// 完全終了した頂点はスルー
if (finished[nv]) continue;
// サイクルを検出
if (seen[nv] && !finished[nv]) {
pos = nv;
return;
}
// 再帰的に探索
dfs(G, nv, v);
// サイクル検出したならば真っ直ぐに抜けていく
if (pos != -1) return;
}
hist.pop();
finished[v] = true;
}
int main() {
// 頂点数 (サイクルを一つ含むグラフなので辺数は N で確定)
int N; cin >> N;
// グラフ入力受取
Graph G(N);
for (int i = 0; i < N; ++i) {
int a, b;
cin >> a >> b;
--a, --b; // 頂点番号が 1-indexed で与えられるので 0-indexed にする
G[a].push_back(b);
G[b].push_back(a);
}
// 探索
seen.assign(N, false), finished.assign(N, false);
pos = -1;
dfs(G, 0, -1);
// サイクルを復元
set<int> cycle;
while (!hist.empty()) {
int t = hist.top();
cycle.insert(t);
hist.pop();
if (t == pos) break;
}
// クエリに答える
int Q; cin >> Q;
for (int _ = 0; _ < Q; ++_) {
int a, b;
cin >> a >> b;
--a, --b;
if (cycle.count(a) && cycle.count(b)) cout << 2 << endl;
else cout << 1 << endl;
}
}
5. 発展的話題
ここでは深さ優先探索 (DFS) を用いたアルゴリズムのさらなる発展について簡単に紹介します。これらの詳細な解説は他資料に譲り、ここでは他資料へのポインタを示すこととします。
5-1. 動的計画法
グラフ探索の考え方と、動的計画法とは密接な関係にあります。そもそも動的計画法とは、グラフ上の各辺を緩和する考え方が主軸となっています (動的計画法入門記事を参照)。そして DAG においては DFS 再帰関数の帰りがけ時に、キャッシュにメモするという行為を行うだけで動的計画法になります。
5-2. 木の直径
木の場合について考えます。特に、予め根の指定されていない無向グラフを想定します。木は
- 木上の $2$ 頂点 $u, v$ を選ぶと、$u-v$ パスが一意に定まる
- したがって $2$ 頂点 $u, v$ の距離を $u-v$ パスの長さとして定義できる
という特徴をもっていますが、この $2$ 頂点 $u, v$ の距離が最大となるときの $u-v$ パスを木の直径 (diameter) といいます。直径は複数通り考えられることもあります。木の直径は DFS を二回行うことで求めることができます。
- まず木上の点 $w$ を一つ選んで探索を行い、$w$ との距離が最も遠い点 $u$ を求める
- 再び $u$ を始点とした探索を行い、$u$ との距離が最も遠い点 $v$ を求める
とすることで得られる $u-v$ パスが求める直径になります。
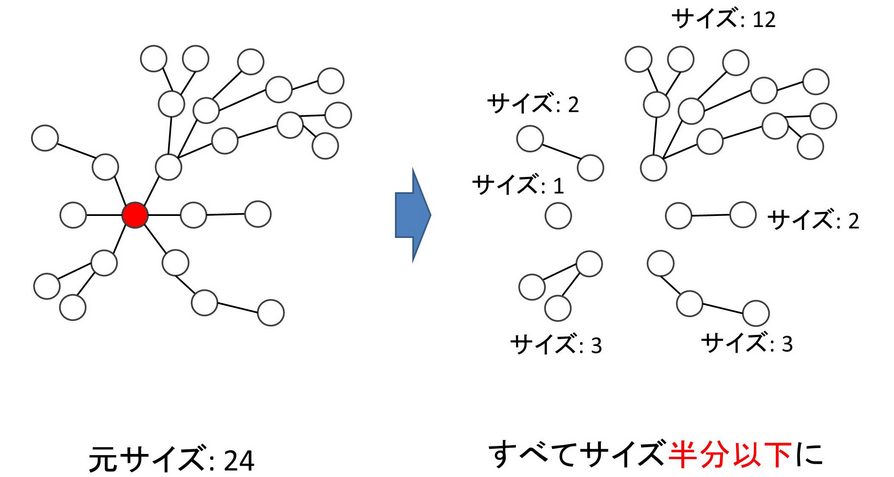
5-3. 木の重心
木の重心とは、その頂点を取り除くことで元の木を複数個の木に分解したとき、その分解された木のすべてについて、サイズが元の木のサイズの半分以下になるような頂点のことをいいます。木の重心は DFS によって自然に求めることができます。詳しくは
を読んでいただけたらと思います。
5-4. オイラー閉路 (一筆書き)
一般のグラフについての話題に戻ります。有向グラフでも無向グラフでもよいですし、多重辺があってもよいですが、連結であるとします。このとき、グラフの各辺をちょうど一回ずつ通る閉路 (オイラー閉路といいます) が存在するかどうか、すなわち与えられたグラフを一筆書きして、最後に始点に戻って来れるようにできるかどうかという有名問題があります。以下の定理が成立します。
連結グラフがオイラー閉路をもつための必要十分条件は、
- 無向グラフの場合は、すべての頂点の次数が偶数であること
- 有向グラフの場合は、すべての頂点の入次数と出次数が等しいこと
である
このうちの必要条件を Euler が示したことがグラフ理論の始まりと言われています。十分条件 (グラフが条件を満たせば実際に一筆書きで一周できること) については DFS によって具体的にオイラー路を構成することで示すことができます。
余談ですが、僕が普段用いているアイコンは、Euler が一筆書きできないことを示したグラフで、ケーニヒスベルクの橋の問題に登場するものです。

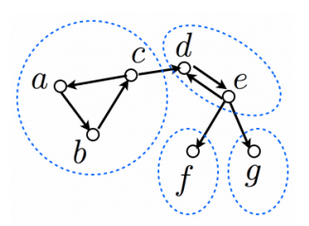
5-5. 強連結成分分解
有向グラフの場合を考えます。下図 (このページから引用) のように、「お互いに行き来できる ⇔ 同じグループ」を満たすように頂点をグループ分けすることを強連結成分分解といいます。
強連結成分分解は二回の DFS を行うことで実現できます。詳しくは
を参照していただけたらと思います。その際には、3-4 節で解説した行きがけ順・帰りがけ順について馴染んでいると、理解しやすいと思います。
5-6. 橋と関節点
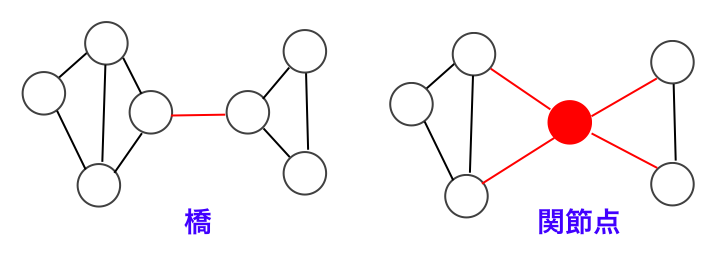
無向グラフの場合を考えます。
橋 (bridge) とは、その辺を取り除くとその辺を含む連結成分が分断するような辺のことをいいます。同様に関節点 (articulation vertex) とは、その頂点およびその頂点に接続している辺を取り除くと、その頂点を含む連結成分が分断するような頂点のことをいいます。
いずれもネットワークの頑健性や脆弱性に関する重要な概念となっています。
橋や関節点は、DFS を用いた low-link と呼ばれるアルゴリズムによって求めることができます。詳しくは
などを参照していただけたらと思います。また、橋や関節点によってグラフ全体を分解することをそれぞれ二重辺連結成分分解・二重頂点連結成分分解と呼びます。
二重辺連結成分分解によって得られた各連結成分は、どの 2 頂点をとってもその間に 2 本の辺素な (互いに辺を共有しない) パスをとることができます2。また二重頂点連結成分分解によって得られた各連結成分は、どの 2 頂点をとってもその間に 2 本の点素な (互いに頂点を共有しない) パスをとることができます。
なお、一般に二頂点 $s, t$ に対して、辺素な $s-t$ パスを $k$ 本とることができて、$k+1$ 本とることはできないとき、$s-t$ 間の辺連結度 (edge-connectivity) は $k$ であるといいます。同様に点素な $s-t$ パスを $k$ 本とることができて、$k+1$ 本とることはできないとき、$s-t$ 間の点連結度 (vertex-connectivity) は $k$ であるといいます。辺連結度も点連結度も、ネットワークの耐故障性を評価する重要な指標となります。
5-7. ネットワークフロー
ネットワークフロー理論は、グラフ理論の中でも非常に美しく深淵な一分野です。それについてもまた別途詳しく記事を書きたいと思います。
ネットワークフロー・アルゴリズムでは頻繁に DFS や BFS をサブルーチンとして用います。ここまで来ると、DFS はグラフ理論の重要な基礎であることが一段と実感できます。
6. おわりに
深さ優先探索 (DFS) は動的計画法 (DP) と並んで、アルゴリズム学習の登竜門となっている印象があります。最初はとっつきにくくイメージが掴みづらいかもしれません。しかしながら「習うより慣れろ」の精神で触れ続けることで、徐々にワカッタ感覚を磨いていける分野でもあります。本記事を通してグラフ探索のイメージを深めていただけたらならば、とても嬉しいです。
7. 参考文献
本記事を書く上で参考にした資料や、今後のさらなる勉強の助けになる資料たちを紹介します。
7-1. アルゴリズム系全般
グラフ理論に限らず、アルゴリズム全般を学べる書籍たちです。
- 杉原厚吉: データ構造とアルゴリズム, 共立出版 (2001).
アルゴリズムを数学的にしっかり勉強するための書籍としては、とても平易かつ簡潔に書かれています。真にわかりやすい説明とは、くどい記述で何とか伝わるようにする説明というよりは、「一言で伝わるような簡潔な説明」だと思います。この書籍はそのような真にわかりやすい説明を体現したものだと言えます。
- 渋谷哲郎: 情報工学 アルゴリズム, 丸善出版 (2016).
各種アルゴリズムについて数学的にしっかりとした記述がなされている書籍です。ページ数の割に扱っている内容が多く、一つ一つのテーマの記述がかなり簡潔ですが、数学書を読むことに慣れている方にとっては読みやすいと思います。
- J. Kleinberg and E. Tardos: Algorithm Design, Pearson/Addison-Wesley (2006). (邦訳: アルゴリズムデザイン)
アルゴリズムの世界的教科書の一つです。多くの書籍では各アルゴリズム自体をわかりやすく説明することのみに終始している中、この書籍では各アルゴリズムの詳細を学ぶだけでなく、実問題を解決するアルゴリズムをいかにして設計するかにまで焦点を当てた名著です。
- T. H. Cormen, C. E. Leiserson, R. L. Rivest and C. Stein: Introduction to Algorithms 3rd ed., MIT Press (2009). (邦訳: アルゴリズムイントロダクション 第3版 総合版)
同じくアルゴリズムの世界的教科書です。アルゴリズムデザインがアルゴリズムの使い方に焦点を当てた本だとすると、アルゴリズムイントロダクションはアルゴリズムの原理に焦点を当てた本だと言えます。直観的には正しいと思えるような様々なアルゴリズムの正当性がきっちりと議論されています。こうしたことをしっかりと学んでおくことは、自力で未知の問題に対するアルゴリズムを開発していく上で大変重要になります。
7-2. アルゴリズムの「実装」も含めて学べる書籍たち
アルゴリズムの「実装」も含めて学べる書籍たち
いわゆるプログラミングコンテストの攻略本と呼べる書籍たちを挙げます。
- 秋葉拓哉, 岩田陽一, 北川宜稔: プログラミングコンテストチャレンジブック [第2版], マイナビ出版 (2012).
プログラミングコンテスト界のバイブル、蟻本です!
6 年前に日本人世界ランカー達によって執筆されて以来、誰もが手にするバイブルとなりました。現在では競技プログラミング用参考書という域を超えて、世界的なアルゴリズムの教科書の 1 つと言える立ち位置までになっています。大きな特長として、洗練された C++ による実装が載っていることが挙げられるでしょう。行間をぎゅっと絞っているので、スピード感があって爽快な反面、説明を読み解くのが難しいという声も多々聞きます。しかしながら蟻本に書いてある内容は、読み解くことさえできたならば、非常に濃密なものと感じられます。
- 渡部有隆: プログラミングコンテスト攻略のためのアルゴリズムとデータ構造, マイナビ出版 (2015).
蟻本が難しいと感じる方のためのプログラミングコンテスト書籍です。通称螺旋本と呼ばれています。対象層はアルゴリズム学習の入門を終えた初中級者向けで、あらゆる層の人にとって読みやすい書籍と言えそうです。掲載されている例題たちはすべて自分でソースコードを実装して、AOJ 上でジャッジできるようになっています。
- 高橋直大: 最強最速アルゴリズマー養成講座 プログラミングコンテストTopCoder攻略ガイド, SBクリエイティブ (2012).
今流行りの AtCoder 社長による競技プログラミング入門用書籍、通称チーター本です。蟻本は対象者層が中上級者向けで難しいと言われていますが、チーター本は競技プログラミングを始めたばかりの人に目線を合わせた真の入門書です。丁寧なわかりやすい解説が売りで、C++ だけでなく Java や C# による実装も載っているのが特長です (現在なら Python もあった方が嬉しいかもなので続報期待)。ただし丁寧な反面、やや重いのが弱点です。「これを読まないと螺旋本・蟻本に進めない」と思ってしまうと気が遠くなるので、もっと気軽に読むと「強くなるための良いヒントが沢山書いてある」本です。
Google, Microsoft, Facebook, Amazon, Apple などでは選考過程で実際にコーディングを行うことはすっかり有名になりました。国内でも、選考過程に AtCoder システムを用いてコーディング試験を課す企業も急増しています。それらのプログラミング試験に合格して採用されるための攻略本として絶大な人気を誇るベストセラー書となっています。なお新版もあるのですが日本語訳に誤植が多く注意が必要です。
とても面白いです!
アルゴリズムを体系的に解説するよりも、具体的な楽しいパズルのような問題たちを解いていくことで、自然に楽しくアルゴリズムの使い方や、アルゴリズムコーディング技術が身に着くようになっています。
7-3. グラフ理論
グラフ理論に関する内容が充実している書籍たちです。
組合せ最適化の世界的教科書です。少し難しめですが、グラフ理論や離散数学に関連するアルゴリズムの話題が豊富に集められており、学ぶ要素は非常に多いです。
組合せ最適化に関するサーベイは、2003 年までの分についてはこれ一冊でできると言われるほど、グラフ理論や離散数学に関するアルゴリズムを集大成した本です。1881 ページにも及ぶ世界的名著は、組合せ最適化分野における世界的研究者 Alexander Schrijver によって書かれました。
グラフ理論に関する古典的な話題を一通り扱っていて、大変面白いです。読み終えた頃にはグラフと慣れ親めた気持ちになることができます。