0. はじめに --- 二部マッチング問題は実世界で超頻出
はじめまして。NTTデータ数理システムでアルゴリズムを探求している大槻 (通称、けんちょん) です。
好きなアルゴリズムはタイトルにもある二部マッチングですが、会社ではなぜか「DP が好きな人」と呼ばれています。
以前に動的計画法 (DP) の典型パターンを整理した記事を執筆したのですが、DP と並んで超頻出の話題として二部マッチング問題があります。二部マッチング問題とは、例えばマッチングアプリなどに見られるように、2 つのカテゴリ間で最適なマッチングを構成していく問題です。実問題で登場する二部マッチングは以下のように多岐にわたります:
- マッチングアプリで男女のペアを最適化する (「男」と「女」)
- インターネット広告分野で、ユーザの興味に合う広告を出す (「ユーザ」と「広告」)
- 企業検索サービスなどで、ユーザの検索履歴に合う企業をレコメンドする (「ユーザ」と「企業」)
- 従業員シフト割当問題などで、従業員全員の不満の少ない割当をする (「従業員」と「シフト」)
- トラック配送計画問題などで、どの荷物をどのトラックに割当てるかを最適化する (「荷物」と「トラック」)
- 輸送問題などで、どの工場からどの店舗へどの分量の製品を輸送するかを最適化する (「工場」と「店舗」)
- スポーツのチーム対抗戦などで勝てる確率が最大になるように対戦割当をする (「自チームメンバー」と「相手チームメンバー」)
- 箱根駅伝でチームの総合タイムが最小となるように選手を各区に割当てる (「選手」と「区」)
-
ProjectSelection問題: 考えられる仕事をすべてこなすことが現実的でなく、仕事間の依存関係が複雑な場面において、確実にこなす仕事を選択する (「選ぶ仕事」と「選ばない仕事」)
このように様々な分野で二部マッチング問題が発生します。なお、実際のビジネス現場において、二部マッチングに相当するものを輸送問題と呼んでいるケースも多いようです。本記事では二部マッチングと呼び名を統一して、二部マッチング問題を解く手法を整理していきます。
また、下の方で簡単な例題について実際に解いていますので参考にしていただければと思います。
1. 問題の分類
一口に二部マッチング問題といっても様々なバリエーションが考えられます。
1-1. 最大二部マッチング問題
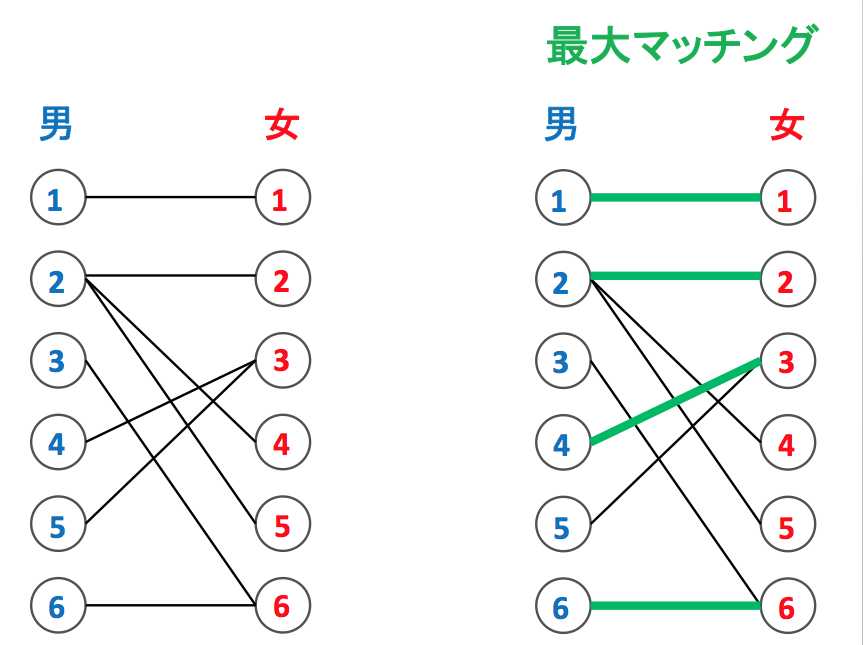
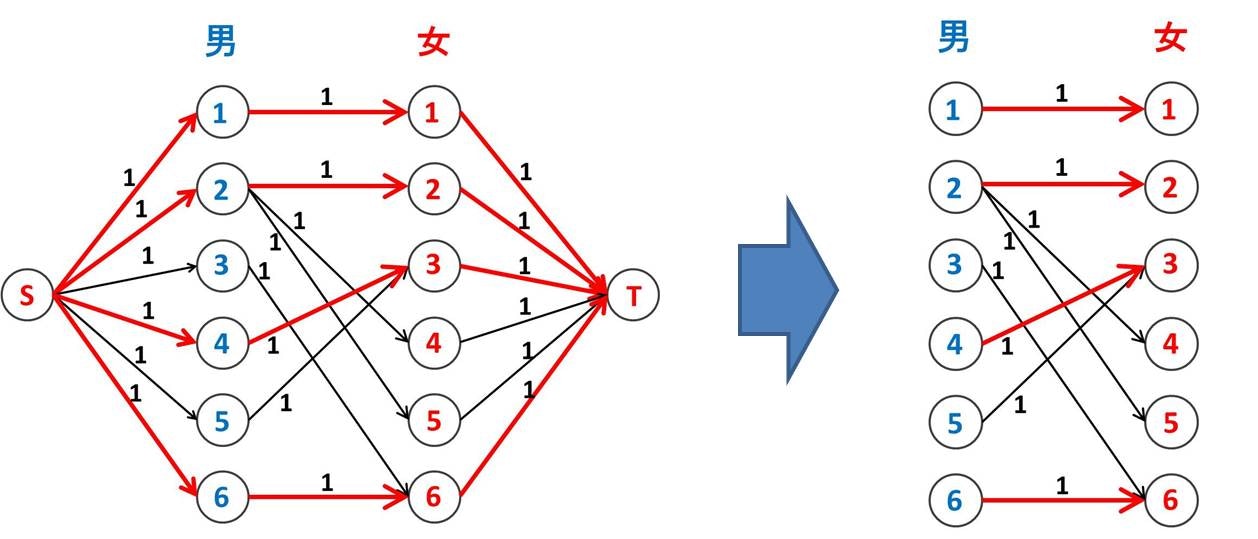
例えば下左図のように何人かの男と女 (◯で表しています) がいて、ペアになってもいいという2人の間には線を引かれています。できるだけ多くのペアを作ろうとしたときに最大で何組のペアができるかを求める問題です。
この場合の答えは下右図のように 4 組になります。注意点としては、最大マッチングは必ずしも一通りとは限りません。例えば下右図では (1, 1), (2, 2), (4, 3), (6, 6) がペアとなっていますが、(1, 1), (2, 2), (3, 6), (5, 3) なども同じく 4 組のマッチングとなっています。
このように最適解は必ずしも一通りではないという意識は、数理最適化の技術をビジネス現場に適用するときに大変重要になって来ます。同じ最適値をもつ最適解でも「現場の人にとって違和感のない最適解」と「現場の人にとって違和感のある最適解」とがあることが多いです。
1-2. 重みつき最大二部マッチング問題
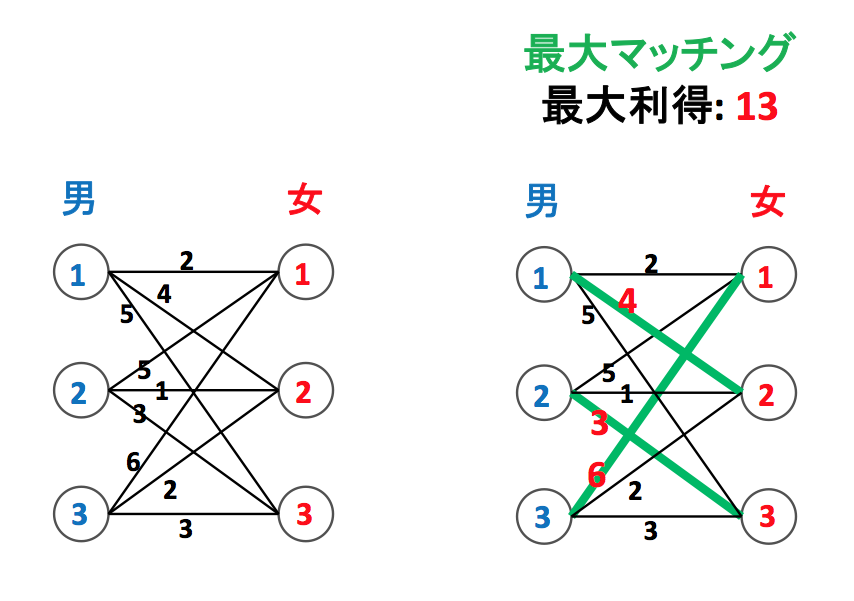
重みつき最大二部マッチング問題は様々なバリエーションが考えられるのですが、ここでは左下図のように男女間の各ペアについて「そこがペアになったらお互いどれだけ嬉しいか」が数値化されている状態を考えます。そこからペアリングして各ペアの利得の総和が最大になるようにする問題です。
下図の場合は (1, 2), (2, 3), (3, 1) をペアリングして得られる利得 13 が最大です。必ずしもそれぞれの男・女にとって一番理想の相手とペアになっているわけではないことに注意しましょう。例えば男 1 にとっては女 3 が一番いいのですが、残りのペアをどう結び付けても全体の利得は小さくなってしまいます。
このように二部マッチング問題というのは基本的に全体最適を目指す考え方です。マッチングアプリの例で言えば、個人最適を追い求めすぎると人気の男女に「いいね」が殺到してしまうため、運営側としては二部マッチング問題的な手法を取り入れることで全体最適な方向性に引っ張っていくことが重要になると考えられます。
1-3. その他のバリエーション
これらの問題と類似の設定で、様々なバリエーションの問題が考えられます。以下に例示します:
- 「1 対 1」のペアリングに限らず二股など「多 対 多」を許したマッチング問題
- 工場から店舗への輸送問題 に見られるように「どの工場からどの店舗に輸送するか」だけでなくその輸送量も最適化する問題
- またその輸送量に上限制約 (店舗側の在庫のキャパの問題) や下限制約 (工場側が満たすべき需要の問題) があるバージョン
- 重みつき最大マッチング問題において、利得最大化をするのではなくコスト最小化をするバージョン
- 重みつき最大マッチング問題において、「このペアはペアリングしてはいけない」という制約があるバージョン
- 重みつき最大マッチング問題において、全員をマッチングさせるのではなく決められた数のペアを作るバージョン
- 重みつき最大マッチング問題において、全員をマッチングさせるのではなく決められた数以下のペアを作るバージョン
2. 二部マッチング問題の解法の分類
大きく分けて 2 つの方向性があるように思います。
- ネットワークフローアルゴリズム、あるいは類似のアルゴリズムを用いる
- 数理最適化ソルバーを用いる
前者は実装も簡単で、無料で利用できるソースコードが世の中に多数溢れているのが魅力です。簡単なものであれば 30 行ほどで実装することができます。しかしながら解きたい問題設定が複雑になって来ると職人技のようなテクニックが必要になったり、そもそもネットワークフローアルゴリズムでは効率よく解くことが不可能な状態に陥りやすい側面があります。
後者は自前で実装するのは非常に大変です。glpk など無料で利用できるソフトウェアも世の中に存在していますが、大規模な問題に適用しようとなると厳しいので結局は有料のものに頼らざるを得ない場面も多いでしょう。国内製で柔軟に扱えるソルバーとして弊社の Numerical Optimizer があります。ある程度最適化問題への定式化に習熟してしまえば、様々な制約に柔軟に対応できるのが魅力です。
どの程度の規模の問題が解けるか
上にあげた 2 つの問題のうちの 1 つめの最大二部マッチング問題の方については、ネットワークフローアルゴリズムを用いることで非常に高速に求めることができます。「ペアになってもいいという組の個数」がある程度小さいこと (そのような性質をスパース性といいます) が必要になりますが、場合によっては「数百万 × 数百万」程度のサイズのマッチング問題を現実的な時間で解くことができます。
2 つめの重みつき最大二部マッチング問題については、いずれの方法を用いたとしても、現実的な時間で最適解を導くことができるのは「数万 × 数万」程度までという規模感です。それより規模が大きい問題については最適解を導くことは諦めて、現実的な時間内に少しでもよりよい解を探索するアプローチをとることになります。
なお、条件設定が複雑になって来ると、解くことが本質的に難しい問題になってしまうことが少なくありません。例えば各荷物を各トラックに割り当てる問題において、各トラックには複数の荷物を積むことができるものの、それぞれ積載重量の上限値が決まっているような状況が考えられます。荷物の方も重量がまちまちであるため、各トラックに「どの荷物の集まり」であれば積載可能であるかという部分が非常に複雑になります。このような問題はネットワークフローアルゴリズムで解くことはできず、近似解 (実務では準最適解と慣用的に呼ぶこともあります) を求める専用のアルゴリズムを考案するか、数理計画ソルバーに頼ることになります。このような問題に対してきちんと最適解を求めることができる問題のサイズの上限は「数百〜数千」程度になることが多いです。
3. ネットワークフロー問題への帰着
最大二部マッチング問題は最大流問題に帰着し、重みつき最大二部マッチング問題は最小費用流問題に帰着して解きます。最大流問題と最小費用流問題はどちらもネットワークフロー問題と総称される問題群に属しています。
3-1. 最大流問題
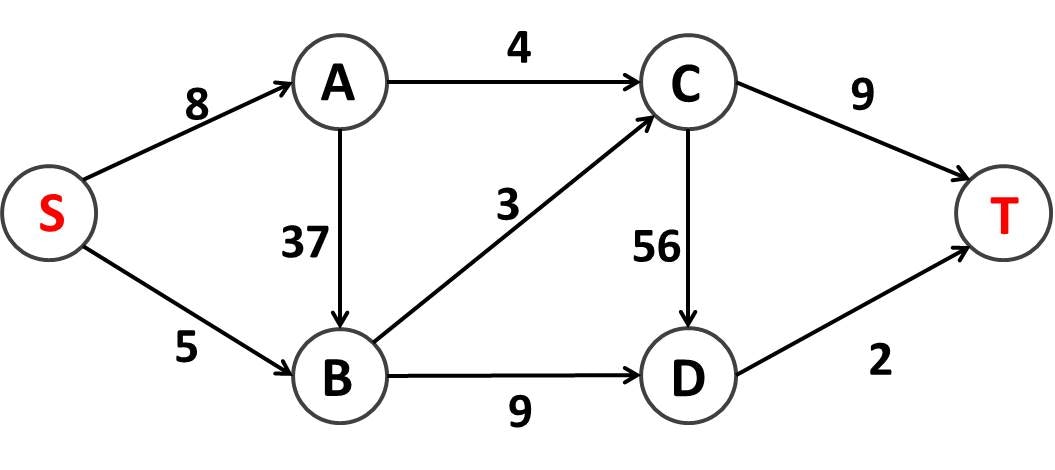
最大流問題とは、例えば下図のような物流ラインにおいて、供給地である地点 S から需要地である地点 T へと「もの」をできるだけたくさん運ぶ方法を考える問題です。ただし、各輸送経路には運べる量の上限が設けられています。たとえば、地点 A から地点 B へは 37 トンの荷物を運ぶことができますが、地点 A から地点 C へは 4 トンの荷物しか運べません。また、地点 S と地点 T 以外の場所では物流を滞らせてもいけません。つまり、例えば地点 B に地点 S と地点 A から合計して 6 トンの荷物が届いているならば、地点 B からは地点 C と地点 D へと合計して 6 トンの荷物を送らなければいけません。
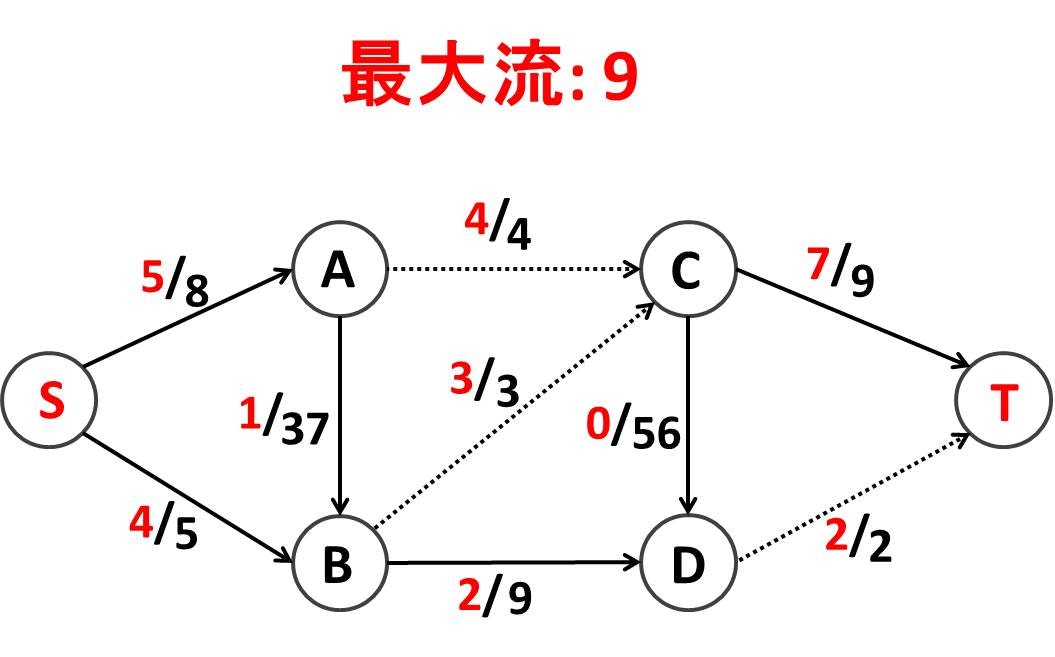
さてこの輸送ネットワークでは最大で何トンの荷物を地点 S から地点 T へと送り出すことができるでしょうか?答えは以下のようになります (物流が上限一杯の経路は点線で示しています)!
各輸送経路につき何トンの荷物を送るべきかを赤字で示しています。合計 9 トンです。地点 S からは地点 A と地点 B にそれぞれ 5 トン、4 トンと合計 9 トン送り出しているのがわかります。地点 T には地点 C と地点 D からそれぞれ 7 トン、2 トンと合計 9 トンが届いているのがわかります。また、物流が滞っていないかどうかを確かめるために地点 B を見てみましょう。地点 A と地点 S から合計 5 トンの荷物が届いていて、地点 C と地点 D へと合計 5 トンの荷物を送りだしていることがわかります。
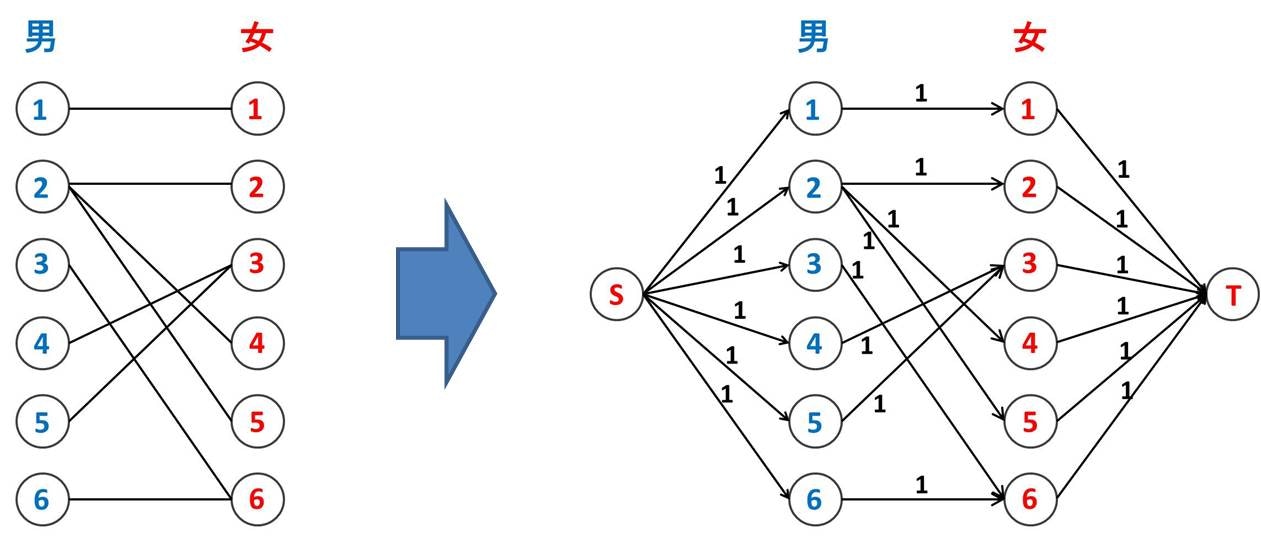
最大二部マッチング問題を最大流問題に帰着する
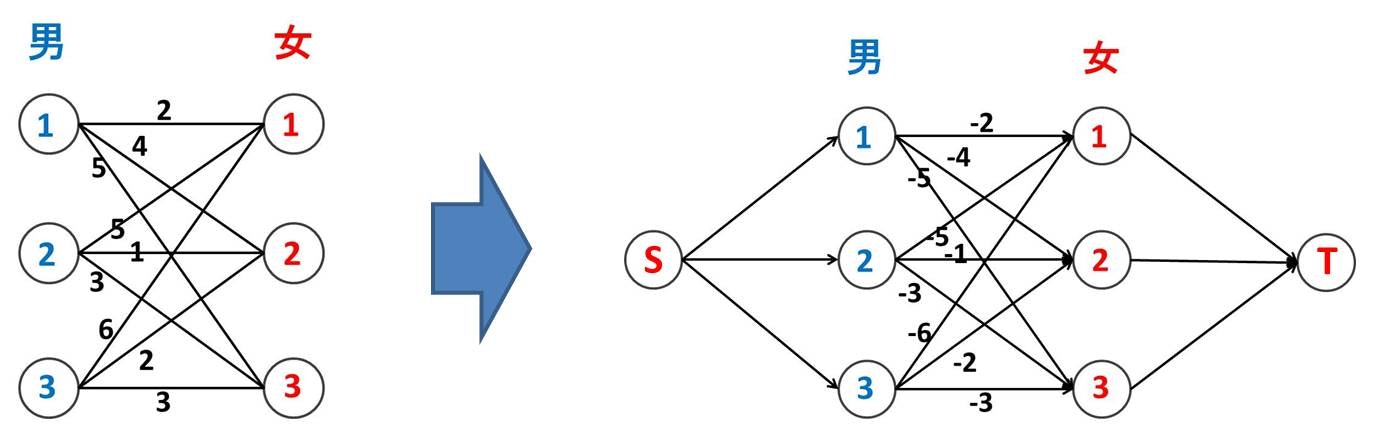
やり方は簡単です。下図のように、新たなノード S, T を設けてネットワークを作ります。
元の二部マッチングでは辺に向きはありませんでしたが、S と T を加えたネットワークには辺に向きがあります。また各辺の上限容量は 1 としておきます。
こうして作ったネットワークで最大流を流します。最後に再び S と T を取っ払うと、最大二部マッチングが求まっています。
3-2. 最小費用流問題
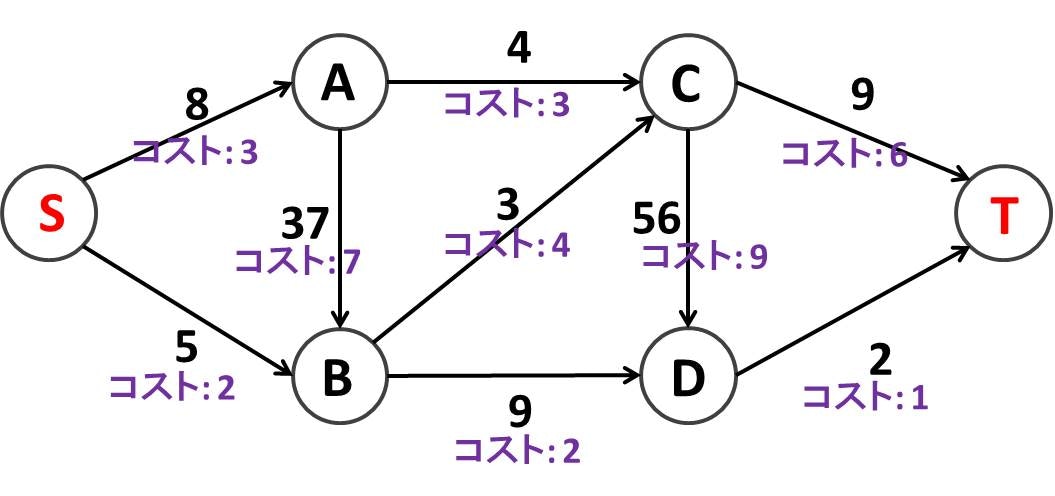
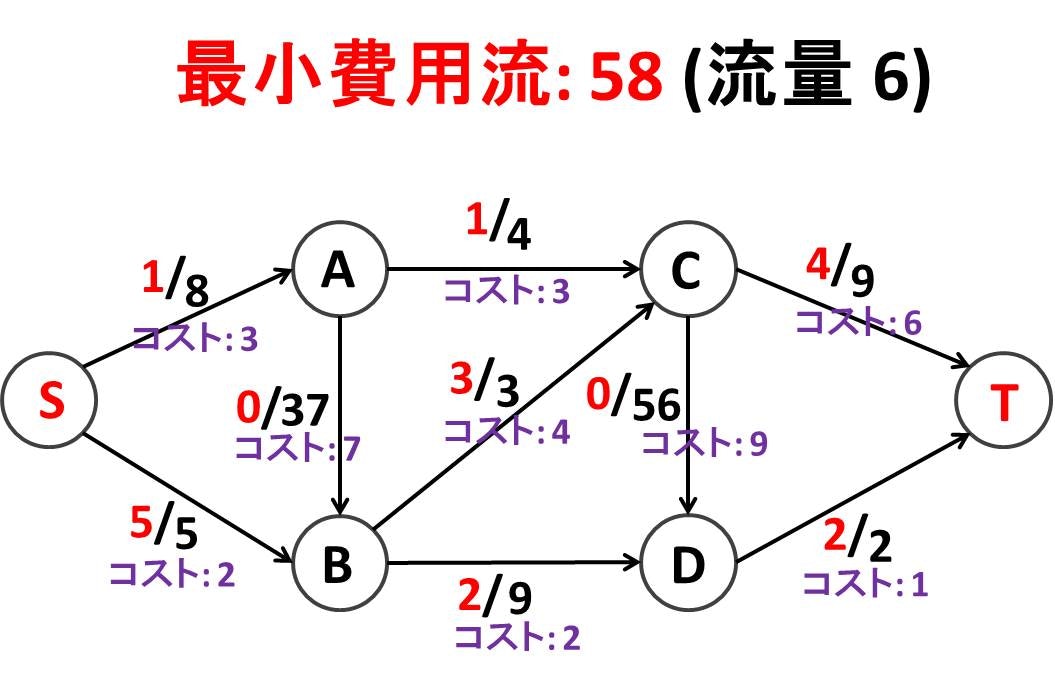
続いて最小費用流問題です。最大流問題は「できるだけ多くの量を運ぶ」問題でしたが、最小費用流問題は「決められた量をできるだけ小さなコストで運ぶ」問題です。例えば下図のような物流ラインを考えます。先程は各辺に乗っている値は上限容量だけでしたが、今回はそれに加えて単位フローあたりのコストが付け加えられています。このネットワークには最大で大きさ 9 のフローを流すことができますが、今回は無理をせず 6 のフローを流すことにして、最小のコストを求めてみましょう。
見るからに複雑ですが、答えは以下のようになります。コストは S-A が 3 × 1 = 3, S-B が 2 × 5 = 10, A-B が 7 × 0 = 0, A-C が 3 × 1 = 3, B-C が 4 × 3 = 12, B-D が 2 × 2 = 4, C-D が 9 × 0 = 0, C-T が 6 × 4 = 24, D-T が 1 × 2 = 2 で合計 58 となっています。
重みつき最大二部マッチング問題を最小費用流問題に帰着する
やり方はさっきとほぼ一緒です。下図のように、新たなノード S, T を設けてネットワークを作ります。また各辺の上限容量は 1 としておきます (図が見えづらくなるので省略)。元々の利得はコストになるのですが、ここで注意点が必要です。利得は大きくしたいものですがコストは小さくしたいものです。こういうときに用いるテクニックとして、マイナスをつけるというのがあります。マイナスを付けたネットワークでコスト最小化をしておけば、元のネットワークでは利得最大化をしたことになります。
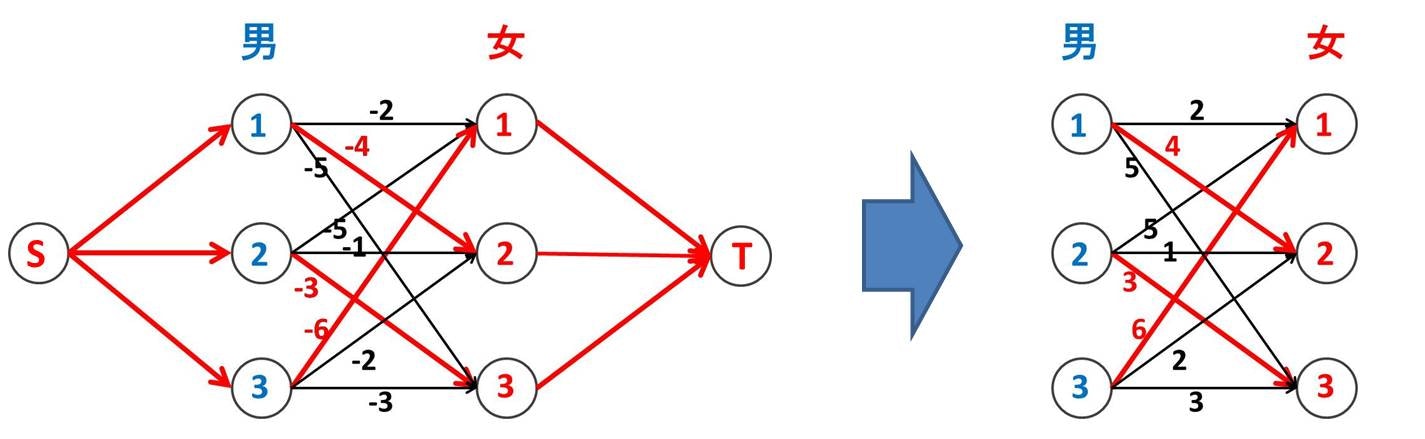
こうして作ったネットワークで大きさ 3 (男女の人数) の最小費用流を流します。最後に再び S と T を取っ払うと、重みつき最大二部マッチングが求まっています。
4. 最大流問題、最小費用流問題を解く
前章で二部マッチング問題が最大流問題、最小費用流問題に帰着されたので、あとはそれを解けばよいです。ネットワークフロー問題はとても歴史が長く、世界中の研究者が活発に研究し続けて来たテーマですので、現在に至るまで様々なアルゴリズムが提案されており、無料で使える実装が世の中に多数存在しています。
なお、最大流問題、最小費用流問題を解くアルゴリズムの理論的背景については以下のスライドがとても参考になります。
4-1. 最大流問題を解くアルゴリズム
歴史的に最初の最大流アルゴリズムは 1956 年に Ford-Fulkerson によって提案されました。その後幾多の改良が続けられて現在に至っています。実装のしやすさと実用上の計算速度の観点から Dinic のアルゴリズムがよく用いられており、場合によってはサイズが数百万規模の問題も解くことができます。Dinic のアルゴリズムを実装したものとして、例えば以下のものがあります。
また、Python にも最大流を求めるライブラリがありますのでそれを簡単に利用することができます。実行例として以下の記事が参考になります。
最大二部マッチング問題の適用例
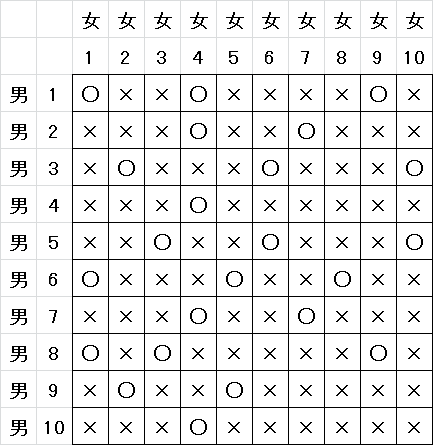
例として以下のような問題を解いてみましょう。男女がそれぞれ 10 人ずついて、お互いにカップルになってもよいという部分には「○」、そうでない部分には「×」がついています。最大で何組のカップルが成立し得るかを求めてみましょう。
以下のような入力ファイルを作っておきます。
10 10
o x x o x x x x o x
x x x o x x o x x x
x o x x x o x x x o
x x x o x x x x x x
x x o x x o x x x o
o x x x o x x o x x
x x x o x x o x x x
o x o x x x x x o x
x o x x o x x x x x
x x x o x x x x x x
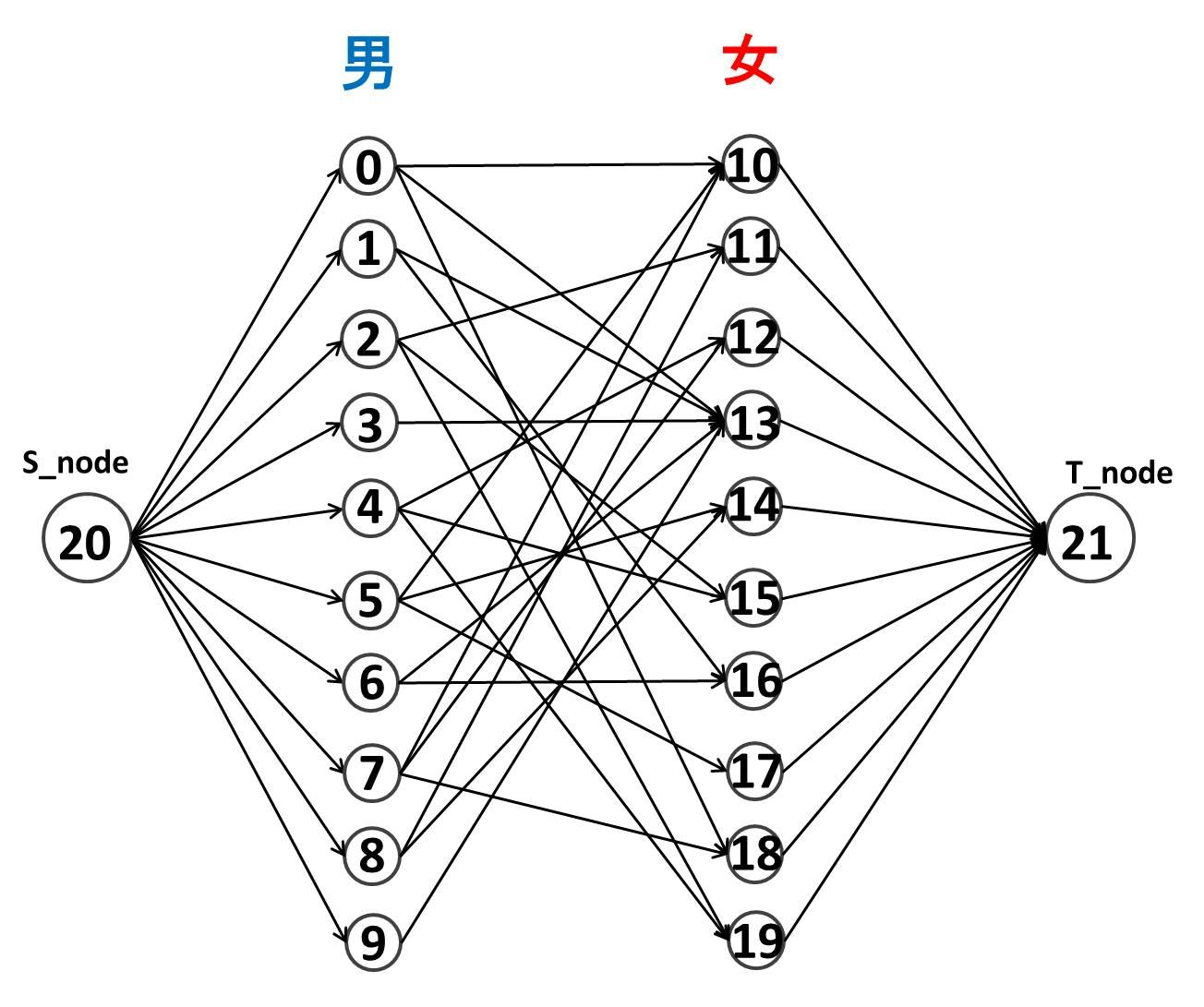
今回は先に挙げた実装のうち、プログラミングコンテストチャレンジブックに載っている Dinic のアルゴリズムの実装をアレンジしたものを用いてみます。構成しているネットワークは以下の感じです。張っている辺の容量はすべて 1 です。
# include <iostream>
# include <vector>
# include <queue>
# include <cstring>
using namespace std;
typedef int FLOW; // フローを表す型、今回は int 型
const int MAX_V = 100; // グラフの最大ノード数
const FLOW INF = 100000000; // 十分大きい値
// グラフの辺の構造体
struct Edge {
int rev, from, to;
FLOW cap, icap;
Edge(int r, int f, int t, FLOW c) : rev(r), from(f), to(t), cap(c), icap(c) {}
friend ostream& operator << (ostream& s, const Edge& E) {
if (E.cap > 0) return s << E.from << "->" << E.to << '(' << E.cap << ')';
else return s;
}
};
// グラフ構造体
struct Graph {
int V;
vector<Edge> list[MAX_V];
Graph(int n = 0) : V(n) { for (int i = 0; i < MAX_V; ++i) list[i].clear(); }
void init(int n = 0) { V = n; for (int i = 0; i < MAX_V; ++i) list[i].clear(); }
void resize(int n = 0) { V = n; }
void reset() { for (int i = 0; i < V; ++i) for (int j = 0; j < list[i].size(); ++j) list[i][j].cap = list[i][j].icap; }
inline vector<Edge>& operator [] (int i) { return list[i]; }
Edge &redge(Edge e) {
if (e.from != e.to) return list[e.to][e.rev];
else return list[e.to][e.rev + 1];
}
void addedge(int from, int to, FLOW cap) {
list[from].push_back(Edge((int)list[to].size(), from, to, cap));
list[to].push_back(Edge((int)list[from].size() - 1, to, from, 0));
}
};
// 最大流を求めるサブルーチンたち
static int level[MAX_V];
static int iter[MAX_V];
void dibfs(Graph &G, int s) {
for (int i = 0; i < MAX_V; ++i) level[i] = -1;
level[s] = 0;
queue<int> que;
que.push(s);
while (!que.empty()) {
int v = que.front();
que.pop();
for (int i = 0; i < G[v].size(); ++i) {
Edge &e = G[v][i];
if (level[e.to] < 0 && e.cap > 0) {
level[e.to] = level[v] + 1;
que.push(e.to);
}
}
}
}
FLOW didfs(Graph &G, int v, int t, FLOW f) {
if (v == t) return f;
for (int &i = iter[v]; i < G[v].size(); ++i) {
Edge &e = G[v][i], &re = G.redge(e);
if (level[v] < level[e.to] && e.cap > 0) {
FLOW d = didfs(G, e.to, t, min(f, e.cap));
if (d > 0) {
e.cap -= d;
re.cap += d;
return d;
}
}
}
return 0;
}
// 最大流を求めるメイン関数
FLOW Dinic(Graph &G, int s, int t) {
FLOW res = 0;
while (true) {
dibfs(G, s);
if (level[t] < 0) return res;
memset(iter, 0, sizeof(iter));
FLOW flow;
while ((flow = didfs(G, s, t, INF)) > 0) {
res += flow;
}
}
}
int main() {
int men[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
int women[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
// 男の人数と、女の人数
int NUM_MEN = 0, NUM_WOMEN = 0;
cin >> NUM_MEN >> NUM_WOMEN;
// グラフの定義 (ノード数を引数に)
Graph G(NUM_MEN + NUM_WOMEN + 2); // +2 は S, T の分
// スーパーノード S, T の index
int S_node = NUM_MEN + NUM_WOMEN;
int T_node = NUM_MEN + NUM_WOMEN + 1;
// グラフに枝を張っていく
for (int i = 0; i < NUM_MEN; ++i) {
for (int j = 0; j < NUM_WOMEN; ++j) {
char isok;
cin >> isok;
if (isok == 'o') {
// 男 i から、女 j (index は j + NUM_MEN) へと、容量 1 の枝を張る
G.addedge(i, j + NUM_MEN, 1);
}
}
}
for (int i = 0; i < NUM_MEN; ++i) {
// S から男 i へと、容量 1 の枝を張る
G.addedge(S_node, i, 1);
}
for (int j = 0; j < NUM_WOMEN; ++j) {
// 女 j から T へと、容量 1 の枝を張る
G.addedge(j + NUM_MEN, T_node, 1);
}
// 最大流を求める
FLOW res = Dinic(G, S_node, T_node);
// 出力
cout << "Max Size of Matching: " << res << endl;
// 誰が誰とマッチしたのかを出力する
for (int i = 0; i < NUM_MEN; ++i) {
for (auto e : G[i]) {
// 元々の容量 (e.icap) が 1 で、フローが流れて容量 (e.cap) が 0 になった部分が割り当てられたところ
if (e.icap == 1 && e.cap == 0) {
cout << "Man " << men[i] << " and " << "Woman " << women[e.to - NUM_MEN]
<< " are matched" << endl;
}
}
}
return 0;
}
結果は以下のようになりました。
Max Size of Matching: 8
Man 1 and Woman 1 are matched
Man 2 and Woman 4 are matched
Man 3 and Woman 6 are matched
Man 5 and Woman 3 are matched
Man 6 and Woman 5 are matched
Man 7 and Woman 7 are matched
Man 8 and Woman 9 are matched
Man 9 and Woman 2 are matched
今回は人気の女 4 をゲットしたのは男 2 でした。もちろんカップル成立数が最大で 8 組というのは正しいですが、同じく 8 組を達成できる組合せは他にも色々考えられます。
4-2. 最小費用流問題を解くアルゴリズム
最小費用流問題もまた研究の歴史が長いです。最小費用流アルゴリズムを C++ で実装したものとして以下のものがあります。問題設定にもよりますが、場合によってはサイズが数万規模の問題も解くことができます。
また同じく Python にも最小費用流を求めるライブラリがありますので簡単に利用できます。実行例として以下の記事が参考になります。
重みつき最大二部マッチングの適用例
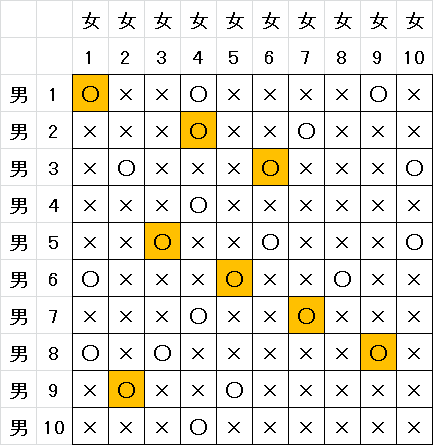
例として以下のような問題を解いてみましょう。従業員が 5 人いて、仕事が 10 個あります。A さん~ E さんにそれぞれ 2 個ずつ仕事を割り振りたいとします。それぞれの従業員にとってそれぞれの仕事がどのくらい得意かが数値化されているとします。うまく全体最適化するように仕事を割り振ってみましょう。
以下のような入力ファイルを作っておきます。
5 10
8 9 12 16 21 2 12 15 20 3
7 12 5 14 13 10 16 12 18 11
19 2 14 7 16 5 8 7 1 4
3 7 8 2 9 1 4 3 1 2
20 27 33 39 26 21 15 30 28 19
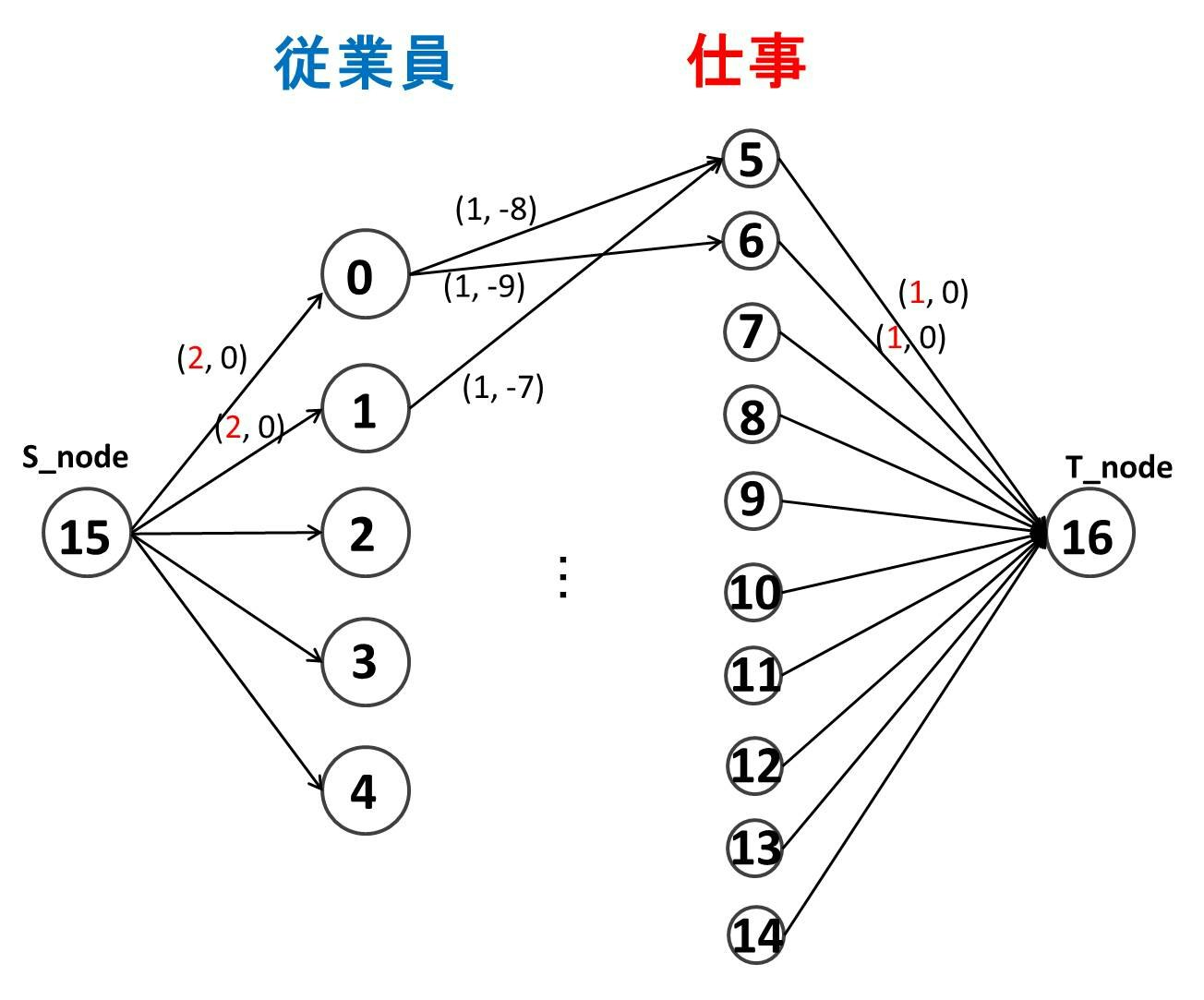
今回は先に挙げた実装のうち、プログラミングコンテストチャレンジブックに載っている実装をアレンジしたものを用いてみます。構成しているネットワークは以下の感じです。(,) 表記は (上限容量, コスト) を表しています。注意点として今回は各従業員に 2 個ずつ仕事が割り振られるので、S_node から各従業員へは容量が 2 の辺を張っています。
# include <iostream>
# include <vector>
using namespace std;
typedef int FLOW; // フローを表す型、今回は int 型
typedef int COST; // コストを表す型、今回は int 型
const int MAX_V = 100; // グラフの最大ノード数
const COST INF = 100000000; // 十分大きい値
// グラフの辺の構造体
struct Edge {
int rev, from, to;
FLOW cap, icap;
COST cost;
Edge(int r, int f, int t, FLOW ca, COST co) : rev(r), from(f), to(t), cap(ca), icap(ca), cost(co) {}
};
// グラフ構造体
struct Graph {
int V;
vector<Edge> list[MAX_V];
Graph(int n = 0) : V(n) { for (int i = 0; i < MAX_V; ++i) list[i].clear(); }
void init(int n = 0) { V = n; for (int i = 0; i < MAX_V; ++i) list[i].clear(); }
void resize(int n = 0) { V = n; }
void reset() { for (int i = 0; i < V; ++i) for (int j = 0; j < list[i].size(); ++j) list[i][j].cap = list[i][j].icap; }
inline vector<Edge>& operator [] (int i) { return list[i]; }
Edge &redge(Edge &e) {
if (e.from != e.to) return list[e.to][e.rev];
else return list[e.to][e.rev + 1];
}
void addedge(int from, int to, FLOW cap, COST cost) {
list[from].push_back(Edge((int)list[to].size(), from, to, cap, cost));
list[to].push_back(Edge((int)list[from].size() - 1, to, from, 0, -cost));
}
};
// 最小費用流を求める関数
COST MinCostFlow(Graph &G, int s, int t, FLOW inif) {
COST dist[MAX_V];
int prevv[MAX_V];
int preve[MAX_V];
COST res = 0;
FLOW f = inif;
while (f > 0) {
fill(dist, dist + G.V, INF);
dist[s] = 0;
while (true) {
bool update = false;
for (int v = 0; v < G.V; ++v) {
if (dist[v] == INF) continue;
for (int i = 0; i < G[v].size(); ++i) {
Edge &e = G[v][i];
if (e.cap > 0 && dist[e.to] > dist[v] + e.cost) {
dist[e.to] = dist[v] + e.cost;
prevv[e.to] = v;
preve[e.to] = i;
update = true;
}
}
}
if (!update) break;
}
if (dist[t] == INF) return 0;
FLOW d = f;
for (int v = t; v != s; v = prevv[v]) {
d = min(d, G[prevv[v]][preve[v]].cap);
}
f -= d;
res += dist[t] * d;
for (int v = t; v != s; v = prevv[v]) {
Edge &e = G[prevv[v]][preve[v]];
Edge &re = G.redge(e);
e.cap -= d;
re.cap += d;
}
}
return res;
}
int main() {
char workers[5] = { 'A', 'B', 'C', 'D', 'E' };
int jobs[10] = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
// 従業員数と、仕事数
int NUM_WORKER = 0, NUM_JOB = 0;
cin >> NUM_WORKER >> NUM_JOB;
// グラフの定義 (ノード数を引数に)
Graph G(NUM_WORKER + NUM_JOB + 2); // +2 は S, T の分
// スーパーノード S, T の index
int S_node = NUM_WORKER + NUM_JOB;
int T_node = NUM_WORKER + NUM_JOB + 1;
// グラフに枝を張っていく
for (int i = 0; i < NUM_WORKER; ++i) {
for (int j = 0; j < NUM_JOB; ++j) {
int gain;
cin >> gain;
// 従業員 i から、仕事 j (index は j+NUM_WORKER) へと、容量 1, コスト -gain の枝を張る
G.addedge(i, j + NUM_WORKER, 1, -gain);
}
}
for (int i = 0; i < NUM_WORKER; ++i) {
// S から従業員 i へと、容量 2, コスト 0 の枝を張る
G.addedge(S_node, i, 2, 0);
}
for (int j = 0; j < NUM_JOB; ++j) {
// 仕事 j から T へと、容量 1, コスト 0 の枝を張る
G.addedge(j + NUM_WORKER, T_node, 1, 0);
}
// 最小費用流を求める
COST res = MinCostFlow(G, S_node, T_node, NUM_JOB);
// 出力
cout << "Max Gain: " << -res << endl;
// 誰がどの仕事に割当てられたかを出力する
for (int i = 0; i < NUM_WORKER; ++i) {
for (auto e : G[i]) {
// 元々の容量 (e.icap) が 1 で、フローが流れて容量 (e.cap) が 0 になった部分が割り当てられたところ
if (e.icap == 1 && e.cap == 0) {
cout << "Worker " << workers[i] << " and " << "Job " << jobs[e.to - NUM_WORKER]
<< " are matched (gain: " << -e.cost << ")" << endl;
}
}
}
return 0;
}
結果は以下のようになりました。
Max Gain: 178
Worker A and Job 5 are matched (gain: 21)
Worker A and Job 9 are matched (gain: 20)
Worker B and Job 7 are matched (gain: 16)
Worker B and Job 10 are matched (gain: 11)
Worker C and Job 1 are matched (gain: 19)
Worker C and Job 3 are matched (gain: 14)
Worker D and Job 2 are matched (gain: 7)
Worker D and Job 6 are matched (gain: 1)
Worker E and Job 4 are matched (gain: 39)
Worker E and Job 8 are matched (gain: 30)
こうしてみると、必ずしも「それぞれの Worker が一番得意とするものはひとまず割り当ててしまう」のが全体最適を導くとは限らないことがわかります。Worker B, D は自分が最も得意とする仕事を割り当てられてはいないです。
さらなるテクニック
重みつき最大二部マッチング問題を最小費用流問題に帰着するとき、利得にマイナスをつけて、それをコストと考えて帰着して来ましたが、もしマッチングサイズが予め決まっているのならば、
- gain に単にマイナスをつけて -gain とする代わりに
- 十分大きい値 M から gain を引いた値 M - gain を用いる
というテクニックがあります。こうすることでコストが非負になりますので、
- コストが非負の場合に特化したより高速な最小費用流アルゴリズム (具体的には、サブルーチンの Bellman-Ford 法を Dijkstra 法に置き換えたもの)
を用いることができて、より高速な求解が可能になります。
5. プログラミングコンテストのススメ: 細かい要求に強くなる!
ここまでに解いて来た問題たちは理想化されたモデルの問題でした。現実世界で生じる二部マッチング問題は、様々な制約が絡んで来たり、最適化対象も複数にまたがるケースも少なくありません。
しかしながら、ある程度のことは最大流問題、最小費用流問題を解くグラフネットワークを工夫することで対応できます。1 章の最後の「その他のバリエーション」で挙げたことはすべて対応できるので、それについては別途記事にしたいと考えております。
そのような対応力を磨くのに有効な方法として、プログラミングコンテストに参加したり過去問を解いたりして鍛錬するというのがあります。プログラミングコンテストがどのようなものかを知ることができる資料として、以下のものがあります:
- プログラミングコンテストはエンジニアを育てるのか。AtCoder高橋CEOに聞いてみた
- 【初心者向け】腕を磨くのに最適!プログラミングコンテストとは?
- 強くなるためのプログラミング -様々なプログラミングコンテストとそのはじめ方-
また、最近は競技プログラミングという単語をよく目にするようになりました。これはプログラミングコンテストのうち、特にアルゴリズム系コンテストのことを指します。
ネットワークフローアルゴリズムに限らず、実問題の多様な制約・要求を解決するテクニックを身につけるという意味では、このうち競技プログラミングと呼ばれている種のコンテストがオススメです。定期的に開催されている競技プログラミングコンテストは、以下の 4 つが世界的にも有名です:
- AtCoder: 日本発のコンテスト運営会社, 初心者向けの ABC (AtCoder Beginner Contest), 中上級者向けの ARC (AtCoder Regular Contest), 最上級者も楽しめる AGC (AtCoder Grand Contest) が定期的に開催されています。また事業の一環として、優秀な学生を発掘して各企業におけるソフトウエアエンジニア採用の支援を行う事業 (例: CODE FESTIVAL, ドワンゴからの挑戦状) や、ソフトウェアエンジニアの能力判定 (例: TOPSIC) なども行っています。
- Codeforces: ロシア発のコンテストサイト。世界的には最大規模。
- topcoder: 世界四大定期開催コンテスト (AtCoder, Codeforces, topcoder, CSAcademy) の中では最も歴史が長いです。
- CS Academy: 新しいです。四大コンテストの中で問題の質は高めです。
日本人としては日本語で参加できる AtCoder が魅力的であり、世界的にも良質の問題が出題されることで有名です。
6. どうしても解けない問題は数理計画ソルバーへ!
現実世界の実問題は往々にして非常に複雑な制約条件が絡み、ネットワークフローアルゴリズムで解くことは厳しいことも多いです。そんなときは問題に応じて近似解法を考案するか、数理計画問題として定式化して数理計画ソルバーに解かせましょう。数理最適化ソルバーを用いるとかなり複雑な制約条件も加味して考えることができます。具体的なソルバーとしては、glpk など無償のものから、弊社の Numerical Optimizer といった商用のものまで様々なものがあります。
数理計画問題とは
先ほどの問題を今度は数理計画問題に定式化することで解いてみましょう!
数理計画問題とは以下のようなものです:
Maximize:
3x + 1
Subject to:
x <= 10
これは、x <= 10 の範囲内で 3x + 1 の最大値を求める問題です (答えは x = 10 のとき 31 です)。
このように数理計画問題は、意思決定の選択肢を表す変数 (上の例では x) と、最適化したい目的関数 (上の例では 3x + 1) と、制約条件 (上の例では x <= 10) から成っています。
この例は中学数学の一次関数のところで習うくらい簡単なものですが、一次式の表現力はものすごいです。非常に多くの数理計画問題が一次式を用いて記述することができます!
さて、先ほどの問題を再掲します。
従業員が 5 人いて、仕事が 10 個あります。A〜E さんにそれぞれ 2 個ずつ仕事を割り振りたいとします。それぞれの従業員にとってそれぞれの仕事がどのくらい得意かが数値化されているとします。うまく全体最適化するように仕事を割り振ってみましょう。
変数
今度は変数として以下のものを考えます:
x[\rm{person}, \rm{work}] = \left\{
\begin{array}{ll}
1 & (従業員 \rm{person} を仕事 \rm{work} に割り当てるとき) \\
0 & (従業員 \rm{person} を仕事 \rm{work} に割り当てないとき)
\end{array}
\right.
ここで、person は {A, B, C, D, E} の 5 個の値をとり、work は {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} の 10 個の値をとるので、変数は全部で 50 個になります (具体的に書くと、x[A, 1], x[A, 2], x[A, 3], ... と続きます)。また各変数は 0 か 1 の値のみをとりえます。このような変数を binary 変数と呼びます。
目的関数
次に最適化したい目的関数がどのようになるかを考えます。まず、従業員 person が仕事 work に割り当てられたときの利得を gain[person, work] と表すことにします (例えば、gain[C, 7] = 8 です)。
このとき、目的関数は以下のように表せます:
\sum_{\rm{person}} \sum_{\rm{work}} (\rm{gain}[\rm{person}, \rm{work}] × x[\rm{person}, \rm{work}])
50個の項の足し算ですね。これは、(person, work) の 50 個のペアのうち、$x$[person, work] = 1 となっている箇所、すなわち person が work に割り当てられている箇所についてのみ、gain[person, work] を足しあげる式になっています。
制約条件
制約条件としては以下の 2 つがあります:
- どの従業員も 2 つの仕事が割り当てられる
- どの仕事も 1 人によってのみ行われる
それぞれ以下のようになります:
\sum_{\rm{work}} x[\rm{person}, \rm{work}] = 2 (\rm{person} = A, B, C, D, E それぞれに対して) \\
\sum_{\rm{person}} x[\rm{person}, \rm{work}] = 1 (\rm{work} = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 それぞれに対して)
少し難しいかもしれませんが、例えば従業員 B に割り当てられる仕事が 2 つであるという式を抜き出して書くと、
\sum_{\rm{work}} x[\rm{B}, \rm{work}] = 2
すなわち
x[\rm{B}, 1] + x[\rm{B}, 2] + x[\rm{B}, 3] + x[\rm{B}, 4] + x[\rm{B}, 5] + x[\rm{B}, 6] + x[\rm{B}, 7] + x[\rm{B}, 8] + x[\rm{B}, 9] + x[\rm{B}, 10] = 2
となります。
まとめ
まとめると以下のようになります:
Maximize:
$\sum_{\rm{person}} \sum_{\rm{work}} (\rm{gain}[\rm{person}, \rm{work}] × x[\rm{person}, \rm{work}])$
Subject to:
$\sum_{\rm{work}} x[\rm{person}, \rm{work}] = 2$ (person = A, B, C, D, E それぞれに対して)
$\sum_{\rm{person}} x[\rm{person}, \rm{work}] = 1$ (work = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 それぞれに対して)
$x$[person, work] は binary 変数
ここまで定式化できれば、あとは数理計画ソルバーに解かせるのみです!
なお、ここで解いた問題と類似の問題を実際に Numerical Optimizer を用いて解く話がこのページにありますので、参考にしていただければと思います。
7. おわりに
二部マッチング問題やそれに類した問題は現実世界の様々な場面で直面します。二部マッチング問題はそれ自体重要な問題ではありますが、しばしば「最大流問題や最小費用流問題の応用例の 1 つである」という語られ方をしているため、なかなか欲しい情報がヒットしづらい現状があるのではないかと感じて本記事を執筆しました。もしどこかでなんらかの課題の解決に寄与することができたならば、とても嬉しく思います。