はじめに
大きなサイズの問題を扱っていると、元の問題のサイズを半分以下にしたい場面がしばしば登場します。二分探索もそうですし、分割統治法もそうです。
ツリーに関する問題に対しても、サイズを半分以下にしたい場面がしばしば登場します。そんなときに重要な概念になるのがツリーの重心です。
ツリーの重心とは
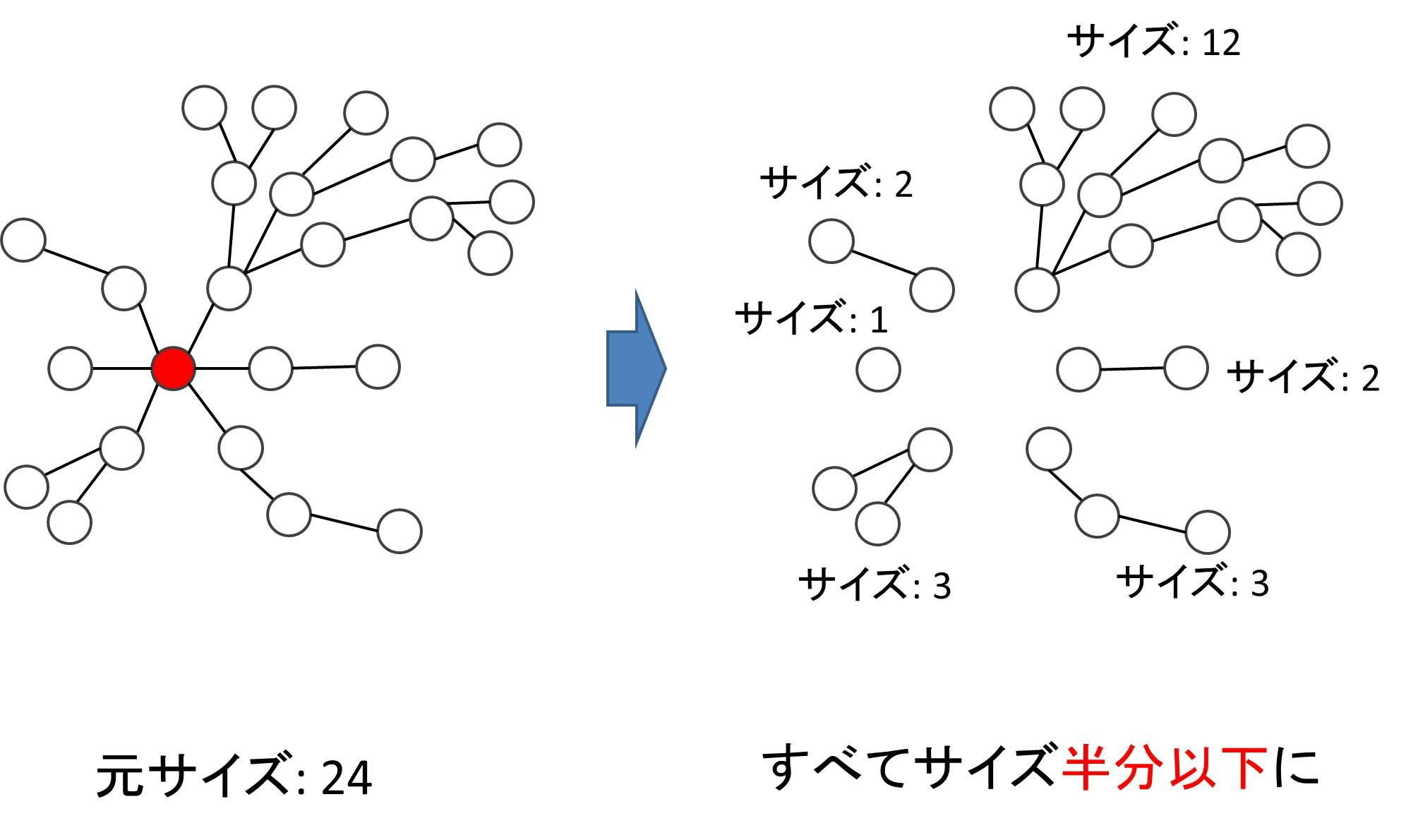
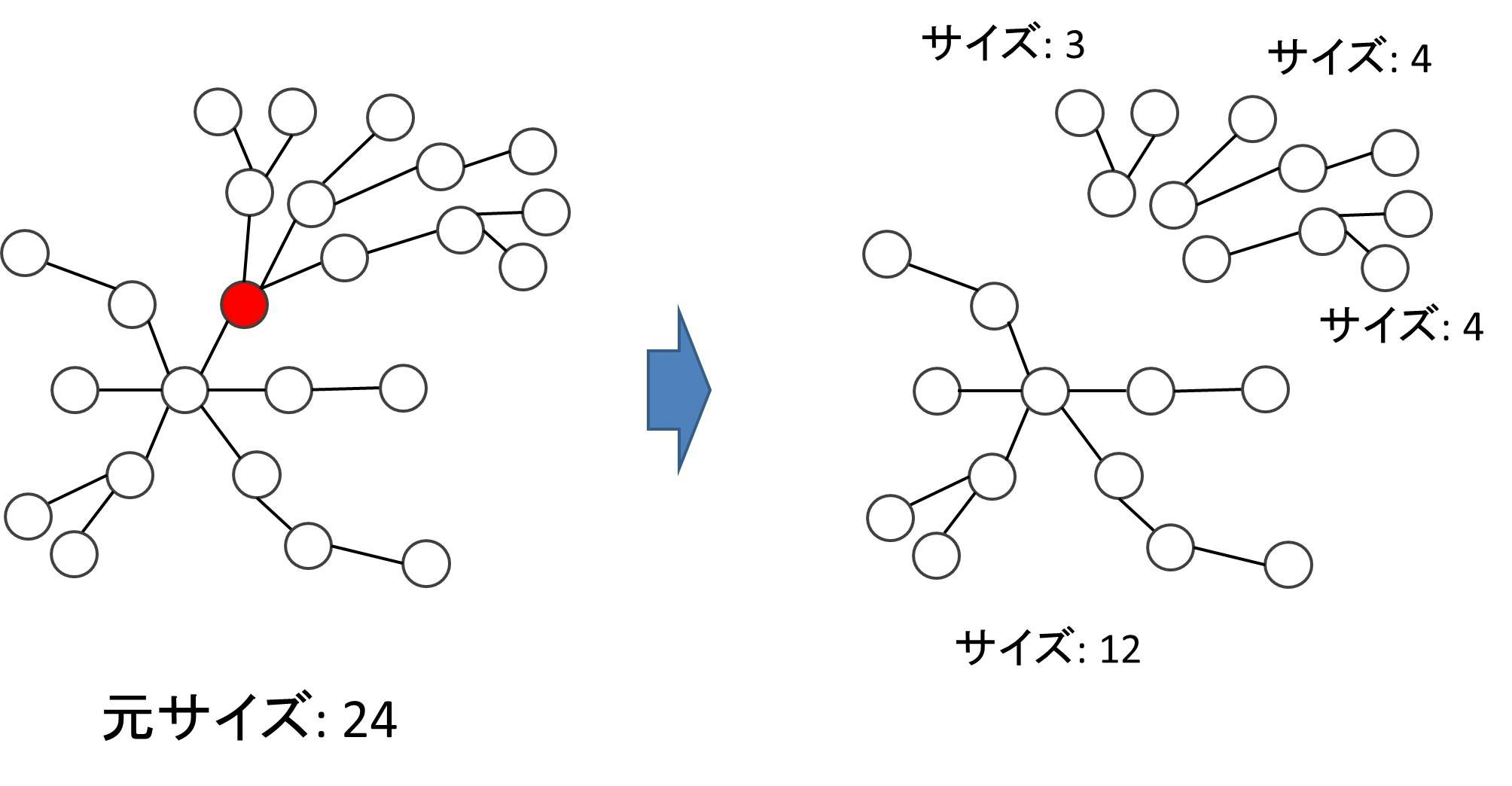
ツリーである頂点を取り除くと、元のツリーは何個かのツリーに分裂します。そのすべての部分ツリーのサイズが元のツリーのサイズの半分以下になるような頂点がツリーの重心です。
なおこの図の場合、もう一つ重心があることがわかります。
一般に、ツリーの重心は 1 個または 2 個になります。多くのツリーでは重心は 1 個だけですが、この例については、2 つの重心を結んでいる枝の両端からなる部分木がともに元のサイズの半分ずつになっています。このような状況が発生する場合のみ、重心が 2 個になります。なお、重心が 2 個以下であることの詳しい証明は、以下のこうきさんの記事
に記載があります。

ツリーの重心が必ず存在すること
ツリーに対してサイズを半分以下にしながら問題を解きたい場面では、ツリーの重心が存在するかどうかはとても重要な問題です。ツリーの重心が必ず存在することは、パッと見ではそんなに自明ではないです。
しかしながら次の章に示すように、ツリーの重心の求め方を見れば、重心の存在が明らかになります。
ツリーの重心を求める (ツリーの重心の存在証明)
ツリー DP の心得があれば簡単に求めることができます (N: ツリーの頂点数)。
- 根を適当に決めて根付き木にする
- 各ノード v を根とした部分木のサイズ sizeSubtree[v] をツリー DP によって求めていく
- 任意の v の子ノード ch に対して sizeSubtree[ch] <= N/2 が成り立ち、かつ N - sizeSubtree[v] <= N/2 を満たすような v を列挙する
これだけです。以下が実装例になります。
const int MAX_V = 2100; // ツリーのサイズのありうる最大値
int N; // ツリーのサイズ
vector<int> tree[MAX_V]; // ツリーを隣接リスト形式のグラフ構造で表したもの
int sizeSubtree[MAX_V]; // sizeSubtree[v] := v を根とする部分ツリーのサイズ
vector<int> centroids; // 重心列挙の答えがここに入る
/* ツリーDP */
void SubFindCentroids(int v, int parent_of_v = -1) {
sizeSubtree[v] = 1;
bool isCentroid = true;
for (auto ch : tree[v]) {
if (ch == parent_of_v) continue;
SubFindCentroids(ch, v);
if (sizeSubtree[ch] > N / 2) isCentroid = false;
sizeSubtree[v] += sizeSubtree[ch];
}
if (N - sizeSubtree[v] > N / 2) isCentroid = false;
if (isCentroid) centroids.push_back(v);
}
void FindCentroids() {
centroids.clear();
SubFindCentroids(0, N); // これを呼び出すと centoroids に重心を列挙したものが入る
}
なお、プログラミングコンテストチャレンジブックの P.320 には、より重心の存在証明を意識した構成方法が以下のように示されています:
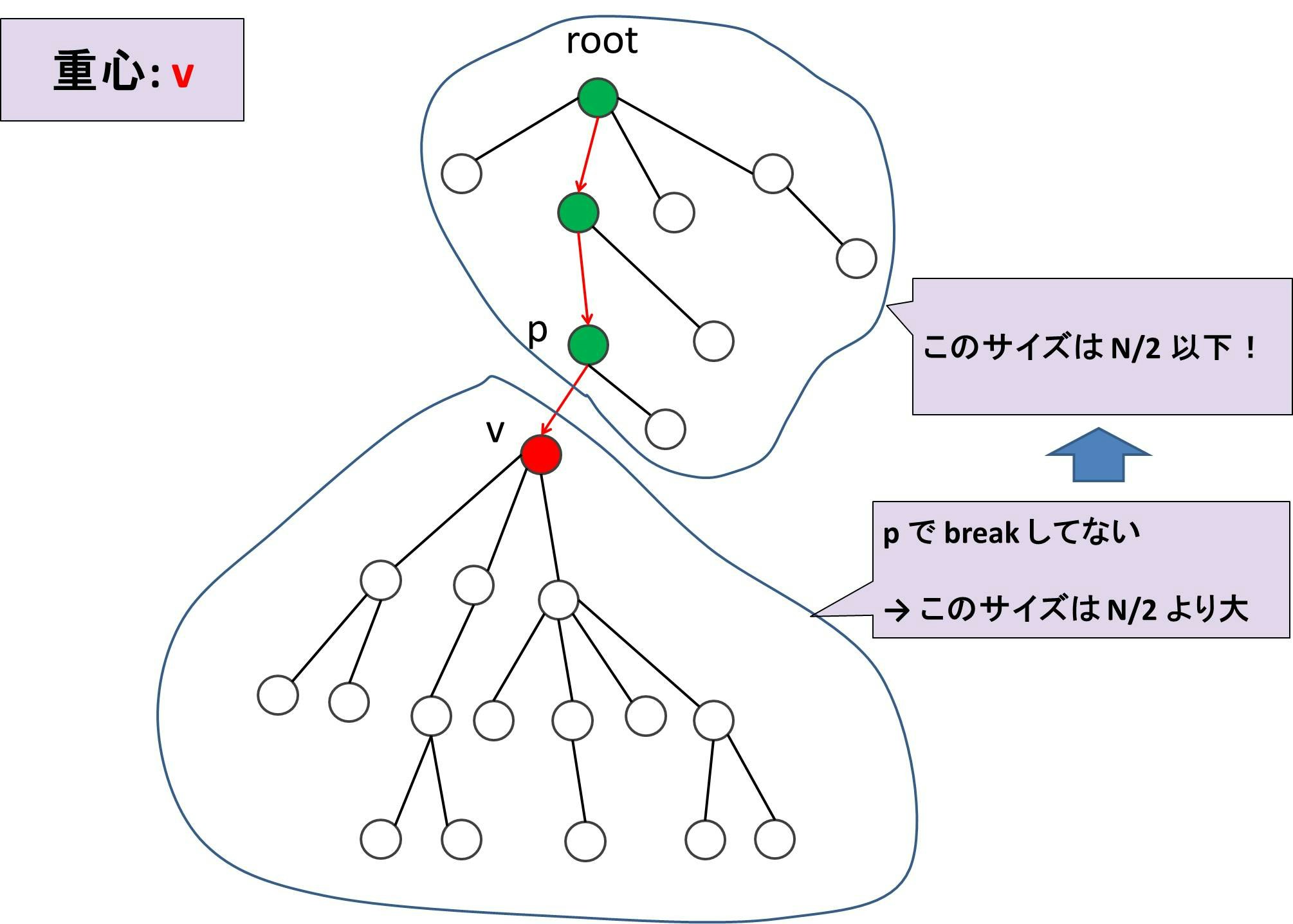
- 根を適当に決めて根付き木とし、v ← 根とする
- While True:
- If v の子ノードたちからなる部分木たちのサイズがすべて N/2 以下:
- v を重心として break
- v の子ノードのうち、最も部分木のサイズが大きいものを ch として、v ← ch
つまり root から出発して、「子ノードを根とする部分木のうち一番大きいやつに侵入」を繰り返して、初めて「子供が全員 N/2 以下」になる部分で break します。このアルゴリズムが停止することは明らかです。root から出発して、最悪 leaf まで行けば部分木たちのサイズの最大値が 0 になるので、それまでにどこかで停止します。
そしてよくよく考えるとこのアルゴリズムが停止したときの v は重心になっています!
v の子供たちはみんなサイズ N/2 以下ですが、図のように v の親のサイズも N/2 以下になっていることがわかります。以上から、重心が常に存在することもわかりました。
ツリー上の分割統治法: ツリーの重心分解を再帰的に行う方法
ツリーの重心分解は単発で行うケースもありますが、多くの場合は再帰的に重心分解していきます。
再帰的に重心分解していく上で難しいのは
- 再帰的に作られていく部分ツリーをどのように表現するか
- 重心分解によって作られた部分ツリーにさらに重心分解を適用するときに、その部分ツリー全体の頂点数を予め知ること
1 つ目については、既に取り除かれた頂点をフラグ管理しておけば実装することができます。
2 つ目については、ここでは重心を求めるために使用したツリーDPの結果をフル活用する方針で書いてみます。
再帰的な重心分解を意識した実装例を以下に示します。
より実践的な分割統治の書き方については、こうきさんの記事にまとまっています。
const int MAX_V = 2100; // ツリーのサイズのありうる最大値
int N; // ツリーのサイズ
vector<int> tree[MAX_V]; // ツリーを隣接リスト形式のグラフ構造で表したもの
int sizeSubtree[MAX_V]; // sizeSubtree[v] := v を根とする部分ツリーのサイズ (分割統治の毎ステップごとに再利用)
bool isRemoved[MAX_V]; // isRemoved[v] := v が既に取り除かれたかどうか
int whoIsParent[MAX_V]; // whoIsParent[v] := ツリーDP時に v の親が誰だったか
// メイン処理
vector<int> centroids;
void FindCentroidRecursive(int v, int size, int p = -1) {
sizeSubtree[v] = 1;
whoIsParent[v] = p;
bool isCentroid = true;
for (auto ch : tree[v]) {
if (ch == p) continue;
if (isRemoved[ch]) continue;
FindCentroidRecursive(ch, size, v);
if (sizeSubtree[ch] > size / 2) isCentroid = false;
sizeSubtree[v] += sizeSubtree[ch];
}
if (size - sizeSubtree[v] > size / 2) isCentroid = false;
if (isCentroid) centroids.push_back(v);
}
// 初期化
void Init() {
for (int i = 0; i < MAX_V; ++i) {
isRemoved[i] = false;
}
}
// first: 重心, second: (重心の子ノード, 子部分木のサイズ) からなるベクトル
pair<int, vector<pair<int,int> > > FindCentroid(int root, int size) {
vector<pair<int, int> > subtrees;
centroids.clear();
FindCentroidRecursive(root, size);
int center = centroids[0];
for (auto ch : tree[center]) {
if (isRemoved[ch]) continue;
if (ch == whoIsParent[center]) {
subtrees.push_back(make_pair(ch, size - sizeSubtree[center]));
}
else {
subtrees.push_back(make_pair(ch, sizeSubtree[ch]));
}
}
return make_pair(center, subtrees);
}
ツリーの重心分解を用いる具体的な問題たち
とてもよくまとまっている記事たちがあるのでそれらへのポインタを示します:
おわりに
本記事ではツリーの重心という概念の図解を試みました。