再帰関数を学ぶと、どんな世界が広がるか

0. はじめに

再帰関数は初めて学ぶときに壁になりがちで

• なんとなくわかった...けれど
• どんな場面で使えるのだろう...いい感じの例を探したい！

という気持ちになりがちです。再帰関数は、なかなかその動きを直感的に想像することが難しいため、掴み所が無いと感じてしまいそうです。

そこで本記事では

• 再帰関数の動きを追いまくることで、再帰関数自体に慣れる
• 再帰的なアルゴリズムの実例に多数触れることで、世界を大きく広げる！

ことを目標とします。特に「再帰関数がどういうものかはわかったけど、使いどころがわからない」という方のモヤモヤ感を少しでも晴らすことができたら嬉しいです。なお本記事では、ソースコード例に用いるプログラミング言語として C++ を用いておりますが、基本的にはプログラミング言語に依存しない部分についての解説を行っています。

追記

1. 再帰関数とは

再帰の意味はとても広いです。自分自身を呼び出す関数を再帰的 (recursive) であると呼び、再帰的な関数のことを再帰関数 (recursive function) と呼びます。また再帰的に関数を呼び出すことを再帰呼び出し (recursive call) と呼びます。とにかく、自分自身を呼び出しさえすれば、再帰的であると言えます。広い概念ですね！！！！！

再帰関数は一般に次のような形式で記述します。物によっては「再帰呼び出し」「その前後で色々やる」「答えを返す」をまとめて一行でやってしまうこともあります。

戻り値の型 func(引数) {
  if (ベースケース) {
    return ベースケースに対する値;
  }
  
  func(次の引数); // 再帰呼び出しします。その前後でも色々やります。
  return (答え);
}

ポイントとしては、以下の条件を満たすように再帰関数を設計します。

• ベースケースに対して return する処理を必ず入れる
• 再帰呼び出しを行ったときの問題が、元の問題よりも小さな問題となるように再帰呼び出しを行い、そのような「より小さい問題の系列」が最終的にベースケースに辿り着くようにする

まず「ベースケースに対する処理」がとても大切です。これをやらないと再帰呼び出しを無限に繰り返すようなこととなり、逮捕に繋がってしまうかもしれません¹。「より小さい問題の系列」に関する話はわかりにくいかもしれません。最初に具体的な再帰関数の例を見てみます。

再帰関数の最初の例として、よく教科書などにも載っているように「$n$ 以下の正の整数の総和 ($1 + 2 + \dots + n$) を計算するプログラム」を取り上げます。

int func(int n) {
    if (n == 0) return 0;
    return n + func(n-1);
}

これを用いて以下のプログラムを実行してみます。

#include <iostream>
using namespace std;

int func(int n) {
    if (n == 0) return 0;
    return n + func(n-1);
}

int main() {
    for (int n = 0; n <= 10; ++n) {
        cout << n << " までの和 = " << func(n) << endl;
    }
}

結果は以下のようになりました:

0 までの和 = 0
1 までの和 = 1
2 までの和 = 3
3 までの和 = 6
4 までの和 = 10
5 までの和 = 15
6 までの和 = 21
7 までの和 = 28
8 までの和 = 36
9 までの和 = 45
10 までの和 = 55

確かに、例えば「$5$ までの和」のところを見ると

$5 + 4 + 3 + 2 + 1 = 15$

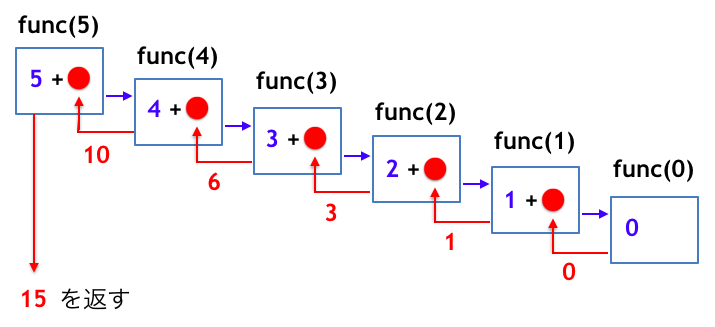
になっていますね。func(n) の n に色々な値を代入すると何が起こるのか、詳しく見て行きましょう。先立って func(5) を呼び出した時の様子を図示してみます。

n = 0 のとき

まずは一番基本のベースケースからです。func(0) を呼び出すと、

if (n == 0) return 0;

によって一瞬で 0 が返って来ます。

n = 1 のとき

次に n = 1 のときはどうでしょう。まず func(1) を呼び出すと、

return n + func(n-1)

の行に入ることがわかります。ここでの処理は

• 1 + func(0) を計算しようとして、func(0) を呼び出す
• func(0) は、0 を返す (すでに述べた通り)
• よって、1 + func(0) = 1 + 0 = 1 となる
• その値を return する

という流れになっています。よって 1 が返って来ることになります。

n = 2 のとき

少しずつ難しくなります。まず func(2) を呼び出すと

• 2 + func(1) によって func(1) が呼び出される
• func(1) の中では 1 + func(0) によって、func(0) が呼び出される
• func(0) では 0 を返す

という流れになりますので、結局

2 + func(1)

の func(1) のところが

2 + 1 + func(0)

になって、これが

2 + 1 + 0

となるイメージですね。その結果、3 が返って来ます。

n = 5 のとき

一気に進めて n = 5 を見てみましょう。まず func(5) の中身で

5 + func(4)

になって、func(4) はその中で 4 + func(3) になるので func(3) が呼ばれて

5 + 4 + func(3)

になって、func(3) はその中で 3 + func(2) になるので func(2) が呼ばれて

5 + 4 + 3 + func(2)

になって、func(2) はその中で 2 + func(1) になるので func(1) が呼ばれて

5 + 4 + 3 + 2 + func(1)

になって、func(1) はその中で 1 + func(0) になるので func(0) が呼ばれて

5 + 4 + 3 + 2 + 1 + func(0)

になって、最終的に func(0) = 0 によって

5 + 4 + 3 + 2 + 1 + 0

となります。答えとして 15 が返って来ます。注意点として、ここでは最終的に「5 + 4 + 3 + 2 + 1 + 0」になるという言い方をしたのですが、実際には func(5) は、

• 5 + func(4)

となったときに、func(4) はその中で色々ごちゃごちゃごちゃ〜〜〜とするうちに 10 という値を返して来て、最後に 5 + 10 = 15 として 15 を返すという感じになります。

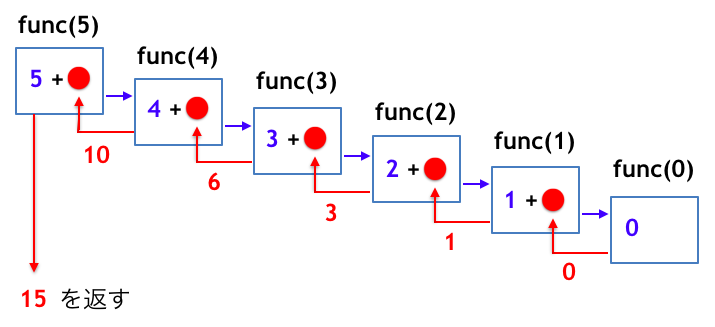
func(5) を呼び出したときの動きのイメージを再び図示すると次のようになります。

1-1. 再帰関数の有限停止性について

再帰関数の動きの一例を追ったところで、再帰関数を設計するときの考え方がハッキリして来たと思います:

• ベースケースに対して return する処理を必ず入れる
• 再帰呼び出しを行ったときの問題が、元の問題よりも小さな問題となるように再帰呼び出しを行い、そのような「より小さい問題の系列」が最終的にベースケースに辿り着くようにする

ベースケースがないと、再帰呼び出しが延々と続いてしまうことになります。そしてベースケースに対する処理を書いていたとしても、例えば、再帰呼び出し時の問題を元の問題とまったく同じにしてしまうと、大変なことになってしまいます。例えば下のようなソースコードを実行してみると、ひたすら "hyogo" が出力されるはずです。

#include <iostream>
using namespace std;

void func(int n) {
    if (n == 0) return;
    cout << "hyogo" << endl;
    func(n);
}

int main() {
    func(10);
}

1-2. 再帰呼び出しが複数回の場合: フィボナッチ数列

上記の例では、再帰関数の中で再帰呼び出しを行うのは 1 回だけでした。ここで再帰呼び出しを複数回行う例も見てみましょう。例としてフィボナッチ数列を求める再帰関数を考えてみます。フィボナッチ数列は

• $F_0 = 0$
• $F_1 = 1$
• $F_{n} = F_{n-1} + F_{n-2}$ ($n = 2, 3, \dots$)

によって定義される数列でした。$0, 1, 1, 2, 3, 5, 8, 13, 21, \dots$ と続いていきます。フィボナッチ数列の第 $n$ 項 $F_n$ を計算する再帰関数は、上記の漸化式を参考に、自然に書くことができます。

#include <iostream>
using namespace std;

int fibo(int n) {
    // ベースケース
    if (n == 0) return 0;
    else if (n == 1) return 1;

    // 再帰呼び出し
    return fibo(n-1) + fibo(n-2);
}
    
int main() {
    for (int n = 0; n <= 10; ++n) {
        cout << n << " 項目の値: " << fibo(n) << endl;
    }
}

今回はベースケースは $n = 0, 1$ の $2$ 通りになりました。そして fibo($n$) の中での再帰呼び出しも

• fibo($n-1$)
• fibo($n-2$)

の $2$ つを呼び出しています。上のコードを実行した結果は以下のようになります。

0 項目の値: 0
1 項目の値: 1
2 項目の値: 1
3 項目の値: 2
4 項目の値: 3
5 項目の値: 5
6 項目の値: 8
7 項目の値: 13
8 項目の値: 21
9 項目の値: 34
10 項目の値: 55

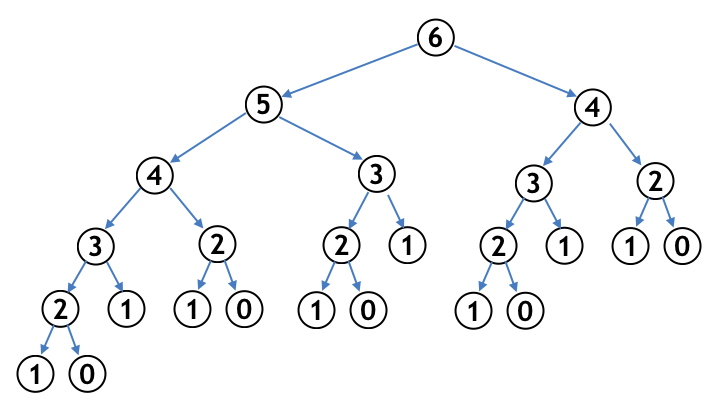
また、今回は再帰関数の中で再帰呼び出しを $2$ 回行っていることから、再帰呼び出しの流れは複雑になります。fibo($6$) を呼び出したときに呼び出される fibo 関数の引数の流れを下図に示します。

1-3. 動的計画法 (メモ化再帰) へ

実は上記の再帰関数は「同じ計算を何度も実行することなって大変効率が悪い」という問題を抱えています。上図を見ると、fibo($6$) を計算するのに実に $25$ 回もの関数呼び出しを行っていることがわかります。$25$ 回程度ならまだいいのですが、fibo($50$) ともなると計算量が爆発してしまい、とても現実的な時間で答えを求めることができなくなってしまいます²！！！

しかし違和感を感じる方も多いでしょう。フィボナッチ数列の計算は $F_0 = 0, F_1 = 1$ から出発して「前の二項を順々に足して行く」という風にすれば

$0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \dots$

とすぐに計算できそうです。$n$ 項目を求めるまでに実施する足し算回数は僅か $n-1$ 回で済みます。つまり以下のように for 文反復コードによって十分高速に求めることができます。

#include <iostream>
#include <vector>
using namespace std;

int main() {
    vector<long long> F(50);
    F[0] = 0, F[1] = 1;
    for (int n = 2; n < 50; ++n) {
        F[n] = F[n-1] + F[n-2];
        cout << n << " 項目: " << F[n] << endl;
    }
}

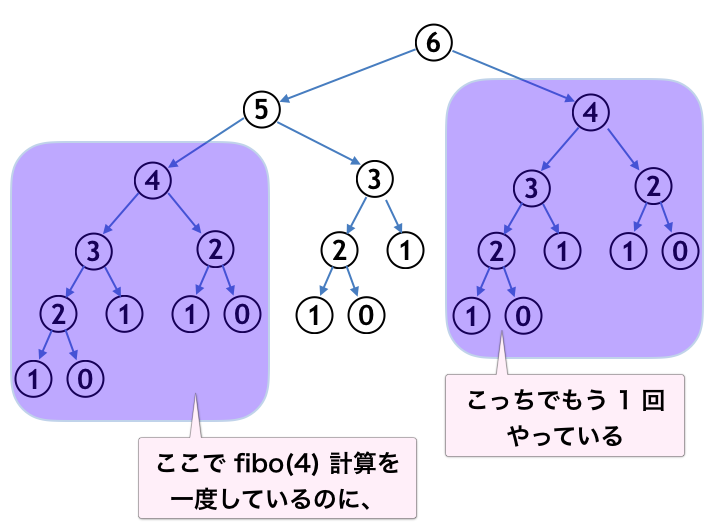
なぜ再帰関数を用いたフィボナッチ数列計算は、計算量が爆発してしまうのでしょうか。それは例えば下図のような無駄があるからです。

fibo(4) に限らず、fibo(3) の計算なども $3$ 回繰り返していることもわかります。このような無駄を省くためには

• 同じ引数に対する答えをメモする

という方法が大変有効です。具体的には

• memo[v] := v 項目の答えを格納する、未計算時は -1 を格納する

といった配列を用意してあげて、再帰関数の中で計算済みであれば「再帰呼び出しを行わずに直接リターンする」としてあげます。これによって大幅な高速化を実現することができて、計算量的には for 文ループを用いた方法と同等なものになります。

#include <iostream>
#include <vector>
using namespace std;

long long fibo(int n, vector<long long> &memo) {
    // ベースケース
    if (n == 0) return 0;
    else if (n == 1) return 1;

    // メモをチェック (既に計算済みなら答えをリターンする)
    if (memo[n] != -1) return memo[n];

    // 答えをメモしながら、再帰呼び出し
    return memo[n] = fibo(n-1, memo) + fibo(n-2, memo);
}
    
int main() {
    // メモ用配列 (-1 は未計算であることを表す)
    vector<long long> memo(50, -1);
    for (int n = 0; n < 50; ++n) {
        cout << n << " 項目の値: " << fibo(n, memo) << endl;
    }
}

以上の方法は、実は動的計画法と呼ばれるフレームワークを再帰関数によって実現したものになっています。動的計画法の実現方法として、メモ化処理を施した再帰関数を用いたものを、特にメモ化再帰と呼ぶことがあります。動的計画法・メモ化再帰は極めて汎用的で強力なアルゴリズムなので、興味のある方は

• 動的計画法超入門！ Educational DP Contest の A ～ E 問題の解説と類題集

などを参照していただけたらと思います。

2. 再帰関数の使いどころ

さて、上記の「$1 + 2 + \dots + n$ を計算するプログラム」は、再帰関数を理解するための最初の例としてはわかりやすいですが、再帰関数を用いる必要性の薄いものでした。使用言語にも依りますが、手続き型プログラミングのできる言語であれば for 文ループで書くのも自然です:

int sum = 0;
for (int i = 1; i <= n; ++i) {
    sum += i;
}

一方では再帰関数を用いることで簡潔かつ明快な記述ができるアルゴリズムも多々あります。例えば以下の表のような場面で再帰関数が大活躍します。本記事ではこのうちの

• 部分和問題
• 数独ソルバー
• グラフ上の探索

について簡単に触れてみます。グラフ上の探索については非常に重要なテーマなのでまた別途記事を書きたいのですが、その考え方について簡単に触れてみます。また再帰関数を用いた再帰的なアルゴリズムたちについては、詳細な解説を行ってる文献へのリンクを示します。さらに分割統治法を用いたクイックソートやマージソートについては、

• ソートを極める！ 〜 なぜソートを学ぶのか 〜

に詳しく書いたので参考にしていただけたらと思います。

場面	例
$n$ 重の for 文を書きたくなるケース	数独ソルバー, 虫食算ソルバー, 部分和問題など
グラフ上の探索	トポロジカルソート, サイクル検出, 二部グラフ判定など
再帰的なアルゴリズム	Euclid の互除法, 繰り返し自乗法, Union-Find 木の経路圧縮, 再帰下降構文解析など
分割統治法・縮小法	マージソート, クイックソート, median of median など
動的計画法 (メモ化再帰)	超多数

3. n 重の for 文を書きたい

まずは再帰関数を用いることで明快に記述できる探索アルゴリズムを挙げます。

3-1. 部分和問題

for 文ループのネストは二重三重までであれば登場するケースも多いでしょう。例えば $500$ 円のコインが $A$ 枚、$100$ 円のコインが $B$ 枚、$50$ 円のコインが $C$ 枚あって、その中から何枚か選んで合計金額がちょうど $X$ 円になる方法が何通りあるかを求める問題は、以下のように三重の for 文を用いると簡単に解くことができます。

• 500 円コインを用いる枚数を $a$ とすると $a$ は $a = 0, 1, \dots, A$ の $A+1$ 通りの候補がある
• 100 円コインを用いる枚数を $b$ とすると $b$ は $b = 0, 1, \dots, B$ の $B+1$ 通りの候補がある
• 50 円コインを用いる枚数を $c$ とすると $c$ は $c = 0, 1, \dots, C$ の $C+1$ 通りの候補がある

ということで、全部で $(A+1)(B+1)(C+1)$ 通りの場合があります。これを全探索して、そのうち合計金額が $X$ 円になるものをカウントします。

#include <iostream>
using namespace std;

int main() {
    // 入力
    int A, B, C, X;
    cin >> A >> B >> C >> X;

    // 求める
    int num = 0;
    for (int a = 0; a <= A; ++a) {
        for (int b = 0; b <= B; ++b) {
            for (int c = 0; c <= C; ++c) {
                // 条件を満たしていたらカウント
                if (500*a + 100*b + 50*c == X) {
                    ++num;
                }
            }
        }
    }

    // 答えを出力
    cout << num << endl;
}

それではコインの種類を増やして $n$ 種類のコインがあるとします。コインの金額はそれぞれ $a_0, a_1, \dots, a_{n-1}$ 円であるとします。簡単のため、今回はコインはそれぞれ $1$ 枚のみとします。これらのコインの中から何枚か選んで、合計金額を $X$ 円にする方法は何通りあるでしょうか？？？

この問題は実は部分和問題と呼ばれる有名問題です。まずは先ほどと同様の全探索を考えてみましょう。

• $a_0$ 円のコインについて「$0$ 個選ぶ (選ばない)」「$1$ 個選ぶ」の $2$ 通りの選択肢がある
• $a_1$ 円のコインについて「$0$ 個選ぶ (選ばない)」「$1$ 個選ぶ」の $2$ 通りの選択肢がある
• ...
• $a_{n-1}$ 円のコインについて「$0$ 個選ぶ (選ばない)」「$1$ 個選ぶ」の $2$ 通りの選択肢がある

ということで全部で $2^n$ 通りの選択肢があります。どうしたらこの $2^n$ 通りの選択肢を調べることができるでしょうか。コインが $3$ 種類のみであった場合と同様に

for (int i0 = 0; i0 <= 1; ++i0) {
    for (int i1 = 0; i1 <= 1; ++i1) {
        for (int i2 = 0; i2 <= 1; ++i2) {
            for (int i3 = 0; i3 <= 1; ++i3) {
                for (int i4 = 0; i4 <= 1; ++i4) {
                    ...

という風にできたら良いのですが、for 文が何重にもループするのは見栄えが悪いですし、何より $n$ の値を予め知らなければ何重にすればよいのかもわかりません。こんなとき、再帰関数が活躍します！

最初に大まかなイメージを掴んでおきましょう。われわれは $n$ 個の整数 $a_0, a_1, \dots, a_{n-1}$ から何個か選んで総和を $X$ にできるかどうかを知りたいです。これは以下のように場合分けできるでしょう:

• $a_{n-1}$ を選ばないとき、$n-1$ 個の整数 $a_0, a_1, \dots, a_{n-2}$ から $X$ を作れるならば OK
• $a_{n-1}$ を選ぶとき、$n-1$ 個の整数 $a_0, a_1, \dots, a_{n-2}$ から $X - a_{n-1}$ を作れるならば OK

この $2$ 通りの場合のうちどちらかが OK なら元の問題の答えも OK であることがわかります。こうして問題は $n$ 個の整数についての問題から、$n-1$ 個の整数についての問題へと帰着することができました。以降同様にして、$n-1$ 個の整数についての問題を $n-2$ 個の整数についての問題へと帰着して、それを $n-3$ 個の整数についての問題へと帰着して...と再帰的に繰り返して行きます。

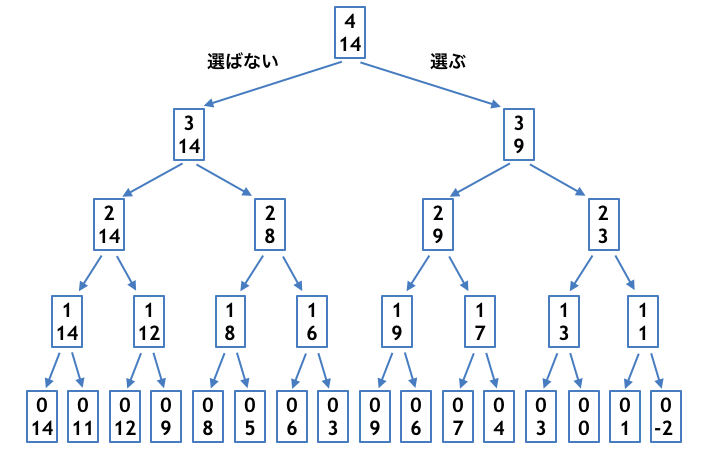
例えば $n = 4, a = (3, 2, 6, 5), X = 14$ に対する再帰的アルゴリズムの挙動を図にすると上図のようになるでしょう。図の各ノードの上の数値は「何個の整数についての問題か」を表していて、下の数値は「何の値を作りたいか」を表しています。そして末端のノードに一つでも答えが Yes になるものがあれば、大元のノードの答えも Yes になります。

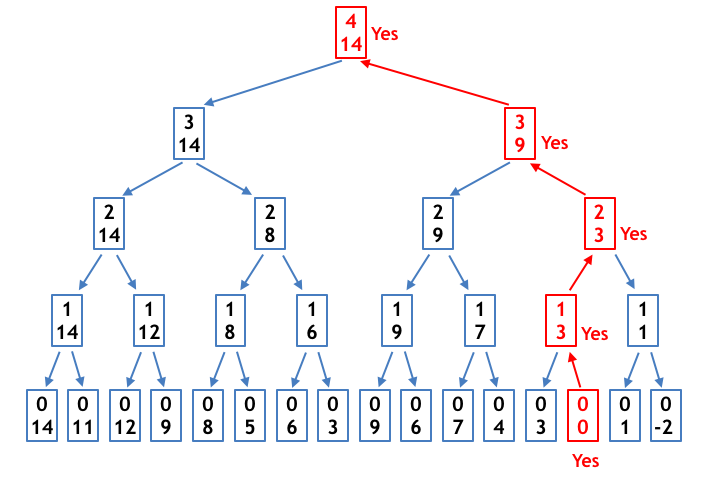
さらに具体的な部分和の選び方も復元することができて、図の一番下の $(0, 0)$ から上へ辿って行くと、

• $a_0 = 3$ は選ぶ ($(1, 3)$ の状態になります)
• $a_1 = 2$ は選ばない ($(2, 3)$ の状態になります)
• $a_2 = 6$ は選ぶ ($(3, 9)$ の状態になります)
• $a_3 = 5$ は選ぶ ($(4, 14)$ の状態になります)

とすることで、総和を $14$ にできることもわかります。

具体的には再帰関数を

• func(int i, int x):=　$a_0, a_1, \dots, a_{n-1}$ のうちの最初の $i$ 個 ($a_0, a_1, \dots, a_{i-1}$) から何個か選んで総和を $x$ にできるかどうかを返す

と定義してあげます。func($n$, $X$) が最終的な答えです。以下のように実装できるでしょう。注意点として、func(i-1, x, a) が true であったならば、func(i-1, x-a[i-1], a) を調べるまでもなく true なので、その時点で return true; としています。

#include <iostream>
#include <vector>
using namespace std;

bool func(int i, int x, const vector<int> &a) {
    // ベースケース
    if (i == 0) {
        if (x == 0) return true;
        else return false;
    }

    // a[i-1] を選ばない場合 (func(i-1, x, a) が OK なら OK)
    if (func(i-1, x, a)) return true;

    // a[i-1] を選ぶ場合 (func(i-1, x-a[i-1], a) が OK なら OK)
    if (func(i-1, x-a[i-1], a)) return true;

    // どっちもダメだったらダメ
    return false;
}

int main() {
    // 入力
    int n; cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; ++i) cin >> a[i];
    int X; cin >> X;

    // 再帰的に解く
    if (func(n, X, a)) cout << "Yes" << endl;
    else cout << "No" << endl;
}

入力ケースとして例えば $n = 5, a = (3, 5, 1, 2, 9), X = 8$ とすると "Yes" が出力されますし、$n = 5, a = (9, 8, 3, 1, 3), X = 19$ を入力すると "No" が出力されます。

なお、このアルゴリズムの計算時間ですが、最悪ケース³では $2^n$ 通りの場合を考えているので少しでも $n$ が大きくなると膨大な時間がかかってしまいます。現実的な時間内に答えが求められるのは $n = 30$ 程度まででしょう。決して効率的とは言えないアルゴリズムです。

部分和問題に対するメモ化

しかしながら $a_i$ や $X$ が正の整数で、$X$ の値がそれほど大きくない場合にはより効率的なアルゴリズムが存在します。$n = 100$ 程度であっても解くことができます。実は上記の実装をほんの少し改良するだけで実現できます。

フィボナッチ数列を求める再帰関数に対して施したメモ化による改良とまったく同様に、

• dp[i][x] := func(i, x) についての答え

をメモしておく配列を用意しましょう。そうすると以下のように自然に動的計画法に基づくアルゴリズムを作ることができます。これによって計算量は $O(NX)$ となり、$2^N$ 通りの選択肢を調べていた状態から大きく改善しました。

#include <iostream>
#include <vector>
using namespace std;

bool func(int i, int x, const vector<int> &a, vector<vector<int> > &dp) {
    // ベースケース
    if (i == 0) {
        if (x == 0) return true;
        else return false;
    }
    if (x < 0) return false;
    
    // メモをチェック
    if (dp[i][x] != -1) return dp[i][x];
    
    // a[i-1] を選ばない場合
    if (func(i-1, x, a, dp)) return dp[i][x] = 1; // true をメモしながらリターン
    
    // a[i-1] を選ぶ場合
    if (func(i-1, x-a[i-1], a, dp)) return dp[i][x] = 1; // true をメモしながらリターン
    
    // どっちもダメだったらダメ
    return dp[i][x] = 0; // false をメモしながらリターン
}

int main() {
    // 入力
    int n; cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; ++i) cin >> a[i];
    int X; cin >> X;
    
    // 再帰的に解く
    const int MAX = 100000; // 例えば X の取りうる最大値を 100000 としてみます
    vector<vector<int> > dp(n+1, vector<int>(MAX+1, -1)); // -1 は未確定を表す
    if (func(n, X, a, dp)) cout << "Yes" << endl;
    else cout << "No" << endl;
}

ナップサック問題へ

動的計画法というと、ナップサック問題を思い浮かべる方も多いと思います。上記の部分和問題に対する動的計画法をほんの少し変更するだけで、ナップサック問題に対する動的計画法も設計することができます。それについて関心のある方は

• 動的計画法超入門！ Educational DP Contest の A ～ E 問題の解説と類題集
• 典型的な DP (動的計画法) のパターンを整理 Part 1 ～ ナップサック DP 編 ～

などを読んでいただけたらと思います。

3-2. 数独

再帰関数を用いた全探索に慣れて来たところで、少し面白い例に進みます。数独ソルバーを実装してみましょう！下画像は wikipedia に載っている問題です。

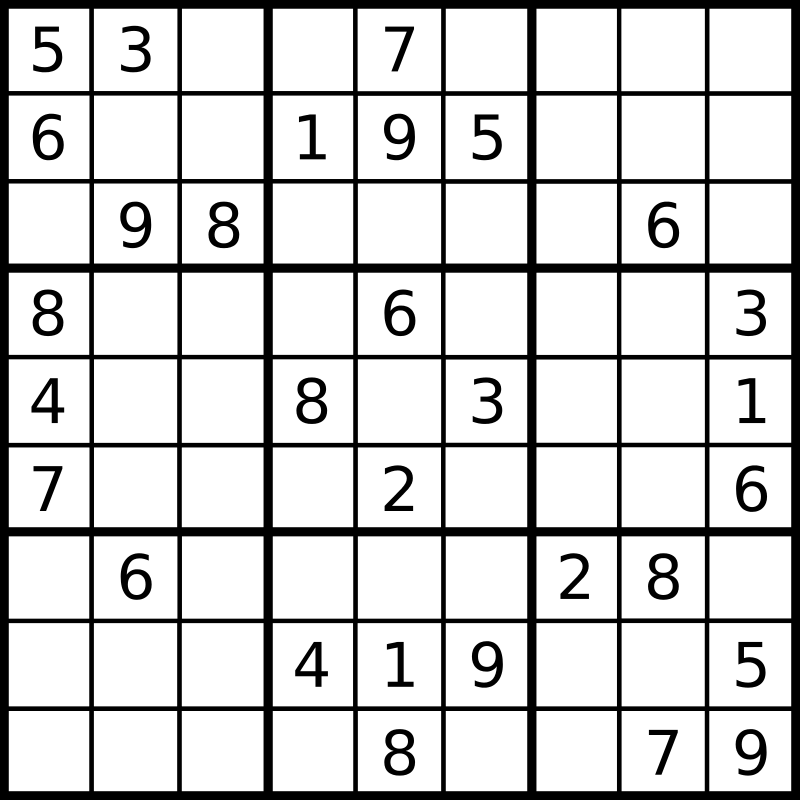
これを解くにはどうしたらよいでしょうか。部分和問題を解いたときと同じような全探索をする気持ちになると

• 各マスに対して $1$〜$9$ を入れて行く (マスの個数を $n$ とすると $9^n$ 通りの選択肢がある)
• そのうち条件を満たすものを求める

という風にすれば良さそうです。さて、第一感では $9^n$ 通りの選択肢を調べるのは厳しそうに感じられるかもしれないですが、実際は再帰関数の途中で「そのマスにどの数字を入れてもダメだと判明したら打ち切る」という枝刈りを行うことで、現実的な時間で素早く解を求めることができます。

以下に挙げる実装は、特別な工夫は施していない大変シンプルなものですが、それでも試しに

53**7****
6**195***
*98****6*
8***6***3
4**8*3**1
7***2***6
*6****28*
***419**5
****8**79

という入力を与えると、

5 3 4 6 7 8 9 1 2 
6 7 2 1 9 5 3 4 8 
1 9 8 3 4 2 5 6 7 
8 5 9 7 6 1 4 2 3 
4 2 6 8 5 3 7 9 1 
7 1 3 9 2 4 8 5 6 
9 6 1 5 3 7 2 8 4 
2 8 7 4 1 9 6 3 5 
3 4 5 2 8 6 1 7 9 

という答えが、$1$ 秒もかからずに出力されます。

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
using Field = vector<vector<int> >; // 盤面を二次元配列で表す

// res に見つかった答えを格納する, 答えが一つとは限らないので res を vector<Filed> 型とする
void rec(Field &field, vector<Field> &res) {
    // 空きマスを探す
    int emptyi = -1, emptyj = -1;
    for (int i = 0; i < 9 && emptyi == -1; ++i) {
        for (int j = 0; j < 9 && emptyj == -1; ++j) {
            if (field[i][j] == -1) {
                emptyi = i, emptyj = j;
                break;
            }
        }
    }

    // ベースケース (すべて埋めて空きマスがない)
    if (emptyi == -1 || emptyj == -1) {
        res.push_back(field);      
        return;
    }

    // 空きマスに入れられる数字を求める
    vector<bool> canuse(10, 1); // canuse[v] := 空きマスに v を入れられるかどうか
    for (int i = 0; i < 9; ++i) {
        // 同じ列に同じ数字はダメ
        if (field[emptyi][i] != -1) canuse[field[emptyi][i]] = false;

        // 同じ行に同じ数字はダメ
        if (field[i][emptyj] != -1) canuse[field[i][emptyj]] = false;

        // 同じブロックに同じ数字はダメ
        int bi = emptyi / 3 * 3 + 1, bj = emptyj / 3 * 3 + 1; // 同じブロックの中央
        for (int di = bi-1; di <= bi+1; ++di) 
            for (int dj = bj-1; dj <= bj+1; ++dj)
                if (field[di][dj] != -1)
                    canuse[field[di][dj]] = false;
    }

    // 再帰的に探索
    for (int v = 1; v <= 9; ++v) {
        if (!canuse[v]) continue;
        field[emptyi][emptyj] = v; // 空きマスに数値 v を置く
        rec(field, res);
    }

    // 数値を置いていた空きマスを元の空きマスに戻す (この処理をバックトラックと呼ぶ)
    field[emptyi][emptyj] = -1;
}

int main() {
    // 入力
    Field field(9, vector<int>(9, -1)); // -1 は未確定
    for (int i = 0; i < 9; ++i) {
        string line; cin >> line;
        for (int j = 0; j < 9; ++j) {
            if (line[j] == '*') continue;

            // line[j] は char 型の '0' 〜 '9'　なので、これらを 0 〜 9 にする
            int num = line[j] - '0'; 
            field[i][j] = num;
        }
    }

    // 再帰的に解く
    vector<Field> res;
    rec(field, res);

    // 答えを出力する
    if (res.size() == 0) cout << "no solutions." << endl;
    else if (res.size() > 1) cout << "more than one solutions." << endl;
    else {
        Field ans = res[0];
        for (int i = 0; i < 9; ++i) {
            for (int j = 0; j < 9; ++j) {
                cout << ans[i][j] << " ";
            }
            cout << endl;
        }
    }
}

以上の実装は、特別な工夫をほとんどしていない大変シンプルな探索ですが、それでも市販されているような数独問題のほとんどを $1$ 秒以内に解くことができます。試しに世界一難しい数独にチャレンジしてみます。

**53*****
8******2*
*7**1*5**
4****53**
*1**7***6
**32***8*
*6*5****9
**4****3*
*****97**

こちらも $1$ 秒かからずに以下の答えを出力することができました:

1 4 5 3 2 7 6 9 8 
8 3 9 6 5 4 1 2 7 
6 7 2 9 1 8 5 4 3 
4 9 6 1 8 5 3 7 2 
2 1 8 4 7 3 9 5 6 
7 5 3 2 9 6 4 8 1 
3 6 7 5 4 2 8 1 9 
9 8 4 7 6 1 2 3 5 
5 2 1 8 3 9 7 6 4 

より性能の高いソルバーを作りたい場合には「どのマスから順番に数字を置いて行くか」という探索順序などについて工夫を行います。

4. グラフ上の探索

部分和問題や数独を解く再帰関数を設計して来ましたが、このような探索は「グラフ上の探索」と考えると見通しがよくなります。グラフとは

• ノードの集まり
• エッジ (ノードとノードの繋がりを表すもの) の集まり

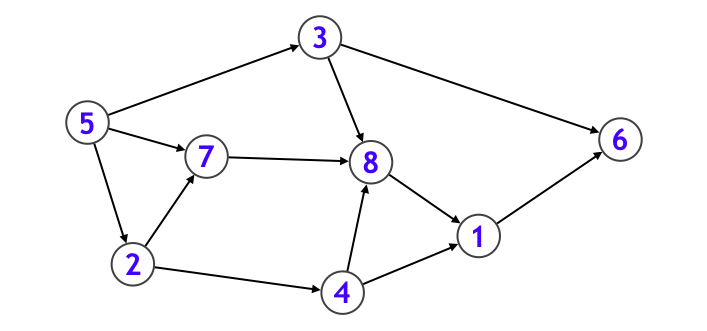
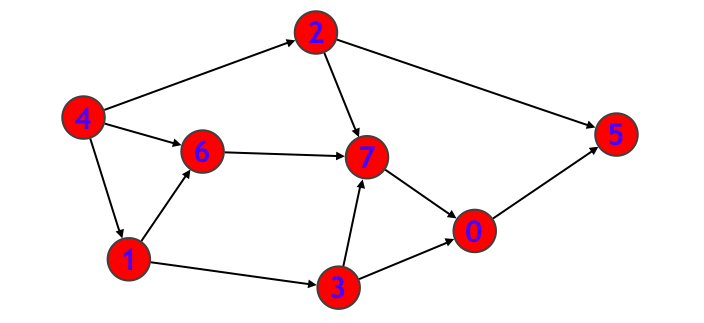
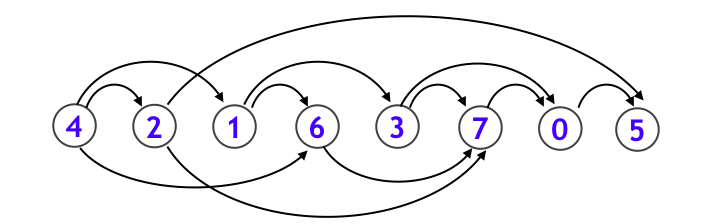
を表すもので、下図のように描画されることが多いです。ノードは丸で、エッジは矢印で表しています。また各ノードには番号を付けています。

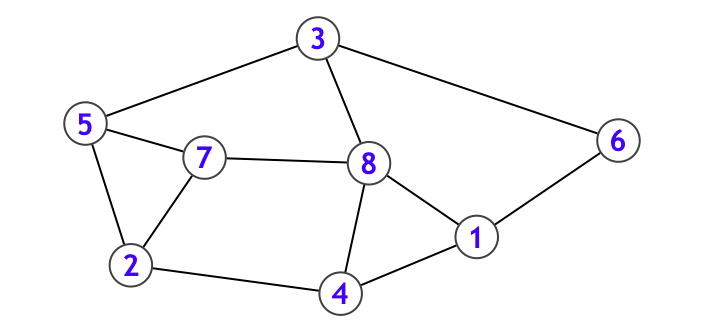
ここでは各エッジに向きがあるバージョンを考えていましたが、各エッジに向きがないバージョンもあります。その場合はエッジは矢印ではなく線分で表すことが多いです。なお、エッジに向きのあるグラフを有向グラフ、向きのないグラフを無向グラフと呼びます。

4-1. グラフを表すデータ構造

まずグラフは隣接リスト形式で表すことにします。すなわち C++ では

using Graph = vector<vector<int> >;

という感じの型で表すことにします。このとき Graph 型の変数を G としたとき G[v] は「ノード v から 1 ステップで行くことのできるノードの集まり」を表しています。例えば下図のようなグラフであれば、

• G[0] = {5}
• G[1] = {3, 6}
• G[2] = {5, 7}
• G[3] = {0, 7}
• G[4] = {1, 2, 6}
• G[5] = { }
• G[6] = {7}
• G[7] = {0}

となります。

4-2. グラフ上の探索

上記のようなグラフデータ構造を用いて、グラフのノードを一通り探索するコードは以下のように書くことができます。ただし

• seen[v] := ノード v を既に訪れたかどうか

で定義される配列 seen を用いることで、同じノードを二度訪問することがないようにしています。下記の実装は一見すると再帰関数のベースケースに対する処理を書いていないように見えるのですが、実は「ノード v から行くことのできるノードがないとき」は再帰呼び出しを行うことはないので、それが自然にベースケースになっています。

#include <iostream>
#include <vector>
using namespace std;
using Graph = vector<vector<int> >; // グラフ

// ノード v を探索し、v から 1 ステップで行くことのできるノードたちを再帰的に探索する
void rec(int v, const Graph &G, vector<bool> &seen) {
    seen[v] = true;
    for (auto next : G[v]) {
        if (seen[next]) continue; // 既に訪問済みなら探索しない
        rec(next, G, seen);
    }
}

int main() {
    int N, M; cin >> N >> M; // 頂点数と枝数
    Graph G(N); // 頂点数 N のグラフ
    for (int i = 0; i < M; ++i) {
        int a, b;
        cin >> a >> b; // ノード a からノード b へと有向辺を張る
        G[a].push_back(b);
    }

    // 探索
    vector<bool> seen(N, 0); // 初期状態では全ノードが未訪問
    for (int v = 0; v < N; ++v) {
        if (seen[v]) continue; // 既に訪問済みなら探索しない
        rec(v, G, seen);
    }
}

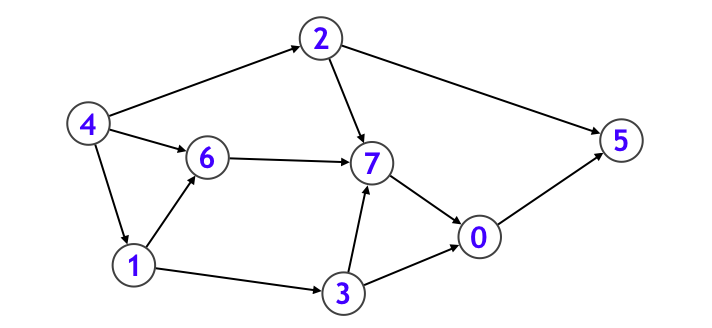
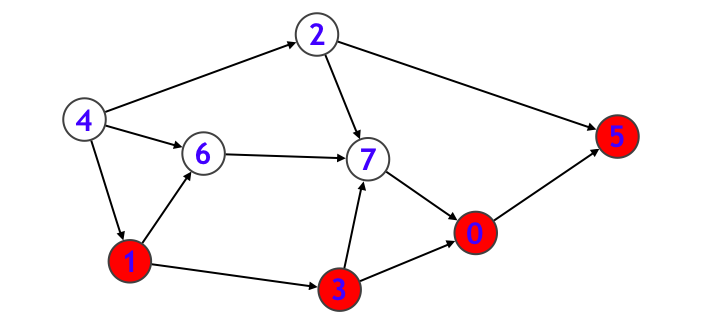
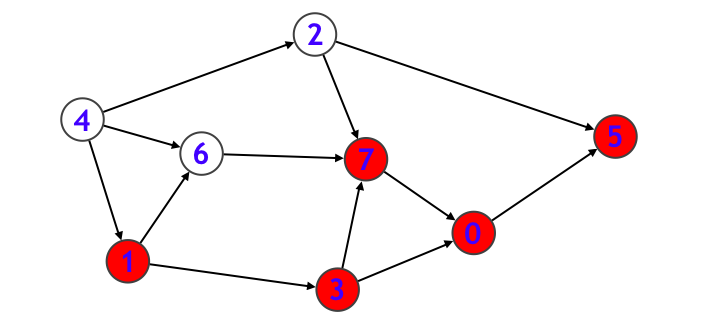
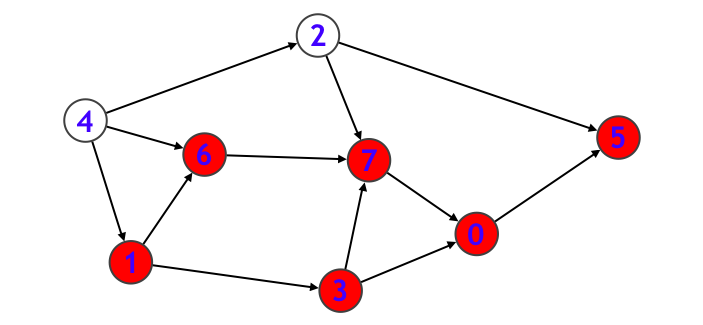
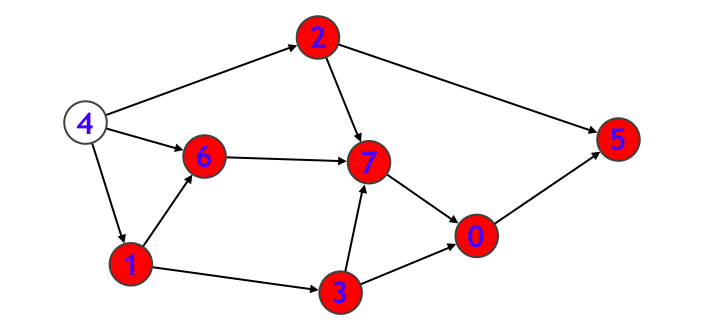
例えば上記のグラフであれば、

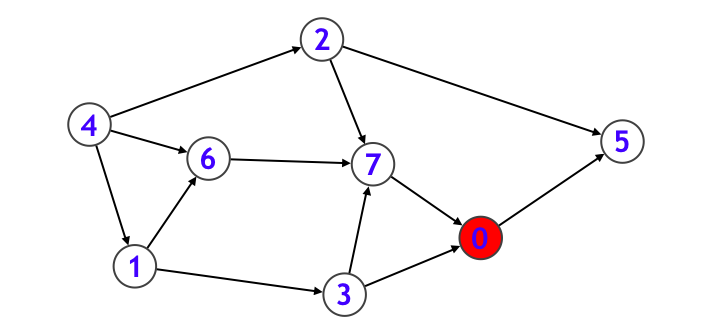
• まずノード $0$ に入り、ノード $0$ が探索済みになります。

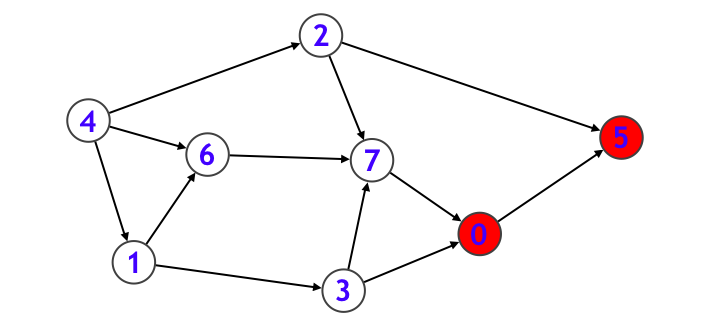
• ノード $0$ から行くことのできるノード $5$ に入り、その後ノード $5$ から行けるノードはないので一旦再帰関数から抜けます。

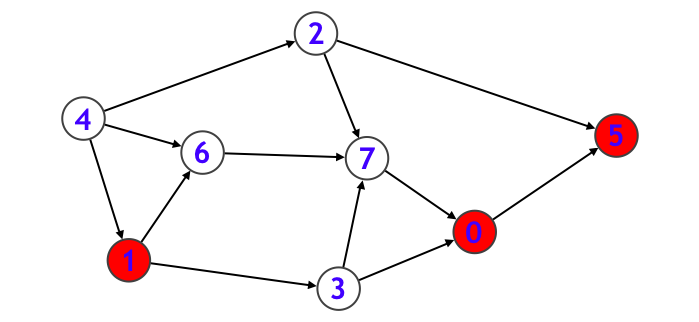
• 次に元の main 関数中の for 文ループに戻り、v = 1 のケースを呼び出す。そしてノード $1$ に入ります。

• ノード $1$ に隣接しているノードは $3$ と $6$ の二種類があります。まずノード番号の小さい $3$ の方から再帰呼び出しを行うとします。

• ノード $3$ に隣接しているノードは $0$ と $7$ の 2 種類がありますが、$0$ は既に探索すみなので、ノード $7$ に入ります。

• ノード $7$ からはノード $0$ へと行けますが、それは探索済みなのでノード $7$ に関する処理は終わり、さらにノード $3$ に関する処理も終わるので、ノード $1$ に戻ります。そしてノード $1$ から行くことのできるもう 1 つのノード $6$ に進みます。

• ノード $6$ から行けるノードはすべて探索済みなのでノード $6$ に関する処理を終えて、さらにノード $1$ に関する処理も終えるので、一旦再帰関数から抜けます。次に元の main 関数中の for 文ループの v = 2 のケースになります。

• ノード $2$ から行くことのできるノードはすべて探索済みなので速攻で再帰関数を抜けて、最後に元の main 関数中の for 文ループの v = 4 のケースを実行して終わります。

以上のような挙動によって、このグラフ上のすべてのノードの探索を行うことができました。実践的には、各ノードの探索を行いながら、様々な処理をついでに行うことで様々なアルゴリズムを設計することができます。代表的な例としてトポロジカルソートを紹介します。

4-3. DAG のトポロジカルソート

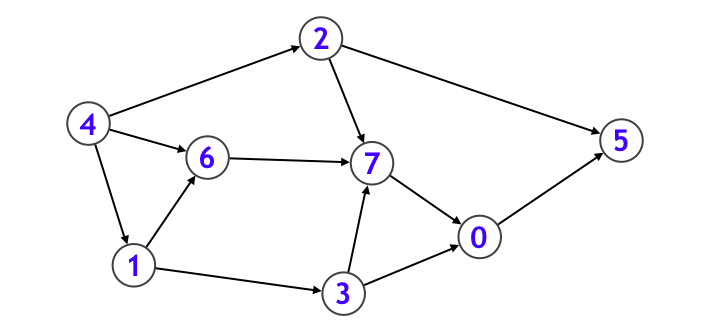
トポロジカルソートとは以下のような有向グラフに対し、

下図のように、辺の向きに沿うように一列に並べることです。応用例としては makefile などに見られるような、依存関係を解決する処理などは、まさにトポロジカルソートそのものです。

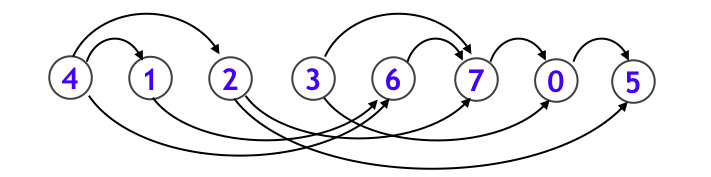
注意点として、基本的に有向グラフを扱うのですが、「サイクルがない」ことが条件となります。つまり、どの頂点から出発しても、その頂点には戻って来れないことが条件になります。そのような有向グラフを DAG (Directed Acyclid Graph) と呼びます。DAG は必ず上記のようなトポロジカルソートが可能です。また、DAG のトポロジカルソートは一般には答えが一通りではなく、上のグラフでも下図のような別の並び替え方もあります。

さて、トポロジカルソート順を求めるアルゴリズムは、実は上述の再帰的探索アルゴリズムにほんの少し手を加えるだけで実現することができます。上のグラフに対して、「どのノードから順番に再帰関数から抜けたか」を整理すると以下のようになります。

• 最初にノード $5$ に関する再帰関数の処理を終えて
• 次にノード $0$ に関する再帰関数の処理を終えます
• 次にノード $7$
• その次にノード $3$
• その次にノード $6$
• その次にノード $1$
• そしてノード $2$
• 最後にノード $4$

という順序で再帰関数から抜けています。ここで、ノード $5$ よりもノード $0$ の方が先に再帰関数内に入っていることから、ノード $5$ が最初に終わるということに違和感を感じる方もいるかもしれません。しかし再帰関数を抜けるタイミングを考えると、先にノード $5$ を抜けてからノード $0$ も抜ける順序になっていることがわかります。

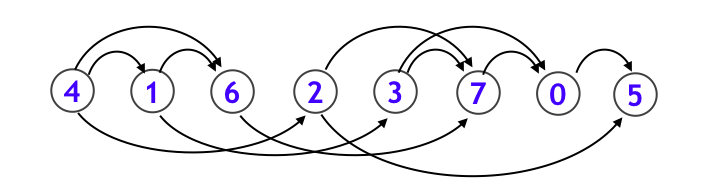
さて、実はこれを逆順に並べなおすとトポロジカルソート順になっています！実際並べてみると下図のようになります。

実装もほんの少し手を加えるだけでできます:

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
using Graph = vector<vector<int> >; // グラフ

// トポロジカルソートする
void rec(int v, const Graph &G, vector<bool> &seen, vector<int> &order) {
    seen[v] = true;
    for (auto next : G[v]) {
        if (seen[next]) continue; // 既に訪問済みなら探索しない
        rec(next, G, seen, order);
    }
    order.push_back(v);
}

int main() {
    int N, M; cin >> N >> M; // 頂点数と枝数
    Graph G(N); // 頂点数 N のグラフ
    for (int i = 0; i < M; ++i) {
        int a, b;
        cin >> a >> b; // ノード a からノード b へと有向辺を張る
        G[a].push_back(b);
    }
    
    // 探索
    vector<bool> seen(N, 0); // 初期状態では全ノードが未訪問
    vector<int> order; // トポロジカルソート順
    for (int v = 0; v < N; ++v) {
        if (seen[v]) continue; // 既に訪問済みなら探索しない
        rec(v, G, seen, order);
    }
    reverse(order.begin(), order.end()); // 逆順に
    
    // 出力
    for (auto v : order) cout << v << " -> ";
    cout << endl;
}

5. 再帰的なアルゴリズムたち

再帰関数を用いることで明快に記述できるアルゴリズムたちについて、詳細に解説している文献を挙げていきます。

5-1. Euclid の互除法

2 つの整数 $a, b$ の最大公約数を求めるアルゴリズムです。以下のようなコードで計算できるのですが、詳しくは

• 拡張ユークリッドの互除法 〜 一次不定方程式 ax + by = c の解き方 〜

を参考にしていただけたらと思います。

long long GCD(long long a, long long b) {
    if (b == 0) return a;
    else return GCD(b, a % b);
}

5-2. 繰り返し自乗法

整数 $a, n, m$ に対して、$a^n$ を $m$ で割った余りを求めます。詳しくは

• 繰り返し自乗法　(satanic さん)

を参考にしていただけたらと思います。

long long modpow(long long a, long long n, long long m) {
    if (n == 0) return 1;
    long long half = modpow(a, n/2, m);
    long long res = half * half % m;
    if (n & 1) res = res * a % m;
    return res;
}

5-3. Union-Find 木の経路圧縮

Union-Find 木とは、グループ分けを管理するデータ構造です。最初はバラバラのグループに属している $n$ 個の要素 $(0, 1, 2, \dots, n-1)$ に対して、

• 要素 $a$ を含むグループと要素 $b$ を含むグループを併合する。
• 要素 $a$ と要素 $b$ が同じグループに属するかを調べる。

という処理を高速に実行することができます。実現方法など詳しくは

• Union find(素集合データ構造)　(AtCoder 公式資料)

を参考にしていただけたらと思います。

struct UnionFind {
    vector<int> par, rank;
    
    UnionFind(int n) : par(n , -1), rank(n, 0) { }
    void init(int n) { par.assign(n, -1), rank.assign(n, 0); }
    
    int root(int x) {
        if (par[x] == -1) return x;
        else return par[x] = root(par[x]);
    }
    
    bool issame(int x, int y) {
        return root(x) == root(y);
    }
    
    bool merge(int x, int y) {
        x = root(x); y = root(y);
        if (x == y) return false;
        if (rank[x] < rank[y]) swap(x, y);
        if (rank[x] == rank[y]) ++rank[x];
        par[y] = x;
        return true;
    }
};

5-4. 再帰下降構文解析

構文解析とは例えば

((6 - 3) * 2 + 10 / 5) * (-3)

のような文字列が与えられたときに、それを解釈して計算を実行するような問題です。上の例で言えば、$-24$ と出力します。詳しくは

• Java 再帰下降構文解析 超入門　(@7shi さん)

を参考にしていただけたらと思います。下記のコードを実行すると、それぞれのケースで $9, 6, -24$ を出力します。

#include <iostream>
#include <vector>
#include <string>
using namespace std;


// 再帰下降パーサ
template<class T> struct Parser {
    // results
    int root;                       // vals[root] is the answer
    vector<T> vals;                 // value of each node
    vector<char> ops;               // operator of each node ('a' means leaf values)
    vector<int> left, right;        // the index of left-node, right-node
    vector<int> ids;                // the node-index of i-th value
    int ind = 0;
    
    void init() {
        vals.clear(); ops.clear(); left.clear(); right.clear(); ids.clear();
        ind = 0;
    }
    
    // generate nodes
    int newnode(char op, int lp, int rp, T val = 0) {
        ops.push_back(op); left.push_back(lp); right.push_back(rp);
        if (op == 'a') {
            vals.push_back(val);
            ids.push_back(ind++);
        }
        else {
            if (op == '+') vals.push_back(vals[lp] + vals[rp]);
            else if (op == '-') vals.push_back(vals[lp] - vals[rp]);
            else if (op == '*') vals.push_back(vals[lp] * vals[rp]);
            else if (op == '/') vals.push_back(vals[lp] / vals[rp]);
            ids.push_back(-1);
        }
        return (int)vals.size() - 1;
    }
    
    // main solver
    T solve(const string &S) {
        int p = 0;
        string nS = "";
        for (auto c : S) if (c != ' ') nS += c;
        root = expr(nS, p);
        return vals[root];
    }
    
    // parser
    int expr(const string &S, int &p) {
        int lp = factor(S, p);
        while (p < (int)S.size() && (S[p] == '+' || S[p] == '-')) {
            char op = S[p]; ++p;
            int rp = factor(S, p);
            lp = newnode(op, lp, rp);
        }
        return lp;
    }
    
    int factor(const string &S, int &p) {
        int lp = value(S, p);
        while (p < (int)S.size() && (S[p]== '*' || S[p] == '/')) {
            char op = S[p]; ++p;
            int rp = value(S, p);
            lp = newnode(op, lp, rp);
        }
        return lp;
    }
    
    int value(const string &S, int &p) {
        if (S[p] == '(') {
            ++p;                    // skip '('
            int lp = expr(S, p);
            ++p;                    // skip ')'
            return lp;
        }
        else {
            T val = 0;
            int sign = 1;
            if (p < (int)S.size() && S[p] == '-') sign = -1;
            while (p < (int)S.size() && S[p] >= '0' && S[p] <= '9') {
                val = val * 10 + (int)(S[p] - '0');
                ++p;
            }
            return newnode('a', -1, -1, val);
        }
    }
};


int main() {
    Parser<int> parse;
    cout << parse.solve("6 + 3") << endl;
    cout << parse.solve("3 + (10 - 4) / 2") << endl;
    cout << parse.solve("((6 - 3) * 2 + 10 / 5) * (-3)") << endl;
}

6. スタックオーバーフローと末尾再帰最適化について

最後に、本記事では主に再帰関数のアルゴリズム的側面に焦点を当てた解説を行ってきたのですが、実際に再帰関数を用いるときに極めて重要な視点であるメモリ管理について言及したいと思います。

一般にタスクが関数を実行するとき、スタック領域と呼ばれるメモリ領域に、関数の戻り先アドレスの情報や、引数・ローカル変数といった情報などが記録されます。スタック領域に push された情報は、通常は関数が終了した時点で pop されます。しかし再帰関数の場合には、再帰呼び出しが深くなるとスタック領域に情報が次々と積み上がっていきます。こうしてスタック容量を溢れさせてしまうことで、他の用途で確保されているメモリ空間を破壊するなどした状態がいわゆるスタックオーバーフローです。

タスクに割り当てられるスタックサイズの小さな組み込み系では「再帰呼び出しはご法度」とまで言われていますし、通常の Linux や Windows 環境であっても、スタックオーバーフローについて留意することがとても重要です。

そしてプログラミング言語によっては、再帰関数における再帰呼び出しが、その関数内の計算における最後のステップであるような形式で記述することで、スタックオーバーフローが発生しない状態に最適化することができるようになります。このような形式の再帰を末尾再帰と呼び、末尾再帰を用いた最適化を末尾再帰最適化または末尾呼出し最適化と呼びます。末尾再帰最適化については

• 末尾再帰による最適化

にて、わかりやすく解説されています。

7. おわりに

初学者にとって大きな壁となっている再帰関数について特集してみました。少しでも再帰関数の豊かな実例に触れていただいて、再帰的なアルゴリズムを設計することの楽しさを感じていただけたならばとても嬉しいです。

1. 実際は徐々にスタック領域を潰してメモリを食って行くので、有限資源を用いている限りはいつかはスタックオーバーフローを起こします。 ↩

2. 詳細な解析は省略するのですが、fibo($n$) の計算は $O((\frac{1+\sqrt{5}}{2})^n)$ の計算量になります。$n$ について指数的に増大することがわかります。 ↩

3. func(i-1, X, a) が true であった場合には func(i-1, X-a[i-1], a) を調べずに return true としているので、上手くアタリを引けば高速に "Yes" を出力する可能性はあります。 ↩