0. はじめに
NTTデータ数理システムでアルゴリズムの探求をしている大槻 (通称、けんちょん) です。好きなアルゴリズムは二部マッチングです。
アルゴリズムという言葉を聞いたことがある方は多いかもしれません。アルゴリズムとは「問題を解くための手順」のことです。しかしそのように聞いても、具体的なイメージが沸かない方が多いかもしれません。
本記事ではアルゴリズムとは何か、というのを具体例を交えて紹介します。特に前半は文系の方が読んでもわかる記述になったと思います。本記事では各アルゴリズムを雰囲気で掴むことを目標としましたが、より詳しく学びたい方向けに詳細な解説・プログラミング方法へのポインタも示しました。また最後の章にて、アルゴリズムを学ぶ意義について個人的に思うことを書いています。
アルゴリズムを理解するためには「実際に手を動かしてアルゴリズムをプログラミングする」のが一番だと思います。そのような実装込みの勉強ができるサービスとして、AtCoder が最近話題になっています。AtCoder を始めるためのチュートリアル記事:
も執筆してみましたので、興味のある方は読んでいただけたらと思います。
アルゴリズム本を出版! (2020/9/30)
僕は、アルゴリズムの面白さ・考え方を伝える記事を、Qiita 上に多数執筆してきました。それらを有機的にまとめあげる形で、アルゴリズム本を出版しました。
アルゴリズムをより深く学びたい方は、ぜひ読んでみてください。
本記事で扱うアルゴリズムたち
「アルゴリズムとは何か」を紹介する多くの資料では「線形探索」や「ソート」がメインに取り上げられていると思います。アルゴリズムの Hello World なテーマであり、応用情報技術者試験で頻出のテーマであることも影響しているでしょう。これらについても記事を書いています:
これらのテーマはアルゴリズムを腰を据えて勉強しようとなったときには最初に通る道です。計算量オーダーといった重要な概念についてもソートを題材にして学ぶ方も多いでしょう。しかしここではもっと気軽にアルゴリズムの面白さに触れられるようなテーマを 6 個取り上げます。「気軽に面白いテーマ」と言っても、掲載しているアルゴリズムたちは本格的かつ正統派なものになっています。
| 問題 | アルゴリズム | |
|---|---|---|
| 年齢当てゲーム | 二分探索法 / 二分法 | 応用情報でもお馴染みです |
| マッチング問題 | マッチング法 | 面白いです |
| 虫食算パズル | 深さ優先探索法 (DFS) | すべての基礎です |
| 迷路 | 幅優先探索法 (BFS) | 同じく重要な基礎です |
| 音声認識パターンマッチ問題 | 動的計画法 (DP) | DP はとても用途が広いです |
| ディープラーニング | 勾配降下法 | 超流行中です |
1. アルゴリズムとは
アルゴリズムと聞くと、私たちの生活には関係ないような難しい概念と感じられるかもしれませんが、実際はとても身近なものです。
ちょっとした年齢当てゲームを考えてみましょう!
1-1. 年齢当てゲームに学ぶ、二分探索法
A さんの年齢を当てようとしています。
A さんが、20 歳以上 36 歳未満だというのはわかっているとしましょう。あなたは A さんに 4 回だけ Yes / No で答えられる質問をすることができます。A さんの年齢を当てられるでしょうか???
それができるのです!!!!!
まず、現在わかっている年齢幅は 20 歳以上 36 歳未満 と 16 歳分もの幅がありますが、「28 歳以上ですか?」と聞いてみます。
- Yes なら: 28 歳以上 36 歳未満だとわかり、選択肢が一気に 8 歳分まで絞れます
- No なら: 20 歳以上 28 歳未満だとわかり、やはり選択肢が一気に 8 歳分まで絞れます
どっちの答えだったとしても、選択肢が半減するのです!!!
これを繰り返すと、A さんが 31 歳だったとして、以下のようにストーリーが進行するでしょう:
| 人物 | セリフ | 備考 |
|---|---|---|
| あなた | 「A さんは 28 歳以上ですか?」 | |
| A さん | Yes | |
| あなた | 「A さんは 32 歳以上ですか?」 | 28 以上 36 未満に絞れているので、その真ん中で切ります |
| A さん | No | |
| あなた | 「A さんは 30 歳以上ですか?」 | 28 以上 32 未満に絞れている (28, 29, 30, 31 のどれか) ので、その真ん中で |
| A さん | Yes | |
| あなた | 「A さんは 31 歳以上ですか?」 | 30 以上 32 未満に絞れている (30 か 31 か) ので、その真ん中で |
| A さん | Yes | |
| あなた | 「A さんは 31 歳ですね!」 | 決まりました! |
| A さん | 正解です |
今の場合は A さんが 31 歳の場合のストーリーでしたが、A さんが 20 歳~ 35 歳のうちのどの年齢であったとしても、似たようなストーリーで必ず 4 回の質問で当てることができます!(他の例も是非考えてみてください。)
ちなみに、このような「真ん中で切ってどちらかに絞って行く」タイプのアルゴリズムには二分探索法という名前がついています。応用情報技術者試験でも頻出のテーマですので馴染みのある方も多いと思います。
1-2. つまり、アルゴリズムとは
上の年齢当てゲームという問題では、相手の年齢を当てる「方法・手順」を二分探索法に基づいて導きました。このようにアルゴリズムとは、
問題を解くための方法・手順
のことです。さて、アルゴリズムと聞くと「コンピュータ上で実装されたプログラム」のことを思い浮かべる方も多いと思いますが、必ずしもコンピュータと関係がある必要はなく、日常生活でも多々登場します。例えばキャンプにおいてテントを組み立てるときの組立手順書が示すものもアルゴリズムの一種です。他にもコンビニの仕事でお客さんにお釣りを渡す場面において渡す紙幣やコインの枚数を最小にするためには、
- まず 10000 円札を渡せるだけ渡す
- 残りを 5000 円札を渡せるだけ渡す
- 残りを 1000 円札を渡せるだけ渡す
- 残りを 500 円玉を渡せるだけ渡す
- 残りを 100 円玉を渡せるだけ渡す
- 残りを 50 円玉を渡せるだけ渡す
- 残りを 10 円玉を渡せるだけ渡す
- 残りを 5 円玉を渡せるだけ渡す
- 残りを 1 円玉を渡せるだけ渡す
とすればよいですが、このような手順も立派なアルゴリズムであるといえます。

このようにアルゴリズムとはあくまで問題を解くための方法・手順のことであって、その手順を実現する手段については問いません。原理的には人手で実行できるものです。
しかしながら現実世界の大きな問題を解決する場合には、人手では実行速度や正確さにおいて限界があります。そのため通常、アルゴリズムはコンピュータプログラムとして実装して計算実行することになります。
1-3. アルゴリズムのすごいところ
アルゴリズムのすごいところは、ある決まった問題に対して
- 想定内であれば、どんな場合に対しても
- 同じやり方で
答えを導けることです。つまり 1 つのプログラムであらゆる場合を処理できるということです (想定内であればです)。今の世の中は既にそういうシステムが溢れています。カーナビを使えば現在地がどこであっても目的地までの経路を示してくれますし、銀行口座は預金額と引出額がいくらであっても正しくお金を引き出すことができます。こういったシステムはアルゴリズムによって支えられています。
アルゴリズムのもう 1 つのすごいところとして、コンピュータプログラムとして実装することにより、人手では到底調べ切れない問題を解決できることが挙げられます。現実世界で直面する多くの問題は「答えは原理的にはある」しかし「それが人手ではわからない」というものです。例えば、練馬駅を 2018 年 3 月 18 日 11:34 に出発して、最速で神保町駅にたどり着く方法というのは、原理的にはあるはずです。しかしそれが人手ではパッとはわかりません。一方でこれは、コンピュータなら一瞬で計算できますし、そういうアプリもあります。
このような「原理的にはあるはずの答え」を見つけ出すのがアルゴリズムです。
2. マッチング問題に学ぶ、マッチング法
年齢当てゲームに続いて次の問題を考えてみたいと思います。マッチングアプリと呼ばれる恋活・婚活サービスが流行している昨今、マッチングという言葉を聞いたことのある方は非常に多いと思います。マッチングアプリはユーザ側から見ても面白いサービスですが、運営側から見ても考えることの多い楽しい題材です。世界的にも "Online Dating" というキーワードで盛んに研究されているテーマです。
- ユーザ 1 人 1 人に合いそうな異性をどうやってレコメンドするか?
- 男性ユーザと女性ユーザの顔の好みの相性をどうやって推定するか?
- 男性ユーザと女性ユーザの性格の相性をどうやって推定するか?
- 特定の個人に「いいね」が集中しすぎないようにするにはどうするか?
古典的な輸送問題から、今流行りの機械学習手法や、ディープラーニング技術まで、幅広いテクニックを総動員して挑む甲斐のある面白い題材だと言えるでしょう。
さて、ここではマッチングを題材にした次のような問題を考えてみましょう:
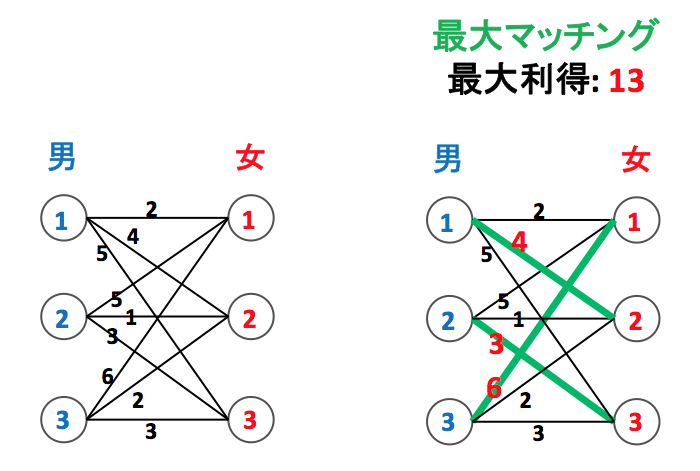
左下図のように男女間の各ペアについて「そこがペアになったらお互いどれだけ嬉しいか」が数値化されている状態を考えます。そこからペアリングして各ペアの利得の総和が最大になるようにする問題です。
この図の場合は (1, 2), (2, 3), (3, 1) をペアリングして得られる利得 13 が最大です (他の組み合わせを色々試してみてください)。必ずしも、それぞれの男・女にとって一番理想の相手とペアになっているわけではないことに注意しましょう。例えば男 1 にとっては女 3 が一番いいのですが、そこを結びつけてしまうと、残りのペアをどう結び付けても全体の利得は小さくなってしまいます。
このように二部マッチング問題というのは基本的に全体最適を目指す考え方です。マッチングアプリの例で言えば、個人最適を追い求めすぎると人気の男女に「いいね」が殺到してしまうため、運営側としては二部マッチング問題的な手法を取り入れることで全体最適な方向性に引っ張っていくことが重要になると考えられます。
二部マッチングは、男女間のマッチング問題に限らず、
- インターネット広告分野で、ユーザの興味に合う広告を出す (「ユーザ」と「広告」)
- 従業員シフト割当問題で、従業員全員の不満の少ない割当をする (「従業員」と「シフト」)
- トラック配送計画問題で、どの荷物をどのトラックに割当てるかを最適化する (「荷物」と「トラック」)
- 輸送問題で、どの工場からどの店舗へどの分量の製品を輸送するかを最適化する (「工場」と「店舗」)
- 箱根駅伝で、チームの総合タイムが最小となるように選手を各区に割当てる (「選手」と「区」)
といった様々な場面で応用ができます。具体的なアルゴリズムなど詳しくは
を読んでいただけたらと思います。
3. 虫食算パズルに学ぶ、深さ優先探索法 (DFS)
虫食算は、筆算のうちのいくつかの数値が □ や文字に置き換えられてしまったものが与えられ、元の筆算を復元するパズルです。ルールとしては、
- 同じ文字には同じ数字が入り、異なる文字には異なる数字が入る
- □ マスにはどんな数字が入ってもよい (他の文字と数字が被ってもよい)
となっています。

虫食算パズルを解くテクニックはもちろん色々あるのですが、このくらいの問題はコンピュータによって力任せに探索を行うことで簡単に解くことができます。そのように言うと、昔ながらのパズル愛好家さんたちに嫌がられてしまうのですが、コンピュータを用いてパズルを解く営みにも、様々な工夫を凝らす楽しみがあります。左上の「211」の虫食算を「深さ優先探索法 (DFS)」で解くとこんな感じです。

このように、深さ優先探索法 (DFS) は
- 「とりあえず仮定して突き進む」ことを、行き詰るまで繰り返す
- 行き詰ったら一歩戻って、次の選択肢を試す
というのを繰り返す探索アルゴリズムです。基本的には力任せの全探索アルゴリズムなのですが、探索順序を工夫することで劇的な性能差が出ることも珍しくないです (例えば「虫食算を作るアルゴリズム」を参照)。深さ優先探索は様々なアルゴリズムの基本となるアルゴリズムで、応用範囲も広いです:
- 数独も解ける (数独は、人間的には探索ではなく理詰めで解くものではありますが...)
- フリーセルも解ける
- Ponanza などのコンピュータ将棋ソフトでも使われているようなゲーム木探索
- makefile の仕組みはトポロジカルソートで根本的には DFS
- メモしながら DFS すれば動的計画法 (DP) にもなる
- ネットワークフローアルゴリズムのサブルーチンでもある
なお、上での深さ優先探索法の説明では、「グラフ上の探索」という言い方をしなかったのですが、深さ優先探索 (DFS) も次の節の幅優先探索 (BFS) も、グラフ上の探索と考えると見通しがよくなります。関心のある方は是非
を読んでいただけたらと思います。
4. 迷路に学ぶ、幅優先探索法 (BFS)
以下のような迷路で、スタート (S) からゴール (G) まで行きたいです。ただし茶色マスには入れません。いくつか考えられる行き方のうち、最短のものはどのように求められるでしょうか。

まず、スタートから 1 手で行ける場所に「1」と書きます。

続いて、「1」のマスから 1 手で行ける場所に「2」と書きます。これはスタートから 2 手で行ける場所でもあります。

続いて、「2」のマスから 1 手で行ける場所に「3」と書いて...

これを繰り返していくと、G のマスは「16」となりました。

ここまで来たら、あとは数字をさかのぼるようにして最短経路を復元できます:

このように幅優先探索 (BFS) も、深さ優先探索 (DFS) と同様に基本的には力任せの全探索アルゴリズムですが、「なにかを達成するための最小手順を知りたい」という場面で活躍することが多いです。以下のような応用があります:
-
ルービックキューブの最小手数「神の数字」
- 必ず 20 手以内で揃えられることが最近完全解析された!(God's Number is 20 参照)
- 解析のベースは BFS を改良した IDA$^{*}$ だと思われます
-
トポロジカルソート
- DFS の章でも応用例として挙げた makefile の仕組み
- DFS でもできますが、BFS でもできます
-
最短経路問題
- カーナビにも代表されるような最短経路問題は Dijkstra 法が定番ですが、特殊な場合には BFS の方がより効果的に使えます
そして幅優先探索 (BFS) も深さ優先探索 (DFS) と同様に、グラフ上の探索と考えると見通しがよくなります。関心のある方は是非
を読んでいただけたらと思います。
5. 音声認識パターンマッチ問題に学ぶ、動的計画法 (DP)
動的計画法はとにかく実用的なアルゴリズムです!
スケジューリング問題、最短経路問題、ナップサック問題から、パターンマッチ問題まで、実世界の極めて多くの現場で活躍するアルゴリズムです。DP の使われ方は多彩過ぎて紹介しきれないので、ここでは典型的応用例の 1 つであるパターンマッチング問題、特に最小コスト弾性マッチング問題を取り挙げます。
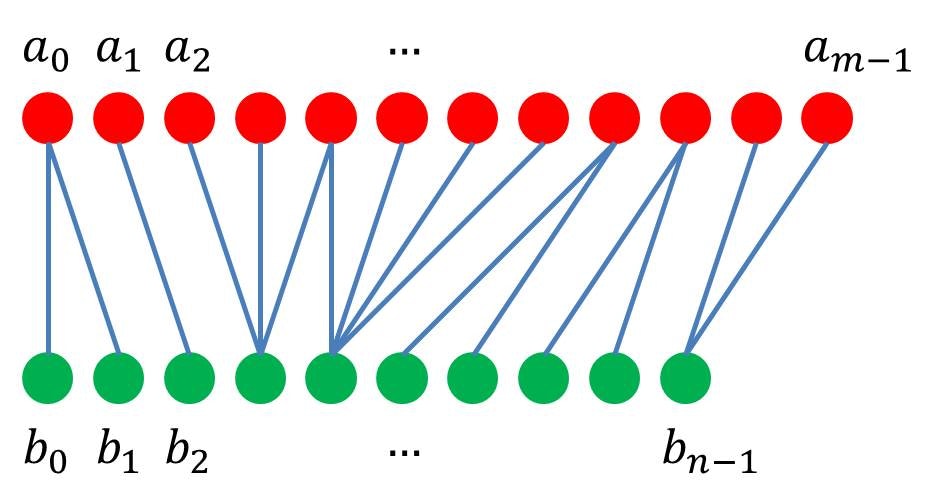
最小コスト弾性マッチング問題とは、下図のように 2 つの系列 $A = (a_0, a_1, \dots, a_{m-1})$, $B = (b_0, b_1, \dots, b_{n-1})$ が与えられて、それらがどの程度「似ているか」を測る問題です。類似度の測り方としては、ペア $(a_i, b_j)$ をマッチさせたときのコストは $c(i, j)$ で与えられて、左から順番に最適なマッチングを構成していきます。マッチングを最適化したときのコストの総和の最小値を「類似度」とします。
注意点として「2. マッチング問題」で挙げたマッチング問題との違いは、「左から順番に詰めるようにマッチングを構成しないといけなくて、ペア同士が交叉してはいけない」という制約があることです。
このフレームワークに類似した考え方が具体的に適用可能な場面として以下が考えられます:
-
diff コマンド
- いわゆる編集距離
-
スペルチェッカー
- 直したい単語が、どの単語に近いかを推測
-
バイオインフォマティクス
- 今熱い応用例です、2 つの DNA の間の類似度を測ります
-
空間認識・画像認識
- 近年はディープラーニングが盛んだが DP マッチングも有効なケースも多いです (「画像認識」参照)
-
音声認識
- 未知の音声波形が何の単語を表しているかを推測
- 「音声認識・画像認識に用いられる弾性マッチングのアルゴリズムって一体」を参照
それでは具体的なアルゴリズムを記述していきます。少し理系寄りの話で難しくなります。高校数学で学ぶ「漸化式」に馴染みのある方であれば、無理なく理解できると思います。難しく感じた場合には、先に
を読んでいただけたらと思います。これを読んだ後であれば自然なものに思えると思います。
まず DP テーブルの定義を以下のようにします:
${\rm dp}[i][j]$ := $A$ のうち最初の $i$ 個までと、$B$ のうち最初の $j$ 個までについての弾性マッチングの最小コスト
そして、${\rm dp}[i][j]$ を算出する漸化式を立てることを考えると、以下のようになります:
<DP漸化式>
$${\rm dp}[i][j] = \min({\rm dp}[i-1][j-1], {\rm dp}[i][j-1], {\rm dp}[i-1][j]) + c(i-1, j-1)$$
<DP初期条件>
$${\rm dp}[0][0] = 0$$
<求める類似度>
$${\rm dp}[m][n]$$
あとはこれに従って素直に実装すればよいです。実装など含めて DP を詳細に学びたい方はこの記事を読んでいただけたらと思います。
6. ディープラーニングに学ぶ、勾配降下法
今はどこへ行ってもディープラーニングの話題で溢れ返っています。圧倒的な AI ブームに沸き立つ中、「とりあえず AI という用語を入れた提案書は通りやすい」といった話も頻繁に耳にします。
「ディープラーニング」という言葉をよく耳にするが具体的なことがよくわからない方向けに、実際のビジネス現場で登場しやすい「画像処理」「自然言語処理」への応用を念頭においた入門スライド資料を執筆してみました。比較的最新に近い話題も盛り込んでいます。
ディープラーニングが魔法のようなことをしているイメージのある方も多いかもしれませんが、多くの場合、手法自体はごく単純な「勾配降下法」です。勾配降下法はざっくりと言ってしまえば「関数の最小値を求める一般的なテク」とでも言うべきもので考え方は単純です。関数 $L(w)$ を最小化したいときに
- 初期値 $w_0$ を用意する
- 毎ステップ $t$ ごとに $w_{t+1} = w_{t} - \epsilon \frac{\partial L}{\partial w}$ に従って $w$ を更新していく
とするだけです。
$$w_{t+1} = w_{t} - \epsilon \frac{\partial L}{\partial w}$$
の意味は単純明快で、$L$ が小さくなる方向に $w$ を動かす、というイメージです。どのくらい動かすのかを $\epsilon$ という値で調節していて学習率と呼びます。学習率のチューニングは学習の成否を大きく分ける重要な要素になります。
さて、勾配降下法において関数 $L$ を様々なものにすることで様々な学習を行うことができます。一般的な考え方としてはディープラーニングに限らず、関数 $L$ はなんらかの形式で「予測結果と正解とのズレの大きさ」を表すもので損失関数と呼ばれます。「複雑なニューラルネットワークモデルによって表された損失関数が小さくなるように勾配降下法を適用する」というのが、昨今耳にするディープラーニングの中身であることが多いです。ディープラーニングにおいて損失関数 $L$ を具体的にどのように設計するかについては、上のスライドを見ていただけたらと思います。
7. アルゴリズムの何が難しいか: 計算量について
ここまで様々な問題を見て来ましたが、多くの諸問題に対しては、
「無尽蔵の計算実行時間さえかければ確実に答えが求まる」ようなアルゴリズムを、とりあえず導くことは簡単!!!
です。「全探索」と呼ばれる種類の様々な探索技術を身につけると大抵の問題に対しては全探索アルゴリズムがパッと作れるようになります。応用情報技術者試験のアルゴリズムの設問でも全探索からの話題が極めて多いのは、やはり全探索がすべての基礎になるからです。難しいのは、単純な全探索から改良して
「現実的な制限時間内に答えが求まる」ようなアルゴリズムを、導くことは難しいことが多い!!!
です。将棋の必勝法を求めるアルゴリズム (「ゲームを解く!! 〜 将棋の必勝法を求めるアルゴリズム 〜」を参照) も、計算にものすごく時間のかかる単純なアルゴリズムでよいなら、情報系のプログラミングに慣れた人なら比較的簡単に実装できるでしょう。ここで「ものすごく」というのは言葉の迫力が全然足りなくて、宇宙が誕生してから今までの時間を 5000 兆回繰り返しても終わらないような時間です。
- 似た例の動画: 『フカシギの数え方』 おねえさんといっしょ! みんなで数えてみよう!
(非常に話題になった動画です。科学未来館などでも展示されていました。YouTube にありますのでこのタイトルで検索してみください)
(すべて動画より引用)
つまりアルゴリズムには圧倒的なまでの「良し悪し」があるのです。アルゴリズムの研究とは、様々な問題に対して、少しでも早く答えを求めることのできる良いアルゴリズムを見つけるというものです。アルゴリズムの良さを測る具体的な指標として「計算量オーダー」と呼ばれるものがあります。計算量については
を参考にしていただけたらと思います。
8. 参考資料
アルゴリズムの世界へと入っていくための書籍たちを紹介していきます。
8-1. 一般の方にもわかりやすい書籍
まずは一般の方も読めるような、アルゴリズムの世界に足を踏み入れるための書籍たちを挙げます。
様々なアルゴリズムを図解してわかりやすく解説した本です。数学的にしっかり書かれた書籍をいきなり読むのが難しいと感じる方向けです。反対にアルゴリズムの動きを数学的にしっかりと理解したい方には、逆にわかりにくく感じるかもしれません。アルゴリズムの理解の仕方は個人差が非常に大きいので、自分に合った学び方を見出すのが大切だと思います。
同じくアルゴリズムのわかりやすく図解することを試みた書籍です。イラストが豊富で、アルゴリズムの数学的記述を見てもよくわからない場合には待望の書籍と言えます。
アルゴリズムが世界を変える!
現在の私たちの生活のなかには、アルゴリズム的技術革命によってもたらされた恩恵に溢れるデバイスに溢れています。何気なく使用している Google 検索エンジンも、世界中のセキュリティを支えている暗号も、アルゴリズム革命によってもたらされました。そういった事柄が楽しく描かれた面白い書籍です。
「世界でもっとも強力な9のアルゴリズム」に比べると、アルゴリズムそのものの解説の印象が薄いものの、アルゴリズムがどのように世界を変えていくのかを感じ取れる面白い読み物です。
8-2. アルゴリズムの教科書
アルゴリズムを本格的に学ぶためには、図解するだけでは物足りないでしょう。数学的にしっかりと学べる書籍たちです。
アルゴリズムを数学的にしっかり勉強するための書籍としては、とても平易かつ簡潔に書かれています。真にわかりやすい説明とは、くどい記述で何とか伝わるようにする説明というよりは、「一言で伝わるような簡潔な説明」だと思います。この書籍はそのような真にわかりやすい説明を体現したものだと言えます。
アルゴリズムの世界的教科書の 1 つです。プログラミングコンテスト攻略本として名高い蟻本が出版されてからはこの本で勉強する日本人は少なくなりましたが、現在なお色褪せない価値のある本です。様々なアルゴリズムの詳細を学ぶだけでなく、実世界においてアルゴリズムをどのように使うべきかに焦点を当てた貴重な一冊です。
同じくアルゴリズムの世界的教科書です。アルゴリズムデザインがアルゴリズムの使い方に焦点を当てた本だとすると、アルゴリズムイントロダクションはアルゴリズムの原理に焦点を当てた本だと言えます。直観的には正しいと思えるような様々なアルゴリズムの正当性がきっちりと議論されています。こうしたことをしっかりと学んでおくことは、自力で未知の問題に対するアルゴリズムを開発していく上で大変重要になります。
8-3. アルゴリズムの「実装」も含めて学べる書籍たち
いわゆるプログラミングコンテストの攻略本と呼べる書籍たちを挙げます。
- プログラミングコンテストチャレンジブック (通称、蟻本)
プログラミングコンテスト界のバイブル、蟻本です!
6 年前に日本人世界ランカー達によって執筆されて以来、誰もが手にするバイブルとなりました。現在では競技プログラミング用参考書という域を超えて、世界的なアルゴリズムの教科書の 1 つと言える立ち位置までになっています。大きな特長として、洗練された C++ による実装が載っていることが挙げられるでしょう。行間をぎゅっと絞っているので、スピード感があって爽快な反面、説明を読み解くのが難しいという声も多々聞きます。しかしながら蟻本に書いてある内容は、読み解くことさえできたならば、非常に濃密なものと感じられます。
- プログラミングコンテスト攻略のためのアルゴリズムとデータ構造 (通称、螺旋本)
蟻本が難しいと感じる方のためのプログラミングコンテスト書籍です。通称螺旋本と呼ばれています。対象層はアルゴリズム学習の入門を終えた初中級者向けで、あらゆる層の人にとって読みやすい書籍と言えそうです。掲載されている例題たちはすべて自分でソースコードを実装して、AOJ 上でジャッジできるようになっています。
- 最強最速アルゴリズマー養成講座 プログラミングコンテストTopCoder攻略ガイド (通称、チーター本)
今流行りの AtCoder 社長による競技プログラミング入門用書籍です。蟻本は対象者層が中上級者向けで難しいと言われていますが、チーター本は競技プログラミングを始めたばかりの人に目線を合わせた真の入門書です。丁寧なわかりやすい解説が売りで、C++ だけでなく Java や C# による実装も載っているのが特長です (現在なら Python もあった方が嬉しいかもなので続報期待)。ただし丁寧な反面、やや重いのが弱点です。「これを読まないと螺旋本・蟻本に進めない」と思ってしまうと気が遠くなるので、もっと気軽に読むと「強くなるための良いヒントが沢山書いてある」本です。
Google, Microsoft, Facebook, Amazon, Apple などでは選考過程で実際にコーディングを行うことはすっかり有名になりました。国内でも、選考過程に AtCoder システムを用いてコーディング試験を課す企業も急増しています。それらのプログラミング試験に合格して採用されるための攻略本として絶大な人気を誇るベストセラー書となっています。なお新版もあるのですが日本語訳に誤植が多く注意が必要です。
とても面白いです!
アルゴリズムを体系的に解説するよりも、具体的な楽しいパズルのような問題たちを解いていくことで、自然に楽しくアルゴリズムの使い方や、アルゴリズムコーディング技術が身に着くようになっています。
8-4. 各分野ごとのアルゴリズム系書籍
組合せ最適化の世界的教科書です。少し難しめですが、グラフ理論や離散数学に関連するアルゴリズムの話題が豊富に集められており、学ぶ要素は非常に多いです。
組合せ最適化に関するサーベイは、2003 年までの分についてはこれ一冊でできると言われるほど、グラフ理論や離散数学に関するアルゴリズムを集大成した本です。1881 ページにも及ぶ世界的名著は、組合せ最適化分野における世界的研究者 Alexander Schrijver によって書かれました。
文字列を高速に処理するアルゴリズムについての書籍です。
計算幾何分野に関する書籍です。
整数論や数列など、いわゆる数学ゲーと呼ばれる分野に関する書籍です。
ゲーム分野に関する書籍です。
具体的な問題に挑む上で解けない問題 (NP-hard, NP-complete, #P-complete) を知ることは大切です。この本を勉強すると、解けない問題を知覚するスキルが磨かれます。
深層学習に関してよくまとめられた書籍たちです
8-5. インターネット上の資料など
アルゴリズム好きの集うプログラミングコンテスト界隈では情報共有が非常に活発で、皆が勉強したことを盛んに発信しています。そのため無料で読むことのできる資料が非常に充実しています。ここではその一例を示します。
- AtCoder に登録したら次にやること ~ これだけ解けば十分闘える!過去問精選 10 問 ~
- AtCoder 版!蟻本 (初級編)
- AtCoder 版!蟻本 (中級編)
- AtCoder 版!蟻本 (上級編)
- AtCoder 版!蟻本 (発展的トピック編)
アルゴリズムを実装しながら楽しく学べるサイト AtCoder の始め方から、のめり込み方までを記載しました。
- 各種アルゴリズムの C++ による実装 (前原さん)
- spaghetti-source/algorithm (前原さん)
通称 spaghetti-source。競技プログラマ以外にも有名なライブラリ集です。様々なアルゴリズムが C++ で実装されています。
- 競技プロ的なアルゴリズムのスライドのまとめ (kroton さん)
今までに公開された良質なスライドたちを集めています。
- coursera 講座: Machine Learning (Andrew Ng 先生)
- Deep Learning Papers Reading Roadmap (floodsung さん)
非常に評判のよい、機械学習・深層学習の入門資料たちです。
9. おわりに 〜 「アルゴリズム」とは結局何か 〜
本記事では「年齢当てゲーム」「二部マッチング」「虫食算パズル」「迷路の最短路」「パターンマッチング」「ディープラーニング」といった問題を考えて来ましたが、アルゴリズムとはそれらの問題の解を見つけるための手順のことです。アルゴリズムのすごいところは、例えば年齢当てゲームでは相手の年齢が何歳であっても当てられますし、虫食算パズルでは数字の配置が変わっても解けますし、迷路の最短路では迷路の形状が変わっても解けます。アルゴリズムを学ぶ意義としては以下のものが挙げられるでしょう:
世界が変わる
僕は「アルゴリズム」を学んでから、世の中の諸問題と対峙する上での世界観に革命が起きたのを覚えています。アルゴリズムを学ぶ前は「問題を解決する」とは「具体的な解を提示する」ことだと無意識に思っていました。しかしアルゴリズムを学んでからは、具体的な解が陽に書き下せなくても「問題の解を構成する手順を与えればよい」という見方ができるようになり、問題解決手段が大きく拡がったように思います。
休日出勤しないで済む
本記事では「アルゴリズムの性能差」については深く触れなかったですが、同じ問題を解くことのできるアルゴリズムでも実行時間・実行メモリ量に莫大な差が出ることもしばしばです。アルゴリズムの性能差が重要な事例として、
が参考になります。
バグを生みにくい実装が高速にできるようになる
多くの方にとってこの効果が最も重要かもしれません。特に競技プログラミングを通してアルゴリズムを学んだ人は、実装がとにかく速く正確です。単にアルゴリズムの知識があってコーディング慣れしているから実装が速いというだけではなく、ロジックをシンプルにする能力が自然と備わるため、スッキリとしたコーディングができるようになります。そうすると自然にバグを埋め込みにくくなり、デバッグに要する時間も格段に短くなります。最近話題の就職・転職サービス AtCoder Jobs はプログラミングコンテストを通した応募者の能力ランク付けを行っていますが、応募者たちのアルゴリズムエキスパートとしての活躍の場は限られていても、「実装がシンプルで正確で速く、デバッグスキルも高い」といったことも重宝されるように思います。
なお、アルゴリズムとは何かを数学的にきちんと定義するならば、
- そもそも「問題」とは何か
- そして「アルゴリズム」とは何か (チューリングマシンを用いて定義)
といったステップを踏んでいくのが一般的ですが、本記事では「具体的な面白い問題たちを解く手順を示すことで、雰囲気でアルゴリズムを理解する」ことを目標にしました。チューリングマシンを用いてきちんと理解したい方には、参考書籍にも挙げた「Computers and Intractability: A Guide to the Theory of Np-Completeness」が参考になると思います。
「アルゴリズム」という言葉に対して怖いイメージを抱いていた方は多いかもしれません。しかし実際にはアルゴリズムはとても身近で実用的で楽しいものです。また最近では AtCoder や AOJ をはじめ、アルゴリズムを実際に手を動かして学ぶための環境が整っており、とても勉強しやすい状態になっています。本記事をきっかけにアルゴリズムの世界に関心を抱き、アルゴリズムの世界へと踏み込んで行く方が増えたならばとても嬉しい気持ちでいっぱいです。