NTT データ数理システムでアルゴリズムの探求をしている大槻 (通称、けんちょん) です。好きなアルゴリズムは二部マッチングです。今回は、歴史の記録に残る最古のアルゴリズムの 1 つとして知られるユークリッドの互除法について書きます。
ユークリッドの互除法は、最大公約数を求めたり、一次不定方程式 $ax + by = c$ に応用したりなど、大学受験でもお馴染みのアルゴリズムですが、整数論的アルゴリズムや数え上げアルゴリズムにおいて根幹を成す重要なものでもあります。
今回の記事では特に、一次不定方程式 $ax + by = c$ の整数解を一般に求めるアルゴリズムとして知られる「拡張ユークリッドの互除法」の理解を目指します。
1. ユークリッドの互除法とは
ユークリッドの互除法は、2 つの整数 $a$, $b$ の最大公約数を効率よく求めるアルゴリズムです。本記事では $a$ と $b$ の最大公約数を ${\rm gcd}(a, b)$ と表すことにします。大学受験でもお馴染みの表記法です。
1-1. ユークリッドの互除法のやり方
300 と 780 の最大公約数を求めたいとします。このとき、以下の手順で求めることができます:
- 780 を 300 で割る: 780 ÷ 300 = 2 ・・・ 180
- 300 を 180 で割る: 300 ÷ 180 = 1 ・・・ 120
- 180 を 120 で割る: 180 ÷ 120 = 1 ・・・ 60
- 120 を 60 で割る: 120 ÷ 60 = 2
- 割り切れたらおしまいで、最後に割った数が答え: 60
すなわち、${\rm gcd}(300, 780) = 60$ です。このように以下のフロートチャートのような手順を繰り返すアルゴリズムです。
このアルゴリズムの核心部分は「大きい方から小さい方を割り、大きい方を余りで置き換える」のところにあります。具体的な動きは以下のようになります。(780, 300) で言えば、大きい方から小さい方で割ると 780 ÷ 300 = 2 ・・・ 180 で、780 を余りの 180 で置き換えると、(180, 300) になります。再び大きい方から小さい方で割ると 300 ÷ 180 = 1 ・・・ 120 で (180, 120) になります。
フロートチャートが終了する瞬間を確認すると、最後は (120, 60) に対して 120 ÷ 60 = 2 で、余りは 0 なので (0, 60) になります。一方が 0 になったので答えはもう一方の 60 です。
1-2. ユークリッドの互除法がなぜ必要か
私たちが最大公約数・最小公倍数といった概念に最初に出会うのは、小学校で教わる
- 分数の約分 (分子分母を最大公約数で割る)
- 分数の通分 (分母を最小公倍数に揃える)
といったあたりでしょうか。でもそこで「ユークリッドの互除法」を教わった人はほとんどいなさそうです。多くの方は
- 素因数分解
- すだれ算
をしていたのではないかと思います。例えば 160 と 1200 の最大公約数を求めるとき、
【素因数分解】
$160 = 2^5 × 5$
$1200 = 2^4 × 3 × 5^2$
なので、${\rm gcd}(160, 1200) = 2^4 × 5 = 80$ という感じです。
【すだれ算】
これが多くの方の記憶に残っているやり方かもしれません。
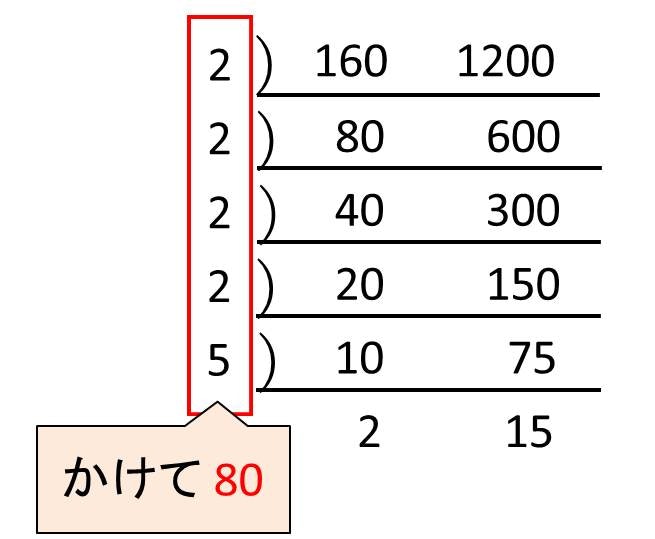
これらの素因数分解、すだれ算といった方法に馴染んでいると、ユークリッドの互除法は必要ないものに思えるかもしれません。しかし、9876543210 と 123456789 の最大公約数を求めてくださいと言われたらどうでしょう。これを素因数分解やすだれ算でやろうにも、気が遠くなりそうです。しかしユークリッドの互除法を使えば、
9876543210 ÷ 123456789 = 80 ・・・ 90
123456789 ÷ 90 = 1371742 ・・・ 9
90 ÷ 9 = 10
より、簡単な計算で最大公約数が 9 だとわかります。
このように最大公約数を求めたい 2 数が大きくなればなるほど、ユークリッドの互除法の効率良さが際立って来るようになります。1-4 節にて、計算量オーダーの観点からユークリッドの互除法の効率良さについて述べます。
1-3. ユークリッドの互除法のプログラム
この節はプログラミングを学んでいる方向けになります。上に示したフローチャートをプログラムに起こすのはそれほど難しくなく、再帰関数を用いると綺麗に実装できます。C++ での実装例を示します。
注意点として、下の実装では「a と b のうちのどちらの方が大きいか」の判定もせずに済ませています。a < b であっても a % b = a なので、GCD(b, a) が再帰的に呼ばれることになり、a と b がここで入れ替わるので問題ないです。
そして一度 a >= b を満たしたならば b >= a%b となるので、再帰的に呼ばれる関数たちは常に a >= b を満たし続けることになります。
/* a と b の最大公約数を返す関数 */
long long GCD(long long a, long long b) {
if (b == 0) return a;
else return GCD(b, a % b);
}
1-4. ユークリッドの互除法の計算量
ユークリッドの互除法の計算量に関する議論をします。ここではユークリッドの互除法の計算ステップ回数を「除算の回数」で評価することにします。まずはざっくりと評価してみます。$a \ge b$ とします。
$a$ を $b$ で割って、$a = qb + r$ ($q$ は商, $r$ は余り) としたとき、$q \ge 1$ より、$a \ge b + r \ge 2r$ ($b \ge r$ より) となるので、$r \le a/2$ が成り立ちます。
よってユークリッドの互除法のステップを 2 回繰り返して $(a, b)$ -> $(b, r_1)$ -> $(r_1, r_2)$ となったとき、$a$ や $b$ は半分以下になったことになります。よってざっくりと $2\log{a}$ 回の計算ステップ回数ということになります。したがってユークリッドの互除法の計算ステップ回数は $O(\log{a})$ になります。
計算ステップ回数が最悪になるケース
ユークリッドの互除法の計算回数がどんな場合に最悪になるのかを考えてみます。それはフィボナッチ数列の隣接 2 項です。フィボナッチ数列は
$1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...$
というものですが、${\rm gcd}(89, 144)$ を計算すると
${\rm gcd}(144, 89)$ = ${\rm gcd}(89, 55)$ = ${\rm gcd}(55, 34)$ = ${\rm gcd}(34, 21)$ = ${\rm gcd}(21, 13)$ = ${\rm gcd}(13, 8)$ = ${\rm gcd}(8, 5)$ = ${\rm gcd}(5, 3)$ = ${\rm gcd}(3, 2)$ = ${\rm gcd}(2, 1)$ = ${\rm gcd}(1, 0) = 1$
となり、長い道のりです。フィボナッチ数列の一般項が
$a_n = \frac{1}{\sqrt{5}} ((\frac{1+\sqrt{5}}{2})^{n} - (\frac{1-\sqrt{5}}{2})^{n})$
であることを考えると (このページ参照)、$\gamma = \frac{1+\sqrt{5}}{2}$ ($\gamma$ はいわゆる黄金数) として、計算ステップ回数は $O(\log_{\gamma}{a})$ だけ要することになります。
ラメの定理
以上の考察に基づいた以下の定理が 19 世紀には示されていました (ラメの定理):
$a, b$ を非負整数とし、小さい方の数を十進法で表したときの桁数を $d$ とする。このとき、ユークリッドの互除法を用いて $a$ と $b$ の最大公約数を求めるときの計算回数は、$5d$ 回以下となる。
証明はフィボナッチ数列を用いた上の考察をきちんと詰めれば難しくないです。このページにきちんとした証明があります。冷静に考えるとすごい主張で、
1,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000
といった 100 桁の整数に対しても、高々 500 回の計算ステップで最大公約数が求められることになります。しかもこれは相当に最悪なケースの話であり、実際上平均的にはもっと遥かに少ない計算回数で最大公約数が求められます。
素因数分解による方法との比較
2 つの整数 $a, b$ ($a \ge b$) の最大公約数を求めるアルゴリズムとして、素因数分解と比べるとユークリッドの互除法は著しく効率がよいです。計算量の観点から比較してみます。
- 素因数分解はナイーブなアルゴリズムでは、例えば $1$ から $a$ まで順に試し割りをすると $O(a)$ かかります
- ユークリッドの互除法は $O(\log{a})$ で計算できます
この差は歴然で、$a$ が大きくなると深刻な差に拡大して行きます。特に前者は指数時間アルゴリズム (その理由はここを参照) で、後者は多項式時間アルゴリズムになっています。素因数分解はもう少し工夫することができて例えばちょっと考えると $O(\sqrt{a})$ なアルゴリズムが得られます。しかしどれほど工夫を重ねても素因数分解に対しては現在のところ多項式時間アルゴリズムは得られていませんし、今後も得られそうもないと言われています。
2. ユークリッドの互除法の原理
なぜユークリッドの互除法によって整数 $a, b$ の最大公約数が求められるのかを理解することは重要です。以下の定理に依っています。なお、証明中で用いている $a | b$ といった記法は「$b$ が $a$ の倍数であること」「$a$ が $b$ の約数であること」を表しています。
$a, b, q$ を整数とすると ${\rm gcd}(a, b) = {\rm gcd}(a - qb, b)$ が成り立つ
【証明】
$d = {\rm gcd}(a, b)$ とおくと、$a$ も $b$ も $d$ の倍数なので、$a - qb$ も $d$ の倍数である。よって、$a - qb$ も $b$ も $d$ で割り切れるので $d$ | ${\rm gcd}(a - qb, b)$ すなわち ${\rm gcd}(a, b)$ | ${\rm gcd}(a - qb, b)$ が成り立つ。
逆に $a' = a - qb$ とおくと、$a = a' + qb$ となる。ここで $d' = {\rm gcd}(a', b)$ とおくと先ほどとまったく同様の議論によって、$d'$ | ${\rm gcd}(a' + qb, b)$ すなわち ${\rm gcd}(a - qb, b)$ | ${\rm gcd}(a, b)$ が導かれる。
以上により、${\rm gcd}(a, b) = {\rm gcd}(a - qb, b)$ が従う。
(証明終)
上の定理から特に、 整数 $a$ と $b$ に対して $a = qb + r$ ($q$ は商, $r$ は余り) として ${\rm gcd}(a, b) = {\rm gcd}(a - qb, b)$ が従うので、ユークリッドの互除法の正当性が示されました。
そしてこの証明の副産物として、$q$ が「$a$ を $b$ で割ったときの商」でなくてもいいことがわかります。特に ${\rm gcd}(a, b) = {\rm gcd}(a - b, b)$ が成り立ちますし、
$a ≡ c$ $({\rm mod}.b)$ ならば ${\rm gcd}(a, b) = {\rm gcd}(c, b)$
が成り立ちます。
3. 一次不定方程式 ax + by = c の整数解
$6x + 8y = 10$ の整数解を求めよ、といった問題は大学入試でも頻出です。そしてこれはユークリッドの互除法の典型的な活用例でもあり、「拡張ユークリッドの互除法」とも呼ばれています。実は整数論的にもより高度な環論へと繋がる重要な話題だったりします (下の主張は「整数環が単項イデアル整域であること」を示すものに他ならないです)。
3-1. 一次不定方程式 ax + by = c が整数解をもつ条件
$a, b, c$ を $0$ 以外の整数とする。一次不定方程式 $ax + by = c$ が整数解をもつための必要十分条件は $c$ が ${\rm gcd}(a, b)$ で割り切れることである。
【略証】
まず、一次不定方程式 $ax + by = c$ が整数解をもつならば $c$ が ${\rm gcd}(a, b)$ で割り切れる必要があることは明らかである。$d = {\rm gcd}(a, b)$ とおくと、$a$ も $b$ も $d$ で割り切れることから $ax + by$ も $d$ で割り切れるからである。
逆に $c$ が ${\rm gcd}(a, b)$ で割り切れるとき、$ax + by = c$ が整数解をもつことを示す方が難しいです。具体的に整数解を構成することによって示します。まず $c$ が ${\rm gcd}(a, b)$ で割り切れるので、$c = c'{\rm gcd}(a, b)$ とおくと、$ax + by = c'{\rm gcd}(a, b)$ となります。
そして実は $ax + by = {\rm gcd}(a, b)$ を満たす整数 $x, y$ が存在することが知られています。その解説は 3-3 や 3-4 で行います。$ax + by = {\rm gcd}(a, b)$ を満たす $x, y$ が存在したならば、両辺 $c'$ 倍して
$a(c'x) + b(c'y) = c$
となるので、$(c'x, c'y)$ が $ax + by = c$ の整数解になっています。
(証明終)
3-2. 一次不定方程式 ax + by = c の整数解を求める具体例
実際に具体的な不定方程式 $111x + 30y = 12$ を解いてみます。${\rm gcd}(111, 30) = 3$ より、まずは $111x + 30y = 3$ を満たす $x, y$ を求めます。ユークリッドの互除法を適用すると
| 割り算 | かけ算の式に直す | さらに式変形する |
|---|---|---|
| $111 ÷ 30 = 3$ あまり $21$ | $111 = 3×30 + 21$ | $21 = 111 - 3×30$ |
| $30 ÷ 21 = 1$ あまり $9$ | $30 = 1×21 + 9$ | $9 = 30 - 1×21$ |
| $21 ÷ 9 = 2$ あまり $3$ | $21 = 2×9 + 3$ | $3 = 21 - 2×9$ |
| $9 ÷ 3 = 3$ |
となるので、ここから逆にたどっていきます:
$3 $
$= 21 - 2×9$
$= 21 - 2×(30 - 1×21) (9 を置き換える)$
$= (-2)×30 + 3×21$
$= (-2)×30 + 3×(111 - 3×30) (21 を置き換える)$
$= 3×111 + (-11)×30$
となりました。よって、$(x, y) = (3, -11)$ が $111x + 30y = 3$ を満たすので、これを 4 倍して $(x, y) = (12, -44)$ が $111x + 30y = 12$ を満たします。
すべての解を求める
整数解を 1 つ求めるだけでなくすべて求めたい場合には以下のようにします:
$111x + 30y = 12$
$12×111 + (-44)×30 = 12$
を辺々引くと
$111(x-12) + 30(y+44) = 0$
⇔ $37(x-12) = -10(y+44)$ (両辺を 3 で割った)
37 と 10 は互いに素なので $x-12$ は 10 の倍数になります。したがって $t$ を任意の整数として
$x - 12 = 10t$
と表せて、これを代入すると $y + 44 = -37t$ となります。よって一般解は $(x, y) = (10t + 12, -37t - 44)$ と求まりました。これが実際に解になっていることは代入すれば確かめられます。
3-3. ax + by = gcd(a, b) の整数解が存在することの一般論
前節で具体的な $a, b$ の数値が与えられている場合の解法を与えました。大学入試では抽象的に一般の整数 $a, b$ に対して $ax + by = {\rm gcd}(a, b)$ を満たす整数 $(x, y)$ が存在することを証明させる出題もあります。方法としては大きく分けて
- 「拡張ユークリッドの互除法」を具体的に記述する (3-4 にて)
- $ax + by$ で表される最小の正の整数を $d_0$ とおいて $d_0 = {\rm gcd}(a, b)$ を示す
- $a$ を法として $a$ と互いに素な整数たちが乗法群をなすことを活用する (本記事では省略、このページに高校数学で理解できる記述があります)
の 3 つの方法がメジャーです。次節で 1 番目の方法を示し、本節では 2 番目の方法を示します。本節の証明方法は大学受験業界でもよく見られる証明方法です。
【証明】
$ax + by$ の形で表される最小の正の整数を $ax_0 + by_0 = d_0$ とおく。
このとき、$ax + by$ で表される整数 $k$ はすべて $d_0$ の倍数になることを示す。
$k$ を $d_0$ で割った余りを $r$ ($0 \le r < d_0$) として
$k = qd_0 + r$
とおく。このとき $r = 0$ になることを示せばよい。
$r = k - qd_0 = (ax + by) - q(ax_0 + by_0) = a(x - qx_0) + b(y - qy_0)$
であるから、$r$ もまた $ax + by$ の形で表される整数となっている。ここでもし仮に $r > 0$ であると仮定すると、$r < d_0$ より、$d_0$ が $ax + by$ の形で表される最小の正の整数であることに矛盾する。従って $r = 0$ であることが示された。
以上より、$ax + by$ で表される整数はすべて $d_0$ の倍数である。これから $d_0$ を具体的に求める。まず、$d = gcd(a, b)$ とおくと、$a$ も $b$ も $d$ の倍数であるから、$ax + by$ は必ず $d$ の倍数である。従って $d$ | $d_0$ である。
次に $d_0$ | $d$ を示す。$a$ 自身も $ax + by$ の形で表される整数であるから ($a×1 + b×0 = a$ より)、$a$ は $d_0$ の倍数であり、同様にして $b$ も $d_0$ の倍数である。従って、$d_0$ は $a$ と $b$ の公約数である。すなわち $d_0$ は $d = gcd(a, b)$ の約数であって、$d_0$ | $d$ が成立する。
以上より、$d_0 = d = gcd(a, b)$ であることが示された。特に $ax + by = d$ となるような整数 $(x, y)$ が存在することが示された。
(証明終)
3-4. 拡張ユークリッドの互除法のアルゴリズム的記述
$ax + by = {\rm gcd}(a, b)$ を満たす $(x, y)$ を求めるアルゴリズムを具体的に導出します。このアルゴリズムを特に拡張ユークリッドの互除法と呼びます。これもやはり再帰関数を用いることで簡潔に実現できます。$d = {\rm gcd}(a, b)$ とおきます。
まずは普通のユークリッドの互除法と同様に $a$ を $b$ で割って
$a = qb + r$
とします。これを元の方程式に代入すると、
$(qb + r)x + by = d ⇔ b(qx + y) + rx = d$
となります。これによって $(a, b)$ に関する問題が、それより数値の小さな $(b, r)$ に関する問題に帰着できました。これを再帰的に解くのが拡張ユークリッドの互除法です。具体的には $(b, r)$ に関する小問題を解いて
$bs + rt = d$
を満たす解 $(s, t)$ が再帰的に得られたとすると、
$qx + y = s, x = t ⇔ x = t, y = s - qt$
という風に、元の問題の解を構成できます。ここで気になるのは、$bs + rt = d$ を満たす $(s, t)$ が本当に再帰的に得られるかどうかです。それを示すためにユークリッドの互除法の終了条件を考えてみます。ユークリッドの互除法は最後は $(d, 0)$ の形になります。つまりは、
$dx + 0y = d$
を満たす $(x, y)$ を求める問題まで降りて来ます。この解は $(x, y) = (1, 0)$ で明らかです。よってここから再帰的にドンドン上へ遡ることで元の方程式の解が構成できます。
以上のアルゴリズムを C++ で実装すると以下のようになります:
// 返り値: a と b の最大公約数
// ax + by = gcd(a, b) を満たす (x, y) が格納される
long long extGCD(long long a, long long b, long long &x, long long &y) {
if (b == 0) {
x = 1;
y = 0;
return a;
}
long long d = extGCD(b, a%b, y, x);
y -= a/b * x;
return d;
}
さきほどの $111x + 30y = 3$ について確かめてみます。
# include <iostream>
using namespace std;
// extGCD は略
int main() {
long long x, y;
extGCD(111, 30, x, y);
cout << x << ", " << y << endl;
}
実行結果は以下のようになりました:
3, -11
確かにさきほど手で求めた結果に一致しています。
4. ユークリッドの互除法と、素因数分解の一意性との関係 (おまけ)
通常の整数の世界において「素因数分解の一意性」が成立することはよく知られています。実は複素整数の世界でも「素因数分解の一意性」は成立します。この両者の根底にはともに
- ユークリッドの互除法が適用できる
という共通の構造があります。環論において一般に以下のような定理が成り立っています:
- ユークリッド整域は単項イデアル整域である
- 単項イデアル整域は一意分解整域である (素因数分解の一意性が成り立つ)
ユークリッド整域とはざっくり、ユークリッドの互除法が適用できる整域のことです。通常の整数環も複素整数環もユークリッド整域です。そして整域 $R$ が単項イデアル聖域であるとはまさに {$a_1 x_1 + a_2 x_2 + ... + a_n x_n | x_1, x_2, ..., x_n \in R$} で表される元がすべて単一の元 $d$ の倍数になるようなもののことを言います。「3-3. ax + by = gcd(a, b) の整数解が存在することの一般論」でやった議論は、まさにユークリッド整域が単項イデアル整域であることの証明の特殊ケースになっていました。一般論もほぼ同様に証明できます。
さらに単項イデアル整域において素因数分解の一意性が成立することを示すには、「既約元」「素元」という概念を定義して、それらの等価性を示していくことになります。それほど難しい議論ではないので、
といった書籍たちが参考になると思います。
5. おわりに
歴史上最古のアルゴリズムとして馴染みの深いユークリッドの互除法について特集してみました。本記事で特集した通り、ユークリッドの互除法は大学受験数学の整数問題において頻出のテーマであり、整数論的アルゴリズムの根幹を支えるものでもあります。また数え上げアルゴリズムでは「逆元」の計算を要する場面も多く、ユークリッドの互除法が有効に用いられます。
このようにユークリッドの互除法は、単に歴史上最古のアルゴリズムとしての記念碑であるにとどまらず、数学やアルゴリズムの根底に根ざしているものでもあります。本記事を通して、整数論や整数論的アルゴリズムの面白さを感じ取っていただけたならばとても嬉しい気持ちでいっぱいです。