0. はじめに

基本的なデータ構造として大学の授業や情報系の各種試験などによく登場するものの一つに、スタックとキューがあります。

スタックとキューについて学ぶ場面の多くでは、「スタックは LIFO (Last-In-First-Out)、キューは FIFO (First-In-First-Out)」と呪文のように覚えたり、

スタックは、例えば超忙しいときに新しい課題がぶっこまれたときとかにとりあえずそれを先に片付けるような感じ
キューは、人気ラーメン屋に並ぶ人々の待ち行列のように先に並んだ人が先にお店に入る感じ

という風に、日常の事物に対応づけて説明したりする文化が多く見受けられます。「タスクが次々と降ってくる状況をどう扱っていくか」というのは、日常生活を生きる人間にとっても、コンピュータ上の処理であっても自然に登場する普遍的な問題意識ですので、その最も基本的な思想であるところのスタックやキューについて、日常生活における状況になぞらえて理解するのは自然な試みではあります¹。しかしながらスタックやキューの考え方が様々な問題に対してどういう風に使えるのか、もっと掘り下げてみてもよいと感じています。

そもそも、スタックやキューは特別難しいデータ構造ではなく、配列や連結リストを用いて比較的簡単に実現することができます。したがってそれ自体の構造を深く学ぶべきものというよりは

データ構造としてはなんら特別なものではなく、配列や連結リストの上手な使い方の一つに過ぎないものである
その使い所についての理解が重要なものである

としてとらえるのが良さそうに思います (ただし組み込み系においてはスタックやキューの実現方法自体が重要な問題意識となるケースも多いです)。本記事では、主にアルゴリズム的な側面から、スタックやキューの考え方が有効に用いられるような問題例を特集してみます。

1. スタックとキュー

1-1. スタックとキューとは

まずスタックとキューとは何かについてです。「スタックは LIFO (Last-In-First-Out) で、キューは FIFO (First-In-First-Out) である」という知識はあっても、具体的にどういうものを指すのかについては摑みどころがないと感じている方も多いと思います。

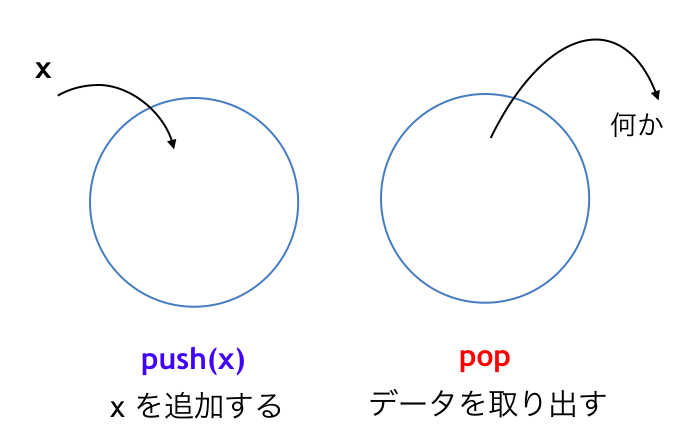
スタックもキューも、以下のようなフレームワークに則った「データの持ち方 (データ構造)」のことです。

push(x): 要素 x をデータ構造に追加する
pop(): データ構造から要素を取り出す
isEmpty(): データ構造が空かどうかを調べる (おまけ)

ここで push する要素 x がどのようなデータを指すかについては、用途によって様々です。「新しく降って来たタスク」だったり「チケットのキャンセル待ちデータ」だったり「スクリプトが呼び出した関数」だったり「採点待ちの提出コード」だったりします。

追加された処理待ちデータをどの順番で pop するかについては、場面によって様々な思想が考えられます。その思想として最も基本的かつ典型的なものを表すのがスタックとキューです:

データ構造	pop の仕様
スタック	データ構造に入っている要素のうち、最後に push した要素を取り出す
キュー	データ構造に入っている要素のうち、最初に push した要素を取り出す

これでスタックとキューの仕様が定まりました。なお注意点として、ここではスタックとキューを統一的に説明するために、キューに対しても push, pop という用語を用いました²が、これらはそれぞれ enqueue, dequeue と呼ぶことが多いです。以降は enqueue, dequeue という用語を用います。

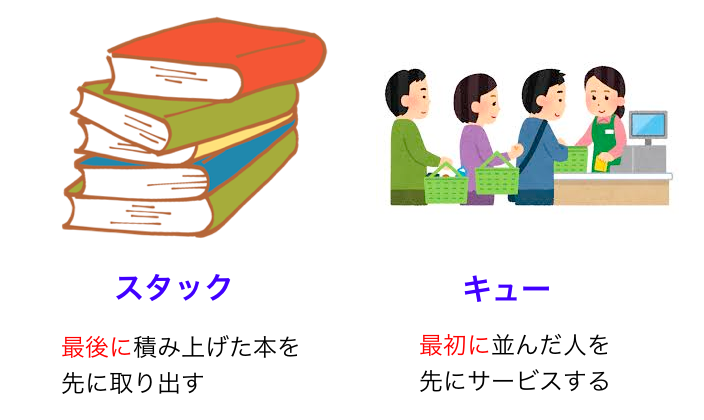
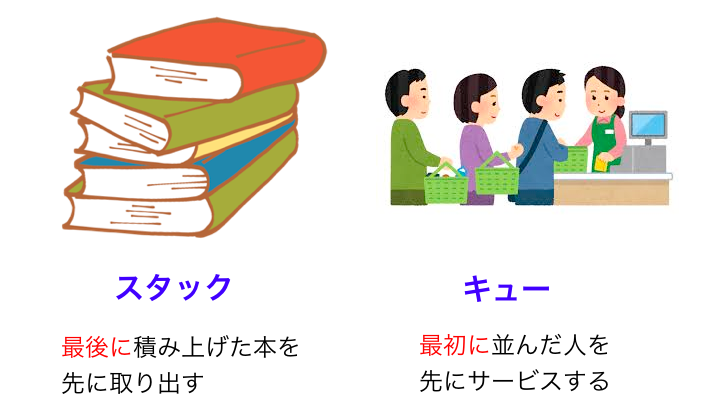
スタックとキューの思想については、下図 (再掲) のように日常生活の具体的な状況をイメージするとわかりやすいと思います。

1-2. スタック・キューの使用場面

スタックもキューも、「降って来たタスクなり要素なりをどういう順序で処理していくか」という普遍的な問いに対する、最も基本的かつ典型的な思想を表すデータ構造です。それゆえに、日常生活からコンピュータサイエンスの全域に至るまで、幅広い領域で暗に使われています。ここでは基本的な使われ方をいくつか紹介し、さらなる応用例については 3 章, 4 章で紹介します。

1-2-1. スタックの用途

スタックは「最後に追加した要素を最初に取り出す (LIFO)」というものでした。日常生活では「積み上げられた本」や「タスクをこなしているときにかかって来た電話にとりあえず答えるような状態」などにたとえられます。コンピュータサイエンスにおける典型的用途としては

再帰関数の再帰呼び出し
Web ブラウザの訪問履歴 (戻りボタンで pop)
テキストエディタでの Undo 系列

といったものが挙げられます。

1-2-2. キューの用途

キューは「最初に追加した要素を最初に取り出す (FIFO)」というものでした。日常生活では「ラーメン屋の行列」などにたとえられます。古いデータから先に処理していくイメージです。コンピュータサイエンスにおける典型的用途としては

印刷機のジョブスケジューリング
航空券予約のキャンセル待ち処理
ファイル IO などにおける非同期データ転送

といったものが挙げられます。

2. スタック・キューの詳細と実装

いよいよスタックとキューの動作について、具体的に追うことで理解を深めていきたいと思います。スタックとキューはいずれも配列を用いて実現することができます。スタックとキューを配列を用いて理解することは、スタックとキューの仕組みそのものを理解することに直結しています。

具体例の後に、スタック・キューの配列を用いた簡易実装を示します。あくまでスタック・キューの概念を示すための簡易実装ですので、「配列サイズを超えて要素を挿入しようとした場合にバッファ領域を新たに確保するような処理」などは行っていませんし、構造体やクラスとしてまとめることもしていません。実際上は特にキューについては、2-5 で例示するように、各言語において標準で提供されているライブラリを用いるのが良いと思います。

2-1. スタックの詳細

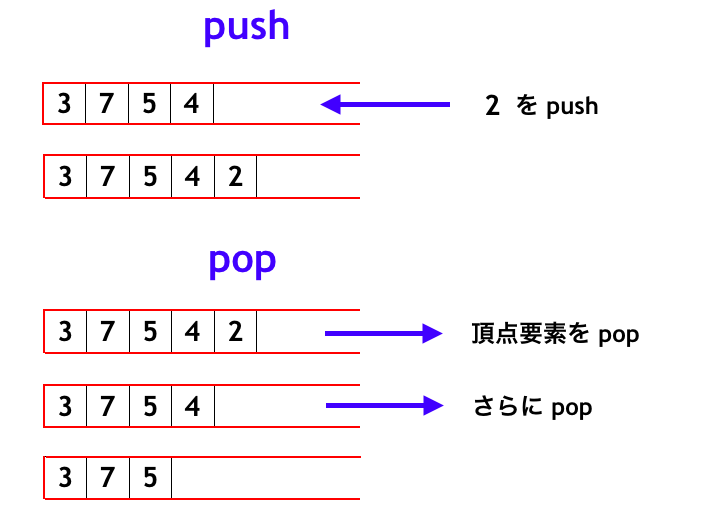
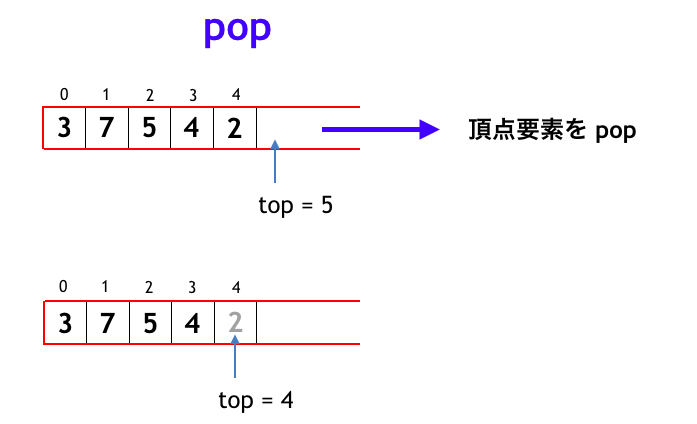
スタックの動きを配列ベースできちんと考えると下図のようになります。まず push については、例えば追加された順に「3, 7, 5, 4」となっているスタックに「2」を push すると「3, 7, 5, 4, 2」となります。この状態で pop すると「2」が取り出されて「3, 7, 5, 4」となります。さらに pop すると「4」が取り出されて「3, 7, 5」になります。

スタックを実装するためには、下図のように、スタック中の最後に追加された要素の次の index (次に新たに要素を push するときにそれを格納する index) を示す変数 top を用いると簡明です。このとき top は同時に「スタックに格納されている要素数」でもあります。push については下図のように top に追加要素を格納して、top をインクリメントします。

pop するときは、top の位置にある要素を出力して、top をデクリメントします。このとき配列において pop した要素をどうするかは実装依存ですが、そのままにしておいても差し支えないです。

以上の処理を実装すると例えば以下のようになるでしょう。ここではスタックを実現するための配列のサイズを固定した状態で実装しています。またここではスタックに追加する要素を int 型としていますが、他に様々な型を扱うこともできます (C++ の std::stack ではテンプレートを用いています)。また push や pop は std::stack のメソッドでも用いられている関数名ですので、本来は注意が必要です。また

スタックが空のとき (top = 0 のとき) に pop しようとする場合
スタックが満杯のとき (top == MAX のとき) に push しようとする場合

については例外処理するようにしています。

スタックの簡易実装例

#include <iostream>
#include <vector>
using namespace std;
const int MAX = 100000; // スタック配列の最大サイズ

int st[MAX]; // スタックを表す配列
int top = 0; // スタックの先頭を表すポインタ

// スタックを初期化する
void init() {
    top = 0; // スタックポインタを初期位置に
}

// スタックが空かどうかを判定する
bool isEmpty() {
    return (top == 0); // スタックサイズが 0 かどうか
}

// スタックが満杯かどうかを判定する
bool isFull() {
    return (top == MAX); // スタックサイズが MAX かどうか
}

// push (top を進めて要素を格納)
void push(int v) {
    if (isFull()) {
        cout << "error: stack is full." << endl;
        return;
    }
    st[top++] = v; // st[top] = v; と top++; をまとめてこのように表せます
}

// pop (top をデクリメントして、top の位置にある要素を返す)
int pop() {
    if (isEmpty()) {
        cout << "error: stack is empty." << endl;
        return -1;
    }
    return st[--top]; // --top; と return st[top]; をまとめてこのように表せます
}

int main() {
    init(); // スタックを初期化

    push(3); // スタックに 3 を積む {} -> {3}
    push(5); // スタックに 5 を積む {3} -> {3, 5}
    push(7); // スタックに 7 を積む {3, 5} -> {3, 5, 7}

    cout << pop() << endl; // {3, 5, 7} -> {3, 5} で 7 を出力
    cout << pop() << endl; // {3, 5} -> {3} で 5 を出力

    push(9); // 新たに 9 を積む {3} -> {3, 9}
    push(11); // {3, 9} -> {3, 9, 11}

    pop(); // {3, 9, 11} -> {3, 9}
    pop(); // {3, 9} -> {3}
    pop(); // {3} -> {}

    // 空かどうかを check: empty の方を出力
    cout << (isEmpty() ? "empty" : "not empty") << endl;
}

出力結果は以下のようになりました:

7
5
empty

2-2. キューの詳細

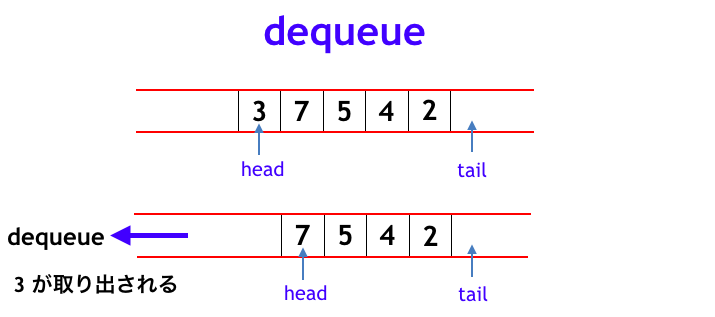
スタックの配列を用いた実現方法は「左側が閉じている」「行き止まりのトンネルの中に要素を突っ込んでいる」ようなイメージでしたが、キューは下図のように「両端が開いている」イメージです。例えば追加された順に「3, 7, 5, 4」となっているキューに「2」を enqueue すると「3, 7, 5, 4, 2」となります。この状態で dequeue すると「3」が取り出されて「7, 5, 4, 2」となります。

スタックでは「3, 7, 5, 4, 2」の状態で pop すると「3, 7, 5, 4」になるのでした。

スタックでは、次に新たに要素を push するときにそれを格納する index を表す変数 top を用いることで簡単に実装できましたが、キューでは

最初に追加された要素の index を表す変数 head
最後に追加された要素の次の index を表す変数 tail

の両方を用いることで実装できます。しかしここで一つ問題が生じます。キューで enqueue と dequeue を繰り返していると、tail だけでなく head も右へ右へ進んで行くので、head も tail もドンドン右に移動することになります。このままでは途方もない配列サイズが必要となってしまいます。

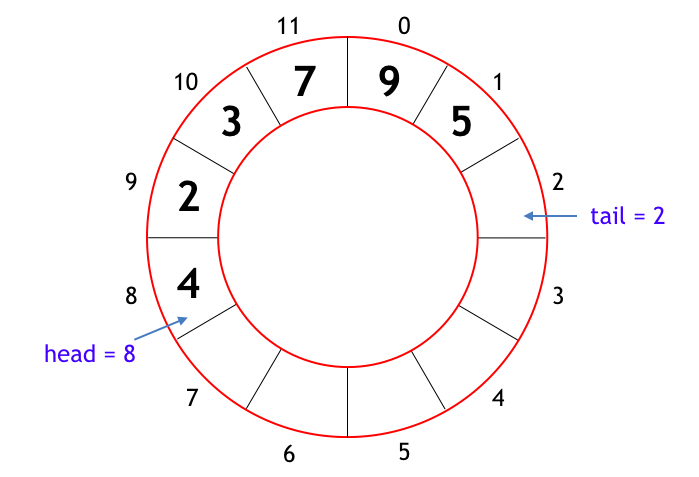
これを解決する仕組みとして広く用いられているのがリングバッファと呼ばれる配列の使い方です。といっても実態は今までの配列と変わらないです。配列サイズを N としたとき配列の index は 0, 1, 2, ..., N-1 で表されますが、例えば tail = N-1 の状態からインクリメントするとき、tail = N とするのではなく tail = 0 に戻ります。head についても同様です。これによって、キューに追加された要素数が配列サイズを超えない限り、head や tail がいくらでもインクリメントしても大丈夫です。下図 (バッファサイズが 12 の場合を表しています) のようなリング中をひたすら要素たちが回転するような動きになります。

キューの実装は例えば以下のようにできます。ただしここではリングバッファのサイズを固定した簡易実装ゆえにシンプルな実装におさまっていますが、実際上は「キューに追加されている要素数の増加に伴ってリングバッファ領域を新たに確保するような処理」を実現したいと考えた場合には結構大変です。またスタックの場合と同様に

キューが空のとき (head == tail のとき) に pop しようとする場合
キューが満杯のとき (head == (tail + 1) % MAX のとき) に push しようとする場合

については例外処理するようにしています。ここでキューが満杯かどうかの判定基準ですが、ここでは「あと 1 個要素を追加したらリングバッファの先頭と最後尾が繋がってしまう状態」としています。すなわちバッファに追加されている要素が MAX - 1 個の状態を満杯であるとしています。

キューの簡易実装例

#include <iostream>
#include <vector>
using namespace std;
const int MAX = 100000; // キュー配列の最大サイズ

int qu[MAX]; // キューを表す配列
int tail = 0, head = 0; // キューの要素区間を表す変数

// キューを初期化する
void init() {
    head = tail = 0;
}

// キューが空かどうかを判定する
bool isEmpty() {
    return (head == tail);
}

// スタックが満杯かどうかを判定する
bool isFull() {
    return (head == (tail + 1) % MAX);
}

// enqueue (tail に要素を格納してインクリメント)
void enqueue(int v) {
    if (isFull()) {
        cout << "error: queue is full." << endl;
        return;
    }
    qu[tail++] = v;
    if (tail == MAX) tail = 0; // リングバッファの終端に来たら 0 に
}

// dequeue (head にある要素を返して head をインクリメント)
int dequeue() {
    if (isEmpty()) {
        cout << "error: stack is empty." << endl;
        return -1;
    }
    int res = qu[head];
    ++head;
    if (head == MAX) head = 0;
    return res;
}

int main() {
    init(); // キューを初期化

    enqueue(3); // キューに 3 を積む {} -> {3}
    enqueue(5); // キューに 5 を積む {3} -> {3, 5}
    enqueue(7); // キューに 7 を積む {3, 5} -> {3, 5, 7}

    cout << dequeue() << endl; // {3, 5, 7} -> {5, 7} で 3 を出力
    cout << dequeue() << endl; // {5, 7} -> {7} で 5 を出力

    enqueue(9); // 新たに 9 を積む {7} -> {7, 9}
    enqueue(11); // {7, 9} -> {7, 9, 11}

    dequeue(); // {7, 9, 11} -> {9, 11}
    dequeue(); // {9, 11} -> {11}
    dequeue(); // {11} -> {}

    // 空かどうかを check: empty の方を出力
    cout << (isEmpty() ? "empty" : "not empty") << endl;
}

出力結果は以下のようになりました:

3
5
empty

2-3. デックと優先度付きキュー

スタック・キュー以外にも「降って来たタスクなり要素なりをどういう順序で処理していくか」についての思想を反映したデータ構造は様々なものが考えられます。代表的なものとして、デックと優先度付きキューがあります。

データ構造	機能	C++ ライブラリ
デック	スタックとキューの両方の機能を兼ね備えたもの	std::deque
優先度付きキュー	キューに優先度をつけて要素を追加して、優先度の高い要素から取り出す	std::priority_queue

デックは両端キューとも呼ばれ、データ構造中の要素が一列に並んでいることを前提として

先頭にも末尾にも要素を追加できる
先頭からも末尾からも要素を取り出せる

というデータ構造となっています。優先度付きキューは多くの場合、ヒープと呼ばれるデータ構造を用いて実装されます。

2-4. 連結リストを用いたスタック・キューの実装方法

スタックとキューの実現方法としては配列を用いるのが一般的ですが、連結リストを用いて実現することもできます。詳細はここでは省略しますが、連結リスト構造における

head に追加する
head を削除する
tail に追加する

といった処理を用いることで、以下のように簡単に実現できます。「削除」操作を含んだ連結リストは通常は双方向連結リストを用いて実装しますが、head の削除だけであれば片方向連結リストでも十分実現することができます。

データ構造	push (enqueue)	pop (dequeue)
スタック	head に追加	head を削除
キュー	tail に追加	head を削除

2-5. C++ ライブラリ

スタックやキューは自分で実装してもいいのですが、特にキューについては少し面倒です (スタックは配列を用いて自分でパッと実装してもいいと思います)。そこで多くのプログラミング言語ではスタックやキューの実装が標準ライブラリとして用意されています。

例えば C++ ではスタック、キューはそれぞれ std::stack, std::queue を簡便に用いることができます。以下に使用例を挙げます。注意点として std::stack や std:queue を用いるときは、今までの pop の 2 つの動作「先頭要素を取り出す」「先頭要素を削除する」をそれぞれ top(), pop() 関数を用いて分けて行うことになります。

std::stackの使用例

stackの使用例

#include <iostream>
#include <stack>
using namespace std;

int main() {
    /* スタック */
    stack<int> S;

    S.push(3); // スタックに 3 を積む {} -> {3}
    S.push(5); // スタックに 5 を積む {3} -> {3, 5}
    S.push(7); // スタックに 7 を積む {3, 5} -> {3, 5, 7}

    cout << S.size() << endl; // スタックのサイズを出力: 3 が出る

    cout << S.top() << endl; // スタックの頂点要素: 7 が出る
    S.pop(); // {3, 5, 7} -> {3, 5}

    cout << S.top() << endl; // スタックの頂点要素: 5 が出る
    S.pop(); // {3, 5} -> {3}

    S.push(9); // 新たに 9 を積む {3} -> {3, 9}
    cout << S.top() << endl; // スタックの頂点要素: 9 が出る

    S.push(11); // {3, 9} -> {3, 9, 11}
    S.pop(); // {3, 9, 11} -> {3, 9}
    S.pop(); // {3, 9} -> {3}
    cout << S.top() << endl; // スタックの頂点要素: 3 が出る

    S.pop(); // {3} -> {}

    // 空かどうかを check: empty の方を出力
    cout << (S.empty() ? "empty" : "not empty") << endl;
}

これを実行すると、以下の結果になりました:

3
7
5
9
3
empty

std::queueの使用例

queueの使用例

#include <iostream>
#include <queue>
using namespace std;

int main() {
    /* キュー */
    queue<int> Q;

    Q.push(3); // キューに 3 を追加 {} -> {3}
    Q.push(5); // キューに 5 を追加 {3} -> {3, 5}
    Q.push(7); // キューに 7 を追加 {3, 5} -> {3, 5, 7}

    cout << Q.size() << endl; // キューのサイズを出力: 3 が出る

    cout << Q.front() << endl; // キューの先頭要素: 3 が出る
    Q.pop(); // {3, 5, 7} -> {5, 7}

    cout << Q.front() << endl; // キューの先頭要素: 5 が出る
    Q.pop(); // {5, 7} -> {7}

    Q.push(9); // 新たに 9 を追加 {7} -> {7, 9}
    cout << Q.front() << endl; // キューの先頭要素: 7 が出る

    Q.push(11); // {7, 9} -> {7, 9, 11}
    Q.pop(); // {7, 9, 11} -> {9, 11}
    Q.pop(); // {9, 11} -> {11}
    cout << Q.front() << endl; // キューの先頭要素: 11 が出る

    Q.pop(); // {11} -> {}

    // 空かどうかを check: empty の方を出力
    cout << (Q.empty() ? "empty" : "not empty") << endl;
}

これを実行すると、以下の結果になりました:

3
3
5
7
11
empty

3. スタック・キューを用いて問題を解く

前章にて、スタック・キューの詳細を具体的に見ると同時に、コンピュータ内部のおける典型的な使われ方について見てきました。ここではスタック・キューを単なる「降りかかってくるタスクを処理する順序の思想を表すもの」としてとらえる枠組みを超えて、アルゴリズム的な種々の問題たちを効率よく解くのにも使えることがある、というのを特集します。いくつかのものについては概要のみにとどめて、詳細な解説へのリンクを掲載します。

3-1. 括弧列の整合性チェック (スタック)

(())(())((()())))()))()

のような括弧列があたえられたとき、左括弧と右括弧の対応関係を整理したり、括弧列が全体として整合がとれているかどうかを判定する問題は重要です。この問題はスタックを用いることで鮮やかに解くことができます。

最初はスタックを空の状態にしておく
括弧列を左から順番に見て行き、
- 左括弧 '(' が来たらスタックに push する
- 右括弧 ')' が来たら
  - もしスタックが空だった場合にはエラーを返す
  - スタックが空でなかった場合は、top 要素を pop する (ここで pop した '(' と手元にある ')' が互いに対応します)

以上の処理を終えたとき、もしスタックが空であれば、括弧列は整合がとれていたことがハッキリとします (具体的な対応関係も明らかにできています！)。

空でなかった場合には左括弧が余っていたことが判明するのでエラーを返します。

括弧列の対応をとる

#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <stack>
using namespace std;

bool check(const string &S) {
    stack<int> st; // 左括弧の index を格納するスタック
    vector<pair<int,int> > ps; // 対応を表すペア

    // ループを回す
    for (int i = 0; i < (int)S.size(); ++i) {
        if (S[i] == '(') st.push(i);
        else {
            if (st.empty()) {
                cout << "error" << endl;
                return false;
            }
            int t = st.top();
            st.pop();
            ps.push_back({t, i});
        }
    }

    // スタックが空でなかったら左括弧が過剰
    if (!st.empty()) {
        cout << "too many (" << endl;
        return false;
    }

    // 整合を出力
    sort(ps.begin(), ps.end());
    for (int i = 0; i < (int)ps.size(); ++i) {
        if (i) cout << ", ";
        cout << "(" << ps[i].first << ", " << ps[i].second << ")";
    }
    cout << endl;
    return true;
}

int main() {
    check("((()())())"); // (0, 9) (1, 6), (2, 3), (4, 5), (7, 8)
    check("())"); // error
    check("(()"); // too many (
}

なお、左括弧と右括弧の対応を正確にとる必要はなく、括弧列全体の整合性を判定するだけであれば、明示的にスタックを用いなくても、スタックポインタ top に相当する変数を 1 個管理するだけでも簡潔に実装することができます。

括弧列の整合性判定

#include <iostream>
#include <string>
using namespace std;

bool check(const string &S) {
    int top = 0;
    for (auto c : S) {
        if (c == '(') ++top;
        else {
            if (top == 0) return false;
            --top;
        }
    }
    if (top) return false;
    else return true;
}

int main() {
    cout << check("((()())())") << endl; // true
    cout << check("())") << endl; // false
    cout << check("(()") << endl; // false
}

3-2. 逆ポーランド記法 (スタック)

逆ポーランド記法とは、数式の記法の一種であり、

(3 + 4) * (1 - 2)

といった演算順序の解析が複雑な数式に対し、

3 4 + 1 2 - *

という風に、演算子をオペランドの後に記述する方法であり、括弧が不要になるメリットがあります。逆ポーランド記法で与えられた数式の計算にはスタックを用いることができます。上例の場合は以下のようになります:

処理順序	処理内容	スタック状態
初期状態		{}
3	スタックに 3 を push する	{3}
4	スタックに 4 を push する	{3, 4}
+	スタックの先頭から二要素を pop (ここでは 3 と 4) して、3 + 4 = 7 と計算し、計算結果 7 をスタックに push する	{7}
1	スタックに 1 を push する	{7, 1}
2	スタックに 2 を push する	{7, 1, 2}
-	スタックの先頭二要素を pop して演算結果を push する	{7, -1}
*	スタックの先頭二要素を pop して演算結果を push する	{-7}

こうして計算結果が -7 であることがわかりました。

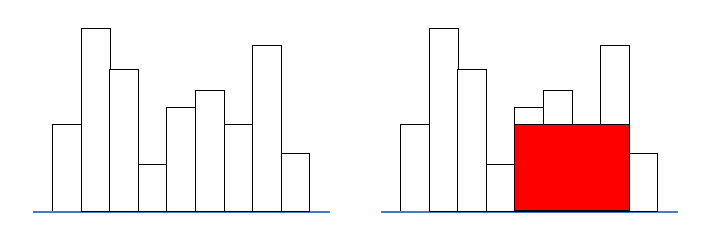
3-3. ヒストグラム中の面積最大の長方形 (スタック)

スタックを用いることで効率よく解くことのできる有名な問題として、ヒストグラム中に含まれる面積最大の長方形を求める問題があります。下図の左のようなヒストグラムが与えられたとき、右の赤い長方形のようなヒストグラムに包含される長方形のうち、面積が最大のものを求める問題です。

この問題の解法については、蟻本に載っていますので該当ページを見ていただくか、

ヒストグラム中の最大の長方形の面積

を読んでいただけたらと思います。

3-4. スパン (スタック)

数列 $A_1, A_2, \dots, A_N$ の各要素 $A_i$ に対して、$A_j \ge A_i$ を満たすような最大の $j (< i)$ を求める問題を考えます。ただしそれが存在しない場合は $0$ を答えます。例えば

6, 2, 4, 1, 3, 5, 7

に対しては

0, 1, 1, 3, 3, 1, 0

となります。愚直に計算すれば各要素に対して、それより前の要素をすべて探索することで $O(N^2)$ の計算時間で実施することができますが、スタックを用いると以下のように $O(N)$ ですべて求めることができます。

スパンを求める

#include <iostream>
#include <vector>
#include <stack>
using namespace std;
const int INF = 100000000; // 十分大きい値

int main() {
    // 入力
    int N; cin >> N;
    vector<int> A(N);
    for (int i = 0; i < N; ++i) cin >> A[i];

    // スタック
    stack<pair<int,int> > st;
    st.push({INF, 0}); // 番兵
    for (int i = 0; i < N; ++i) {
        // 条件を満たすまで pop し続ける
        while (A[i] > st.top().first) st.pop();

        // 答えを出力
        cout << st.top().second << ", ";

        // 新たに push
        st.push({A[i], i+1});
    }
    cout << endl;
}

3-5. ラウンドロビン・スケジューリング (キュー)

オペレーションシステムにおけるプロセスのスケジューリング規則として考えられるものについて、簡単なモデルをキューを用いて実装してみます。CPU が $N$ 個のプロセス ($i$ 番目のプロセスは ${\rm name}_{i}$ という名前で、${\rm time}_{i}$ の処理時間を必要とするものとします) を順に処理していくのですが、各プロセスは最大で $Q$ の時間だけ処理が実行されるものとします。各プロセスについて、$Q$ の時間だけ処理を行っても完了しなかった場合には、そのプロセスはプロセス待機列の最後尾に移動して、次のプロセスを実行するようにします。

以上の処理をキューを用いて実装してみましょう。なおこの問題に対してはこちらのページで処理をシミュレートするプログラムを書いて提出して、正しく答えられているかどうかをジャッジすることができます。

ラウンドロビン・スケジューリングのシミュレーション

#include <iostream>
#include <string>
#include <queue>
using namespace std;

int main() {
    // 入力, キューにまずは順に要素を追加します
    int N;
    int Q; // クオンタム
    cin >> N >> Q;
    queue<pair<string,int> > que;
    for (int i = 0; i < N; ++i) {
        string name;
        int time;
        cin >> name >> time;
        que.push({name, time});
    }

    // ラウンドロビンスケジーリング
    int cur_time = 0;
    while (!que.empty()) {
        auto cur = que.front();
        que.pop();

        // Q 秒以上かかるとき、Q 秒処理してまたキューに追加
        if (cur.second > Q) {
            cur_time += Q;
            cur.second -= Q;
            que.push(cur);
        }
        // Q 秒以内に終了するときは、処理を終えてプログラムを出力する
        else {
            cur_time += cur.second;
            cout << cur.first << " " << cur_time << endl;
        }
    }   
}

3-6. 後退解析 (キュー)

後退解析とは、どうぶつしょうぎや将棋のような、局面の状態がループしうるようなゲームの解析に使われる手法です。どうぶつしょうぎは実際に後退解析によって完全解析がなされています³。

後退解析はキューを用いたグラフ探索手法の一種です。その考え方はゲームの解析のみならず、有向グラフのサイクルを検出したり、DAG をトポロジカルソートしたりする問題などにも使うことができて、応用がとても広いです。いくつかの例については

などを読んでいただけたらと思います。

3-7. スライド最小値 (デック)

3 章の最後に、デックを用いて効率よく解くことのできる問題として、スライド最小値を紹介します。スライド最小値とは、長さ $N$ の数列 $A_1, A_2, \dots, A_N$ に対して以下の $Q$ 個のクエリに素早く答える問題です。ここで、クエリ番号 $i$ に対して $l_i$ も $r_i$ も広義単調増加であることを仮定します。

$i$ 番目のクエリは $2$ つの整数 $1 \le l_i \le r_i \le N$ が与えらえて、$\min_{l_i \le j \le r_i} A_j$ の値を答える

各クエリに対して愚直に $A_{l_i}, A_{l_i + 1}, \dots, A_{r_i}$ の値をすべて調べて最小値をとるのでは、最悪 $O(QN)$ の計算時間を必要としますが、デックを用いて効率よく $O(Q + N)$ の計算量ですべてのクエリに答えることができます。その詳細については

スライド最小値

を読んでいただけたらと思います。

4. 深さ優先探索 (DFS) と幅優先探索 (BFS)

最後にスタック・キューの思想を探索問題に適用してみます。探索とは、様々な形式のデータを順に走査していくもので、あらゆるアルゴリズムの基本となるものです。例えばネットサーフィンを行うときは、次々とリンクをたどっていくわけですが、そのときの探索行為は

新しくページを開くごとに、次に飛びたいページ内リンクたちが「これから見るバッファ」に push され、
そのバッファから pop して実際に新しくページを見に行く

という風にとらえることができます。ここでその pop の仕方がスタック寄りかキュー寄りかは人によって性格が出る部分だと思います。

「一度飛びたいリンクを見つけたら次々とリンクを飛んで行く」というスタンスはスタック的
「飛びたいリンクを一旦タブで全部開いておいて一個一個順に見て行き、それが済んでから新たなリンクを開拓する」というスタンスはキュー的

であると言えます。実はこれらの探索様式には名前がついています。前者を深さ優先探索 (DFS)、後者を幅優先探索 (BFS) と呼びます。以上の事情をもう少しグラフという概念を用いて整理してみましょう。

4-1. グラフ

まず大前提として、大抵の物事はグラフを用いて整理できることに注意します。グラフとは

ノードの集まり
エッジ (ノードとノードの繋がりを表すもの) の集まり

を表すもので、下図のように描画されることが多いです。ノードは丸で、エッジは矢印で表しています。また各ノードには番号を付けています。ここでは各エッジに向きがあるバージョンを考えていましたが、各エッジに向きがないバージョンもあります。その場合はエッジは矢印ではなく線分で表すことが多いです。なお、エッジに向きのあるグラフを有向グラフ、向きのないグラフを無向グラフと呼びます。

グラフを用いることで、以下に例示するような様々な事物を抽象的に統一的に整理することができます:

Web ページのリンク (ノード: Web ページで、エッジ: リンク)
人間同士の友人関係 (ノード: 人間、エッジ: 友達関係)
論文著者の共著関係 (ノード: 著者、エッジ: 共著関係)
家系図 (ノード: 人、エッジ: 親子関係や兄弟関係など)
鉄道の路線図 (ノード: 駅、エッジ: 路線)
道路ネットワーク (ノード: 交差点, エッジ: 道路)
タスクの依存関係 (ノード: タスク、エッジ: 依存関係)
将棋や囲碁の局面 (ノード: 局面、エッジ: 手)

4-2. グラフ上の探索

以上のように、様々な物事を探索する問題は、グラフ上の探索問題ととらえることができます。このようにとらえることで様々な問題を統一的に扱えるメリットがあります。例えば、(現実的には計算資源的に不可能ですが) 将棋や囲碁の必勝法を見出したいと考えた場合には、原理的には将棋の全局面の遷移を表したグラフを探索し尽くすことで、それを実現することができます。

ノード $v_0$ を出発点としたグラフの探索は、一般的には下のようなフレームワークで記述することができます。ここで $v_0$ は将棋であれば初期盤面、ネットサーフィンであればホームページといったものを表します。

v0からの探索

seen := グラフの各ノードについて、そのノードが訪問済みかどうかを表す配列
to_visit := これから訪問するノードの集合を表すスタックやキュー

seen をすべて false に初期化する
seen[v0] = true
to_visit.push(v0)
while (to_visit が空でない) {
  cur_v = to_visit.pop()
  for (next_v : (cur_v から行くことのできるノード集合)) {
    // next_v が訪問済みならスルーして、未訪問なら to_visit に追加
    if (!seen[next_v]) {
      seen[next_v] = true
      to_visit.push(next_v)
    }
  }
}

to_visit をスタックにすれば深さ優先探索 (DFS)、キューにすれば幅優先探索 (BFS) になります。双方に強みと弱みがありますので、場面場面に応じて使いこなしたいところです。なお深さ優先探索については、スタックを明示的に用いる代わりに再帰関数を用いることで、より柔軟に様々な処理を明快に実装できることも多いです。グラフ上の探索については、また別の機会に詳しく記事にしたいと思います。

さらに to_visit を優先度付きキュー (各頂点 v の優先度は「現時点でわかっているスタートから v への最短距離」が小さい順とする) とすれば、最短路アルゴリズムとしてお馴染みのダイクストラ法にもなります。このように、スタック・キューといった枠のみにとらわれることなく、柔軟な設計を行うことで様々な探索を実現することもできます。

ここでは一例として、下図のような迷路についてスタート (S マス) からゴール (G マス) まで辿り着くまでの最短路を求めるアルゴリズムを実装してみましょう。毎ステップごとに上下左右のいずれかに進むことができますが、黄色マスには進むことができないものとします。

これはキューを用いた幅優先探索で明快に解くことができます。ここではスタートからゴールまでの最短距離も求めることができるようにするため、上に挙げたグラフ探索疑似コードにおいて

seen[v] := ノード v (この場合は各マス) が訪問済みかどうか

としていた配列を

dist[x][y] := スタートからマス (x, y) まで最短で何ステップでいけるか (ただし未訪問の場合は -1 としておく)

という配列で置き換えます。そして

マス (x, y) が訪問済みかどうか
マス (x, y) が訪問済みの場合には、スタートから何ステップで到達できたか⁴

という情報を更新していきます。こうすることで、スタートから各マスまでの最短距離も同時に求めることができるようになります。なお、迷路の入力形式としては以下のように

1 行目に迷路のサイズ
2 行目以降に迷路のマップ ('S': スタート、'G': ゴール、'.': 通路、'#': 壁)

を表すものとします。

8 8
.#....#G
.#.#....
...#.##.
#.##...#
...###.#
.#.....#
...#.#..
S.......

さていよいよ迷路を解いてみましょう。なお、スタートからゴールまでの最短距離がわかった後で具体的な最短経路を復元する方法については

意外と解説がない！動的計画法で得た最適解を「復元」する一般的な方法

を読んでいただけたらと思います。

迷路の最短路を幅優先探索で解く

#include <iostream>
#include <queue>
#include <vector>
#include <string>
#include <iomanip>
using namespace std;

/* 4 方向への隣接頂点への移動を表すベクトル */
const int dx[4] = { 1, 0, -1, 0 };
const int dy[4] = { 0, 1, 0, -1 };


int main() {

    ////////////////////////////////////////
    /* 入力受け取り */
    ////////////////////////////////////////

    /* 縦と横の長さ */
    int height, width;
    cin >> height >> width;

    /* 盤面 */
    vector<string> field(height);
    for (int h = 0; h < height; ++h) cin >> field[h];

    /* スタート地点とゴール地点 */
    int sx, sy, gx, gy;
    for (int h = 0; h < height; ++h) {
        for (int w = 0; w < width; ++w) {
            if (field[h][w] == 'S') {
                sx = h;
                sy = w;
            }
            if (field[h][w] == 'G') {
                gx = h;
                gy = w;
            }
        }
    }


    ////////////////////////////////////////
    /* 幅優先探索の初期設定 */
    ////////////////////////////////////////

    // 各セルの最短距離 (訪れていないところは -1 としておく)
    vector<vector<int> > dist(height, vector<int>(width, -1)); 
    dist[sx][sy] = 0; // スタートを 0 に

    // 探索中に各マスはどのマスから来たのかを表す配列 (最短経路長を知るだけなら、これは不要)
    vector<vector<int> > prev_x(height, vector<int>(width, -1));
    vector<vector<int> > prev_y(height, vector<int>(width, -1));

    // 「一度見た頂点」のうち「まだ訪れていない頂点」を表すキュー
    queue<pair<int, int> > que; 
    que.push(make_pair(sx, sy)); // スタートを push


    ////////////////////////////////////////
    /* 幅優先探索を実施 */
    ////////////////////////////////////////    

    /* キューが空になるまで */
    while (!que.empty()) {
        pair<int, int> current_pos = que.front(); // キューの先頭を見る (C++ ではこれをしても pop しない)
        int x = current_pos.first;
        int y = current_pos.second;
        que.pop(); // キューから pop を忘れずに

        // 隣接頂点を探索
        for (int direction = 0; direction < 4; ++direction) {
            int next_x = x + dx[direction];
            int next_y = y + dy[direction];
            if (next_x < 0 || next_x >= height || next_y < 0 || next_y >= width) continue; // 場外アウトならダメ
            if (field[next_x][next_y] == '#') continue; // 壁はダメ

            // まだ見ていない頂点なら push
            if (dist[next_x][next_y] == -1) {
                que.push(make_pair(next_x, next_y));
                dist[next_x][next_y] = dist[x][y] + 1; // (next_x, next_y) の距離も更新
                prev_x[next_x][next_y] = x;  // どの頂点から情報が伝播して来たか、縦方向の座標をメモ
                prev_y[next_x][next_y] = y;  // どの頂点から情報が伝播して来たか、横方向の座標をメモ
            }
        }
    }


    ////////////////////////////////////////
    /* 結果出力 */
    ////////////////////////////////////////    

    int x = gx, y = gy;
    while (x != -1 && y != -1) {
        field[x][y] = 'o'; // 通過したことを示す

        // 前の頂点へ行く
        int px = prev_x[x][y];
        int py = prev_y[x][y];
        x = px, y = py;
    }
    for (int h = 0; h < height; ++h) {
        for (int w = 0; w < width; ++w) {
            cout << std::setw(3) << field[h][w];
        }
        cout << endl;
    }
}

このプログラムに先ほどの入力を与えると、以下のような出力になりました:

  .  #  o  o  o  .  #  o
  .  #  o  #  o  o  o  o
  .  o  o  #  .  #  #  .
  #  o  #  #  .  .  .  #
  o  o  .  #  #  #  .  #
  o  #  .  .  .  .  .  #
  o  .  .  #  .  #  .  .
  o  .  .  .  .  .  .  .

5. おわりに

基本的なデータ構造として、どのアルゴリズム系入門書にも載っているスタック・キューについて、考え方・実装から応用例まで特集してみました。しかしながらやはりスタック・キューは、コンピュータサイエンスの全域で基本的な考え方ではありますが、データ構造としては「配列の上手な使い方の一つ」という域を出ていない印象です。現代では、もっともっとあっと驚くようなデータ構造がいくつも考案されています。是非それらの世界へと足を踏み入れて行くと、楽しい世界が待っています。

6. 参考文献

本記事を書くうえで参考にした文献、またさらなる知見を得るために参考になる文献たちを紹介します。

渡辺有隆 (著), Ozy (協力), 秋葉拓哉 (協力): プログラミングコンテスト攻略のためのアルゴリズムとデータ構造, マイナビ出版 (2015).
N. Karumanchi: Data Structures and Algorithms Made Easy: Data Structures and Algorithmic Puzzles, CareerMonk Plublications (2011).
T. H. Cormen, C. E. Leiserson, R. L. Rivest, C. Stein: Introduction to Algorithms 3rd ed., MIT Press (2009).

頼まれたタスクが積み上がったときに、その処理する順番がスタック的な人とキュー的な人がいるね、という世間話はあちこちで耳にしますね。 ↩
C++ の std::queue では push, pop というメソッド名が用いられています。 ↩
田中哲郎: 「どうぶつしょうぎ」の完全解析, 情報処理学会研究報告, Vol.2009-GI-22 No.3, pp.1-8, (2009), http://id.nii.ac.jp/1001/00062415/ ↩
幅優先探索を行うとこれが実は最短になることは、本当はきちんとした証明が必要です。 ↩

スタックとキューを極める！ 〜 考え方と使い所を特集 〜

0. はじめに

1. スタックとキュー

1-1. スタックとキューとは

1-2. スタック・キューの使用場面

1-2-1. スタックの用途

1-2-2. キューの用途

2. スタック・キューの詳細と実装

2-1. スタックの詳細

2-2. キューの詳細

2-3. デックと優先度付きキュー

2-4. 連結リストを用いたスタック・キューの実装方法

2-5. C++ ライブラリ

std::stackの使用例

std::queueの使用例

3. スタック・キューを用いて問題を解く

3-1. 括弧列の整合性チェック (スタック)

3-2. 逆ポーランド記法 (スタック)

3-3. ヒストグラム中の面積最大の長方形 (スタック)

3-4. スパン (スタック)

3-5. ラウンドロビン・スケジューリング (キュー)

3-6. 後退解析 (キュー)

3-7. スライド最小値 (デック)

4. 深さ優先探索 (DFS) と幅優先探索 (BFS)

4-1. グラフ

4-2. グラフ上の探索

5. おわりに

6. 参考文献

スタックとキューを極める！〜考え方と使い所を特集〜