0. はじめに
の続きです。DP ってなんだろうという方は先に上の記事を見ていただけたらと思います。それにしても、EDPC (Educational DP Cotest)、本当に素敵な DP 学習コンテンツが登場しましたね!
今回は F 〜 J 問題を扱います。DP は「最適化問題」に限らず
- 数え上げ問題
- 確率問題
- 期待値問題
などに対しても、適用できるということを学べるセットになっています。
F 問題 - LCS
【問題概要】
文字列 $s$ および $t$ が与えられます。
$s$ の部分列かつ $t$ の部分列であるような文字列のうち、最長のものをひとつ求めよ。
【制約】
- $1 \le |s|, |t| \le 3000$
キーポイント
- index が二次元になった DP
- 復元
解法 (メイン部分)
もしこの問題が「$s$ の部分列かつ $t$ の部分列であるような文字列の長さの最大値を求めよ」という問題だったならば、超有名な最長共通部分列問題 (LCS) です。その解法自体はこの記事にも書いてみました。
A 問題から E 問題までの DP は
- ${\rm dp[i + 1]}$ := ${\rm i}$ 番目までの何か
- ${\rm dp[i + 1][j]}$ := ${\rm i}$ 番目で何かが ${\rm j}$ になるような制約下での何か
といった「系列に沿って進んでいくインデックス」が $1$ 個だけのものばかりでした。それに対して、今回の DP は「系列に沿って進んでいくインデックス」が $2$ 個になります。
$\rm{dp}[i+1][j+1]$ := ${\rm s}$ の ${\rm i}$ 文字目までと ${\rm t}$ の ${\rm j}$ 文字目まででの LCS の長さ
とします。今までは、$\rm{dp}[i]$ を使って $\rm{dp}[i+1]$ を表したりしましたが、今回は $\rm{dp}[i][j]$, $\rm{dp}[i+1][j]$, $\rm{dp}[i][j+1]$ を使って $\rm{dp}[i+1][j+1]$ を表すことを考えると次のようになります。
- ${\rm s[i] == t[j]}$ ならば、$\rm{dp}[i][j]$ に対して、${\rm s}$ の ${\rm i}$ 文字目と ${\rm t}$ の ${\rm j}$ 文字目を付け加えれば 1 文字伸びるので、
$${\rm chmax(dp[i+1][j+1], dp[i][j] + 1)}$$
- $\rm{dp}[i+1][j]$ に対して、${\rm t}$ の ${\rm j}$ 文字目を考慮しても特に LCS の長さは変わらず、
$${\rm chmax(dp[i+1][j+1], dp[i+1][j])}$$
- $\rm{dp}[i][j+1]$ に対して、${\rm s}$ の ${\rm i}$ 文字目を考慮しても特に LCS の長さは変わらず、
$${\rm chmax(dp[i+1][j+1], dp[i][j+1])}$$
以上をまとめると
if (s[i] == t[j]) chmax(dp[i+1][j+1], dp[i][j] + 1);
chmax(dp[i+1][j+1], dp[i+1][j]);
chmax(dp[i+1][j+1], dp[i][j+1]);
という感じにすればよいです。そして最長共通部分列の長さは、$n = |s|$, $m = |t|$ として ${\rm dp[n][m]}$ となります。
解法 (復元部分)
以上の DP によって「最長共通部分列の長さ」までは求まります。さらに「最長共通部分列を具体的にどれか 1 つ」求める方法を考えます。基本的な考え方としては DP テーブルの終端ノード ${\rm dp[n][m]}$ から出発して順に「どのノードから更新されて来たのか、その元となる部分を辿って行く」ことになります。その方法は大きくわけて
- DP テーブルの値を見ながら、今いるノード ${\rm (i, j)}$ がどのノードから更新されて来たのかを特定する
- あらかじめ DP 更新と同時に、各ノード ${\rm (i, j)}$ がどのノードから更新されているのかをメモしておく
といった方針が考えられます。様々な強い人のコードを見ていても、どちらも書き方も見受けられました。方針 2 の考え方についてはこの記事に書きました。ここでは方針 1 で実装してみます。素朴な実装だと思います。
# include <iostream>
# include <string>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
const long long INF = 1LL<<60;
// 入力
string s, t;
// DPテーブル
int dp[3100][3100] = {0}; // 初期値も初期条件も 0
int main() {
cin >> s >> t;
// DPループ
for (int i = 0; i < s.size(); ++i) {
for (int j = 0; j < t.size(); ++j) {
if (s[i] == t[j]) chmax(dp[i+1][j+1], dp[i][j] + 1);
chmax(dp[i+1][j+1], dp[i+1][j]);
chmax(dp[i+1][j+1], dp[i][j+1]);
}
}
// 復元
string res = "";
int i = (int)s.size(), j = (int)t.size();
while (i > 0 && j > 0)
{
// (i-1, j) -> (i, j) と更新されていた場合
if (dp[i][j] == dp[i-1][j]) {
--i; // DP の遷移を遡る
}
// (i, j-1) -> (i, j) と更新されていた場合
else if (dp[i][j] == dp[i][j-1]) {
--j; // DP の遷移を遡る
}
// (i-1, j-1) -> (i, j) と更新されていた場合
else {
res = s[i-1] + res; // このとき s[i-1] == t[j-1] なので、t[j-1] + res でも OK
--i, --j; // DP の遷移を遡る
}
}
cout << res << endl;
}
類題
まずは系列が二次元になった DP たちです:
- AOJ Course 編集距離 (よく似た二次元ナップサック DP です)
- Indeedなう C - Optimal Recommendations (今度は三次元です)
続いて、復元を要する DP を挙げてみます:
- AOJ 0155 スパイダー人 (典型的な復元問題です)
- CSAcademy 064 DIV2 E - Classic Task (やはり典型的な復元問題です)
- AOJ 2517 ホテル探し (辞書順最小な復元を要求されます、その場合には後ろから DP するのが有効です)
G 問題 - Longest Path
【問題概要】
$N$ 頂点 $M$ 辺の有向グラフ $G$ が与えられます。
$G$ には有向閉路がないです (DAG = Directed Acyclic Graph と呼びます)。
$G$ の有向パスのうち、最長のものの長さを求めよ。
【制約】
- $2 \le N \le 10^5$
- $1 \le M \le 10^5$
キーポイント
- DAG 上の DP
- 更新順序が非自明な場合にはメモ化再帰が有効
- トポロジカルソート
解法 1: メモ化再帰
問題 A では「for 文を回す DP」と「メモ化再帰」とで大きな違いはないと書きました。しかしメモ化再帰が大きなメリットを生む状況があります。それは
DP の更新順序が非自明
という場合です。for 文を回すタイプの DP は「ノード from からノード to への更新をするときにはノード from の値の更新が完了している必要がある」というのを意識する必要がありました。そのため、for 文回すタイプの DP でこの問題を解くためには
- まずトポロジカルソートする
- それによって DP を回していくべきノード順が決まるので、DP する
としてあげる必要があります。それも一つの解法ですが、メモ化再帰で書けばトポロジカルソートを陽にはせずに実現することができます。メモ化再帰では
int dp[]
int rec(int v) {
if (dp[v] が更新されている) return dp[v];
for (nv : 何か) {
rec(nv)
}
}
みたいなことをしますが、更新順序のことを何も考えずに rec(v) についての処理を、rec(nv) についての処理に押し付けてしまうことができます。補足として、実際にはメモ化再帰を回していくとき、更新が完了する順を (逆順に) 辿ればそれが自然にトポロジカルソート順になっています。したがってメモ化再帰は、「トポロジカルソートしなくていい」というよりはむしろ、「トポロジカルソートしながら DP している」といえるでしょう。
さて、
- dp[v] := ノード v を始点としたときの、$G$ の有効パスの長さの最大値
としましょう。このとき求めたい dp[v] の値を res として、ノード v から直接行くことのできる各ノード nv に対して
chmax(res, rec(nv) + 1)
としてあげればよいです。
# include <iostream>
# include <vector>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
const long long INF = 1LL<<60;
// 入力
int N, M;
vector<vector<int> > G; // グラフ
// メモ化再帰
int dp[100100];
int rec(int v) {
if (dp[v] != -1) return dp[v]; // 既に更新済み
int res = 0;
for (auto nv : G[v]) {
chmax(res, rec(nv) + 1);
}
return dp[v] = res; // メモしながらリターン
}
int main() {
// 入力受け取り
cin >> N >> M;
G.assign(N, vector<int>());
for (int i = 0; i < M; ++i) {
int x, y; cin >> x >> y;
--x, --y; // 0-indexed にする
G[x].push_back(y);
}
// 初期化
for (int v = 0; v < N; ++v) dp[v] = -1;
// 全ノードを一通り更新しながら答えを求める
int res = 0;
for (int v = 0; v < N; ++v) chmax(res, rec(v));
cout << res << endl;
}
解法 2: BFS 式にトポロジカルソートしながら DP
トポロジカルソートには DFS っぽくやる方法と、BFS っぽくやる方法とがありました。
メモ化再帰による解法が「DFS っぽくトポロジカルソートしながら DP する」解法と言えるならば、「BFS っぽくトポロジカルソートしながら DP する」解法も考えられるでしょう。まずトポロジカルソートを BFS で実現する方法を思い出すと以下のようになります (wikipedia から引用)。
L ← トポロジカルソートした結果を蓄積する空リスト
S ← 入力辺を持たないすべてのノードの集合を表すキュー
while S が空ではない do
S からノード n を削除する
L に n を追加する
for each n の出力辺 e とその先のノード m do
辺 e をグラフから削除する
if m がその他の入力辺を持っていなければ then
m を S に追加する
これをやりながら、DP もまとめてやってしまえばよいでしょう。具体的には以下のようにすればよいです。
- 最初の $S$ を初期化する段階でノード ${\rm v}$ をキュー $S$ に突っ込むなら、${\rm dp[v] = 0}$ とする
- 最終行の ${\rm m}$ をキュー $S$ に突っ込む段階で、${\rm chmax(dp[m], dp[n] + 1)}$ とする
# include <iostream>
# include <vector>
# include <queue>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
const long long INF = 1LL<<60;
// 入力
int N, M;
vector<vector<int> > G; // グラフ
vector<int> deg; // 各頂点の入次数
int dp[100100];
int main() {
// 入力受け取り, 入次数も管理する
cin >> N >> M;
G.assign(N, vector<int>());
deg.assign(N, 0);
for (int i = 0; i < M; ++i) {
int x, y; cin >> x >> y;
--x, --y; // 0-indexed にする
G[x].push_back(y);
deg[y]++;
}
// source をキューに突っ込む
queue<int> que;
for (int v = 0; v < N; ++v) if (deg[v] == 0) que.push(v);
// BFS
while (!que.empty()) {
int v = que.front(); que.pop();
for (auto nv : G[v]) {
deg[nv]--; // エッジ (v, nv) を破壊する
if (deg[nv] == 0) {
que.push(nv); // それによって入次数が 0 にあったならキューに突っ込む
chmax(dp[nv], dp[v] + 1); // さらにソースから nv までの再長距離が確定する
}
}
}
// 答え
int res = 0;
for (int v = 0; v < N; ++v) chmax(res, dp[v]);
cout << res << endl;
}
類題
DP 更新順序が非自明なためにメモ化再帰が有効になる類題を挙げます:
- AOJ 2503 プロジェクト管理 (よく似た問題です)
- ABC 037 D - 経路 (まさに DP 更新順序が非自明な問題なのでピッタリです)
- SRM 313 DIV2 Hard ParallelProgramming (DAG 上の DP です)
H 問題 - Grid 1
【問題概要】
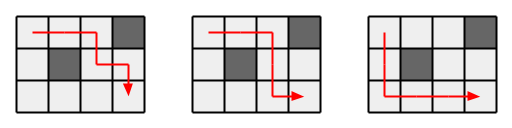
下図のような、$H × W$ のグリッドがあり、左上のマスから右下のマスまで移動したいです。ただし
- 毎ターン「右」か「下」にしか進めません。
- 壁のあるマスには進めません。
左上から右下まで行く経路は何通りあるかを、$1000000007$ で割ったあまりで求めよ。
【制約】
- $2 \le H, W \le 1000$
キーポイント
- グリッド上の DP
- 数え上げ DP
解法
F 問題、G 問題と難しめでしたが、H 問題でまた少し難易度が下がりました。小休憩といったところでしょう。そして今までの DP は最大化問題や最小化問題でしたが、ついに数え上げ問題が登場しました!!!!!
$1000000007$ で割ったあまりを求めさせる問題への取り組み方についてはこの記事を参考にしていただけたらと思います。また、今までの DP の緩和式は
chmax(dp[to], dp[from] + なにか);
chmin(dp[to], dp[from] + なにか);
という形をしていましたが、数え上げ DP では
dp[to] += dp[from];
や
dp[to] += dp[from] * なにか;
といった緩和式になります。また
- DP 初期化: テーブル全体を $0$ に初期化
- DP 初期条件: スタートノードを $1$ とする
という感じになります。この違いに適応できさえすれば今までと同じ感覚で DP を組めると思います。例によって 0-indexed として、
- ${\rm dp[i][j]}$ := マス $(0, 0)$ からマス ${\rm (i, j)}$ までの経路の本数 (ただし $10000000007$ で割ったあまり)
とします。このとき配る DP で書くと
- マス ${\rm (i + 1, j)}$ が空マスならば、${\rm dp[i+1][j]}$ += ${\rm dp[i][j]}$
- マス ${\rm (i, j + 1)}$ が空マスならば、${\rm dp[i][j+1]}$ += ${\rm dp[i][j]}$
としてあげればよいです。初期条件は ${\rm dp[0][0] = 1}$ です。適宜 $1000000007$ で割るのを怠らないようにします。
# include <iostream>
# include <vector>
# include <string>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
// MOD
const int MOD = 1000000007;
// 入力
int H, W;
vector<string> a;
// DP テーブル
int dp[1100][1100] = {0};
// add
void add(int &a, int b) {
a += b;
if (a >= MOD) a -= MOD;
}
int main() {
cin >> H >> W;
a.resize(H);
for (int i = 0; i < H; ++i) cin >> a[i];
// DP 初期化: すでに配列全体が 0 に初期化されているので OK
// DP 初期条件
dp[0][0] = 1;
// DP ループ
for (int i = 0; i < H; ++i) {
for (int j = 0; j < W; ++j) {
if (i+1 < H && a[i+1][j] == '.') add(dp[i+1][j], dp[i][j]);
if (j+1 < W && a[i][j+1] == '.') add(dp[i][j+1], dp[i][j]);
}
}
cout << dp[H-1][W-1] << endl;
}
類題
グリッド上の DP たちです。
- AOJ 0515 通学経路 (JOI 2006 予選 F)
- AOJ 0530 ぴょんぴょん川渡り (JOI 2007 本選 D)
- AOJ 0541 散歩 (JOI 2008 本選 D)
- AOJ 0547 通勤経路 (JOI 2009 予選 E)
I 問題 - Coins
【問題概要】
$N$ を正の奇数とする。
$N$ 枚のコインがあって $i$ 枚目のコインの表が出る確率は $p_i$ で与えられている。
$N$ 枚すべてのコインを投げたとき、表の出た枚数が裏の出た枚数より多くなる確率を求めよ。
【制約】
- $1 \le N \le 2999$
キーポイント
- 確率 DP
解法
今度は確率 DP です!!!
- ${\rm dp[i][j]}$ := 最初の ${\rm i}$ 枚のコインを投げたときに、表が $j$ 枚となる確率
とすると緩和式は
- 次のコインが表のとき: ${\rm dp[i+1][j+1]}$ += ${\rm dp[i][j] * p}$
- 次のコインが裏のとき: ${\rm dp[i+1][j]}$ += ${\rm dp[i][j] * (1 - p)}$
となります。
# include <iostream>
# include <vector>
# include <iomanip>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
// 入力
int N;
vector<double> p;
// DP テーブル
double dp[3100][3100];
int main() {
cin >> N;
p.resize(N);
for (int i = 0; i < N; ++i) cin >> p[i];
// 初期条件
dp[0][0] = 1.0;
// DP ループ
for (int i = 0; i < N; ++i) {
for (int j = 0; j <= i; ++j) {
dp[i+1][j+1] += dp[i][j] * p[i];
dp[i+1][j] += dp[i][j] * (1.0 - p[i]);
}
}
// 答え
double res = 0.0;
for (int j = N/2 + 1; j <= N; ++j) res += dp[N][j];
cout << fixed << setprecision(10) << res << endl;
}
J 問題 - Sushi
【問題概要】
$N$ 枚の皿があって、$i$ 枚目の皿には寿司が $a_i$ 個置かれている。すべての寿司がなくなるまで
- $1, 2, \dots, N$ の中からランダムに 1 つ選び
- その皿に寿司があるなら食べて、ないなら何もしない
という操作を行う。すべての寿司がなくなるまでの操作回数の期待値を求めよ。
【制約】
- $1 \le N \le 300$
- $1 \le a_i \le 3$
キーポイント
- 期待値 DP
- DP 状態変数を圧縮することを考える
- DP 遷移式の自己ループは式変形によってなくす
解法
今度は期待値 DP です!!!
...という感じにスパッと言えればいいのですが、この問題は前半の中では圧倒的に難しい問題のようです。一見すると
- ${\rm dp[i][j][k] ... []}$ := それぞれの皿の寿司の個数が ${\rm i, j, k, ...}$ という状態から寿司がなくなるまでの操作回数の期待値
という感じの式を立てたくなります。しかしこれでは最悪 $300$ 次元配列になってしまいますし、各皿の寿司の個数は $0, 1, 2, 3$ の $4$ 通りがありうるので $4^{300}$ もの状態量になってしまいます。こういうときは DP の状態量をもっと圧縮できないかを考えることになります。少し考えてみると、
残寿司数が同じ皿同士は区別する必要がない
ということに気がつきます。そうすると、
- 残 $0$ 個になった皿の枚数
- 残 $1$ 個になった皿の枚数
- 残 $2$ 個になった皿の枚数
- 残 $3$ 個になった皿の枚数
の情報だけでよいことに気がつきます。そしてこれらの総和は $N$ で一定なので、残 $1, 2, 3$ 個の皿の枚数の情報だけでいいです。そこで DP は
- ${\rm dp[i][j][k]}$ := 寿司が残り $1$ 個の皿が ${\rm i}$ 枚、$2$ 個の皿が ${\rm j}$ 枚、$3$ 個の皿が ${\rm k}$ 枚の状態から、寿司をすべてなくすのに必要な操作回数の期待値
としてあげます。これを表す漸化式を考えます。
| 次の引き | その確率 | 行き先 |
|---|---|---|
| 残 $0$ 枚の皿 | ${\rm \frac{N-i-j-k}{N}}$ | ${\rm dp[i][j][k]}$ |
| 残 $1$ 枚の皿 | ${\rm \frac{i}{N}}$ | ${\rm dp[i-1][j][k]}$ |
| 残 $2$ 枚の皿 | ${\rm \frac{j}{N}}$ | ${\rm dp[i+1][j-1][k]}$ |
| 残 $3$ 枚の皿 | ${\rm \frac{k}{N}}$ | ${\rm dp[i][j+1][k-1]}$ |
これをまとめると以下のような式が立式できます。期待値 DP に慣れていないとこのような立式は少し難しく感じるかもしれません。式の最後の「$+1$」がまさに行う操作を表しています。
{\rm dp[i][j][k]
= (dp[i][j][k] × \frac{N-i-j-k}{N} \\
+ dp[i-1][j][k] × \frac{i}{N} + dp[i+1][j-1][k] × \frac{j}{N} + dp[i][j+1][k-1] × \frac{k}{N}) + 1}
さてこれを素直に実装すればいいかと思いきや、なんと、左辺にも右辺にも ${\rm dp[i][j][k]}$ が登場しています!!!
このままだと、${\rm dp[i][j][k]}$ の値を求めるのに自分自身を参照することになってしまいます。そこでよくやるテクとして、式変形して自己ループを除去します。そうすると以下のようになります:
{\rm dp[i][j][k] \\
= (dp[i-1][j][k] × \frac{i}{N} + dp[i+1][j-1][k] × \frac{j}{N} + dp[i][j+1][k-1] × \frac{k}{N} + 1) × \frac{N}{i+j+k} \\
= (dp[i-1][j][k] × i + dp[i+1][j-1][k] × j + dp[i][j+1][k-1] × k + N) × \frac{1}{i+j+k}}
これでようやく DP が回せる式になりました。注意点として ${\rm i, j, k}$ が $0$ の場合に気をつける必要があります。添字の順序がややこしく見えたのでメモ化再帰で実装することにしました。
# include <iostream>
# include <cstring>
# include <iomanip>
using namespace std;
template<class T> inline bool chmax(T& a, T b) { if (a < b) { a = b; return true; } return false; }
template<class T> inline bool chmin(T& a, T b) { if (a > b) { a = b; return true; } return false; }
// 入力
int N;
// DP テーブル
double dp[310][310][310];
double rec(int i, int j, int k) {
if (dp[i][j][k] >= 0) return dp[i][j][k];
if (i == 0 && j == 0 && k == 0) return 0.0;
double res = 0.0;
if (i > 0) res += rec(i-1, j, k) * i;
if (j > 0) res += rec(i+1, j-1, k) * j;
if (k > 0) res += rec(i, j+1, k-1) * k;
res += N;
res *= 1.0 / (i + j + k);
return dp[i][j][k] = res;
}
int main() {
cin >> N;
int one = 0, two = 0, three = 0;
for (int i = 0; i < N; ++i) {
int a; cin >> a;
if (a == 1) ++one;
else if (a == 2) ++two;
else ++three;
}
// 初期化
memset(dp, -1, sizeof(dp));
// 答え
cout << fixed << setprecision(10) << rec(one, two, three) << endl;
}
類題
自己ループを除去する系の問題を挙げてみます:
- TDPC J ボール (この後登場する bitDP も使います)
- SRM 488 DIV1 Easy TheBoredomDivOne
-1. おわりに
To be continued...