NTTデータ数理システムでアルゴリズムを探求している大槻 (通称、けんちょん) です。
好きなアルゴリズムは最小カットやマッチングですが、会社ではなぜか「動的計画法が好きな人」と呼ばれています。今回は動的計画法を用いて得られた最適解を復元するための汎用的な方法について紹介します。
0. はじめに
動的計画法を用いて効率的に解くことのできる最適化問題は数多くあります。パッと思いつくだけでも
などなど、多種多様な分野の問題を動的計画法によって効率よく解くことができます。このように、分野横断的な活用をできることが、動的計画法をはじめとした数理工学的手法の特長であり醍醐味であると常々感じています。今回は動的計画法によって得られた解を復元する一般的なテクについて紹介したいと思います。というのも、様々な書籍や解説資料において
動的計画法を用いて、解きたい最適化問題の最適値を求める方法の詳細な解説はあっても、最適解そのものを求める方法はサラッとしか書かれていないことが多い
と感じたからです。今回は迷路やナップサック問題など様々な実例を通して、具体的な実装例も含めて、動的計画法で得た最適解を復元する方法を紹介します。
1. 動的計画法の最適解を復元する 2 つの方法
例えば、下図のような迷路の最短路問題を例にとってみます。

'S' から 'G' へ至る最短の経路を求める問題を考えてみましょう。これは以下のように、
- 'S' から 1 手で行ける場所
- 'S' から 2 手で行ける場所 (= 'S' から 1 手で行ける場所から 1 手で行ける場所)
- 'S' から 3 手で行ける場所 (= 'S' から 2 手で行ける場所から 1 手で行ける場所)
- ...
をメモして行くことで解くことができます。

こうして、最短手数が 16 手であることがわかりました。今回の記事の問題意識は、「最短手数が 16 手であること」を知るだけでなく、「具体的に 16 手で到達する経路を復元すること」です。
方法 1: 素朴なやり方
具体的な最適解の復元を実現するための 1 つの方法としては、
- 16 のマスの周りで 15 になっている場所を探して
- 15 のマスの周りで 14 になっている場所を探して
- 14 のマスの周りで 13 になっている場所を探して
- ...
と繰り返して行けば、下図のように経路復元することができます。

とても素朴な実装方法です。欠点としては「各マスの近傍」の探索範囲が非常に大きくなる場合には復元に時間がかかってしまいますし、場合によってはオーダーレベルで計算量が悪化してしまうこともあります。
そこで、そのような場合にも通用するような汎用的な方法を次に紹介します。
方法 2: 汎用的に使える良い方法
上記の方法の効率悪い部分を解決できる有力な方法は
各マスの値を更新するときに、ついでに、どのマスから伝播して来たかをメモしておく
というものです。今回の問題では下図のような感じです。
各マスについて、どこから伝播して来たのかを矢印で表しています。例えば黄色で示した「11」のマスを見ると、右隣の「10」のマスから伝播して来たことがわかります。

このような矢印テーブルを別途求めておけば、ゴールのマスから矢印を辿ることで最適解を復元することができます。注意点として、マスによっては矢印が複数方向を指しているものもありますが、その場合はどちらを選んでもよいです。また実装依存ですが、そもそも矢印が 1 方向しか指さないようにするケースが多いかもしれません。
2 つの方法の比較
DP テーブルの各ノードの近傍の探索に時間がかかる場合には、方法 2 を用いるのがよいでしょう。それ以外については、どちらで実装しても良さそうです。復元のためのデータ構造などをなにも考えずに方法 1 を用いるのが楽なケースも多いような気もします。本記事では方法 2 によって実装して行きます。
2. 動的計画法の最適解復元の具体例
習うより慣れろの精神で、いくつかの例について経路復元をしてみます。
2-1. 迷路の最短路の復元
まずは上記の迷路についてです。入力形式は以下のように
- 1 行目に迷路のサイズ
- 2 行目以降に迷路のマップ ('S': スタート、'G': ゴール、'.': 通路、'#': 壁)
を表すものとしてみます。
8 8
.#....#G
.#.#....
...#.##.
# .##...#
...###.#
.#.....#
...#.#..
S.......
'S' から 'G' へと至る最小手数を求める方法として幅優先探索 (BFS)を用います。幅優先探索はキュー (queue) を用いることでシンプルに実現できるのですが、幅優先探索の具体的な実装方法についてはこの記事などを参考にしてもらえたらと思います。
まず、経路復元を意識せずに幅優先探索の部分のみを実装すると以下のようになるでしょう。以下のコードでは、'S' から 'G' に到達するまでの最小手数だけでなく、'S' から任意の通路マスへの最小手数も出力しています。
# include <iostream>
# include <queue>
# include <vector>
# include <string>
# include <iomanip>
using namespace std;
/* 4 方向への隣接頂点への移動を表すベクトル */
const int dx[4] = { 1, 0, -1, 0 };
const int dy[4] = { 0, 1, 0, -1 };
int main() {
////////////////////////////////////////
/* 入力受け取り */
////////////////////////////////////////
/* 縦と横の長さ */
int height, width;
cin >> height >> width;
/* 盤面 */
vector<string> field(height);
for (int h = 0; h < height; ++h) cin >> field[h];
/* スタート地点とゴール地点 */
int sx, sy, gx, gy;
for (int h = 0; h < height; ++h) {
for (int w = 0; w < width; ++w) {
if (field[h][w] == 'S') {
sx = h;
sy = w;
}
if (field[h][w] == 'G') {
gx = h;
gy = w;
}
}
}
////////////////////////////////////////
/* 幅優先探索の初期設定 */
////////////////////////////////////////
// 各セルの最短距離 (訪れていないところは -1 としておく)
vector<vector<int> > dist(height, vector<int>(width, -1));
dist[sx][sy] = 0; // スタートを 0 に
// 「一度見た頂点」のうち「まだ訪れていない頂点」を表すキュー
queue<pair<int, int> > que;
que.push(make_pair(sx, sy)); // スタートを push
////////////////////////////////////////
/* 幅優先探索を実施 */
////////////////////////////////////////
/* キューが空になるまで */
while (!que.empty()) {
pair<int, int> current_pos = que.front(); // キューの先頭を見る (C++ ではこれをしても pop しない)
int x = current_pos.first;
int y = current_pos.second;
que.pop(); // キューから pop を忘れずに
// 隣接頂点を探索
for (int direction = 0; direction < 4; ++direction) {
int next_x = x + dx[direction];
int next_y = y + dy[direction];
if (next_x < 0 || next_x >= height || next_y < 0 || next_y >= width) continue; // 場外アウトならダメ
if (field[next_x][next_y] == '#') continue; // 壁はダメ
// まだ見ていない頂点なら push
if (dist[next_x][next_y] == -1) {
que.push(make_pair(next_x, next_y));
dist[next_x][next_y] = dist[x][y] + 1;
}
}
}
////////////////////////////////////////
/* 結果出力 */
////////////////////////////////////////
/* 各マスへのスタートからの最短距離を見てみる */
for (int h = 0; h < height; ++h) {
for (int w = 0; w < width; ++w) {
if (field[h][w] != '.' && field[h][w] != 'G') cout << std::setw(3) << field[h][w];
else cout << std::setw(3) << dist[h][w];
}
cout << endl;
}
cout << endl;
}
このコードに例示した入力を与えると以下のような出力になります。確かに各マスに対して、'S' から到達するための最短手数が求められているのが読みとれます。
9 # 9 10 11 12 # 16
8 # 8 # 12 13 14 15
7 6 7 # 13 # # 16
# 5 # # 12 11 10 #
3 4 5 # # # 9 #
2 # 4 5 6 7 8 #
1 2 3 # 5 # 7 8
S 1 2 3 4 5 6 7
さて、上のコードで動的計画法らしい部分と言えば、
// まだ見ていない頂点なら push
if (dist[next_x][next_y] == -1) {
que.push(make_pair(next_x, next_y));
dist[next_x][next_y] = dist[x][y] + 1;
}
の部分でしょう。このうちの特に「dist[next_x][next_y] = dist[x][y] + 1;」とする部分は、動的計画法のテーブル更新の部分を実行しています。すなわち、マス (next_x, next_y) の情報を、マス (x, y) から情報を受け取ることで更新しています。
動的計画法で得た解を最後に復元することを意識するときは、ここに処理を付け加えます。まずは各マスに対して「どのマスからテーブル更新情報が伝播して来たか」を表す情報をもたせます:
vector<vector<int> > prev_x(height, vector<int>(width, -1)); // prev_x[i][j] = マス (i, j) への伝播元マスの縦方向の座標
vector<vector<int> > prev_y(height, vector<int>(width, -1)); // prev_y[i][j] = マス (i, j) への伝播元マスの横方向の座標
これを用いて、動的計画法のテーブル更新部分に対して処理を追加します:
// まだ見ていない頂点なら push
if (dist[next_x][next_y] == -1) {
que.push(make_pair(next_x, next_y));
dist[next_x][next_y] = dist[x][y] + 1;
prev_x[next_x][next_y] = x; // どの頂点から情報が伝播して来たか、縦方向の座標をメモ
prev_y[next_x][next_y] = y; // どの頂点から情報が伝播して来たか、横方向の座標をメモ
}
prev_x, prev_y テーブルさえ構築してあれば、ゴールから順にたどることで簡単に最短経路を復元することができます。最短経路を復元するパートも含めて、コード全体の実装例としては以下のようになるでしょう:
# include <iostream>
# include <queue>
# include <vector>
# include <string>
# include <iomanip>
using namespace std;
/* 4 方向への隣接頂点への移動を表すベクトル */
const int dx[4] = { 1, 0, -1, 0 };
const int dy[4] = { 0, 1, 0, -1 };
int main() {
////////////////////////////////////////
/* 入力受け取り */
////////////////////////////////////////
/* 縦と横の長さ */
int height, width;
cin >> height >> width;
/* 盤面 */
vector<string> field(height);
for (int h = 0; h < height; ++h) cin >> field[h];
/* スタート地点とゴール地点 */
int sx, sy, gx, gy;
for (int h = 0; h < height; ++h) {
for (int w = 0; w < width; ++w) {
if (field[h][w] == 'S') {
sx = h;
sy = w;
}
if (field[h][w] == 'G') {
gx = h;
gy = w;
}
}
}
////////////////////////////////////////
/* 幅優先探索の初期設定 */
////////////////////////////////////////
// 各セルの最短距離 (訪れていないところは -1 としておく)
vector<vector<int> > dist(height, vector<int>(width, -1));
dist[sx][sy] = 0; // スタートを 0 に
// 探索中に各マスはどのマスから来たのかを表す配列 (最短経路長を知るだけなら、これは不要)
vector<vector<int> > prev_x(height, vector<int>(width, -1));
vector<vector<int> > prev_y(height, vector<int>(width, -1));
// 「一度見た頂点」のうち「まだ訪れていない頂点」を表すキュー
queue<pair<int, int> > que;
que.push(make_pair(sx, sy)); // スタートを push
////////////////////////////////////////
/* 幅優先探索を実施 */
////////////////////////////////////////
/* キューが空になるまで */
while (!que.empty()) {
pair<int, int> current_pos = que.front(); // キューの先頭を見る (C++ ではこれをしても pop しない)
int x = current_pos.first;
int y = current_pos.second;
que.pop(); // キューから pop を忘れずに
// 隣接頂点を探索
for (int direction = 0; direction < 4; ++direction) {
int next_x = x + dx[direction];
int next_y = y + dy[direction];
if (next_x < 0 || next_x >= height || next_y < 0 || next_y >= width) continue; // 場外アウトならダメ
if (field[next_x][next_y] == '#') continue; // 壁はダメ
// まだ見ていない頂点なら push
if (dist[next_x][next_y] == -1) {
que.push(make_pair(next_x, next_y));
dist[next_x][next_y] = dist[x][y] + 1; // (next_x, next_y) の距離も更新
prev_x[next_x][next_y] = x; // どの頂点から情報が伝播して来たか、縦方向の座標をメモ
prev_y[next_x][next_y] = y; // どの頂点から情報が伝播して来たか、横方向の座標をメモ
}
}
}
////////////////////////////////////////
/* 結果出力 */
////////////////////////////////////////
/* 各マスへのスタートからの最短距離を見てみる */
for (int h = 0; h < height; ++h) {
for (int w = 0; w < width; ++w) {
if (field[h][w] != '.') cout << std::setw(3) << field[h][w];
else cout << std::setw(3) << dist[h][w];
}
cout << endl;
}
cout << endl;
/* ゴールに至るまでの最短経路を復元してみる */
int x = gx, y = gy;
while (x != -1 && y != -1) {
field[x][y] = 'o'; // 通過したことを示す
// 前の頂点へ行く
int px = prev_x[x][y];
int py = prev_y[x][y];
x = px, y = py;
}
for (int h = 0; h < height; ++h) {
for (int w = 0; w < width; ++w) {
cout << std::setw(3) << field[h][w];
}
cout << endl;
}
}
先ほどの入力ケースに対して、結果は以下のようになりました:
9 # 9 10 11 12 # G
8 # 8 # 12 13 14 15
7 6 7 # 13 # # 16
# 5 # # 12 11 10 #
3 4 5 # # # 9 #
2 # 4 5 6 7 8 #
1 2 3 # 5 # 7 8
S 1 2 3 4 5 6 7
. # o o o . # o
. # o # o o o o
. o o # . # # .
# o # # . . . #
o o . # # # . #
o # . . . . . #
o . . # . # . .
o . . . . . . .
2-2. ナップサック問題の最適解の復元
続いて動的計画法の例題として頻繁に取り上げられるナップサック問題です。なお、このナップサック問題は、最適値を求めるプログラムを実装して、
http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=DPL_1_B&lang=jp
で提出することでジャッジできます。実際にソースコードを記述して提出してみると理解が深まると思います。
ナップサック問題
$n$ 個の品物があり、$i$ 番目の品物のそれぞれ重さと価値が $\rm{weight}[i], \rm{value}[i]$ となっている ($i = 0, 1, ..., n-1$)。
これらの品物から重さの総和が $W$ を超えないように選んだときの、価値の総和の最大値を求めよ。
【制約】
- $1 \le n \le 100$
- $\rm{weight}[i], \rm{value}[i]$ は整数
- $1 \le \rm{weight}[i], \rm{value}[i] \le 1000$
- $1 \le W \le 10000$
【数値例】
1)
$n = 6$
$(\rm{weight},\rm{value}) = {(2,3), (1,2), (3,6), (2,1), (1,3), (5,85)}$
$W = 8$
答え: $91$ ($(3,6), (5,85)$ を選んだときが最大です)
ナップサック問題に対する動的計画法の概説
ナップサック問題を動的計画法によって解く解法の詳細は以下の記事を参考にしていただけたらと思います:
ここでは簡単に概説します。まず、ナップサック問題を解くための動的計画法テーブルは以下のように設定します:
【DP テーブルの定義】
- $\rm{dp}[i][w]$ := 最初の $i$ 個の品物の中から重さが $w$ を超えないように選んだときの、価値の総和の最大値
そして $\rm{dp}[i+1][w]$ $(w = 0, 1, \dots, W)$ の値を、$\rm{dp}[i][w]$ $(w = 0, 1, \dots, W)$ の値を用いて更新することを考えます。それは以下のように整理できます:
【DP 更新式】
-
品物 $(\rm{weight}[i], \rm{value}[i])$ を選ぶ場合 ($w \ge \rm{weight}[i]$ の場合のみ)
- $\rm{dp}[i+1][w]$ の値が $\rm{dp}[i][w-\rm{weight}[i]] + \rm{value}[i]$ よりも小さかったら、$\rm{dp}[i+1][w]$ の値をそれで置き換える
-
品物 $(\rm{weight}[i], \rm{value}[i])$ を選ばない場合
- $\rm{dp}[i+1][w]$ の値が $\rm{dp}[i][w]$ よりも小さかったら、$\rm{dp}[i+1][w]$ の値をそれで置き換える
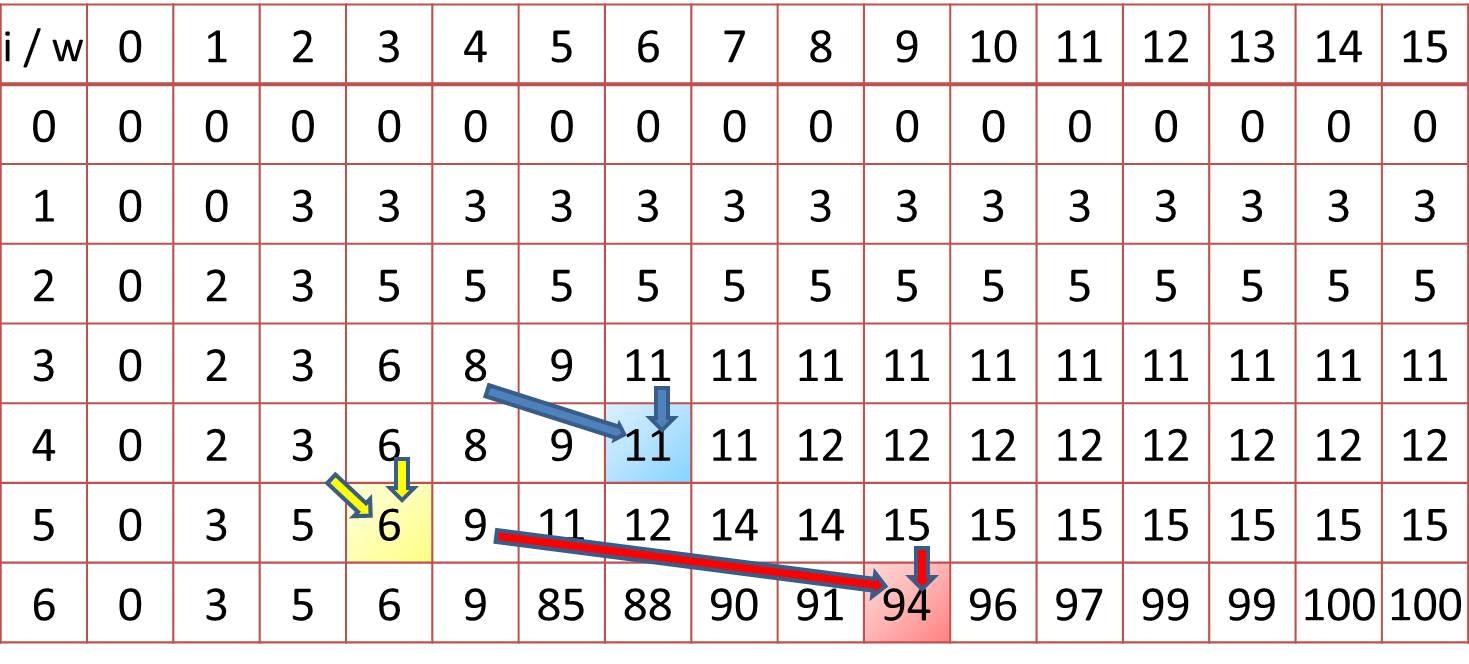
何をしているのかが難しく感じられる方も多いかもしれませんが、下図を見るとイメージが湧くかもしれません。例えば、赤マスの $\rm{dp}[6][9]$ の値 ($6$ 個の品物の中から、合計重さが $9$ 以下で選んだ最大値) を更新したいと思ったときは、
- $6$ 番目の品物 (重さ $5$, 価値 $85$) を選ぶ場合は、$\rm{dp}[5][4]$ ($5$ 個の品物の中から、合計重さが $9-5 = 4$ 以下で選んだ最大値) に $85$ を足した値 ($94$ になります) と見比べる
- $6$ 番目の品物 (重さ $5$, 価値 $85$) を選ばない場合は、$\rm{dp}[5][9]$ ($5$ 個の品物の中から、合計重さが $9$ 以下で選んだ最大値) そのものの値 ($15$ です) と見比べる
という風にしています。この 2 種類の更新のうち、前者の「選ぶ」方が大きいので前者が採用されています。反対に水色の $\rm{dp}[4][6]$ の値を見ると、
- $4$ 番目の品物 (重さ $2$, 価値 $1$) を選ぶ場合には、$\rm{dp}[3][4]$ に $1$ を足した値 ($9$ になります)
- $4$ 番目の品物 (重さ $2$, 価値 $1$) を選ばない場合には、$\rm{dp}[3][6]$ そのものの値 ($11$ です)
とを見比べて後者の「選ばない」方が大きいので後者が採用されています。
以上の処理を素直に書くと、以下のようになるでしょう:
# include <iostream>
using namespace std;
// 入力
int n, W;
int weight[110], value[110]; // 品物の個数は 100 個なので少し余裕持たせてサイズ 110 に
// DPテーブル
int dp[110][10010] = {0}; // テーブルの初期値はすべて 0 にしておきます
int main() {
// 入力受け取り
cin >> n >> W;
for (int i = 0; i < n; ++i) cin >> value[i] >> weight[i];
// DPループ
for (int i = 0; i < n; ++i) {
for (int w = 0; w <= W; ++w) {
// i 番目の品物を選ぶ場合を考える
if (w >= weight[i]) {
if (dp[i+1][w] < dp[i][w-weight[i]] + value[i]) {
dp[i+1][w] = dp[i][w-weight[i]] + value[i];
}
}
// i 番目の品物を選ばない場合を考える
if (dp[i+1][w] < dp[i][w]) {
dp[i+1][w] = dp[i][w];
}
}
}
// 最適値の出力
cout << dp[n][W] << endl;
}
今回はさらに進んで、実際にどの品物を選ぶのが最適であるかを「復元」することまでやってみます。先ほどの迷路の場合と同様に、復元のためのテーブルを用意します。prev_w[i+1][w] は、dp[i+1][w] が dp[i][prev_w[i+1][w]] によって更新されたことを表しています。
// 復元用テーブル
int prev_w[110][10010];
そうして、DP 更新部分に処理を追加すると以下のようになるでしょう。最適解の復元処理も行なっています。
# include <iostream>
using namespace std;
// 入力
int n, W;
int weight[110], value[110]; // 品物の個数は 100 個なので少し余裕持たせてサイズ 110 に
// DPテーブル
int dp[110][10010] = {0}; // テーブルの初期値はすべて 0 にしておきます
// 復元用テーブル
int prev_w[110][10010];
int main() {
// 入力受け取り
cin >> n >> W;
for (int i = 0; i < n; ++i) cin >> value[i] >> weight[i];
// DPループ
for (int i = 0; i < n; ++i) {
for (int w = 0; w <= W; ++w) {
// i 番目の品物を選ぶ場合を考える
if (w >= weight[i]) {
if (dp[i+1][w] < dp[i][w-weight[i]] + value[i]) {
dp[i+1][w] = dp[i][w-weight[i]] + value[i];
prev_w[i+1][w] = w - weight[i];
}
}
// i 番目の品物を選ばない場合を考える
if (dp[i+1][w] < dp[i][w]) {
dp[i+1][w] = dp[i][w];
prev_w[i+1][w] = w;
}
}
}
// 最適値の出力
cout << dp[n][W] << endl;
// 復元
cout << "Selected items are..." << endl;
int cur_w = W;
for (int i = n-1; i >= 0; --i) {
// 選んでいた場合
if (prev_w[i+1][cur_w] == cur_w - weight[i]) {
cout << i << " th item (weight = " << weight[i] << ", value = " << value[i] << ")" << endl;
}
// 復元テーブルをたどる
cur_w = prev_w[i+1][cur_w];
}
}
これに最初の数値例を与えると以下の出力になりました。
91
Selected items are...
5 th item (weight = 5, value = 85)
4 th item (weight = 1, value = 3)
0 th item (weight = 2, value = 3)
2-3. レーベンシュタイン距離
ここからは長くなるので簡単な紹介に留めたいと思います。レーベンシュタイン距離とは、2 つの文字列の類似度を表すものです。類似度は、一方の文字列に対して「1 文字置き換え」「1 文字削除」「1 文字追加」を行なってもう一方の文字列へと変換する手数の最小手数で測ります。例えば "qiita" と "iota" との編集距離は 2 です。
- "qiita" から q を削除して、"iita"
- "iita" の 2 文字目を 'o' にして "iota"
と 2 回のステップで変換できるので編集距離は 2 になります。注意すべきこととして、どちらの文字列からスタートしても最小手数は一緒になります (「削除」と「追加」は逆変換であることから)。
レーベンシュタイン距離も、簡単な動的計画法によって求めることができます。ここでは詳細は省略して、このページなどを参考にしてもらえたらと思います。
そしてこれまでと同様な方法によって、文字列の変換方法を復元することができます。これにより、簡単な diff コマンドのようなものを自作することもできます。
3. おわりに
動的計画法をはじめとした数理計画手法には、様々な分野に対して横断的に活用ができる強みがあります。この強みこそが弊社の理念の拠り所とするところでもあり、時代とともに流行の対象が移り変わっても、数理工学的手法は常に何らかの形で生き続けるものと考えております。動的計画法で得た最適解の復元手法を通して、横断的に活躍できる数理の一端を垣間見ていただけたらならば、とても嬉しく思います。
最後に、動的計画法の解の復元に関して、少し応用的な話題を紹介して締めたいと思います。
辞書順最小な解の復元: ゴールから動的計画法
一般に最適解というものは複数あることが多いです。そのうちの特に都合のよい最適解を求めることは重要な問題意識です。今回はそのうち特に、辞書順最小な解を復元することについて考えてみます。辞書順最小な解を復元するとは、例えば「グラフの最短路問題」を考えたときに、最短路のうち、たどるグラフのノードの index の列が辞書順最小であるものを求めたいという問題意識です。
その場合は、動的計画法の更新をスタートからではなく、ゴールから行うことで解決することが多いです。
今まで紹介した解の復元はすべて、ゴールからスタートへと prev 配列を辿って行く形で実装していました。動的計画法の更新をゴールから行うことにより、これを「スタートからゴールへと辿る」形にすることができます。そうすることによって、最短路のうち、特に辞書順が最小となるものを選べるようになります。
最適解の数え上げ
類似の問題意識ですが、最適解をすべて数え上げたいという問題を考えます。これは動的計画法の更新部分をほんの少し修正するだけで実現できます。詳しくは「最短経路の個数も一緒に数え上げる最短経路アルゴリズム」を読んでいただけたらと思います。