目次
からの続きです!
前編
| 章 | タイトル | 備考 |
|---|---|---|
| 0. | はじめに | |
| 1. | 探索アルゴリズムとは | ここからサポートしていきます |
| 2. | すべての基本、全探索 | |
| 3. | 種々の全探索 ~bit全探索、順列全探索など~ | 2 章より複雑な構造を扱います |
| 4. | 効率的な探索手法 ~二分探索と三分探索~ | |
| 5. | はやい探索法 ~半分全列挙~ | |
| 6. | 意外と強い、枝刈り全探索 |
後編
| 章 | タイトル | 備考 |
|---|---|---|
| 7. | 「おねえさん問題」で役立つ、全探索 | 後編では探索が役立つ事例を紹介します |
| 8. | 「高次方程式の解の発見」で役立つ、二分法 | |
| 9. | 「15パズル」で役立つ、半分全列挙と枝刈り全探索 | |
| 10. | 更なる探索アルゴリズムの奥深さ | |
| 11. | おわりに |
7. 「おねえさん問題」で役立つ、全探索
1 章では、以下の問題を紹介しました。(俗に「お姉さん問題」1といわれるものです)
$N \times N$ の碁盤目状道路がある。左上座標を $(0, 0)$、右下座標を $(N, N)$ とするとき、左上の座標から右下の座標まで、同じ交差点を通らずに行くような方法は何通りあるか。
例えば、$N = 2$ の場合は $12$ 通りの行き方しか存在しません。
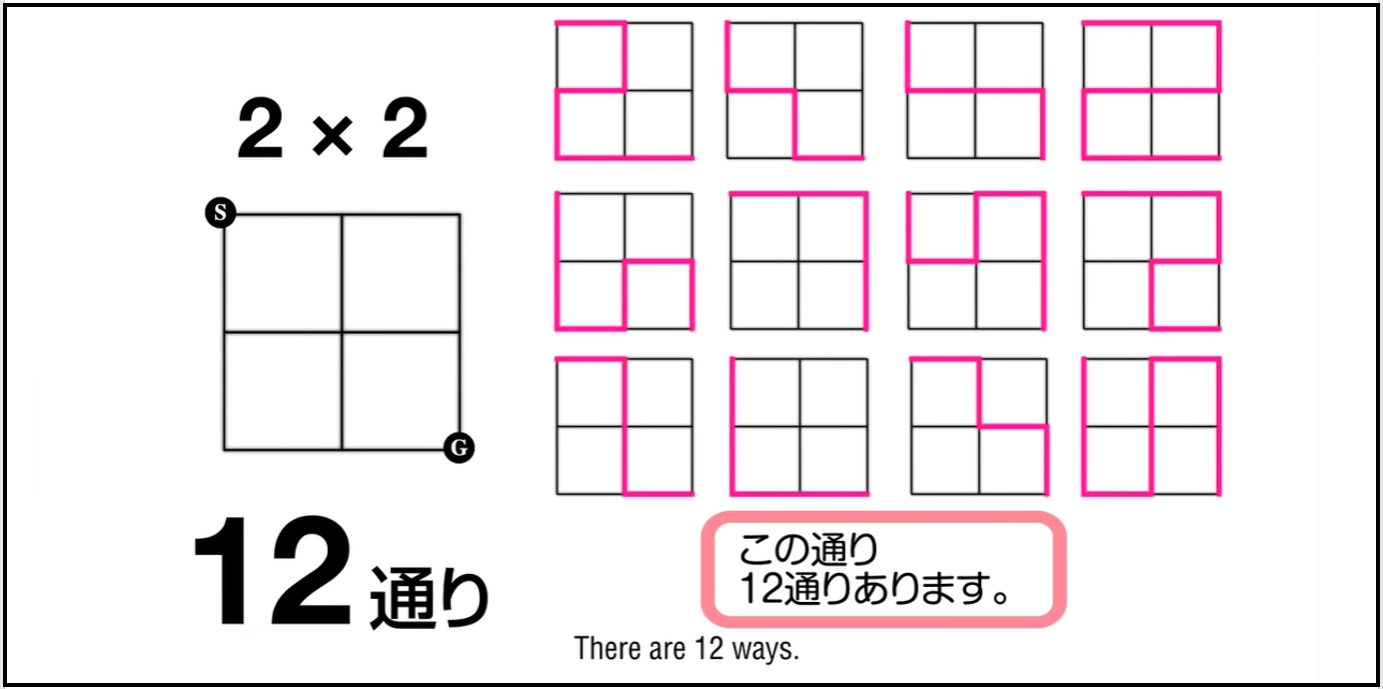
一方で、$N \geq 3$ のとき答えは次表のようになり、$N$ が $1$ 増えたら一気に答えが大きくなる、「組合せ爆発」の有名問題として知られています。2
| $N$ | $1$ | $2$ | $3$ | $4$ | $5$ | $6$ |
|---|---|---|---|---|---|---|
| 答え | $2$ | $12$ | $184$ | $8512$ | $1262816$ | $575780564$ |
7-1. 単純な全探索だと上手くいかない
さて、この問題の答えをどのようにして求めるのでしょうか。できれば $5 \times 5$ くらいまでは数秒で計算したいですが、複雑な構造を扱うため、単純な for 文ループでの全探索をすると、ループが $20$ 重あるいは $30$ 重以上になってしまい、実装が大変なことになってしまいます。
また、どのような行き方をしても、「上下左右の交差点に移動する回数」は高々 $(N+1)^2$ 回です。例えば下のような場合は $(N+1)^2$ 回になります。
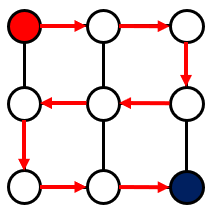
そこで、3-5. 節で扱ったような $3$ 進数以上の bit 全探索を利用して、最大 $(N + 1)^2$ 回の移動の方向を全探索することもできます。しかし、$4$ 方向に移動できるので、計算量が $O(4^{(N + 1) \times (N + 1)})$ などといった莫大なものになります。したがって、$N = 4$ の場合ですら数秒で計算できません。
7-2. ここで役立つ「再帰関数による全探索」
ここで役立つのが 3-3. 節で紹介した「再帰関数を用いた全探索」です。
- 今どの交差点にいるかの情報 $(px, py)$
- 既にどの交差点を通ったかの情報 $S$
という 2 つの状態を管理しながら再帰関数で処理を行うことを考えます。($S$ の情報は struct などで型や構造体を予め作っておくと実装が楽です)
既に通ったことのある交差点は次通ることができないので、例えば $N=2$ で以下の図のような状態の場合、次のように $2$ 通りの遷移ができます。
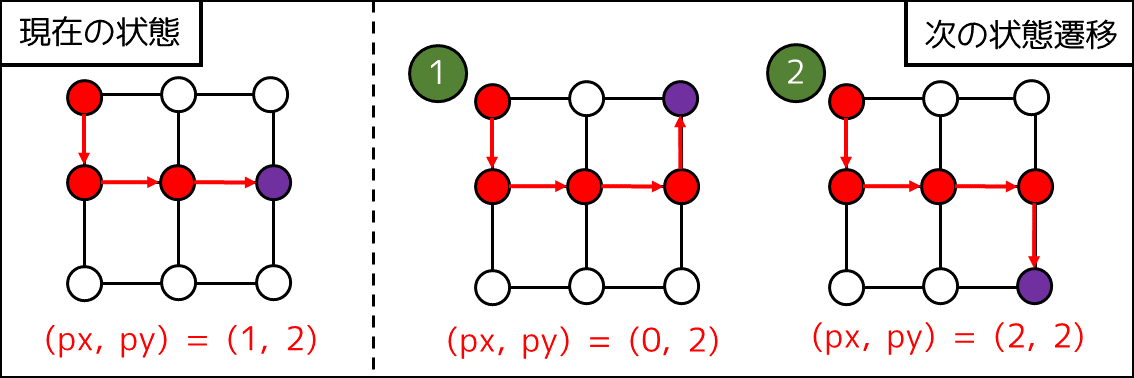
したがって、以下のように実装できます。ここでは dfs が扱う再帰関数です。
# include <iostream>
using namespace std;
struct State {
bool used[7][7];
};
int dx[4] = { -1, 0, 1, 0 };
int dy[4] = { 0, 1, 0, -1 };
int dfs(int N, int px, int py, State S) {
if (px == N && py == N) return 1;
int sum = 0;
for (int i = 0; i < 4; i++) {
// 次通る交差点を (sx, sy) とする
int sx = px + dx[i];
int sy = py + dy[i];
if (sx < 0 || sy < 0 || sx > N || sy > N) continue;
if (S.used[sx][sy] == true) continue;
State NextState = S; NextState.used[sx][sy] = true;
sum += dfs(N, sx, sy, NextState);
}
return sum;
}
int main() {
// 入力
int N; cin >> N;
// 初期化
State InitS;
for (int i = 0; i <= N; i++) {
for (int j = 0; j <= N; j++) InitS.used[i][j] = false;
}
InitS.used[0][0] = true;
// 答えを求める
cout << dfs(N, 0, 0, InitS) << endl;
return 0;
}
計算には次表の通りの時間がかかりました。再帰関数による全探索(深さ優先探索)は意外と無駄が少なく、最大でも答えの数十倍程度の状態数しか探索していないことがわかります。$N = 5$ でも 0.4秒以内で計算できており、とても高速です。
| N | 通り数(答え) | 探索した状態数 | 計算時間 |
|---|---|---|---|
| 2 | 12 通り | 51 個 | 0.023 ミリ秒 |
| 3 | 184 通り | 1271 個 | 0.066 ミリ秒 |
| 4 | 8512 通り | 90111 個 | 2.142 ミリ秒 |
| 5 | 1262816 通り | 18470411 個 | 309.507 ミリ秒 |
補足ですが、現在の最新技術を使えば $N = 16$ でもわずか数分で計算することができます。ZDDのアルゴリズムという効率的な数え上げ手法があるので、興味ある方は是非調べてみてください。また、2013 年に $25 \times 25$ の結果が計算され、世界記録が塗り替えられているように、現在も記録更新が続いている面白い問題です。詳しくは以下の参考文献をお読みください。3
8. 「高次方程式の解の発見」に役立つ、二分法
一次方程式 $ax+b = 0$ の解は、
$$x = -\frac{b}{a}$$
となります。また、二次方程式 $ax^{2} + bx + c$ の解は、
$$x = \frac{-b-\sqrt{b^2-4ac}}{2a}, \frac{-b+\sqrt{b^2-4ac}}{2a}$$
となります。しかし三次方程式以上になると求めるのが難しくなり、特に五次方程式以上であれば解の公式が存在しません。したがって、数値解析的に解く必要があります。しかし、本記事で紹介した二分探索というアルゴリズムを用いると、$N$ 次方程式を $O(N^3 \log 精度の逆数)$ などの高速な計算量で求めることができます。まずは三次方程式から考え、次に一般の $N$ 次方程式の場合に解いてみましょう。
8-1. 三次方程式の解を求める
三次方程式 $ax^3 + bx^2 + cx + d = 0$ を解くことを考えましょう。
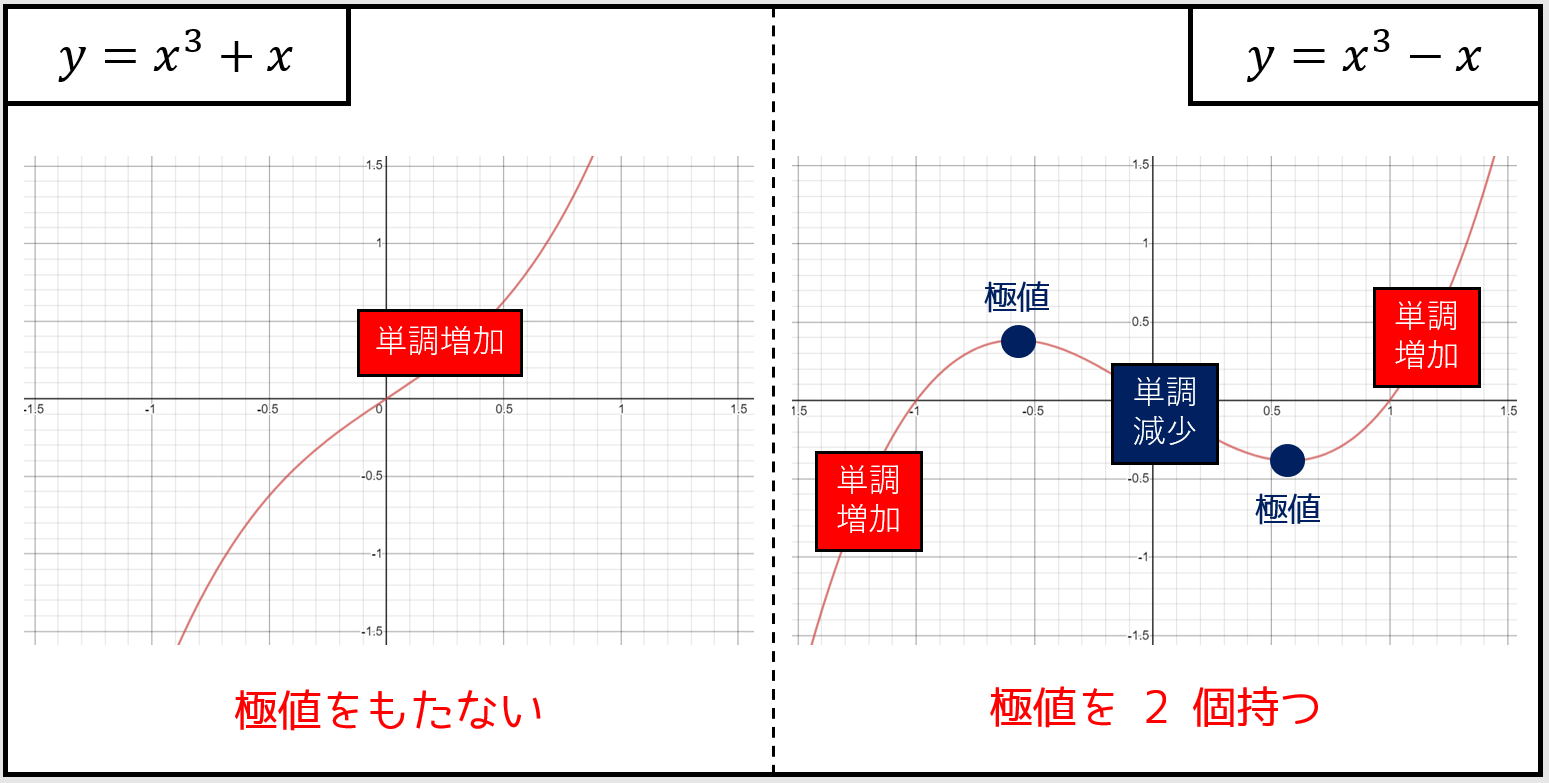
まず、三次関数 $f(x) = ax^3 + bx^2 + cx + d$ は以下の性質を持ちます。
- 極値を高々 $2$ つ持つ。
- 極値と極値の間は、単調増加あるいは単調減少である。
例えば、$y=x^3+x$ と $y=x^3-x$ のグラフは、以下の図の通り条件を満たします。(高校数学が分からない方へ:「極値」は下図のように「山の頂上」「谷の底」のような形をする場所です。)
そこで、以下の 2 パターンに場合分けしてみましょう。
パターン 1. 極値をもたない場合
極値をもたない場合、 $f(x)$ は単調増加か単調減少です。したがって、4-2. 節で扱った「二分法」を利用すれば解くことができます。例として、方程式 $x^3+x-1=0$ の解を求めることを考えます。$0 \leq x \leq 1$ に解があることは簡単にわかるので、以下のようにして解けます。(ここでは、$f(x) = x^3+x-1$ とします)
| 現在分かっている $x$ の範囲 | 行う計算 | 計算結果 |
|---|---|---|
| $0.0000 \leq x \leq 1.0000$ | $f(0.5000) \leq 0$ か? | 正しい($f(0.5000) \fallingdotseq -0.38$) |
| $0.5000 \leq x \leq 1.0000$ | $f(0.7500) \leq 0$ か? | 間違い($f(0.7500) \fallingdotseq 0.17$) |
| $0.5000 \leq x \leq 0.7500$ | $f(0.6250) \leq 0$ か? | 正しい($f(0.6250) \fallingdotseq -0.13$) |
| $0.6250 \leq x \leq 0.7500$ | $f(0.6875) \leq 0$ か? | 間違い($f(0.6875) \fallingdotseq 0.01$) |
| $0.6250 \leq x \leq 0.6875$ | $f(0.6563) \leq 0$ か? | 正しい($f(0.6563) \fallingdotseq -0.06$) |
上の表は $f(x)$ 単調増加の場合の例ですが、$f(x)$ が単調減少の場合も逆のことをすれば、計算量 $O(\log_2 精度の逆数)$ で解くことができます。
パターン 2. 極値をもつ場合
極値 $x=a_1, a_2$ で持つとしましょう。$x^3$ の項が正だと仮定するとき、
- $-\infty \leq x \leq a_1$ の区間では単調増加
- $a_1 \leq x \leq a_2$ の区間では単調減少
- $a_2 \leq x \leq +\infty$ の区間では単調増加
となります。したがって、3 つの区間それぞれについて、パターン 1 と同様に二分法のアイデアを使って解を求めることができます。ただし、3 つのうち 1 つか 2 つの区間に解が存在しない場合があることに注意してください。(例えば中央の区間について、$f(a_1)$ と $f(a_2)$ の間に $0$ が存在しなければ、$a_1 \leq x \leq a_2$ を満たす解が存在しないといえます)
なお、極値は $f(x)$ を微分することで求めることができます。一般に、三次関数 $f(x) = ax^3 + bx^2 + cx + d$ の極値となる $x$ の値は、
$$3ax^2 + 2bx + c = 0$$
の解であるため、解の公式などを用いて二次方程式を解けば、極値を求めることができます。
8-2. 四次以上の方程式の解を求める
次に、$n$ 次多項式
$$a_nx^n + a_{n-1}x^{n-1} + ... + a_{1}x + a_0 = 0$$
の解を求めることを考えましょう。
$$f(x) = a_nx^n + a_{n-1}x^{n-1} + ... + a_{1}x + a_{0}$$
とするとき、$n$ 次関数 $f(x)$ が $x = a_1, a_2, ..., a_t$ で極値を取るとします。そのとき、以下の性質が必ず成り立ちます。
- $-\infty \leq x \leq a_1$ の区間では単調増加 または 単調減少
- $a_1 \leq x \leq a_2$ の区間では単調減少 または 単調増加
- $a_2 \leq x \leq a_3$ の区間では単調増加 または 単調減少
:
- $a_t \leq x \leq +\infty$ の区間では単調増加 または 単調減少
したがって、$n$ 次関数は単調増加または単調減少である $t+1$ 個の区間に分けることができます。$t < n$ なので、区間の数は最大でも $n$ 個です。単調減少あるいは単調増加の区間に対して問題を解くためには、三次方程式の場合と同様に二分法を使えば良いので、$O(nt \times \log 精度の逆数)$ といった計算量で解けます。
最後に、極値はどのようにして求めることができるのでしょうか。一般に、$n$ 次関数
$$f(x) \ = \ a_{n}x^{n} \ + \ a_{n-1}x^{n-1} \ + \ ... \ + \ a_{1}x \ + \ a_{0}$$
の極値は、$n-1$ 次方程式
$$na_nx^{n-1} \ + \ (n-1)a_{n-1}x^{n-2} \ + \ ... \ + \ 2a_{2}x \ + \ a_{1} \ = \ 0$$
の解となります。($f(x)$ を微分すると導出できます)
したがって、$n$ 次方程式は $n-1$ 次方程式に帰着させることができました。
n-1 次方程式に帰着させると…
- $n$ 次方程式は $n-1$ 次方程式に帰着でき、
- $n-1$ 次方程式は $n-2$ 次方程式に帰着でき、
- $n-2$ 次方程式は $n-3$ 次方程式に帰着でき、… (以下省略)
となっていくため、最終的には $1$ 次方程式の解を求めることになります。精度の逆数を $A$ とすると、計算量は以下のようになります。
- $n$ 次方程式を $n-1$ 次方程式に帰着するのに、$O(n^2 \times \log A)$ かかる
- $n-1$ 次方程式を $n-2$ 次方程式に帰着するのに、$O(n(n-1) \times \log A)$ かかる
- $n-2$ 次方程式を $n-3$ 次方程式に帰着するのに、$O(n(n-2) \times \log A)$ かかる …(以下省略)
したがって、合計計算量は以下の通りとなり、$n = 100$ 程度でも数秒で解けます。
$$O(n^2 \times \log A) + O(n(n-1) \times \log A) + ... + O(2n \times \log A) = O(n^3 \times \log A)$$
実装例は次の通りです。(solve は $|A|-1$ 次多項式 $A_{|A|-1}x^{|A|-1}+A_{|A|-2}x^{|A|-2}+...+A_{0}$ を入力し、解となる $x$ を返す関数です)
# include <iostream>
# include <cmath>
# include <vector>
using namespace std;
double getvalue(vector<double> A, double x) {
// f(x) の値を求める
double rem = 0;
for (int i = 0; i < A.size(); i++) rem += 1.0 * A[i] * pow(x, 1.0 * i);
return rem;
}
vector<double> solve(vector<double> A) {
// 1 次方程式の場合
if (A.size() == 2) {
if (A[1] == 0) return vector<double>{};
return vector<double>{-1.0 * A[0] / A[1]};
}
// A を微分して極値 {K1, K2, ..., KT} を得る
vector<double> B(A.size() - 1, 0);
for (int i = 0; i < B.size(); i++) B[i] = 1.0 * (i + 1) * A[i + 1];
vector<double> K = solve(B);
// 各区間に対して二分法をする
vector<double> ret;
for (int i = 0; i <= K.size(); i++) {
double cl = -100000; if (i >= 1) cl = K[i - 1];
double cr = 100000; if (i < K.size()) cr = K[i];
double val1 = getvalue(A, cl), val2 = getvalue(A, cr);
bool flag = false;
if (val1 > val2) { val1 *= -1.0; val2 *= -1.0; flag = true; }
if (val2 < 0.0 || 0.0 < val1) continue;
double cm;
for (int j = 0; j < 60; j++) {
cm = (cl + cr) / 2.0;
double val = getvalue(A, cm); if (flag == true) val *= -1.0;
if (val < 0) { cl = cm; }
else { cr = cm; }
}
ret.push_back(cm);
}
return ret;
}
9. 「15 パズル」で役立つ、半分全列挙と枝刈り探索
最後に紹介する例は「15 パズル」です。
皆さん、「15 パズル」というパズルをご存知でしょうか。
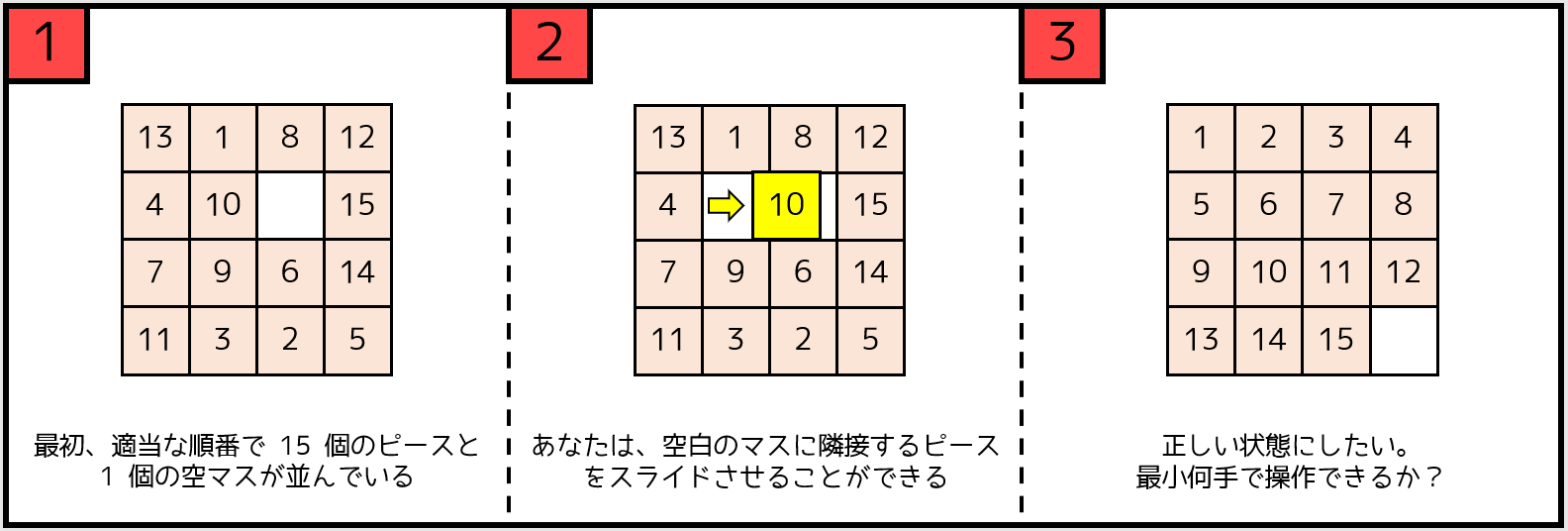
そこで、ある 15 パズルの盤面が与えられたときに、最短手数を求めるためにはどうすれば良いのでしょうか。
9-1. 基本手法 - 全探索
ある状態からスライドさせる(1 手動かす)方法が何通りあるか考えましょう。空マスの上下左右に隣接するピースの個数なので、高々 4 通り です。例えば、以下の場面だと $4$ 通りの手を打つことができます。
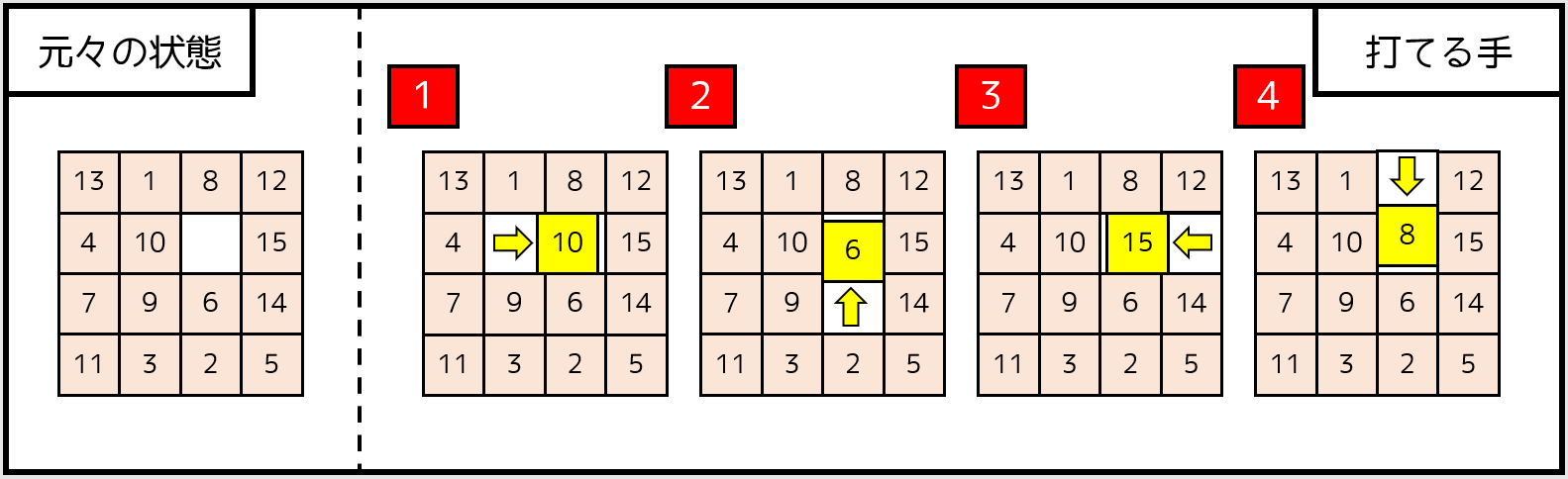
したがって、全探索をする場合、考える最大手数を $A$ としたとき $4^A$ 通り探索する必要があります。したがって、$10$ 手以内までなら解けます。プログラムの実装は、
のいずれかを利用すると、書くことができます。また、以下の図のように「直前の手と逆の向きに動かすのは無駄である」という発想に気づけば、$O(4 \times 3^{A-1})$ 通りに絞ることができ、$15$ 手以内までなら解けます。実際は、近傍が $2$ つや $3$ つのマス(角など)があるので、$20$~$25$ 手くらいまでなら数秒以内で解けます。
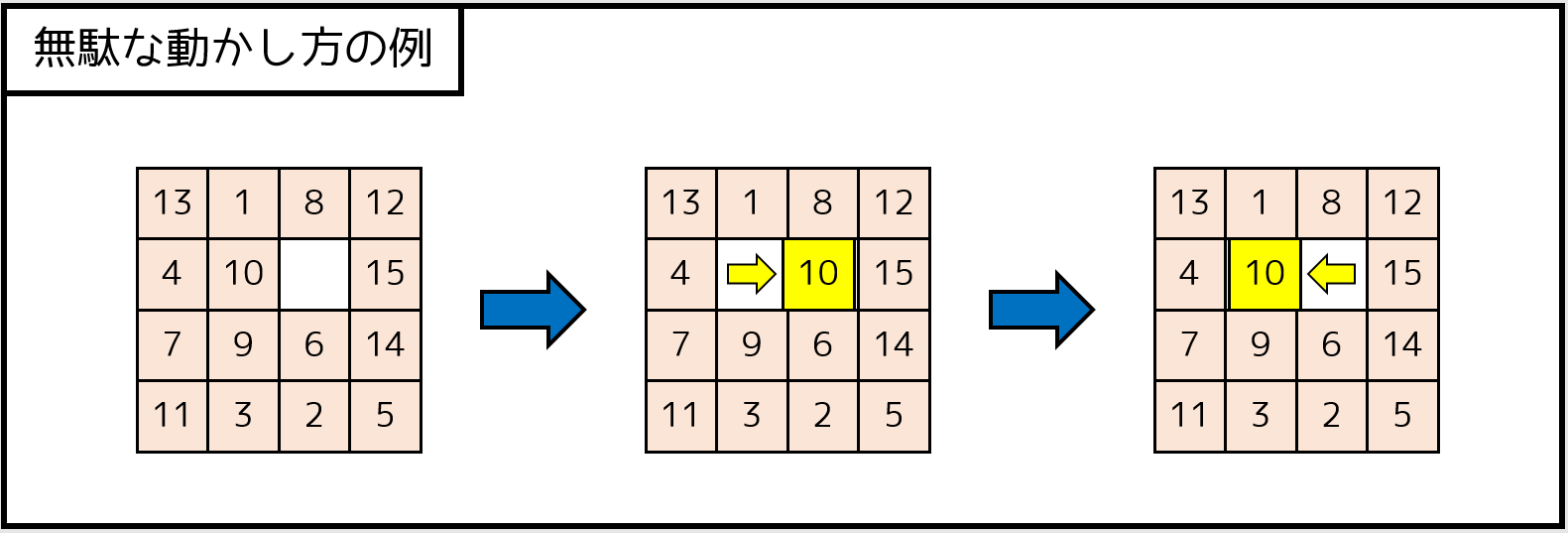
9-2. 半分全列挙を用いた解法
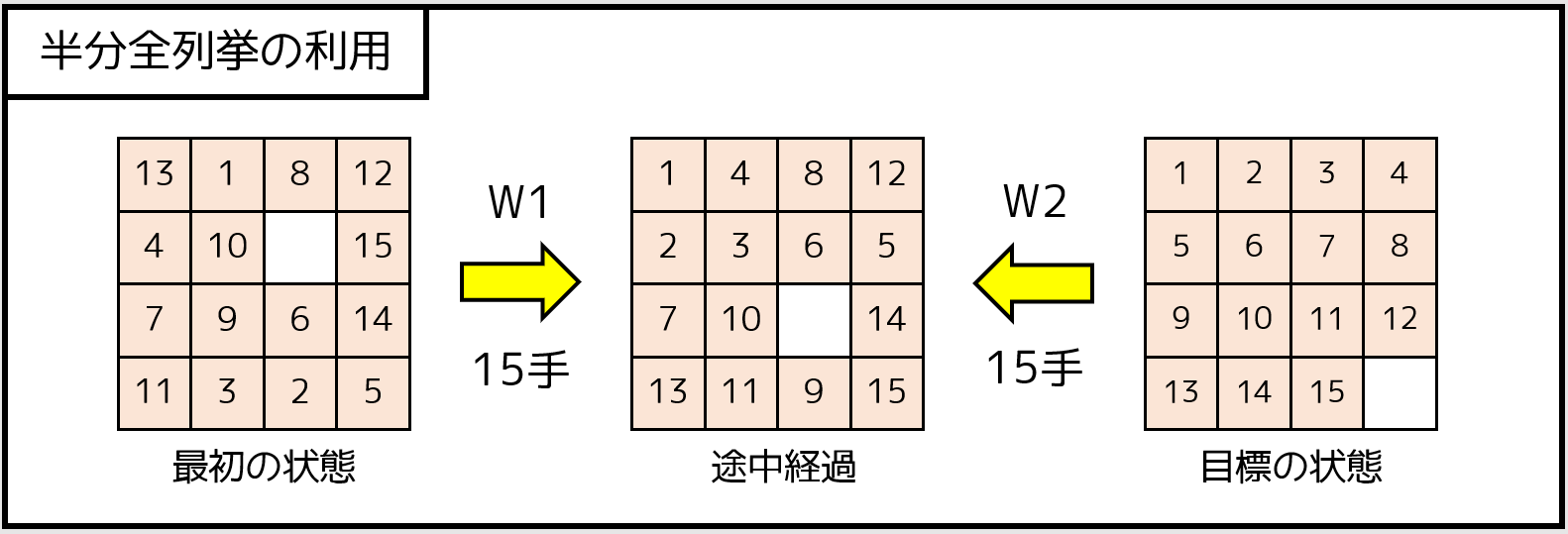
しかし、このままだと 20-25 手までしか探索できません。もっと多くの手数がかかる問題であっても、最適解を見つける方法は存在するのでしょうか。ここで用いるのが半分全列挙のアイデアです。例えば、「ちょうど $30$ 手でゴールできるか」を考えましょう。
- 最初の盤面から $15$ 手動かしたときのあり得る状態を、$(W1_1, W1_2, ..., W1_{T1})$ とする
- 目標の盤面から $15$ 手動かしたときのあり得る状態を、$(W2_1, W2_2, ..., W2_{T2})$ とする
そのとき、$W1_i = W2_j$ となるような $(i, j)$ の組が存在すれば、ちょうど $30$ 手で目標の状態まで動かすことができます。このような組が存在するかは、$W1, W2$ を適切な順序でソートした後、二分探索をすれば判定できます。(map などのデータ構造を用いても解けます)
ただし、この手法だと最初に手数を決めなければ計算できないので、6-2. 節で紹介した「反復深化」のアイデアを利用して、
- $1$ 回ではできるか?
- (できなかった場合)$2$ 回ではできるか?
- (できなかった場合)$3$ 回ではできるか?
- (できなかった場合)$4$ 回ではできるか? …(以下省略)
といった感じに解けば、最短手数が求まります。
半分全列挙を利用したアイデアでは、最短手数約36手まで解くことができます。実際に、$W1, W2$ の大きさは以下の表の通りになり、$36$ 手の場合でも高々数百万程度の状態しか考えなくて良いです。計算量は二分探索とソートがボトルネックになって $O((|W1| + |W2|) \log (|W1| + |W2))$ となるので、数秒で計算できます。
| 操作回数 | 全探索する手数 | $W2$ のサイズ | $W1$ のサイズ(最大値) |
|---|---|---|---|
| 20 | 10 | 2204 | 3666 |
| 24 | 12 | 9880 | 16774 |
| 28 | 14 | 44972 | 75986 |
| 32 | 16 | 204216 | 344758 |
| 36 | 18 | 925980 | 1565618 |
9-3. <発展>ハッシュを用いて計算速度改善
盤面の状態を例えば struct で構造体を作って記録すると、int 型配列をマス目の数と同じ 16 個持つ必要があります。したがって、状態遷移・ソート・二分探索に時間がかかってしまいます。そこで利用するのが、bit 全探索のアイデアのもととなった、盤面の状態を数値として表す手法**「ハッシュ」**です。
左上のマスから順に $1, 2, ..., 16$ マス目として、$i$ マス目に置かれているピースの番号を $P_i$(空マスの場合は $0$)で表します。そのとき、
$$V = 16^0P_0 + 16^1P_1 + 16^2P_2 + 16^3P_3 + ... + 16^{15}P_{15}$$
とすると、盤面の状態を $0$ 以上 $2^{64}$ 未満の $1$ つの 64 ビット型整数で表現できてしまうのです。例えば以下の図の場合は $V = 1147797409030816545$とります。

そうすると、状態遷移・ソート・二分探索にかかる時間が短縮でき、考えるべき状態数が $10^7$ 程度になっても数秒で計算できます。したがって、最短手数約40手の場合まで対応できます。(このように、計算量オーダー自体は改善しないが、処理を単純化するなどして高速化することを、定数倍高速化といいます)
9-4. <発展>IDA* を用いて更に改善
最後に、枝刈り全探索の一つの手法である**「IDA*」**という手法を用いて状態数を絞り込み、さらに手数の多い問題にも対応できるようにします。(ここでは一旦「半分全列挙の解法」を忘れます。)
まず、6-3. 節で紹介した IDA* について再掲しておきます。
IDA* アルゴリズムは、反復深化に枝刈りを加えたものである。「$D$ 手以内に操作してください」という問題を解くとき、現在 $g$ 手操作しており、残りの最短手数の推定値(正確でなくて良い)を $h$ 手するとき、$g + h > D$ の場合枝刈りをして、遷移を打ち切る。
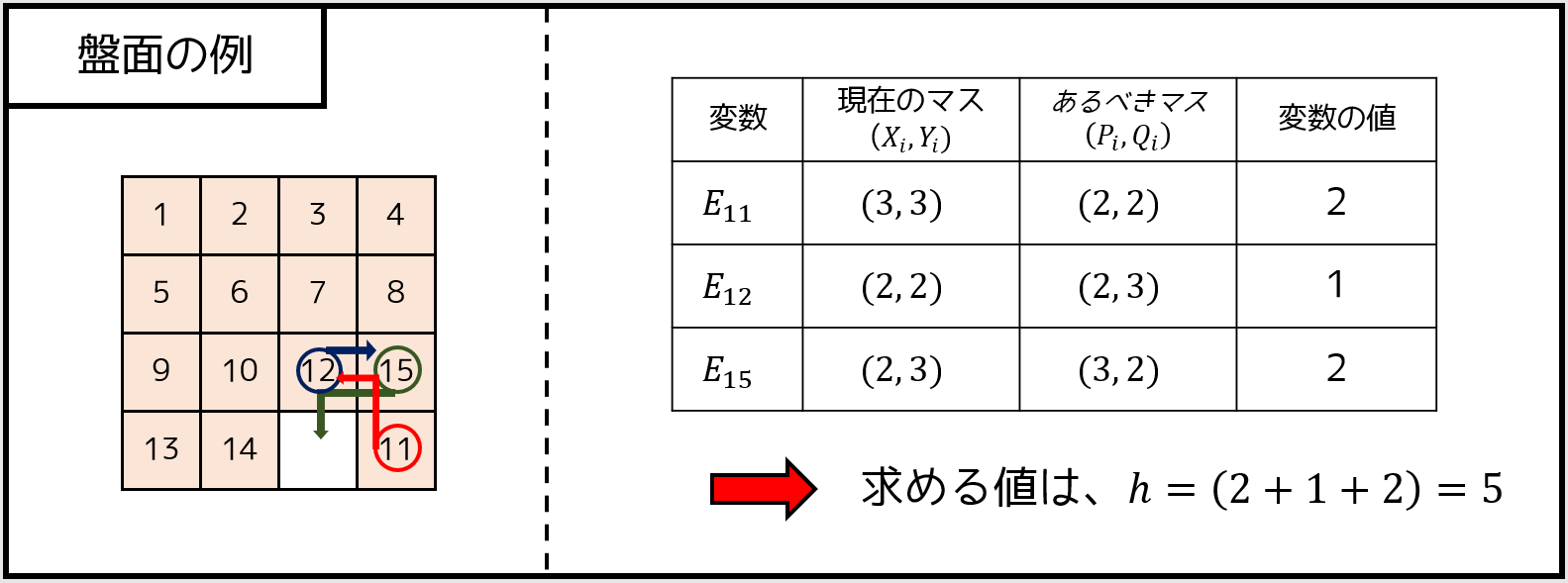
さて、この問題にどうやって IDA* のアルゴリズムが適用できるのでしょうか。例えば、残りの最短手数 $h$ の推定値を以下のように定義できます。
- ピース $i$ の位置を $(X_i, Y_i)$ として、目標状態でのピース $i$ の位置を $(P_i, Q_i)$ とする。
- $E_i = |X_i - P_i| + |Y_i - Q_i|$(2 点間のマンハッタン距離)とする。
- そのとき、$h = E_1 + E_2 + ... + E_{15}$ とする。
例えば、下図の場合は $h = 5$ になります。なお、最短手数は $h$ 以上であることが証明できるので、解を見逃すということは絶対にありません。
このように推定値を計算して、枝刈り全探索を行った場合、探索すべき通り数が大幅に減り、9-1. 節で扱った全探索の10000分の1以下になります。例えば以下の盤面を考えましょう。
14 7 6 4
2 3 1 11
5 9 12 15
13 0 10 8
この盤面における最短手数は $40$ 手ですが、IDA* を用いたアルゴリズムだと 4378257個しか状態を探索する必要がありません。また、ほとんどの 15 パズルでは最短手数となるような動かし方が複数存在し、10 通り以上となるものも多いです。したがって、解が一つ見つかった場合に探索を終了すれば、実質的には 100万個以下の状態探索で解を求めることができるのです。
このように、
- 本節で紹介した IDA* アルゴリズム
- 9-3. 節で紹介したハッシュによる定数倍高速化
を使うと、最短手数 $40$ 手の場合は 0.02秒以内、$55$ 手の場合でも数秒以内に計算を終わらせることができます。とても高速に計算を行うことができました。
ソースコード
この問題で扱ったソースコードは 70 行以上と長いので、リンクを貼り付けておきます。
以下の実装例は、両方 C++ のコードです。
ちなみに、「有限手数で解ける 15 パズル」の解は必ず 80 手以内であることが証明されています。4最も難しい $80$ 手の場合を解くのは難しいですが、IDA* の「残り手数推定値」をもう少し工夫すると、$65$ 手前後の問題でも数秒以内で実行できるようになります。
そして、現在最先端の探索アルゴリズム技術を使えば、$80$ 手のものでもすんなり計算できてしまいます。探索アルゴリズムは単純さがありながら、とても奥深く、応用範囲が広いです。
10. 更なる探索アルゴリズムの奥深さ
7 章・8 章・9 章では、「探索アルゴリズム」が役立つ例として、
を挙げました。しかしながら、探索アルゴリズムが役立つ範囲はそれだけではありません。実際にはもっとたくさんあるのです。皆さんが日常的に使っているモノの中にも「探索アルゴリズム」が役立っていたりするのです。
10-1. 巡回セールスマン問題
以下のような問題を考えてみましょう。
$N$ 個の都市があって、$i$ 個目の都市は座標 $(x_i, y_i)$ にある。$2$ つの都市間を移動するのに、ユークリッド距離だけ時間がかかる。都市 $1$ から出発し、すべての都市を通って都市 $1$ に戻ってくるような移動方法のうち、時間ができるだけ短くなるようなものを出力してください。
制約:$1 \leq N \leq 200$
この問題は、$N \leq 10$ ならば 3-2. 節で紹介した順列全探索のアルゴリズムを利用することで解けます。また、$N \leq 16$ のとき、ビットDP5 という別の方法を使うことで解くことができます。しかし、巡回セールスマン問題は NP 困難6であり、多項式時間7では解けません。
そこで、近似解(最適解にできるだけ近い解)を求めることを考えるのですが、この問題では、全探索と貪欲法アルゴリズムを組み合わせた局所探索法(山登り法)という手法が通用します。局所探索法とは、大まかにいえば「解を少しずつ改善していくこと」を繰り返すことによって、最適に近い解を得るアルゴリズムのことを指します。
特に、巡回セールスマン問題を解くにあたっては、
がよく使われます。それを利用すると、最適解に比べて数パーセントしか悪くない8答えを見つけることができるのです。
10-2. オセロ AI の作成
オセロは、皆さんの多くがプレイしたことのあるような、有名なゲームです。
実はこのオセロでも、「AI の実装」や「現在の形勢判断」に、探索アルゴリズムが使われているのです。例えば、再帰関数を用いた全探索の応用である、
が利用されています。しかし、MiniMax 法には、最善手から悪手まで含めて全部探索してしまうという欠点があります。したがって、$1$ 手読む手数を増やしただけで状態遷移が数十倍に膨れ上がるほど、探索通り数が大きくなってしまいます。それを改善するために利用されているのは、評価値の高い状態を優先して計算する枝刈り探索アルゴリズムの一つである、
です。この手法を用いると、多くの人間に勝てる AI を実装することができます。
一方、最近のAIは…
しかし、最近は探索アルゴリズムではなく機械学習を用いた最適化も主流になっています。例えば将棋 AI では強化学習や機械学習が用いられており、その影響で近年 AI が急激に進化しています。αβ法だけでも相当強いのですが、機械学習によって AI がプロと互角に戦えるようになったり、タイトルを持つような人にも勝てるようになったりしてきています。
11. おわりに
探索アルゴリズムの最も基本的なアルゴリズムは「全探索」で、あり得るものを全通り探索するという本当に単純なものでした。しかし、これを応用すると、現実社会で活用されているような、様々な効率的なアルゴリズムが生まれます。これこそが探索アルゴリズムの奥深さ、難しさ、そして面白さなのです。
プログラムを書くにあたって、アルゴリズムを使うだけでなく、問題を「探索視点で見ること」はとても重要です。本記事を通して少しでも「探索視点の考え方」のイメージを深めていただけたならば、とても嬉しいです。
記事は以上です。高校生が書いた記事ですので、文章が分かりづらかったかもしれませんが、最後までお読みいただきありがとうございました。
-
「おねえさん問題」とは、組合せ爆発のすごさとアルゴリズム技術の重要性を分かりやすく伝えることを目的にした、2012 年 8 月から 2013 年 4 月にかけて日本科学未来館で上映された動画に出てくる問題です。動画は、Youtube のリンクから閲覧することができます。 ↩
-
例えば、$N = 25$ の場合は $8.403 \times 10^{150}$ というものすごい通り数になります。オンライン整数列大辞典 A007764 に載っています。 ↩
-
2020 年 7 月 26 日時点で、$26 \times 26$ までが解かれています。 ↩
-
詳しくは、こちらの Wikipediaのページをご覧ください。 ↩
-
ビットDPについては、ビット演算 (bit 演算) の使い方を総特集! 〜 マスクビットから bit DP まで 〜 の第11章 をご覧ください。 ↩
-
多項式時間とは、処理時間の上界が $N$ の多項式で表現できることを指します。例えば $O(N^{869120})$ は多項式時間ですが、$O(1.001^N)$ は多項式時間ではありません。 ↩
-
例えば、Beneteley は $10^6$ 個の都市を持つような問題について、3~4%程度しか悪くない答えを出しています。こちらの文献の p.415 を参照してください。 ↩