巡回セールスマン問題(traveling salesman problem, TSP)は、都市(頂点)を一回ずつ一筆書きのように通るとき、コスト(例えば経路長)を最小化する問題である。TSPの近似解を求める方法として2-optがある。競技プログラミングのマラソンマッチではたまに利用機会があるが、性質がよくわかっていなかったので、実装し直してみた。
2-optは、2辺をランダムに選び、コストが低くなる方につなぎかえるというものである。以下のように説明されることが多い。(Wikipediaより)
- A B - - A - B -
X ==>
- C D - - C - D -
上の例は、A-DとB-Cが接続していて、それよりもA-BとC-Dのコスト長さの合計が短ければ、それにつなぎ直す。
部分だけだとよくわからないので、全体で考えてみる。rianさんが作ったTSPのVisualizerを使って、以下の10個の頂点の例で説明する。
10
-100.00000000 0.00000000
-80.90169944 58.77852523
-30.90169944 95.10565163
30.90169944 95.10565163
80.90169944 58.77852523
-80.90169944 -58.77852523
-30.90169944 -95.10565163
30.90169944 -95.10565163
80.90169944 -58.77852523
100.00000000 0.00000000
0 1 2 3 4 5 6 7 8 9
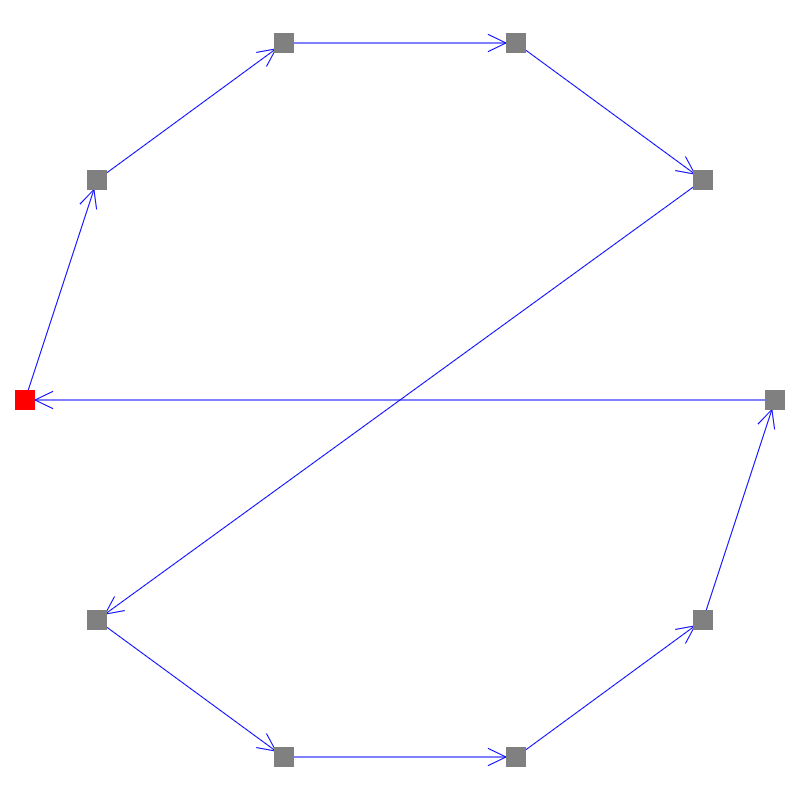
上の例では、以下のように頂点が接続している。
0 -> 1 -> 2 -> 3 -> 4
^ |
| v
9 <- 8 <- 7 <- 6 <- 5
頂点0-9と4-5が接続しているが、0-5と4-9の方が短いので、以下のようにつなぎかえたい。
0 -> 1 -> 2 -> 3 -> 4
^ |
| v
5 <- 6 <- 7 <- 8 <- 9
Visualizerだと以下のデータである。
0 1 2 3 4 9 8 7 6 5

2-optでは、つなぎかえるときに向きを考慮する必要がある。
頂点5と9を交換するだけではだめで、5から9までを逆向きにする必要がある。
このように向きを保持するシンプルなデータ構造として、例えば以下のようなものが考えられる。
(A) 次の頂点を保持するリンクリスト
struct Node {
int next;
}
(B) 配列に次の頂点番号を保持する
+---+---+---+---+---+---+---+---+---+---+
| 1 | 2 | 3 | 4 | 9 | 0 | 5 | 6 | 7 | 8 |
+---+---+---+---+---+---+---+---+---+---+
(C) 配列に頂点番号を保持し、次のインデックスが隣で、末尾は先頭と接続しているものとする
+---+---+---+---+---+---+---+---+---+---+
| 0 | 1 | 2 | 3 | 4 | 9 | 8 | 7 | 6 | 5 |
+---+---+---+---+---+---+---+---+---+---+
去年(B)で実装したのだが、実は(C)でよいということに気づき、実装し直してみた。
以下のように、bがaより後ろのインデックスにあるとき、
+---+---+---+---+---+---+---+---+---+---+
| ? | ? | a | d | ? | ? | b | c | ? | ? |
+---+---+---+---+---+---+---+---+---+---+
配列seqの内容をa-b c-dにつなぎ変えるには、以下のようにdからbを反転させる。(C++)
int x = d, y = b;
while (x < y) {
swap(seq[x++], seq[y--]);
}
ところで、繋ぎ変える部分を反転させればよいので、実はcからaまでを反転させてもよい。その場合は、配列の末尾の先が先頭になるようにアクセスする。
int x = c, y = a + N;
while (x < y) {
swap(seq[x % N], seq[y % N]);
++x, --y;
}
反転する量が小さい方がうれしいはずなので、このようにまとめてみた。(コーナーケースでcがゼロのことがあるが、その場合はd-bを反転させる)
int x = d, y = b;
if (y - x > a + N - c) {
x = c, y = a + N;
}
while (x < y) {
swap(seq[x < N ? x : x - N], seq[y < N ? y : y - N]);
++x, --y;
}
というわけで実装し直してみた。
頂点数を増やすと、ちゃんと動いているらしいことがわかる。(開発中は、つなぎかえたあとに距離が長くなっていないかどうか検証した)
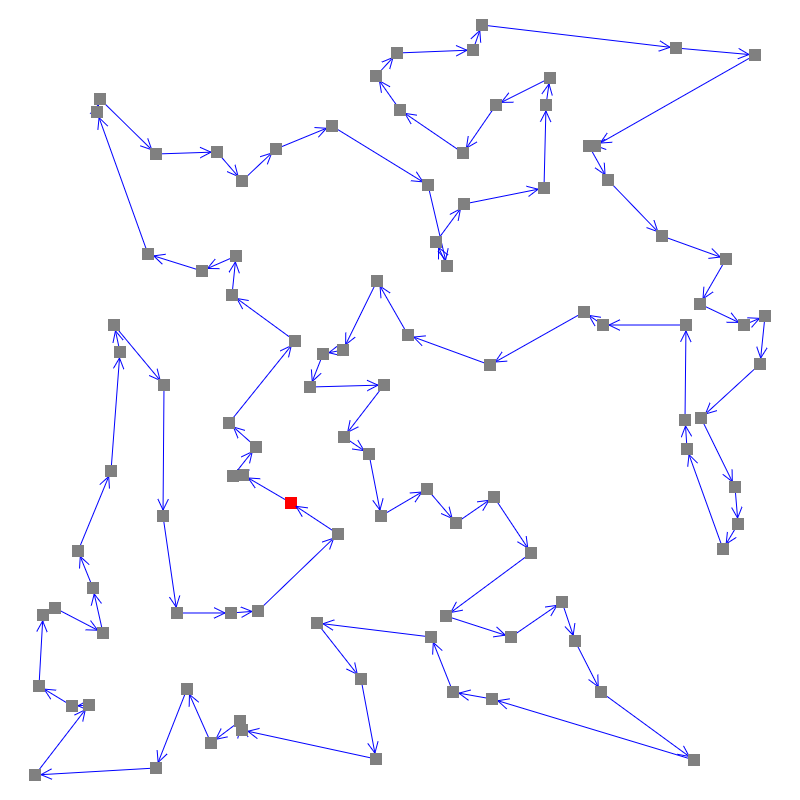
交換回数を減らす工夫だが、交換回数自体は10-20%ほど減るが、全体的な高速化には寄与しなかった。しかしなぜか収束するまでの回数は短くなるようだ。
ランダムのループの回数は、頂点数が10だと100回、100だと数万回、1000だと数百万回でだいたい良い感じになるようだ。他の条件や3-optなどと組み合わせるのが実用的だと思われる。