0. はじめに
「P ≠ NP 予想」とは数学における極めて重要な未解決問題であり、クレイ研究所によって定められたミレニアム懸賞問題の 1 つです。ミレニアム懸賞問題は「これが解けたら 100 万ドル」と懸賞のかけられた問題で、以下の 7 問が選定されています:
非常に有名な「リーマン予想」や「ポアンカレ予想」が含まれています。ポアンカレ予想は既に G. Perelman によって解かれました。残る問題は「P ≠ NP 予想」を含む 6 問です。
1. 計算量について
まず計算量オーダーという概念についてはこちらの記事で解説をしています。計算量オーダーを求める実例集にて
- 多項式時間アルゴリズム
- 弱多項式時間アルゴリズム
- 強多項式時間アルゴリズム
- 擬多項式時間アルゴリズム (多項式時間アルゴリズムではない)
という概念についても紹介しています。
2. 指数時間が遅いこと
多項式時間アルゴリズムは速く、指数時間アルゴリズムは遅い
という考え方の歴史はおよそ 40~50 年前にさかのぼり、J. Edmonds によって提唱されました。そして、P 問題、NP 問題、NP 完全問題、NP 困難問題といった重要な概念たちが次々と登場していきました。これらについては次章で解説します。
さて、指数時間アルゴリズムがいかに遅いかを示す有名な動画があります:
- 『フカシギの数え方』 おねえさんといっしょ! みんなで数えてみよう! (YouTube)
25万年かかった計算が、工夫すると数秒でできるというのは決して極端な話ではなく、しばしば見られる現象です。最短経路を求める Dijkstra 法や、最大流問題を解く Dinic 法や、重み付き二部マッチング問題を解く Hungarian 法 など、現在広く知られている有名な多項式時間アルゴリズムたちの多くは、愚直に全探索しようとすると $O(2^n)$ といった指数時間アルゴリズムになる問題を、見事に多項式時間アルゴリズムに改良できたものたちです。 (注意: 動画の問題はそもそも #P 完全問題であることが知られており、動画の最後に出て来る「最先端のアルゴリズム」は愚直な全探索アルゴリズムよりは高速ですが指数時間アルゴリズムであることには変わりないです)。
3. 「P ≠ NP 予想」とは
3-1. 「P ≠ NP 予想」をざっくり紹介
「P ≠ NP 予想」とはざっくり言えば、多項式時間アルゴリズムは存在しないだろうと広く信じられている判定問題たち (部分和問題など) に対して、
- 本当に多項式時間アルゴリズムが存在しないことを証明する (本命、P ≠ NP)
- 本当は多項式時間アルゴリズムが存在することを示す (大穴、P = NP)
のいずれかを達成することです。
3-2. 「P ≠ NP 予想」をちゃんと紹介
さて、「P ≠ NP 予想」の主張をもう少しきちんと述べます。「P」や「NP」というのは判定問題のクラスを表していて、
- 判定問題が P に属するとき、その問題は多項式時間で解ける
- 判定問題が NP に属するとき、その問題の答えが Yes であったならば、Yes であるための証拠が存在して、その証拠を多項式時間で検証できる
というものです。補足として、判定問題とは、様々な問題のうち「Yes か No かを判定する問題」のことです。素数判定問題や部分和問題は判定問題ですが、素因数分解問題や巡回セールスマン問題は判定問題ではありません。P や NP と言った場合には、そもそも判定問題についてのみ対象にしていることに注意が必要です。
さて、NP が P を含むことは明らかです (下図)。「P ≠ NP 問題」とは、NP が P より真に広いかどうかを決定する問題です。よくある誤解として以下のものがあります:
| 誤解 | 正しくは |
|---|---|
| NP とは Non-P の略である、すなわち多項式時間では解けない問題のクラスである | Non-deterministic Polynomial time の略であり、先述の通り NP は P を含みます |
| NP とは指数時間アルゴリズムで解ける問題のクラスである | そのようなクラスは EXP と言い、EXP は NP を含みます |
1 個目の誤解はアルゴリズム未修者にあるあるですが、2 個目の誤解はアルゴリズムを学んだ方にもあるあるです。NP に属するためには、解の正しさを多項式時間で検証できる必要があります。とはいえ、「多項式時間で解くことが難しい」と言われている有名な難しい問題のほとんどは NP に属します。具体例として部分和問題を考えると、(a[0], a[1], ..., a[n-1]) のうちの具体的な部分集合の総和が $A$ ですと言われたとき、それを確かめる作業は、実際に足し算するだけなので $O(n)$ で検証できます。
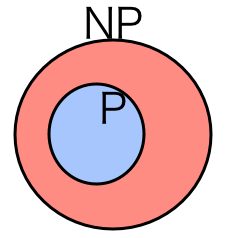
(「P≠NP予想の主張の解説」より引用)
さて、この赤い部分がつぶれてなくなってしまうかどうかが問題となっているわけですが、多くの専門家は赤い部分はつぶれないと信じています。つまり、部分和問題などは NP には属するが P には属さない問題として君臨していると考えられています。
「P ≠ NP 予想」の理解をさらに深めるには、「決定性アルゴリズム」「非決定性アルゴリズム」について理解するのがよいですが、
- Computers and Intractability: A Guide to the Theory of Np-Completeness
- 計算複雑性にまつわる 10の誤解 - 岡本吉央 - 電気通信大学
などを参考にしていただければと思います。
3-3. NP 完全問題
「P ≠ NP」だと広く信じられている理由の 1 つに、非常に多くの問題が「NP 完全問題」に属していることが示されたことが挙げられます。
NP 完全問題とは、ざっくり「NP に属する問題の中で最も難しい問題」のことです。部分和問題など、NP 完全問題に属している問題のうちの 1 つに対して万が一多項式時間アルゴリズムが開発できたならば、NP に属するすべての問題に対して多項式時間アルゴリズムが開発できることが示されています。
このように言うと NP 完全問題はあたかも「NP の中のごく一部の特にヤバい問題たち」というイメージを抱きそうになるのですが、実態はそれとは大きく異なります。驚くべきことに「多項式時間では解けそうもないな」と思われていた問題の多くが次から次へと NP 完全だと示されていったのです。部分和問題単体を見ると、なんか多項式時間で解けても不思議じゃないんじゃないか...という気分にもなるのですが、もし多項式時間で解けてしまったら、ハミルトンパス問題や、3-SAT 問題など、難しそうなありとあらゆる問題が多項式時間で解けることになるのです。そんなことはあり得そうもないな...というのが多くの専門家の感触になっています。
3-4. NP 困難問題
NP 困難問題というのは、NP 完全問題以上に難しい問題のことを指すのですが、実際上は
「判定問題ではないから NP 困難問題と呼ばれているものの、そこから自然に生まれる判定問題が NP 完全問題である」
というタイプの問題を指すことが多いです。自然に生まれるというのは「もし元の NP 困難問題が多項式時間で解けたならば、自然に生まれた NP 完全問題 (判定問題) も多項式時間で解けてしまう」ということを意味しています。標語的に言ってしまえば「多項式時間では解けないと広く信じられている問題のうち、判定問題は NP 完全問題で、それ以外は NP 困難問題」という雰囲気です。具体的には
- 巡回セールスマン問題は、判定問題ではないが、そこから自然に「ハミルトンパス問題」という NP 完全問題が生まれるので NP 困難問題である
- ナップサック問題は、判定問題ではないが、そこから自然に「部分和問題」という NP 完全問題が生まれるので NP 困難問題である
という感じです。なお NP 困難問題とは NP 完全以上に難しい問題のことですので、「NP にも属さないような非常に困難な判定問題」も定義上は含まれます (が、そのような問題に対して NP 困難と言及することはあまりないです)。
4. NP 完全問題や NP 困難問題の意義
NP 完全問題という概念が登場する前は、「この問題は多項式時間では解けそうもない」となったら、
- 自分の能力が低くて多項式時間アルゴリズムが開発できない
- 本当に誰がやっても多項式時間では解けそうもない
の切り分けが困難でした。しかし今や「多項式時間では解けそうもない」と思った問題に対しては NP 完全または NP 困難を示すという手段が使えるのです。挑んでいる問題の NP 完全性を示すということは「世界中のどんな天才たちが挑んでも多項式時間アルゴリズムが開発できそうもない」ということの状況証拠になるわけです!!!!!!
そんなわけで、20 世紀のアルゴリズム研究の歴史は、難しい問題たちを「多項式時間にできたやつ」と「NP 完全または NP 困難であることを証明したやつ」とに振り分ける作業が中心だったと言っても過言ではないでしょう。現在未解決問題と言われるものは
- 多項式時間アルゴリズムも見つかっていない
- NP 完全または NP 困難であることも証明できていない
という意味を表していることが多いです。このどちらかになることが示せれば、その問題について一旦の決着が得られたと言ってよいでしょう。もちろんそれで本当に研究が終わるわけではなく、多項式時間であることがわかったならば少しでもオーダーを小さくする高速化合戦が始まりますし、NP 困難であることがわかったならば、指数時間の中でもより高速なアルゴリズムの開発合戦が始まったり (「指数時間アルゴリズム入門」参照)、よりよい近似比をもつ近似アルゴリズム開発合戦が始まったりします。
5. NP 完全性や NP 困難性を示す実例
後日追記します
6. おわりに
arXiv などを見渡すと、結構な頻度で「P = NP が示せました」という論文を見かけます。3-SAT などの NP 完全に属する問題が多項式時間で解けたと主張しているわけですが、現在のところ正しいと認められたものは出て来ていないです。
アルゴリズムを本格的に学ぶまでは「NP 完全問題のどれか 1 つでも多項式時間アルゴリズムが開発できたら 100 万ドルなのか、夢がある」と思っていたときもありましたが、実際にアルゴリズムを開発しようとしていると、しばしば「あれ、このままだと P = NP になってしまう」という場面に出くわします。そんなときは「きっとどこか間違っている」と思えて修正できることが NP 完全理論の大きな利点の 1 つと言えるかもしれません。
