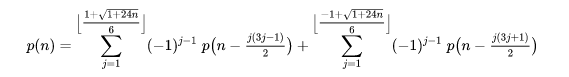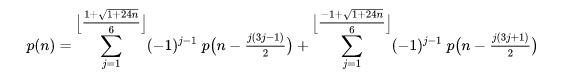0. はじめに: 「数え上げ」という分野について
「条件を満たすものを数え上げる」タイプの問題にはパズルのような楽しさがあります。そのような問題のうち簡単なものは高校数学の「個数の処理・確率」で学ぶのですが、その先にも奥深い世界が待っています。
- 例: 数え上げテクニック集 (DEGwer さん)
- 例: 数え上げおねえさん (ERATO 湊離散構造処理系プロジェクト)
本記事では数え上げ問題を解くと度々登場する「写像12相」について整理します。写像12相の中でも特に高度なスターリング数と分割数をメインに取り上げます。これらのテーマが直接的に登場する問題はあまり多くはないですが、包除原理や動的計画法といった技法を学べる格好の題材です。簡単な部分についても重複組合せなどの教育的要素を多く含んでいます。
そんな事情もあって、chokudai さんも「競プロで使う基礎的な数学は写像12相がわかればとりあえずオッケー」と言っています。写像12相を通して、周辺の数学を整理していきましょう。
1. 写像12相とは
1-1. 写像12相の概要
写像12相とは、一連の 12 個の数え上げ問題たちです。高校時代に誰もが学ぶ順列・組合せといった基礎的なものから、分割数・スターリング数といった高度なものまでを包含する統一的なフレームワークです。
【問題】
0 以上の整数 $n, k$ が与えられます。$n$ 個の玉を $k$ 個の箱に入れる方法は何通りあるでしょうか?
以下のように状況に応じて $12$ パターンあるので、$12$ 個の値を答えてください。
- $n$ 個の玉を互いに区別するかどうか
- $k$ 個の箱を互いに区別するかどうか
- 各箱に入る玉の個数は「1 個以内」「制限なし」「1 個以上」
写像12相をきちんと求めると以下の表のようになります。本記事でこれから 1 マスずつ解き明かして行きます。全体的に難しいのは「箱を区別しない場合」です。
- $S(n, k)$ は第二種スターリング数
- $B(n, k)$ はベル数
- $P(n, k)$ は分割数
| 玉 | 箱 | 1個以内 | 制限なし | 1個以上 |
|---|---|---|---|---|
| 区別する | 区別する | ${}_{k}{\mathrm P}_n$ | $k^n$ | 第 3 章:$\sum_{i=0}^{k} (-1)^{k-i} {}_{k}{\mathrm C}_i i^n$ |
| 区別しない | 区別する | $_{k}{\mathrm C}_n$ | ${}_{n+k-1}{\mathrm C}_{n}$ | ${}_{n-1}{\mathrm C}_{k-1}$ |
| 区別する | 区別しない | 0 or 1 | 第 5 章:$B(n, k)$ | 第 4 章:$S(n, k)$ |
| 区別しない | 区別しない | 0 or 1 | 第 6 章:$P(n, k)$ | 第 6 章:$P(n-k, k)$ |
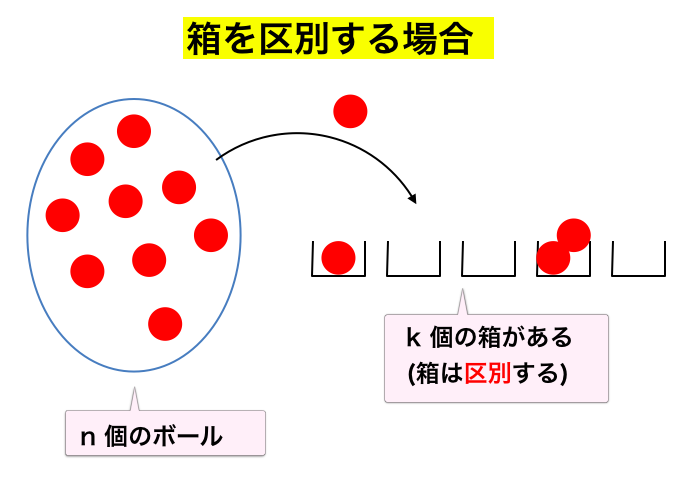
箱を区別するか、しないかによって、問題設定が大きく変わると言ってよいでしょう。箱を区別するときは、
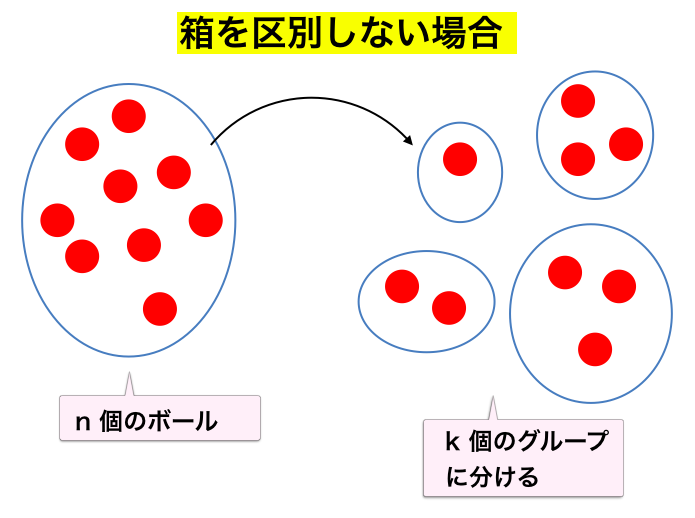
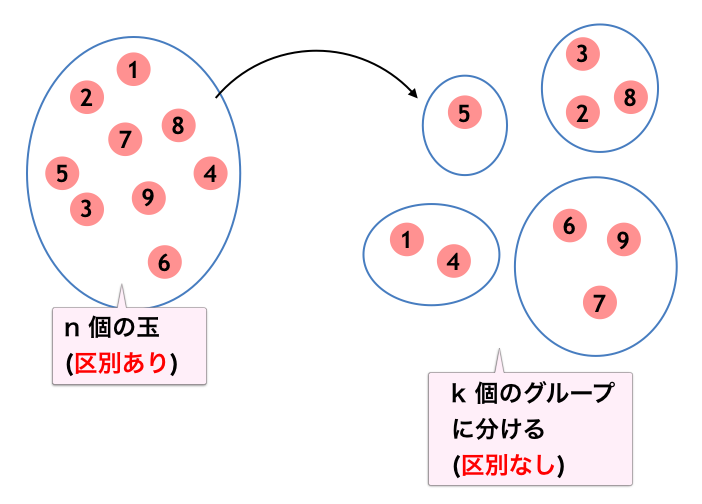
のようなイメージで問題を考えればよい1のですが、箱を区別しないということは要するに「$n$ 個のものを $k$ 個 (以下・ちょうど) のグループに分割する」というイメージの問題を考えていくことになります。
本記事のメインテーマであるスターリング数、分割数はどちらも箱を区別しない問題設定です。
1-2. n と k の大小関係
各箱に入れる玉の個数が「1個以内」「制限無し」「1個以上」に応じて、$n$ と $k$ の大小関係は次のようになります。「1個以内」の場合が比較的自然で考えやすいものになっています。「1個以上」の場合は全体的に難しめです。
| 制約 | $n$ と $k$ の大小関係 |
|---|---|
| 1 個以内 | $k \ge n$ となっていて、$k$ 個の箱の中から $n$ 個選択して玉を入れるような問題になります |
| 制限なし | $n$ の方が大きいことも $k$ の方が大きいこともあります |
| 1 個以上 | $n \ge k$ となっていて、どの箱にも玉が何個か入っている状態になります |
1-3. 写像12相の「写像」とは
$n$ 個の玉を $k$ 個の箱に入れる行為は、$n$ 個の玉それぞれについて $k$ 個の箱のいずれかに対応させる「写像」とみなせます。そう考えると、各箱に入る玉の個数の条件について、
- 1個以下: 写像が単射
- 1個以上: 写像が全射
と言い換えることができて見通しが良くなります。ただし写像12相の問題設定を写像だと思うことにそれほどのメリットはないようにも思います。
2. 簡単なマス
先に簡単なマスを片付けてしまおうと思います。玉を区別する場合の大部分を終わらせます。玉を区別する場合のうち、少し難しい「箱区別」「各箱に1個以上」の場合は第 3 章で紹介します。
| 玉 | 箱 | 1個以内 | 制限なし | 1個以上 |
|---|---|---|---|---|
| 区別する | 区別する | ${}_{k}{\mathrm P}_n$ | $k^n$ | 第 3 章:$\sum_{i=0}^{k} (-1)^{k-i} {}_{k}{\mathrm C}_i i^n$ |
| 区別しない | 区別する | $_{k}{\mathrm C}_n$ | 第 2-1 節:${}_{n+k-1}{\mathrm C}_{n}$ | 第 2-2 節:${}_{n-1}{\mathrm C}_{k-1}$ |
| 区別する | 区別しない | 0 or 1 | 第 5 章:$B(n, k)$ | 第 4 章:$S(n, k)$ |
| 区別しない | 区別しない | 0 or 1 | 第 6 章:$P(n, k)$ | 第 6 章:$P(n-k, k)$ |
まず表のうちの
- $n$ 個の玉を区別しない
- $k$ 個の箱を区別する
- 各箱に入る玉の個数は「1 個以内」 ($k \ge n$)
の場合は簡単です。つまり、$k$ 個の箱の中から、$n$ 個の玉が入る場所を選ぶ問題ので ${}_k{\mathrm C}_n$ 通りになります。$k$ と $n$ の記号の使い方に違和感がある方も多いかもしれない (${}_n{\mathrm C}_k$ の方が馴染みがある方が多そう) ですが、後にスターリング数や分割数について考えるときには、こちらの記号の使い方の方が自然になります。同様に
- $n$ 個の玉を区別する
- $k$ 個の箱を区別する
- 各箱に入る玉の個数は「1 個以内」 ($k \ge n$)
場合も簡単で、$k$ 個の箱の中から、$n$ 個の玉 (今度は玉を区別するので $1, 2, \dots, n$ のラベルがついているとみなせます) が入る場所を選定する問題です。玉は区別するので ${}_{k}{\mathrm P}_{n}$ 通りになります。さらに
- $n$ 個の玉を区別する
- $k$ 個の箱を区別する
- 各箱に入る玉の個数に制限はない
の場合も簡明で、各玉 ($n$ 個) について、どの箱 ($k$ 通りの選択肢) に入れるかを選ぶだけなので、$k^n$ 通りです。最後に
- $n$ 個の玉は区別してもしなくてもよい
- $k$ 個の箱を区別しない
- 各箱に入る玉の個数は「1 個以内」 ($k \ge n$)
の場合は少し考えると自明です。$k \ge n$ であれば、「ボール 1 個ずつからなる $n$ 個のグループ」と「ボール 0 個ずつからなる $k-n$ 個のグループ」とに分ける方法しかないので $1$ 通りです。ただし写像12相の流儀によっては「1 個以内」制約下であっても $k < n$ の場合も含めて考えることもあり、その場合は不可能なので 0 通りになります。
2-1. 「玉区別しない」「箱区別」「制限なし」
この場合は、AtCoder でも頻出の重複組合せです!!!!!
玉を区別しないということは、
- どの箱に何個のボールを入れるか
のみが重要だということです。つまり、箱 $1, 2, \dots, k$ に入れるボールの個数を $x_1, x_2, \dots, x_k$ とすると
- $x_1 + x_2 + \dots + x_k = n$
- $x_i$ は 0 以上の整数
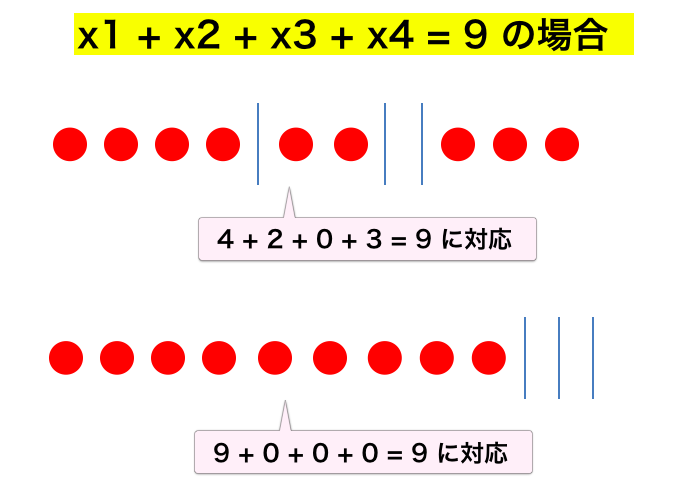
を満たす $(x_1, x_2, \dots, x_k)$ の組が何通りありますか?という問題になります。これは ${}_{k}{\rm H}_{n} = {}_{n+k-1}{\mathrm C}_{n}$ 通りです。考え方としては下図のように
- $x_1 + x_2 + \dots + x_k = n$ を満たす $(x_1, x_2, \dots, x_k$) の組
- $n$ 個の玉と、$k-1$ 個の仕切りの並び
とに一対一に対応させます。
そうすると一般に $a$ 個の玉と $b$ 個の仕切りを並べる方法の数は ${}_{a+b}{\rm C}_{a}$ 通りであることから2、答えは ${}_{n+k-1}{\mathrm C}_{n}$ 通りとなります。
重複組合せの例題
重複組合せは AtCoder でも頻出なので例題を挙げてみます:
- ABC 110 D - Factorization (とても教育的な良問でした)
- ABC 021 D - 多重ループ (重複組合せぴったりです)
- ARC 004 D - 表現の自由 (現代ではすっかり練習問題レベルになりましたね)
2-2. 「玉区別しない」「箱区別」「1個以上」
易しいマスのラストを飾る問題として、今度は 2-1 に「どの箱にも1個以上」という制約がついたバージョンを考えます。すなわち
- $x_1 + x_2 + \dots + x_k = n$
- $x_i$ は 1 以上の整数 (2-1 では 0 以上)
を満たす $(x_1, x_2, \dots, x_k)$ の組が何通りありますか?という問題です。二通りの考え方を紹介します:
- 2-1 の重複組合せに帰着
- 仕切りの考え方を変える
重複組合せに帰着
$x_i \ge 1$ とわかっているので、$y_i = x_i - 1$ とおくと
- $y_1 + y_2 + \dots + y_k = n - k$
- $y_i$ は 0 以上の整数
となります。これは重複組合せに帰着されていて、「$n-k$ 個の玉と $k-1$ 個の仕切りの並べ方」なので、${}_{n-1}{\mathrm C}_{k-1}$ 通りです。
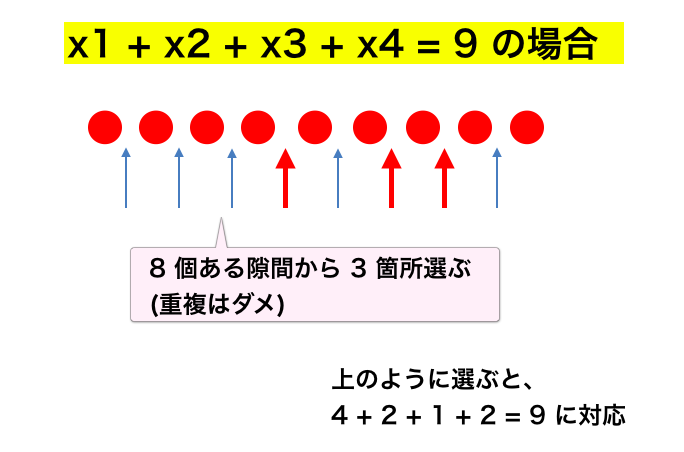
仕切りの考え方を変える
$x_1 + x_2 + \dots + x_k = n$ で $x_i \ge 0$ の場合は「$n$ 個の玉と $k-1$ 個の仕切りの並べ方」でしたが、$x_i \ge 1$ の場合は、
- $n$ 個の玉の隙間 $n-1$ 箇所から、$k-1$ 箇所選んで仕切りを入れる方法
と考えるとピッタリです。よって ${}_{n-1}{\mathrm C}_{k-1}$ 通りです。
3. 「箱を区別する場合」の残された難関
写像12相のうち、「箱を区別する場合」は全体的にやさしめですが、
- $n$ 個の玉を区別する
- $k$ 個の箱を区別する
- 各箱に入る玉の個数は「1 個以上」
の場合だけ少し難しいです。
| 玉 | 箱 | 1個以内 | 制限なし | 1個以上 |
|---|---|---|---|---|
| 区別する | 区別する | ${}_{k}{\mathrm P}_n$ | $k^n$ | 第 3 章:$\sum_{i=0}^{k} (-1)^{k-i} {}_{k}{\mathrm C}_i i^n$ |
| 区別しない | 区別する | $_{k}{\mathrm C}_n$ | 第 2-1 節:${}_{n+k-1}{\mathrm C}_{n}$ | 第 2-2 節:${}_{n-1}{\mathrm C}_{k-1}$ |
| 区別する | 区別しない | 0 or 1 | 第 5 章:$B(n, k)$ | 第 4 章:$S(n, k)$ |
| 区別しない | 区別しない | 0 or 1 | 第 6 章:$P(n, k)$ | 第 6 章:$P(n-k, k)$ |
包除原理に基づいてしっかり考察したいと思います。この考察は次章のスターリング数にも直結します。実際スターリング数は $k$ 個の箱の区別をなくすだけなので、上の場合の数が求まったら $k!$ で割るだけでよいです。
3-1. 包除原理
$n (\ge k)$ 個の玉を $k$ 個の箱にいれる方法は何も制限がなければ $k^n$ 通りです。これは簡単ですが、「各箱に入る玉の個数は 1 個以上」という制約がつくと一気に難しくなります。
慣れて来ると一目で包除原理を用いたくなります。包除原理とは以下のようなものです:
集合 $X$ があって、そのうち $k$ 個の条件があってそれぞれを満たす部分集合を $X_1, X_2, \dots, X_k$ とする。このとき、$k$ 個の条件のうちのいずれかを満たす要素の個数は
$|X_1 \cup X_2 \cup \dots \cup X_k|$
$= \sum_{p}|X_p| - \sum_{p<q}|X_p \cap X_q| + \sum_{p<q<r}|X_p \cap X_q \cap X_r| - \dots + (-1)^{k-1}|X_1 \cap X_2 \cap \dots \cap X_k|$
で与えられる。
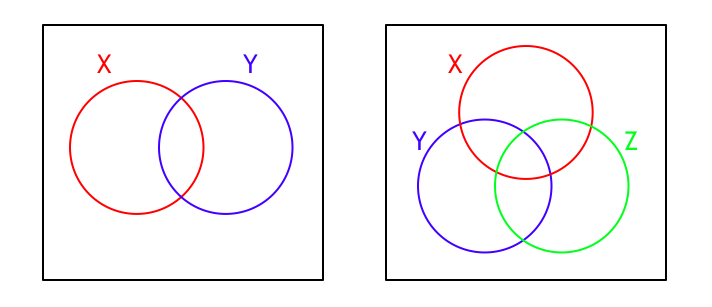
この式が何を表すのかは分かりづらいかもしれないですが、$k = 2, 3$ の場合は高校数学でもお馴染みだと思います。ベン図で表してやるやつです。例えば「$2$ か $3$ で割り切れる数は何通りか」という問題に対して
- 「$2$ で割れる個数」 + 「$3$ で割れる個数」 - 「$6$ で割れる個数」
と計算するのはお馴染みでしょう。
$|X \cup Y| = |X| + |Y| - |X \cap Y| $
$|X \cup Y \cup Z| = |X| + |Y| + |Z| - |X \cap Y| - |Y \cap Z| - |Z \cap X| + |X \cap Y \cap Z| $
これを $k$ 個に一般化すると上のような包除原理になります。お気持ちとしては
- 条件を 1 個ずつ満たすやつを足していったら、条件を 2 個同時に満たすやつをダブルカウントしてしまう (「$2$ で割れる個数」と「$3$ で割れる個数」をそのまま合計したら、どっちでも割れる数をダブルカウントしてしまう感じ)
- そこで条件を 2 個同時に満たすやつを引く...が、今度は 3 個同時に満たすやつを引き過ぎてしまう
- そこで条件を 3 個同時に満たすやつを足す...が、今度は 4 個同時に満たすやつを足し過ぎてしまう
- そこで条件を 4 個同時に満たすやつを引く...が、今度は 5 個同時に満たすやつを引き過ぎてしまう
と繰り返していくうちに最後に帳尻が合う仕組みになっています。ちゃんとした証明は以下の記事が参考になります:
包除原理は「または」の条件を「かつ」の条件の足し引きで表すテクニックと言えます。さて実際の問題設定では、「または」の条件を与えられることは少なくて、むしろ、「かつ」の条件だがそれを上手く扱えない場面が多いです。
例えば、今考えたい問題 ($n$ 個の玉を $k$ 個の箱に入れる方法のうち、どの箱も 1 個以上のボールが入っているものを数え上げる問題) もまさにそのケースで、
- 「1 個めの箱はボールが 1 個以上」かつ「2 個めの箱はボールが 1 個以上」かつ「3 個めの箱はボールが 1 個以上」 ...
という条件は扱いにくいです。そんなときに、この条件を全体集合から引いたもの (余事象) を代わりに求めることを考えると、
- 「1 個めの箱はボールが 0 個」または「2 個めの箱はボールが 0 個」または「3 個めの箱はボールが 0 個」または ...
と「または」で表される条件になり、しかも「〜個めの箱は 0 個」という条件は扱いやすく、包除原理がジャストフィットする形になります。以上のことを踏まえて扱いやすくした包除原理は以下のようになります:
集合 $X$ があって、そのうち $k$ 個の条件があってそれぞれを満たさない部分集合を $X_1, X_2, \dots, X_k$ とする (満たさないやつの方が数えやすい設定)。このとき、$k$ 個の条件をすべて満たす要素の個数は
$|X| - |X_1 \cup X_2 \cup \dots \cup X_k| $
$= |X| - \sum_{p}|X_p| + \sum_{p<q}|X_p \cap X_q| - \sum_{p<q<r}|X_p \cap X_q \cap X_r| + \dots + (-1)^{k}|X_1 \cap X_2 \cap \dots \cap X_k| $
で表される。
イメージ的に言えば、
(条件から 0 個選んで、それらを満たさないようにする場合の数) (これはつまり「全体集合」です)
- (条件から 1 個選んで、それらを満たさないようにする場合の数)
+ (条件から 2 個選んで、それらを満たさないようにする場合の数)
- (条件から 3 個選んで、それらを満たさないようにする場合の数)
+ (条件から 4 個選んで、それらを満たさないようにする場合の数)
- ...
を計算すればよいです。「2 の倍数でも 3 の倍数でも 5 の倍数でもないような整数の個数」を問う問題であれば
(全体)
- (2 の倍数の個数) - (3 の倍数の個数) - (5 の倍数の個数)
+ (6 の倍数の個数) + (15 の倍数の個数) + (10 の倍数の個数)
- (30 の倍数の個数)
です。注意点として、例えば上の (条件から 2 個選んで、それらを満たさないようにする場合の数) というのは、満たさないようにする条件を 2 個決めてしまえば、残りの条件については満たしても満たさなくてもよいです。つまり実際には 3 個以上の条件を満たさないような場合もまとめて数えていることになります。
3-2. 「箱を区別する場合」の最難マス
改めて写像12相のうち、
- $n$ 個の玉を区別する
- $k$ 個の箱を区別する
- 各箱に入る玉の個数は「1 個以上」
の場合を求めます。
$n$ 個の玉を $k$ 個の箱に入れる $k^n$ 通りの方法のうち、各箱 $1, 2, \dots, k$ について「玉が 1 個以上」という条件を満たすものを数え上げます。「玉が 1 個以上」という条件は扱いづらいので、包除原理によって、
(箱を 0 個選んで、それらを空にする場合の数)
- (箱を 1 個選んで、それらを空にする場合の数)
+ (箱を 2 個選んで、それらを空にする場合の数)
- (箱を 3 個選んで、それらを空にする場合の数)
+ (箱を 4 個選んで、それらを空にする場合の数)
- ...
を計算すればよいことがわかります。一般に $i$ について (箱を $i$ 個選んで、それらを空にする場合の数)を計算します。
- $k$ 個の箱から、空にする $i$ 個の箱を選ぶ方法の数は ${}_k{\rm C}_i$ 通り
- 空にする $i$ 個の箱を決めたとき、残りの箱については自由なので $n$ 個の玉それぞれについて残り $k-i$ 個の箱のどこに入れるかを選んで $(k-i)^n$ 通り
これらをまとめて、${}_k{\rm C}_{i} (k-i)^n$ 通りとなります。よって $k$ が奇数のときは引いて、$k$ が偶数のときは足せばよいので、
$$\sum_{i=0}^{k} (-1)^{i} {}_k{\rm C}_{i} (k-i)^n$$
通りとなります。この表式でもいいのですが、実際は $i$ を $k-i$ に変換して
$$\sum_{i=0}^{k} (-1)^{k-i} {}_k{\rm C}_{i} i^n ({}_{k}{\rm C}_{k-i}={}_{k}{\rm C}_{i} を用いた)$$
という表式を用いることが多いです。これで無事に求まりました。箱を区別する場合についてはコンプリートです!この場合の数を求める実装については、以下の記事に示しました。上の式を愚直に計算していますが、各 $i$ について $i^n$ の計算に $O(\log{n})$ の計算時間がかかるので、全体として $O(k\log{n})$ の計算量となっています。
3-3. 包除原理のさらなる応用
今回は包除原理を用いて、
- $n$ 個の玉を区別する
- $k$ 個の箱を区別する
- 各箱に入る玉の個数は「1 個以上」
という場合の答えを導きました。包除原理にはまだまだ深淵な応用の世界が広がっています。その世界を見て行きたい方は是非、つたじぇー⭐︎さんの書いたスライドを読んでみましょう:
4. スターリング数
いよいよメインコンテンツの 1 つであるスターリング数を扱います。スターリング数は
- $n$ 個の玉を区別する
- $k$ 個の箱を区別しない
- 各箱に入る玉の個数は「1 個以上」
という場合です。
| 玉 | 箱 | 1個以内 | 制限なし | 1個以上 |
|---|---|---|---|---|
| 区別する | 区別する | ${}_{k}{\mathrm P}_n$ | $k^n$ | 第 3 章:$\sum_{i=0}^{k} (-1)^{k-i} {}_{k}{\mathrm C}_i i^n$ |
| 区別しない | 区別する | $_{k}{\mathrm C}_n$ | 第 2-1 節:${}_{n+k-1}{\mathrm C}_{n}$ | 第 2-2 節:${}_{n-1}{\mathrm C}_{k-1}$ |
| 区別する | 区別しない | 0 or 1 | 第 5 章:$B(n, k)$ | 第 4 章:$S(n, k)$ |
| 区別しない | 区別しない | 0 or 1 | 第 6 章:$P(n, k)$ | 第 6 章:$P(n-k, k)$ |
以下のようなイメージです。各グループにつき 1 個以上の玉を入れるということはすなわち、$n$ 個の玉全体をちょうど $k$ 個のグループにわけるということです (「制限なし」バージョンは $k$ 個以下のグループにわける方法ということになります)。
ここでは、スターリング数を二通りの求め方で求めます
- 3 章で求めたものを $k!$ で割るだけ
- 漸化式
特に漸化式を用いた方法は応用が効くので是非ともマスターして応用を効かせたいところです。
4-1. 3 章で求めたものを k! で割る
実はスターリング数はすでにほとんど求められていて、3 章でやった
- $n$ 個の玉を区別する
- $k$ 個の箱を区別する
- 各箱に入る玉の個数は「1 個以上」
に対して箱の区別をなくすだけです。つまり $k!$ で割ればよいです。よって答えは
$$S(n, k) = \frac{1}{k!} \sum_{i=0}^{k} (-1)^{k-i} {}_k{\rm C}_{i} i^n$$
となります。アッサリと求められました。$i^n$ の計算に $O(\log{n})$ の計算時間がかかることを考慮して、全体として $O(k\log{n})$ の計算量となります。
4-2. スターリング数を漸化式で求める
次にスターリング数を漸化式 (動的計画法) で計算する方法です。
- $S(n, k) = S(n-1, k-1) + k S(n-1, k)$
という関係式が成立します。これは二項係数における
- ${}_{n}{\rm C}_{k} = {}_{n-1}{\rm C}_{k-1} + {}_{n-1}{\rm C}_{k}$
という式に対応しています。証明も簡単で、$n$ 個の玉 $1, 2, \dots, n$ のうち、特に玉 1 の挙動について以下のような場合分けをします;
- 玉 1 が単独で 1 個だけでグループを形成するとき: 残り $n-1$ 個について $k-1$ グループに分ける方法は $S(n-1, k-1)$ 通り。
- 玉 1 が単独でない場合は、まず 1 以外の $n-1$ 個について $k$ グループに分ける方法が $S(n-1, k)$ 通りあって、その $k$ グループのうち 1 つ選んで 1 を放り込めばよいので、$k S(n-1, k)$ 通り。
以上から合計して、$S(n, k) = S(n-1, k-1) + k S(n-1, k)$ が成立します。この漸化式を用いると、$0 \le i \le n$, $0 \le j \le k$ を満たすすべての $i, j$ についての $S(i, j)$ を $O(nk)$ の計算時間で求めることができます。
応用
この漸化式を用いたスターリング数の求め方の良さとして、似たような対象を数えることに応用が広がることが挙げられます。例を挙げてみます。
各グループにつき r 個以上の場合
スターリング数は各グループにつき「1 個以上」という制約でしたが、各グループにつき「$r$ 個以上」とした場合を $S'(n, k)$ 通りとしても、同様の漸化式を立てることができます。
- 玉 1 が $r$ 個しかないグループに入るとき、玉 1 以外の同グループメンバーを選ぶ方法が ${}_{n-1}{\rm C}_{r-1}$ 通りあって、残りの $n-r$ 個を $k-1$ グループに分ければよいので、${}_{n-1}{\rm C}_{r-1} S'(n-r, k-1)$ 通り。
- 玉 1 が $r$ 個より多いグループに入るとき、まったく同様にして $k S(n-1, k)$ 通り。
これらをまとめて、$S'(n, k) = {}_{n-1}{\rm C}_{r-1} S'(n-r, k-1) + k S'(n-1, k)$ となります。
n 個のうち、何個かを選んで k グループに分ける場合
次に $n$ 個すべてがグループに属する必要はなくて、何個か選んで $k$ グループ作る問題を考えます。$S'(n, k)$ 通りとして、
- 玉 1 が使われないとき:$S'(n−1, k)$ 通り
- 玉 1 が単独で使われるとき: $S'(n−1, k−1)$ 通り
- 玉 1 が単独でなく使われるとき:$k S'(n−1, k)$ 通り
となるので、$S'(n, k) = S'(n−1, k−1) + (k + 1) S'(n−1, k)$ となります。実はこの計算を要求する問題として
があります。
4-3. 第一種スターリング数
これまで見て来たスターリング数は、より正確には第二種スターリング数と呼ばれるものです。第一種スターリング数もあります。そもそも第二種スターリング数と等価な定義として、$(x)_{n} = x(x-1)\dots(x-n+1)$ として
- $x^{n} = \sum_{k = 0}^{n} S(n, k)(x)_{k}$
という恒等式が挙げられます。$(x)_{n}$ は順列 ${}_{x}{\rm P}_{n}$ を $x$ についての関数とみなしたものになっています。この式は、$x$ が正の整数の場合には、$n$ 個のものを $x$ 色用いて塗る $x^n$ 通りの方法のうち、ちょうど $k$ 色が使われるような方法が $S(n, k)(x)_{k}$ 通りであることから自然に導けます (一般に恒等式になってることもすぐに言えます)。
第一種スターリング数 $s(n, k)$ は、逆に
- $(x)_{n} = \sum_{k = 0}^{n} (-1)^{n-k} s(n, k) x^{k}$
あるいは $[x]_{n} = x(x+1) \dots (x+n-1)$ として
- $[x]_{n} = \sum_{k = 0}^{n} s(n, k) x^{k}$
という恒等式を満たすようなものとして定義されます。第二種スターリング数が $x^{n}$ を $(x)_{k}$ で表すときの係数であったのに対し、第一種スターリング数は $(x)_{n}$ を $x^{k}$ で表すときの係数であるということで、ちょうど対称な関係になっています。さて、第一種スターリング数の組合せ論的意味付けは少しわかりづらいですが、「$n$ 個の要素に関する置換 (順列) のうち、$k$ 個の巡回に分解されるようなものの個数」を表しています。
4-4. スターリング数についての tips
二項係数の多数の関係式があるのと同様、スターリング数にも様々な関係式があります。その多くは二項係数についての関係式とアナロジーのあるものになっています。興味のある方は、英語版 wikipedia や、MathWorld に詳しいです。
5. ベル数
次にスターリング数との関係性が深いベル数です。ベル数は
- $n$ 個の玉を区別する
- $k$ 個の箱を区別しない
- 各箱に入る玉の個数に制限はない (ここがスターリング数と異なる)
という場合です。
| 玉 | 箱 | 1個以内 | 制限なし | 1個以上 |
|---|---|---|---|---|
| 区別する | 区別する | ${}_{k}{\mathrm P}_n$ | $k^n$ | 第 3 章:$\sum_{i=0}^{k} (-1)^{k-i} {}_{k}{\mathrm C}_i i^n$ |
| 区別しない | 区別する | $_{k}{\mathrm C}_n$ | 第 2-1 節:${}_{n+k-1}{\mathrm C}_{n}$ | 第 2-2 節:${}_{n-1}{\mathrm C}_{k-1}$ |
| 区別する | 区別しない | 0 or 1 | 第 5 章:$B(n, k)$ | 第 4 章:$S(n, k)$ |
| 区別しない | 区別しない | 0 or 1 | 第 6 章:$P(n, k)$ | 第 6 章:$P(n-k, k)$ |
さて、ベル数はスターリング数との関係性がとても深いです。スターリング数は各箱に入る玉の個数は 1 個以上であったのに対し、ベル数にはそのような制限がありません。これはつまり「$n$ 個の玉全体を $k$ 個以下のグループにわける方法」であるということができます。したがって
- $B(n, k) = S(n, 0) + S(n, 1) + \dots + S(n, k)$
という関係が成り立っています。これを議論の出発点にして、ベル数を効率良く計算する方法を模索します。
5-1. ベル数を直接計算する方法: O(min(n, k) log n)
上の式を変形していくと
$B(n, k)$
$= \sum_{j = 0}^{k} S(n, j)$
$= \sum_{j = 0}^{k} \frac{1}{j!} \sum_{i = 0}^{j} (-1)^{j-i} {}_{j}{\rm C}_{i} i^{n}$
$= \sum_{j = 0}^{k} \sum_{i = 0}^{j} \frac{(-1)^{j-i}}{i!(j-i)!} i^{n}$
$= \sum_{i = 0}^{k} \sum_{j = i}^{k} \frac{(-1)^{j-i}}{i!(j-i)!} i^{n}$ (ここの $\sum$ の入替はわかりづらいかもしれません)
$= \sum_{i = 0}^{k} \sum_{j = 0}^{k-i} \frac{(-1)^{j}}{i! j!} i^{n}$ ($j' = j-i$ と変数変換して $j'$ を $j$ に置き換えます)
$= \sum_{i = 0}^{k} \frac{i^n}{i!} \sum_{j = 0}^{k-i} \frac{(-1)^j}{j!}$
となります。このうちの $\sum_{j = 0}^{k-i} \frac{(-1)^j}{j!}$ については前処理で予め計算しておくことができて、そうするとベル数 $B(n, k)$ を $O(k)$ 個の足し算で計算することができます。$i^n$ の計算に $O(\log{n})$ の計算時間が必要なので全体として $O(\min(n, k)\log{n})$ の計算量となります3。スターリング数の直接計算と同等の計算量です。
5-2. ベル数の漸化式: O(n^2)
ベル数として特に $B(n, n)$ の形のものを改めて $B(n)$ とおいてベル数と呼ぶことも多いです。すなわち $B(n)$ は「$n$ 個の要素を何個かのグループに分ける方法の数」ということになります。$B(n)$ について以下の漸化式が有名です:
- $B(n+1) = \sum_{i = 0}^{n} {}_{n}{\rm C}_{i} B(i)$
これは $O(n^2)$ の計算量で求められます。証明も簡単で、$1, 2, \dots, n$ のうち、要素 $n+1$ と同じグループにならない要素の個数を $i = 0, 1, \dots, n$ とするとその選び方は ${}_{n}{\rm C}_{i}$ 通りあって (それ以外は $n+1$ と一緒になります)、その $i$ 要素のグループ分け方法が $B(i)$ 通りあることから導けます。
5-3. ベル数についての tips
ベル数についても、英語版 wikipedia や、MathWorld に詳しいです。
6. 分割数
最後に残るは分割数です。分割数 $P(n, k)$ を
- $n$ 個の玉を区別しない (ここがベル数と異なる)
- $k$ 個の箱を区別しない
- 各箱に入る玉の個数に制限はない
場合の数として定義します。このとき、各箱に入る玉の個数が 1 個以上の場合についても簡単で、各箱の玉を 1 個ずつ減らせば制限なしの場合に帰着するので $P(n-k, k)$ 通りとなります。よって $P(n, k)$ を基本に考えていきます。
| 玉 | 箱 | 1個以内 | 制限なし | 1個以上 |
|---|---|---|---|---|
| 区別する | 区別する | ${}_{k}{\mathrm P}_n$ | $k^n$ | 第 3 章:$\sum_{i=0}^{k} (-1)^{k-i} {}_{k}{\mathrm C}_i i^n$ |
| 区別しない | 区別する | $_{k}{\mathrm C}_n$ | 第 2-1 節:${}_{n+k-1}{\mathrm C}_{n}$ | 第 2-2 節:${}_{n-1}{\mathrm C}_{k-1}$ |
| 区別する | 区別しない | 0 or 1 | 第 5 章:$B(n, k)$ | 第 4 章:$S(n, k)$ |
| 区別しない | 区別しない | 0 or 1 | 第 6 章:$P(n, k)$ | 第 6 章:$P(n-k, k)$ |
さて、分割数 $P(n, k)$ とは要するに「自然数 $n$ を $k$ 個の 0 以上の整数の和で表す方法の数」です。順序が異なるものは同一視します。例えば $n = 5, k = 3$ であれば、
- $0 + 0 + 5 = 0 + 1 + 4 = 0 + 2 + 3 = 1 + 1 + 3 = 1 + 2 + 2$
の 5 通りの表し方があります。よって $P(5, 3) = 5$ です。なお、上の式で 0 のところを取り除いて考えると、$P(n, k)$ は「自然数 $n$ を $k$ 個以下の 1 以上の整数の和で表す場合の数」とも言い換えられます (蟻本の P. 66 に載っている問題はこれで定義しています)。
6-1. 分割数 P(n, k) を計算する漸化式: O(nk)
分割数については、スターリング数やベル数のような、直接計算する表式が知られていません。専ら漸化式によって計算することになります。分割数の漸化式は
- $P(n, k) = P(n, k-1) + P(n-k, k)$
と表せます。証明は簡単です。$n$ を $k$ 個の 0 以上の整数の和として表す方法のうち、
-
分解に 0 を含むものについては、そのうちのどれかの 0 を取り除いてしまうことで、$n$ を $k-1$ 個の 0 以上の整数の和として表す方法に帰着される。よって、$P(n, k-1)$ 通り。
-
分解に 0 を含まない場合は、$k$ 個の整数がすべて 1 以上なので、それぞれ 1 を引くことで $n-k$ を $k$ 個の 0 以上の整数の和として表す方法に帰着される。よって、$P(n-k, k)$ 通り。
以上から示されました。この漸化式を用いることで $O(nk)$ で計算できます。
応用例: n を k 個の 0 以上 m 以下の整数の和に分割する方法の数
スターリング数の漸化式が様々な応用があったのと同様、分割数の漸化式も色々と応用の余地が考えられます。例えば分割数 $P(n, k)$ は $n$ を $k$ 個の 0 以上の整数の和に分割する方法の数でしたが、分割される各整数に $m$ 以下という制約を課してみましょう。このときの分割する方法の数を $P'(n, k)$ と表すことにします。
-
分割に 0 を含むとき、通常の分割数とまったく同様に、$P'(n, k-1)$ 通り。
-
分割に 0 を含まないとき、以下のようになります:
($n$ を $k$ 個の 1 以上 $m$ 以下の整数に分割する場合の数)
= ($n-k$ を $k$ 個の 0 以上 $m-1$ 以下の整数に分割する場合の数)
= ($n-k$ を $k$ 個の 0 以上 $m$ 以下の整数の分割する場合の数) - (そのうち $m$ を含む場合の数)
この (そのうち $m$ を含む場合の数) は $m$ を 1 個取り除いてしまっても一緒なので $P'(n-k-m, k-1)$ 通りです。以上をまとめると、
- $P'(n, k) = P'(n, k-1) + P'(n-k, k) - P'(n-k-m, k-1)$
となります。このことを利用すると想定解法よりも高速に解ける例題として
があります。このことは怒髪さんによって指摘されました。
6-2. 分割数 P(n) を計算する漸化式: O(n√n)
分割数として特に $P(n, n)$ の形のものを改めて $P(n)$ とおいて分割数と呼ぶことも多いです。すなわち $P(n)$ は「$n$ 個の要素を何個かの整数の和として表す方法の数」ということになります。上の漸化式を用いた方法では $P(n)$ を計算するのに $O(n^2)$ の計算量がかかるのですが、$P(n)$ の計算を $O(n\sqrt{n})$ で済ませてしまう方法もあります。下のような漸化式を用います (OEIS に載っています)。
もう少し直感的な方法として、DEGwer さんによって導かれた方法もあります。
7. 実装
ここまで導いたスターリング数 $S(n, k)$、ベル数 $B(n, k)$、分割数 $P(n, k)$ について実装していきます。ただしいずれも値が大きくなるので素数 MOD (競プロでは MOD = $1000000007$ とすることが多い) で割ったあまりで示します。ここで
を用いています。
7-1. スターリング数の実装
まずはスターリング数です。
7-1-1. スターリング数の直接計算
スターリング数の表式 $S(n, k) = \frac{1}{k!} \sum_{i=0}^{i=k} (-1)^{k-i} {}_k{\rm C}_{i} i^n$ をそのまま実装します。$O(K\log{N})$ の計算量となります。
# include <iostream>
# include <vector>
using namespace std;
// 素数 p で割ったあまりに関する構造体 (特に p = 1000000007 とすることが多い)
template<int MOD> struct Fp {
long long val;
constexpr Fp(long long v = 0) noexcept : val(v % MOD) {
if (val < 0) v += MOD;
}
constexpr int getmod() { return MOD; }
constexpr Fp operator - () const noexcept {
return val ? MOD - val : 0;
}
constexpr Fp operator + (const Fp& r) const noexcept { return Fp(*this) += r; }
constexpr Fp operator - (const Fp& r) const noexcept { return Fp(*this) -= r; }
constexpr Fp operator * (const Fp& r) const noexcept { return Fp(*this) *= r; }
constexpr Fp operator / (const Fp& r) const noexcept { return Fp(*this) /= r; }
constexpr Fp& operator += (const Fp& r) noexcept {
val += r.val;
if (val >= MOD) val -= MOD;
return *this;
}
constexpr Fp& operator -= (const Fp& r) noexcept {
val -= r.val;
if (val < 0) val += MOD;
return *this;
}
constexpr Fp& operator *= (const Fp& r) noexcept {
val = val * r.val % MOD;
return *this;
}
constexpr Fp& operator /= (const Fp& r) noexcept {
long long a = r.val, b = MOD, u = 1, v = 0;
while (b) {
long long t = a / b;
a -= t * b; swap(a, b);
u -= t * v; swap(u, v);
}
val = val * u % MOD;
if (val < 0) val += MOD;
return *this;
}
constexpr bool operator == (const Fp& r) const noexcept {
return this->val == r.val;
}
constexpr bool operator != (const Fp& r) const noexcept {
return this->val != r.val;
}
friend constexpr ostream& operator << (ostream &os, const Fp<MOD>& x) noexcept {
return os << x.val;
}
friend constexpr istream& operator >> (istream &is, Fp<MOD>& x) noexcept {
return is >> x.val;
}
friend constexpr Fp<MOD> modpow(const Fp<MOD> &a, long long n) noexcept {
if (n == 0) return 1;
auto t = modpow(a, n / 2);
t = t * t;
if (n & 1) t = t * a;
return t;
}
};
// 二項係数ライブラリ
template<class T> struct BiCoef {
vector<T> fact_, inv_, finv_;
constexpr BiCoef(int n) noexcept : fact_(n, 1), inv_(n, 1), finv_(n, 1) {
int MOD = fact_[0].getmod();
for(int i = 2; i < n; i++){
fact_[i] = fact_[i-1] * i;
inv_[i] = -inv_[MOD%i] * (MOD/i);
finv_[i] = finv_[i-1] * inv_[i];
}
}
constexpr T com(int n, int k) const noexcept {
if (n < k || n < 0 || k < 0) return 0;
return fact_[n] * finv_[k] * finv_[n-k];
}
constexpr T fact(int n) const noexcept {
if (n < 0) return 0;
return fact_[n];
}
constexpr T inv(int n) const noexcept {
if (n < 0) return 0;
return inv_[n];
}
constexpr T finv(int n) const noexcept {
if (n < 0) return 0;
return finv_[n];
}
};
int main() {
// 1000000007 で割ったあまりのクラス
using mint = Fp<1000000007>;
// 二項係数計算の前処理 (nCk, n, k < 101010 について O(1) でとれるようにする)
BiCoef<mint> bc(101010);
// スターリング数
int n, k;
cin >> n >> k;
mint res = 0;
for (int i = 0; i <= k; ++i) {
mint add = bc.com(k, i) * modpow(mint(i), n);
if ((k-i) % 2 == 0) res += add;
else res -= add;
}
// k! で割る
res *= bc.finv(k); // finv(k) = 1/k!
cout << res << endl;
}
7-1-2. スターリング数の漸化式計算
漸化式 $S(n, k) = S(n-1, k-1) + k S(n-1, k)$ による方法です。$O(nk)$ かかりますが、$0 \le i \le n$, $0 \le j \le k$ に対して $S(i, j)$ がすべて求まります。なおここから modint 構造体ライブラリ・二項係数ライブラリの実装は省略します。
# include <iostream>
# include <vector>
using namespace std;
// スターリング数 (n 個を k グループにわける、n >= k)
template<class T> struct Stirling {
vector<vector<T> > S;
constexpr Stirling(int MAX) noexcept : S(MAX, vector<T>(MAX, 0)) {
S[0][0] = 1;
for (int n = 1; n < MAX; ++n) {
for (int k = 1; k <= n; ++k) {
S[n][k] = S[n-1][k-1] + S[n-1][k] * k;
}
}
}
constexpr T get(int n, int k) {
if (n < 0 || k < 0 || n < k) return 0;
return S[n][k];
}
};
int main() {
// 1000000007 で割ったあまりのクラス
using mint = Fp<1000000007>;
// スターリング数
Stirling<mint> sl(3100); // S(n, k) を n, k < 3100 の範囲で求める
// スターリング数
int n, k;
cin >> n >> k;
cout << sl.get(n, k) << endl;
}
7-2. ベル数の実装
次にベル数です。
7-2-1. ベル数の直接計算
ベル数の表式
$B(n, k) = \sum_{i = 0}^{k} \frac{i^n}{i!} \sum_{j = 0}^{k-i} \frac{(-1)^j}{j!}$
をそのまま実装します。一旦 $\sum_{j = 0}^{k-i} \frac{(-1)^j}{j!}$ の部分を累積和を用いて前処理しておきます。これによって $O(\min(n, k)\log{n})$ の計算量となります。
# include <iostream>
# include <vector>
using namespace std;
// modint
using mint = Fp<1000000007>;
BiCoef<mint> bc(5100); // 二項係数計算
// ベル数
mint Bell(int n, int k) {
if (k > n) k = n;
vector<mint> jsum(k+2, 0);
for (int j = 0; j <= k; ++j) {
mint add = bc.finv(j);
if (j % 2 == 0) jsum[j+1] = jsum[j] + add;
else jsum[j+1] = jsum[j] - add;
}
mint res = 0;
for (int i = 0; i <= k; ++i) {
res += modpow(mint(i), n) * bc.finv(i) * jsum[k-i+1];
}
return res;
}
int main() {
int n, k; cin >> n >> k;
cout << Bell(n, k) << endl;
}
7-2-2. ベル数の漸化式計算
一般的なベル数 $B(n, k)$ については
- $B(n, k) = S(n, 0) + S(n, 1) + \dots + S(n, k)$
を利用すれば、$S(n, k)$ と同様に累積和計算によって $O(nk)$ の計算量でテーブルを用意することができます。一方 $B(n) = B(n, n)$ についてはより簡潔な
- $B(n+1) = \sum_{i = 0}^{n} {}_{n}{\rm C}_{i} B(i)$
という関係式を有効に用いることができます。Codeforces 315 DIV1 B. Symmetric and Transitive がちょうどそれを試せる問題だったので、その問題に対する実装を載せます。
# include <iostream>
# include <vector>
using namespace std;
int main() {
// 1000000007 で割ったあまりのクラス
const int MAX = 5000;
using mint = Fp<1000000007>;
BiCoef<mint> bc(MAX);
// ベル数
vector<mint> Bell(MAX+1, 0);
Bell[0] = 1;
for (int n = 0; n < MAX; ++n) {
for (int i = 0; i <= n; ++i) {
Bell[n+1] += bc.com(n, i) * Bell[i];
}
}
// 答え
int N; cin >> N;
mint res = 0;
for (int M = 0; M < N; ++M) res += bc.com(N, M) * Bell[M];
cout << res << endl;
}
7-3. 分割数の実装
ラストは分割数です。
7-3-1. 分割数 P(n, k) の漸化式計算 O(nk)
分割数 $P(n, k)$ の漸化式
- $P(n, k) = P(n, k-1) + P(n-k, k)$
に基づく実装です。
# include <iostream>
# include <vector>
using namespace std;
// 分割数
template<class T> struct Partition {
vector<vector<T> > P;
constexpr Partition(int MAX) noexcept : P(MAX, vector<T>(MAX, 0)) {
for (int k = 0; k < MAX; ++k) P[0][k] = 1;
for (int n = 1; n < MAX; ++n) {
for (int k = 1; k < MAX; ++k) {
P[n][k] = P[n][k-1] + (n-k >= 0 ? P[n-k][k] : 0);
}
}
}
constexpr T get(int n, int k) {
if (n < 0 || k < 0) return 0;
return P[n][k];
}
};
int main() {
using mint = Fp<1000000007>;
Partition<mint> pt(5100);
int n, k; cin >> n >> k;
cout << pt.get(n, k) << endl;
}
7-3-2. 分割数 P(n) の漸化式計算 O(n√n)
最後に、分割数 $P(n)$ を以下の漸化式に基づいて $O(n\sqrt{n})$ で計算します。
# include <iostream>
# include <vector>
using namespace std;
// 分割数
template<class T> struct PartitionSqrt {
vector<T> P;
constexpr PartitionSqrt(int MAX) noexcept : P(MAX, 0) {
P[0] = 1;
for (int i = 1; i < 100; ++i) {
for (int j = 1, sign = 1; i-(j*j*3-j)/2 >= 0; ++j, sign *= -1) {
P[i] += P[i-(j*j*3-j)/2] * sign;
if (i-(j*j*3+j)/2 >= 0) P[i] += P[i-(j*j*3+j)/2] * sign;
}
}
}
constexpr T get(int n) {
if (n < 0) return 0;
return P[n];
}
};
int main() {
using mint = Fp<1000000007>;
Partition<mint> pt(5100);
PartitionSqrt<mint> pts(5100);
for (int n = 1; n < 100; ++n) {
cout << n << ": " << pt.get(n, n) << ", " << pts.get(n) << endl;
}
}
8. 問題集
写像12相に関する問題集です。
8-1. 基本的な実装を試す問題
AOJ Course Library of Discrete Optimization Problems にて、写像12相の各マスそれぞれについて計算する問題が一通り揃っています。
8-2. 重複組合せ
写像12相の中では比較的易しめのマスですが、重複組合せに関する問題は数多いです。
- AtCoder ABC 110 D - Factorization (とても教育的な良問でした)
- AtCoder ABC 021 D - 多重ループ (重複組合せぴったりです)
- AtCoder ARC 004 D - 表現の自由 (現代ではすっかり練習問題レベルになりましたね)
8-3. スターリング数
スターリング数を計算することが自明な問題から、スターリング数に関連した類似の漸化式を導く問題まで。
- yukicoder No.391 CODING WAR (3 章のテーマそのものです)
- yukicoder No.140 みんなで旅行 (スターリング数がいい感じに出てきます)
- AtCoder ARC 096 E - Everything on It (スターリング数と類似の漸化式を導きます)
- TopCoder SRM 686 Div1 Medium CyclesNumber (第一種スターリング数も登場して難しいです)
8-4. ベル数
続いてベル数です。
- Codeforces #315 Div1 B. Symmetric and Transitive (ベル数がいい感じに出てきます)
- Codeforces Good Bye 2017: E. New Year and Entity Enumeration (ベル数が関係しています)
- TopCoder IIT Roorkee Cognizance DIV1 Hard - StrangeColoring (ベル数の高速計算が要求されます)
- ねねジャッジ 0014 ベル数 (リンク復活して...)
8-5. 分割数
最後に分割数です。やはり分割数を用いることが自明な問題から、分割数に関連した類似の漸化式を導く問題まで。
- yukicoder No.269 見栄っ張りの募金活動 (いい感じの分割数です)
- 第4回 ドワンゴからの挑戦状 予選 C - Kill/Death (分割数を前処理として計算します)
- AOJ 0537 Bingo (分割数と類似の漸化式によって、想定解よりも高速な解法が導けます)
- CSA 032 G Sum of Powers (かなり難しいです)
9. おわりに
スターリング数や分割数そのものが登場する問題はそれほど多いわけではないですが、その考え方を応用できる問題となるとグッと広がる印象があります。写像12相を通して、数え上げの楽しさの一端を感じていただけたら嬉しいです。