0. はじめに
最近では AtCoder がコーディング面接の文脈でも有効なものとしての認識が広まってきています。AtCoder の登竜門といわれる水色を目指すにあたって多くの方が「勉強した」と報告している代表的なアルゴリズム的手法の一つに累積和があります。
今回はそんな累積和をストレスなく機械的に書けるようになることを目標とします。累積和は、そのコンセプト自体は簡明で決して難しくないのですが、
- 添字の扱い方など、頭がゴッチャになりがちである
- 応用範囲が非常に広い
ということから、整理する価値の高い手法です。僕自身、累積和を用いる問題に対して、毎回添字の扱いに神経を尖らせながら頑張っていたのですが、一度実装テンプレートを決め込んでしまえば何も考えなくても書けるようになりました。そうなってからは累積和を実装することにストレスが無くなりました。
そんな体験を共有できたらと思います。
1. 累積和でできること
累積和とは、一言で言えば
適切な前処理をしておくことで、配列上の区間の総和を求めるクエリを爆速で処理できるようになる手法
です。世の中には「データから所望の範囲に関する合計値を出力させるクエリ」が何度も何度も飛んで来る場面に溢れています。例えば
- 昨年 8 月から今年 5 月までの売り上げ高の合計を教えて欲しい
- ある書籍の 114 ページから 514 ページまでの間に「アルゴリズム」という単語が何回登場したのかを教えて欲しい
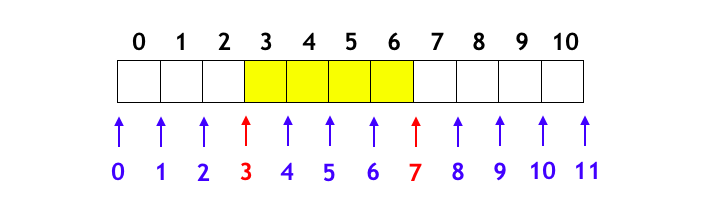
といったクエリが大量に飛んで来る場面が挙げられます。より抽象的には、長さ $N$ の配列があって、下図のように「配列中の範囲が指定されて、その範囲にある値の総和を知りたい」というクエリが大量に飛んで来る場面を考えます。$N$ のサイズ感としては $N = 300,000$ 程度を想定しています1。
ナイーブには範囲の合計を素直に計算すればクエリに答えることができます。例えば配列を a (int 型) として、範囲 [left, right) の総和を知りたいときは、
int sum = 0;
for (int i = left; i < right; ++i) {
sum += a[i];
}
とすれば合計値を求めることができます。しかしこれではクエリが飛んで来る度に配列サイズ $N$ に比例する時間がかかってしまいます。計算量の言葉で言えば $O(N)$ の計算時間を要します。
この状態で処理を例えば $Q = 1,000,000$ 回もこなすようなことをすると、$O(NQ)$ の計算時間がかかってしまいます。これは現在の典型的な市販 PC 上で $1$ 時間かけてようやく終わるかどうかです。
解決策としてとりあえず思いつくのは
- 最初に $\frac{N(N+1)}{2}$ 通り2の合計値をすべて記憶しておけば、それを毎回答えるだけでよいのでは...
という発想でしょう。しかしこれも $O(N^2)$ の記憶容量を必要とするので現実的ではないでしょう。しかも前処理計算にも多くの時間を要します3。そこで
- 前処理に $O(N)$ だけの時間をかける
- 記憶容量は $O(N)$ でよい
- 前処理をしておけば、毎回のクエリに $O(1)$ で爆速で答えることができる
という筋の良い方法があります。それが累積和手法です。まとめると以下のようになります:
| 方法 | 前処理計算時間 | 記憶容量 | クエリ計算時間 |
|---|---|---|---|
| ナイーブ計算 | なし | $O(N)$ | $O(N)$ |
| すべて前処理 | $O(N^2)$ | $O(N^2)$ | $O(1)$ |
| 累積和 | $O(N)$ | $O(N)$ | $O(1)$ |
大量のクエリ処理が重要となる場面では、この中では累積和一択でしょう。
2. 累積和とは
累積和に関するまとめです。
2-1. 累積和とは何か
「累積和は何か」については、すごく簡単です。高校数学の「数列と数学的帰納法」といった単元でも出て来るやつです。
- 配列 $a_0, a_1, a_2, \dots, a_{N-1}$ に対して
- 配列 $s_0, s_1, s_2, \dots, s_{N-1}, s_{N}$ を以下のように定めたもの
- $s_0 = 0$
- $s_1 = a_0$
- $s_2 = a_0 + a_1$
- $s_3 = a_0 + a_1 + a_2$
- $\dots$
- $s_N = a_0 + a_1 + a_2 + \dots + a_{N-1}$
です。例えば $a = $ {$3, 6, 8, 2$} であれば、$s = $ {$0, 3, 9, 17, 19$} です。$s$ の方が $a$ よりも $1$ だけ配列サイズが大きくなっています。これを用いると、例えば配列 $a$ の区間 [$4, 13$) の総和
- $a_4 + a_5 + a_6 + a_7 + a_8 + a_9 + a_{10} + a_{11} + a_{12}$
は
- $s_{13} - s_{4}$
を計算するだけで求めることができます!!!!!
確かに $O(1)$ で計算できることがわかります。確かめてみましょう。
- $s_{13} = a_1 + a_2 + a_3 + a_4 + a_5 + a_6 + a_7 + a_8 + a_9 + a_{10} + a_{11} + a_{12}$
- $s_{4} = a_1 + a_2 + a_3$
ですので、引くと確かに「$a_1 + a_2 + a_3$」の部分が消えて
- $s_{13} - s_{4} = a_4 + a_5 + a_6 + a_7 + a_8 + a_9 + a_{10} + a_{11} + a_{12}$
となっています。
2-2. 累積和を視覚的に理解する
注意点として、配列 $a$ の範囲を例えば [$3, 7$) のように指定するとき、これは $(a_3, a_4, a_5, a_6)$ を表していて、
- 左側 ($a_3$) は含める (閉区間)
- 右側 ($a_7$) は含めない (開区間)
としていました。これは C++ の STL コンテナや、Python の各種コンテナなどでも採用されている一般的な定義方法になっています。例えば $(a_3, a_4, a_5, a_6)$ をソートしたいときは
sort(a+3, a+7);
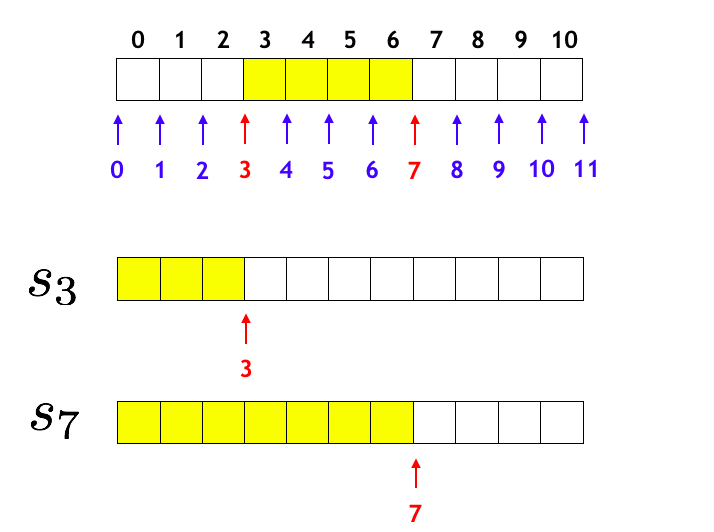
という感じです。このような一見歪な定義をするお気持ちとしては、下図のように、区間 [left, right) の left や right は「配列の両端や隙間のうちのどこを表しているか」と考えればわかりやすいです。
そして、このような捉え方をしたとき、累積和の考え方は大変明快です。
上図のように、
- $s_3$ とは [$0, 3$) の総和 (言い換えると左 $3$ 個分の総和)
- $s_7$ とは [$0, 7$) の総和 (言い換えると左 $7$ 個分の総和)
を表しています。そうすると $s_7$ から $s_3$ を引けば [$3, 7$) の総和が求められることが大変明快です。
2-3. s_0 = 0 の意味
累積和の定義で、
- $s_0 = 0$
というのにぎょっとした方は多いかもしれません。これについて補足してみます。
- $s_3$ は [$0, 3$) の総和
を意味するのならば
- $s_0$ は [$0, 0$) の総和
を意味するものであって欲しいです。区間 [$0, 0$) とは $0$ から $0$ まで。つまり長さ $0$ の何もない区間です。
何も足さない値は $0$ とするのが自然でしょう。さらに気になる方は、累積和の絶対に成り立って欲しい性質である「配列 $a$ の区間 [${\rm left, right}$) の総和が $s_{{\rm right}} - s_{{\rm left}}$ である」という性質が、${\rm left} = 0$ としても整合していることを確かめると良さそうです。
2-4. 累積和の実装
残りは累積和自体の実装方法ですね。累積和の定義を思い出しておくと
- 配列 $a_0, a_1, a_2, \dots, a_{N-1}$ に対して
- 配列 $s_0, s_1, s_2, \dots, s_{N-1}, s_{N}$ を以下のように定めたもの
- $s_0 = 0$
- $s_1 = a_0$
- $s_2 = a_0 + a_1$
- $s_3 = a_0 + a_1 + a_2$
- $\dots$
- $s_N = a_0 + a_1 + a_2 + \dots + a_{N-1}$
でした。この式をよく眺めると $s_{i+1} = s_i + a_i$ という関係が浮かび上がって来ます。具体的には
int N; cin >> N; // 配列サイズ
vector<int> a(N);
for (int i = 0; i < N; ++i) cin >> a[i]; // a の入力
// 累積和
vector<int> s(N+1, 0); // s[0] = 0 になる
for (int i = 0; i < N; ++i) s[i+1] = s[i] + a[i];
という感じで簡単に実装できます。各クエリに対しては
// 区間 [left, right) の総和を求める
int left, right;
cin >> left >> right;
cout << s[right] - s[left] << endl;
という感じで答えることができます。
2-5. 累積和のまとめ
まとめると
配列 $a$ に対して累積和 $s$ を求めると、配列 $a$ の区間 [left, right) の総和が
- $s$[right] - $s$[left]
で $O(1)$ で求められる
ということがわかりました。この事実を丸ごと吸収して機械的に実装すればよいです。
3. 累積和の例題
累積和を用いると解くことのできる例題を何問か解いてみます。
問題 1: AOJ 0516 - 最大の和 (JOI 2006 本選 A)
【問題概要】
$N$ 個の整数 $a_0, a_1, \dots, a_{N-1}$ が与えられる。$K$ 個の連続する整数の和の最大値を求めよ。
(入力形式がやや特殊なので元問題文を参照)。
【制約】
- $1 \le K \le N \le 10^5$
- $-10^4 \le a_i \le 10^4$
【数値例】
$N = 5$
$K = 3$
$a = (2, 5, -4, 10, 3)$
答え: $11$ ($5, -4, 10$ を選ぶのが最大です)
まさに累積和がピッタリはまりそうな問題ですね。
- 区間 [$0, K$) の総和
- 区間 [$1, K+1$) の総和
- 区間 [$2, K+2$) の総和
- ...
- 区間 [$N-K, N$) の総和
の $N-K+1$ 個の値の最大値を求める問題となっています。予め累積和を前計算しておくことで、それぞれの値を $O(1)$ で計算できますので、全体としても $O(N)$ の計算時間で求めることができます。
仮に累積和を使わずに愚直に計算すると、それぞれ $O(K)$ の計算時間がかかりますので全体として $O(NK)$ の計算量を要してしまいます。
# include <iostream>
# include <vector>
using namespace std;
const long long INF = 1LL<<60; // 仮想的な無限大の値
int main() {
// 入力
int N, K;
while (cin >> N >> K) {
if (N == 0) break;
vector<long long> a(N);
for (int i = 0; i < N; ++i) cin >> a[i];
// 累積和を前計算
vector<int> s(N+1, 0);
for (int i = 0; i < N; ++i) s[i+1] = s[i] + a[i];
// 答えを求める
long long res = -INF; // 最初は無限小の値に初期化しておく
for (int i = 0; i <= N-K; ++i) {
long long val = s[K+i] - s[i];
if (res < val) res = val;
}
cout << res << endl;
}
}
問題 2: AtCoder ABC 084 D - 2017-like Number
【問題概要】
$N$ も $(N+1)÷2$ も素数であるような $N$ を「$2017$ に似た数」と呼ぶことにします。
$Q$ 個のクエリが与えられます。クエリ $i$ では奇数 $l_i, r_i$ が与えられるので、$l_i \le x \le r_i$ であって「$2017$ に似た数」となっているような奇数 $x$ の個数を求めよ。
【制約】
- $1 \le Q \le 10^{5}$
- $1 \le l_i \le r_i \le 10^5$
【数値例】
$Q = 2$
$(l, r) = (3, 7), (13, 13)$
答え
$2$
$1$
(一番目の例では、$3, 5$ が $2017$ に似た数です。二番目の例では、$13$ が $2017$ に似た数です。)
初見では累積和っぽくは見えないかもしれないですが、以下のような配列を考えると見えて来ます。
- a[i] := i が「2017 に似た数」なら 1、そうでないなら 0
例えば、
(a[0], a[1], a[2], a[3], a[4], a[5], a[6], a[7], ...)
= (0, 0, 0, 1, 0, 1, 0, 0, ...)
という風になります。そうするとクエリ $(l, r)$ というのは「配列 a の区間 [$l, r+1$) 上の総和を求めよ」ということになります4。
よって問題は配列 a を求める問題に帰着されました。これは例えばエラトステネスのふるいを用いることで効率良く実現することができます。
# include <iostream>
# include <vector>
using namespace std;
int main() {
// エラトステネスのふるい
int MAX = 101010;
vector<int> is_prime(MAX, 1);
is_prime[0] = 0, is_prime[1] = 0;
for (int i = 2; i < MAX; ++i) {
if (!is_prime[i]) continue;
for (int j = i*2; j < MAX; j += i) is_prime[j] = 0;
}
// 2017-like 数かどうか
vector<int> a(MAX, 0);
for (int i = 0; i < MAX; ++i) {
if (i % 2 == 0) continue;
if (is_prime[i] && is_prime[(i+1)/2]) a[i] = 1;
}
// 累積和
vector<int> s(MAX+1, 0);
for (int i = 0; i < MAX; ++i) s[i+1] = s[i] + a[i];
// クエリ処理
int Q; cin >> Q;
for (int q = 0; q < Q; ++q) {
int l, r;
cin >> l >> r;
++r;
cout << s[r] - s[l] << endl;
}
}
問題 3: AtCoder ABC 122 C - GeT AC
【問題概要】
'A', 'C', 'G', 'T' からなる長さ $N$ の文字列 $S$ が与えられます。以下の $Q$ 個のクエリに答えよ。
- $S$ の $l$ 文字目から $r$ 文字目までに "AC" が何回登場するかを答えよ
【制約】
- $2 \le N \le 10^5$
- $1 \le Q \le 10^5$
【数値例】
$N = 8, Q = 3$
$S$ = "ACACTACG"
$(l, r) = (3, 7), (2, 3), (1, 8)$
答え
$2$
$0$
$3$
一番目は "ACTAC", 二番目は "CA", 三番目は "ACACTACG" です。
さきほどの「$2017$ に似た数」の問題とよく似ています。実際同様の解法で解くことができます。少しややこしいのが、
TTTA | CTTACTT | TTTTT
のようなクエリの場合です。このとき
- 区間の右側までに登場する "AC" の個数は $2$ ("TTTACTTACTT")
- 区間の左側までに登場する "AC" の個数は $0$ ("TTTA")
となって愚直に計算すると $2 - 0 = 2$ となりますが、正しい答えは $1$ です。このようなケースに対処するために
- "AC" をまとめて扱うのではなく、「'C' が右隣にあるような 'A' の個数」を数える
という問題だと読み替えることにしましょう。それに合わせて
- 区間 [$l, r+1$) を考えるのではなく、区間 [$l, r$) を考える
というようにします。"TTACTTTA | C" のような「右端の 'A' の右隣に 'C' がある」というような 'A' を除外するためです。ここまで整理すると自然に解くことができます。
# include <iostream>
# include <vector>
# include <string>
using namespace std;
int main() {
int N, Q; cin >> N >> Q;
string str; cin >> str;
// 累積和
vector<int> s(N+1, 0);
for (int i = 0; i < N; ++i) {
if (i+1 < N && str[i] == 'A' && str[i+1] == 'C') s[i+1] = s[i] + 1;
else s[i+1] = s[i];
}
// クエリ
for (int q = 0; q < Q; ++q) {
int l, r; cin >> l >> r;
--l, --r; // 0-indexed にする
cout << s[r] - s[l] << endl;
}
}
問題 4: AtCoder AGC 023 A - Zero-Sum Ranges
【問題概要】
長さ $N$ の整数列 $a_0, a_1, \dots, a_{N-1}$ が与えられる。この整数列の連続する区間であって、その区間内の値の総和が $0$ になるものが何個あるか答えよ。
【制約】
- $1 \le N \le 2 × 10^5$
- $-10^9 \le a_i \le 10^9$
【数値例】
$N = 6$
$a = (1, 3, -4, 2, 2, -2)$
答え
3
($(1, 3, -4)$ と $(-4, 2, 2)$ と $(2, -2)$ が正解です)
AtCoder 200 点問題史上最難問と名高い問題です。400 点が適当なのではないかという声も多々上がっています。それはともかくとして、ここまで累積和の感覚を研ぎ澄ませていると、この問題は自然に思えるのではないでしょうか。
まず「条件を満たす区間の個数を数え上げよ」という問題で検討したいこととして
- 累積和
- しゃくとり法
があると思います。詳細は省略しますが、今回の問題はしゃくとり法が使える構造にはなっていません。代わりに累積和を用いて効率良く解くことができます。累積和 $s_0, s_1, s_2, \dots, s_{N-1}, s_N$ を求めてあげると、各区間の和は
- $i < j$ となる $i, j$ を選んで $s_j - s_i$ の値を計算したもの
にピッタリ対応していることがわかります。よって問題は
- $s_i = s_j$ となるような $(i, j)$ ($i < j$) の組の個数を求めよ
という問題に変換されました。例えば $s = (3, 5, 3, 7, 3, 7, 3)$ であったら、
- $3$ は $4$ 個あるので、$s_i = s_j = 3$ に対応する $i, j$ を選ぶ方法は ${}_{4}{\rm C}_{2} = 6$ 通り
- $5$ は $1$ 個しかないので $s_i = s_j = 5$ に対応する $i, j$ の組は選べない
- $7$ は $2$ 個あるので、$s_i = s_j = 7$ に対応する $i, j$ を選ぶ方法は ${}_{2}{\rm C}_{2} = 1$ 通り
ということになり、合計で $6 + 1 = 7$ 通りあるということになります。一般に $s$ の中にどの数値が何個あるのかがわかれば上記のようにして集計することができます。これは例えば連想配列として使える std::map などを用いると簡単に実現できます。
# include <iostream>
# include <vector>
# include <map>
using namespace std;
int main() {
int N; cin >> N;
vector<long long> a(N);
for (int i = 0; i < N; ++i) cin >> a[i];
// 累積和と連想配列
vector<long long> s(N+1, 0);
map<long long, long long> nums;
for (int i = 0; i < N; ++i) s[i+1] = s[i] + a[i];
for (int i = 0; i < N+1; ++i) nums[s[i]]++;
// 集計処理
long long res = 0;
for (auto it : nums) {
long long num = it.second; // it.first が it.second 個ある
res += num * (num - 1) / 2;
}
cout << res << endl;
}
4. 二次元累積和
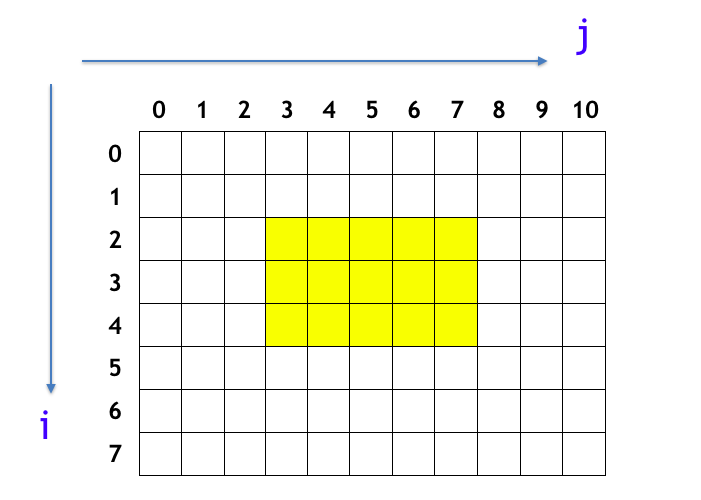
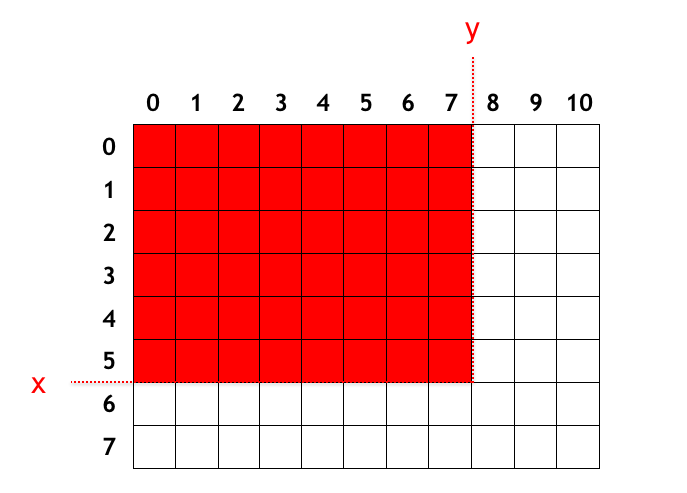
ここまでは一次元配列を考えて来ましたが、二次元配列に対して同様のことがしたいケースもあります。すなわち下図の長方形区域内の値の総和を高速に求めたい場面を考えます。下図は $[2, 5) × [3, 8)$ の長方形区間を表しています。
ここでもやはり、一次元の場合と同様に以下のような配列を考えます:
- $s[x][y] := [0, x) × [0, y)$ の長方形区間の和
図にすると下のようになります。下図は $x = 6, y = 8$ の場合を表しています。
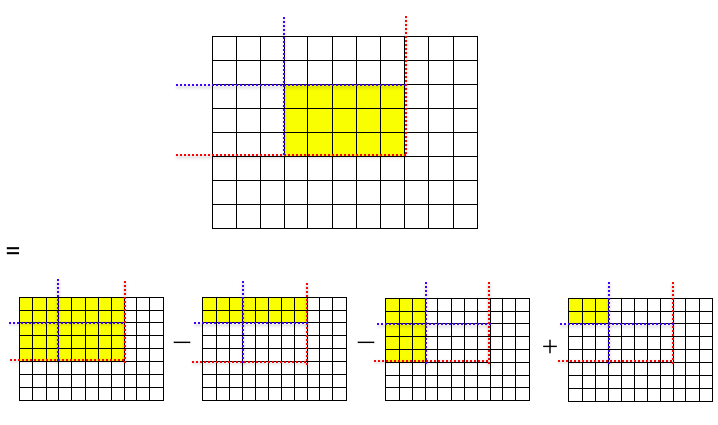
この配列 $s$ を上手く足し引きして、任意の長方形区間を作ることを考えてみましょう。少し複雑ですが、下図のように 4 つの $s$ の足し引きで実現することができます。
最後に $s$ 自体の求め方ですが、これも同様に 4 つの値を足し引きすることで求めることができます。例えば $s[x+1][y+1]$ を求めたいとき、$s[x][y+1]$ や $s[x+1][y]$ は既に求められているものとして
- $s[x+1][y+1] = s[x][y+1] + s[x+1][y] - s[x][y] + a[x][y]$
と求めることができます。累積和を前計算するのに要する計算時間はグリットサイズを $H × W$ として $O(HW)$ となります。是非長方形の絵を描いて確認していただけたらと思います。以上をまとめると、実装例として以下のようになるでしょう。
# include <iostream>
# include <vector>
using namespace std;
int main() {
// 入力: H × W のグリッド
int H, W; cin >> H >> W;
vector<vector<int> > a(H, vector<int>(W));
for (int i = 0; i < H; ++i) for (int j = 0; j < W; ++j) cin >> a[i][j];
// 二次元累積和
vector<vector<int> > s(H+1, vector<int>(W+1, 0));
for (int i = 0; i < H; ++i)
for (int j = 0; j < W; ++j)
s[i+1][j+1] = s[i][j+1] + s[i+1][j] - s[i][j] + a[i][j];
// クエリ [x1, x2) × [y1, y2) の長方形区域の和
int Q; cin >> Q;
for (int q = 0; q < Q; ++q) {
int x1, x2, y1, y2;
cin >> x1 >> x2 >> y1 >> y2;
cout << s[x2][y2] - s[x1][y2] - s[x2][y1] + s[x1][y1] << endl;
}
}
これに対し、例えば
4 5
1 8 7 3 2
9 1 3 4 6
3 5 8 1 4
2 7 3 2 5
3
1 3 2 5
0 2 1 3
0 4 0 5
という入力を与えると出力結果は以下のようになります。
- $1$ 個目は、$3 + 4 + 6 + 8 + 1 + 4 = 26$
- $2$ 個目は、$8 + 7 + 1 + 3 = 19$
- $3$ 個目は、全部の総和で $84$
となっています。
26
19
84
より効率よく二次元累積和を求める
ここでは二次元累積和 $s$ を求めるのに、長方形の足し引き (包除原理) を用いました。しかしより効率よく in-place な計算で求めることもできます。詳しくは以下の記事に記載があります。
問題 5: AtCoder ABC 005 D - おいしいたこ焼きの焼き方
【問題概要】
$N$ × $N$ のグリッドに整数 (マス($i, j$) には $D_{ij}$) が書かれている。以下の $Q$ 個のクエリに答えよ。
- 面積が $P_i$ 以下となるような長方形領域の値の総和として考えられる最大値を求めよ
【制約】
- $1 \le N \le 50$
- $1 \le D_{ij} \le 100$
- $1 \le Q, P_i \le N^2$
【数値例】
$N = 3$
$D =$
$1 2 3$
$4 5 6$
$7 8 9$
$Q = 1$
$P = (5)$
答え
$28$
($5 + 6 + 8 + 9 = 28$ が最大です、面積を $5$ にはできません)
いかにも二次元累積和が使えそうな問題です。累積和な問題で「すべての区間についての総和を求める」という処理をすることは少ないですが、今回はひとまず全ての長方形区域の総和を求めることを考えます。
しかしその場合も、あらゆる長方形区域について愚直に総和を計算したならば
- 長方形区域の個数が $O(N^4)$
- それぞれの長方形区域の総和計算が $O(N^2)$
ということで合計 $O(N^6)$ の計算時間を要してしまいます。流石に間に合いません。しかし累積和を予め前計算しておくことで
- それぞれの長方形区域の総和計算が $O(1)$
でできるようになるため、合計で $O(N^4)$ となって間に合います。すべての長方形区域の「面積」と「総和」がわかってしまえば、
- 面積 $P$ 以下な長方形区域についての「総和」の最大値
も簡単に求めることができます。
# include <iostream>
# include <vector>
using namespace std;
int main() {
int N; cin >> N;
vector<vector<long long> > D(N, vector<long long>(N));
for (int i = 0; i < N; ++i) for (int j = 0; j < N; ++j) cin >> D[i][j];
// 累積和
vector<vector<long long> > S(N+1, vector<long long>(N+1, 0));
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j)
S[i+1][j+1] = S[i][j+1] + S[i+1][j] - S[i][j] + D[i][j];
// すべての長方形区域の面積を集計
vector<long long> val(N*N+1, 0); // val[v] := 面積が v の長方形領域の総和の最大値
for (int x1 = 0; x1 < N; ++x1) {
for (int x2 = x1 + 1; x2 <= N; ++x2) {
for (int y1 = 0; y1 < N; ++y1) {
for (int y2 = y1 + 1; y2 <= N; ++y2) {
long long area = (x2 - x1) * (y2 - y1);
long long sum = S[x2][y2] - S[x1][y2] - S[x2][y1] + S[x1][y1];
val[area] = max(val[area], sum);
}
}
}
}
// ちゃんと集計, val[v] := 面積が v 「以下」の長方形領域の総和の最大値
for (int v = 0; v < N*N; ++v) val[v+1] = max(val[v+1], val[v]);
// クエリに答える
int Q; cin >> Q;
for (int q = 0; q < Q; ++q) {
long long P; cin >> P;
cout << val[P] << endl;
}
}
5. おわりに
競技プログラミングを始めてから、累積和を扱えるようになると、解ける問題の幅が一気に広がって楽しくなります。是非素敵な累積和ライフを!
最後に累積和に関連する発展的トピックを紹介して締めます。
いもす法
累積和と並んで、競技プログラミングで初期に学ぶ楽しい手法です。累積和は
- 区間の総和を求める (区間の値自体は最初に与えられた時点から不変)
というクエリに高速に答える手法でしたが、いもす法は
- 区間に値を加算する (最後に、最終的な区間の値をまとめて知る)
というクエリを高速に扱うことのできる手法になっています。いもす法という名前の由来となったいもすさんによる解説記事を参考にしていただけたらと思います。
しゃくとり法
区間に関する問題において、累積和以外にも検討したい手法として、しゃくとり法があります。ある種の条件設定においては
- 〜という条件を満たす区間を数え上げよ
- 〜という条件を満たす区間の長さの最大値を求めよ
といった問題を効率良く解くことのできるアルゴリズムになっています。詳しくはしゃくとり法を参考にしていただけたらと思います。
「総和」以外にも色々
今回は累積和は「配列の区間の総和を求めるクエリを爆速に処理する」アルゴリズムとして紹介しました。実際には「総和」でなくても、例えば
- 配列の各値は、なんらかの場合の数を $1000000007$ で割ったあまり
- 配列の各区間の値の積を $1000000007$ で割ったあまりを求めるクエリを爆速処理する
といった場面にも自然に使うことができます。他に面白い例としては
- 配列の各区間の値の XOR 和を求めるクエリを爆速処理する
というのもあります。より抽象的には群と呼ばれる構造全般に対して適用することができます。これは上記のいもす法などにも言えることです。柔軟に多彩な応用ができるととても楽しいです。
更新クエリもある場合には BIT やセグメントツリー
今回の問題設定では、「配列の値は常に不変」という状態を扱っていました。実際には
- 配列のある値が更新される
- 配列内のある区間の総和を求めたい
という二種類のクエリが入り乱れる場面も多々あります。そんなときは BIT やセグメントツリーと呼ばれるデータ構造を用いるとピッタリです。
ローリングハッシュ
文字列検索問題において超基本となる手法です。例えば
$S$ = "ACGTACTTGAACCTTATCTAGTTAGGCGATCAGCTCGACGAGCGGCCAT"
という文字列にパターン $T$ = "ACCTTATCTAGTTAG" がどこに登場するのかを検索する問題を考えてみましょう。愚直にやると、$S$ の各 index に対して、そこから先が $T$ と一致するかどうかを調べることになります。これでは $O(|S||T|)$ の計算時間が必要になります。しかし実はローリングハッシュと呼ばれる手法と、累積和のような手法を組合せることで上手に検索することができます。
- $S$ の先頭から $i$ 文字目までを表す累積和ハッシュ
というのを求めることで、さらに
- $S$ の $i$ 文字目から $j$ 文字目までを表すハッシュ値
を $O(1)$ で求めることができるようになります。それによって、それが $T$ を表すハッシュ値と一致するかどうかを調べれば良く、$O(|S| + |T|)$ の計算時間で検索できるようになりました。詳しくは Rolling Hashing を読んでいただけたらと思います。
DP の高速化
やや高度な話題になりますが、動的計画法を設計したときに、
- ${\rm dp}[i] = \sum_{j = f(i)}^{i-1} dp[j] + g(i)$
という形をした遷移式が登場することが多々あります。このとき $\sum_{j = f(i)}^{i-1} dp[j]$ の部分を愚直に計算しては大変ですが、dp 配列の累積和をとることで、この部分の計算を効率化することができます。
-
例えば Qiita ユーザ数は約 $300,000$ 人であり、多くのサービスに付随するデータとして典型的なサイズ感だと思います。 ↩
-
区間の個数は「配列の両端と隙間を合わせて $N+1$ 箇所のうち $2$ 箇所を選んで仕切りを入れる方法の数」と同じですので、${}_{N+1}{\rm C}_{2} = \frac{N(N+1)}{2}$ 個になります。 ↩
-
色んな方法がありますが、どれほど工夫をしても記憶容量だけの時間はかかるので $O(N^2)$ の計算時間を要します。 ↩
-
問題では区間の右側が含まれる形で入力が与えられていますが、累積和を考えるときは区間の右側を含まない形式で考えると明快なので、$r$ に $1$ を足しています。 ↩