ゼータ変換・メビウス変換を理解する

#要約

本記事では、競技プログラミングに頻出のゼータ変換・メビウス変換についてまとめました。
記事中のコードはpythonで記述されています。

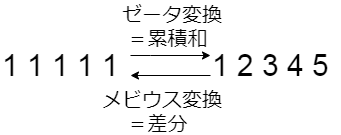
1次元のゼータ変換

###定義
$f[0], \dots, f[N-1]$が与えられている。
このとき、$\displaystyle g[x] = \sum_{i \le x}f[i]$となる$g$を、$f$のゼータ変換という。
また、逆に$f$を$g$のメビウス変換という。

###アルゴリズム
上の定義を落ち着いて読むと、$f$のゼータ変換$g$は$f$の累積和そのものだとわかります。
図で見ると上図のようになります。
累積和を知らない方はdrkenさんの記事を見てください。

念のため累積和の計算を復習しよう。
配列$f$が与えられているとき、$f$のゼータ変換はlist(itertools.accumulate(f))となる。
もしくは、in place に
for i in range(1,n): f[i] += f[i-1]
とできる。もちろん
for i in range(n-1): f[i+1] += f[i]
でもよい（この記事では最初の書き方にあわせる）。
メビウス変換はこれを逆再生すればいいので、in place に
for i in range(n-1,0,-1): f[i] -= f[i-1]
と書ける。つまりただの差分。
計算量はどちらも$O(N)$。

2次元のゼータ変換

###定義
$f[0][0], \dots, f[N-1][N-1]$が与えられている。
このとき、$g[x][y] = \sum_{i \le x, j \le y}f[i][j]$となる$g$を、$f$のゼータ変換という。
また、$f$を$g$のメビウス変換という。

上の定義を落ち着いて読むと、$f$のゼータ変換$g$は$f$の2次元累積和そのものとわかる。
2次元累積和の計算法は、同じく[drkenさんの記事]
(https://qiita.com/drken/items/56a6b68edef8fc605821#4-%E4%BA%8C%E6%AC%A1%E5%85%83%E7%B4%AF%E7%A9%8D%E5%92%8C)にも記述があるが、
そこで紹介されたアルゴリズムでは1つのマスを計算するために4つの値の足し引きが必要になってしまう。
これだと、$d$次元で同じことをやると$2^d$回の足し引きが必要で大変なので、
別のアルゴリズムを紹介する。

###アルゴリズム

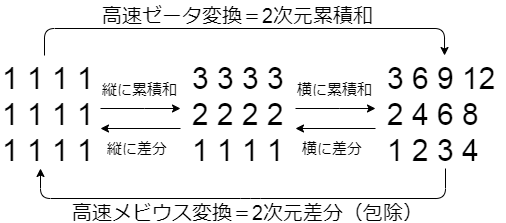
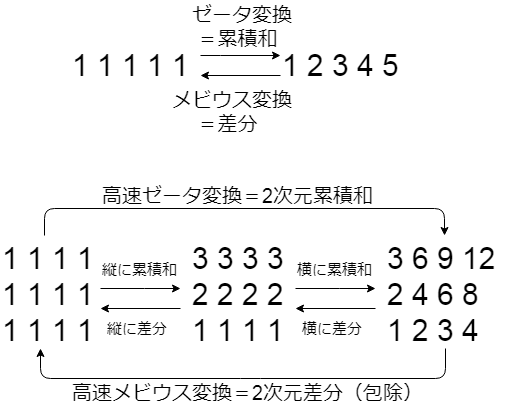
実は、上図のように$f$の2次元累積和は1次元累積和をそれぞれの次元について行えばよい。
つまり、in place に以下のようにして$f$のゼータ変換が計算できる。

#ヨコに累積和
for i in range(n):
    for j in range(n):
        if i: a[i][j] += a[i-1][j]
#タテに累積和
for i in range(n):
    for j in range(n):
        if j: a[i][j] += a[i][j-1]

こうすると、各マスについて足し算が2回ですむ。
メビウス変換はこれを逆再生すればいいので、$g$のメビウス変換は次元ごとの差分で in place に以下のように計算できる。

for i in range(n-1,-1,-1):
    for j in range(n-1,-1,-1):
        if i: a[i][j] -= a[i-1][j]
for i in range(n-1,-1,-1):
    for j in range(n-1,-1,-1):
        if j: a[i][j] -= a[i][j-1]

注意　このアルゴリズムは、$d$次元の場合も含めYatesのアルゴリズムと呼ばれているようだ。
F. Yates, The Design and Analysis of Factorial Experiments, Technical Communication No. 35,
Commonwealth Bureau of Soil Science, Harpenden, UK, 1937

注意　メビウス変換を包除で書くと、例えば2次元の場合
f[i][j] = g[i][j] - g[i-1][j] - g[i][j-1] + g[i-1][j-1]
のようになるが、これだと１マスの計算に$2^d$回の演算が必要なので、よろしくない。

d次元のゼータ変換

きちんとは書かないが、$d$次元のゼータ変換とは$d$次元累積和のこと。
メビウス変換は$d$次元累積和の逆変換のこと。

$d$次元のゼータ変換は、$2$次元のときと同様に、$1$次元累積和を次元ごとに$d$回やればよい。
逆に、$d$次元のメビウス変換は、$1$次元差分を次元ごとに$d$回やればよい。
計算量はどちらも$O(dN^d)$。

#まとめ

• ゼータ変換＝累積和
• メビウス変換＝差分
• 高速ゼータ変換＝ 高速 $d$ 次元累積和 = $1$次元累積和を次元ごとに $d$ 回
• 高速メビウス変換＝ 高速 $d$ 次元差分 = $1$次元差分を次元ごとに $d$ 回

ゼータ変換と畳み込み

もう一回１次元の場合にもどってみよう。
つまり、$f[0], \dots, f[N-1]$および$g[0], \dots, g[N-1]$が与えられているとする。
突然だが、$f$と$g$のmax演算による畳み込み$h$を
$$
h[x] = \sum_{0 \le i,j < N,, \max(i,j)=x} f[i]g[j]
$$
と定義する。各関数$f,g,h$のゼータ変換先を$\zeta f, \zeta g, \zeta h$とかく。
すると畳み込み定理
$$
(\zeta h)[x] = (\zeta f)[x] \cdot (\zeta g)[x]
$$
が成立することが計算によりわかる（右辺は各点積、つまり数と数の積）。
つまり、max演算による$f$と$g$の畳み込み$h$を計算したいときは、

• $f$と$g$をゼータ変換する
• それらの各点積をとる（これが$h$のゼータ変換に等しいというのが畳み込み定理）
• それをメビウス変換する

とすると$h$が計算できる。

$d$次元の場合も同様。
$2$次元格子点どうしのmax演算を $\max((a_1,a_2),(b_1,b_2)) = (\max(a_1,b_1), \max(a_2,b_2))$ で定めておこう。
同様に$d$次元格子点のmax演算を、各成分ごとに$\max$をとるとして定める。
すると、max演算に関する畳み込み定理が、上式そのままの形で成立することがわかる。
（証明は、束に一般化したものが下のほうに書いてある）

もしmin演算で畳み込みたい場合は、ゼータ変換を0から（左下から）ではなく$N-1$から（右上から）やることで達成できる。

#具体例(1) 下位集合の和

###問題

集合$U$を$U={0,1,\dots,d-1}$とおく。
$f$を、$U$のべき集合上の関数とする（つまり、$U$の部分集合$S$に対して$f(S)$が定まる）。
このとき、以下の問いに答えよ。

• $\displaystyle　g(T) = \sum_{S \subset T} f(S)$ をみたす$g(T)$を各$T$について計算せよ
• $\displaystyle　f(T) = \sum_{S \subset T} h(S)$ をみたす$h(S)$を各$S$について計算せよ

###アルゴリズム

この問題は、上で紹介した$d$次元ゼータorメビウス変換で$N=2$の場合に相当する。
つまり、$g$は$f$のゼータ変換、$h$は$f$のメビウス変換となる。
よって$O(d2^d)$でこの問題が解けました。

サンプルコード

# f をゼータ変換
for i in range(d):
    for j in range(1<<d):
        if (j&(1<<i)): f[j] += f[j^(1<<i)]
#g をメビウス変換
for i in range(d):
    for j in range(1<<d):
        if (j&(1<<i)): g[j] -= g[j^(1<<i)]

###競技プログラミングにおけるremark
競プロ界でゼータ変換と呼ばれるのは主にこの形（と、包含を逆にした上位集合の和）のようだ。
名前がつくほどに有名なので、すでにこのテーマについてのたくさんの記事がある。
naoya_tさんの記事にその多くがまとめられているので、参照してください。

###余談・線形変換としてみる
$\mathbb{Z}/2^n\mathbb{Z}$上の離散フーリエ変換は、基底の順番をうまく入れ替えると変換の行列が
$W_n = \begin{bmatrix}
W_{n-1} & DW_{n-1} \
W_{n-1} & -DW_{n-1}
\end{bmatrix}$
のように再帰的に書ける($D$は対角行列)ので、計算量が落ちる。
下位集合のゼータ変換の場合は、基底の順番を自然に（次元ごとに）とれば
$W_n = \begin{bmatrix}
W_{n-1} & 0 \
W_{n-1} & W_{n-1}
\end{bmatrix}$
のようになっているので、同様に計算量が落ちるともいえる。

#具体例(2) 約数系包除
###問題
$f(1), \dots, f(N)$が与えられたとする。$i > N$のとき$f(i) = 0$とする。このとき、

• $\displaystyle　g(n) = \sum_{n|m} f(m)$ をみたす$g(n)$を各$n \le N$について計算せよ
• $\displaystyle　f(n) = \sum_{n|m} h(m)$ をみたす$h(m)$を各$m \le N$について計算せよ

###競技プログラミングにおけるremark
この形の問題（特に$h$を求める問題）は競プロ界では約数系包除として知られている（DEGwerさんの数え上げテクニック集などを参照）。

たとえば$g(n)$を求めるときは、それぞれを定義どおりに計算するとエラトステネスのふるいと同じ$O(N \log N)$で解ける。
これを逆回しすると、$h$を包除原理により同じオーダーで求めることができる（DEGwerさんの数え上げテクニック集参照）。

しかし、noshi91さんの記事が指摘しているように、この問題は高速ゼータ・メビウス変換により$O(N\log\log N)$で解くことができる。

###アルゴリズム

（$d$=$N$以下の素数）として、約数倍数関係から定まる$d$次元の格子を考える。
たとえば$20 = 2^2 \cdot 5$は$(2,0,1,0,0,0,0,...)$に対応させる。
$k = 2^a 3^b 5^c \cdots$ は $(a,b,c,...)$という点に対応させる。
上の図は、最初の２次元（2倍の軸と3倍の軸のみ）を取り出したときの格子の一部である。

すると、この問題はやはりゼータ・メビウス変換を計算することに相当する。
ただし、今までとは逆方向に、「右上（無限大）方向」からの累積和を考えていることに注意。
メビウス変換では「左下（つまり$1$に対応するノード）」から差分をとることになる。

サンプルコード（noshi91さんの記事を参考にしました。）

#注意：あらかじめ素数のリスト primes を作成する
def zeta_divisor(a,primes): #aを約数ゼータ
    n = len(a)-1
    for p in primes:
        for i in range(n//p,0,-1):
            a[i] += a[p*i]
def mobius_divisor(a,primes): #aを約数メビウス
    n = len(a)
    for p in primes:
        for i in range(1,n):
            if i*p >= n: break
            a[i] -= a[p*i] 

#具体例(3) gcd演算による畳み込み
###問題
$f(1), \dots, f(N), g(1) \dots, g(N)$が与えられたとする。$i > N$のとき$f(i) = g(i) = 0$とする。このとき、$f$と$g$のgcd演算による畳み込み$h$を計算せよ。すなわち、
$\displaystyle h(n) = \sum_{\gcd(x,y)=n} f(x)g(y)$ をみたす$h(n)$を各$n \le N$について計算せよ

###アルゴリズム
さきほどと同様に、約数倍数関係の$d$次元格子を考える。
$x$が約数倍数関係の格子において$\boldsymbol{x} =(x_2,x_3,x_5,\dots)$に対応するとしよう。
$y,n$も同様に、$\boldsymbol{y},\boldsymbol{n}$に対応するとしよう。
このとき$\gcd(x,y)=n$という式を約数倍数関係の格子に翻訳すると、
$\min(\boldsymbol{x},\boldsymbol{y})=\boldsymbol{n}$となるので、
gcd演算による畳み込みは格子の世界でまさに（上のほうで紹介した）min演算の畳み込みとなる。

よって$h$を求めるには、

• $f$,$g$を（上で紹介した約数の意味での）ゼータ変換する
• 各点積をとる
• それを約数の意味でメビウス変換する

とすれば求まる。

Historical remark

さまざまな演算に対するconvolutionは多くの研究者が考えている。

László Tóth 2014 のサーベイ(https://arxiv.org/pdf/1310.7053v2.pdf) の参考文献にもあるとおり、
D. H. Lehmer, On a theorem of von Sterneck, Bull. Amer. Math. Soc. 37 (1931), pp. 723–726.
ではすでに畳み込み定理が成り立つ畳み込み演算が調べられていたりする。

lcm演算で畳み込む場合、lcm convolutionという名前で大丈夫そう。
上のサーベイのほかにも、レクチャーノート [http://www.cip.ifi.lmu.de/~grinberg/floor.pdf] にもその名前がある。概念自体、上のLehmer やSterneckでも取り扱われている。

一方で、gcdで畳み込む場合はちょっと事情が異なる。無限級数をgcdで畳み込もうとすると、一般には各項の係数が有限和にならないことがわかる（つまり、$\mathrm{lcm}(a,b)=n$ なる$a,b$は有限個だが、$\mathrm{gcd}(a,b)=n$なる$a,b$は無限個ある）。
そのためか、上のサーベイで定義された「gcd convolution」は本文で紹介したgcdでの畳み込みとは異なっている。調べた限り、gcdでの畳み込みはあまり定着した専門用語がなさそう。競プロでは、計算量の関係からgcdでの畳み込みのほうがよく現れるのでちょっと困る。

#蛇足
以下は蛇足。少しだけ一般化して話をする。

Poset上のメビウス変換

ゼータ変換、メビウス変換は、一般にposet(半順序集合,partially ordered set)上で定義される。
Rota, On the Foundations of Combinatorial Theory I. Theory of Möbius Functions
とか、
Enumerative Combinatoricsのプレプリント [http://math.mit.edu/~rstan/ec/ec1/]
を読めばよさそう？

集合$X$と$X$上の二項関係$\le$ が以下の３条件をみたすとき、$X$は poset であるという。

• 反射律 $x \le x$
• 推移律 $x \le y$, $y \le z$ $\implies$ $x \le z$
• 反対称律 $x \le y$, $y \le x$ $\implies$ $x = y$

たとえば、以下の例はすべてposet

• $X=\mathbb{N}$は非負整数全体, 普通の整数の順序
• $X=\mathbb{N}^2$, $(a,b) \le (c,d) \iff a \le c, b \le d$
• $X=2^U$（集合$U$のべき集合）, $S \subset T$のときに$S \le T$と定める
• $X$は非負整数全体, $a|b$のときに$a \le b$と定める

以下有限posetに限って話を進める。
$X$上の関数$f$のゼータ変換を次で定める：
$$
\begin{align}
f_{\le}(x) &:= \sum_{i \le x}f(i) = f(i)\zeta(i,x) \
f_{\ge}(x) &:= \sum_{i \ge x}f(i) = f(i)\zeta(x,i)
\end{align}
$$
ただし$a \le b$のとき$\zeta(a,b) = 1$,そうでないとき$\zeta(a,b) = 0$.
また、これらの逆変換をメビウス変換という。
メビウス変換はきちんと定まる（$\zeta(x,y)$の逆行列となる）。

いままで紹介してきたゼータ変換は、すべてこの枠組みで解釈できる。
つまり、上のposetの例がそれぞれ1次元累積和、2次元累積和、部分集合、約数倍数に相当する。

##束上の畳み込み

畳み込みを定義するにあたっては、poset だけではすこし構造が弱い。
二元$a,b \in X$について、$a,b$よりも大きいもののなかで最小の元および$a,b$よりも小さいもののなかで最大の元が存在してくれると都合がよい。そういった都合の良い元を結び、交わりといい、$a \vee b$, $a \wedge b$とかく。
そのようなposetを束という。実は、先ほど例に挙げたposetはすべて束となっている。

とくに先ほどの例について、

• $X=\mathbb{N}^2$の例では $(a,b)\vee(c,d)=(\max(a,b),\max(c,d))$
• $X=2^U$（集合$U$のべき集合）の例では $S \vee T = S \cup T$
• $X$は非負整数全体, $a|b$の順序の例では$a \vee b = \mathrm{lcm}(a,b)$

などとなっている。

さて、束上の畳み込みを
$$
\begin{align}
f@g(x) &= \sum_{s \wedge t = x} f(s)g(t)　\
fg(x) &= \sum_{s \vee t = x} f(s)g(t)
\end{align}
$$
と定める（この記号はここだけのものなのでマネしないで下さい）。
このとき以下の畳み込み定理が成立する。
$$
\begin{align}
(f@g)_{\le} = f_{\le} \cdot g_{\le}, \
(fg)_{\ge} = f_{\ge} \cdot g_{\ge}
\end{align}
$$
ただし、右辺の積は各点積。

証明

束を仮定していたので、 $s \le x かつ t \le x \iff s \vee t \le x$ が成立する。よって

\begin{align}
f_{\le}(x) \cdot g_{\le}(x)
&= \sum_{s \le x} f(s) \sum_{t \le x} g(t)  \\\
&= \sum_{s,t\colon\, s,t \le x} f(s)g(t)  \\\
&= \sum_{y\colon\, y \le x} \sum_{s,t\colon\, s \vee t = y} f(s)g(t)  \\\
&= (f*g)_{\le}(x)
\end{align}

フーリエ変換と畳みこみ

$G$が有限群のとき関数環 $\mathbb{C}^G$は半単純で、とある行列環の直積と同型になる。
ここで、左辺の積は畳みこみ積、右辺の積は行列積である。
この対応をフーリエ変換と呼ぶ本もある。

ところでこんなことを知らなくても、$G$が可換のときは関数環が1次元の積に分解できる（行列環がすべて$1$次となる）。
別の見方をすると、指標（つまり$G$から$\mathbb{C}$への準同型）が関数環の基底になっていて、この基底の係数を見ているということ。
もしくは、環の同型
$$\mathbb{C}^{\mathbb{Z}/n\mathbb{Z}}
\simeq \mathbb{C}[x]/(x^n-1)
\simeq \bigoplus_i \mathbb{C}[x]/(x-w^i)
\simeq \bigoplus_i \mathbb{C}
$$
の左辺が関数環、右辺が1次元への分解となってると見ても大丈夫。
で、1次元行列の積はただのスカラーの積なので、分解したほうの積は「各点積」となる。
こうして、左辺の畳みこみ積が、フーリエ変換を通して右辺では各点積という計算が容易なものになる、
というのが離散フーリエ変換の畳み込みというやつだ。
（$G=(\mathbb{Z}/2\mathbb{Z})^n$としたのがWalshの畳み込みだ。）

ところで$L$をfinite meet-semilatticeとすると、
関数環$\mathbb{C}^L$はやはり$L$の演算から畳みこみ積が入る。
この関数環を分解したい。
で、すでにみんな知っている通り、ゼータ変換により環としての同型
$$\mathbb{C}^L
= \bigoplus_{z \in L} \mathbb{C} \mu(z,-) \simeq
\bigoplus_{z \in L} \mathbb{C}
$$
があって、１次元代数の積に分解できる。おまえも半単純だったのか。
こうしてmeet-semilatticeの畳み込みがゼータ変換を通して各点積に化けた。