0. はじめに
気軽な気持ちでプログラムを書いたら計算量オーダーが $O(n^2)$ になってしまって処理がメチャクチャ遅い、というのは大変あるあるです (この記事など)。そういった状況を打破するために、古来から $O(n^2)$ なアルゴリズムを $O(n)$ や $O(n\log{n})$ に改良するテクニックは無数に考案されて来ました。逆に本来なら $O(n)$ で終わるはずの処理を雑に実装したために $O(n^2)$ になってしまうトラップも無数に知られています。その辺りの話は以下に特集してみました:
今回は $O(n^2)$ を $O(n)$ にするテクニックの 1 つであるしゃくとり法について、個人的に思うことを書いて行きます。またしゃくとり法を用いる以下の問題たちを紹介します:
- AOJ Course The Number of Windows (300〜400点相当、最初の例題という感じ)
- POJ 3061 Subsequence (300〜400点相当、蟻本の例題)
- ABC 032 C 列 (300〜400点相当)
- ABC 038 C 単調増加 (400点相当)
- ARC 022 B 細長いお菓子 (400〜500点相当、データ構造を少し考えます)
- ABC 098 D Xor Sum 2 (500点、xor に惑わされないようにしたいです)
- ABC 017 D サプリメント (600〜700点相当、DP との組み合わせ)
- JOI 2013 本選 C バームクーヘン (600点相当、二分探索との組み合わせ)
- JOI 2017 予選 E L番目のK番目の数 (700〜800点相当、二分探索との組み合わせ)
1. しゃくとり法とは
1-1. しゃくとり法が使える場面
しゃくとり法は、以下の形式の問題を解くときに使える可能性のあるテクニックです:
長さ $n$ の数列 $a_1, a_2, \dots, a_n$ において
- 「条件」を満たす区間 (連続する部分列) のうち、最小の長さを求めよ
- 「条件」を満たす区間 (連続する部分列) のうち、最大の長さを求めよ
- 「条件」を満たす区間 (連続する部分列) を数え上げよ
つまりは条件を満たすような区間をすべて求めることができる方法です。愚直に全探索をしようと思うと、$n(n+1)/2$ 個の区間がある (後述) ため $O(n^2)$ の計算量を要します。それを鮮やかに $O(n)$ に改善します。
具体的な問題例は以下の表のように多岐にわたります。一番上の問題 1 で言えば、$a_1, a_2, \dots, a_n$ の連続する部分列のうち総和が $x$ 以下となるものを数え上げる問題です。

|通し番号|問題|条件|求めるもの|備考|
|---|---|---|---|---|---|
|問題 1|AOJ Course The Number of Windows|総和が $x$ 以下|数え上げ||
|問題 2|POJ 3061 Subsequence|総和が $x$ 以上|最小の長さ||
|問題 3|ABC 032 C 列|積が $K$ 以下|最大の長さ||
|問題 4|ABC 038 C 単調増加|単調増加|数え上げ||
|問題 5|ARC 022 B 細長いお菓子|同じ値を複数個含まない|最大の長さ||
|問題 6|ABC 098 D Xor Sum 2|xor 和と総和が等しい|数え上げ||
|問題 7|ABC 017 D サプリメント|同じ値を複数個含まない| - |DP 更新をしゃくとり法っぽく|
|問題 8|JOI 2013 本選 C バームクーヘン| 総和が $x$ 以上 |最小の長さ|$x$ を二分探索|
|問題 9|JOI 2017 予選 F L番目のK番目の数|$x$ 以下の値が $K$ 個以上ある|数え上げ|$x$ を二分探索|
1-2. 半開区間について
しゃくとり法に限らず、区間を考えるときは半開区間 [left, right) で考えるとよいことが多いです。区間 [3, 7) といった場合
- $a_3, a_4, a_5, a_6$
を表していて $a_7$ は含みません。半開区間は以下のように「しきりを入れている」と考えるとイメージしやすいと思います。区間 [3, 7) を以下に図示しています。こうして考えてみると、「区間」は「2 箇所にしきりを入れる方法」に対応します。しきりを入れる箇所の候補は $n+1$ 箇所あるため、区間は全部で $_{n+1}{\mathrm C}_2 = n(n+1)/2$ 個あります。

世の中の「区間」を扱う標準ライブラリの多くは半開区間で設計されています。例として配列 a に対して
std::sort(a, a+n);
と書いた場合には、配列 a の a[0], a[1], ..., a[n-1] をソートしていて a[n] は含まないです。Python のリスト a で a[3:7] のように書いた場合には [a[3], a[4], a[5], a[6]] を表していて a[7] は含まないです。
1-3. しゃくとり法のアイディア・実装
上の問題リストの問題 1 「総和が $x$ 以下となる区間の数え上げ」を見てみます。
問題 1: AOJ Course The Number of Windows
【問題概要】
長さ $n$ の正の整数列 $a_1, a_2, \dots, a_n$ と整数 $x$ が与えられる。整数列の連続する部分列で、その総和が $x$ 以下となるものを数え上げよ (実際の出題は $Q$ 個のクエリがあって各クエリごとに $x$ が与えられる)。
【制約】
- $1 \le n \le 10^5$
- $1 \le Q \le 500$
- $1 \le a_i \le 10^9$
- $1 \le x_j \le 10^{14}$
【数値例】
1)
$n = 6$
$x = 12$
$a = (5, 3, 8, 6, 1, 4)$
答え: $11$
(5), (5, 3), (3), (3, 8), (8), (6), (6, 1), (6, 1, 4), (1), (1, 4), (4) の 11 個です
例として
- $n = 12$
- $a = (4, 6, 7, 8, 1, 2, 110, 2, 4, 12, 3, 9)$
- $x = 25$
について考えてみます。基本的な方針としては区間の左端がどこかで場合分けします。区間の左端で場合分けしてみると以下のようになっています。注意点として、下の表では [4, 4) のような長さ 0 の区間 (left も right も 4 番目の仕切りを指している状態) も記入していますが、個数カウントには含めていないです。
| 左端 left | 条件を満たす右端 right | 区間の個数 | 備考 |
|---|---|---|---|
| 0 | 0, 1, 2, 3, 4 | 4 | [0, 0) の総和は 0、[0, 1) の総和は 4、[0, 2) の総和は 4+6=10、[0, 3) の総和は 4+6+7=17、[0, 4) は総和は 4+6+7+8=25 |
| 1 | 1, 2, 3, 4, 5, 6 | 5 | [1, 6) は総和は 6+7+8+1+2=24 で OK、[1, 7) は 134 で NG |
| 2 | 2, 3, 4, 5, 6 | 4 | [2, 7) はやはり総和 128 で NG |
| 3 | 3, 4, 5, 6 | 3 | |
| 4 | 4, 5, 6 | 2 | |
| 5 | 5, 6 | 1 | [5, 6) は総和 2 で OK |
| 6 | 6 | 0 | left = 6 では right = 6 (区間なし) しかない |
| 7 | 7, 8, 9, 10, 11 | 4 | |
| 8 | 8, 9, 10, 11 | 3 | |
| 9 | 9, 10, 11, 12 | 3 | |
| 10 | 10, 11, 12 | 2 | |
| 11 | 11, 12 | 1 | |
| 合計 | 32 | [4, 4) のようなものは含めないことに注意 |
観察として
- 区間の左端 left を固定すると、条件を満たす右端 right は left から始まる連続自然数になっている
ことがわかります。したがって各左端 left に対して、条件を満たす区間の右端 right の最大値を f(left) (上の表で太字で表した数値) とおいて、これを求めることができればよいです。ひとまず単純に考えれば、right = left, left+1, left+2, ..., と調べて行って、条件を満たさなくなる場所を検出することで実現できます。
# include <iostream>
# include <vector>
using namespace std;
int main() {
/* 入力受け取り */
int n, Q;
cin >> n >> Q;
vector<long long> a(n);
for (int i = 0; i < n; ++i) cin >> a[i];
/* Q 回分のクエリを処理 */
for (int j = 0; j < Q; ++j) {
long long x; cin >> x; // 各クエリ x
/* 合計値 */
long long res = 0;
/* 区間の左端 left で場合分け */
for (int left = 0; left < n; ++left) {
long long sum = 0;
int right = left; // [left, right) の総和が x 以下となる最大の right を求める
/* sum に a[right] を加えても大丈夫なら right を動かす */
while (right < n && sum + a[right] <= x) {
sum += a[right];
++right;
}
/* break した状態で right は条件を満たす最大 */
res += (right - left);
}
cout << res << endl;
}
}
しかしこれでは各 left に対して最悪 $O(n)$ かかるので全体で $O(n^2)$ かかってしまいます。ここからさらに観察を進めると、
- f(left) は広義単調増加関数
という際立った特徴があります。これこそがしゃくとり法の主要なアイディアだと思います。実際上の例に対して left = 0, 1, 2, ... に対する f(left) の値を見ると「4, 6, 6, 6, 6, 6, 6, 11, 11, 12, 12, 12」と単調増加になっています。このことを利用して鮮やかに $O(n)$ に高速化します。具体的には
f(left) まで求まっているときに次の f(left+1) を求めるときは、right = f(left) から出発して条件を満たさなくなるまでインクリメントしていく
という風にやります。具体的な動きとしては下図のようになります。left は下図の左側の太線を、right は下図の右側の太線を辿って行きます。「left を固定して right を右に動かして、今度は left を 1 増やして...」という動きがしゃくとり虫のようなので、しゃくとり法と呼ばれます。

# include <iostream>
# include <vector>
using namespace std;
int main() {
/* 入力受け取り */
int n, Q;
cin >> n >> Q;
vector<long long> a(n);
for (int i = 0; i < n; ++i) cin >> a[i];
/* Q 回分のクエリを処理 */
for (int j = 0; j < Q; ++j) {
long long x; cin >> x; // 各クエリ x
/* 合計値 */
long long res = 0;
/* 区間の左端 left で場合分け */
int right = 0; // 毎回 right を使い回すようにする
long long sum = 0; // sum も使い回す
for (int left = 0; left < n; ++left) {
/* sum に a[right] を加えても大丈夫なら right を動かす */
while (right < n && sum + a[right] <= x) {
sum += a[right];
++right;
}
/* break した状態で right は条件を満たす最大 */
res += (right - left);
/* left をインクリメントする準備 */
if (right == left) ++right; // right が left に重なったら right も動かす
else sum -= a[left]; // left のみがインクリメントされるので sum から a[left] を引く
}
cout << res << endl;
}
}
こうすると、left も right も結局左から右まで順に動くことがわかります。left と right が複雑な動きをしていても、トータルで見ると結局「2 つのポインタを左から右まで動かした」ということに過ぎないです。すなわち計算量は $O(n)$ になります。
なお、しゃくとり法の実装方法は様々な流儀があると考えられますが、以下の形式はそれなりに汎用性が高いのではないかと思います。
int right = 0;
for (int left = 0; left < n; ++left) {
while (right < n && (right を 1 個進めたときに条件を満たす)) {
/* 実際に right を 1 進める */
// ex: sum += a[right];
++right;
}
/* break した状態で right は条件を満たす最大なので、何かする */
// ex: res += (right - left);
/* left をインクリメントする準備 */
// ex: if (right == left) ++right;
// ex: else sum -= a[left];
}
1-3. しゃくとり法が使える条件
しゃくとり法は
- 「条件」を満たす区間 (連続する部分列) のうち、最小の長さを求める
- 「条件」を満たす区間 (連続する部分列) のうち、最大の長さを求める
- 「条件」を満たす区間 (連続する部分列) を数え上げる
といったことを効率良く実現できる手法ですが、「条件」というのが何でもいいわけではないです。「条件を満たす区間」が以下のいずれかの構造になっている場合には、しゃくとり法を適用することができます:
- 区間 [left, right) が「条件」を満たすなら、それに含まれる区間も「条件」を満たす
- 区間 [left, right) が「条件」を満たすなら、それを含む区間も「条件」を満たす
例えば、上の表の問題 1 の条件「総和が $x$ 以下」については 1 個目の構造になっています。逆に問題 2 の条件「総和が $x$ 以上」については 2 個目の構造になっています。
1 個目の構造になっているとき、一般に
- 区間の左端 left に対する、条件を満たす右端の最大値 f(left) は広義単調増加関数
という風になるのでしゃくとり法が使えます。反対に 2 個目の構造になっている場合は
- 区間の左端 left に対する、条件を満たす右端の最小値 f(left) は広義単調増加関数
という風になります。次の節の「問題 2: POJ 3061 Subsequence」でそのような問題を見てみます。
2. しゃくとり法のバリエーション
上で登場した「問題 1: AOJ Course The Number of Windows」の反対バージョンの問題を見てみます。蟻本にも載っている例題です。さっきは条件が「総和が $x$ 以下」だったのに対して、今回は「総和が $x$ 以上」になっています。またさっきは「区間の数え上げ」でしたが今回は「区間の長さの最小値」を求める問題になっています。
問題 2: POJ 3061 Subsequence
【問題概要】
長さ $n$ の正の整数列 $a_1, a_2, \dots, a_n$ と整数 $x$ が与えられる。整数列の連続する部分列で、その総和が $x$ 以上となるもののうち、最小の長さを求めよ (実際の出題は $Q$ 個のクエリがあって各クエリごとに $x$ が与えられ、条件を満たす区間がないときは $0$ を出力)。
【制約】
- $10 \le n \le 10^5$
- $1 \le a_i \le 10^4$
- $1 \le x \le 10^{9}$
【数値例】
1)
$n = 10$
$x = 28$
$a = (5, 1, 2, 5, 10, 7, 4, 9, 2, 8)$
答え: $4$
(10, 7, 4, 9) の総和は 30 となって長さ最小です
例として
- $n = 12$
- $a = (4, 6, 7, 8, 1, 2, 110, 2, 4, 20, 3, 9)$
- $x = 25$
について考えてみると以下の表のようになります。left = 10, 11 に対しては条件を満たす right は存在しないので ∞ としています。
|左端 left |条件を満たす右端 right|区間の長さの最小値|
|---|---|---|---|
|0|4, 5, 6, 7, 8, 9, 10, 11, 12|4|
|1|7, 8, 9, 10, 11, 12|6|
|2|7, 8, 9, 10, 11, 12|5|
|3|7, 8, 9, 10, 11, 12|4|
|4|7, 8, 9, 10, 11, 12|3|
|5|7, 8, 9, 10, 11, 12|2|
|6|7, 8, 9, 10, 11, 12|1|
|7|10, 11, 12|3|
|8|11, 12|3|
|9|12|3|
|10|∞|-|
|11|∞|-|
|トータル||1|
今度は
- 区間の左端 left に対する、条件を満たす右端の最小値 f(left) は広義単調増加関数
という風になっています。実装方法的には、さっきと同じようにできます。注意点としては、 left によっては条件を満たす right が存在しなくなってしまう (上の表の ∞) ので、その判定を怠らないようにします。
# include <iostream>
# include <vector>
using namespace std;
int main() {
/* クエリ回数 */
int Q;
cin >> Q;
for (int query = 0; query < Q; ++query) {
/* 入力受け取り */
int n; cin >> n;
long long x; cin >> x;
vector<long long> a(n);
for (int i = 0; i < n; ++i) cin >> a[i];
/* 区間の長さの最小値 */
int res = n+1; // 上界を入れておく
/* 区間の左端 left で場合分け */
int right = 0;
long long sum = 0;
for (int left = 0; left < n; ++left) {
/* [left, right) の総和が x 以上となる最小の right を求める */
while (right < n && sum < x) {
sum += a[right];
++right;
}
/* 更新 */
if (sum < x) break; // これ以上 left を進めてもダメ
res = min(res, right - left);
/* left をインクリメントする準備 */
if (right == left) ++right; // right が left に重なったら right も動かす
else sum -= a[left]; // left のみがインクリメントされるので sum から a[left] を引く
}
/* res = n+1 のときは解なし */
if (res < n+1) cout << res << endl;
else cout << 0 << endl;
}
}
3. しゃくとり法を様々な視点から
3-1. 二分探索法との類似
しゃくとり法は条件を満たす区間を全列挙する手法だと言えますが、
- 区間の左端 left を固定したときに、条件を満たす区間の右端 right に単調性がある (途中から満たさなくなる or 途中から満たすようになる)
- 区間の左端 left に対して、条件を満たす区間の右端の最大値 or 最小値 f(left) は広義単調増加関数である
という 2 つの性質を上手に活用するものでした。このうちの 1 個目を見ると二分探索法も自然だと思えて来ます。実際、$O(n)$ なしゃくとり法が想定解法の問題において、別解として $O(n\log{n})$ な二分探索法でも解けるケースは多いように思います。
3-2. しゃくとり法の適用範囲を拡げる
しゃくとり法の動きを見ていると、「区間の数え上げ問題」についてはともかく、「区間の長さの最大値 (最小値)」を求める問題に対しては、もう少し一般化できそうです。一般にニ変数関数 $g(x, y)$ ($x, y $ は $0$ 以上 $N$ 以下の整数) があってこれを最大化したいとなったときに、
- $x$ を固定したときに $g(y) = g(x, y)$ は上に凸な関数になる
- $x$ を固定したときに $g$ が最大となるような $y$ を $f(x) := {\rm argmax}_y g(x, y)$ とおくと、$f(x)$ は広義単調増加関数である
という性質を満たしていれば、しゃくとり法を適用して $g(x, y)$ の最大値を求めることができます。この視点を利用して解ける問題やアルゴリズムとして
がありました。後者は比較的難しく三分探索法などの様々な解法があるようですが、$O(n)$ なしゃくとり法で解けます。なお、今までの「条件を満たす区間の長さの最大値」を求めていたしゃくとり法は、このフレームワークの特殊ケースと言えます。実際
g(left, right) := (条件をみたす ? right - left : -∞)
とすれば、これは left を固定したときに上に凸な関数になっています。
3-3. スライド最小値や Convex Hull Trick
さらに、3-2 のような視点を用いることで応用の広がるアルゴリズムとして
- スライド最小値
- Convex Hull Trick
が有名です。スライド最小値とは、
- 区間 [$l, r$) における最小値を求めよ
という大量のクエリたちを爆速に処理する手法であり、$l$ にも $r$ にも単調性があった場合には「区間内の最小値をとる index が単調増加になる」という条件を満たすため、しゃくとり法のような方法がバッチリ決まります。全体としてセグメントツリーを用いるよりも高速に処理できるようになります。実装例としては以下のような感じです:
# include <iostream>
# include <vector>
# include <deque>
# include <algorithm>
using namespace std;
using pll = pair<long long, long long>;
// slide min
template<class VAL, class TIME> struct SlideMin {
const VAL INF = 1LL<<60; // to be set appropriately
const TIME nul = -1; // to be set appropriately
deque<pair<VAL, TIME> > deq;
SlideMin() { }
// get minimum
pair<VAL, TIME> get() {
if (deq.empty()) return make_pair(INF, nul);
return deq.front();
}
// push (v, t), "t is non-decreasing" is necessary
void push(VAL v, TIME t) {
while (!deq.empty() && deq.back().first >= v) deq.pop_back();
deq.emplace_back(v, t);
}
// pop "< t", "t it non-decreasing" is necessary
void pop(TIME t) {
while (!deq.empty() && deq.front().second < t) deq.pop_front();
}
};
さらに、スライド最小値の考え方を有効に用いることのできる DP 高速化手法として Convex Hull Trick が有名です。以下の記事たちがとても読みやすいです:
- Convex-Hull Trick (satanic さん)
- 傾きの単調性が要らない Convex Hull Trick (kazuma さん)
4. 問題例
「条件」を満たす区間を数え上げたり、区間の長さの最大値・最小値を求めたりする問題たちを解いて行きます。
問題 3: ABC 032 C 列
【問題概要】
長さ $n$ の整数列 $a_1, a_2, \dots, a_n$ と整数 $K$ が与えられる。整数列の連続する部分列で、その積が $K$ 以下となるもののうち、最大の長さを求めよ (条件を満たす区間がないときは $0$ を出力)。
【制約】
- $1 \le n \le 10^5$
- $0 \le a_i, X \le 10^9$
【数値例】
1)
$n = 7$
$K = 6$
$a = (4, 3, 1, 1, 2, 10, 2)$
答え: $4$
(3, 1, 1, 2) の積は 6 となって長さ最大です
【解法】
「積が $K$ 以下」という条件は、基本的には「満たしている区間の部分区間も満たす」という構造をしています。それを利用してしゃくとり法します。コーナーケースとして、$a$ の中に $0$ がある場合は実装がイヤなので除外しておきます (全部の積が $0$ になるので答えは $n$)。
# include <iostream>
# include <vector>
using namespace std;
int main() {
/* 入力受け取り */
int n;
long long K;
cin >> n >> K;
vector<long long> a(n);
for (int i = 0; i < n; ++i) cin >> a[i];
/* 0 があったら n をリターン */
for (int i = 0; i < n; ++i) {
if (a[i] == 0) {
cout << n << endl;
return 0;
}
}
/* しゃくとり法 */
int res = 0;
int right = 0;
long long mul = 1;
for (int left = 0; left < n; ++left) {
while (right < n && mul * a[right] <= K) {
mul *= a[right];
++right;
}
res = max(res, right - left); // 更新
if (left == right) ++right;
else mul /= a[left]; // left を除く
}
cout << res << endl;
}
問題 4: ABC 038 C 単調増加
【問題概要】
長さ $n$ の正の整数列 $a_1, a_2, \dots, a_n$ が与えられる。整数列の連続する部分列のうち、単調増加となっているものを数え上げよ。
【制約】
- $1 \le n \le 10^5$
- $1 \le a_i \le 10^5$
【数値例】
1)
$n = 5$
$a = (1, 2, 3, 2, 1)$
答え: $8$
(1), (1, 2), (1, 2, 3), (2), (2, 3), (3), (2), (1) の 8 個です
【解法】
「単調増加」という条件も「満たしている区間の部分区間も満たす」という構造をしているので、しゃくとり法できます。[l, r) という条件は
- r = l+1 なら常に OK
- [l, r-1) が単調増加で a[r-2] < a[r-1] なら OK
という感じです。
# include <iostream>
# include <vector>
using namespace std;
int main() {
/* 入力受け取り */
int n;
cin >> n;
vector<long long> a(n);
for (int i = 0; i < n; ++i) cin >> a[i];
/* しゃくとり法 */
long long res = 0;
int right = 1; // [0, 1) は確実に条件を満たす
for (int left = 0; left < n; ++left) {
// right を 1 個進めたものが条件を満たすかどうか
while (right < n && (right <= left || a[right - 1] < a[right])) {
++right;
}
res += right - left;
if (left == right) ++right;
}
cout << res << endl;
}
問題 5: ARC 022 B 細長いお菓子
【問題概要】
長さ $n$ の正の整数列 $a_1, a_2, \dots, a_n$ が与えられる。整数列の連続する部分列のうち、「同じ数値が 2 箇所以上登場しない」という条件を満たす最大長を求めよ。
【制約】
- $1 \le n \le 10^5$
- $1 \le a_i \le 10^5$
【数値例】
1)
$n = 7$
$a = (1, 2, 1, 3, 1, 4, 4)$
答え: $3$
(2, 1, 3) などが条件を満たします。
【解法】
だんだんと条件が複雑になって来ていますが、「同じ数値が 2 箇所以上登場しない」という条件も今までと同様に「条件を満たす区間の部分区間も条件を満たす」という構造になっています。「同じ数値が 2 箇所以上登場しない」という条件は set や連想配列やバケットなどを用いて管理します。
a[i] の範囲が $10^5$ 以下と小さいのでバケットでもできますが、ここでは set を用いてみます。
# include <iostream>
# include <vector>
# include <set>
using namespace std;
int main() {
/* 入力受け取り */
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; ++i) cin >> a[i];
/* しゃくとり法 */
int res = 0;
int right = 0;
set<int> member;
for (int left = 0; left < n; ++left) {
while (right < n && !member.count(a[right])) {
member.insert(a[right]);
++right;
}
res = max(res, right - left);
if (left == right) ++right;
else {
member.erase(a[left]); // a[left] を削除
}
}
cout << res << endl;
}
問題 6: ABC 098 D Xor Sum 2
【問題概要】
長さ $n$ の正の整数列 $a_1, a_2, \dots, a_n$ が与えられる。整数列の連続する部分列のうち、「xor 和と加算和とが等しい」という条件を満たすものを数え上げよ。
【制約】
- $1 \le n \le 2*10^5$
- $0 \le a_i \le 2^{20}$
【数値例】
1)
$n = 4$
$a = (2, 5, 4, 6)$
答え: $5$
(2), (2, 5), (5), (4), (6) の 5 個です
【解法】
「xor 和と加算和とが等しい」という条件が、「条件を満たす区間の部分区間も条件を満たす」という構造になっていることは非自明かもしれません。そこが示せたら、あとはしゃくとり法を適用するだけになります。
基本的に「xor 和 <= 加算和」が成り立ちます。例えば x = 10101 (二進法)、y = 1001 (二進法) としたとき、
x xor y = 11100 (一の位が消えます)
x + y = 11110 (一の位が繰り上がります)
という感じになり、x + y は繰り上がりが残るのに対し、x xor y は 1 が被ると消えてしまいます。そう考えると
x xor y = x + y
⇔
二進法におけるどの桁を見ても $x$ と $y$ のうちビットが立っているのは高々一方のみ
となります。つまり条件は「どの桁を見てもビットが立っているのは高々 1 個のみ」と同値になります。ここまで来ると確かに「条件を満たす区間の部分区間も条件を満たす」という構造を満たしていることがわかります。
実装上は、「各桁ごとに」という考え方をせずに、直接 sum xor a[right] = sum + a[right] になるかどうかを判定した方が楽です。
# include <iostream>
# include <vector>
# include <set>
using namespace std;
int main() {
/* 入力受け取り */
int n;
cin >> n;
vector<int> a(n);
for (int i = 0; i < n; ++i) cin >> a[i];
/* しゃくとり法 */
long long res = 0;
int right = 0;
int sum = 0; // AND 和
for (int left = 0; left < n; ++left) {
while (right < n && (sum ^ a[right]) == (sum + a[right])) {
sum += a[right];
++right;
}
res += right - left;
if (left == right) ++right;
else {
sum -= a[left]; // a[left] を削除 (sum ^= a[left] でも OK)
}
}
cout << res << endl;
}
問題 7: ABC 017 D サプリメント
【問題概要】
$1$ 以上 $M$ 以下の整数からなる長さ $N$ の数列 $f_1, f_2, \dots, f_n$ が与えられる。数列を前から順番に区切って行く。各区間は「同じ値が二度以上登場しない」という条件を満たすようにしたい。そのような方法が何通りあるかを 1000000007 で割った余りで求めよ。
【制約】
- $1 \le N, M \le 10^5$
【数値例】
1)
$N = 5$
$M = 2$
$f = (1, 2, 1, 2, 2)$
答え: $5$
(1)(2)(1)(2)(2)
(1)(2)(1,2)(2)
(1)(2,1)(2)(2)
(1,2)(1)(2)(2)
(1,2)(1,2)(2)
の 5 通りがあります
【解法】
この辺りから複合的な問題になります。基本的には以下のタイプの DP をします。
dp[i] := 最初の i 個のサプリまで吸収する方法の数 (i 個目を吸収した段階で一旦区切る)
dp[0] = 1
dp[i] = 区間 [j, i) が「複数種類のサプリがない」という条件を満たすような j についての dp[j] の総和
各 i に対して上記のような j の範囲はしゃくとり法によって求めることができます。j の範囲が [left, i) で与えられるとき、
dp[i] = dp[left] + dp[left+1] + ... + dp[i-1]
という風になります。このままでは最悪 $O(n)$ 回の計算をすることになるので DP 全体で $O(n^2)$ かかってしまいそうなのですが、累積和を用いることで解決します:
sum[i+1] = dp[0] + dp[1] + ... + dp[i]
として、
dp[i] = sum[i] - sum[left]
と更新すればよいです。
# include <iostream>
# include <vector>
using namespace std;
const int MOD = 1000000007;
int dp[110000];
int sum[110000];
int main() {
/* 入力 */
int N, M;
cin >> N >> M;
vector<int> f(N);
for (int i = 0; i < N; ++i) cin >> f[i], --f[i];
/* しゃくとり法 */
vector<int> fnum(M, 0); // 区間に種類 i が何個あるか
vector<int> L(N+1, 0); // 各 i に対するしゃくとり法の区間
int left = 0;
for (int right = 0; right < N; ++right) {
fnum[f[right]]++;
while (left < right && fnum[f[right]] > 1) {
--fnum[f[left]];
++left;
}
L[right+1] = left;
}
/* 累積和で高速化した DP */
dp[0] = 1;
sum[0] = 0; sum[1] = 1;
for (int i = 1; i <= N; ++i) {
dp[i] = (sum[i] - sum[L[i]] + MOD) % MOD; // DP
sum[i+1] = (sum[i] + dp[i]) % MOD; // 累積
}
cout << dp[N] << endl;
}
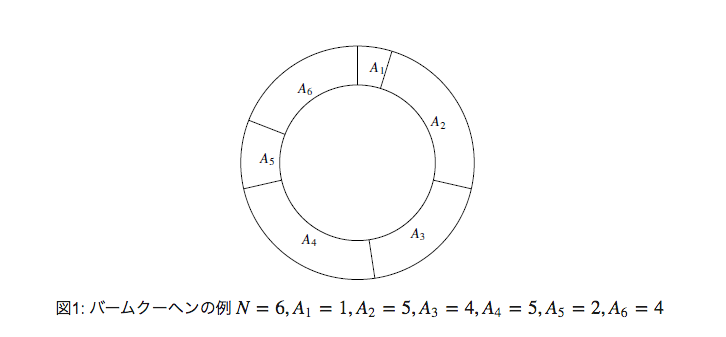
問題 8: JOI 2013 本選 C バームクーヘン
【問題概要】
環状のバームクーヘンを 3 つに分けたい。バームクーヘンは下図 (問題文から引用) のように $N$ 個のピースに分かれていて、それぞれのサイズは $A_1, A_2, \dots, A_N$ となっている。バームクーヘンに 3 箇所切り込みを入れて、3 つの連続するピース列に分割する。その 3 つのピースサイズの最小値が最大になるようにせよ。
【制約】
- $3 \le N \le 10^5$
- $1 \le A_i \le 10^9$
【数値例】
1)
$N = 6$
$A = (5, 4, 5, 2, 4, 1)$
答え: $6$
(4, 5), (2, 4), (1, 5) に切り分けます
【解法】
「最小値の最大化」なので二分探索法が自然です。三区間とも $x$ 以上にできるかどうかを判定する問題が解ければよいです。判定方法としては、バームクーヘンの切り込みを入れる位置を $N$ 通り全探索して、それぞれの場合について「総和が $x$ 以上」になる最小の区間を順に切って行って (ここでしゃくとり法)、最後に残るピースのサイズが $x$ 以上になるかどうかを check すればよいです。
# include <iostream>
# include <vector>
using namespace std;
int main() {
/* 入力 */
int N;
cin >> N;
vector<long long> a(N*2); // 環状の数列を扱うときは二週確保はよくやる
long long total = 0; // バームクーヘン全体のサイズ
for (int i = 0; i < N; ++i) cin >> a[i], a[i+N] = a[i], total += a[i];
/* 二分探索 */
long long low = 0, high = 1LL<<60;
while (high - low > 1) {
/* 3 ピースとも mid 以上にできるかを判定する */
long long mid = low + (high - low) / 2;
/* しゃくとり法により、各切れ目から mid 以上になる最小区間がどこまでかを求める */
vector<int> Next(N, -1);
vector<long long> Size(N, -1);
int right = 0;
long long sum = 0;
for (int left = 0; left < N; ++left) {
while (right < N*2 && sum < mid) {
sum += a[right];
++right;
}
if (sum >= mid) { // mid 以上なら記録
Next[left] = right;
Size[left] = sum;
}
if (right == left) ++right;
else sum -= a[left];
}
/* check */
bool ok = false;
for (int i = 0; i < N; ++i) {
/* 1 ピース目 */
int ni = Next[i];
if (ni == -1) continue;
if (Size[i] >= total) continue;
/* 2 ピース目 */
ni %= N;
int nni = Next[ni];
if (nni == -1) continue;
// 残りが mid 以上なら OK
if (total - Size[i] - Size[ni] >= mid) ok = true;
}
if (!ok) high = mid;
else low = mid;
}
cout << low << endl;
}
問題 9: JOI 2017 予選 F L番目のK番目の数
【問題概要】
長さ $N$ の整数列 $a_1, a_2, \dots, a_N$ が与えられる。整数列の連続する部分列のうち長さが $K$ 以上のものそれぞれについて、その中で $K$ 番目に小さい数を書き出していく。こうして書き出された数のうち $L$ 番目に小さい数を求めよ。
【制約】
- $1 \le K \le N \le 2*10^5$
- $1 \le a_i \le N$
- 書き出される数の個数は $L$ 個以上
【数値例】
1)
$N = 4$
$K = 3$
$L = 2$
$a = (4, 3, 1, 2)$
答え: $3$
長さが 3 以上の区間は (4, 3, 1), (4, 3, 1, 2), (3, 1, 2) の 3 つがあり、それぞれについて 3 番目に小さい値は 4, 3, 3 となる。このうち 2 番目に小さい値は 3 である。
【解法】
$L$ 番目を求める問題において、二分探索法が有効であるケースは多いです。すなわち、$x$ 以下が $L$ 個あるかどうかを判定する問題に帰着させて解きます。
そうするとこの問題は、整数列の部分列のうち「$x$ 以下の値が $K$ 個以上ある」という条件を満たすものを数え上げる問題になります。そのような条件を扱うこと自体が難しめですが、BITを用いることで実現できます。
# include <iostream>
# include <vector>
using namespace std;
/* BIT */
template <class Abel> struct BIT {
vector<Abel> dat;
Abel UNITY_SUM = 0; // to be set
/* [1, n] */
BIT(int n) { init(n); }
void init(int n) {
dat.resize(n + 1);
for (int i = 0; i < (int)dat.size(); ++i) dat[i] = UNITY_SUM;
}
/* a is 1-indexed */
inline void add(int a, Abel x) {
for (int i = a; i < (int)dat.size(); i += i & -i)
dat[i] = dat[i] + x;
}
/* [1, a], a is 1-indexed */
inline Abel sum(int a) {
Abel res = UNITY_SUM;
for (int i = a; i > 0; i -= i & -i)
res = res + dat[i];
return res;
}
/* [a, b), a and b are 1-indexed */
inline Abel sum(int a, int b) {
return sum(b - 1) - sum(a - 1);
}
};
int main() {
/* 入力 */
int N, K;
long long L;
cin >> N >> K >> L;
vector<int> a(N);
for (int i = 0; i < N; ++i) cin >> a[i];
/* 二分探索 */
int low = 0, high = N;
while (high - low > 1) {
/* mid 以下の値が L 個あるかを判定する */
int mid = low + (high - low) / 2;
/* しゃくとり法で、mid 以下の値が K 個以上あるような区間を数え上げる */
BIT<int> bit(N+1);
int right = 0;
long long num = 0;
for (int left = 0; left < N; ++left) {
while (right < N && bit.sum(mid) < K) {
bit.add(a[right], 1);
++right;
}
if (bit.sum(mid) < K) break;
num += N - right + 1;
bit.add(a[left], -1);
}
if (num >= L) high = mid;
else low = mid;
}
cout << high << endl;
}