はじめに
この記事はCompetitive Programming (1) Advent Calendar 2018の9日目の記事となります.
競技プログラミングの題材の裏表に時折登場する,論理演算ならびにその(非負)整数型へのビットごとの拡張であるところの排他的論理和(XOR)について基本的な事柄をまとめてみました.
どうでもいいですが私のアイコンは競技プログラミングを始めた頃,あまりにXORが分からなかった哀しみからXORの回路記号を使用しています.
排他的論理和とは
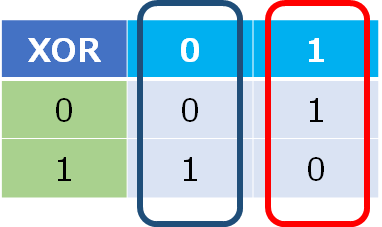
論理演算としての排他的論理和は以下の真理値表であらわされます.0をfalse,1をtrueとして,
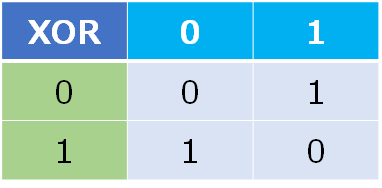
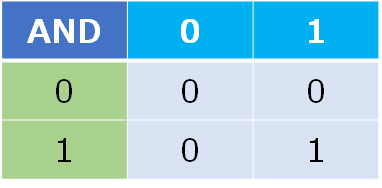
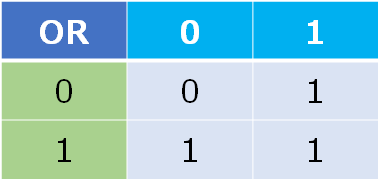
見慣れた論理積(AND)や論理和(OR)と比べると少し直感的には分かりにくいでしょうか.
どうみるか
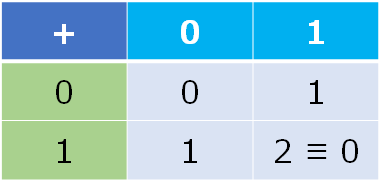
Z/2Zの足し算
2で割った剰余の世界( $\mathbb{Z} / 2 \mathbb{Z}$ )の足し算と思うことができます.
イネーブル付きの反転スイッチ
片方がもう片方に作用していると考えると,元の値に対して0を作用させても何も変わらず,1を作用させると値が反転する.
ビットワイズXOR
ANDやORと同じく,2進数であらわしたときのビットごとのXORを考えたものを(ビットワイズ)XORと定義している.C系の言語では$\mathbin{\text{^}}$が用いられている.(以降特に断らない限り,XORはbitwise XORを指すこととする.)
// 0b は2進数リテラルのヘッダ
int a = 0b11010110
int b = 0b01110101
a ^ b == 0b10100011 // bitwise XOR
a & b == 0b01010100 // bitwise AND
a | b == 0b11110111 // bitwise OR
XORの性質
- 可換(左右について対象)
a ^ b == b ^ a // ビットごとに見て可換なので全体でも可換
- 結合的
(a ^ b) ^ c == a ^ (b ^ c) // ビットごとに見て結合的なので
- 2回作用させると元に戻る.これは特に作用$\mathbin{\text{^}}$$x$が作用$\mathbin{\text{^}}$$x$の逆元になっていることであり,さらに言うと逆元を持つことから単射の作用になっている.
a ^ x ^ x == a // ^x 自身が逆元になる.(ビットごとに見て確認できる)
a ^ x == b ^ x <=> a == b // ^x を作用させることでつぶれたりしない.
a != b <=> a ^ x != b ^ x // ^x を作用させることでつぶれたりしない.
- (普通の和と違って)各位のビットが桁あふれしない.特に $a$ $\mathbin{\text{^}}$ $b$ は数値としての大小で $a+b$を超えない.
int a = 0b11010110
int b = 0b01110101
a ^ b == 0b10100011 // a ^ b のビット長は a, b のMaxビット長を超えない.
a + b == 0b101001011 // a + b のビット長は a, b のMaxビット長を超えることもある.
a ^ b <= a + b // 桁あふれするビットのcarryの分だけ等号が成り立たなくなる.
基本的な性質はここに挙げた4つですが,手軽に非自明な変換を作ることが可能なため競技プログラミングの問題の題材やテクニックとしてよく登場します.
使い方・使われ方
- ビット演算:特定のビットを反転する時に使う(enableするときにはOR/disableする時には反転マスクのANDを使うのが普通ですね)(181213修正)
int mask = 0b00100110
mask |= (1 << 3); // mask == 0b00101110
mask |= (1 << 3); // mask == 0b00101110 (念のためもう一回やっても大丈夫(やりません))
mask &= ~(1 << 2); // mask == 0b00101010
mask &= ~(1 << 2); // mask == 0b00101010 (念のためもう一回やっても大丈夫(やりません))
mask ^= (1 << 5); // mask == 0b00001010
mask ^= (1 << 5); // mask == 0b00101010 (念のためもう一回やると大惨事)
- Nim/Grundy数:
Nimやそれに帰着される2人ゲームにおいて,山が複数に分かれるようなものはそれぞれの山のgrundy数の総XOR和で全体の局面のgrundy数が計算できる. - 区間XOR和,累積XOR和: 普通の区間和/累積和と同じように計算できる.引き算(逆元操作)も前述のとおりXORなので,それを利用する.区間XOR和はセグメント木やBITに乗せたりもできる.
int[] a = {3, 8, 9, 2};
// 例えば,自分以外のXORをそれぞれの要素に対し求めたいときに,
int total = 0;
for(int i=0;i<4;i++) total ^= a[i];
for(int i=0;i<4;i++) {
int totalWithoutMe = total ^ a[i]; // 自分だけ総XOR和から引く
}
- XOR自体はビット間で独立であることから,ビット毎に考える方針が有効な問題もちらほらある.
- 特に値の大小が問題となる場合は,(XORに限ったことではないが)大小が決定するビットを全探索するのが有効なことが多い?
- XORで生成できる数の個数:32bit整数が複数与えられたときにそれらのXORで生成できる数の個数は,32次元の$\mathbb{Z} / 2 \mathbb{Z}$ のベクトル空間 $\prod_{i=1}^{32 }\mathbb{Z} / 2 \mathbb{Z} $ とみなしたときの,基底の数で計算できる.掃き出し法が素直に使える.
int[] a = {3, 8, 9, 2};
a[0] == 0b0011
a[1] == 0b1000
a[2] == 0b1001
a[3] == 0b0010
// 掃き出してやると 0b1000, 0b0010, 0b0001 が作れるので,2^^3 = 8通りの数が作れる.
- XORshift :XORとビットシフトを使った疑似乱数生成のアルゴリズム.ここに詳しい挙動があって参考になります.
- ハッシュ値の生成:ある程度均等(等確率)に数値が存在してほしいハッシュ値のようなものの計算にXORがしばしば使われます.C#だと例えば64bit整数longのハッシュ値は上位32bitと下位32bitのXORで計算しています.同一盤面除去などに使われるZobrist hashingでもハッシュ値はXORで生成します.
- XOR swap: インラインで数値のスワップができる有名な奴(ここ)
他にもいろいろあると思うので教えてくださいね.
おまけ Xor Sum (AtCoder Regular Contest 066 D問題)
この何年かのAtCoderで出題された問題の中で,XORを冠する問題の中でも最も悪名(いい意味で)高いXor Sumを,XORを題材にした本投稿で避ける訳にはいかないのではという内面からのプレッシャーから,自分なりの解説を載せます.
(まぁ既に@259_Momone さんの記事 で大筋は紹介されているのですが)
問題概要は以下です.
正の整数 N が与えられた時に,
0 <= u, v <= N なる(u, v)のペアであって,
「この(u, v)はなんらかの非負整数 (a, b)で u = a ^ b, v = a + b と書ける」ようなものの個数を求めよ.
- ある v を一つ決めた時に,uとしてありうる値がどうなるかを考えてみます.例えば v = 8とすると
v a b u
8 0 8 0 ^ 8 = 8
8 1 7 1 ^ 7 = 6
8 2 6 2 ^ 6 = 4
8 3 5 3 ^ 5 = 6
8 4 4 4 ^ 4 = 0
8 5 3 5 ^ 3 = 6
8 6 2 6 ^ 2 = 4
8 7 1 7 ^ 1 = 6
8 8 0 8 ^ 0 = 8
// (u, v) のうち,v = 8 としては (8, 8), (6, 8), (4, 8), (0, 8) の4つがある
ここで,(u, v) = (6, 8) となる組み合わせを ビット表記でみると
a 7 0b111
b 1 0b001
a 5 0b101
b 3 0b011
a 3 0b011
b 5 0b101
a 1 0b001
b 7 0b111
これらを1つになるように数え上げる方法を考えるという方針から,aとbのどちらか片方にしか1が無いようなものは,aにのみ1が立つものだけを考えられるようにできればよいと考えられます.そうすると,元の問題は
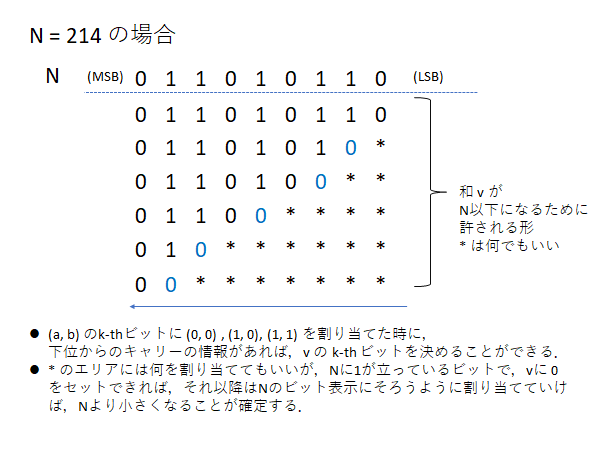
(a, b) の各ビットにそれぞれ (1, 1) , (0, 0), (1, 0) を任意に割り付けていく操作を考える.
出来上がった(a, b) に対して, u = a ^ b, v = a + b を計算したときに,0 <= u, v <= N となるようなものは
いくつ作ることができるか
という問題に読み替えることができるようになります.さらに言うと, 一般に a ^ b <= a + b なので,結局は vだけがN以下になるようにケアすればいいという事になります.これを桁dpで解きます.私は下位の桁から決めて行くことにしました.
実装するうえでは,* 部分を計算するdp1とN以下が確定してからNのビット表示をなぞる計算をするdp2を同時に更新する感じで書くことができます.
public void Solve(){
long N = long.Parse(Console.ReadLine());
// ビット表示を配列にしておく(単に見易さのため)
int M = 63;
int[] B = new int[M];
for(int i=0;i<M;i++){
B[i] = (int)((N >> i) & 1);
}
// mlong は mod剰余付き64bit整数クラス
// dp[m][c] : 下位 m ビット目に carry c で到達する組み合わせの個数.
// dp1: 自由に生成するdp
// dp2: Nのビット表示をなぞる選択肢のみ許容する.
mlong[][] dp1 = new mlong[M][];
mlong[][] dp2 = new mlong[M][];
for(int i=0;i<M;i++){
dp1[i] = new mlong[2];
dp2[i] = new mlong[2];
}
dp1[0][0] = 1;
dp2[0][0] = 1;
for(int i=0;i<M-1;i++){
// i-th ビットに carry = c で到達したときに (ai,bi) を割り当てると
// vの i-th ビットは (ai + bi + c) % 2
// vの (i+1) ビットへのcarryは (ai + bi + c) / 2 になる.
// i-th ビットの値は明示的に持つ必要はない
dp1[i + 1][0] += dp1[i][0]; // (0, 0);
dp1[i + 1][0] += dp1[i][0]; // (1, 0);
dp1[i + 1][1] += dp1[i][0]; // (1, 1);
dp1[i + 1][0] += dp1[i][1]; // (0, 0);
dp1[i + 1][1] += dp1[i][1]; // (1, 0);
dp1[i + 1][1] += dp1[i][1]; // (1, 1);
// Nにビット1が立っている桁では vの i-th ビットが0になる分岐でdp2に移行することでN未満が確定する.
if(B[i] == 1){
dp2[i + 1][0] += dp1[i][0]; // (0, 0);
dp2[i + 1][1] += dp1[i][0]; // (1, 1);
dp2[i + 1][1] += dp1[i][1]; // (1, 0);
}
// dp2は vの i-th ビットが Nのi-th ビットと一致する遷移だけを許容する.
if(B[i] == 1){
dp2[i + 1][0] += dp2[i][0]; // (1, 0);
dp2[i + 1][0] += dp2[i][1]; // (0, 0);
dp2[i + 1][1] += dp2[i][1]; // (1, 1);
}
if(B[i] == 0){
dp2[i + 1][0] += dp2[i][0]; // (0, 0);
dp2[i + 1][1] += dp2[i][0]; // (1, 1);
dp2[i + 1][1] += dp2[i][1]; // (1, 0);
}
}
Console.WriteLine(dp2[M-1][0]);
}