年も明けて冬休みの宿題も一段落したので自己紹介もかねて記事をかいてみます(テストも研究も一段落してないですが)
自己紹介
高校二年生もはや三年生になってしまいましたのMMNMMです(おわり)
今回はわたしの一番好きな問題(解法がいっぱいあっておもしろいし, 自分の解法も思いついたので)Xor Sumについて記事をかきます(他の解法を理解し次第追記するかもしれません)
Xor Sum
2016年12月18日に開催されたAtCoder Regular/Beginner ContestのD問題(Writer : maroon_kuriさん)
正の整数 $N$ が与えられます。 $2$ つの整数 $u, v (0≦u, v≦N) $ であって、ある非負整数 $a, b$ が存在して、$a \ \ \mathit{xor}\ \ b=u、a+b=v$ となるようなものが何通りあるかを求めてください。 ここで、$\mathit{xor}$ はビットごとの排他的論理和を表します。 なお、答えは非常に大きくなることがあるので、$10^9+7$ で割った余りを求めてください。
(コンテスト問題ページから引用)
かんたんに言うと $u \leqq v \leqq N$ なる $(u, v) = (a \ \ \mathit{xor} \ \ b, a + b)$ が何通りあるかという問題です
制約は $1\leqq N \leqq 10^{18}$ です
Writerさん解
上から桁DPを行っていくものです
$dp[i][j]$ の定義を $v$ の上位 $i$ 桁と$N$の上位 $i$ 桁の差が $j$であるような組み合わせの数とします
そうすることによって 上位 $i$ 桁より下位の桁が $2$ 以上繰り上がることはないので$j > 2$ の場合は $j = 2$ と同様に扱ってよく、 $0 \leqq j \leqq 2$ とできることがわかります
$dp[i][j]$ は $N$の上から $i$ 桁目の偶奇と $\{0, 1, 2\}$ の値をとるパラメータによって決定される値の総和となるので、それぞれの桁で高々9回の計算をします
なので、$dp[i][j]$ を計算していって $O(\log N)$ で解けます
解けました
rng_58さん解
$a, b$ の各桁 $a_i, b_i$ について必ず $a_i \geqq b_i$ が成り立つようにして $(u, v)$ と $(a, b)$ を一対一対応させます
ここで, $\displaystyle \begin{cases}a\ \ +\ \ b &\leqq S \\ a \ \ \mathit{xor}\ \ b &\leqq X\end{cases}$ (およびうえの各桁についての条件)を満たす正整数 $(a, b)$ の組の個数を返す関数 $f(S, X)$ を考えます
$f(S, X)$は, 条件を満たす $(a, b)$ について $(a$ が奇数 $, b$ が奇数$), (a$ が奇数 $, b$ が偶数$), (a$ が偶数 $, b$ が偶数$)$ のそれぞれの場合の組の個数の合計となっています
それぞれの場合について$\displaystyle \Big\lfloor{\frac{a}{2}}\Big\rfloor, \Big\lfloor\frac{b}{2}\Big\rfloor$ とそれに対する $S, X$ を考えると,
f(S, X)\\
= f(\Big\lfloor{\frac{S}{2}}\Big\rfloor, \Big\lfloor{\frac{X}{2}}\Big\rfloor) + f(\Big\lfloor{\frac{S - 1}{2}}\Big\rfloor, \Big\lfloor{\frac{X - 1}{2}}\Big\rfloor) + f(\Big\lfloor{\frac{S - 2}{2}}\Big\rfloor, \Big\lfloor{\frac{X}{2}}\Big\rfloor)
となります
これをメモ化して計算していくと, 第一引数および第二引数は3つの呼び出しで互いに高々$1$しか異ならないので, 計算量は $O(\log N)$ となって解けます
解けました
と思ったらこれは罠らしくメモ化の方針によっては $O\big((\log N)^2\big)$程度になってしまうそうです(たぶん通ると思いますけど)
わたしの思いついた解
まず, 題意を満たす $(u, v)$ の組を$uv$ 平面上にプロットすると, パスカルの三角形(というかシェルピンスキーのギャスケット)ができることがわかります(証明はかんたんです)
このパスカルの三角形を縦の直線で切ったときに, 直線の左側にいくつの黒い点があるか($f(N)$ とします)を数えればよいです
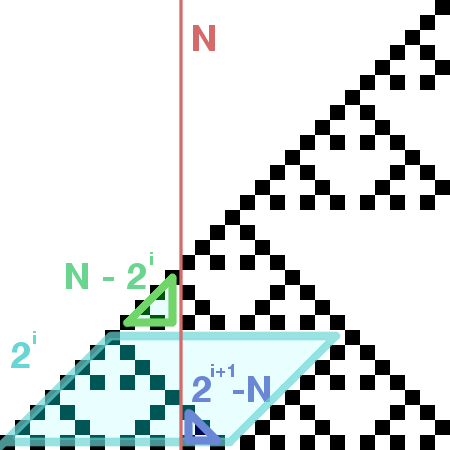
ここで, 求める黒い点の数は, 下の図の $($水色の部分の点の数$)+($緑色の部分の点の数$)-($青色の部分の点の数$)$ と等しいことがわかります
つまり, 適切な $i$ について $f(N) = f(N - 2^i) - f(2^{i+1} - N) + ($水色の部分の点の数$)$となります
水色の部分の点の数はシェルピンスキーのギャスケットの性質から $3^i$ 個であるので, $f(N) = f(N - 2^i) - f(2^{i+1} - N) + 3^i$ が成り立ちます
それぞれの $f$ の呼び出しで引数は半分以下になっていて, さらに呼び出される数字は$2$進数で $N$ あるいは $\lnot N\ (N$の反転$)$ のSuffixになっているので高々 $\log N$ 個しかありませんからメモ化したらいけます
がもうちょっと考えてみます
$N$ と $\lnot N$ のそれぞれのSuffixは $N$ のほうは符号が必ず$+$で, $\lnot N$のほうは必ず$-$で呼び出されます
また, たとえば$N = 1011110100000101_{[2]}$のsuffixである$101_{[2]}$については$f\left(100000101_{[2]} \right)$の第一項と, $f\left(11111010_{[2]}\right), f\left(1111010_{[2]}\right), f\left(111010_{[2]}\right), f\left(11010_{[2]}\right), f\left(1010_{[2]}\right)$の第二項で呼び出されます
ここからわかるように, その場で足踏みをするフィボナッチ数列みたいなものになります1
符号と合わせてそれぞれのSuffixが呼び出される回数 $\{a_n\}$ は次のような感じで計算できます
M = ((++N) ^ (N / 2));
for(i = 64; i; ++c){
if(M & (o << --i)){
swap(k, l);
l = (l + k * c) % m;
c = 0;
}
a[i] = (N & (o << i)) ? l : (m - l);
}
あとはこれと $\{b_n\} = \{3^n\}$ との inner_productをとるなどすれば解けます
解けました
DEGwerさん解
すごいかんじです(まだわかっていません)
int s = ((num&(1LL << i)) != 0);
if (s == 0)
{
dp[i + 1][0][0][0] += dp[i][0][0][0];
dp[i + 1][0][1][1] += dp[i][0][0][0];
dp[i + 1][1][0][0] += dp[i][0][0][0];
dp[i + 1][0][0][1] += dp[i][1][0][0];
dp[i + 1][1][1][0] += dp[i][1][0][0];
dp[i + 1][1][0][1] += dp[i][1][0][0];
dp[i + 1][0][1][0] += dp[i][0][1][0];
dp[i + 1][0][1][1] += dp[i][0][1][0];
dp[i + 1][1][1][0] += dp[i][0][1][0];
dp[i + 1][0][1][1] += dp[i][1][1][0];
dp[i + 1][1][1][0] += dp[i][1][1][0];
dp[i + 1][1][1][1] += dp[i][1][1][0];
dp[i + 1][0][0][1] += dp[i][0][0][1];
dp[i + 1][0][1][1] += dp[i][0][0][1];
dp[i + 1][1][0][1] += dp[i][0][0][1];
dp[i + 1][0][0][1] += dp[i][1][0][1];
dp[i + 1][1][1][1] += dp[i][1][0][1];
dp[i + 1][1][0][1] += dp[i][1][0][1];
dp[i + 1][0][1][1] += dp[i][0][1][1];
dp[i + 1][0][1][1] += dp[i][0][1][1];
dp[i + 1][1][1][1] += dp[i][0][1][1];
dp[i + 1][0][1][1] += dp[i][1][1][1];
dp[i + 1][1][1][1] += dp[i][1][1][1];
dp[i + 1][1][1][1] += dp[i][1][1][1];
}
else
{
dp[i + 1][0][0][0] += dp[i][0][0][0];
dp[i + 1][0][0][0] += dp[i][0][0][0];
dp[i + 1][1][0][0] += dp[i][0][0][0];
dp[i + 1][0][0][0] += dp[i][1][0][0];
dp[i + 1][1][0][0] += dp[i][1][0][0];
dp[i + 1][1][0][0] += dp[i][1][0][0];
dp[i + 1][0][0][0] += dp[i][0][0][1];
dp[i + 1][0][0][1] += dp[i][0][0][1];
dp[i + 1][1][0][0] += dp[i][0][0][1];
dp[i + 1][0][0][1] += dp[i][1][0][1];
dp[i + 1][1][0][0] += dp[i][1][0][1];
dp[i + 1][1][0][1] += dp[i][1][0][1];
dp[i + 1][0][0][0] += dp[i][0][1][0];
dp[i + 1][0][1][0] += dp[i][0][1][0];
dp[i + 1][1][0][0] += dp[i][0][1][0];
dp[i + 1][0][0][0] += dp[i][1][1][0];
dp[i + 1][1][1][0] += dp[i][1][1][0];
dp[i + 1][1][0][0] += dp[i][1][1][0];
dp[i + 1][0][0][0] += dp[i][0][1][1];
dp[i + 1][0][1][1] += dp[i][0][1][1];
dp[i + 1][1][0][0] += dp[i][0][1][1];
dp[i + 1][0][0][1] += dp[i][1][1][1];
dp[i + 1][1][1][0] += dp[i][1][1][1];
dp[i + 1][1][0][1] += dp[i][1][1][1];
}
for (int p = 0; p < 8; p++)dp[i + 1][(p & 4) >> 2][(p & 2) >> 1][p & 1] %= mod;
(DEGwerさんのコード引用)
...すごい...
Writerさん解の$dp[i][0], dp[i][1], dp[i][2]$がそれぞれDERwerさん解の$\displaystyle dp[i][0][0][0], dp[i][0][0][0] + dp[i][0][0][1] + dp[i][0][1][0] + dp[i][0][1][1] + dp[i][1][0][0] + do[i][1][1][0], \sum^1_{j=0}\sum^1_{k=0}\sum^1_{l=0}dp[i][j][k][l]$ に対応しているみたいな感じがしますが結局何を表しているのかわかりません...(わかるひとおしえてください)
まとめ
Xor Sumはいろんなアプローチといろんな綺麗な構造があって好きな問題です
きっとほかにもいっぱい解法があるのではないかと思っているので把握したら追記したいと思います
私はコンテスト時間中に解ききれなかったのでこういったのがすばやく解けるひとになりたいなあと思って精進していきます
謝辞
面白い問題を作ってくださったmaroon_kuriさん、コンテストを開いてくださったAtCoder社の方々、ありがとうございます
あとwriter解とか解説動画とかをしっかり見て実装していて今回とてもありがたかった友達のaddeightくんに感謝!
-
もちろん正式な用語ではありません(たぶん)へにゃっとした説明になりますけれど同じ項がいくつも続いてそれだけ直後の異なる項に足す数が大きくなるという感じです(結局へにゃっとしてしまっている...)
もう少し良い感じの説明をすると $\displaystyle \sum^k_{i=0}w_i = N$ なる正整数列 ${w_i}$ に対して群数列 $\begin{cases} a_0 = 0 \\ a_1 = \{1\} \times w_1 \\ a_n = \{a_{n-2}[0] + a_{n-1}[0] \times w_{n-1}\}\times w_n\end{cases}$ を構成してその群数列をそのまま数列にしたものを考えています(はい) ↩