はじめに、二部マッチングに関してこちらの記事を読んでいただければと思います。
早見表
二部グラフの最大マッチング、最小点被覆、最大安定集合、最小辺被覆についての結論を最初にまとめます。$|V|$ はグラフの頂点数、$|M|$ は最大マッチングのサイズです。
なお、本記事の内容のあらすじは簡単に以下のスライドにまとめました。
https://www.slideshare.net/drken1215/ss-86894312
1. はじめに
グラフ上の最適化問題として、最大マッチング問題、最小点被覆問題、最大安定集合問題、最小辺被覆問題がよく知られています。最大マッチング問題、最小辺被覆問題は一般のグラフでも多項式時間で解けますが、最小点被覆問題、最大安定集合問題は一般には NP-hard であることが知られています。しかしながら、グラフの構造が特殊であればこれらの NP-hard な問題も多項式時間で解ける場合があります。そのようなグラフのクラスとして
- 二部グラフ (ネットワークフロー問題に帰着します)
- 木 (木DPに帰着します)
- 区間グラフ (Greedy アルゴリズムが適用できます)
などがあります。これらをすべて包含する枠組みとして完璧グラフ (Perfect Graph, 完全グラフとは異なります) と呼ばれるクラスが知られていますが、本記事では二部グラフに対して最大マッチング、最小点被覆、最大安定集合、最小辺被覆を具体的に構成します。なお最大流問題を解くアルゴリズムについては既知であると仮定します。
まず最初にこれらの問題の定義を書いていきます。これらの問題自体は二部グラフに限らず一般のグラフに対しても定義されます。
最大マッチング問題
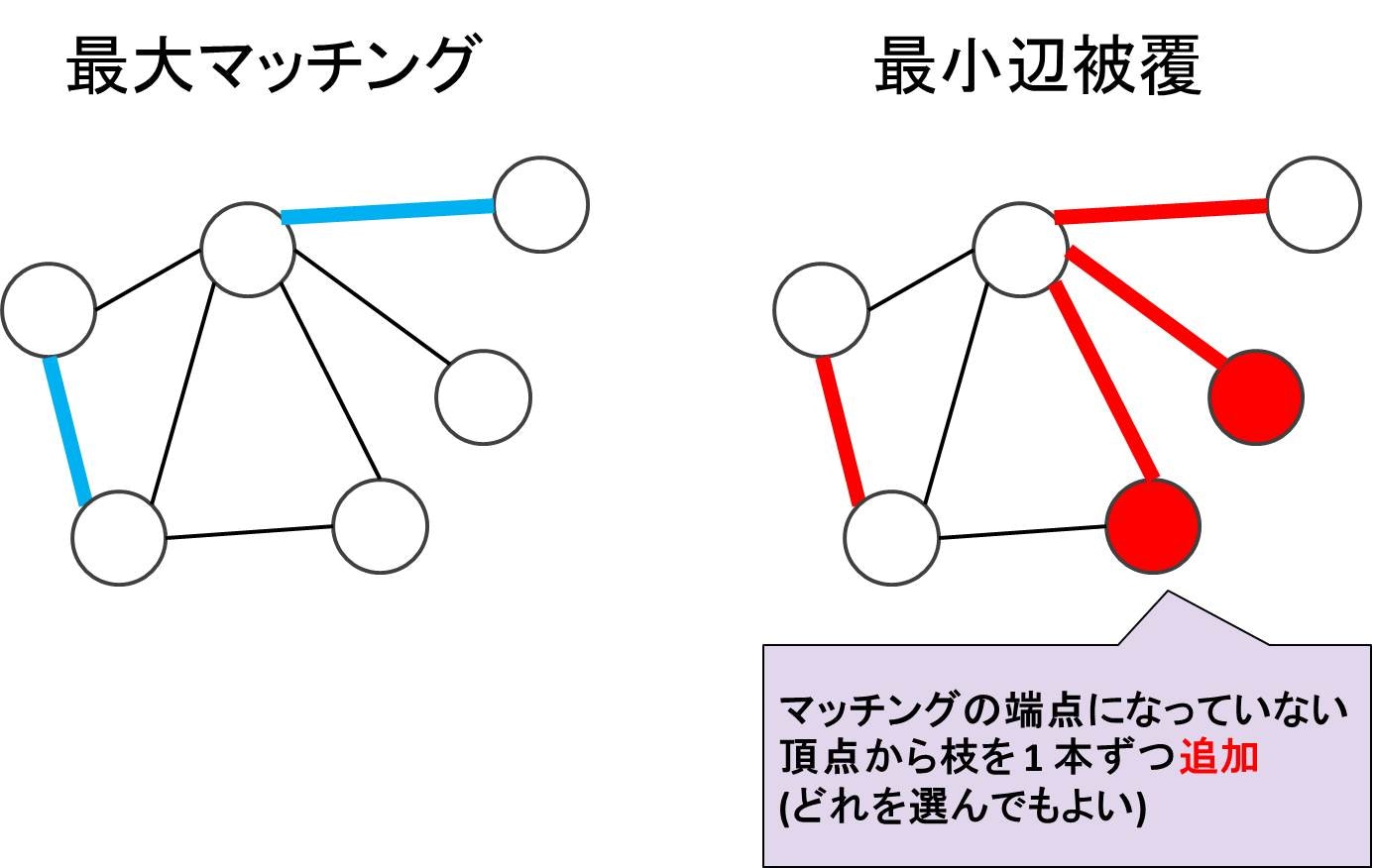
辺からなる集合のうち、どの 2 辺も端点を共有しないようなものをマッチングと呼び、最大サイズのマッチングを求める問題です。下図のグラフでは赤太線で示した 2 本の辺集合が最大マッチングの一例になっています。一見 3 本とれそうにも見えるのですがよく見ると 3 本とれないことがわかります。

最小点被覆問題
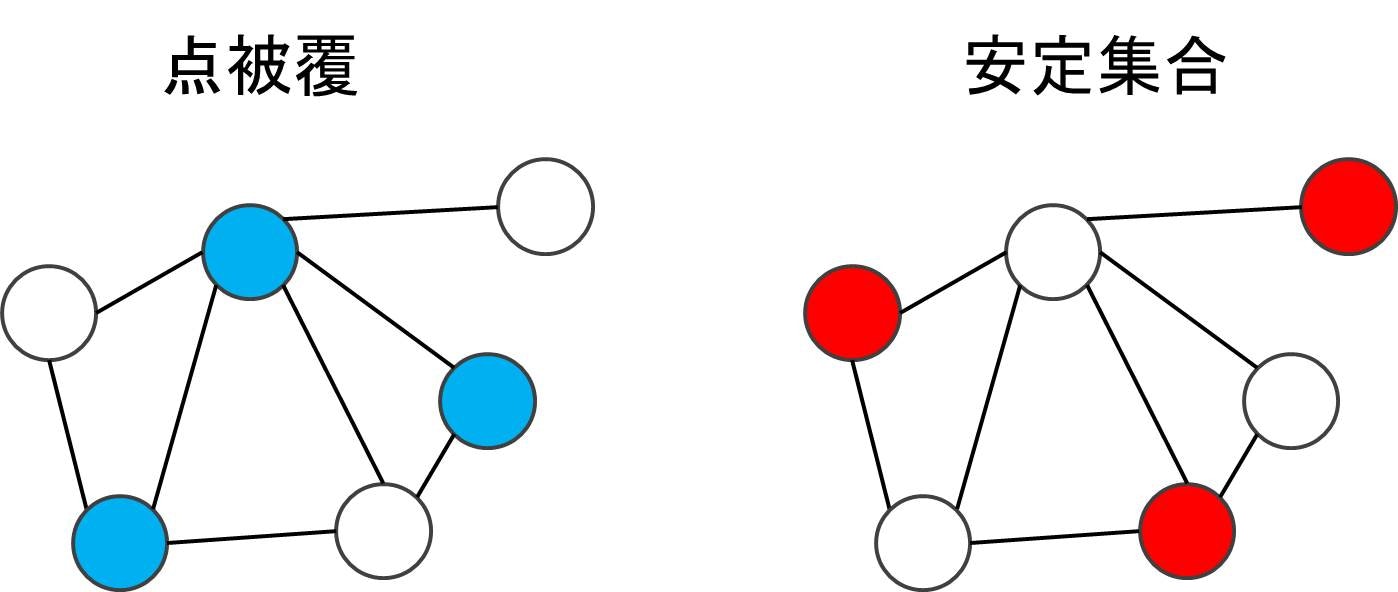
頂点からなる集合のうち、それらの頂点から出ている辺をすべて集めるとすべての辺を覆うようなものを点被覆とよび、最小サイズの点被覆を求める問題です。下図では赤丸で示した 3 頂点が最小点被覆の一例になっています。

最大安定集合問題
頂点からなる集合のうち、どの 2 頂点も辺で結ばれていないようなものを安定集合とよび、最大サイズの安定集合を求める問題です。下図では赤丸で示した 3 頂点が最大安定集合の一例になっています。

最小辺被覆問題
辺からなる集合のうち、それらの辺の両端点をすべて集めるとすべての頂点を覆うようなものを辺被覆とよび、最小サイズの辺被覆を求める問題です。下図では赤太線で示した 4 辺が最小辺被覆の一例になっています。

二部グラフの最大マッチングを求めるアルゴリズムについて
二部グラフの最小点被覆問題、最大安定集合問題、最小辺被覆問題はすべて二部グラフの最大マッチング問題に帰着させて解くので、二部グラフの最大マッチングを求めるアルゴリズムが必要になります。
二部グラフの最大マッチング (最大二部マッチング) を求めるアルゴリズムについては、別途記事を書いたので参考にしていただければと思います。
またその他には以下の記事が参考になります:
- 高校数学の美しい物語 - 二部グラフの最大マッチングと増加道 (二部グラフの最大マッチングの数学的性質の解説)
- プログラミングコンテストチャレンジブック第二版の P.195〜197 (最大流問題に帰着する)
一般のグラフの最大マッチングを求めるアルゴリズムについて
最大マッチング問題と最小辺被覆問題については一般のグラフでも多項式時間で求めることができます。大きく分けて 2 通りの方法がよく知られています。
- 行列補完を用いる方法 (最大マッチングサイズ求めるだけなら $O(|V|^{\omega})$, 構成も含めると $O(|V|^{\omega+1})$)
- Edmonds の花アルゴリズム ($O(|V|^3)$, 実装はとても大変)
一般のグラフの最大独立集合、最小点被覆を求めるアルゴリズムについて
一般のグラフでは最大独立集合問題、最小点被覆問題は NP-hard であり、効率よく解けるアルゴリズムは存在しないと信じられています。しかしながらこれらを $O(1.381^{|V|})$ で求められるアルゴリズムがあります。指数時間アルゴリズムですが、$|V| \le 50$ 程度であれば 1s 以内に十分解くことができます。
- CODE THANKS FESTIVAL 2017 G - Mixture Drug に提出した僕のコード, 全提出者内最速タイ ($O(1.381^{|V|})$ のアルゴリズムの実装)
- 指数時間アルゴリズム入門 ($O(1.381^{|V|})$ のアルゴリズムの解説があります)
2. 一般のグラフで言える 2 つの重要な定理
二部グラフの最小点被覆、最大安定集合、最小辺被覆の具体的な構成について考えていきたいのですが、最小点被覆だけ考えれば十分です。なぜなら二部グラフに限らず、一般のグラフで以下の 2 つのことが成り立つからです。
点被覆と安定集合との関係
一般の無向グラフにおいて、点被覆の補集合は安定集合をなし、安定集合の補集合は点被覆をなす。
点被覆とは「すべての辺の端点のいずれかが点被覆に含まれている」という状態です。
安定集合とは「安定集合に含まれるどの 2 頂点も辺で結ばれていない」とう状態です。
さて、点被覆が下図のように与えられているとします (青頂点)。
このとき、青頂点の補集合を赤く塗るとそれが安定集合になることを示します。もし「赤 - 赤」な辺が存在すると仮定すると、その辺は青頂点に被覆されないので、青頂点たちが点被覆であることに矛盾します。
反対もまったく同様に示せます。
最小辺被覆と最大マッチングとの関係
孤立点のない一般の無向グラフで最大マッチングが得られているとする。
マッチングの端点となっていない頂点それぞれにつき 1 本ずつ枝を追加すると、それが最小辺被覆になる。
辺被覆とは「すべての頂点について、そこから出ている辺のいずれかが辺被覆に含まれている」という状態です。
左図のように最大マッチングが得られているとして、マッチングの端点になっていない頂点それぞれに 1 本ずつ枝を追加していったものが最小辺被覆になります。マッチングの端点になっていない頂点同士が辺に結ばれることはないので、追加される枝数は $|V| - 2|M|$ 本。したがって最小辺被覆のサイズは $|M| + (|V| - 2|M|) = |V| - |M|$ となります。
3. 二部グラフの最小点被覆、最大安定集合、最小辺被覆の構成
二部グラフの最小点被覆、最大安定集合、最小辺被覆の具体的な構成方法を slideshare にアップロードしました!
https://www.slideshare.net/drken1215/ss-86894312
最小点被覆の図
これで求められる理由
少々難しいです。
証明のあらすじを記述していきます。より詳細を学びたい方は離散凸解析と最適化アルゴリズムの「第3章 マッチング問題」を参考にしていただければと思います。
さて、まず大前提として、2部グラフに限らず一般のグラフにおいて最大マッチング問題と最小点被覆問題との間には弱双対性が成り立ちます。
ここでいう弱双対性とは、
一般グラフ $G$ の最大マッチング $\le$ 一般グラフ $G$ の最小点被覆
という性質です。これは自明です。最大マッチングをなす辺をすべて覆うためには、最低でも最大マッチングサイズ分の頂点が必要です!
二部グラフではなんと、さらに強双対性 (上の不等式がイコールになること) が成り立つというのがミソです。それを示すには具体的に、最大マッチングサイズを $k$ として、サイズ $k$ の点被覆を構成してあげればよいです。
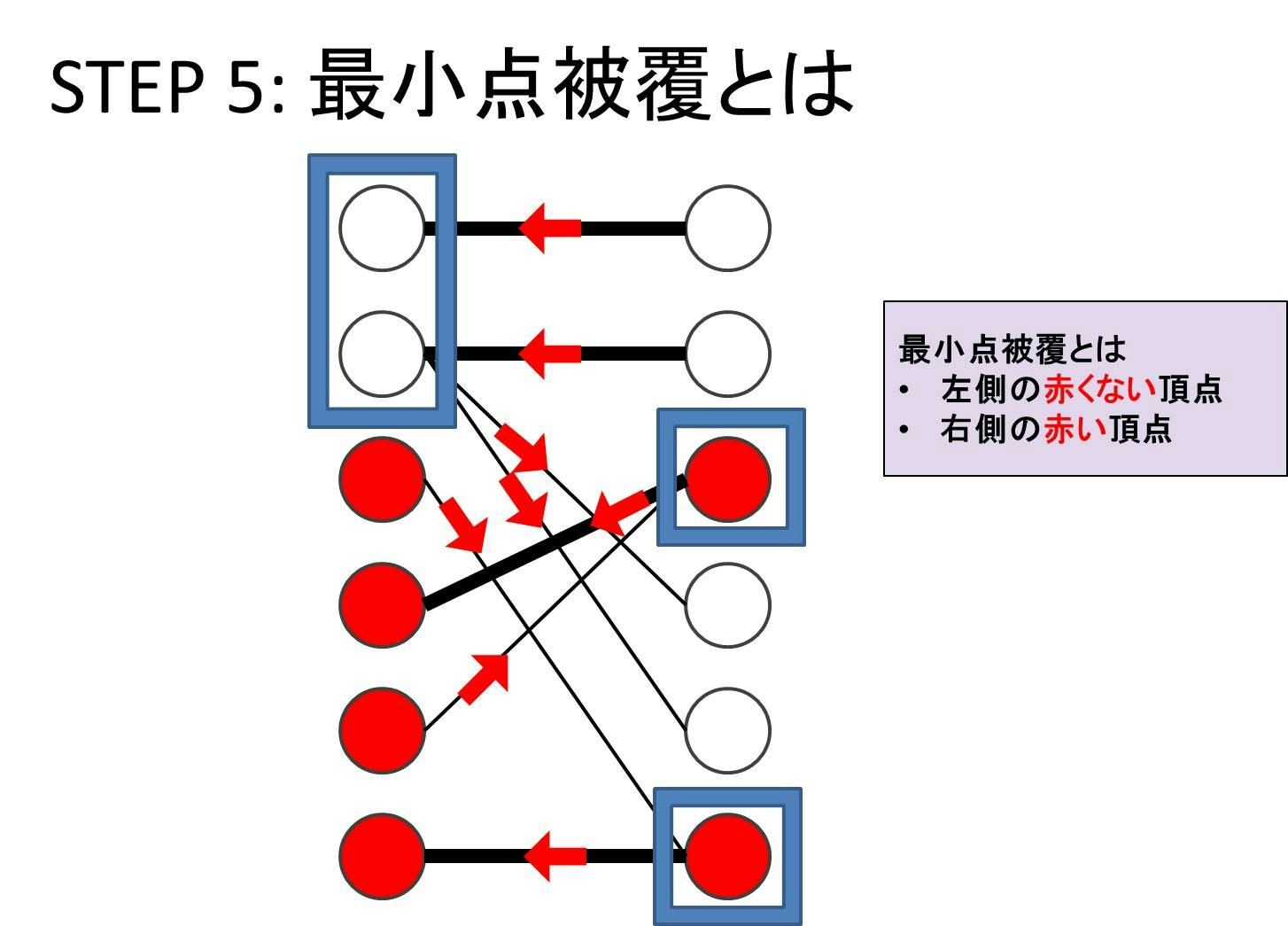
さて、2 部グラフの枝は実は以下の 3 パターンしかないことが少し考えるとわかります。これにより、(左側の白) + (右側の赤) が点被覆であることが言えました!!!
- 白 - 白
- 白 - 赤
- 赤 - 赤
あとは (左側の白) + (右側の赤) のサイズが実際に $k$ であることが言えれば終了です。実は
- 左側の白はマッチングの端点にしかならない
- 右側の赤はマッチングの端点にしかならない
が言えます。もしそうでないと仮定すると、マッチングサイズを増やすことができる (増加路が存在します) ので、$k$ が最大マッチングサイズであることに矛盾します。
このことから、(左側の白) + (右側の赤) のサイズが $k$ であることが従います。
なお以上の議論は、増加路を用いて二部グラフの最大マッチングを求めるアルゴリズムの正当性の証明にもなっています。サイズ $k$ の点被覆の存在が、マッチングが最大サイズになっていることの証拠になっています。
4. 具体的な問題
易しめ
- SoundHound Inc. Programming Contest 2018 (春) C - 広告 (最大安定集合)
- POJ 3041 Asteroids (最小点被覆)
- GCJ 2016 Round 1B C - Technobabble (最小辺被覆)
難しめ
- SRM 303 DIV1 Medium Knights (最小点被覆)
- CSAcademy Round #23 : E. No Prime Sum (最小点被覆)
- SRM 594 DIV1 Medium FoxAndGo3 (最大安定集合)
5. おわりに
世の中の様々な問題はしばしば最大安定集合問題や最小点被覆問題に落ちます。ほとんどのケースでは NP-hard なのでヒューリスティク解法を考えようという動きになるのですが、二部グラフであれば最大マッチング問題に帰着して効率よく解くことができます。そんなときに帰着方法をすぐに参照できるような記事を目指しました。