競技プログラミングでよく使うデータ構造第1位(勝手に決めました、要出典)の、Segment Treeに関する記事です。前編では、Segment Treeの主な理論や実装などについて扱います。後編では、発展形である遅延Segment Treeなどについて扱います。
Segment Treeとは
シンプルなSegment Tree(いわゆる「うし木」)は、おおざっぱには、数列に対して次のような処理を行うデータ構造です。
- 数列のどこかの値になんらかの演算をする。(変更する、値を加算するなど)
- 数列の一部の区間になんらかの演算をした結果を求める。(最小値を求める、総和を求めるなど)
これらの処理を、数列の長さを $N$ として、一回 $O(\log N)$ で行えるのがSegment Treeです。
要件
Segment Treeにのせる演算は、次の要件を満たす必要があります。
- 数列の各要素と、区間に対して行う演算が結合法則を満たす。(交換法則は満たさなくてよい)
他の操作を付け加えたり拡張したりすると要件が増えますが、最低限必要なのはこれだけです。
Segment Treeの発想
Segment Treeの大まかな発想は次の通りです。
- 先に、いくつかの区間に対してそこに演算を行ったときの結果を計算しておく。
- 結果を求めるときは、上で計算した結果を適当に用いて、計算を節約しつつ求めたい結果を出す
- 値に演算を加えるときは、計算しておいた結果の一部を更新する。
ここで大事になってくるのが先に挙げた結合法則です。
結合法則が成り立つことを利用して、一部の区間を先にまとめて計算しておいても、それを使って正しい値を求めることができます。
構造
実際のSegment Treeの構造は、次の図のようになっています。
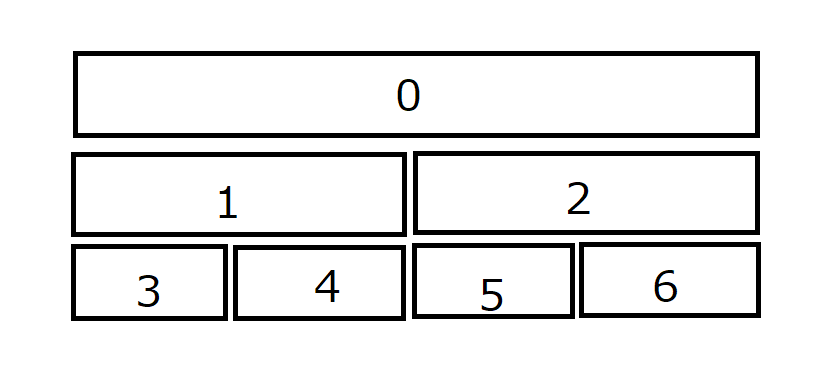
数列の長さは、簡単のため2のべき乗とします。
2のべき乗の長さで区間を統合していき、それらの区間に対して演算を行った結果を格納しておきます。
木の高さは $O(\log N)$ になり、全体のセグメント数は $O(N)$ になります。
実はここでは、ノードの番号は1-indexedにしておくとかえって便利です。
最初は、結合法則を利用して下から計算していけば、$O(N)$ でそれぞれのノードの値が計算できます。
区間についての演算結果を求めたいときは、ノードを高々 $O(\log N)$ 個組み合わせて、結合法則を利用して順番に計算すれば任意の区間についての演算結果を求められます。
値に対する演算をしたいときは、一番下のノードに演算をし、上にさかのぼっていけばよいです。これは、下から素直にさかのぼっていく実装でもよいですし、上から見ていって再帰を利用する実装でもよいです。
実装
基本的な実装は、蟻本に載っているものを使えばよいですが、ここでは僕が適当に実装した例を載せます。
ここでは、Segment Treeの例としてよく使われる、値の変更とRMQ(Range Minimum Query, 区間の最小値を求める)を実装します。
const int INF=1000000000;
int N,node[400010];
void init(int N_){
while(N<N_)N*=2;
for(int i=0;i<2*N-1;i++)node[i]=INF;
}
void update(int a,int x){
a+=size-1;
node[a]=x;
while(a>0){
a=(a-1)/2;
node[a]=min(node[2*N],node[2*N+1]);
}
}
int query(int a,int b,int k=0,int l=0,int r=N){
if(b<=l||r<=a)return INF;
if(a<=l&&r<=b)return node[k];
int vl=query(a,b,2*k+1,l,(l+r)/2);
int vr=query(a,b,2*k+2,(l+r)/2,r);
return min(vl,vr);
}
再帰を使わずに書く方法もあります。そちらのほうが高速ですが、再帰のほうが理解はしやすいです。今回は再帰で書きました。
練習問題
AOJ DSL2-A Range Minimum Query(典型的なSegment Treeです)
AOJ DSL2-B Range Sum Query(典型的なSegment Treeです)
ABC153-F Silver Fox vs Monster(使わなくても解けますがセグ木があると楽です)
ARC008-D タコヤキオイシクナール
暇なときに追加します。
おわりに
短い記事になりましたが、基本的なセグ木の考え方は実はこれで網羅できています。
2べきで区間を分けて前計算をしておき、更新クエリではそれらを書き換える、という処理だけで高速なクエリへの応答が可能になります。
後編では、Segment Treeの発展形である、遅延Segment Treeなどを扱います。
遅延Segment Treeまでを学ぶと応用できる域が大きく広がり、日本情報オリンピックの春合宿で出題される問題なども解けるようになります。
Segment Treeをマスターして、解ける問題の幅を広げましょう!