競技プログラミングでよく使うデータ構造第1位(勝手に決めました、要出典)の、Segment Treeに関する記事です。前編では、Segment Treeの主な理論や実装などについて扱います。後編では、発展形である遅延Segment Treeなどについて扱います。
遅延Segment Tree
遅延Segment Treeは、前編で紹介したSegment Treeに工夫を加え、値の変更や値の加算を区間に対して行えるようにしたものです。つまり、遅延Segment Treeでできる操作は次のようになります。
- 数列のどこかの区間になんらかの演算をする。(変更する、値を加算するなど)
- 数列の一部の区間になんらかの演算をした結果を求める。(最小値を求める、総和を求めるなど)
さて、これを前編で紹介したような単純なSegment Treeを用いて実装するとどうなるでしょうか。
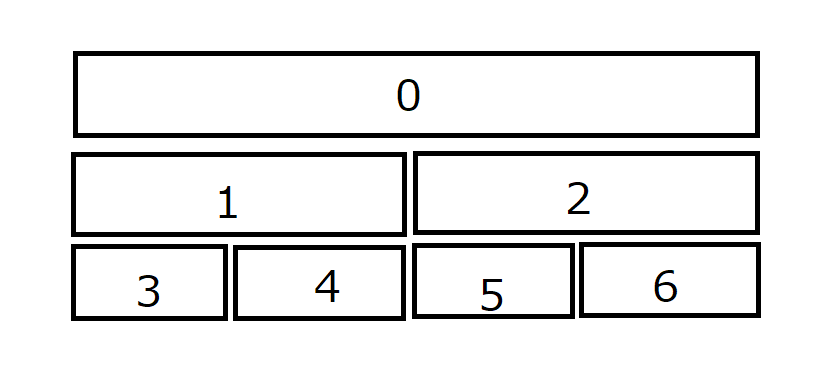
たとえばこの図で、0番目から2番目までを更新しようとすると、更新する必要があるノードはどこになるでしょうか。
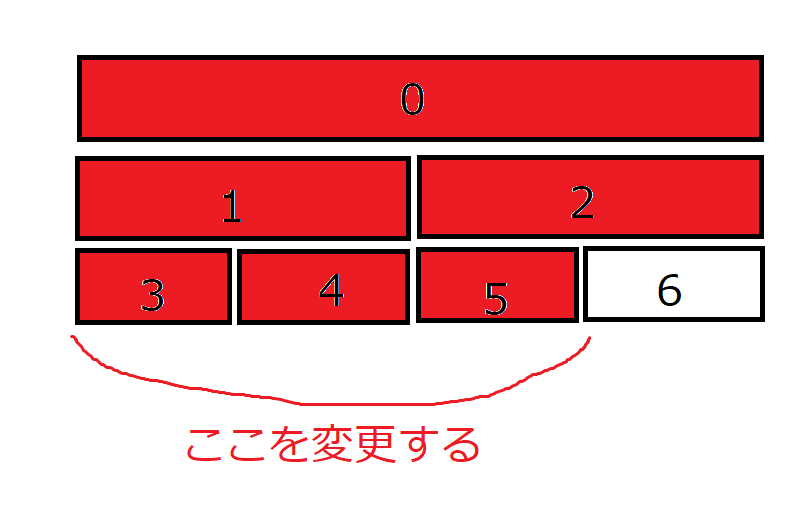
このように、色のついた部分全部、6個ものノードの更新が必要になってしまいます。
ここで、遅延伝播を行うことで計算量を $O(\log N)$ に抑えたまま区間へのクエリに対応できます。
遅延配列の利用
ここで、Segment Treeに、遅延配列と呼ばれるもうひとつの要素集合を用意しておきます。
以下からは、Segment Treeの図に、ベースの配列の中の値と遅延配列の中の値をスラッシュで併記しながら説明を進めます。
次のような状態から、$0$ 番目から $2$ 番目の値に $3$ 加算することを考えます。区間に対しての取得クエリは最小値(RMQ)とします。
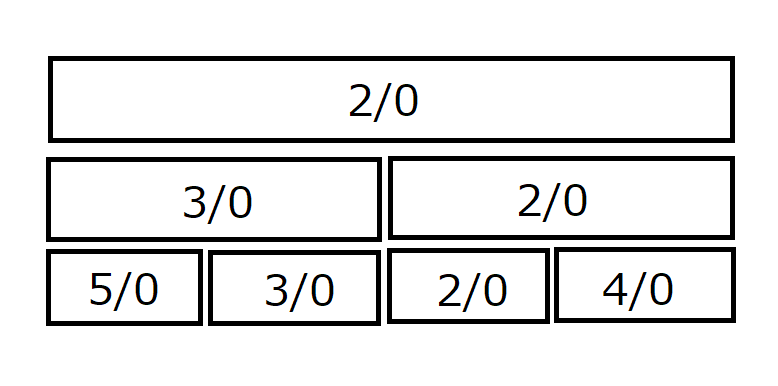
この状態から遷移した後は、次のように遅延配列に値を書き込まれます。
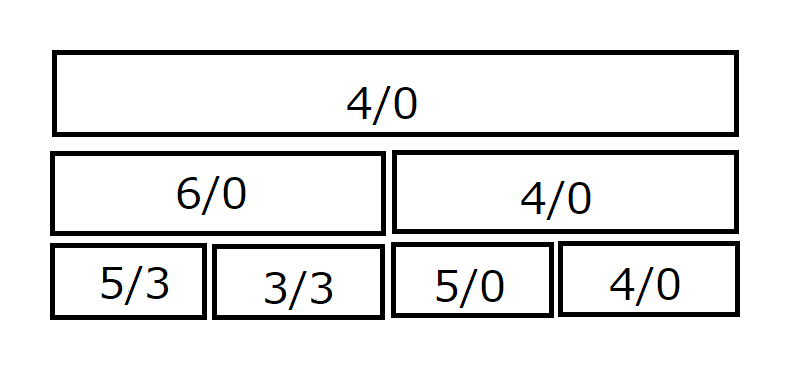
操作に該当する区間に値を加算し、その子に、加算しなければいけない値を伝播させます。
こうすることで、次に来る取得クエリに対しての応答が可能になります。
ここで、$1$ 番目から $3$ 番目までに対する取得クエリを考えてみましょう。
色を付けた部分がクエリの対象になります。
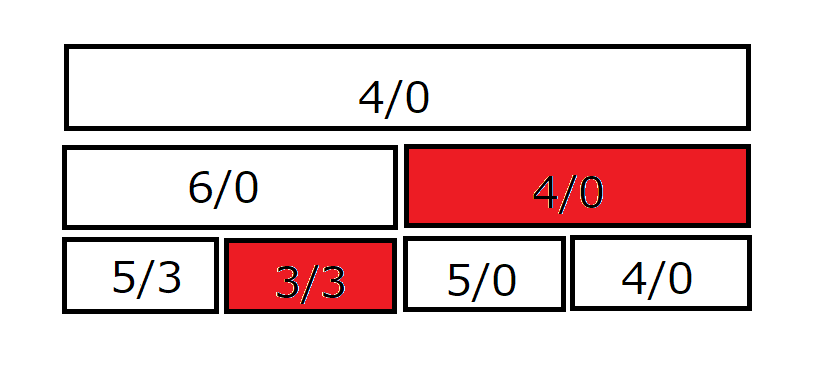
そして、これらのノードに伝播処理を行います。
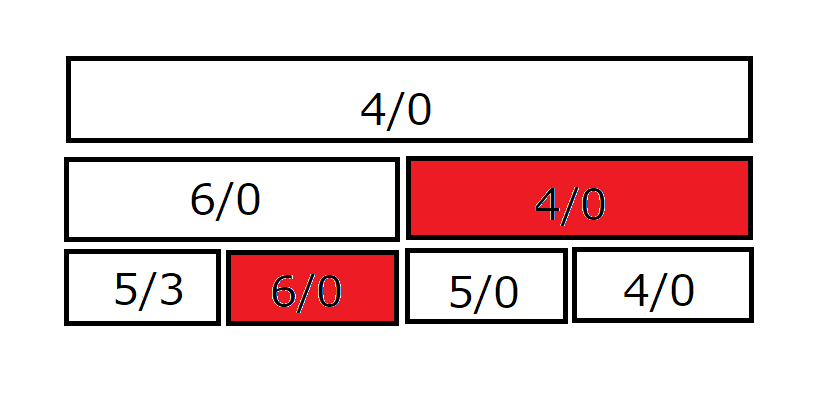
これで、区間の最小値、$4$ が求まります。
これが遅延Segment Treeの構造です。
要件
この構造を考えることで、次のような要件が浮かんできます。
- 区間に対する取得クエリの演算に、結合法則が成り立つ。(これは通常のSegment Treeと同じです。)
- 遅延配列の中での伝播を行える。(たとえば、今回は同じ値を子の配列に書き込めばいいだけでしたが、取得クエリが総和だった場合などは、子の配列に書く値を半分にしなければなりません。)
- 遅延配列からベースの配列への伝播を行える。(今回は最小値クエリなので配列の値に加算をするだけでしたが、総和クエリなら下にある要素の数を書ける必要があります)
値の更新や値への加算、最小値/最大値の取得と総和の取得はすべてこの条件を満たすので、Segment Treeでの処理が可能です。
稀に、Segment Treeが使えない処理が出題されることがあるので、そのような場合は平方分割など、似たようなテクニックを使うといいでしょう。
また、さらに稀ですが、最小値/最大値などの典型的なクエリだけでなく、ad-hocな問題でセグメントツリーが要求されることもあります。頭を柔らかくして問題に向き合うことも大切です。
実装
実装は、要旨だけ抑えておけば実は結構簡単です。
少し練習すれば書けるようになると思います。
int N,node[400010],lazy[400010];
bool flag[400010];
void init(int N_){
N=1;
while(N<N_)N*=2;
rep(i,2*N-1){
node[i]=((int)1<<31)-1;
flag[i]=false;
}
}
void eval(int k,int l,int r){
if(flag[k]){
node[k]=lazy[k];
if(l+1<r){
lazy[2*k+1]=lazy[2*k+2]=lazy[k];
flag[2*k+1]=flag[2*k+2]=true;
}
flag[k]=false;
}
}
void update(int a,int b,int x,int k=0,int l=0,int r=N){
eval(k,l,r);
if(r<=a||b<=l)return;
if(a<=l&&r<=b){
flag[k]=true;
lazy[k]=x;
eval(k,l,r);
}
else{
update(a,b,x,2*k+1,l,(l+r)/2);
update(a,b,x,2*k+2,(l+r)/2,r);
node[k]=min(node[2*k+1],node[2*k+2]);
}
}
int query(int a,int b,int k=0,int l=0,int r=N){
eval(k,l,r);
if(r<=a||b<=l)return INF;
if(a<=l&&r<=b)return node[k];
int vl=query(a,b,2*k+1,l,(l+r)/2);
int vr=query(a,b,2*k+2,(l+r)/2,r);
return min(vl,vr);
}
練習問題
全国統一プログラミング王決定戦本選-D Deforestation
AOJ DSL2-F RMQ and RUQ
AOJ DSL2-G RSQ and RAQ
AOJ DSL2-H RMQ and RAQ
AOJ DSL2-I RSQ and RUQ
暇なときに追加します。
おわりに
今回は、要旨だけを軽めに説明した記事になりました。
Segment Treeは非常に幅広い範囲で使える便利なデータ構造です。Segment Treeを使いこなせるようになれば、解ける問題の幅が大きく広がります。また、日本情報オリンピックの春合宿などでは、Segment Treeを使わないと解けない問題が大量に出題されるので、中高生には特に重要です。
2020年度本選でも、シンプルなSegment Treeを使うだけで取れる部分点がたくさんありました。
ぜひ、Segment Treeをマスターしましょう!!!