LoginSignup
198
216

More than 3 years have passed since last update.

@e869120(E869120)

アルゴリズム・AtCoder のための数学【後編：数学的考察編】

Last updated at Posted at 2021-04-26

0. はじめに

こんにちは、大学 1 年生になったばかりの E869120 です。本記事は、

からの続きです！！！
※前編・中編を読んでいなくても理解できる、独立したトピックになっているので、ご安心ください。

後編から読む方へ

21 世紀も中盤に入り、情報化社会が急激に進行していく中、プログラミング的思考やアルゴリズムの知識、そしてアルゴリズムを用いた問題解決力が日々重要になっています。

しかし、アルゴリズム構築能力・競プロの実力は、単純にプログラミングの知識を学ぶだけでは身につきません。近年、数学的なスキルが重要になりつつあります。実際、私はこれまでの経験で「数学の壁で躓いた競プロ参加者」をたくさん見てきました。そこで本記事では、

AtCoder のコンテストで戦ったり、様々なアルゴリズムを習得していくために必要な数学的知識や数学的考察テクニックを習得し、アルゴリズムと数学の密接さに気づいてもらうこと

を最大の目標にしています。前編・中編では、競プロの問題文の理解、そしてアルゴリズムの理解のために要求される数学的知識について、理解を深めるための演習問題などを交えて解説しましたが、後編では様々な問題解決に要求される数学的考察に絞って記します。

独立したトピックとして理解できる内容になっていますので、前編・中編を読んでいない方も、是非お読みください。


後編のレベル感について

主にプログラミング初心者から水色コーダー・青色コーダーになるために要求される数学的考察テクニックをまとめています。私が調べたところ、過去 2 年間で

  • AtCoder Beginner Contest (ABC)
  • AtCoder Regular Contest (ARC)

に出題された「数学的考察が要求される問題」の中で、水色コーダーが解いてほしい問題の 75% 以上が、本編にまとめられたテクニックを用いて解くことができます。したがって、後編の主な対象は競技プログラミング未経験～水色コーダーです。


目次

前編

章 タイトル 備考
1. はじめに
2. これが分からないと問題が理解できない！ ～最重要ポイント 12 選～ ここからサポートします
3. アルゴリズムと密接に関わる数学＜初級編＞ 本記事のメインです（1 ～ 11 個目のトピックを扱います）

中編

章 タイトル 備考
4. アルゴリズムと密接に関わる数学＜中級編＞ 本記事のメインです（12 ～ 19 個目のトピックを扱います）
5. これだけ解けば理解が深まる！　～演習問題 32 問～ 2 章から 4 章の内容をサポートします

後編

章 タイトル 備考
6. なぜ数学的考察が重要か？ 後編では数学的考察を扱います
7. 競プロで頻出！ ～汎用的な数学的考察 7 選～
8. 問題特有の数学的考察テクニック 14 選 後編のメインです
9. おわりに
10. 参考文献




6. なぜ数学的考察が重要か？

数学的考察の重要性を理解してもらう前に、次の問題を考えてみましょう。

AtCodeer くんは二次元平面上で旅行をしようとしています。彼の旅行プランでは、時刻 $0$ に点 $(0, 0)$ を出発し、時刻 $T$ に点 $(X, Y)$ を訪れる予定です。
AtCodeer くんが時刻 $t$ に点 $(x, y)$ にいる時、時刻 $t+1$ には

  • 点 $(x+1, y)$
  • 点 $(x-1, y)$
  • 点 $(x, y+1)$
  • 点 $(x, y-1)$

のいずれかに存在することができます。その場にとどまることができないことに注意してください。彼の旅行プランが実現可能かどうかを判定してください。
（出典： AtCoder Beginner Contest 086 C - Traveling 改題）

結論から書くと、次の 2 条件両方を満たす場合 Yes、そうでなければ No が答えになります。

条件1　$|X| + |Y| \leq T$ である。
条件2　$|X + Y|$ と $T$ の偶奇は同じである。

実際、以下のプログラムを書くと正解できてしまうのです。でも、どうやって「これが答えだ！」と思いつくことができるのでしょうか。このために要求されるのが数学的考察です。

#include <iostream>
#include <cmath>
using namespace std;

int main() {
    int X, Y, T;
    cin >> X >> Y >> T;
    if (abs(X) + abs(Y) <= T && abs(X + Y) % 2 == T % 2) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}


この問題で要求される数学的考察

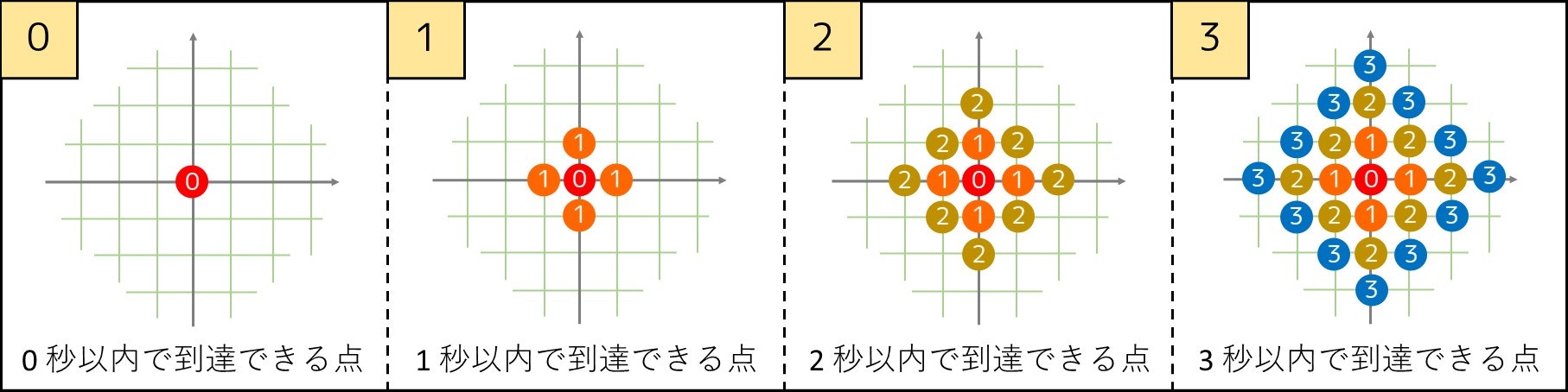
まず、Atcodeer 君は 1 秒ごとに上下左右に 1 だけ移動しているので、座標 $(X, Y)$ に行くためにかかる時間は最低でも $|X| + |Y|$ 秒必要なことはすぐに理解できると思います。実際に、

  • 1 秒以内で到達できる範囲はどれか？
  • 2 秒以内で到達できる範囲はどれか？
  • 3 秒以内で到達できる範囲はどれか？

といった感じで T が小さい場合を考えていくと、下図のように広がることが分かります。
このような考察で、条件 1 の $|X| + |Y| \leq T$ が導出できるのです。（7-4. 節参照）
46.jpg
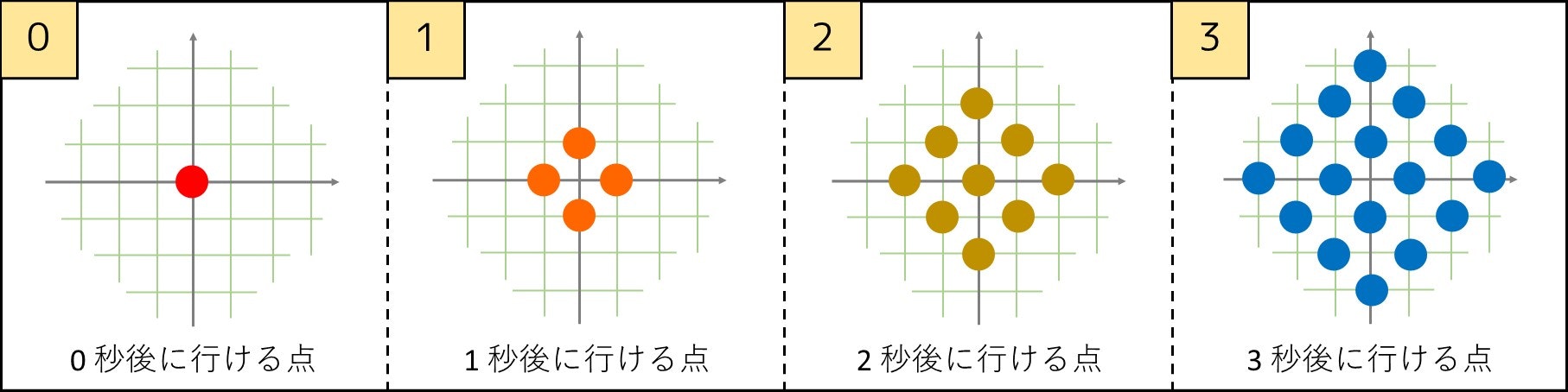
しかし、それで考察が終わった訳ではありません。実は、x 座標を $x$、y 座標を $y$ と表すとき、$1$ 回の移動で $x + y$ の偶奇が必ず入れ変わることが分かります。実際、例えば点 $(869, 120)$ から $1$ 秒後に移動できる点は、

  • x 座標を 1 増やした場合：$(870, 120)$ → $x+y$ は偶数
  • x 座標を 1 減らした場合：$(868, 120)$ → $x+y$ は偶数
  • y 座標を 1 増やした場合：$(869, 121)$ → $x+y$ は偶数
  • y 座標を 1 減らした場合：$(869, 119)$ → $x+y$ は偶数

となり、すべて偶奇が入れ替わっていることが分かります。このような性質をパリティといい、詳しくは 8-3. 節で紹介します。

このように考えていくと、点 $(0, 0)$ から出発するため、$x+y$ の偶奇は「偶数→奇数→偶数→奇数→…」と動いていくことが分かります。したがって、$X + Y$ の偶奇と $T$ の偶奇は一致し、条件2 を導出することができるのです。実際、ちょうど $T$ 秒後に到達し得る点は次図のようになります。
47.jpg


結局、なぜ数学的考察パターンの理解が大切か？

本章の最初に紹介した問題では、二分探索や動的計画法のような典型的なアルゴリズム、そして前編・中編で述べた数学的知識をほとんど使っていません。しかし、次のような数学的考察が見えなければ解けないのです。

  • $T = 1, 2, 3, ...$ のような、小さいケースを考える
  • パリティ（偶奇）の性質を考える

他にも数学的考察が要求される問題は AtCoder などで数えきれないほど出題されているほか、実社会に隠れている様々な問題も数学的考察を使って解けることがあります。確かに

こういう数学的考察は「ひらめかない」と思いつかない…

というイメージを持つ人も多いですが、実は「典型的なパターン」があります。つまり、

重要なアルゴリズムだけでなく、いくつかの「数学的考察パターン」を理解すれば、「解ける問題」の幅が大きく広がり、問題解決力が大幅アップする

ということになるのです。このような面で、数学的考察はプログラミングコンテストにおいて、そしてプログラマ全体にとっても極めて重要だといって良いと思います。

そこで、7 章・8 章では重要な数学的考察パターンを計 21 個に分けて整理し、トピックごとにまとめました。引き続きお読みいただけると嬉しいです。




7. 競プロで頻出！ ～汎用的な数学的考察 7 選～

競プロやアルゴリズム、そして問題解決において求められる数学的考察には、いろいろなものがありますが、大きく分けて 2 種類に大別されます。

  • 多くの問題に使える汎用的な考察の仕方
  • 特定のタイプの問題（例：数え上げ問題）に使える数学的考察テクニック

そこで、本章では主に前者について、以下の 7 点に絞って説明していきたいと思います。

数学系問題に限らず、かなり広範囲に使えるテクニックですので、是非お読みください。


7-1. ギリギリを考える（レベル：:star:1）

まず、次の問題を考えてみましょう。（出典：ABC178B）

整数 $a, b, c, d$ が与えられます。$a \leq x \leq b, c \leq y \leq d$ を満たす整数 $x, y$ について、$x \times y$ の最大値はいくつですか。
制約：$-10^{9} \leq a \leq b \leq 10^{9}, -10^{9} \leq c \leq d \leq 10^{9}$

最初に思いつくアルゴリズムとしては、「以下のように全部の (x, y) の組に対して全探索をする」といった方法が考えられます。

long long Answer = -(1LL << 60);
for (int x = a; x <= b; x++) {
    for (int y = c; y <= d; y++) Answer = max(Answer, 1LL * x * y);
}
cout << Answer << endl;

しかし、家庭用コンピューターでは 1 秒当たり $10^8 \sim 10^9$ 回の計算しかできません。したがって、例えば入力が $(a, b, c, d) = (-10^9, 10^9, -10^9, 10^9)$ の場合、$10^{18}$ 回以上の計算が必要であることを考えると、数秒以内にプログラムの実行が終わることはなく、実行時間制限超過（TLE）となってしまいます。

そこで、次のような性質を使うと、簡単に解くことができます。

$x \times y$ が最大となるような値は、$(x, y) = (a, c), (a, d), (b, c), (b, d)$ のいずれかである。

実際、例えば $(a, b, c, d) = (-3, 2, 5, 17)$ の場合、下表の通り、表の角の部分（条件ギリギリの境界値）が最大値になっています。
48.jpg
したがって、次のようにプログラムを書くと、正解が得られます。

#include <iostream>
#include <algorithm>
using namespace std;

int main() {
    long long a, b, c, d;
    cin >> a >> b >> c >> d;
    cout << max({a * c, a * d, b * c, b * d}) << endl;
    return 0;
}

このように、ギリギリの値や境界値を考えることで解ける問題は数多く存在します。今回のような問題に限らず、特に計算幾何系の問題では「ギリギリを考える」テクニックが頻出です。類題として、

などが挙げられます。


7-2. N や答えが小さい場合を考える（レベル：:star:1）

まず、次の問題を考えてみましょう。（出典：ABC198C）

座標 $(0, 0)$ に高橋君がいます。彼は $1$ 歩歩くことで、距離がちょうど $R$ である点に動くことができます。彼が点 $(X, Y)$ に到達するために必要な歩数の最小値を求めてください。

この問題は少し考察が必要で、一瞬で解法が分かる読者は少ないと思います。そこで、1 歩で到達できる範囲、2 歩で到達できる範囲、3 歩で到達できる範囲、…を図で表してみましょう。次のようになります。
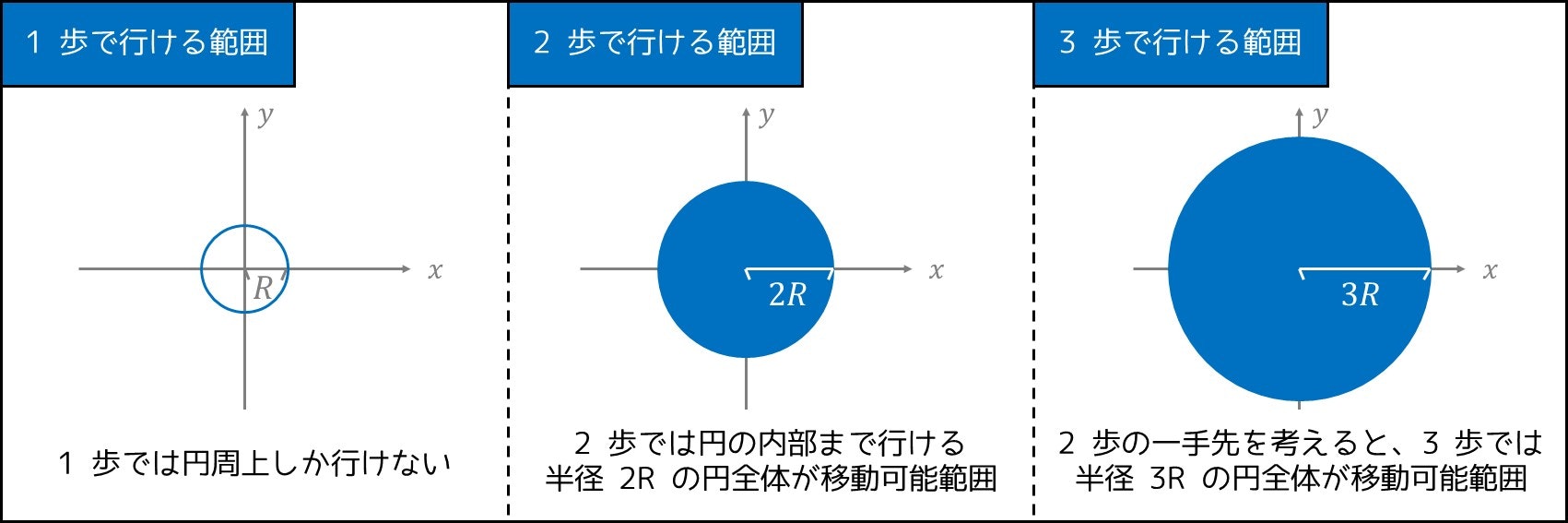
49.jpg
ここまで来ると一気に考察が見えやすくなり、さらに歩数 $T = 2, 3, 4, 5, \cdots$ と順番に考えていくと、半径 $R \times T$ の円の内部であれば $T$ $(\geq 2)$ 歩以内で移動できることも察しが付くと思います。

また、次のような理由で不正解（WA）を出してしまう人もいます。

答えを $\lceil \sqrt{X^2 + Y^2} \div R \rceil$ にしてしまった。
半径 $R$ の円の内部にあっても、移動に $2$ 回かかることを完全に忘れていた。

しかし、小さい場合を考えておくと、このようなコーナーケース（特殊ケース）にはまる確率も減り、一石二鳥です。

実際、次のようなプログラムで正解を出すことができます。

#include <iostream>
using namespace std;

int main() {
    long long R, X, Y; cin >> R >> X >> Y;

    // 1 回で移動できる場合
    if (R * R == X * X + Y * Y) { cout << "1" << endl; return 0; }

    // 2 回以上かかる場合
    for (long long i = 2; i <= 1000000; i++) {
        long long V = (R * i) * (R * i);
        if (V >= X * X + Y * Y) { cout << i << endl; return 0; }
    }
    return 0;
}

このように、解法が分からない場合は、

  • $N = 1, 2, 3$、$M = 1, 2, 3$ など入力サイズが小さい場合
  • 今回紹介した問題のように、答えが $1, 2, 3$ と小さい場合
  • それ以外にも、$A_1 = A_2 = A_3 = \cdots = A_N$、グラフが木の場合などの特殊なケース1

などを考えると、解法に一気に近づく場合もあります。このようなテクニックを使うと解きやすくなる問題の例として、他にも

などが挙げられます。


7-3. いろいろなケースで実験して解く（レベル：:star:1）

まず、次の問題を考えてみましょう。（出典：PANASONIC2020-B）

$H$ 行 $W$ 列の盤面があります。この盤面の左下隅のマスに角行の駒が置かれています。駒を $0$ 回以上移動させることで到達できるマス目は何個あるでしょうか？

この問題も考察が必要で、一瞬で解法が思いつく読者は少ないと思います。そこで下図のように、（入力例を含む）いくつかのテストケースについて、紙の上で手を動かし実験をしてみることを考えます。
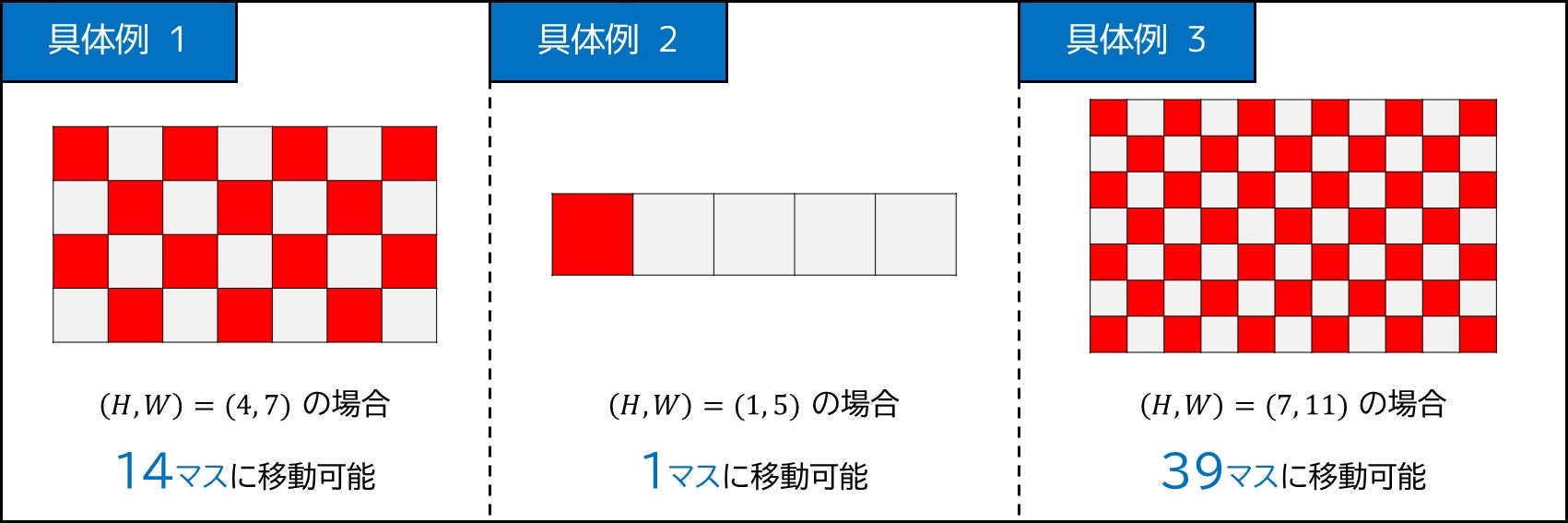
50.jpg
そうすると、次のような事実について、察しが付くと思います。

  • $H=1$ または $W=1$ の場合は 1 マスにしか移動できない
  • そうでない場合は市松模様の赤いマス、つまり合計 $\lceil H \times W \div 2 \rceil$ マスに移動可能

このように、一見難しい問題も、いくつかの例で試すと法則性が見えることもあります。

このような「実験をして法則性を導く」テクニックは、ゲーム系の問題にも応用することができます。例えば、以下の問題を考えてみましょう。

$N$ 個の石があります。各ターンでは $1 \sim 3$ 個の石を取ることができます。初めて石を取れなくなった方が負けです。整数 $N$ が与えられるとき、先手と後手どちらが勝つか出力してください。

この問題も、$N = 1, 2, 3, \cdots, 10$ の場合を手で試してみましょう。次表の通りです。

N 1 2 3 4 5 6 7 8 9 10
勝つ方 先手 先手 先手 後手 先手 先手 先手 後手 先手 先手

この結果から「石の数 $N$ が $4$ の倍数の場合後手必勝」といった法則性が見え、解法に至ることができます。特にこのようなゲーム系の問題では、実験により考察が進むことも少なくありません。2


7-4. 答えや条件を式で表す（レベル：:star:2）

まず、次の問題を考えてみましょう。（出典：ABC190D）

整数からなる公差 $1$ の等差数列のうち、総和が $N$ であるようなものはいくつあるでしょうか？（制約：$1 \leq N \leq 10^{12}$）

問題文が短く一見簡単に見えますが、そのままの形だと頭の中で整理しきれず、考察と実装が大変になります。そこで、「$a$ から始まり $b$ で終わる等差数列の総和が $N$ であること」の条件を式で表してみましょう。次のようになります。

$$
a + (a + 1) + \cdots + b = \sum_{i=a}^{b} i = \frac{(a+b)(b-a+1)}{2} = N
$$

ここまで来ると、$b-a+1$ の値を決め打てば良さそうなことが分かります。実際、$b-a+1$ は $2N$ の約数であり、$M$ の約数の列挙は本記事 3-8. 節で述べた方法により時間計算量 $O(\sqrt{M})$ で行えるので、実行時間制限には余裕を持って間に合います。例えば次のようなプログラムを提出すると正解です。

#include <bits/stdc++.h>
using namespace std;

int main() {
    long long N, Answer = 0;
    cin >> N;

    vector<long long> yakusuu;
    for (long long i = 1; i * i <= 2LL * N; i++) {
        if ((2LL * N) % i != 0LL) continue;
        yakusuu.push_back(i);
        if (i * i != 2LL * N) yakusuu.push_back((2LL * N) / i);
    }

    for (int i = 0; i < (int)yakusuu.size(); i++) {
        long long A_plus_B = (2LL * N) / yakusuu[i];
        if (A_plus_B % 2LL != yakusuu[i] % 2LL) Answer += 1;
    }
    cout << Answer << endl;
    return 0;
}

このように、条件などを解きやすい形の式で表すのは典型的なテクニックです。考察をしていく過程で、頭の中が複雑になってこんがらがることはごく自然なことです。しかし、式で表し、それを紙に書いてみることで、一気に考察が整理されることもあるのです。

また、条件だけでなく答えを式で表すテクニックもあります。例えば次の問題を考えてみましょう。（出典：ABC167B）

$1$ が書かれたカードが $A$ 枚、$0$ が書かれたカードが $B$ 枚、$-1$ が書かれたカードが $C$ 枚あります。ちょうど $K$ $(\leq A + B + C)$ 枚を選ぶとき、取ったカードに書かれた数の和として、あり得る値の最大値はいくつですか。

この問題は簡単ですが、式を書かずに頭の中で考えているだけだと、

  • 境界判定を間違える（例えば $\leq$ と $<$ を間違える）
  • 正負の符号を逆にしてしまう

などの理由で不正解（WA）を出してしまうリスクがあります。したがって以下のように、紙に式を書いて整理するテクニックが有効です。

ケース1　$K \leq A$ の場合：全部 1 なので総和は $K$
ケース2　$A < K \leq A+B$ の場合：全部 1 か 0 なので総和は $A$
ケース3　$A+B < K \leq A+B+C$ の場合：-1 が $K-A-B$ 個含まれるので総和は $A-(K-A-B)=2A+B-K$

他にも、式で表すことで考察がしやすくなる問題はたくさんあります。類題として、

などが挙げられます。


7-5. 部分問題に分解する（レベル：:star:3）

まず、次の問題を考えてみましょう。（出典：JSC2021C）

整数 $A, B$ $(\leq 200000)$ が与えられます。整数 $x, y$ を $A \leq x < y \leq B$ となるように選ぶときの、$gcd(x, y)$ の最大値を求めてください。

一見簡単に見えますが、そのままの形では解くことが難しいです。実際、$(x, y)$ の組を全探索すると二重ループになり、本問題の制約下では実行時間制限超過（TLE）をしてしまいます。そこで、いくつかの部分問題に分解することを考えます。
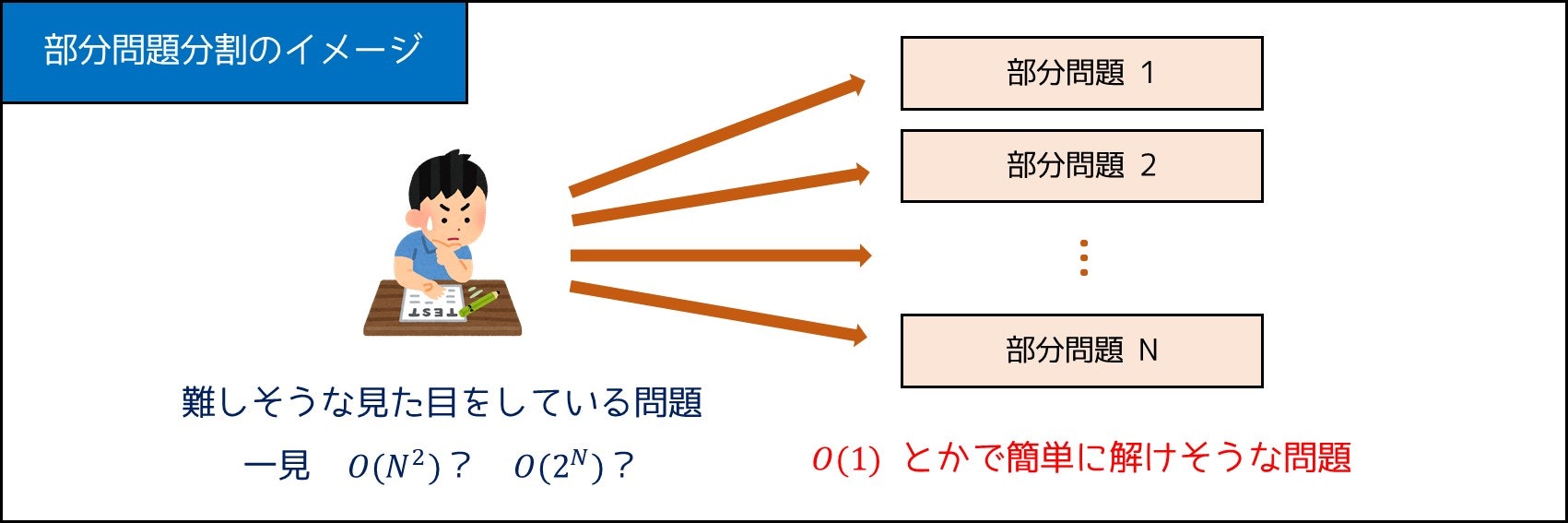
51.jpg
例えば今回の問題の場合、次のような分け方が適切です。

  • $x, y$ 両方が $1$ で割れるようにできるか？
  • $x, y$ 両方が $2$ で割れるようにできるか？
  • $x, y$ 両方が $3$ で割れるようにできるか？
  • $\vdots$
  • $x, y$ 両方が $A$ で割れるようにできるか？

このように分解すると、問題がかなり簡単に見えます。実際、

$A \leq x < y \leq B$ の範囲で、$x, y$ 両方が $u$ で割れるようにできるか？

という問題は、$x$ を「$A$ 以上で最小の $u$ の倍数」、$y = x + u$ とした上で $y \leq B$ かどうかをチェックするだけで解けます。実際、次のようなコードで正解を出すことができるのです。

#include <iostream>
using namespace std;

int A, B, Answer = 0;
bool bubun_mondai(int u) {
    int x = (A + u - 1) / u * u;
    int y = x + u;
    if (y <= B) return true;
    return false;
}

int main() {
    cin >> A >> B;
    for (int i = 1; i <= B; i++) {
        if (bubun_mondai(i) == true) Answer = i;
    }
    cout << Answer << endl;
    return 0;
}

このように、一見難しい問題を、適切にいくつかの簡単な問題に分解するテクニックは非常に有効であり、適用範囲も広いです。類題としては、

などが挙げられます。


7-6. 条件を減らした場合を考える（レベル：:star:2）

まず、次の問題を考えてみましょう。（出典：ARC117A）

次の条件をすべて満たす数列 $E = (E_1, E_2, ..., E_{A+B})$ を構成してください。
条件1　$E_1 + E_2 + \cdots + E_{A+B} = 0$ である。
条件2　数列の要素のうち正のものは $A$ 個ある。
条件3　数列の要素のうち負のものは $B$ 個ある。
条件4　数列の要素はすべて相異なる。
条件5　すべての $i$ について $-10^{9} \leq E_i \leq 10^{9}, E_i \neq 0$ である。

この問題は満たすべき条件が非常に多く、整理しきれない方も多いと思います。このような問題に対しては、いくつかの条件を排除した場合を考えるのが得策となることがあります。そこで条件1を考慮せず、それ以外の条件をすべて満たす数列を考えてみましょう。
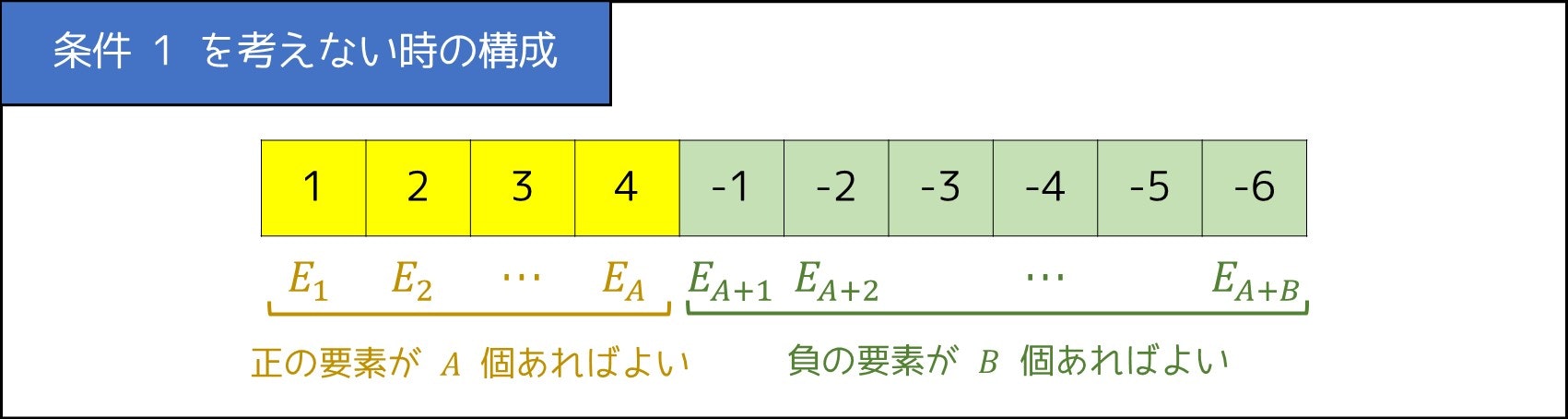
52.JPG
このように、とても簡単に数列を構成することができます。最後に条件1を追加しますが、数列の総和 $E_1 + E_2 + \cdots + E_{A + B}$ が $0$ になっていれば良いので、

  • 数列の要素の和が正であれば、最小の要素 $E_{A+B}$ をさらに減らす
  • 数列の要素の和が負であれば、最大の要素 $E_{A}$ をさらに増やす

といったように、1 つ変えるだけで 5 条件すべて満たす数列を構成することができました。
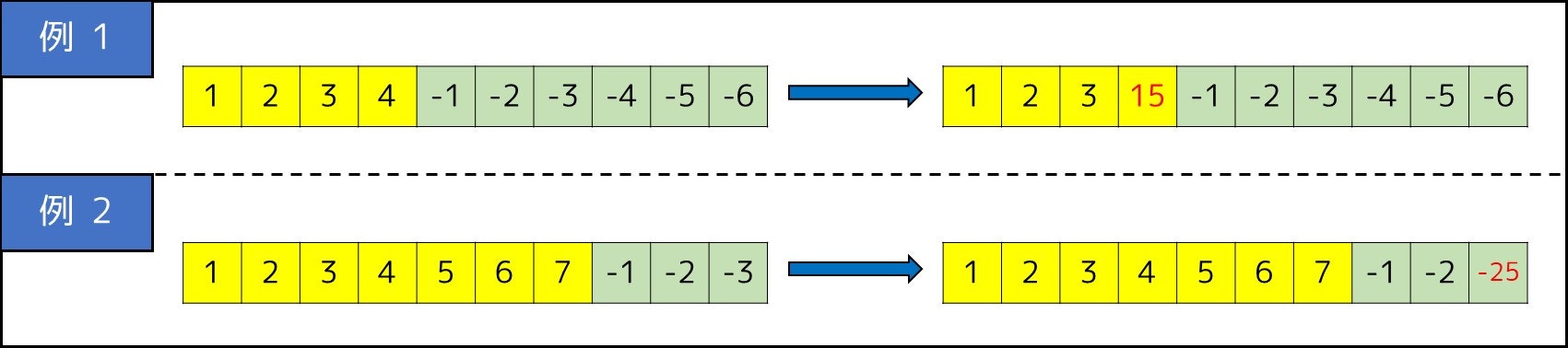
53.jpg
このように、たくさんの条件を含む問題の場合は、

  • 1 つか 2 つの条件を外した「より簡単な問題」を考える
  • その後、それを（少し）変えるだけで問題が解けるかどうかを考える

といった、2 段階の考察テクニックが有効となることもあります。特に、

など、条件を満たす構成を 1 つ出力するタイプの問題（構築問題）ではよく使われます。


7-7. 入出力例（サンプル）から推測する（レベル：:star:1）

本章の最後に、プログラミングコンテストに出題されるような問題を解決するための「裏技的数学的考察」について記します。このうち一つは、各問題に付いている入出力例を活用することです。
52.JPG
皆さんは入出力例をどのように使っているでしょうか。おそらく大半の人は、

自分のプログラムが明らかに間違っているか、それとも正しそうかを提出する前に確認するため。また、デバッグの手助けにするため。

と答えると思います。しかし、それ以外の使い道もあります。例として挙げられるのは、入出力例から解法を予測する方法です。例えば以下の問題を考えてみましょう。（出典：ABC159C）

正の整数 $L$ が与えられます。縦・横・高さ（整数でなくてもよい）の合計が $L$ の直方体としてあり得る体積の最大値を求めてください。

この問題は、直感的に「もしかしたら縦・横・高さ全部同じ場合が最適なのではないか…」と当たりを付けやすいと思います。そこで、入出力例 2 を見てみましょう。

入力: 999
出力: 36926037.00000000000000000

なんと、答えが $333^3 = 36926037$ となっているのです。そうすると自分の直感が正しそうなことが分かりますね。実は入出力例はヒントなのです。このように、入出力例から答えの法則性を見出したりすることも一つの手段です。3

入出力例を活用できる問題はそこまで多くないですが、例えば

などが挙げられます。場合によっては、答えが $N^2$ や $N!$ といった単純な形になっていることもあるので、平方数・立方数・三角数・フィボナッチ数・2 のべき乗・階乗などの値は 20 番目くらいまで覚えても損はないと思います。

ここまで 7 個のポイントに分けて、数学問題に限らず比較的多くの問題で使える汎用的な「数学的考察テクニック」を紹介しました。しかし、問題特有の数学的考察が要求される場合もあるのです。そこで 8 章では、主に水色コーダー程度の問題解決力を付けるために必要な数学的考察テクニックを 14 個に分けてまとめます。是非お読みください。




8. 問題特有の数学的考察テクニック 14 選

7 章では数学問題に限らず多くの問題に利用できる「汎用的な考察テクニック」を 7 つのポイントに絞ってまとめました。しかし、灰色コーダー・茶色コーダー・緑色コーダーが解くべき問題だけを考えても、数学的考察のテクニックはまだまだたくさんあります。例えば、

  • パリティ（偶奇）を考えると解ける（6 章で述べました）
  • 9 の倍数の「各位の数字の和」は 9 の倍数であるという性質を使うと解ける
  • 誤差問題はすべて整数で処理する

など、問題特有の考察が要求される場合もあるのです。そこで 8 章では主に 14 個のポイントに分けて、数学的考察テクニックを紹介したいと思います。皆さんに数学的考察の重要性を体感してもらい、解決できる問題の幅を広げることが最大の目標です。

なお、8 章の構成は次のようになっています。数学的考察の記事ですので、「答えで二分探索」「文字列一致は Rolling Hash で判定する」などといった、数学と関係の薄い典型考察テクニックは省略させていただきます。
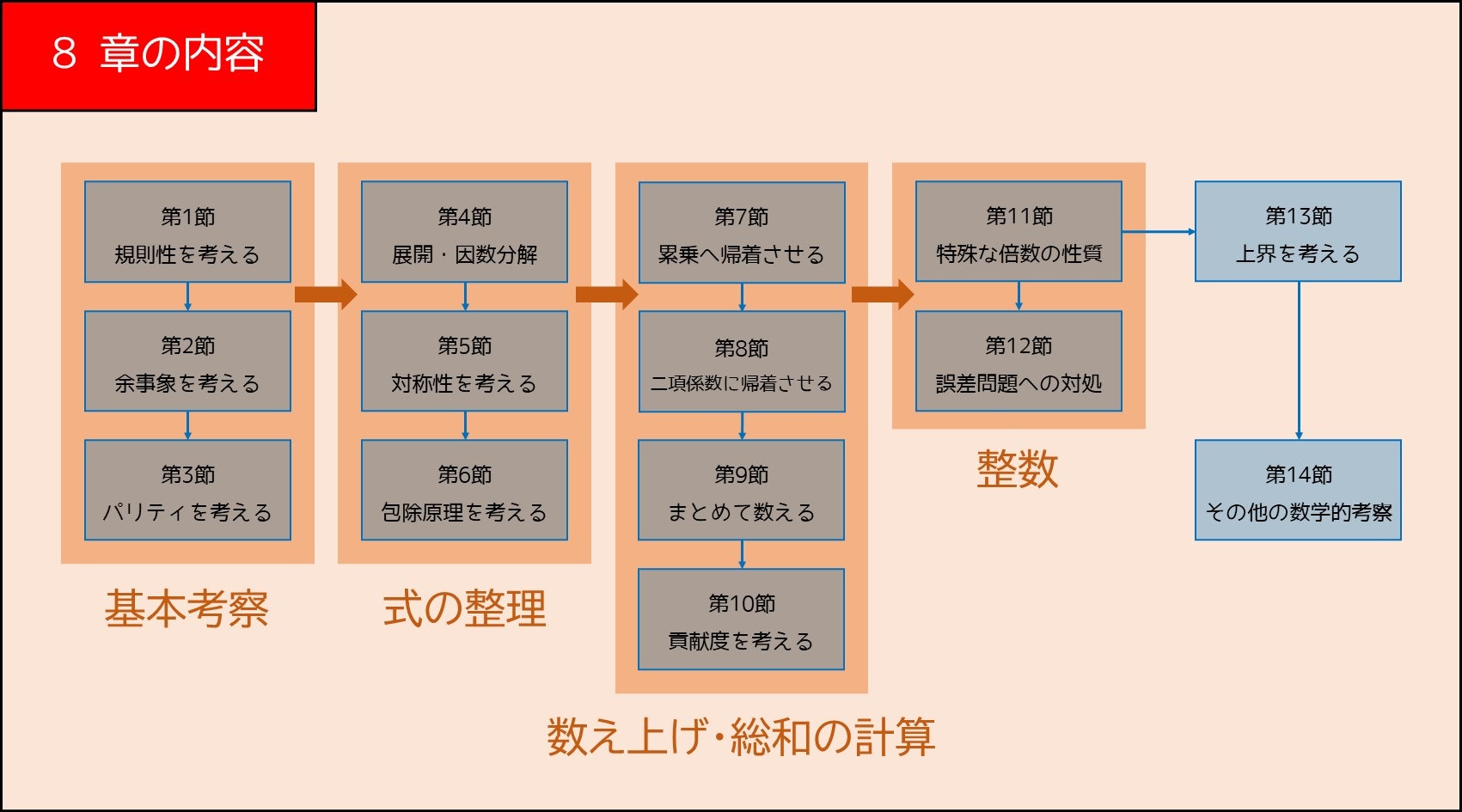
54.jpg


8-1. 規則性・周期性を考える（レベル：:star:2）

まず、次の問題を考えてみましょう。（出典：ARC113B）

正の整数 $A, B, C$ $(\leq 10^{9})$ が与えられます。$A^{(B^C)}$ の 10 進法での 1 の位を求めてください。つまり、$A^{(B^C)}$ を 10 で割った余りを求めてください。

そのまま計算しようとすると、そもそも $B^C$ の計算の時点で桁数が 10 億桁以上となり、大変なことになってしまいます。そこで、次のものを表にしてみましょう。

  • $(A, B^C)$ の値と $A^{B^C}$ の 1 の位の関係

例えば $(A, B, C) = (13, 2, 2)$ の場合 $A^{B^C} = 13^4 = 28561$ ですが、確かに「$A$ の値を 10 で割った余り」が 3、「$B^C$ の値」が 4 の場合、1 の位の値は 1 になっています。
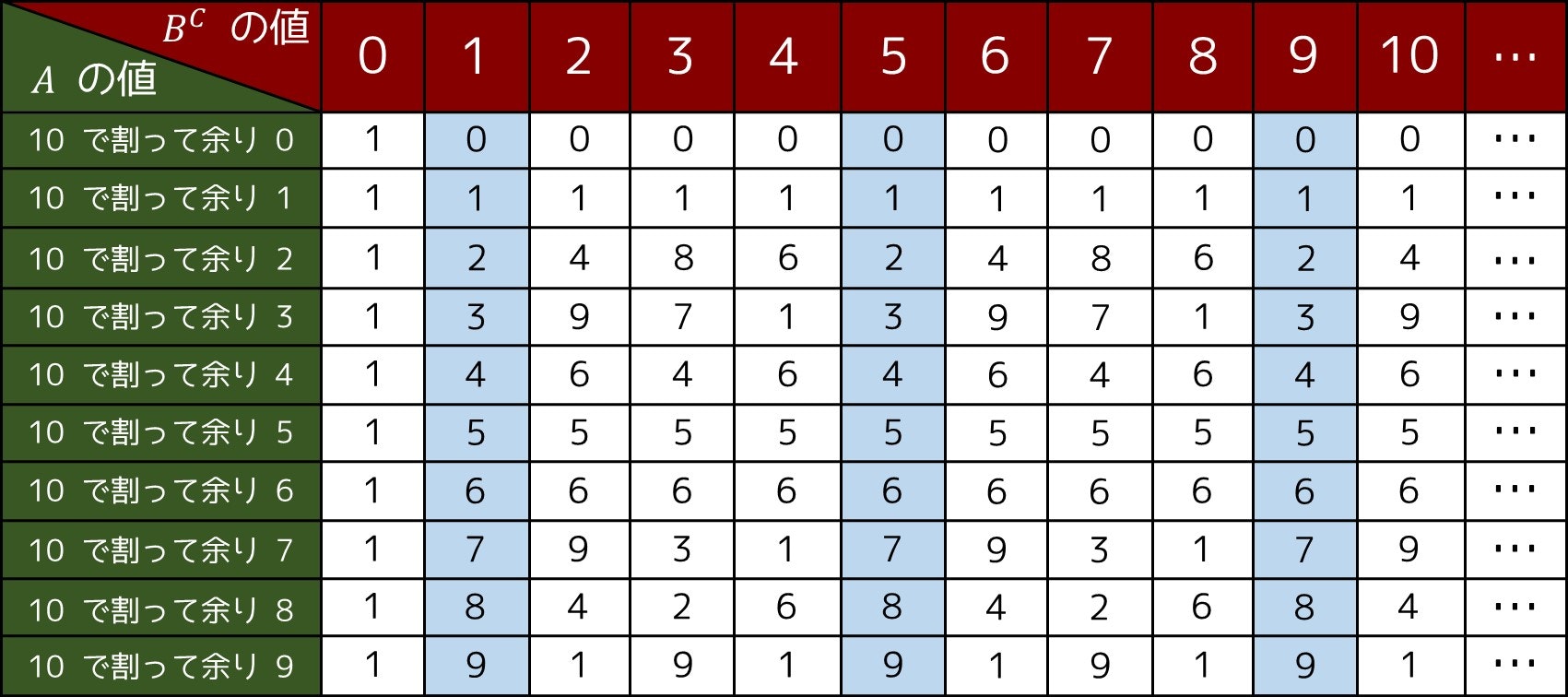
55.jpg
そこで、勘のいい人は「$B^C$ を 4 で割った余りに周期性があるのではないか」と気づくわけです。そうすると、次のような手順で答えを出すことができます。

  • 繰り返し二乗法を使って、$B^C \bmod 4$ の値を計算する
  • $A$ と $B^C \bmod 4$ の値が分かったので、表の通りに答えを求める。

このように、問題によっては、周期性や規則性が重要なヒントになることもあります。

もうひとつの問題例を考えてみましょう。

フィボナッチ数列の第 $N$ $(\leq 10^{18})$ 項を 100 で割った余り $A_N$ を求めてください。
ただし、フィボナッチ数列は $fib_1 = 1, fib_2 = 1, fib_N = fib_{N-1} + fib_{N-2}$ $(N \geq 3)$ で定義されるものとします。

この問題でも規則性を使うことができます。$N$ が小さい場合を調べてみましょう。$A_{301} = 1, A_{302} = 1$ であるため、この数列が前の 2 項によって決まっていることを考えると、「フィボナッチ数列を 100 で割った余り」は 300 項ごとの周期性を持つのです。つまり、以下の等式が成り立ちます。

$$
A_i = A_{i+300} = A_{i + 600} = A_{i + 900} = \cdots = A_{i + 300n} = \cdots
$$

したがって、第 $N$ 項をそのまま計算しなくても、第 $(N \bmod 300)$ 項を計算するだけで答えが分かってしまい、計算にかかる時間が大幅に削減できるのです。

このように、規則性や周期性を使える問題はたくさんあります。類題として、

などが挙げられます。


8-2. 余事象を考える（レベル：:star:2）

まず、次の問題を考えてみましょう。

$1$ 以上 $N$ 以下の整数 $X$ の中で、$3^a + 5^b = X$（$a, b$ は非負整数）の形で表せないようなものはいくつ存在しますか。（制約：$N \leq 10^{18}$）

この問題は $N$ の制約が大きいため、$1$ から $N$ の整数をそれぞれ判定していくことができません。そこで、$3^a + 5^b$ の形で表される整数が非常に少ないことに注目し、

  • $3^a + 5^b = X$ の形で表される整数 $X$ の個数を数える

ことを考えます。実際、次の式が成り立ちます。

$$
（本問題の答え）= N -（3^a + 5^b = X の形で表される整数 X の個数）
$$

そこで、$3^{38} > 10^{18}, 5^{26} > 10^{18}$ より、$0 \leq a \leq 37, 0 \leq b \leq 25$ を満たす $(a, b)$ について調べ上げると、$3^a + 5^b = X$ の形で表される $N$ 以下の整数 $X$ を全列挙できます。したがって、次のような実装をすることで、正解を導くことができるのです！！！

long long pow3[40], pow5[40];

long long solve(long long N) {
    pow3[0] = 1; for (int i = 1; i <= 37; i++) pow3[i] = 3LL * pow3[i - 1];
    pow5[0] = 1; for (int i = 1; i <= 25; i++) pow5[i] = 5LL * pow5[i - 1];

    vector<long long> vec;
    for (int i = 0; i <= 37; i++) {
        for (int j = 0; j <= 25; j++) {
            if (pow3[i] + pow5[j] <= N) vec.push_back(pow3[i] + pow5[j]);
        }
    }
    sort(vec.begin(), vec.end());
    vec.erase(unique(vec.begin(), vec.end()), vec.end());
    return N - (long long)vec.size();
}

このように、「問題文の条件を満たすものの個数」を数えるために、「問題文の条件を満たさないもの（余事象や補集合といいます）の個数」を数えるテクニックは、特に余事象の方が数えやすい場合に非常に有効です。
56.jpg
他にも、例えば次のような問題で余事象のテクニックが活用できます。


8-3. パリティを考える（レベル：:star:2）

まず、次の問題を考えてみましょう。（出典：競プロ典型90問｜24問目）

数列 $A = (A_1, A_2, \cdots, A_N)$ と $B = (B_1, B_2, \cdots, B_N)$ が与えられます。以下の操作をちょうど $K$ 回行うことで、数列 $A$ を $B$ に一致させられるか判定してください。

  • 操作：$A$ の要素を 1 つ選び、+1 か -1 する。

この問題は初心者には難しく、すぐに解法がわかる読者は決して多くないと思います。しかし、次のような考察ステップを踏むことで解けます。（6 章でも紹介されたテクニックです）

考察 1

差の絶対値の総和（$|A_1 - B_1| + |A_2 - B_2| + \cdots + |A_N - B_N|$）は各操作で $1$ しか変わらない。したがって、$|A_1 - B_1| + \cdots + |A_N - B_N| > K$ であれば、$K$ 回の操作では絶対に一致させることができない。逆に、常に $A$ を $B$ に近づける方向で操作を行った場合、最短で $|A_1 - B_1| + |A_2 - B_2 | + \cdots + |A_N - B_N|$ 回で一致させられる。

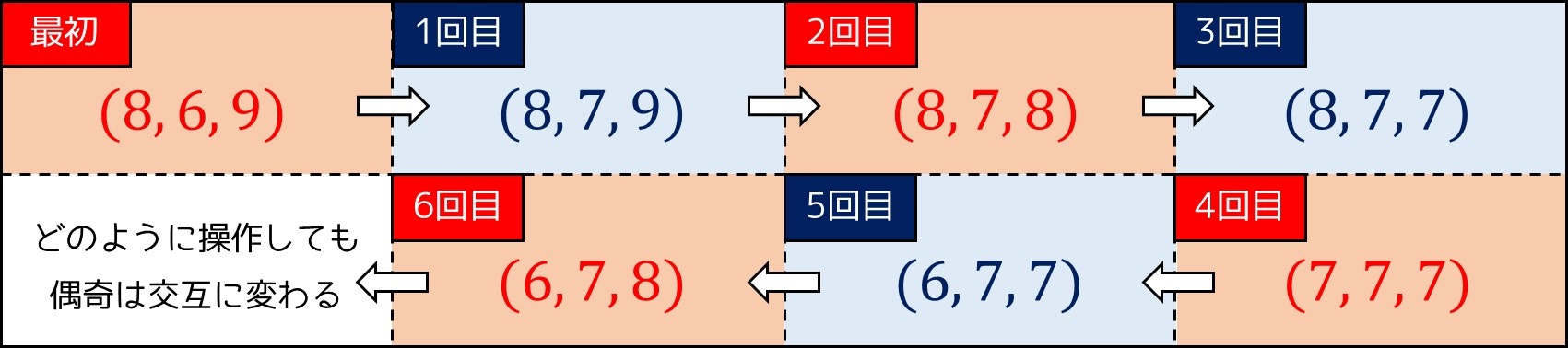
考察 2（本質）

$A_1 + A_2 + \cdots + A_N$ のパリティ（偶奇）は、操作を行うと必ず変わる。例えば最初の数列が $A = (869, 120)$ の場合、数列の総和は奇数であるが、1 回操作を行うと、

  • $A = (870, 120)$
  • $A = (868, 120)$
  • $A = (869, 121)$
  • $A = (869, 119)$

のいずれかとなり、必ず総和は偶数になる。したがって、操作を行うと数列の総和は「奇数→偶数→奇数→偶数→…」といった感じで交互に変わる。よって、$A_1 + A_2 + \cdots + A_N$ の偶奇と $B_1 + B_2 + \cdots + B_N$ の偶奇が同じ場合は $K$ が偶数でなければ一致させられない。偶奇が違う場合は $K$ が奇数でなければ一致させられない。
57.jpg
したがって、次のようなプログラムで正解を出すことができます。

int main() {
    long long Diff = 0, SumA = 0, SumB = 0;
    cin >> N >> K;
    for (int i = 1; i <= N; i++) { cin >> A[i]; SumA += A[i]; }
    for (int i = 1; i <= N; i++) { cin >> B[i]; SumB += B[i]; }
    for (int i = 1; i <= N; i++) Diff += abs(A[i] - B[i]);
    if (Diff > K) cout << "No" << endl;
    else if (SumA % 2LL != SumB % 2LL && K % 2LL == 0LL) cout << "No" << endl;
    else if (SumA % 2LL == SumB % 2LL && K % 2LL == 1LL) cout << "No" << endl;
    else cout << "Yes" << endl;
    return 0;
}

このように、問題によってはパリティ（偶奇）を考えると、考察が非常にやりやすくなる場合もあります。パリティの考え方を使う問題の例として、

などが挙げられます。


8-4. 展開・因数分解を考える（レベル：:star:2）

まず、次の問題を考えてみましょう。

九九表のように、$1 \times 1$ から $N \times N$ までの掛け算が載っている表を「$N \times N$ 九九」といいます。「$N \times N$ 九九」の答え全部の和はいくつか、$10^9 + 7$ で割った余りを求めてください。（制約：$N \leq 10^6$）

この問題は制約が $N \leq 10^6$ と大きいため、例えば次のように、二重ループを用いて表の各セルの値をそのまま計算することはできず、実行時間制限超過（TLE）となってしまいます。

long long Answer = 0;
for (int i = 1; i <= N; i++) {
    for (int j = 1; j <= N; j++) {
        Answer += 1LL * i * j;
        Answer %= 1000000007LL;
    }
}
cout << Answer << endl;

そこで、次のように因数分解のようなことをやってみましょう。

$$
(1 \times 1) + (1 \times 2) + \cdots + (N \times N) = (1 + 2 + \cdots + N) \times (1 + 2 + \cdots + N)
$$

そうすると、$1$ から $N$ までの総和を計算するだけで解くことができます。このように、

  • 答えを式の形で表す（7-4. 節参照）
  • この式を上手い形に因数分解する

といった 2 つの考察ステップを踏むことで、この問題を解くことができるのです！！！
58.jpg
その他にも、約数の個数・約数の和などが、因数分解のテクニックとしては頻出です。軽く解説をしておくと、例えば $175 = 5^2 \times 7$ の約数の和は次のように表すことができます。

$$
1 + 5 + 7 + 25 + 35 + 175 = (1 + 5 + 25)(1 + 7) = 248
$$

実際に、$N = p^a \times q^b \times r^c \times \cdots$ と表される整数における約数の和は、

$$
(1 + p + p^2 + \cdots + p^a)(1 + q + q^2 + \cdots + q^b)(1 + r + r^2 + \cdots + r^c)
$$

となります。詳しく知りたい方は、こちらの記事をお読みください。

プログラミングコンテストでは、式を適切に展開する・因数分解する手法で解ける問題がたくさん出題されています。例えば、

などが挙げられます。


8-5. 対称性を考える（レベル：:star:3）

まず、次の問題を考えてみましょう。（出典：ABC177C）

$N$ 個の整数 $A_1, A_2, \cdots, A_N$ が与えられます。
$1 \leq i < j \leq N$ を満たす全ての組 $(i, j)$ についての $A_i \times A_j$ の和を $\bmod 10^9 + 7$ で求めてください。（制約：$N \leq 200000$）

この問題も制約が大きく、$i, j$ で二重ループを回して計算すると実行時間制限超過（TLE）となってしまいます。そこで、対称性を用いて、次のように問題を言い換えてみましょう。

$N$ 個の整数 $A_1, A_2, \cdots, A_N$ が与えられます。
$1 \leq i \leq N, 1 \leq j \leq N$ を満たす全ての組 $(i, j)$ についての $A_i \times A_j$ の和を $\bmod 10^9 + 7$ で求めてください。（制約：$N \leq 200000$）

実は、1 つ目の問題の答えを $P_1$、2 つ目の問題の答えを $P_2$ とすると、

$$
P_1 = \frac{1}{2} \times \left(P_2 - A_1 \times A_1 - A_2 \times A_2 - \cdots - A_N \times A_N\right)
$$

という式が成り立つのです。理由は、$i < j$ のとき $A_i \times A_j = A_j \times A_i$ であるからです。
59.jpg
そこで、$P_2$ の値は 8-4. 節で紹介した因数分解のテクニックを使うと、

$$
P_2 = (A_1 + A_2 + \cdots + A_N)(A_1 + A_2 + \cdots + A_N)
$$

と表すことができます。あとは前述した通り、適切に 2 で割ると、この問題の答え $P_1$ を出すことができるのです！！！

このように、対称性を利用することで簡単に答えを出すことができる問題はたくさんあります。特に、対称となる部分と値の合計などが等しいときは、全体を求めて 2 で割るテクニックが有効です。類題として、

などが挙げられます。


8-6. 包除原理を考える（レベル：:star:2）

まず、次の問題を考えてみましょう。（出典：競プロ典型90問｜4問目）

$H$ 行 $W$ 列のマス目があります。上から $i$ 行目、左から $j$ 列目にあるマス $(i, j)$ には整数 $A_{i, j}$ が書かれています。$1 \leq i \leq H, 1 \leq j \leq W$ を満たす全ての $(i, j)$ について、「マス $(i, j)$ と同じ行または列にあるマス（自分自身を含む）に書かれている整数をすべて合計した値」を計算してください。（制約：$H, W \leq 2000$）

各 $(i, j)$ について「同じ行または列にあるマスの数値」すべてにアクセスし、単純に足していくと、計算量が $O(HW(H+W))$ となります。しかし、制約が大きいため、この解法だと実行時間制限超過（TLE）となってしまうのです。

int getans(int i, int j) {
    int Answer = 0;
    for (int k = 1; k <= H; k++) Answer += A[k][j];
    for (int k = 1; k <= W; k++) { if (k != j) Answer += A[i][k]; }
    return Answer;
}

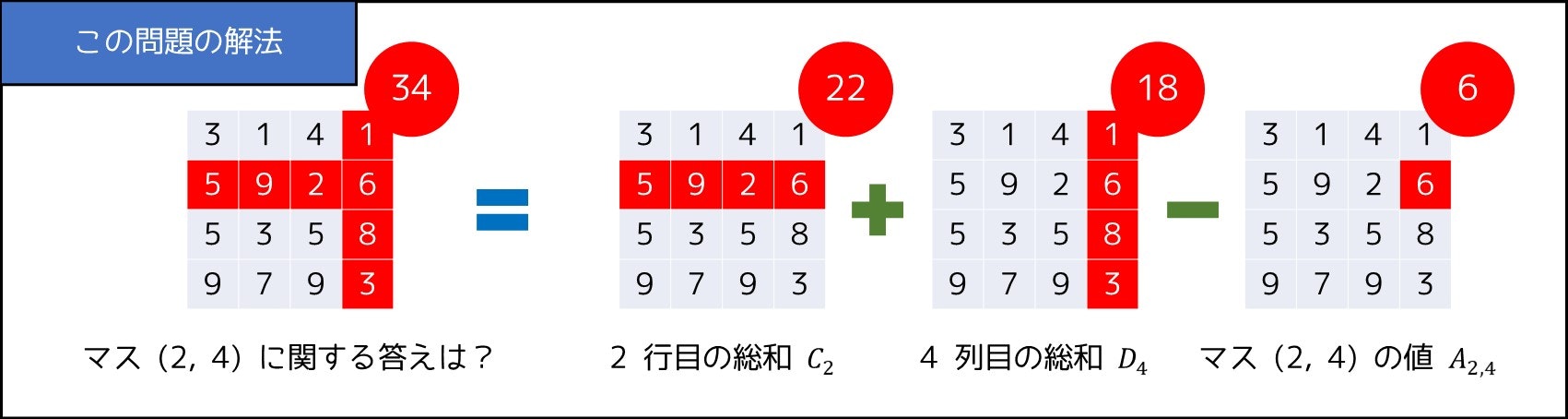
そこで、下図のようなアイデアを使います。そうすると、あらかじめ

  • 各行に書かれた整数の和（$i$ 行目の和を $C_i$ とする）
  • 各列に書かれた整数の和（$j$ 列目の和を $D_j$ とする）

を計算することで、各 $(i, j)$ について計算量 $O(1)$ で答えを出すことができるのです！！！
60.jpg
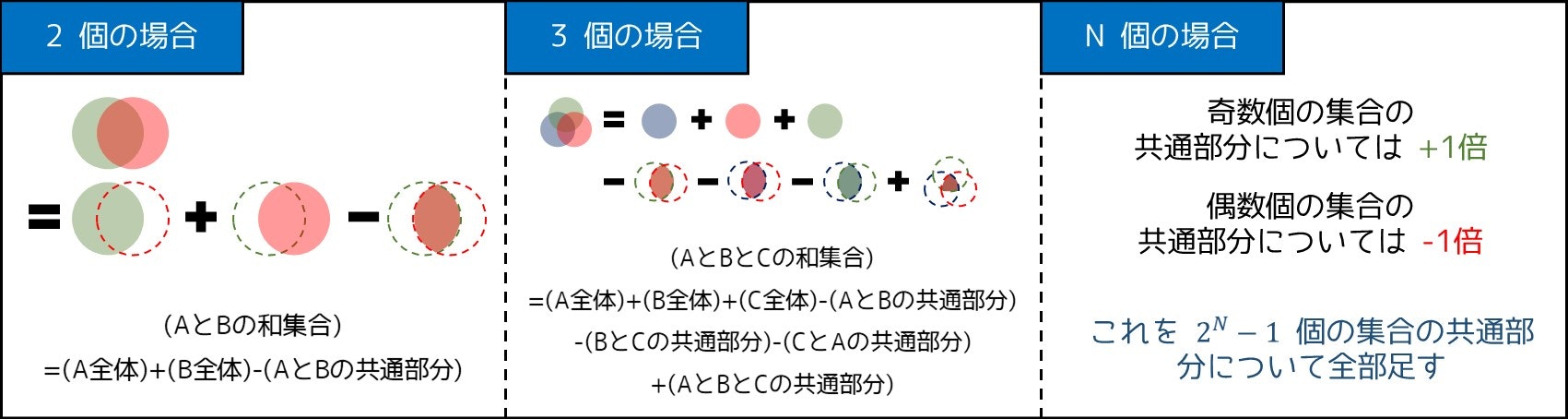
このように、集合 $P$ と $Q$ の和集合（少なくとも一方に含まれる部分）が、

$$
(集合 P) + (集合 Q) - (集合 P と Q の共通部分)
$$

となる性質を包除原理といいます。このような性質は、集合が 2 つの場合のみならず、3 つ以上の場合にも拡張することができます。（詳しくはこちらの記事をご覧ください）
61.jpg
包除原理のテクニックは、共通部分は計算しやすいのに和集合は計算しにくいタイプの数え上げ問題でよく利用され、動的計画法と一緒に使われることもあります4。類題として、

などが挙げられます。


8-7. 累乗に帰着させる（レベル：:star:2）

まず、次の問題を考えてみましょう。（出典：JSC2021D）

整数 $N$ と $P$ が与えられます。次の条件を両方満たす数列 $A = (A_1, A_2, \cdots, A_N)$ はいくつあるでしょうか。$10^9 + 7$ で割った余りを出力してください。
条件1　$1 \leq A_i \leq P-1$ を満たす。
条件2　どのような $i$ $(1 \leq i \leq N)$ についても、$A_1 + \cdots + A_i$ は $P$ の倍数ではない。

この問題は少し難しいですが、次のような考察をすることで、答えが $(P-1) \times (P-2)^{N-1}$ であることが分かります。

  • まず、$A_1$ は $1$ から $P-1$ の範囲で自由に選べるので、選び方は $P-1$ 通り
  • $A_2$ 以降については、$A_i = (P - (A_1 + A_2 + \cdots + A_{i-1}) \bmod P)$ にしてしまった場合、条件2を満たさなくなってしまう。それ以外の選び方は全部 OK なので、$P-2$ 通り

したがって、次のようなプログラムを書くと正解を出すことができます。（べき乗を高速に計算する繰り返し二乗法のアルゴリズムを使っています。）

#include <iostream>
using namespace std;

long long modpow(long long a, long long b, long long m) {
    long long p = 1, q = a;
    for (int i = 0; i < 60; i++) {
        if ((b & (1LL << i)) != 0LL) { p *= q; p %= m; }
        q *= q; q %= m;
    }
    return p;
}

int main() {
    long long N, P, mod = 1000000007;
    cin >> N >> P;
    cout << (P - 1) * modpow(P - 2, N - 1, mod) % mod << endl;
}

このように、ある数のべき乗が答えになる場合もあります。では、どのような問題に「累乗」が使えるのでしょうか。3 つのパターンに分けて整理してみましょう。

パターン 1. 独立な「選べるもの」が N 個あるとき

今回の問題のように、「$P$ 通りの中から 1 つ選ぶこと」を $N$ 回行うとき、全体の選び方の総数は $P \times P \times \cdots \times P = P^N$ 通りです。例えば、次の場合を考えてみましょう。

$10$ 個のボールが一列に並べられており、各ボールには赤青緑の $3$ 種類のうちいずれかの色を塗らねばならない。そのとき、全体の色の塗り方として考えられる場合の数を求めよ。

これは「3 通りの中から 1 つ選ぶこと」を 10 回行うので、求める数は $3^{10}$ 通りです。また、

$N$ 文字の英小文字（a～z）からなる文字列

についても「26 通りの中から 1 つ選ぶこと」を $N$ 回行うので、求める総数は $26^{N}$ 通りとなります。ただし、「赤色の隣には青色を塗ってはならない」など、互いに独立に考えられない条件があった場合、この手法は使えないことがあるのでご注意ください。

パターン 2. N 個のうちいくつかを選ぶ方法

$N$ 個のモノから $0$ 個以上 $N$ 個以下を選ぶ方法は $2^N$ 通りであり、累乗を使って表すことができます。なぜなら、各モノについて「選ぶ」「選ばない」の 2 通りの選択を独立に行うことができ、結局はパターン 1 の

「2 通りの中から 1 つ選ぶこと」を $N$ 回行う場合

に帰着できるからです。同様に考えると、大きさ $N$ の集合の部分集合の数が $2^N$ 個であることが分かります。

パターン 3. 二項係数の和

二項係数に帰着させられる問題については 8-8. 節で詳しく述べますが、それに関連して次の等式が成り立ちます。（二項係数の表記が分からない方は 2-12. 節をご覧ください）

\begin{pmatrix}
N \\
0
\end{pmatrix}
+
\begin{pmatrix}
N \\
1
\end{pmatrix}
+
\begin{pmatrix}
N \\
2
\end{pmatrix}
+
\cdots
+
\begin{pmatrix}
N \\
N
\end{pmatrix}
= 2^N

\begin{pmatrix}
N \\
0
\end{pmatrix}
+
\begin{pmatrix}
N \\
2
\end{pmatrix}
+
\begin{pmatrix}
N \\
4
\end{pmatrix}
+
\cdots
= 2^{N-1} \ (N \geq 1)

実は二項係数の和は 2 のべき乗になっているのです。しかし、これは「$N$ 個から 0 個選ぶ方法」「$N$ 個から 1 個選ぶ方法」…「$N$ 個から $N$ 個選ぶ方法」を全部足していると考えると、案外自然なことです。

このように、累乗は非常に多くの場面で活用できます。特にパターン 1 は活用範囲が広いです。答えがそのままべき乗になっていることはそれほど多くないですが、7-5. 節で述べた通りいくつかの部分問題に分解したときに、その部分問題の答えが「累乗」になっているケースはかなり多いです。例えば、

などが挙げられます。


8-8. 二項係数に帰着させる（レベル：:star:3）

まず、以下の問題を考えてみましょう。（出典：ABC145D）

点 $(0, 0)$ にチェスのナイトの駒があります。この駒が点 $(i, j)$ にあるとき、1 回の移動では $(i+1, j+2)$ または $(i+2, j+1)$ のいずれかに動かせます。ナイトを点 $(X, Y)$ まで移動させる方法は何通りありますか。$10^9 + 7$ で割った余りを出力してください。

この問題は難しいですが、少し考察をすると次のようなことが分かります。

  • 1 回の移動で (x 座標) + (y 座標) の値が 3 増えるので、$(X+Y) \bmod 3 \neq 0$ の場合、移動方法は存在しない
  • そうでない場合、合計 $(X+Y) \div 3$ 回の移動を行う。その中でちょうど $Y - (X + Y) \div 3$ 回赤色の移動を行う必要がある。

さらに後述のパターン1の考察によって、答えが $C((X + Y) \div 3, Y - (X + Y) \div 3)$ 通りであることが分かります。例えば $(X, Y) = (8, 10)$ の場合は全体で 6 回、そのうち赤色の移動が 4 回なので、求める場合の数は $C(6, 2)=15$ 通りです。
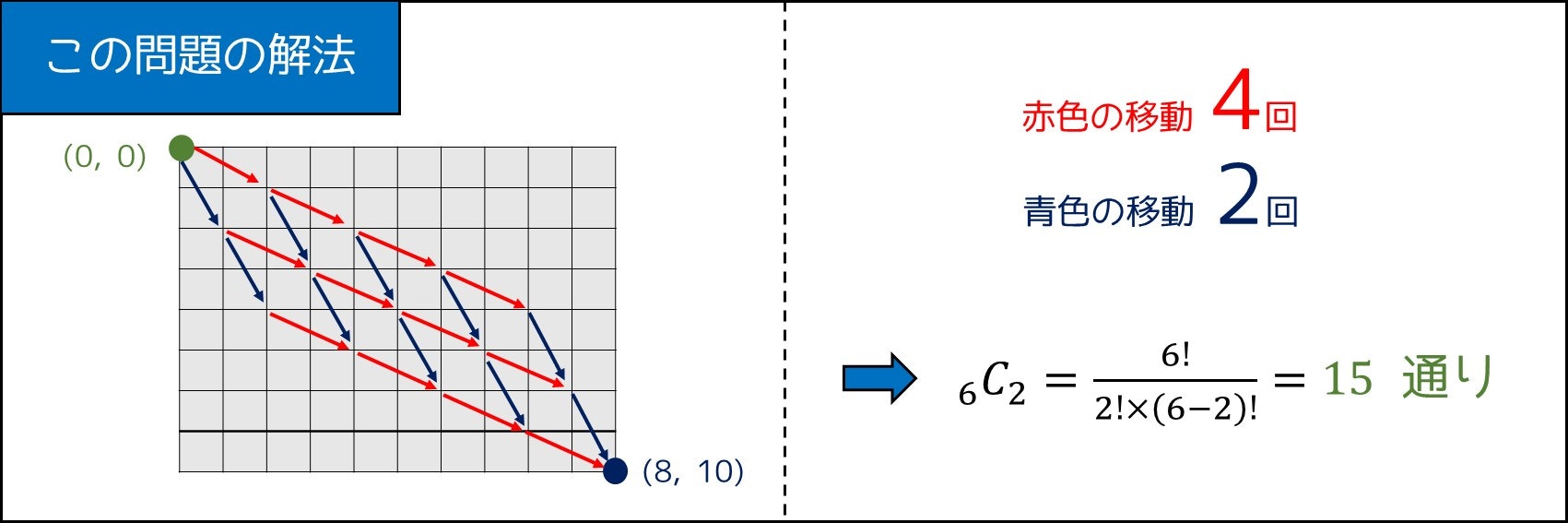
62.jpg
このように、二項係数が答えになることもあります。では、どのような問題に「二項係数」が使えるのでしょうか。3 つのパターンに分けて整理してみましょう。

パターン 1. N 個の中から M 個選ぶ場合の数

これは二項係数の定義そのままです。例えば 6 人の中から 3 人の代表を選ぶ方法の数は、次の式で表されます。

C(6, 3) = 
\begin{pmatrix}
6 \\
3
\end{pmatrix}
= \frac{6!}{3! \times 3!} = 20

このような考え方は、経路の問題にも使われます。例えば格子点上を、点 $(0, 0)$ から点 $(H, W)$ まで最短経路で移動したい場合、次の条件を満たさなければなりません。

  • 移動回数は合計 $H+W$ 回
  • その中で「x 座標が増える方向に移動する回数」は $H$ 回

結局 $H+W$ 個から $H$ 個を選ぶ問題に帰着でき、方法は $C(H+W, H)$ 通りとなるのです。

パターン 2. 和が S である長さ N の正整数列の場合の数

実は、長さ $N$ の正整数列5 $A = (A_1, A_2, \cdots, A_N)$ で総和が $S$ となるものは $C(S-1, N-1)$ 通りです。下図のように「$S-1$ 個の切れ目の中から $N-1$ 個を選び、仕切りを入れる」ことを考えれば自然だと思います。
63.jpg

パターン 3. 和が S である長さ N の非負整数列の場合の数

実は、長さ $N$ の非負数列6 $A = (A_1, A_2, \cdots, A_N)$ で総和が $S$ となるものは $C(N+S-1, N-1)$ 通りです。一見複雑に見えますが、数列の全要素を 1 加算すると、

長さ $N$ の正整数列 $A$ の中で、総和が $N+S$ となるものは何通りか？

というパターン2の問題に帰着できるので、自然なことだと思います。

このように、二項係数は非常に多くの問題で活用できます。答えがそのまま二項係数になっていることはそれほど多くないですが、7-5. 節で述べた通りいくつかの部分問題に分解したときに、その部分問題の答えが「二項係数」になっているケースはかなり多いです。例えば、

などが挙げられます。なお、二項係数を高速に計算する方法について知りたい方は、本記事 3-10. 節をご覧ください。


8-9. 数えやすいものをまとめて数え上げる（レベル：:star:2）

まず、次の問題を考えてみましょう。

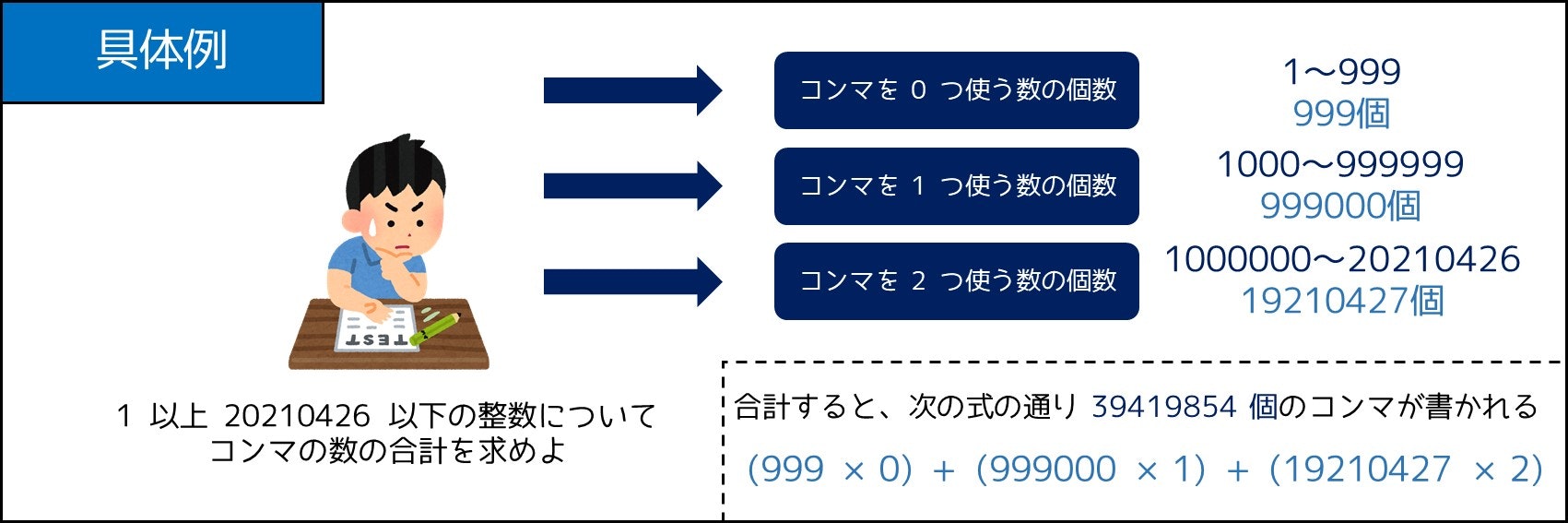
高橋君は整数を書くとき、下から $3$ 桁ごとにコンマで区切って書きます。例えば 1234567 であれば 1,234,567、777 であれば 777 と書きます。彼が $1$ 以上 $N$ 以下の整数を一度ずつ書くとき、コンマは合計で何回書かれますか？（制約：$N \leq 10^{15}$）

この問題も 8-4. 節や 8-5. 節で紹介した問題と同様、制約が大きいため、$1, 2, \cdots, N$ それぞれのコンマの個数を計算量 $O(N)$ かけて求めると実行時間超過（TLE）になってしまいます。

そこで、 7-5. 節で紹介した「いくつかの部分問題に分けるテクニック」を使い、次のような「たくさんの簡単な問題」に分けることを考えます。

  • コンマがちょうど $0$ 回書かれる $N$ 以下の整数はいくつあるか？
  • コンマがちょうど $1$ 回書かれる $N$ 以下の整数はいくつあるか？
  • コンマがちょうど $2$ 回書かれる $N$ 以下の整数はいくつあるか？
  • コンマがちょうど $3$ 回書かれる $N$ 以下の整数はいくつあるか？
  • コンマがちょうど $4$ 回書かれる $N$ 以下の整数はいくつあるか？
  • コンマがちょうど $5$ 回書かれる $N$ 以下の整数はいくつあるか？

そこで、コンマが $P$ 回書かれる数の範囲は $1000^P \leq x < 1000^{P+1}$ なので、「$N$ 以下であること」と重なる個数を計算すれば良いだけです。このように、まとめて数えやすい形を考えて、これが適用できるような部分問題に分ける考察テクニックが有効な場合もあります。7-5. 節で紹介したテクニックは、数え上げ問題にも応用できるのです。
64.jpg
他にも、このような数学的考察は、例えば次の問題で使うことができます。


8-10. 「答えへの貢献度」を考える（レベル：:star:3）

まず、次の問題を考えてみましょう。（出典：ABC186D 改題）

$N$ 個の整数 $A_1, A_2, \cdots, A_N$ があり、$A_1 < A_2 < \cdots < A_N$ を満たしています。そのとき、$1 \leq i < j \leq N$ を満たす全ての $(i, j)$ の組についての $A_j - A_i$ の和を求めてください。（制約：$N \leq 10^5$）

この問題も、次のように $i, j$ で二重ループを回したプログラムを書くと、計算量が $O(N^2)$ となり、実行時間超過（TLE）と判定されてしまいます。

long long Answer = 0;
for (int i = 1; i <= N; i++) {
    for (int j = i + 1; j <= N; j++) Answer += (A[j] - A[i]);
}
cout << Answer << endl;

そこで、次のことを考えてみましょう。

各 $i \ (1 \leq i \leq N-1)$ について、$X_{i+1} - X_i$ の区間が最終的な答えにどの程度寄与しているのだろうか？

実際、下図のように、すべての $(i, j)$ $[1 \leq i < j \leq N]$ の組に対して $X_i$ から $X_j$ に向かう線を引いたとき、区間 $[X_i, X_{i+1}]$ を完全に含むものは $i \times (N-i)$ 個あるので、答えへの貢献度は $(X_{i+1} - X_i) \times i \times (N-i)$ となります。このように考えると、最終的な答えは

$$
Answer = \sum_{i=1}^{N-1} (X_{i+1} - X_i) \times i \times (N-i)
$$

であることが導出できるのです。
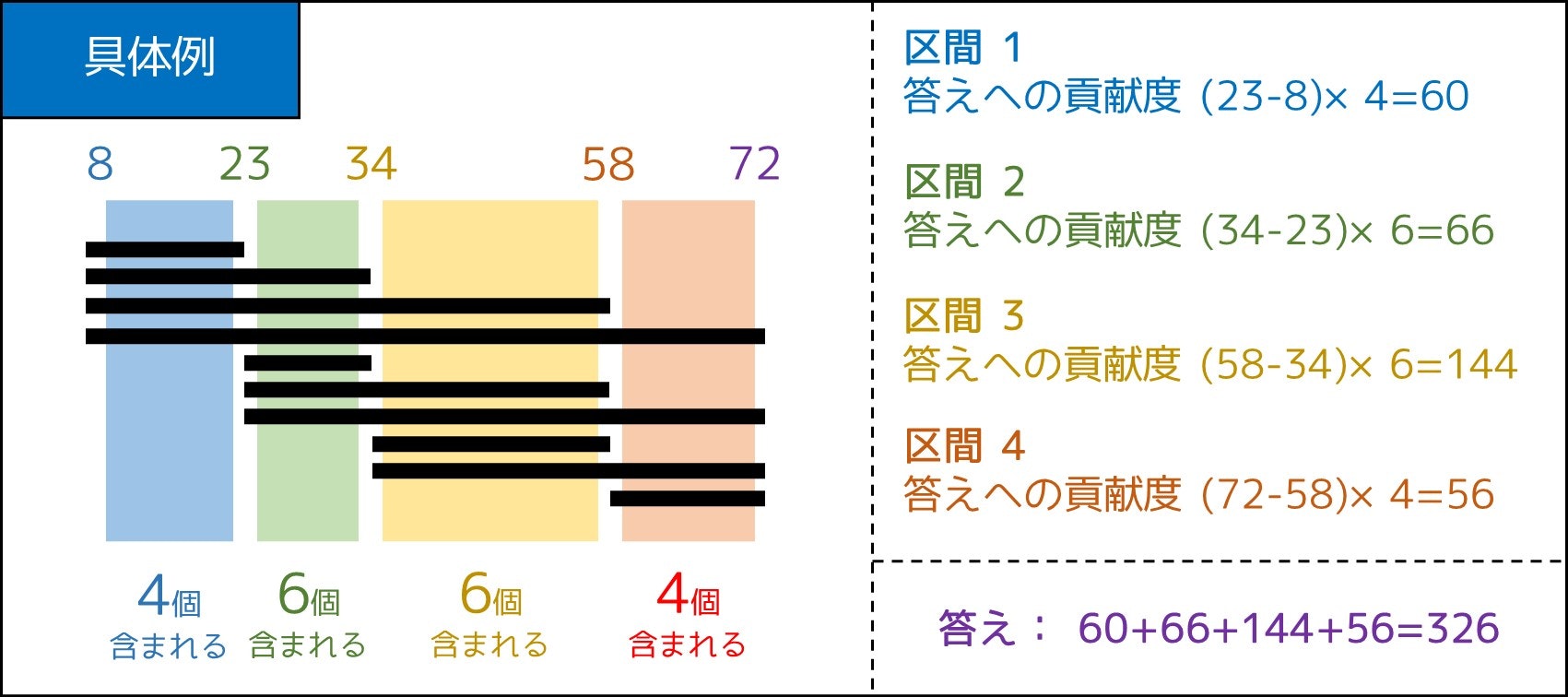
65.jpg
このように、答えへの貢献度を考えると一気に考察が進むこともあります。

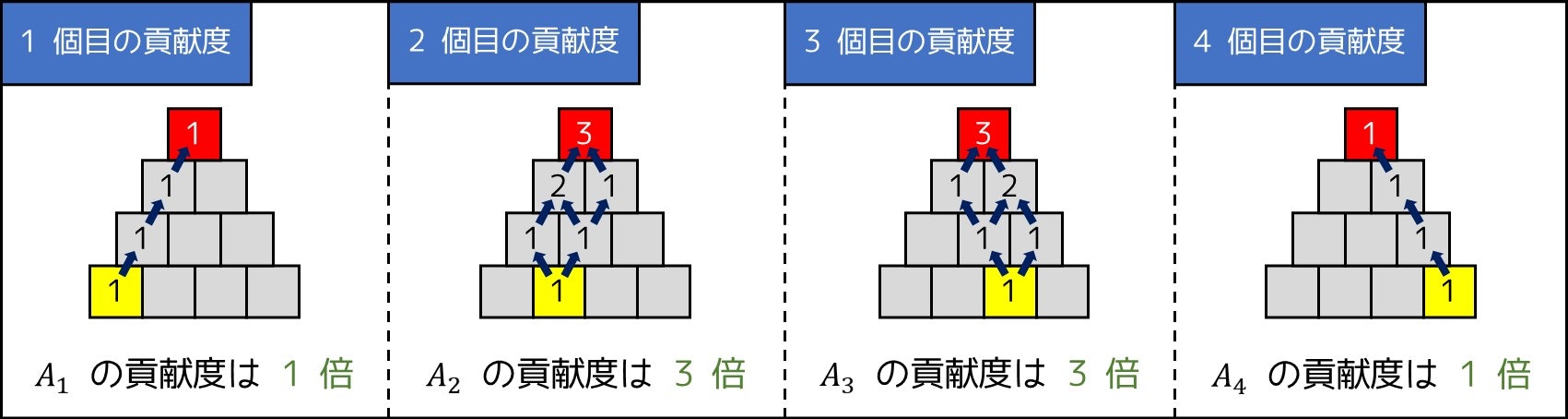
念のため、もうひとつ問題を考えてみましょう。（やや難しいです。この問題も単純にシミュレーションすると二重ループになり、実行時間超過（TLE）と判定されてしまいます。）
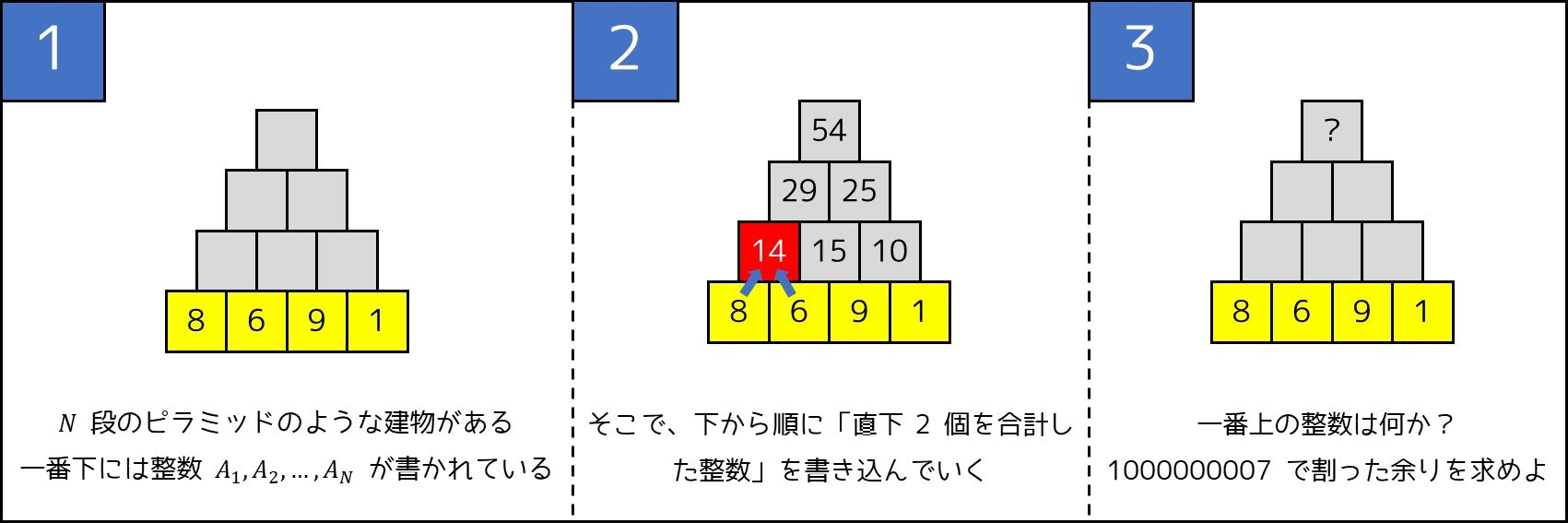
66.jpg
しかし、「答えへの貢献度」を考えるテクニックを使えば解けます。実際、左から $i$ 番目のブロックの貢献度は、二項係数を用いて $C(N-1, i-1) \times A_i$ で表すことができるので、最終的な答えは次の通りになります。

Answer = 
\begin{pmatrix}
N-1 \\
0
\end{pmatrix}
\times A_1 + 
\begin{pmatrix}
N-1 \\
1
\end{pmatrix}
\times A_2 + \cdots + 
\begin{pmatrix}
N-1 \\
N-1
\end{pmatrix}
\times A_N

なお、「答えへの寄与分」に二項係数が掛けられていることは、1 段目のブロックから右上または左上に移動することを繰り返して一番上に行く方法の通り数が二項係数の式で表されることを考えると、理解しやすいと思います。（8-8. 節参照）
67.jpg

このように、答えへの貢献度を考えるテクニックは多くの問題で有効です。また、この種の議論をさらに発展させると、例えば次のようなテクニックにも応用することができるのです。

  • 「期待値の線形性」を使うテクニック（詳しくはこちら）
  • ビット演算において、桁ごとに考えるテクニック
  • x 座標・y 座標を独立に考えるテクニック

類題として、

などが挙げられます。


8-11. 特殊な倍数の性質を使おう（レベル：:star:1）

まず、次の問題を考えてみましょう。（出典：ABC176B 改題）

整数 $N$ が与えられます。$N$ が $9$ の倍数であるか判定してください。（制約：$N < 10^{200000}$）

この問題は $N$ が非常に大きいため、次のようなプログラムで単純に判定することはできません。実際、long long 型でも高々 $2^{63}-1$ までの整数しか表すことができないのです。

long long N;
cin >> N;
if (N % 9LL == 0LL) cout << "Yes"<< endl;
else cout << "No" << endl;

そこで、$N$ が $9$ の倍数であることと、$N$ の各位の数字の和が $9$ の倍数であることは同値です。そのことを利用すると、例えば $N$ を文字列型（string 型など）で受け取っても、次のようなプログラムで正解を出すことができます。

string N; int Digit_Sum = 0;
cin >> N;
for (int i = 0; i < N.size(); i++) Digit_Sum += (N[i] - '0');
if (Digit_Sum % 9 == 0) cout << "Yes" << endl;
else cout << "No" << endl;

このように、特殊な倍数の性質を使うと問題が解ける場合もあるのです。特に 2・3・4・5・8・9・10・11 の倍数は頻出で、主な性質は次表の通りです。

倍数 性質
2 の倍数 1 の位が 0, 2, 4, 6, 8 のいずれかである
3 の倍数 各位の数字の和が 3 の倍数
4 の倍数 下 2 桁が 4 の倍数
5 の倍数 1 の位が 0, 5 のいずれかである
8 の倍数 下 3 桁が 8 の倍数
9 の倍数 各位の数字の和が 9 の倍数
10 の倍数 1 の位が 0 である
11 の倍数 奇数桁目の数字の和と、偶数桁目の数字の和の、差が 11 の倍数 ​

例えば次のような問題で、倍数の性質を使うことができます。


8-12. 誤差問題は整数で処理しよう（レベル：:star:2）

まず、次のような問題を考えてみましょう。（出典：PANASONIC2020-C）

$\sqrt{a} + \sqrt{b} < \sqrt{c}$ ですか？（制約：$1 \leq a, b, c \leq 10^9$）

最も自然に実装すると、例えば次のようになります。7

#include <iostream>
#include <cmath>
using namespace std;

int main() {
    long long a, b, c;
    cin >> a >> b >> c;
    if (sqrt(a) + sqrt(b) < sqrt(c)) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

しかし残念ながら、これはたとえば $(a, b, c) = (249999999, 250000000, 999999998)$ などのケースで WA となってしまいます。本当は、

$$
\sqrt{249999999} + \sqrt{250000000} < \sqrt{999999998}
$$

となるはずなのですが、何故か間違って No と出力されてしまっているのです。そこで、次のコードで実験してみましょう。

int main(){
    printf("%.30f\n", sqrt(249999999));
    printf("%.30f\n", sqrt(250000000));
    printf("%.30f\n", sqrt(249999999) + sqrt(250000000));
    printf("%.30f\n", sqrt(999999998));
    return 0;
}

このときの出力は次の通りです。

15811.388269219120047637261450290680
15811.388300841896125348284840583801
31622.776570061017991974949836730957
31622.776570061017991974949836730957

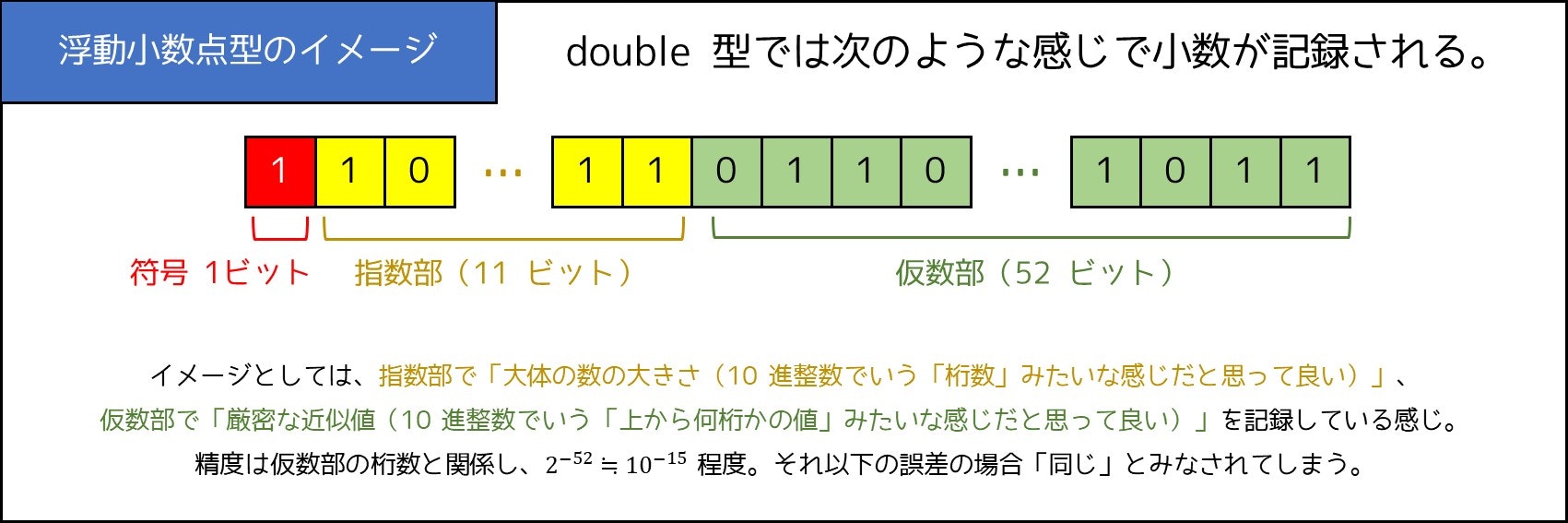
本当は 2 つの値が異なるはずなのに、「等しい」と判定されてしまっています。なぜなら、sqrt 関数の呼び出しにより小数を扱う際に、浮動小数点型（float, double, long double など）が用いられているため、実数が近似的に扱われてしまっているからです。

実際、最もよく使われる double 型の場合、およそ $2^{-52}$ 以下の相対誤差は無視されてしまい、仮に 2 つの値の間にそれ以下の小さい差があったとしても「同じだ」とみなされてしまうのです。したがって、このような非常に小さい誤差によって答えが変わるタイプの問題では、小数を使うことがあまり得策ではありません。
68.jpg
そこで安全のため、全部整数で判定を行うことを考えます。問題文の式は、次のように式変形することができます。

\sqrt{a} + \sqrt{b} < \sqrt{c} \\
(\Leftrightarrow) \ a + 2 \times \sqrt{ab} + b < c \\
(\Leftrightarrow) \ 2 \times \sqrt{ab} < c - b - a \\

そこで、$c - b - a < 0$ の場合は条件が成り立たず、そうでない場合は両辺を 2 乗して、

4ab < (c - b - a)^2

と変形することができます。したがって、以下のソースコードを書くと正解が得られます。

int main() {
    long long a, b, c;
    cin >> a >> b >> c;
    if (c - b - a < 0LL) cout << "No" << endl;
    else if (4LL * a * b < (c - b - a) * (c - b - a)) cout << "Yes" << endl;
    else cout << "No" << endl;
    return 0;
}

このように、非常に細かい誤差によって答えが変わるような問題の場合は、すべて整数で計算することが重要です。さもなければ、プログラム上は一見正しいことをしているように見えても、実際には誤差のせいで不正解（WA）と判定されてしまうのです。他にも、

などの問題では、自然に実装すると誤差が原因となって不正解が出てしまいます。


8-13. 上界を考える（レベル：:star:3）

本章の最後に、次の問題を考えてみましょう。（出典：ABC139D）

整数 $N$ に対して、$\{1, 2, 3, \cdots, N \}$ を並び替えた数列 $\{P_1, P_2, \cdots, P_N \}$ を選びます。そして、各 $i = 1, 2, \cdots, N$ について、$i$ を $P_i$ で割った余りを $M_i$ とします。そのとき、$M_1 + M_2 + \cdots + M_N$ の最大値を求めてください。（制約：$N \leq 10^9$）

この問題は初心者には難しく、一瞬で解法、そして解法の証明までが分かる読者は決して多くないと思います。しかし、次のような考察ステップを踏むことで解けるのです。

ステップ 1. 上界を考える

$i$ を $P_i$ で割った余りが $M_i$ なので、明らかに $M_i \leq P_i-1$ を満たします。したがって、

$$
(M_1 + \cdots + M_N) \leq (P_1 + \cdots + P_N) - N = \frac{N(N+1)}{2} - N = \frac{N(N-1)}{2}
$$

が成り立つことを考えると、最大値の上界が $\frac{N(N-1)}{2}$ であること（つまり、それを超える最大値になることは絶対にありえないこと）が分かります。

ステップ 2. 上界となる構成を考える

次に、$P_i = i+1$（ただし $P_N = 1$）とすることを考えてみましょう。この場合、

$$
M_N = 0, \ M_i = i \ (1 \leq i \leq N-1)
$$

が成り立つため、$M_1 + M_2 + \cdots + M_N = \frac{N(N-1)}{2}$ となり、上界と一致します。

このように、以下の 2 つのステップで考察を行うと、答えが $B$ であることが分かるだけでなく、解法の証明までをすることができます。

ステップ1　頑張って上界が $B$ となる証明を考える
ステップ2　スコアが上界 $B$ と一致する構成を考える

また、解法の大筋は分かったが自信がない場合にも、上界の値を考えることで、自分の解法に自信を持つことができる場合もあります。


8-14. その他の数学的考察テクニック（レベル：:star:4）

7 節と 8 節合わせて、合計で 20 個の数学的考察テクニックを紹介してきました。しかし、AtCoder の出題範囲は広いため、青色コーダー・黄色コーダーとレベルが上がっていくにつれ、ここまでの内容以外の考察が要求される割合も増えていきます。

そこで、本節では紙面の都合上紹介できなかった数学的考察テクニックをリストアップすることで、後編を締めたいと思います。なお、比較的難易度が高いので、読み飛ばしていただいても構いません。

問題を適切に言い換える

問題によっては、別の問題設定に置き換えて考えたり、条件を緩和した問題に言い換えたりすることで、一気に解きやすくなる場合があります。例えば、次のような問題で「問題の言い換え」が使えます。

演算順序を工夫してオーバーフローしないようにする

問題によっては、適切に実装しなければ計算途中で値が $2^{63}$ を超えてしまい、long long 型でもオーバーフローする場合があります。例えば以下のような問題では、割り算を先に行うなど、計算順序を工夫することでオーバーフローを防ぐ必要があるのです。

「写像 12 相」のアイデアを使う

例えば以下の問題のように、重複組合せ・スターリング数・ベル数・分割数など、「写像 12 相」と呼ばれる一連の有名な数え上げ問題に帰着できる場合があります。

操作を後ろから見る

問題文の通りに操作を行っても、「解法が見えない」「計算量が悪くなってしまう」といったことはよくあります。そこで、操作を逆順に考える（つまり $N$ 個の操作があったとき、$N$ 番目の操作から順に考えていく）ことによって、一気に考察が見えやすくなる場合もあります。

差の最小化は中央値

次のようなすごい性質があります。

$\sum_{i=1}^{N} |A_i - x| = \left( |A_1 - x| + |A_2 - x| + \cdots + |A_N - x| \right)$ の値が最小になる $x$ の値は、数列 $A = (A_1, A_2, \cdots, A_N)$ の中央値である。

この性質は、例えば次のような問題で利用することができます。

カッコ列の性質を使う

競プロの文脈では、以下のようなカッコ列を「正しいカッコ列」と定義することが多いです。

性質1　() は正しいカッコ列である
性質2　$S$ が正しいカッコ列であるとき、文字列 ( + $S$ + ) は正しいカッコ列である
性質3　$S, T$ が正しいカッコ列であるとき、文字列 $S$ + $T$ は正しいカッコ列である
性質4　それ以外のカッコ列はすべて正しくない

そこで、文字列 $C$ が正しいカッコ列であるための必要十分条件は、次のように言い換えることができます。

条件1　すべての $i$ $(1 \leq i \leq |C|)$ について、左から $i$ 文字目までの時点で ( より ) の方が多くなることはない
条件2　文字列 $C$ は ( と ) から成り、これら 2 つが同数出現する。

このような性質を使うと、例えば次のような問題を解くことができます。

マンハッタン距離は 45 度回転

二次元平面を 45 度回転することによって、ある点からマンハッタン距離 $K$ 以内となる範囲が「各辺が $x, y$ 軸に平行な正方形」になるため、計算処理がしやすくなるテクニックがあります。（詳しくはこちらの記事をお読みください。）

この考え方は、次のような問題に応用することができます。




9. おわりに

本記事では、アルゴリズムを学ぶうえで必要となる数学的知識、そして様々な問題を解決する上で必要となる数学的考察テクニックについてまとめました。

私は、アルゴリズム構築能力・問題解決力の上達を目指すにあたって、プログラミング知識のみならず、数学的知識や数学的考察力を身に付けることも重要だと考えています。しかし、現状 AtCoder 参加者などでも数学の壁でつまずく人も多いと聞きます。そこで、少しでもこのような壁を取り除きたいと思い、この「アルゴリズム・AtCoder のための数学」という記事を完成させた次第です。

最後に、本記事が一人でも多くの「数学力を鍛えたい！」と思っているプログラマの役に立つことができれば、とても嬉しい気持ちです。前編・中編・後編合わせて約 60,000 字と長い記事になりましたが、最後までお読みいただきありがとうございました。


10. 参考文献・参考資料

今後、数学的知識や数学的考察をさらに身に付けたいと考えている読者のために、参考になりそうな本や記事をいくつか載せておきます。

  1. 他にも、特にグラフや木構造を扱う問題では、「グラフがパスの場合」「グラフがウニの場合（$1 \to 2, 1 \to 3, 1 \to 4, \cdots, 1 \to N$ に辺がある場合）」「二分木の場合」などを考えると上手くいく場合も多いです。また、数列がソートされている場合（$A_1 < A_2 < \cdots < A_N$ の場合）などの特殊ケースがヒントになる場合もあります。 ↩

  2. 大きいケースも含めて実験したい場合、自分で（計算速度が遅い）プログラムを書いてコンピュータに実験させるという手もあります。 ↩

  3. もしかしたら、人によっては「縦・横・長さが全部同じ場合が最適」であるという直感が働かないかもしれません。しかし、入出力例を上手く活用して素因数分解をすると、「入力例 1 では 1=1×1×1、入力例 2 では 36926037=333×333×333 なのでもしかしたらそうかもしれない」と逆の発想を働かせることもできます。 ↩

  4. 例えば「約数系包除原理」と呼ばれている、約数ごとに場合の数などをメモしていくテクニックなどが挙げられます。 ↩

  5. すべての要素が $1$ 以上の整数である数列のことを指します。つまり、$A_1 \geq 1, A_2 \geq 1, \cdots, A_N \geq 1$ を満たします。 ↩

  6. すべての要素が $0$ 以上の整数である数列のことを指します。つまり、$A_1 \geq 0, A_2 \geq 0, \cdots, A_N \geq 0$ を満たします。 ↩

  7. この問題の解法説明に関しては、一部パナソニックプログラミングコンテスト 2020 公式解説から引用しています。 ↩

198
216
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
198
216