安全で爆速なRollingHashの話

要約

ロリハ(RollingHash)のModを$2^{61}-1$にすると安全で爆速になってむちゃくちゃ幸せになれます。

前提知識

bit演算に関する基礎的な知識を要求します。
また、RollingHashについては以下で解説しますが、分からない場合は別の記事を読んだほうがいいかもしれません。

RollingHashとは?

開く

「文字列を一つの大きな整数として見る」というのがRollingHashのアイデアです。
まず、0-9のみの数字を含んだ文字列s = "1234567890"を考えてみます。

ここで、この文字列のHash値を文字列を10進数と解釈したときの数値と定義します。
また、$s$の$a$文字目から$b$文字目の前までの部分文字列を$s[a..b]$と書くことにします。
例えば、s = "1234567890"について、$s[1..3]$は1文字目から3文字目の前までの部分文字列なので、"23"となります。
よって、$\mbox{hash}(s[0..10])$(文字列全体のHash)は$1234567890$、$\mbox{hash}(s[3..7])$は$4567$となります。

また、$\mbox{hash}(s[0..7])=1234567$、$\mbox{hash}(s[0..3])=123$なので、$\mbox{hash}(s[3..7])=\mbox{hash}(s[0..7])-\mbox{hash}(s[0..3])\cdot 10^4$として計算できることが分かります。一般に、$\mbox{hash}(s[a..b])=\mbox{hash}(s[0..b])-\mbox{hash}(s[0..a])\cdot \mbox{base}^{b-a}$となります。ここで、$\mbox{base}$はHashの法、つまり10進法の10です。(証明はしませんが、$\mbox{hash}(s)=\sum_{i=0}^{n-1} s_i\cdot \mbox{base}^{n-i-1}$という式から容易に導出することができます。)
そのため、$\mbox{base}^0$から$\mbox{base}^n$、$\mbox{hash}(s[0..0])$から$\mbox{hash}(s[0..n])$を前計算しておけば、任意の$a$,$b$($a \le b$)について$\mbox{hash}(s[a..b])$を(演算を定数時間として)$O(1)$で求めることができます。

これを一般の文字列について拡張してみます。例えば、小文字アルファベットのみを含んだ文字列の場合は\mbox{base}を27とし、a=1,b=2,c=3...y=25,z=26とすることによって上記のような操作が可能になります。

また、Hashが大きくなりすぎる問題を解決するため、Hashは特定の素数でModを取った状態で保存します。Modを取った整数同士では、整数と同じように定数時間で加算/乗算ができるためです。

安全にRollingHashを使うために～衝突の回避～

RollingHashで最も気をつけるべきこととして、2つの異なる文字列が同じHashを取ることがあります。(これをHashの衝突と呼びます。)
基本的なこととして、数字への割当が0となる文字を作ってはいけません。例えば、a=0とした場合にbとbaaa等の文字列のHashが全て衝突します。
また、全てのHashはModを取られるため、Mod未満となります。そのため、Mod以上の個数のHashを生成した場合、必ずどこかのペアがHashの衝突を起こします。そのため、できる限り大きいModを取ることが求められます。
また、Hashの衝突がどこか一回でも起こる確率は想像以上に高いです(誕生日のパラドックス)。Hashが0～modの間でランダムに分布すると仮定した場合、衝突がp%の確率で発生する試行回数は以下の表のようになります。(Wikipediaより)

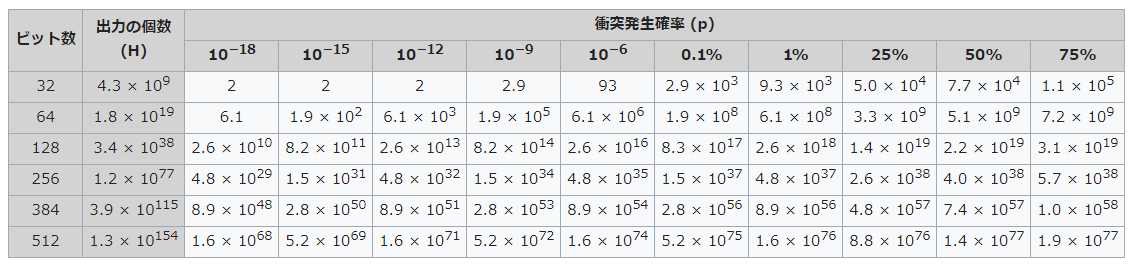
これを見ると、32bitのMod一つでRollingHashを行った場合、$10^5$個程度のHashを生成するだけでも半分以上の確率でどこかのHashが衝突していることが分かります。怖いですね。
また、Hackで撃墜される可能性があるCodeForces等のコンテストでは、十分に大きなModを取っても故意にぶつけられる可能性があります。これを回避するには、$\mbox{base}$を実行時にランダムに決定すると良いです。(Modをランダムにしても良いですが、定数での除算はコンパイラによって最適化が掛けられて早くなるため、実行時依存のModはできる限り避けるべきです。)
また、$2^{64}$等の2の冪乗をModとすることは避けるべきです。その場合、$\mbox{base}$がランダムであっても衝突するケースを作成することが可能なためです。
詳しくはEtoNagisaさんのスライド(Rolling Hashを殺す話)を参照してください。

まとめ:
空間は大きく取ろう(64bitのModを使うか、32bitの互いに素なModを2個使えば十分)
$\mbox{base}$はランダムに取ろう

高速なロリハを求めて～メルセンヌ素数mod～

Modを取る演算は最適化を鑑みても高速ではないため、できるならばMod2つは避けたいです。しかし、32bitより大きいModを使用した場合、2つの数の乗算後に64bitでもオーバーフローしてしまう可能性があります。

a･b mod 2^61-1をオーバーフローなしで計算する

ここで、Modに$2^{61}-1$を採用することを考えます。この数は素数であり、十分に大きいため安全性は十分です。
また、$2^{61} \equiv 1 \pmod{2^{61}-1}$なため、$a\cdot 2^{61} \equiv a \pmod{2^{61}-1}$です。これを利用すると、$a \cdot b \bmod 2^{61}-1$を64bitの範囲内で求めることができます。

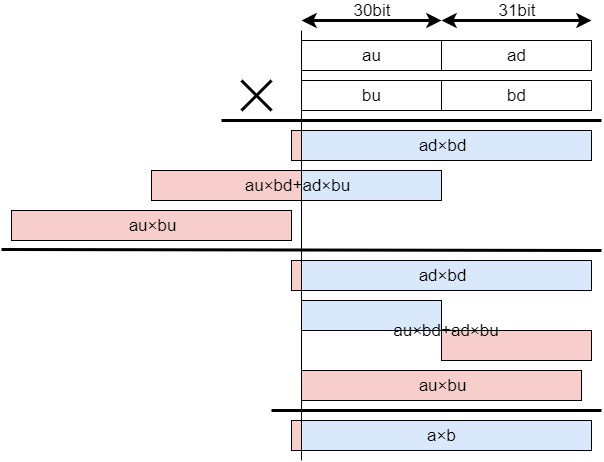
まず、a,bをそれぞれ$a=au\cdot 2^{31}+ad,b=bu\cdot 2^{31}+bd (ad,bd \lt 2^{31})$のように分割します。すると、以下の図のように64bit以内で計算を行うことができます。

正確には、$a\cdot b=au\cdot bu\cdot 2^{62}+(au\cdot bd+ad\cdot bu)\cdot 2^{31}+ad\cdot bd$の各項について、以下のように処理すれば良いです。

• $au\cdot bu\cdot 2^{62}$

$au\cdot bu\cdot 2^{62} \equiv au\cdot bu\cdot 2 \pmod{2^{61}-1}$なため、$au\cdot bu\cdot 2$を足せば良いです。

• $(au\cdot bd+ad\cdot bu)\cdot 2^{31}$

簡略化のために$mid = au\cdot bd+ad\cdot bu$とします。
$mid = midu\cdot 2^{30}+midd(midd \lt 2^{30})$と分割することにより、$mid\cdot 2^{31} = midu\cdot 2^{61}+midd\cdot 2^{31} \equiv midu+midd\cdot 2^{31} \pmod{2^{61}-1}$となります。これを足せば良いです。

• $ad\cdot bd$

$ad\cdot bd$はそのまま足せば良いです。

これをまとめると、$au\cdot bu\cdot 2+midu+midd\cdot 2^{31}+ad\cdot bd$となります。最大ケースを考えてみると分かりますが、これは$2^{64}$以上にならないので、オーバーフローすることはありません。最後に、この値についても$2^{61}-1$でModを取れば良いです。
これは単純に剰余を行っても良いですが、$a\cdot 2^{61} \equiv a \pmod{2^{61}-1}$を利用することによってもう少し効率良く実装することができます。
$x$を剰余を計算したい64bit整数とします。$x=xu \cdot 2^{61} + xd (xd \lt 2^{61})$と分割することで、$xu \cdot 2^{61} + xd \equiv xu + xd\pmod{2^{61}-1}$となります。$x$は64bit整数なので、$x \lt 2^{64} \Rightarrow xu \lt 2^3$が成り立ちます。これにより、$xu+xd \lt 2^3+2^{61}$と分かるので、$xu+xd \ge 2^{61}-1$となった場合は$xu+xd-(2^{61}-1)\lt2^3\lt2^{61}-1$となるため、$xu+xd-(2^{61}-1)$が求めたい剰余の値であることが分かります。

au,bu,ad,bdが求められれば高速に計算できることが分かったため、a,bからau,bu,ad,bdを求めることを考えます。au,buを求めるには$2^{31}$で切り捨て除算をすれば良く、これは31bit右シフトをするのと等価です。ad,bdを求めるためには$2^{31}$で割ったあまりを求めれば良く、これは$2^{31} - 1$($0\mbox{b}\underbrace{111\cdots 111}_{30個}$)とand演算をすることと等しいです。これらは高速な演算なので、au,bu,ad,bdは高速に求めることができます。
上の考えは、$2^{30}$による分割(midu/midd)、$2^{61}$による分割(xu/xd)についても同じく適用することができます。

以下に実装を示します。

const ulong MASK30 = (1UL << 30) - 1;
const ulong MASK31 = (1UL << 31) - 1;
const ulong MOD = (1UL << 61) - 1;
const ulong MASK61 = MOD;

//a*b mod 2^61-1を返す関数(最後にModを取る)
ulong Mul(ulong a, ulong b)
{
    ulong au = a >> 31;
    ulong ad = a & MASK31;
    ulong bu = b >> 31;
    ulong bd = b & MASK31;
    ulong mid = ad * bu + au * bd;
    ulong midu = mid >> 30;
    ulong midd = mid & MASK30;
    return CalcMod(au * bu * 2 + midu + (midd << 31) + ad * bd);
}

//mod 2^61-1を計算する関数
ulong CalcMod(ulong x)
{
    ulong xu = x >> 61;
    ulong xd = x & MASK61;
    ulong res = xu + xd;
    if (res >= MOD) res -= MOD;
    return res;
}

RollingHashに組み込む際に工夫すると良いこと

この項では、解説の項に出てきた記法と同じ記法を用います。
具体的には、$s$の$a$文字目から$b$文字目の前までの部分文字列を$s[a..b]$と書き、文字列$s$のHashを$\mbox{hash}(s)$と書くことにします。

以下に示すような工夫をすると、より高速に$\bmod{2^{61}-1}$でのRollingHashの実装を行うことができます。
まず、上の実装例で示した関数Mulについて、最後にModを取らないように書き換えます。(return前のCalcModを省略するだけで良いです。)

//au*bu*2+midu+midd*2^31+ad*bdそのものを返す関数(最後にModを取らない)
ulong Mul(ulong a, ulong b) { /*実装略*/ }
//mod 2^61-1を計算する関数
ulong CalcMod(ulong val) { /*実装略*/ }

ここで、RollingHashの配列を計算する処理について考えてみます。$\mbox{hash}(s[0..n+1])=\mbox{hash}(s[0..n]) \cdot \mbox{base} + s[n]$となるため、ソースコードでは以下の通りとなります。

ulong[] hash = new ulong[n + 1]; //要素数n+1の配列を初期化
for (int i = 0; i < n; i++) hash[i + 1] = CalcMod(Mul(hash[i], Base) + s[i]);

Mul(a, b)の最大値は、$a,b \lt mod$であった場合は$mod \cdot 4$未満です¹。そのため、各文字の最大値(asciiの場合は127、32bitだとしても$2^{32}-1$)を足したところでオーバーフローすることはありません。そのため、各計算につき最後に一度だけModを計算するだけで十分であることが分かります。

また、部分文字列についてのHashを求める処理については少し注意が必要です。部分文字列のHashは$\mbox{hash}(s[a..b])=\mbox{hash}(s[0..b])-\mbox{hash}(s[0..a])\cdot \mbox{base}^{b-a}$として求められますが、減算が出てくるために負方向へのオーバーフローが発生する可能性があります。
ここで、Mul(a, b)の最大値が$mod \cdot 4$未満であったことを思い出します。つまり、$\mbox{hash}(s[0..b])$にあらかじめ$mod \cdot 4$以上で$n \equiv 0 \pmod{2^{61}-1}$となるような整数$n$を足しておくことで、演算結果を変えずに負方向へのオーバーフローを免れることができます。
これを実装すると以下のようになります。

const ulong POSITIVIZER = MOD * 4;
ulong hash = CalcMod(hash[end] + POSITIVIZER - Mul(hash[begin], powMemo[end - begin]))

実装のサンプルはこちらにあります。(C#です。)

余談(128bit環境における実装の簡易化の話)

この記事では、一般的に使用可能な64bit環境における高速化について説明をしてきました。しかし、一部の環境においてはSIMD命令等で128bit整数を使用することが可能です。
これを用いると、以下のように愚直な方法で複雑な工夫なしにmodを求めることができます。

i128 t = a * b;
t = (t >> 61) + (t & MOD);

if (t >= MOD) return t - MOD;
return t;

この実装は本記事で扱った実装と同等か、それ以上に高速になる場合があります。(検証実装)

速度

ABC141-Eを用いて計測を行いました。

	2^61-1	32bit 1つ	32bit 2つ
最大実行時間	298ms	370ms	656ms
合計実行時間	8906ms	11123ms	18695ms

C#で実装したため、速度はC++などの言語とは違うと思います。実際に、C++だと32bit 1つの方が早かったというケースもありました。しかし、安全でかつ早いRollingHashを作るのであれば$2^{61}-1$をModとすることをお勧めします。

1. max(Mul(a, b)) < (2^61 - 2^32 + 2) + (2^62 - 2^32 + 1) + (2^61 - 1) < (2^61 - 1) * 4 ↩