【数学溢れ話】【Token】ベン図(Venn Diagram)と組み合わせ計算(Combination Calculation)と確率演算(Probability Operation)

今一つ掲題の3分野の統合が脳内で出来てない気がするので、そのプログラム表現も含めまとめてみました。新たに分かった新事実。「人類は難度が急激に高まる3次元以上の行列演算を諦め、2次元行列演算を洗練させる事で全ての事象を扱える様にする方向に進化してきた。同様に集合論についても急激に難度が高まる4個以上の集合についての集合についての考察を諦めたので、その機能は最先端のプログラム言語にも実装されていない」。要するに、この領域にまで「(無限微分と無限積分の組み合わせなどにより)N次元データを2次元配列化する」人類の英知は及んだ様なのです。だがどうやって？

#ベン図(Venn Diagram)と組み合わせ計算(Combination Calculation)と確率演算(Probability Operation)の関係について。
まずはベン図(Venn Diagram)のプログラム表現について。
Python matplotlib-venn でベン図を描く

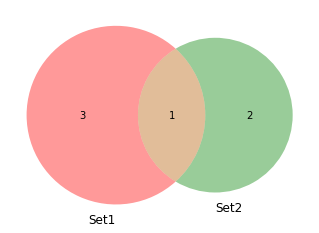
統計学や確率論では起りうることがらを事象と呼びます。事象を表す場合、標本の数に係わらず標本空間を長方形で表しその他の事象を内部に円を描いて表すことが行われます。この図はベン図(Ven diagram)と呼ばれます。

Python には、matplotlib-venn·PyPIというライブラリがあり、このライブラリを用いることでベン図を描くことができます。

ライブラリのインストール方法などは引用元をご覧ください。現代の我々が用いている集合論の演算体系は主に19世紀に入ってから急速に整備されました。
数学記号の由来について－集合論で使用される記号（⊃、⊂、∩、∪等）－

###事象集合(Event Set)2個の重なり具合

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt
venn2(subsets=(3, 2, 1),set_labels = ('Set1', 'Set2'))
plt.show()

###事象集合(Event Set)3個の重なり具合

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
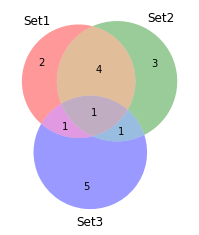
venn3(subsets = (2, 3, 4, 5, 1, 1, 1), set_labels = ('Set1', 'Set2', 'Set3'))
plt.show()

この実装に従って、既存の集合概念の表現を試みます。
###補事象集合(Complementary Event Set)

Complement=Set^{c}

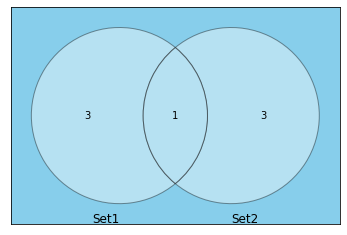
まずは「事象集合1,2の和集合の補事象」のイメージ。

背景を設定すると、ベン図の色にも影響するようでいい感じに描画できませんでした。

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt
v = venn2(subsets=(3, 3, 1),set_labels = ('Set1', 'Set2'))

# ベン図の色を変更する   
v.get_patch_by_id('10').set_color('white')
v.get_patch_by_id('10').set_edgecolor('black')
v.get_patch_by_id('11').set_color('white')
v.get_patch_by_id('11').set_edgecolor('black')
v.get_patch_by_id('01').set_color('white')
v.get_patch_by_id('01').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('skyblue')
plt.show()

「ただ一つの事象集合に対する補集合」を表示する方法はなく、だから「事象1,事象2の差集合が0の場合の補集合」といった方便でも用いるしかありません。

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt
v = venn2(subsets=(0, 0, 3),set_labels = ('Set1', 'Set2'))

# ベン図の色を変更する   
v.get_patch_by_id('10').set_color('white')
v.get_patch_by_id('10').set_edgecolor('black')
v.get_patch_by_id('11').set_color('white')
v.get_patch_by_id('11').set_edgecolor('black')
v.get_patch_by_id('01').set_color('white')
v.get_patch_by_id('01').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('skyblue')
plt.show()

方便? 実はこのライブラリにおける補集合の定義自体が「事象集合1,2と差集合を持たない事象集合3」といった内容なのかもしれません。そして普通は0と想定するので図上に現れないと考える訳です。

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
v=venn3(subsets = (2, 3, 4, 5, 0, 0, 0), set_labels = ('Set1', 'Set2', 'Complement'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('white')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('white')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('010').set_color('white')
v.get_patch_by_id('010').set_edgecolor('black')
v.get_patch_by_id('001').set_color('skyblue')
v.get_patch_by_id('001').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("Sample Venn Diagram")
plt.show()

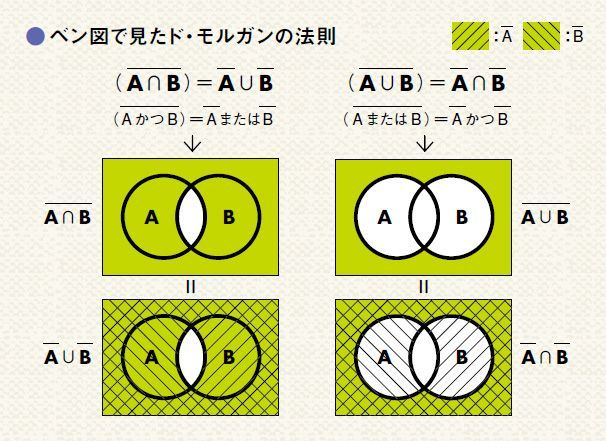
考え方としてはN次元演算において、数値の存在しない高次元軸は存在しないものとして扱う約束と似ています。集合論的においてはその直前までの事象の総和を全体集合(Universal Set)Cと呼び、これについて事象集合Aの任意の事象a($A(\forall a \in A)$)と事象集合Bの任意の事象b($B(\forall b \in B)$)の和集合(Sum Event Set)$A \cup B$と積集合(Product Event Set)$A \cap B$の関係を以下のド・モルガンの法則(De Morgan's Law)によって規定するのです(証明は参照サイト参考の事)。
【基本】補集合
【標準】ド・モルガンの法則（集合）

(A\cup B)^c = A^c \cap B^c \\
(A\cap B)^c = A^c \cup B^c

なぜ女性の食べ物の好みの伝え方は難解か

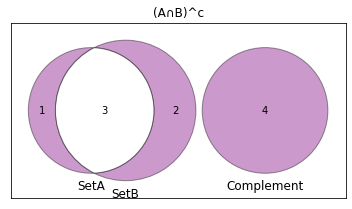
(A\cap B)^c

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
v=venn3(subsets = (1, 2, 3, 4, 0, 0, 0), set_labels = ('SetA', 'SetB', 'Complement'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('purple')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('white')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('010').set_color('purple')
v.get_patch_by_id('010').set_edgecolor('black')
v.get_patch_by_id('001').set_color('purple')
v.get_patch_by_id('001').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("(A∩B)^c")
plt.show()

(A\cup B)^c

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
v=venn3(subsets = (1, 2, 3, 4, 0, 0, 0), set_labels = ('SetA', 'SetB', 'Complement'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('white')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('white')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('010').set_color('white')
v.get_patch_by_id('010').set_edgecolor('black')
v.get_patch_by_id('001').set_color('purple')
v.get_patch_by_id('001').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("(A∪B)^c")
plt.show()

A^c

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
v=venn3(subsets = (1, 2, 3, 4, 0, 0, 0), set_labels = ('SetA', 'SetB', 'Complement'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('white')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('white')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('010').set_color('blue')
v.get_patch_by_id('010').set_edgecolor('black')
v.get_patch_by_id('001').set_color('blue')
v.get_patch_by_id('001').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("A^c")
plt.show()

B^c

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
v=venn3(subsets = (1, 2, 3, 4, 0, 0, 0), set_labels = ('SetA', 'SetB', 'Complement'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('red')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('white')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('010').set_color('white')
v.get_patch_by_id('010').set_edgecolor('black')
v.get_patch_by_id('001').set_color('red')
v.get_patch_by_id('001').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("B^c")
plt.show()

A^c \cup B^c =(A \cup B)^c + A \setminus B + B \setminus A

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
v=venn3(subsets = (1, 2, 3, 4, 0, 0, 0), set_labels = ('SetA', 'SetB', 'Complement'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('red')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('white')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('010').set_color('blue')
v.get_patch_by_id('010').set_edgecolor('black')
v.get_patch_by_id('001').set_color('purple')
v.get_patch_by_id('001').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("A^c∪B^c")
plt.show()

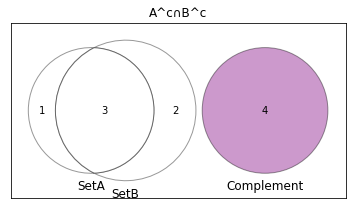
A^c \cup B^c = (A \cap B)^c - A \setminus B - B \setminus A

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
v=venn3(subsets = (1, 2, 3, 4, 0, 0, 0), set_labels = ('SetA', 'SetB', 'Complement'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('white')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('white')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('010').set_color('white')
v.get_patch_by_id('010').set_edgecolor('black')
v.get_patch_by_id('001').set_color('purple')
v.get_patch_by_id('001').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("A^c∩B^c")
plt.show()

やはり全体集合(Universal Set)の最頂点として現れる補集合の要素数を0と考えれば全体像がスッキリしそうです。かかる考え方を閉世界仮説（Closed World Assumption）といい、方便上無限リストを有限リストに縮約し、コンピューター処理可能とします。

閉世界仮説とは - Weblio辞書

現時点で真であると判明していないことは偽であると仮定することを意味する。例えばある企業の従業員を集合関係で分類する名簿が存在する時、その名簿に記載のない人物は従業員でないと想定する。論理学では、Raymond Reither が閉世界仮説を形式化した。閉世界仮説の逆を開世界仮説（Open world assumption）と呼び、知識の欠如を偽とは見なさない。

• 例えばLISP(LISt Processor,1958年~)やPlolog(PROgramming in LOGic,1972年頃~)といったリスト処理言語は有限リスト$X_n=(x_1,x_2,x_3,…,x_n)$について、頻繁に「リストが空になるまで要素$x_n$を左端から取り出し続ける」操作を繰り返す。実はその裏側でこの様な形で閉世界仮説が採用されていた訳である。
  憧れの関数型言語Lispは古くて最新のプログラミング言語
  Prologをご存じですか？

数学の世界においては線形性(linearity)を共有する諸概念を一時結合表記(Linear Combination Expression)で表されるベクトル空間(Vector Space)の概念で束ねますが、この前提さえ受容すれば集合もまた線形性を備えたベクトルの一種として扱えそうです。
高校数学における線形性の8つの例

期待値演算の線形性:E(aX+bY)=aE(X)+bE(Y)

上掲の性質ゆえに確率分布(Probability Distribution)は確率ベクトル(Probability Vector,全体の合計が1となる要素行列)とその要素それぞれに加えられるスカラー(Scalar)に分解可能であり、それで「ギャンブルにおいて掛け金に対して戻ってくる【見込み】の金額」とも表現される期待値(Expected Value)が確率変数(スカラー)のすべての値に確率の重みをつけた加重平均(Weighted Average)とされるのです。
期待値 - Wikipedia

• 加重平均(Weighted Average)の概念はある意味、それぞれ線型独立(Linearly Independent)した基底(Base)ごとのスカラー量を示す線形結合表記(Linear Combination Expression)で表されるベクトル計量空間(Metric Vector Space)概念そのものなのだが、そこに見受けられるスカラー概念と基底概念の概念の主客転倒のせいで、かえって本質を理解する妨げとなっている気もしないではない。というか私自身、これまですっかり騙されてきた。
  証券用語解説集:加重平均（かじゅうへいきん）

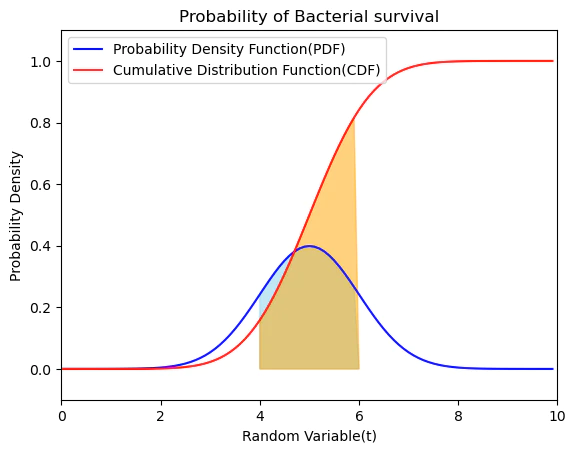
そう確率ベクトルは確率変数(Random Variable)を定義域(Domain)とし、その値域(Range)が微積分によって確率密度分布(Probability Density Distribution)と累積分布(Cumulative distribution)の間を往復する様な確率分布座標系(Probability Distribution Coordinate System)においてある種の基底(Base)として機能するのです。この意味合いにおいて集合論(Set Theory)は特に確率ベクトルの性質に注目した分野とも考えられる訳です。
【Pyrhon演算処理】確率密度空間と累積分布空間②中心極限定理の可視化
【Pyrhon演算処理】確率密度空間と累積分布空間①記述統計との狭間

###排反事象集合(Exclusive Event Set)

Set_A(\forall a \in A) \cap Set_B(\forall b \in B)= \emptyset

事象集合Aの任意の事象aと事象集合Bの任意の事象bは同時に起こる事はなく、事象集合Aの任意の事象aが発生した場合、事象集合Bの任意の事象bはどれも起こらない事を示します。

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt

# 重なる部分の領域の割合を0にする   
v = venn2(subsets=(3, 3, 0),set_labels = ('SetA', 'SetB'))

# ベン図の色を変更する   
v.get_patch_by_id('10').set_color('skyblue')
v.get_patch_by_id('10').set_edgecolor('black')
v.get_patch_by_id('01').set_color('skyblue')
v.get_patch_by_id('01').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("Exclusive Event Set")
plt.show()

###和事象集合(Sum Event Set)

Set_A(\forall a \in A) \cup Set_B(\forall b \in B)

事象集合Aの任意の事象aと事象集合Bの任意の事象bの少なくともどちらか(あるいは両方)が発生する確率を和集合(Union)によって示します。

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt

# 重なる部分の領域の割合を1にする   
v = venn2(subsets=(3, 3, 1),set_labels = ('SetA', 'SetB'))

# ベン図の色を変更する   
v.get_patch_by_id('10').set_color('skyblue')
v.get_patch_by_id('10').set_edgecolor('black')
v.get_patch_by_id('11').set_color('skyblue')
v.get_patch_by_id('11').set_edgecolor('black')
v.get_patch_by_id('01').set_color('skyblue')
v.get_patch_by_id('01').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("Sum Event Set")
plt.show()

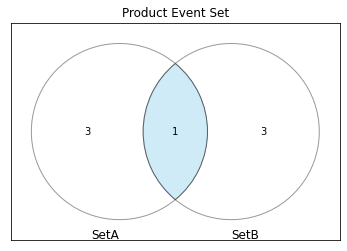
###積事象集合(Product Event Set)

Set_1(\forall a \in A) \cap Set_2(\forall b \in B)

事象集合Aの任意の事象aと事象集合Bの任意の事象bが同時に発生する確率を積集合(Intersection)によって示します。

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt

# 重なる部分の領域の割合を0にする   
v = venn2(subsets=(3, 3, 1),set_labels = ('SetA', 'SetB'))

# ベン図の色を変更する   
v.get_patch_by_id('10').set_color('white')
v.get_patch_by_id('10').set_edgecolor('black')
v.get_patch_by_id('11').set_color('skyblue')
v.get_patch_by_id('11').set_edgecolor('black')
v.get_patch_by_id('01').set_color('white')
v.get_patch_by_id('01').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("Product Event Set")
plt.show()

###差事象集合(Difference Event Set)

Set_A(\forall a \in A) \setminus Set_B(\forall b \in B)\\
Set_B(\forall b \in B) \setminus Set_A(\forall a \in A)

事象集合Aの任意の事象aが起こり、事象集合Bの任意の事象bが起こらない確率、あるいは事象集合Bの任意の事象bが起こり、事象集合Aの任意の事象aが起こらない確率を示します。

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt

# 重なる部分の領域の割合を0にする   
v = venn2(subsets=(3, 3, 1),set_labels = ('SetA', 'SetB'))

# ベン図の色を変更する   
v.get_patch_by_id('10').set_color('skyblue')
v.get_patch_by_id('10').set_edgecolor('black')
v.get_patch_by_id('11').set_color('white')
v.get_patch_by_id('11').set_edgecolor('black')
v.get_patch_by_id('01').set_color('white')
v.get_patch_by_id('01').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("Difference Event Set")
plt.show()

組み合わせ計算(Combination Calculation)${}_2 C_2$より2通り存在する事になる訳です(二項定理により二次方程式$x^2+2xy+y^2$の二番目の係数2に対応)。事象集合が3個ある場合、${}_3 C_2$より6通り存在します(二項定理により三次方程式$x^3+3x^2y+3xy^2+y^3$の二番目と三番目の係数の和に対応)。
【Python演算処理】パスカルの三角形と二項定理または二項展開
【Python演算処理】階乗と順列と組み合わせ

PythonにおいてSympyは三次元配列を扱えず、Pandasはバージョンアップに従ってその機能を切り捨ててしまいました。どうやら数学の世界は原則としてそんな機能を必要としない方向に進化してきた様なのです。
【Python演算処理】三次元配列を扱えるのはnumpyと…xarray？

#ベン図(Venn Diagram)と確率ベクトル(Probability Vector)とパスカルの三角形(Pascalian Triangle)
この様な表示機能を有するpythonのmatplotlib-venn·PyPIライブラリの応用範囲について、もっと細かく見ていきましょう。

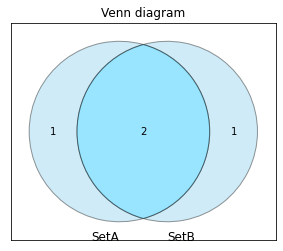
###事象集合2個の重なり。

venn2=(A \setminus B,B \setminus A,A \cup B)

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt
venn2(subsets=(1, 2, 3),set_labels = ('SetA', 'SetB'))
plt.show()

均等分布で全ての区分を埋めるのに最小限必要なのは2要素×2集合=4、各要素の重み付け±0とすればスカラー(ここでは要素数の単純合計)は4。これで集合全体を割った結果が「合計が1になる」確率ベクトルとなります。

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt
v=venn2(subsets=(1, 1, 2),set_labels = ('SetA', 'SetB'))

# ベン図の色を変更する   
v.get_patch_by_id('10').set_color('skyblue')
v.get_patch_by_id('10').set_edgecolor('black')
v.get_patch_by_id('01').set_color('skyblue')
v.get_patch_by_id('01').set_edgecolor('black')
v.get_patch_by_id('11').set_color('deepskyblue')
v.get_patch_by_id('11').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("Venn diagram")
plt.show()

見事に二次方程式$x^2+2xy+y^2$に対応してその領域分布がパスカルの三角形の3行目の係数「1・2・1」、それぞれを埋める最小要素数がx分布「2・1・0」に対応していますね(それぞれ独特の形でさらにこの集合の外側に広がる補集合0を意識する)。従ってその確率ベクトルは以下となります。

import sympy as sp

sp.var('a1,a2, a3') 
A = sp.Matrix([a1,a2,a3])
A1=A.subs([(a1,sp.Rational(1,4)),(a2,sp.Rational(1,4)),(a3,sp.Rational(2,4))])

sp.init_printing()
display(A)
display(A1)
print(sp.latex(A)+"="+sp.latex(A1))

\left[\begin{matrix}a_{1}\\a_{2}\\a_{3}\end{matrix}\right]=\left[\begin{matrix}\frac{1}{4}\\\frac{1}{4}\\\frac{1}{2}\end{matrix}\right]

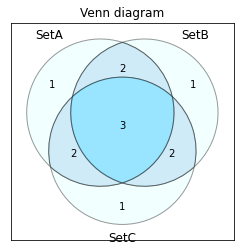
###事象集合3個の重なり。

venn3=(A \setminus (B \cap C),B \setminus (A \cap C),(A \cup B) \setminus C,C \setminus (A \cap B),(A \cup C) \setminus B,(B \cup C) \setminus A,A \cup B \cup C)

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
venn3(subsets = (1, 2, 3, 4, 5, 6, 7), set_labels = ('SetA', 'SetB', 'SetC'))
plt.show()

均等分布で全ての区分を埋めるのに最小限必要なのは4要素×3集合=12、各要素の重み付け±0とすればスカラー(ここでは要素数の単純合計)は12。これで集合全体を割った結果が「合計が1になる」確率ベクトルとなります。

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
v=venn3(subsets = (1, 1, 2, 1, 2, 2, 3), set_labels = ('SetA', 'SetB', 'SetC'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('lightcyan')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('skyblue')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('101').set_color('skyblue')
v.get_patch_by_id('101').set_edgecolor('black')
v.get_patch_by_id('001').set_color('lightcyan')
v.get_patch_by_id('001').set_edgecolor('black')
v.get_patch_by_id('011').set_color('skyblue')
v.get_patch_by_id('011').set_edgecolor('black')
v.get_patch_by_id('101').set_color('skyblue')
v.get_patch_by_id('101').set_edgecolor('black')
v.get_patch_by_id('010').set_color('lightcyan')
v.get_patch_by_id('010').set_edgecolor('black')
v.get_patch_by_id('111').set_color('deepskyblue')
v.get_patch_by_id('111').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("Venn diagram")
plt.show()

見事に三次方程式$x^3+3x^2y+3xy^2+y^3$に対応してその領域分布がパスカルの三角形の4行目の係数「1・3・3・1」、それぞれを埋める最小要素数がx分布「3・2・1・0」に対応していますね(それぞれ独特の形でさらにこの集合の外側に広がる補集合0を含める)。従ってその確率ベクトルは以下となります。

import sympy as sp

sp.var('a1,a2, a3,a4,a5,a6,a7') 
A = sp.Matrix([a1,a2,a3,a4,a5,a6,a7])
A1=A.subs([
    (a1,sp.Rational(1,12)),
    (a2,sp.Rational(1,12)),
    (a3,sp.Rational(2,12)),
    (a4,sp.Rational(1,12)),
    (a5,sp.Rational(2,12)),
    (a6,sp.Rational(2,12)),
    (a7,sp.Rational(3,12))])

sp.init_printing()
display(A)
display(A1)
print(sp.latex(A)+"="+sp.latex(A1))

\left[\begin{matrix}a_{1}\\a_{2}\\a_{3}\\a_{4}\\a_{5}\\a_{6}\\a_{7}\end{matrix}\right]=\left[\begin{matrix}\frac{1}{12}\\\frac{1}{12}\\\frac{1}{6}\\\frac{1}{12}\\\frac{1}{6}\\\frac{1}{6}\\\frac{1}{4}\end{matrix}\right]

同時表示出来ないのが返すがえすも残念ですが、二次方程式を2x2の平方行列で表す表記に対して三次方程式を2x2x2の立方行列で表す表記が発達しなかった様に、三集合のベン図もまた現代数学/最新プログラミングの世界から切り捨てられてしまったのだから、いかしかたありません。
【Python演算処理】パスカルの三角形と二項定理または二項展開

###そしてベン図は4集合以上重ねられない?
そういえばこの話をすっかり失念していました。
4つの円のベン図がかけない理由を超簡単に教えてください！
Pythonで４つ以上のベン図を書く方法

• 「オイラーの多面体定理」にまつわる過去投稿でも、同様の壁に突き当たった。幾何学もまた扱う図形が正三角形、正方形、正六角形**…そして正四面体、正六面体、正八面体といった「身近な範囲」を超えた途端、突然その荒々しい本性を剥き出しにしてくるのである。プラトン立体の残された2つ、すなわち正十二面体や正二十面体を巡る数理すら、到底人類の手なんて及ばない感が…
  【オイラーの多面体定理と正多面体】内接円/球面の半径と外接円/球面の半径の狭間
  
• 反対の極限たる円/球面から迫っても同様の壁に突き当たる。そもそも鍵を握る複素関数$i^{ax}$についての解説とか見た事がなくて…
  【無限遠点を巡る数理】オイラー座標系②複素等比数列による整数概念の再構築
  

そう、いわゆる「高校数学」と「大学数学」の狭間にはこうして近世数学までの伝統的パラダイムが行き詰まり、微積分概念などと組み合わせた平方行列で全てを解く方向に舵を切った歴史が隠されていたのです。

• 考えてみれば現代数学はある意味「近代数学の完成者」ガウス（Johann Carl Friedrich Gauß/Carolus Fridericus Gauss、1777年~1855年）やコーシー（Augustin Louis Cauchy, 1789年~1857年）の不興を買ったノルウェーの数学者アーベル（Niels Henrik Abel、1802年~1829年）、そしてそのアーベルには理解を示したヤコビ（Carl Gustav Jacob Jacobi, 1804年~1851年）からさえ嫌悪され、コーシーとフーリエ（Jean Baptiste Joseph Fourier, Baron de、1768年~1830年）に提出した論文を紛失されて窮地に追い込まれたガロア（Évariste Galois,1811年~1832年）の不遇とそれ故の夭折から出発する。何処に如何なるパラダイムシフトがあったかちゃんと見据えない限り数学史全体が見通せない。ただ確実に言えるのは、歴史のその時点においては群論はおろか(後にベクトル空間の概念で統合される)線形代数/行列演算も関数空間論も統計学も存在せず、下手をしたらそれまでの数学の伝統にはその登場を阻む要因すら存在したかもしれないという事なのである。現代数学の難解さのうち少なくとも一部は、この辺りの誤魔化しに起因するのではなかろうか?
  【Python演算処理】環論に立脚した全体像再構築③ベクトル空間としての構成
  【数理考古学】無限遠点(Infinity)としての正規分布と分散概念の歴史

そもそも上掲の歴史感覚では明らかに現代数学以前の数学者に分類されるヤコビが(過去の伝統の限界を振り切って新境地を切り開いた)ヤコビ行列(Jacobian)の発案者に名前を連ねてる辺り、特に闇が深く感じます。やはり突破口となったのは解析学だったの?
【Python演算処理】半径・直径・円周長・円の面積・球の表面積・球の体積の計算上の往復

{\int U(x,y,z)dV=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}U(r,θ,φ)r^2\sinθdrdθdφ\\
=\int_{0}^{2π}\int_{0}^{π}\int_{0}^{1}\begin{vmatrix}
\frac{∂x}{∂r} & \frac{∂x}{∂θ}  & \frac{∂x}{∂φ}\\
\frac{∂y}{∂r} & \frac{∂y}{∂θ}  & \frac{∂y}{∂φ}\\
\frac{∂z}{∂r} & \frac{∂z}{∂θ} & \frac{∂z}{∂φ}
\end{vmatrix} drdθdφ
}

プログラム言語から入ると、集合の要素を操作する関数が完全に別個のものとして存在しているせいで、ますますこうした考え方から遠ざかる事になります。この辺りはノード理論に統合されたから、もういいの？
Python, set型で集合演算（和集合、積集合や部分集合の判定など）
読書ノート » SymPy 利用ノート » 集合

#事象部分集合(Event Subset)と真事象部分集合(Proper Event Subset)
【初心者向け】集合論①部分集合と真部分集合について

事象部分集合(Event Subset)は以下の場合を含みます。

Set_A(\forall a \in A) \supseteq Set_B(\forall a \in B)

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt

# 重なる部分の領域の割合を0にする   
v = venn2(subsets=(0,0,3),set_labels = ('SetA', 'SetB'))

# ベン図の色を変更する   
v.get_patch_by_id('10').set_color('white')
v.get_patch_by_id('10').set_edgecolor('black')
v.get_patch_by_id('11').set_color('skyblue')
v.get_patch_by_id('11').set_edgecolor('black')
v.get_patch_by_id('01').set_color('white')
v.get_patch_by_id('01').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("Subevent Set")
plt.show()

逆をいえば、この場合を含まないのが真事象部分集合(Proper Event Subset)となります。

Set_A(\forall a \in A) \supsetneq Set_B(\forall b \in B)

%matplotlib inline
from matplotlib_venn import venn2
from matplotlib import pyplot as plt

# 重なる部分の領域の割合を0にする   
v = venn2(subsets=(3, 0,1),set_labels = ('SetA', 'SetB'))

# ベン図の色を変更する   
v.get_patch_by_id('10').set_color('white')
v.get_patch_by_id('10').set_edgecolor('black')
v.get_patch_by_id('11').set_color('skyblue')
v.get_patch_by_id('11').set_edgecolor('black')
v.get_patch_by_id('01').set_color('white')
v.get_patch_by_id('01').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("True Subevent Set")
plt.show()

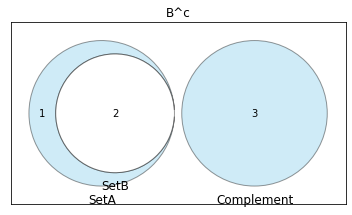
Set_B^c

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt
v=venn3(subsets = (1, 0, 2, 3, 0, 0, 0), set_labels = ('SetA', 'SetB', 'Complement'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('skyblue')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('white')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('001').set_color('skyblue')
v.get_patch_by_id('001').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("B^c")
plt.show()

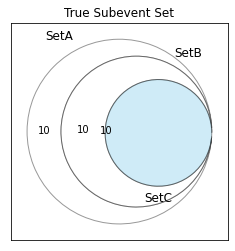
Set_A(\forall a \in A) \supsetneq Set_B(\forall a \in B)  \supsetneq Set_C(\forall c \in C)

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt

v=venn3(subsets = (10, 0, 10, 0, 0, 0, 10), set_labels = ('SetA', 'SetB', 'SetC'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('white')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('white')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('111').set_color('skyblue')
v.get_patch_by_id('111').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("True Subevent Set")
plt.show()

やはり閉世界仮説（Closed World Assumption）を採用して全体集合(Universal Set)の最頂点として現れる補集合の要素数を0と考えた方がスッキリする様に見受けられます。

#十進環(Decimal Ring)概念の類型としての確率ベクトル(Probability Vector)概念
上掲の最後の二重真部分集合の例では何となく十進法を意識していましたが、考えてみれば実際の十進法は以下の様な(ある意味集合表示ライブラリの想定する範囲を超えた)特殊な部分集合として定義される訳です。

%matplotlib inline
from matplotlib_venn import venn3
from matplotlib import pyplot as plt

v=venn3(subsets = (0, 0, 10, 0, 0, 0, 0), set_labels = ('1XX', 'X1X', 'XX1'))

# ベン図の色を変更する   
v.get_patch_by_id('100').set_color('white')
v.get_patch_by_id('100').set_edgecolor('black')
v.get_patch_by_id('110').set_color('skyblue')
v.get_patch_by_id('110').set_edgecolor('black')
v.get_patch_by_id('010').set_color('white')
v.get_patch_by_id('010').set_edgecolor('black')

# 背景色を変更する
plt.gca().set_axis_on()
plt.gca().set_facecolor('white')
plt.title("Decimal Set(3 digits)")
plt.show()

上掲プログラムにおいては、3桁の整数が以下の様に分類されています。

• 集合1XXは0XX~9XXの10要素で構成される部分集合
• 集合X1XはX0X~X9Xの10要素で構成される部分集合
• 集合XX1はXX0~XX9の10要素で構成される部分集合

完全に重なっていてそれぞれの要素数も同じですね。この場合の組み合わせは$10^3=1000$通り(0~999)。各要素の算出過程を線的結合表記(Linear Connection Expression)で表すと以下となります。

10^2a+10^1b+10^0c(a,b,c \in (0,1,2,3,4,5,6,7,8,9))

この考え方だと容易に無限周期拡張(Infinite Periodic Extension)を導入する事が出来ます。

D_n=10^∞n_{∞}+10^{∞-1 }n_{∞-1}+,…,10^2n_2+10^1n_1+10^0n_0(n \in (0,1,2,3,4,5,6,7,8,9))

さらに10^0N_0を単位元Iと規定し、$D_nD_n^{-1}=D_n^{-1}D_n=I$となる小数点下の展開を追加すれば「実数列と同型(Isomorphism,すなわち全単射/双射=Bijective Function, Bijection可能)の十進環(Decmal Ring)の出来上がりです(同時に加法群としても成立する事は自明の利?)。

D_n=10^∞n_{∞}+10^{∞-1 }n_{∞-1}+,…,10^2N_2+10^1n_1+10^0n_0+10^{-1}n_{-1}+10^{-2}n_{-2}(n \in (0,1,2,3,4,5,6,7,8,9))

• 同時に閉世界仮説（Closed World Assumption）を採用して全体集合(Universal Set)の最頂点として現れる補集合の要素数を0と考える概念も視野に入ってくる。例えばお金に関してなら、ルネサンス期欧州に複式簿記(Double-Entry Bookkeeping)が広まった時代まで遡る桁管理技術(とはいえ最新技術を投入しても、今日なお「Exelの桁あふれ」みたいな悲劇は起こり続けている)。そしてまさに金額の頭につける「通貨単位マーク」こそ…
• その一方で当然、十進環を含むN進環は全て、例えば垂直軸に(加法単位元0を原点に-∞方向と+∞方向に伸びる)加法実数列、水平軸に(半径1の乗法単位元を原点に$\frac{1}{∞}$倍方向と∞倍方向に放射展開する)乗法実数列を配した円筒座標系(Cylindrical Coordinate System)といった形でイメージされるベクトル空間を構成する実数環(Real Reng)に包括される訳である。
  【Python演算処理】環論に立脚した全体像再構築①空環と実数環
  
  
  

群論においては$e^x/log(x)$演算を採用した乗法群(Multiplicative Group)やModN演算を採用した商群(Quotient Group,Factor Group)の一種で、さらに厳密な定義がp進数論で得られますが、ここではその辺りまでは踏み込みません。当座の目的を果たすには理論上「十進環単体で既に実数列上の全てを表す(近似する)事が可能である」という考え方だけで十分だからです。
【初心者向け】N進法(N-ary)とp進数(p-adic)
整数環とp進整数環の関係

以前(1次元)ベクトル空間(Vector Space)について触れた時、その特徴たる「スカラー倍可能」のスカラー尺度が外挿的にしか与えられない事について触れました。
【Python演算処理】環論に立脚した全体像再構築③ベクトル空間としての構成

確かにそれはこの様な全く独自の数理展開(Mathematical Expansion)によって構築されるのです。そんな感じで以下続報…