More than 3 years have passed since last update.

もう諦めない圏論入門―圏と関手―

Last updated at 2020-03-27Posted at 2019-08-16

圏論入門前の準備運動―集合と写像―
もう諦めない圏論入門―対象と射―
- 具体例を通して圏の定義を受け入れる
- 直積と余直積に触れて圏を理解した気になる
もう諦めない圏論入門―圏と関手―
- 具体例を通して関手の定義を受け入れる
- Hom 関手に触れて関手を理解した気になる
もう諦めない圏論入門―関手と自然変換―
- 具体例を通して自然変換の定義を受け入れる
- 随伴関手に触れて自然変換を理解した気になる
もう諦めない圏論付録―ストリング・ダイアグラム―
もう諦めない圏論基礎―極限からカン拡張へ―
もう諦めない圏論基礎―モノイドからモナドへ―
もう諦めない圏論基礎―高次元圏と変換手―

関手の定義

まずは定義を見てみましょう。
具体例を考えたとき、それが関手の定義を満たしているのか、
確認したくなったらここに戻ってくれば良い。

確認を重ねるうちに定義には慣れてくるはずだ。

圏と関手

圏 $\boldsymbol{C}$ と圏 $\boldsymbol{D}$ の対応 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ すなわち
対象の対応 $F \colon \mathrm{Obj}(\boldsymbol{C}) \longrightarrow \mathrm{Obj}(\boldsymbol{D})$ と
射の対応 $F \colon \mathrm{Mor}(\boldsymbol{C}) \longrightarrow \mathrm{Mor}(\boldsymbol{D})$ を考える。

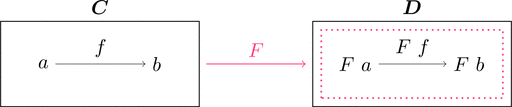
対象の対応 $F$ は、
対象 $a\in\mathrm{Obj}(\boldsymbol{C})$ から
対象 $F\ a \in\mathrm{Obj}(\boldsymbol{D})$ への対応である。

射の対応 $F$ は、
圏 $\boldsymbol{C}$ における射の集合 $\boldsymbol{C}(a,b)$ から
圏 $\boldsymbol{D}$ における射の集合 $\boldsymbol{D}(F\ a,F\ b)$ への
写像 $F \colon \boldsymbol{C}(a,b) \longrightarrow \boldsymbol{D}(F\ a,F\ b)$ である。

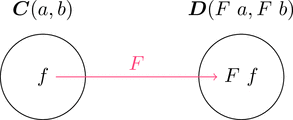
射 $f\in\boldsymbol{C}(a,b)$ に対し $F\ f \in\boldsymbol{D}(F\ a,F\ b)$ すなわち
$\mathrm{dom}(F\ f) = F\ \mathrm{dom}(f)$ かつ $\mathrm{cod}(F\ f) = F\ \mathrm{cod}(f)$ である。

次の２つの条件を満たすとき、$F$ は関手である。

（恒等射の保存）$F\ \mathrm{id}_{a} = \mathrm{id}_{F\ a}$ が成り立つ。
（合成の保存）$F\ (f \ggg g) = F\ f \ggg F\ g$ が成り立つ。

合成の保存により、図を描くとき $F\ (f \ggg g)$ は省略できる。

対象 $a$ と射 $f$ と言う型が異なりうるものを同じ記号で
$F\ a$ や $F\ f$ と書くことに最初は戸惑ったような気がする。

オーバーロードと思えばプログラマには馴染み深いだろう。

合成関手

関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{E}$ の
合成関手 $F \cdot G \colon \boldsymbol{C} \longrightarrow \boldsymbol{E}$ を
対象の対応 $(F \cdot G)\ a = G\ (F\ a)$ と
射の対応 $(F \cdot G)\ f = G\ (F\ f)$ で定義する。

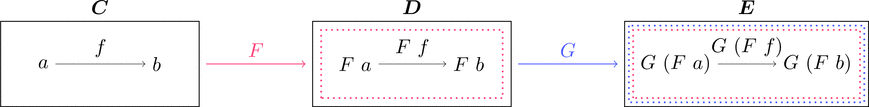
このとき $F \cdot G$ が関手であることを確認できる。

（恒等射の保存）
$(F \cdot G)\ \mathrm{id}_{a} = G\ (F\ \mathrm{id}_{a}) = G\ \mathrm{id}_{F\ a}$
$G\ \mathrm{id}_{F\ a} = \mathrm{id}_{G\ (F\ a)} = \mathrm{id}_{(F \cdot G)\ a}$ が成り立つ。
（合成の保存）
$(F \cdot G)\ (f \ggg g) = G\ (F\ (f \ggg g)) = G\ (F\ f \ggg F\ g)$
$G\ (F\ f \ggg F\ g) = G\ (F\ f) \ggg G\ (F\ g) = (F \cdot G)\ f \ggg (F \cdot G)\ g$ が成り立つ。

恒等関手

恒等関手 $\mathrm{id}_{\boldsymbol{C}} \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}$ を
対象の対応 $\mathrm{id}_{\boldsymbol{C}}\ a = a$ と
射の対応 $\mathrm{id}_{\boldsymbol{C}}\ f = f$ で定義する。

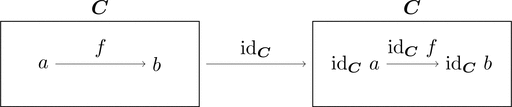
このとき $\mathrm{id}_{\boldsymbol{C}}$ が関手であることを確認できる。

（恒等射の保存）
$\mathrm{id}_{\boldsymbol{C}}\ \mathrm{id}_{a} = \mathrm{id}_{a} = \mathrm{id}_{\mathrm{id}_{\boldsymbol{C}}\ a}$ が成り立つ。
（合成の保存）
$\mathrm{id}_{\boldsymbol{C}}\ (f \ggg g) = f \ggg g = \mathrm{id}_{\boldsymbol{C}}\ f \ggg \mathrm{id}_{\boldsymbol{C}}\ g$ が成り立つ。

対象と射それぞれの対応を定義し
２つの条件を確認せねばならず面倒ではあるが、
ゆっくりと考えれば難しくはないだろう。

圏の圏

関手を圏から圏への射とみなすこともできる。
つまり、圏(が対象)の圏 $\mathbf{Cat}$ を構成可能である。

合成射を合成関手で、恒等射を恒等関手で定義すれば

$\mathbf{Cat}$ は[__圏の定義__](https://qiita.com/norkron/items/f90d851daf05a2efa567#圏の定義)を満たすことが確認できる。

合成関手や恒等関手の定義を眺めていると、
対象の対応と射の対応が同じ形式をしていることに気づく。
そこで $F\ a$ や $F\ f$ をまとめて $F\ -$ とあらわす。

（結合律）
射(すなわち関手) $F, G, H \in \mathrm{Mor}(\mathbf{Cat})$ に対して
$(F \cdot (G \cdot H))\ - = (G \cdot H)\ (F\ -) = H\ (G\ (F\ -))$ と
$((F \cdot G) \cdot H)\ - = H\ ((F \cdot G)\ -) = H\ (G\ (F\ -))$ から
$F \cdot (G \cdot H) = (F \cdot G) \cdot H$ が成り立つ。
（単位律）
射(すなわち関手) $\mathrm{id}_{\boldsymbol{C}}, F, \mathrm{id}_{\boldsymbol{D}} \in \mathrm{Mor}(\mathbf{Cat})$ に対して
$(\mathrm{id}_{\boldsymbol{C}} \cdot F)\ - = F\ (\mathrm{id}_{\boldsymbol{C}}\ -) = F\ -$ と
$(F \cdot \mathrm{id}_{\boldsymbol{D}})\ - = \mathrm{id}_{\boldsymbol{D}}\ (F\ -) = F\ -$ から
$\mathrm{id}_{\boldsymbol{C}} \cdot F = F \cdot \mathrm{id}_{\boldsymbol{D}} = F$ が成り立つ。

対象の対応と射の対応を考えねばならない関手であったが、
圏から圏への射だと思えば単純に感じられるような気もする。

関手の具体例

定義ばかりじゃ何も見えてこないので、
具体例を通して定義の理解を深める。

関手が定義できると何が嬉しいのかは置いておいて、
以下の例が関手なことを定義と照らし合わせ考えよう。

Maybe 関手

対象が型で射が関数な圏を $\mathbf{H}$ と呼ぶことにする。

対象(すなわち型) $\mathrm{Char}, \mathrm{Int}, \mathrm{Bool} \in \mathrm{Obj}(\mathbf{H})$ であり
射(すなわち関数) $\mathrm{id}_{\mathrm{Char}}, \mathrm{id}_{\mathrm{Int}}, \mathrm{id}_{\mathrm{Bool}}, \mathrm{f}, \mathrm{g}, \mathrm{h} \in \mathrm{Mor}(\mathbf{H})$ である。

この圏 $\mathbf{H}$ からの関手 $\mathrm{Maybe}$ を考える。

Maybe は Functor の instance に標準でなっている。

Maybe

data Maybe a = Nothing | Just a

instance Functor Maybe where
    fmap _ Nothing  = Nothing
    fmap f (Just a) = Just (f a)

型構築子 Maybe の種を見て見ると

Maybe :: * -> *

また、高階関数 fmap の型を見てみると

fmap :: (a -> b) -> Maybe a -> Maybe b

ここで (->) は右結合であるから

fmap :: (a -> b) -> (Maybe a -> Maybe b)

対象(すなわち型) $a \in \mathrm{Obj}(\mathbf{H})$ と射(すなわち関数) $f \in \mathrm{Mor}(\mathbf{H})$ に対し
型構築子 Maybe で対象の対応 $\mathrm{Maybe}\ a =$ Maybe a が
高階関数 fmap で射の対応 $\mathrm{Maybe}\ f =$ fmap f が定義される。

絵で描くとこんな感じになる。

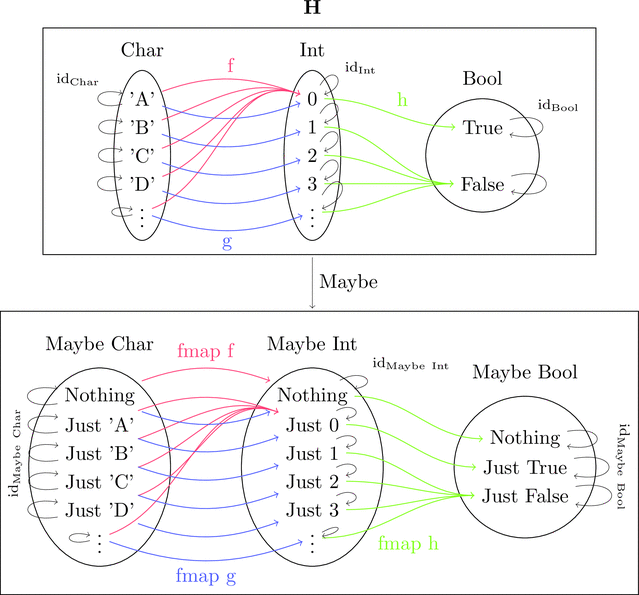
データ構築子 Just ではなく型構築子 Maybe が
対象(すなわち型)の対応をあらわしていることに注意が必要だろう。

例によって、丸で囲まれた対象内部の構造を潰して点 $\bullet$ とみなすと

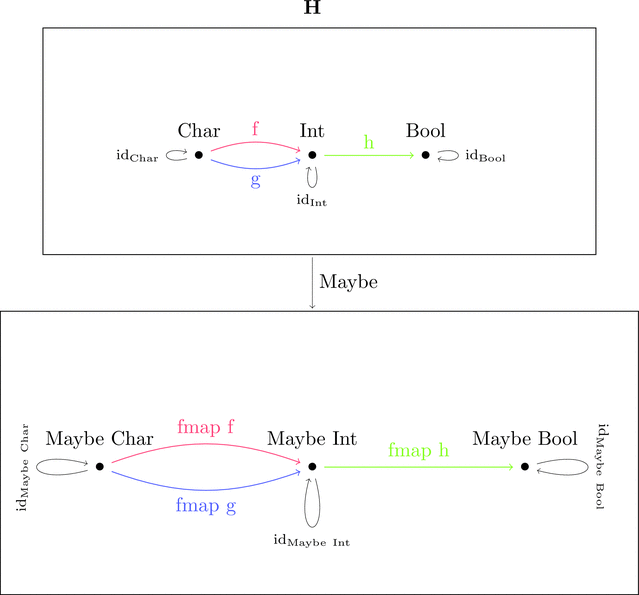
こう見ると型構築子 Maybe が対象の対応をあらわすのは明らかだ。

さらに、四角で囲まれた圏内部の構造を潰して点 $\scriptscriptstyle\blacksquare$ とみなすと

圏の圏になる。

List 関手

Maybe 関手の場合と同様に、
$\mathbf{H}$ からの関手 $\mathrm{List}$ を考える。

List は Functor の instance に標準でなっている。

List

data [] a = [] | a : [a]

instance Functor [] where
    fmap _ []     = []
    fmap f (x:xs) = f x : fmap f xs

Maybe 関手の場合と同様に、
対象(すなわち型) $a \in \mathrm{Obj}(\mathbf{H})$ と射(すなわち関数) $f \in \mathrm{Mor}(\mathbf{H})$ に対し
型構築子 [] で対象の対応 $\mathrm{List}\ a =$ [a] が
高階関数 fmap で射の対応 $\mathrm{List}\ f =$ fmap f が定義される。

絵で描くとこんな感じになる。

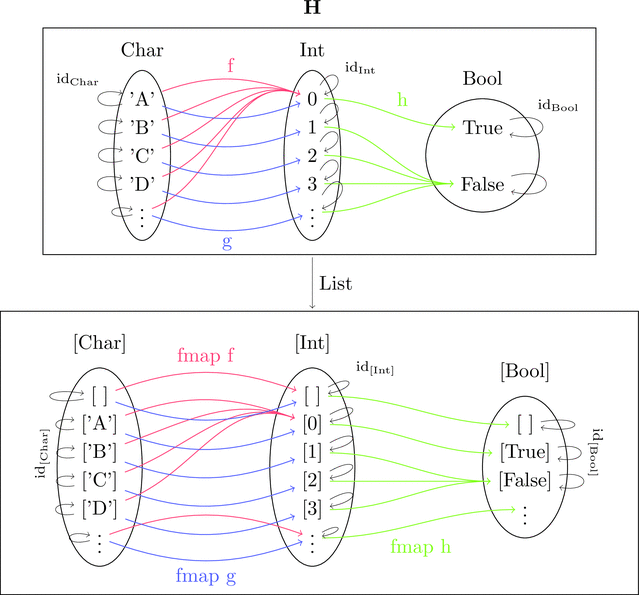
型構築子 [] が対象(すなわち型)の対応をあらわしている。

例によって、丸で囲まれた対象内部の構造を潰して点 $\bullet$ とみなすと

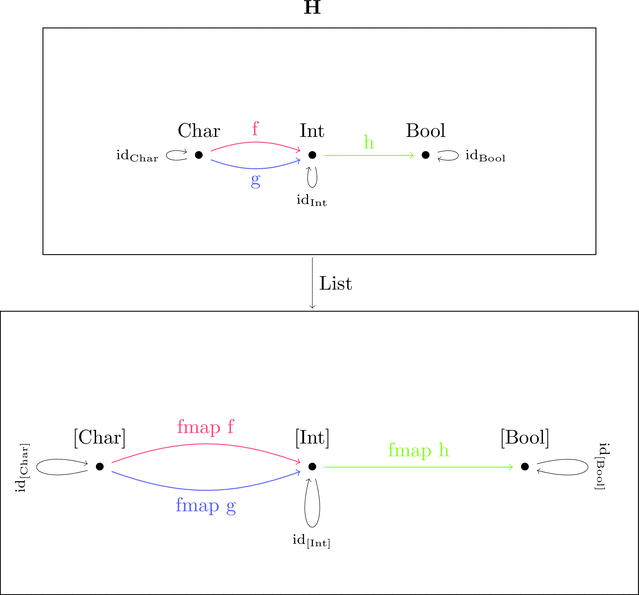
そろそろ対象内部の構造に興味を持たなくても大丈夫な気がする。

さらに、四角で囲まれた圏内部の構造を潰して点 $\scriptscriptstyle\blacksquare$ とみなすと

圏の圏になる。

自己関手

Haskell の全ての型を対象、Haskell の全ての関数を射
とした圏 $\mathbf{Hask}$ を考えれば、Maybe 関手も List 関手も
圏 $\mathbf{Hask}$ から圏 $\mathbf{Hask}$ への関手と言うことができる。

圏 $\mathbf{H}$ は圏 $\mathbf{Hask}$ の部分圏すなわち $\mathbf{H} \subset \mathbf{Hask}$ である。

自分自身に戻ってくるような関手を自己関手と言う。
対象１つで射が整数値の圏に似た絵でモノイドと関係しそう。
自己関手、、、、、、モノイド、、どこかで見たような¹。

Hom 関手

関手の定義をある程度は理解したところで、
もう少し難しげな例として Hom 関手を考えてみたい。

米田の補題²と関係があるらしいのできっと興味深い。

Hom 集合

圏 $\boldsymbol{C}$ の対象 $a, b \in \mathrm{Obj}(\boldsymbol{C})$ に対して
始域 $a$ で終域 $b$ な射の集合を $\mathrm{Hom}_{\boldsymbol{C}}(a, b)$ と呼ぶ。
射 $f\in\mathrm{Mor}(\boldsymbol{C})$ のうち $f \colon a \longrightarrow b$ な射の集合だ。

集合の内包的記法を用いて次のように書くと分かりやすいだろうか。
$\mathrm{Hom}_{\boldsymbol{C}}(a, b) = \{f \in \mathrm{Mor}(\boldsymbol{C}) \mid \mathrm{dom}(f) = a \land \mathrm{cod}(f) = b\}$

Hom 集合は部分集合すなわち $\mathrm{Hom}_{\boldsymbol{C}}(a, b) \subset \mathrm{Mor}(\boldsymbol{C})$ ぽい。

集合の圏

集合 $A$ から集合 $B$ への写像 $f \colon A \longrightarrow B$ を考える。

元 $a \in A$ と元 $b \in B$ として、
元の対応 $f \colon a \longmapsto b$ により写像 $f$ は定められる。

集合を対象、写像を射とした圏を
集合(が対象)の圏 $\mathbf{Set}$ と呼ぶ。

Hom 集合も対象となり、$\mathrm{Hom}_{\boldsymbol{C}}(a, b) \in \mathrm{Obj}(\mathbf{Set})$ である。
上図は集合の圏 $\mathbf{Set}$ における対象と射のごく一部を描いている。

集合の元が対象なのではなく、集合が対象なことに注意しよう。

集合の元を対象にし、恒等射のみを考えると、
これも圏になるのでややこしく感じるかもしれない。

関手 $f \colon A \longrightarrow B$ は
対象の対応 $f\ a = b$ と
射の対応 $f\ \mathrm{id}_{a} = \mathrm{id}_{b}$ で定義される。

共変関手

圏 $\boldsymbol{C}$ から集合の圏 $\mathbf{Set}$ への
対応 $F \colon \boldsymbol{C} \longrightarrow \mathbf{Set}$ を考えてみよう。

対象の対応 $F \colon \mathrm{Obj}(\boldsymbol{C}) \longrightarrow \mathrm{Obj}(\mathbf{Set})$ に関しては、
$a \in \mathrm{Obj}(\boldsymbol{C})$ とし、$F\ b = \mathrm{Hom}_{\boldsymbol{C}}(a, b)$ で定義する。

射の対応 $F \colon \mathrm{Mor}(\boldsymbol{C}) \longrightarrow \mathrm{Mor}(\mathbf{Set})$ に関しては、
圏 $\boldsymbol{C}$ における合成射を定める写像
$\ggg \colon \mathrm{Hom}_{\boldsymbol{C}}(a, b) \times \mathrm{Hom}_{\boldsymbol{C}}(b, b') \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(a, b')$
に部分適用を行い、$F\ g = - \ggg g$ と定義する。

この対応 $F$ を $\mathrm{Hom}_{\boldsymbol{C}}(a, -)$ と書く。

対応 $\mathrm{Hom}_{\boldsymbol{C}}(a, -) \colon \boldsymbol{C} \longrightarrow \mathbf{Set}$ は
$b\in\mathrm{Obj}(\boldsymbol{C})$ を $\mathrm{Hom}_{\boldsymbol{C}}(a, b)\in\mathrm{Obj}(\mathbf{Set})$ に対応させ
$g\in\mathrm{Mor}(\boldsymbol{C})$ を $\mathrm{Hom}_{\boldsymbol{C}}(a, g)\in\mathrm{Mor}(\mathbf{Set})$ に対応させる。

ここで、$\mathrm{Hom}_{\boldsymbol{C}}(a, g) = \mathrm{id}_{a} \ggg - \ggg g$ である。

関数が Functor の instance になるという理解で良いはず。

Hom

{-# LANGUAGE GeneralizedNewtypeDeriving #-}
import Control.Category (Category, (>>>))

newtype Hom a b = Hom { getHom :: a -> b } deriving Category

instance Functor (Hom a) where
    fmap g = (>>> Hom g)

絵で描くとこんな感じになる。

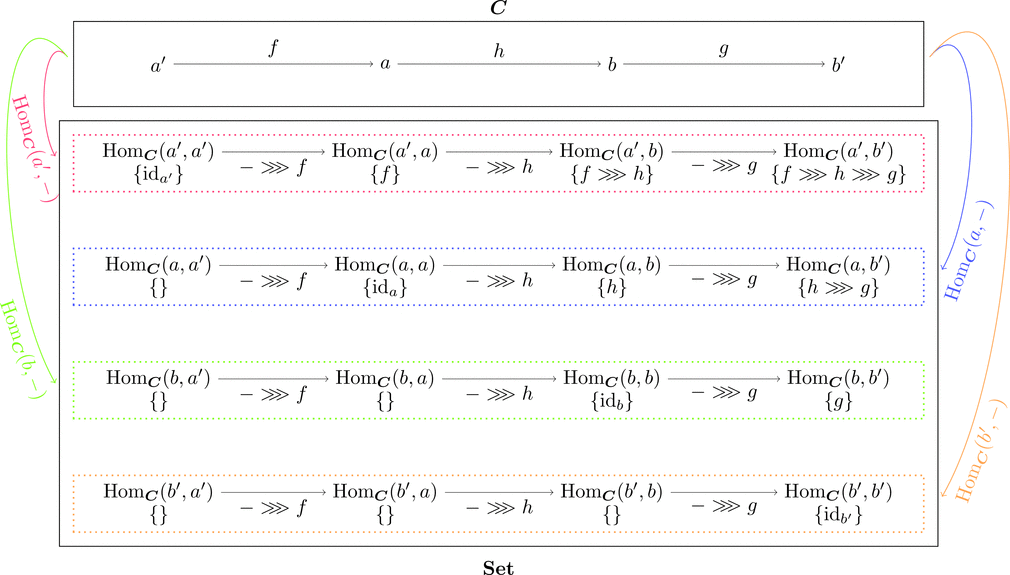
圏 $\boldsymbol{C}$ と圏 $\mathbf{Set}$ で射が同じ向きになっている。
このような対応を共変関手というらしい。

反変関手

圏 $\boldsymbol{C}$ から集合の圏 $\mathbf{Set}$ への
対応 $F \colon \boldsymbol{C} \longrightarrow \mathbf{Set}$ を考えてみよう。

対象の対応 $F \colon \mathrm{Obj}(\boldsymbol{C}) \longrightarrow \mathrm{Obj}(\mathbf{Set})$ に関しては、
$b \in \mathrm{Obj}(\boldsymbol{C})$ とし、$F\ a = \mathrm{Hom}_{\boldsymbol{C}}(a, b)$ で定義する。

射の対応 $F \colon \mathrm{Mor}(\boldsymbol{C}) \longrightarrow \mathrm{Mor}(\mathbf{Set})$ に関しては、
圏 $\boldsymbol{C}$ における合成射を定める写像
$\ggg \colon \mathrm{Hom}_{\boldsymbol{C}}(a', a) \times \mathrm{Hom}_{\boldsymbol{C}}(a, b) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(a', b)$
に部分適用を行い、$F\ f = f \ggg -$ と定義する。

この対応 $F$ を $\mathrm{Hom}_{\boldsymbol{C}}(-, b)$ と書く。

対応 $\mathrm{Hom}_{\boldsymbol{C}}(-, b) \colon \boldsymbol{C} \longrightarrow \mathbf{Set}$ は
$a\in\mathrm{Obj}(\boldsymbol{C})$ を $\mathrm{Hom}_{\boldsymbol{C}}(a, b)\in\mathrm{Obj}(\mathbf{Set})$ に対応させ
$f\in\mathrm{Mor}(\boldsymbol{C})$ を $\mathrm{Hom}_{\boldsymbol{C}}(f, b) \in\mathrm{Mor}(\mathbf{Set})$ に対応させる。

ここで、$\mathrm{Hom}_{\boldsymbol{C}}(f, b) = f \ggg - \ggg \mathrm{id}_{b}$ である。

絵で描くとこんな感じになる。

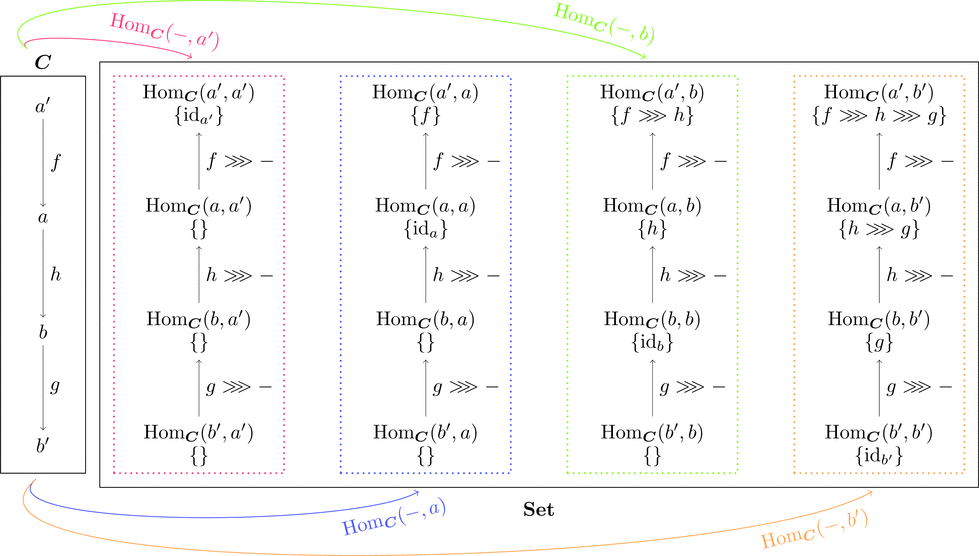
圏 $\boldsymbol{C}$ と圏 $\mathbf{Set}$ で射が逆の向きになっている。
このような対応を反変関手というらしい。

反対圏

圏 $\boldsymbol{C}$ の反対圏 $\boldsymbol{C}^{\mathrm{op}}$ を図のように定める。

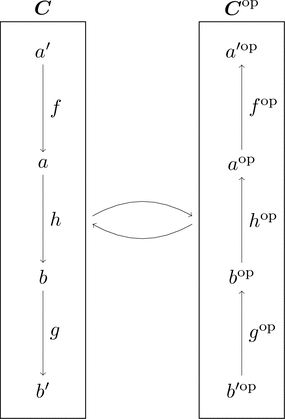
圏 $\boldsymbol{C}^{\mathrm{op}}$ から圏 $\mathbf{Set}$ への対応 $\mathrm{Hom}_{\boldsymbol{C}}(-, b) \colon \boldsymbol{C}^{\mathrm{op}} \longrightarrow\mathbf{Set}$
を考えることで反変関手を共変関手とみなすことができる。

確かに射が同じ向きになるのは分かるけど、
対象や射に付いてる $\scriptstyle \mathrm{op}$ を気にせずにすむ理屈
が良く分かっていないのでいつか理解したい³。

関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ があるとき

関手 $F^{\mathrm{op}} \colon \boldsymbol{C}^{\mathrm{op}} \longrightarrow \boldsymbol{D}^{\mathrm{op}}$ が以下のように定まる。

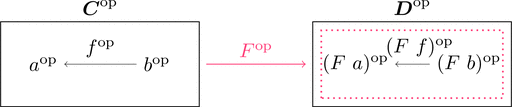
対象の対応 $F^{\mathrm{op}}\ a^{\mathrm{op}} = (F\ a)^{\mathrm{op}}$ および
射の対応 $F^{\mathrm{op}}\ f^{\mathrm{op}} = (F\ f)^{\mathrm{op}}$ である。

双関手

圏の圏 $\mathbf{Cat}$ では圏が対象となるため、
圏の直積と余直積を考えることができるだろう。

圏 $\boldsymbol{C}$ と圏 $\boldsymbol{D}$ の直積 $\boldsymbol{C}\times\boldsymbol{D}$ は
対象 $(c,d)\in\mathrm{Obj}(\boldsymbol{C})\times\mathrm{Obj}(\boldsymbol{D})=\mathrm{Obj}(\boldsymbol{C}\times\boldsymbol{D})$ と
射 $(f,g)\in\mathrm{Hom}_{\boldsymbol{C}}(c,c')\times\mathrm{Hom}_{\boldsymbol{D}}(d,d')=\mathrm{Hom}_{\boldsymbol{C}\times\boldsymbol{D}}((c,d), (c',d'))$
で定められる。

$\mathrm{Hom}_{\boldsymbol{C}\times\boldsymbol{D}}((c,d), (c',d')) \subset \mathrm{Mor}(\boldsymbol{C}\times\boldsymbol{D})$ である。

絵で描くとこんな感じになる。

射の合成は次のように成分ごとに射を合成する。
$(f,\mathrm{id}_{b}) \ggg (\mathrm{id}_{a},g) = (f \ggg\mathrm{id}_{a},\mathrm{id}_{b} \ggg g) = (f,g)$

圏 $\boldsymbol{C}\times\boldsymbol{C}$ から圏 $\mathbf{Set}$ への
対応 $\mathrm{Hom}_{\boldsymbol{C}}(-, -) \colon \boldsymbol{C}\times\boldsymbol{C} \longrightarrow \mathbf{Set}$ を考えてみよう。

反変関手と共変関手とを合わせた感じで、
対応 $\mathrm{Hom}_{\boldsymbol{C}}(-, -) \colon \boldsymbol{C}\times\boldsymbol{C} \longrightarrow \mathbf{Set}$ は
$(a,b)\in\mathrm{Obj}(\boldsymbol{C}\times\boldsymbol{C})$ を $\mathrm{Hom}_{\boldsymbol{C}}(a, b)\in\mathrm{Obj}(\mathbf{Set})$ に対応させ
$(f,g)\in\mathrm{Mor}(\boldsymbol{C}\times\boldsymbol{C})$ を $\mathrm{Hom}_{\boldsymbol{C}}(f, g) \in\mathrm{Mor}(\mathbf{Set})$ に対応させる。

ここで、$\mathrm{Hom}_{\boldsymbol{C}}(f, g) = f \ggg - \ggg g$ である。

絵で描くとこんな感じになる。

圏 $\boldsymbol{C}\times\boldsymbol{C}$ と圏 $\mathbf{Set}$ で縦方向の射が逆の向きになっている。

圏 $\boldsymbol{C}^{\mathrm{op}}\times\boldsymbol{C}$ から圏 $\mathbf{Set}$ への
対応 $\mathrm{Hom}_{\boldsymbol{C}}(-,-) \colon \boldsymbol{C}^{\mathrm{op}}\times\boldsymbol{C} \longrightarrow\mathbf{Set}$
を考えることで双関手⁴とみなすことができる。

圏 $\boldsymbol{C}^{\mathrm{op}}\times\boldsymbol{C}$ と圏 $\mathbf{Set}$ で射が同じ向きになっている。

圏 $\boldsymbol{C}$ の対象 $a\in\mathrm{Mor}(\boldsymbol{C})$ ごとに存在する関手
$\mathrm{Hom}_{\boldsymbol{C}}(a, -)$ による対応が色点線で囲まれている。

これらの関手と関手との間にも何か対応がありそうだ。

まとめ

Functor は箱⁵のイメージが強い場合には
fmap の引数の順序に悩んでしまうけれども、
関手と思えばこの順序が気持ちよく感じる。

Functor は圏 $\mathbf{Hask}$ から圏 $\mathbf{Hask}$ への関手⁶、
つまり射が関数な場合にしか使えないので、
Category から Category への関手を定義⁷して
instance を作ってみると楽しいかもしれない。

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up