圏論入門前の準備運動―集合と写像―
もう諦めない圏論入門―対象と射―
- 具体例を通して圏の定義を受け入れる
- 直積と余直積に触れて圏を理解した気になる
もう諦めない圏論入門―圏と関手―
- 具体例を通して関手の定義を受け入れる
- Hom 関手に触れて関手を理解した気になる
もう諦めない圏論入門―関手と自然変換―
- 具体例を通して自然変換の定義を受け入れる
- 随伴関手に触れて自然変換を理解した気になる
もう諦めない圏論付録―ストリング・ダイアグラム―
もう諦めない圏論基礎―極限からカン拡張へ―
もう諦めない圏論基礎―モノイドからモナドへ―
もう諦めない圏論基礎―高次元圏と変換手―

自然変換の定義

まずは定義を見てみましょう。
具体例を考えたとき、それが自然変換の定義を満たしているのか、
確認したくなったらここに戻ってくれば良い。

確認を重ねるうちに定義には慣れてくるはずだ。

関手と自然変換

$\boldsymbol{C}$ と $\boldsymbol{D}$ を圏とし、関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ から
関手 $G \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ への変換 $\theta \colon F \Longrightarrow G$ を考える。

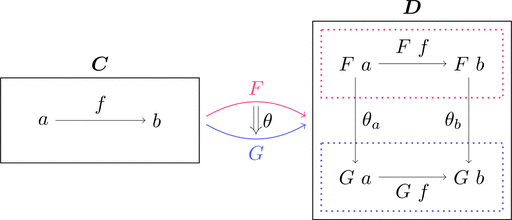
変換は $\theta_{a} \colon F\ a \longrightarrow G\ a$ により定義される。 $\theta$ は射の族で、
各対象 $a\in\mathrm{Obj}(\boldsymbol{C})$ に対して射 $\theta_{a}\in\mathrm{Mor}(\boldsymbol{D})$ が存在する。

次の条件を満たすとき、$\theta$ は自然変換である。

（自然性）$F\ f \ggg \theta_{b} = \theta_{a} \ggg G\ f$ が成り立つ。

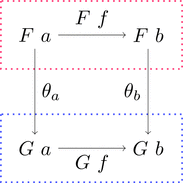
つまり $\theta$ が自然変換の場合にはこれが可換図式となる。

式だけ見ていると到底覚えられそうに無いけれど、
図を描くと満たして欲しそうな式が何となく分かるだろう。

垂直合成

圏 $\boldsymbol{C}$ から圏 $\boldsymbol{D}$ への関手 $F, G, H$ に対して、
自然変換 $\theta \colon F \Longrightarrow G$ と自然変換 $\sigma \colon G \Longrightarrow H$ の
垂直合成 $\theta \ggg \sigma \colon F \Longrightarrow H$ を考える。

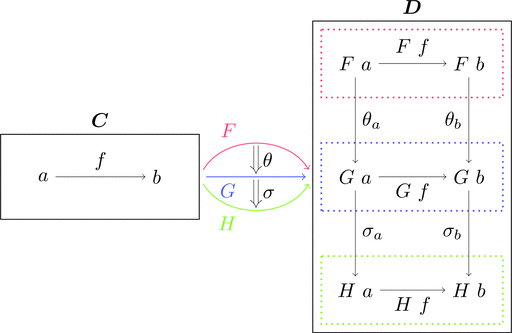
$\theta$ と $\sigma$ が自然変換であることから

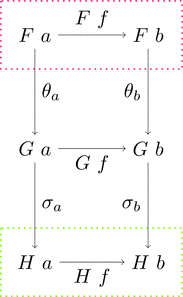
は可換図式であり、射の族を $(\theta \ggg \sigma)_{a} = \theta_{a} \ggg \sigma_{a}$
と定義することで垂直合成 $\theta \ggg \sigma$ は自然変換となる。

左辺 $\theta \ggg \sigma$ の $\ggg$ が自然変換の合成をあらわすのに対して、
右辺 $\theta_{a} \ggg \sigma_{a}$ の $\ggg$ は射の合成をあらわすことに注意しよう。

何か普通の合成っぽいことが感じられるだろう。
自然変換の合成には次の水平合成も存在する。

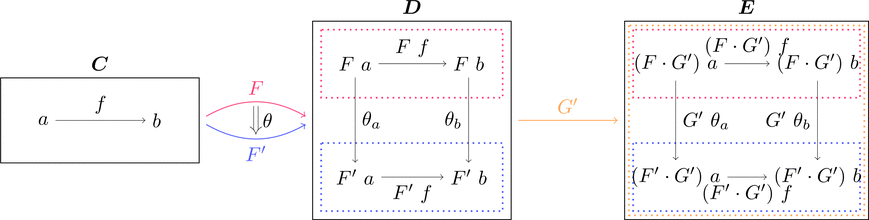
水平合成

圏 $\boldsymbol{C}$ から圏 $\boldsymbol{D}$ への関手 $F, F'$ と
圏 $\boldsymbol{D}$ から圏 $\boldsymbol{E}$ への関手 $G, G'$ に対して、
自然変換 $\theta \colon F \Longrightarrow F'$ と自然変換 $\sigma \colon G \Longrightarrow G'$ の
水平合成 $\theta \cdot \sigma \colon F \cdot G \Longrightarrow F' \cdot G'$ を考える。

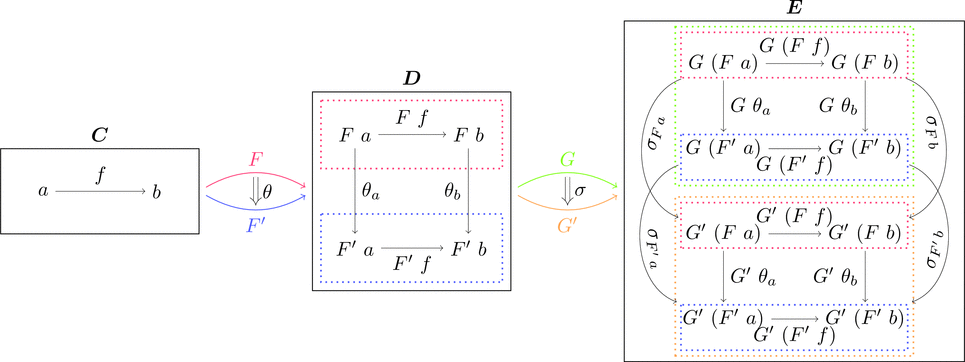
$\theta$ と $\sigma$ が自然変換であることから

は可換図式であり、射の族を
$(\theta \cdot \sigma)_{a} = G\ \theta_{a} \ggg \sigma_{F'\ a} = \sigma_{F\ a} \ggg G'\ \theta_{a}$
と定義することで水平合成 $\theta \cdot \sigma$ は自然変換となる。

この合成は複雑なので、関手の圏の双関手として
まとめて考えたほうが分かりやすいように思う。

恒等変換

圏 $\boldsymbol{C}$ から圏 $\boldsymbol{D}$ への関手 $F$ に対して、
恒等変換 $\mathrm{id}_{F} \colon F \Longrightarrow F$ を考える。

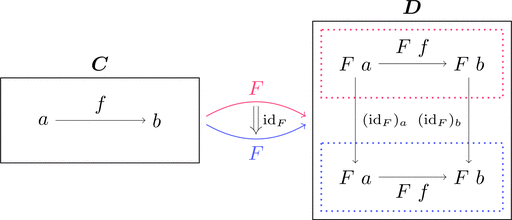
射の族を $(\mathrm{id}_{F})_{a} = \mathrm{id}_{F\ a}$ と定義することで

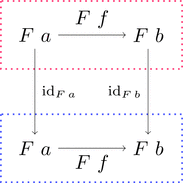
は可換図式、すなわち恒等変換 $\mathrm{id}_{F}$ は自然変換となる。

関手の圏

自然変換を関手から関手への射とみなすこともできる。
つまり、関手(が対象)の圏 $\boldsymbol{D}^\boldsymbol{C}$ を構成可能である。

圏 $\boldsymbol{C}$ から圏 $\boldsymbol{D}$ への関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ を対象、
$F,G\in\mathrm{Obj}(\boldsymbol{D}^\boldsymbol{C})$ に対して自然変換 $\theta \colon F \Longrightarrow G$ を射とする。

合成射を垂直合成で恒等射を恒等変換で定義すれば

$\boldsymbol{D}^\boldsymbol{C}$ は圏の定義を満たすことが確認できる。

（結合律）
射(すなわち自然変換) $\theta,\sigma,\tau\in\mathrm{Mor}(\boldsymbol{D}^\boldsymbol{C})$ に対して
$(\theta \ggg (\sigma \ggg \tau))_{a} = \theta_{a} \ggg (\sigma \ggg \tau)_{a} = \theta_{a} \ggg \sigma_{a} \ggg \tau_{a}$ と
$((\theta \ggg \sigma) \ggg \tau)_{a} = (\theta \ggg \sigma)_{a} \ggg \tau_{a} = \theta_{a} \ggg \sigma_{a} \ggg \tau_{a}$ から
$\theta \ggg (\sigma \ggg \tau) = (\theta \ggg \sigma) \ggg \tau$ が成り立つ。
（単位律）
射(すなわち自然変換) $\mathrm{id}_{F},\theta,\mathrm{id}_{G}\in\mathrm{Mor}(\boldsymbol{D}^\boldsymbol{C})$ に対して
$(\mathrm{id}_{F} \ggg \theta)_{a} = (\mathrm{id}_{F})_{a} \ggg \theta_{a} = \mathrm{id}_{F\ a} \ggg \theta_{a} = \theta_{a}$ と
$(\theta \ggg \mathrm{id}_{G})_{a} = \theta_{a} \ggg (\mathrm{id}_{G})_{a} = \theta_{a} \ggg \mathrm{id}_{G\ a} = \theta_{a}$ から
$\mathrm{id}_{F} \ggg \theta = \theta \ggg \mathrm{id}_{G} = \theta$ が成り立つ。

圏の圏 $\mathbf{Cat}$ では射(すなわち関手)に対してさらに射(すなわち自然変換)
を考えることができる。こうした射の射という概念が重要な気がする。

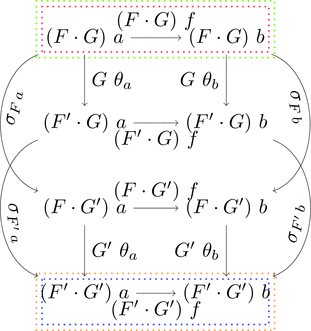
双関手

関手の圏 $\boldsymbol{D}^{\boldsymbol{C}}, \boldsymbol{E}^{\boldsymbol{D}}, \boldsymbol{E}^{\boldsymbol{C}}$ とし、
双関手 $- \cdot - \colon \boldsymbol{D}^\boldsymbol{C} \times \boldsymbol{E}^\boldsymbol{D} \longrightarrow \boldsymbol{E}^\boldsymbol{C}$ を考える。

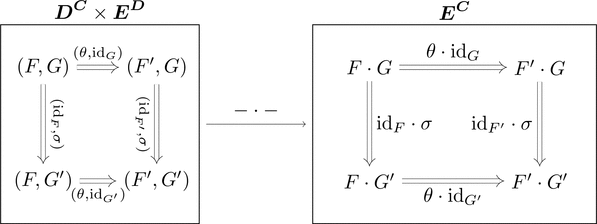
$(F,G) \in \mathrm{Obj}(\boldsymbol{D}^\boldsymbol{C} \times \boldsymbol{E}^\boldsymbol{D})$ を $F \cdot G \in \mathrm{Obj}(\boldsymbol{E}^\boldsymbol{C})$ に対応させ、
$(\theta,\sigma) \in \mathrm{Mor}(\boldsymbol{D}^\boldsymbol{C} \times \boldsymbol{E}^\boldsymbol{D})$ を $\theta \cdot \sigma \in \mathrm{Mor}(\boldsymbol{E}^\boldsymbol{C})$ に対応させる。

合成関手 $F \cdot G$ および水平合成 $\theta \cdot \sigma$ である。

このとき $- \cdot -$ が関手であることを確認できる。

(恒等射の保存)
$(\mathrm{id}_{F} \cdot \mathrm{id}_{G})_{a} = G\ (\mathrm{id}_{F})_{a} \ggg (\mathrm{id}_{G})_{F\,a} = G\ \mathrm{id}_{F\,a} \ggg \mathrm{id}_{G\,(F\,a)} = \mathrm{id}_{(F \cdot
G)\,a}$
すなわち $\mathrm{id}_{F} \cdot \mathrm{id}_{G} = \mathrm{id}_{F \cdot G}$ が成り立つ。
(合成の保存)
$((\theta \ggg \theta') \cdot (\sigma \ggg \sigma'))_{a} = G\ (\theta \ggg \theta')_{a} \ggg (\sigma \ggg \sigma')_{F''\,a}$
$ = G\ (\theta_{a} \ggg \theta'_{a}) \ggg (\sigma_{F''\,a} \ggg \sigma'_{F''\,a})= (G\ \theta_{a} \ggg G\ \theta'_{a}) \ggg (\sigma_{F''\,a} \ggg \sigma'_{F''\,a})$
$= G\ \theta_{a} \ggg (G\ \theta'_{a} \ggg \sigma_{F''\,a}) \ggg \sigma'_{F''\,a} = G\ \theta_{a} \ggg (\sigma_{F'\,a} \ggg G'\ \theta'_{a}) \ggg \sigma'_{F''\,a}$
$= (G\ \theta_{a} \ggg \sigma_{F'\,a}) \ggg (G'\ \theta'_{a} \ggg \sigma'_{F''\,a}) = (\theta \cdot \sigma)_{a} \ggg (\theta' \cdot \sigma')_{a}$
すなわち $(\theta \ggg \theta') \cdot (\sigma \ggg \sigma') = (\theta \cdot \sigma) \ggg (\theta' \cdot \sigma')$ が成り立つ。

左セクション

双関手 $- \cdot - \colon \boldsymbol{D}^\boldsymbol{C} \times \boldsymbol{E}^\boldsymbol{D} \longrightarrow \boldsymbol{E}^\boldsymbol{C}$ の第１引数に
関手 $F$ を部分適用し、関手 $F \cdot - \colon \boldsymbol{E}^{\boldsymbol{D}} \longrightarrow \boldsymbol{E}^{\boldsymbol{C}}$ を考える。

$G \in \mathrm{Obj}(\boldsymbol{E}^{\boldsymbol{D}})$ を $F \cdot G \in \mathrm{Obj}(\boldsymbol{E}^{\boldsymbol{C}})$ に対応させ、
$\sigma \in \mathrm{Mor}(\boldsymbol{E}^{\boldsymbol{D}})$ を $F \cdot \sigma = \mathrm{id}_{F} \cdot \sigma \in \mathrm{Mor}(\boldsymbol{E}^{\boldsymbol{C}})$ に対応させる。

このとき $F \cdot -$ が関手であることを確認できる。

任意の双関手 $B \colon \boldsymbol{C}\times\boldsymbol{D} \longrightarrow \boldsymbol{E}$ に対して
対象の対応 $F(c)\ d = B\ (c,d)$ と
射の対応 $F(c)\ f = B\ (\mathrm{id}_{c},f)$ で
関手 $F(c) \colon \boldsymbol{D} \longrightarrow \boldsymbol{E}$ を定義できる。

(恒等射の保存)
$F(c)\ \mathrm{id}_{d} = B\ (\mathrm{id}_{c},\mathrm{id}_{d}) = \mathrm{id}_{B\,(c,d)}$
すなわち $F(c)\ \mathrm{id}_{d} = \mathrm{id}_{F(c)\,d}$ が成り立つ。
(合成の保存)
$F(c)\ (f \ggg g) = B\ (\mathrm{id}_{c},f \ggg g) = B\ (\mathrm{id}_{c},f) \ggg B\ (\mathrm{id}_{c},g)$
すなわち $F(c)\ (f \ggg g) = F(c)\ f \ggg F(c)\ g$ が成り立つ。

右セクション

双関手 $- \cdot - \colon \boldsymbol{D}^\boldsymbol{C} \times \boldsymbol{E}^\boldsymbol{D} \longrightarrow \boldsymbol{E}^\boldsymbol{C}$ の第２引数に
関手 $G$ を部分適用し、関手 $- \cdot G \colon \boldsymbol{D}^{\boldsymbol{C}} \longrightarrow \boldsymbol{E}^{\boldsymbol{C}}$ を考える。

$F \in \mathrm{Obj}(\boldsymbol{D}^{\boldsymbol{C}})$ を $F \cdot G \in \mathrm{Obj}(\boldsymbol{E}^{\boldsymbol{C}})$ に対応させ、
$\theta \in \mathrm{Mor}(\boldsymbol{D}^{\boldsymbol{C}})$ を $\theta \cdot G = \theta \cdot \mathrm{id}_{G} \in \mathrm{Mor}(\boldsymbol{E}^{\boldsymbol{C}})$ に対応させる

このとき $- \cdot G$ が関手であること確認できる。

任意の双関手 $B \colon \boldsymbol{C}\times\boldsymbol{D} \longrightarrow \boldsymbol{E}$ に対して
対象の対応 $F(d)\ c = B\ (c,d)$ と
射の対応 $F(d)\ f = B\ (f,\mathrm{id}_{d})$ で
関手 $F(d) \colon \boldsymbol{C} \longrightarrow \boldsymbol{E}$ を定義できる。

(恒等射の保存)
$F(d)\ \mathrm{id}_{c} = B\ (\mathrm{id}_{c},\mathrm{id}_{d}) = \mathrm{id}_{B\,(c,d)}$
すなわち $F(d)\ \mathrm{id}_{c} = \mathrm{id}_{F(d)\,c}$ が成り立つ。
(合成の保存)
$F(d)\ (f \ggg g) = B\ (f \ggg g,\mathrm{id}_{d}) = B\ (f,\mathrm{id}_{d}) \ggg B\ (g,\mathrm{id}_{d})$
すなわち $F(d)\ (f \ggg g) = F(d)\ f \ggg F(d)\ g$ が成り立つ。

結合律と単位律

圏の圏で見たように、
合成関手 $F \cdot G$ に関して結合律と単位律が成り立つ。

また、水平合成 $\theta \cdot \sigma$ に関しても

結合律と単位律が成り立つことを確認できる。

（結合律）
$\theta\in\mathrm{Mor}(\boldsymbol{D}^\boldsymbol{C}), \sigma\in\mathrm{Mor}(\boldsymbol{E}^\boldsymbol{D}), \tau\in\mathrm{Mor}(\boldsymbol{F}^\boldsymbol{E})$ に対して
$(\theta \cdot (\sigma \cdot \tau))_{a}= (G \cdot H)\ \theta_{a} \ggg (\sigma \cdot \tau)_{F'\ a}$
$ = H\ (G\ \theta_{a}) \ggg H\ \sigma_{F'\ a} \ggg \tau_{G'\ (F'\ a)}$ と
$((\theta \cdot \sigma) \cdot \tau)_{a} = H\ (\theta \cdot \sigma)_{a} \ggg \tau_{(F' \cdot G')\ a}$
$ = H\ (G\ \theta_{a} \ggg \sigma_{F'\ a}) \ggg \tau_{G'\ (F'\ a)}$ から
$\theta \cdot (\sigma \cdot \tau) = (\theta \cdot \sigma) \cdot \tau$ が成り立つ。
（単位律）
$\mathrm{id}_{\mathrm{id}_{\boldsymbol{C}}}\in\mathrm{Mor}(\boldsymbol{C}^\boldsymbol{C}),\theta\in\mathrm{Mor}(\boldsymbol{D}^\boldsymbol{C}), \mathrm{id}_{\mathrm{id}_{\boldsymbol{D}}}\in\mathrm{Mor}(\boldsymbol{D}^\boldsymbol{D})$ に対して
$(\mathrm{id}_{\mathrm{id}_{\boldsymbol{C}}} \cdot \theta)_{a} = F\ (\mathrm{id}_{\mathrm{id}_{\boldsymbol{C}}})_{a} \ggg \theta_{\mathrm{id}_{\boldsymbol{C}}\ a} = F\ \mathrm{id}_{\mathrm{id}_{\boldsymbol{C}}\ a} \ggg \theta_{a}$
$ = F\ \mathrm{id}_{a} \ggg \theta_{a} = \mathrm{id}_{F\ a} \ggg \theta_{a} = \theta_{a}$ と
$(\theta \cdot \mathrm{id}_{\mathrm{id}_{\boldsymbol{D}}})_{a} = \mathrm{id}_{\boldsymbol{D}}\ \theta_{a} \ggg (\mathrm{id}_{\mathrm{id}_{\boldsymbol{D}}})_{F'\ a} = \theta_{a} \ggg \mathrm{id}_{\mathrm{id}_{\boldsymbol{D}}\ (F'\ a)}$
$ = \theta_{a} \ggg \mathrm{id}_{F'\ a} = \theta_{a}$ から
$\mathrm{id}_{\mathrm{id}_{\boldsymbol{C}}} \cdot \theta = \theta \cdot \mathrm{id}_{\mathrm{id}_{\boldsymbol{D}}} = \theta$ が成り立つ。

したがって、双関手 $- \cdot -$ に対して以下となる。

（結合律）$(- \cdot -) \cdot - = - \cdot (- \cdot -)$ が成り立つ。
（単位律）$\mathrm{id}_{\boldsymbol{C}} \cdot - = - \cdot \mathrm{id}_{\boldsymbol{D}} = \mathrm{id}_{\boldsymbol{D}^\boldsymbol{C}}$ が成り立つ。

関手と自然変換の合成

関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と自然変換 $\sigma \colon G \Longrightarrow G'$ の
合成 $F \cdot \sigma \colon F\cdot G \Longrightarrow F\cdot G'$ を考える。

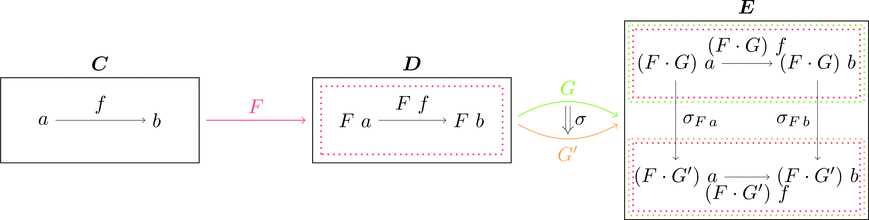
同様に
関手 $F' \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と自然変換 $\sigma \colon G \Longrightarrow G'$ の
合成 $F' \cdot \sigma \colon F'\cdot G \Longrightarrow F'\cdot G'$ を考える。

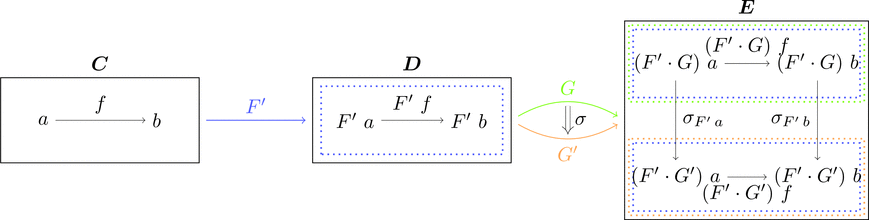
これらの合成は左セクションにおける定義と一致する。
射の族 $(F \cdot \sigma)_{a} = (\mathrm{id}_{F} \cdot \sigma)_{a} = G\ (\mathrm{id}_{F})_{a} \ggg \sigma_{F\ a} = \sigma_{F\ a}$ であり、
射の族 $(F' \cdot \sigma)_{a} = (\mathrm{id}_{F'} \cdot \sigma)_{a} = G\ (\mathrm{id}_{F'})_{a} \ggg \sigma_{F'\ a} = \sigma_{F'\ a}$ である。

自然変換と関手の合成

自然変換 $\theta \colon F \Longrightarrow F'$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{E}$ の
合成 $\theta \cdot G \colon F\cdot G \Longrightarrow F'\cdot G$ を考える。

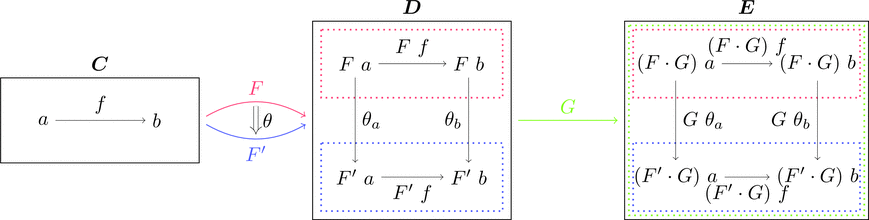
同様に
自然変換 $\theta \colon F \Longrightarrow F'$ と関手 $G' \colon \boldsymbol{D} \longrightarrow \boldsymbol{E}$ の
合成 $\theta \cdot G' \colon F\cdot G' \Longrightarrow F'\cdot G'$ を考える。

これらの合成は右セクションにおける定義と一致する。
射の族 $(\theta \cdot G)_{a} = (\theta \cdot \mathrm{id}_{G})_{a} = G\ \theta_{a} \ggg (\mathrm{id}_{G})_{F'\,a} = G\ \theta_{a}$ であり、
射の族 $(\theta \cdot G')_{a} = (\theta \cdot \mathrm{id}_{G'})_{a} = G'\ \theta_{a} \ggg (\mathrm{id}_{G'})_{F'\,a} = G'\ \theta_{a}$ である。

交替律

これらの関手や自然変換の合成を用いることで、
$\theta \cdot \sigma = \theta \cdot G \ggg F' \cdot \sigma = F \cdot \sigma \ggg \theta \cdot G'$
と水平合成 $\theta \cdot \sigma$ を記述することができる。

自然変換が関わる合成は煩雑なので、
ストリング・ダイアグラムを眺めながら
定義を確認すると理解が早いかもしれない。

自然変換の具体例

定義ばかりじゃ何も見えてこないので、
具体例を通して定義の理解を深める。

自然変換が定義できると何が嬉しいのかは置いておいて、
以下の例が自然変換なことを定義と照らし合わせ考えよう。

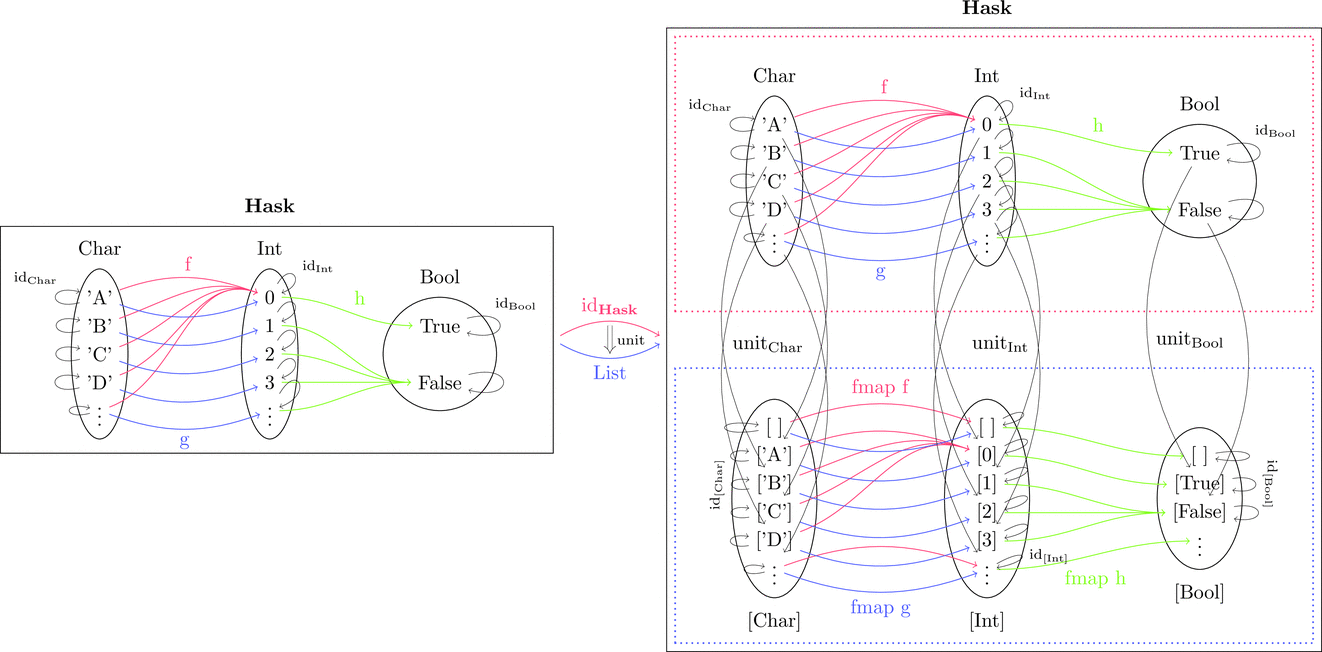
恒等関手から List 関手への自然変換

恒等関手 $\mathrm{id}_{\mathbf{Hask}} \colon \mathbf{Hask} \longrightarrow \mathbf{Hask}$ と
List 関手 $\mathrm{List} \colon \mathbf{Hask} \longrightarrow \mathbf{Hask}$ に対して
自然変換 $\mathrm{unit} \colon \mathrm{id}_{\mathbf{Hask}} \Longrightarrow \mathrm{List}$ を考える。

自然変換を射の族 $\mathrm{unit}_{a}$ により定義する。

unit

{-# LANGUAGE ExplicitForAll #-}

unit :: forall a. a -> [a]
unit a = [a]

パラメタ多相すなわち型変数 a で
各対象(すなわち型)に対して定義を行う。

射の族っぽさを出すために明示的に forall
としているだけなので、こう書く必要性は無い。

絵で描くとこんな感じになる。

例によって、丸で囲まれた対象内部の構造を潰して点 $\bullet$ とみなすと

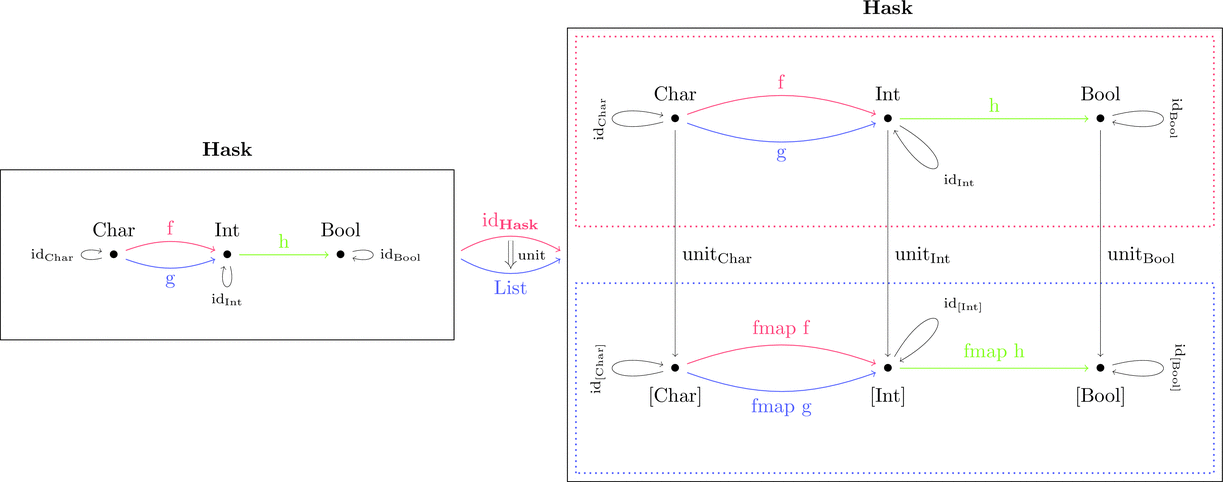
さらに、四角で囲まれた圏内部の構造を潰して点 $\scriptscriptstyle\blacksquare$ とみなすと

圏の圏になる。

関手を対象とみなし、自然変換を射とみなすと

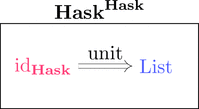
関手の圏になる。
自分自身に戻ってくるような関手なので自己関手の圏だ。

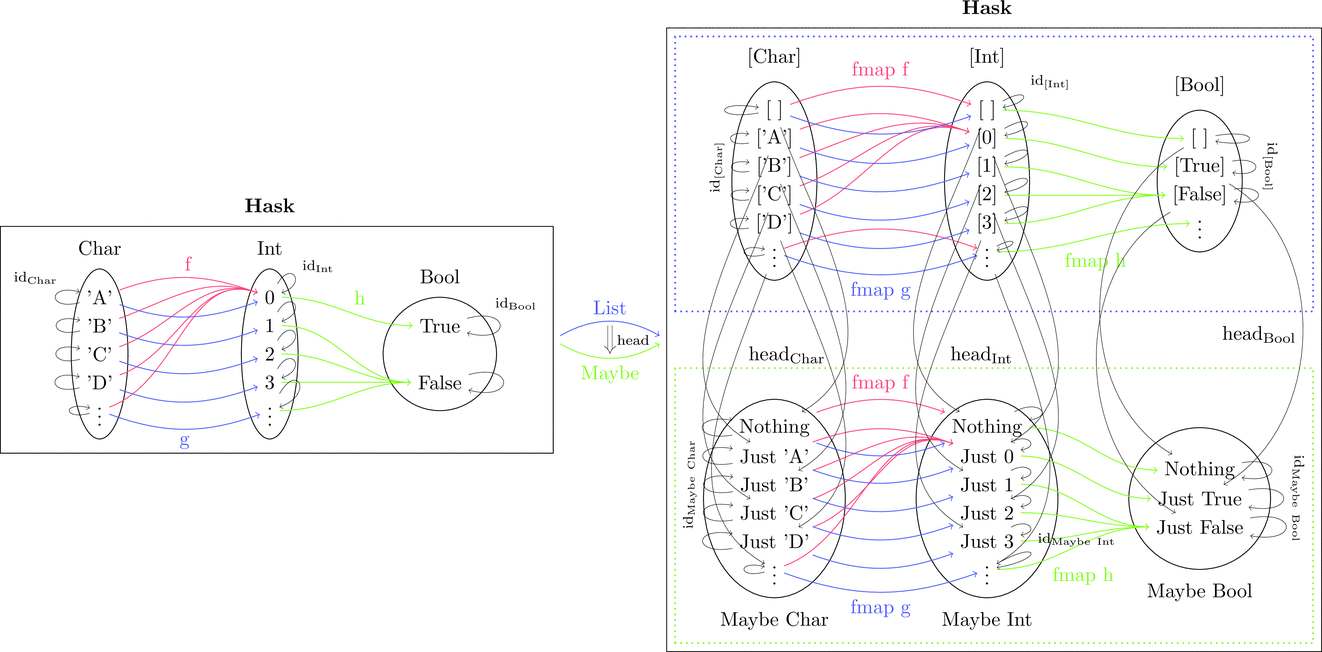
List 関手から Maybe 関手への自然変換

List 関手 $\mathrm{List} \colon \mathbf{Hask} \longrightarrow \mathbf{Hask}$ と
Maybe 関手 $\mathrm{Maybe} \colon \mathbf{Hask} \longrightarrow \mathbf{Hask}$ に対して
自然変換 $\mathrm{head} \colon \mathrm{List} \Longrightarrow \mathrm{Maybe}$ を考える。

自然変換を射の族 $\mathrm{head}_{a}$ により定義する。

head

{-# LANGUAGE ExplicitForAll #-}

import Prelude hiding (head)

head :: forall a. [a] -> Maybe a
head []    = Nothing
head (x:_) = Just x

パラメタ多相すなわち型変数 a で
各対象(すなわち型)に対して定義を行う。

射の族っぽさを出すために明示的に forall
としているだけなので、こう書く必要性は無い。

絵で描くとこんな感じになる。

例によって、丸で囲まれた対象内部の構造を潰して点 $\bullet$ とみなすと

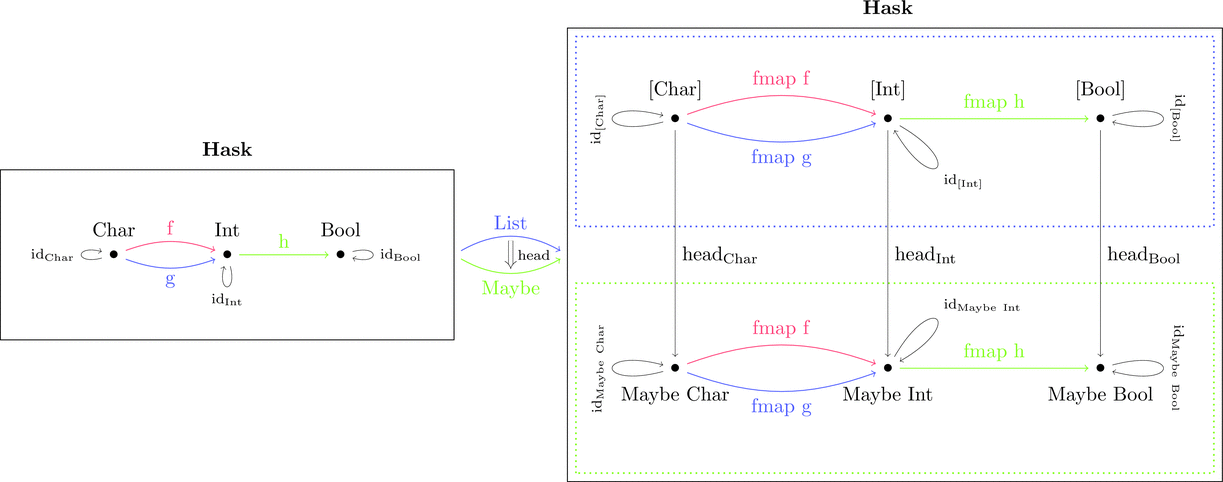
さらに、四角で囲まれた圏内部の構造を潰して点 $\scriptscriptstyle\blacksquare$ とみなすと

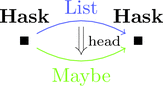
圏の圏になる。

関手を対象とみなし、自然変換を射とみなすと

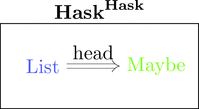
関手の圏になる。
自分自身に戻ってくるような関手なので自己関手の圏だ。

Hom 関手から Hom 関手への自然変換

Hom 関手の間に何か対応があるように見えていたが、
Hom 関手から Hom 関手への自然変換が存在する。

関手 $\mathrm{Hom}_{\boldsymbol{C}}(a,-) \colon \boldsymbol{C}\longrightarrow\mathbf{Set}$ を関手の圏における対象とし、
関手 $G \colon \boldsymbol{C}^{\mathrm{op}} \longrightarrow \mathbf{Set}^{\boldsymbol{C}}$ を考える。

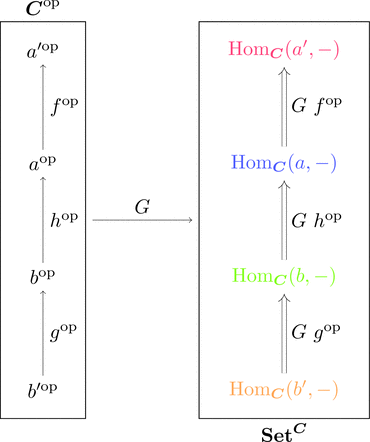
対象の対応 $G\ a^{\mathrm{op}} = \mathrm{Hom}_{\boldsymbol{C}}(a,-)$ と
射の対応 $(G\ f^{\mathrm{op}})_{b} = \mathrm{Hom}_{\boldsymbol{C}}(f,\mathrm{id}_{b}) = f \ggg -$
により関手を定義することができ、
関手の圏 $\mathbf{Set}^{\boldsymbol{C}}$ における射 $G\ f^{\mathrm{op}}$ が自然変換となっている。

関手 $\mathrm{Hom}_{\boldsymbol{C}}(-,b) \colon \boldsymbol{C}^{\mathrm{op}} \longrightarrow\mathbf{Set}$ を関手の圏における対象とし、
関手 $Y \colon \boldsymbol{C} \longrightarrow \mathbf{Set}^{\boldsymbol{C}^{\mathrm{op}}}$ を考える。

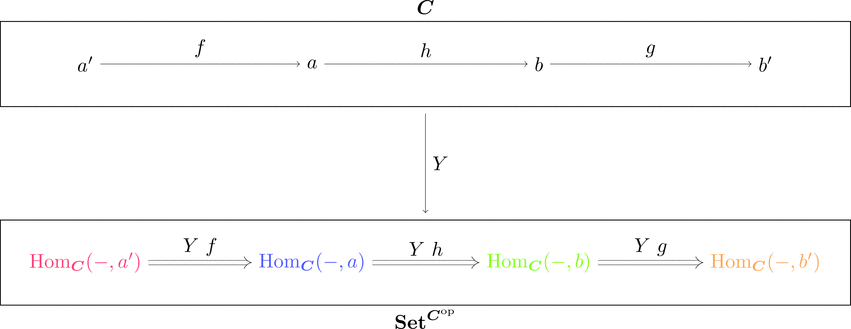
対象の対応 $Y\ b = \mathrm{Hom}_{\boldsymbol{C}}(-,b)$ と
射の対応 $(Y\ g)_{a} = \mathrm{Hom}_{\boldsymbol{C}}(\mathrm{id}_{a},g) = - \ggg g$
により関手を定義することができ、
関手の圏 $\mathbf{Set}^{\boldsymbol{C}^{\mathrm{op}}}$ における射 $Y\ g$ が自然変換となっている。

この関手 $Y$ を米田埋め込みと言うらしい。

随伴関手

自然変換の定義をある程度は理解したところで、
もう少し難しげな例として随伴関手を考えてみたい。

カン拡張¹と関係があるらしいのできっと興味深い。

随伴関手は２つの圏の間の関係を記述する関手らしい。

同型射

射 $f \colon a \longrightarrow b$ に対してある射 $g \colon b \longrightarrow a$ が存在して
$f \ggg g = \mathrm{id}_{a}$ と $g \ggg f = \mathrm{id}_{b}$ が成り立つとき
$a$ と $b$ が同型であると言い、$a \cong b$ とあらわす。

この $f$ を同型射と言い、射が対象間の関係を記述する。

集合の圏 $\mathbf{Set}$ における同型射 $f$ は全単射であり、
射が対象 $A,B$ 間の関係をあらわす感じが分かると思う。

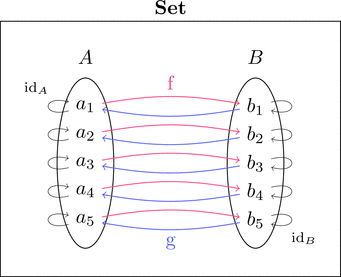
元の間に一対一対応があれば、
集合 $A$ と集合 $B$ を同一視 $A \cong B$ しても
とくに問題ないような気がして来るだろう。

型(が対象)の圏 $\mathbf{Hask}$ において newtype は同型だ。

同型

import Control.Category ((>>>))

newtype F a = F { g :: a }

データ構築子 F :: a -> F a に対して
関数 g :: F a -> a が存在して
F >>> g $=$ id :: a -> a と
g >>> F $=$ id :: F a -> F a が
成り立つので同型 a $\cong$ F a である。

同型関手

圏の圏における同型射を考える。

関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ に対してある関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ が存在して
$F \cdot G = \mathrm{id}_{\boldsymbol{C}}$ と $G \cdot F = \mathrm{id}_{\boldsymbol{D}}$ が成り立つとき
$\boldsymbol{C}$ と $\boldsymbol{D}$ が圏同型であると言い、 $\boldsymbol{C} \cong \boldsymbol{D}$ とあらわす。

この $F$ を同型関手と言い、関手が圏間の関係を記述する。

自然同型

関手の圏における同型射を考える。

自然変換 $\theta \colon F \longrightarrow G$ に対してある自然変換 $\sigma \colon G \longrightarrow F$ が存在して
$\theta \ggg \sigma = \mathrm{id}_{F}$ と $\sigma \ggg \theta = \mathrm{id}_{G}$ が成り立つとき
$F$ と $G$ が自然同型であると言い、 $F \cong G$ とあらわす。

この $\theta$ すなわち射の族 $\theta_{a} \colon F\ a \longrightarrow G\ a$ を
自然な同型射と言い、自然変換が関手間の関係を記述する。

圏同値

圏の圏 $\mathbf{Cat}$ では射の射を考えられるため、
圏間の関係を記述する別の関手を定義することができる。

関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ に対してある関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ が存在して
$F \cdot G \cong \mathrm{id}_{\boldsymbol{C}}$ と $G \cdot F \cong \mathrm{id}_{\boldsymbol{D}}$ が成り立つとき
$\boldsymbol{C}$ と $\boldsymbol{D}$ が圏同値であると言い、 $\boldsymbol{C} \simeq \boldsymbol{D}$ とあらわす。

等号 $=$ が同型 $\cong$ に変わっただけなことが分かる。
関手が一致すると言う厳しすぎる条件を緩めているらしい。

関手間の等号 $=$ や自然同型 $\cong$ を定めているのは
自然変換であることに注意し、圏同型と圏同値の定義
を見直すと以下のようになる。

圏同型: 関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ に対して
$\eta \colon \mathrm{id}_{\boldsymbol{C}} \Longrightarrow F \cdot G$ と $\varepsilon \colon G \cdot F \Longrightarrow \mathrm{id}_{\boldsymbol{D}}$ を恒等変換とする。
このとき $\boldsymbol{C}$ と $\boldsymbol{D}$ が圏同型すなわち $\boldsymbol{C} \cong \boldsymbol{D}$。
圏同値: 関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ に対して
$\eta \colon \mathrm{id}_{\boldsymbol{C}} \Longrightarrow F \cdot G$ と $\varepsilon \colon G \cdot F \Longrightarrow \mathrm{id}_{\boldsymbol{D}}$ を自然な同型射とする。
このとき $\boldsymbol{C}$ と $\boldsymbol{D}$ が圏同値すなわち $\boldsymbol{C} \simeq \boldsymbol{D}$。

上記の $\eta$ や $\varepsilon$ はある性質を持つ自然変換であり、
随伴は次のような性質を持つ自然変換により定まる。

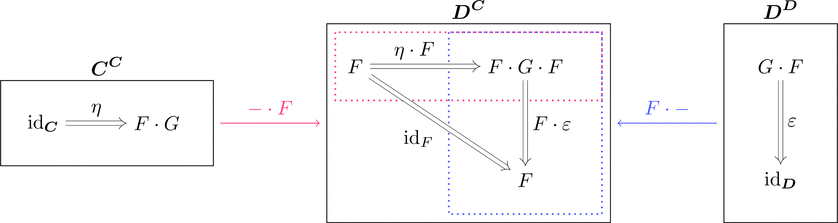
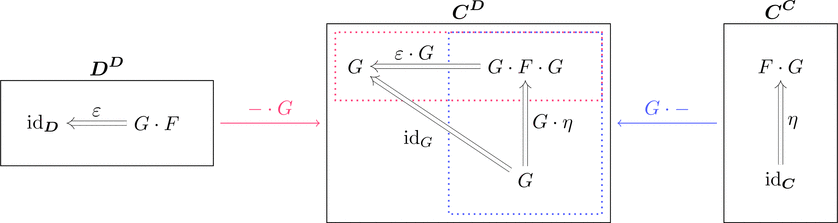
定義

関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ に対して
$\eta \colon \mathrm{id}_{\boldsymbol{C}} \Longrightarrow F \cdot G$ と $\varepsilon \colon G \cdot F \Longrightarrow \mathrm{id}_{\boldsymbol{D}}$ を自然変換とする。

次の２つの条件を満たすとき、随伴と言い $F \dashv G$ とあらわす。

$\eta \cdot F \ggg F \cdot \varepsilon = \mathrm{id}_{F}$ が成り立つ。
$G \cdot \eta \ggg \varepsilon \cdot G = \mathrm{id}_{G}$ が成り立つ。

$F$ を $G$ の左随伴関手と呼び、
$G$ を $F$ の右随伴関手と呼ぶ。
また、単位 $\eta$、余単位 $\varepsilon$ と呼ぶ。

関手 $F \cdot G$ と $\mathrm{id}_{\boldsymbol{C}}$ の関係および関手 $G \cdot F$ と $\mathrm{id}_{\boldsymbol{D}}$ の関係が
等号 $=$ でも同型 $\cong$ でもないそれ以外の何かにより
定められていることが分かればひとまず問題ないだろう。

条件が等号 $=$	条件が同型 $\cong$	条件がそれ以外
圏同型	圏同値	随伴

１つめの等式は上図の三角形が可換図式となることをあらわし、

２つめの等式は上図の三角形が可換図式となることをあらわす。

自然変換 $\eta$ と自然変換 $\varepsilon$ より下図の四角形が可換図式となる。

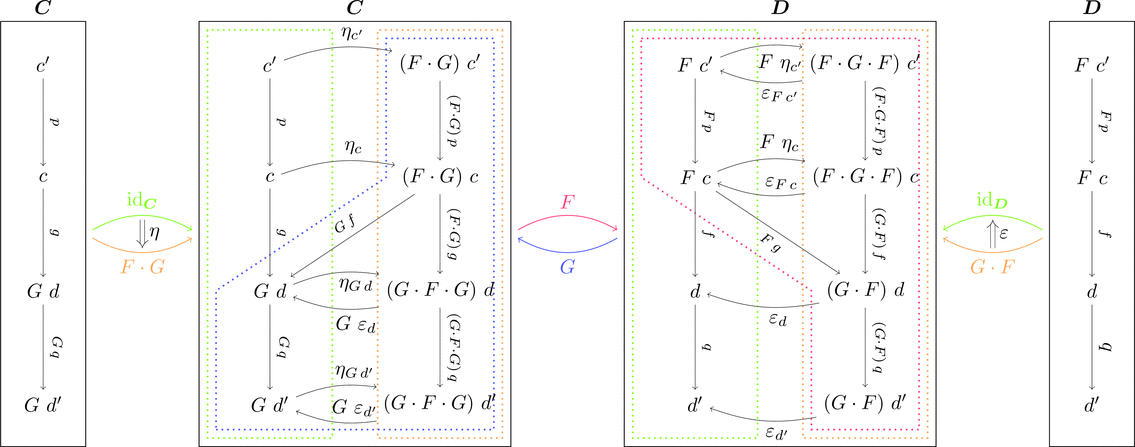
$\eta_{c'} \ggg G\ (F\ p)=p \ggg \eta_{c}$ と $F\ (G\ q) \ggg \varepsilon_{d'}=\varepsilon_{d} \ggg q$ を
後に見る変換が自然変換であることを示すために用い、
$F\ (G\ f) \ggg \varepsilon_{d} = \varepsilon_{F\ c} \ggg f $ と $\eta_{c} \ggg G\ (F\ g) = g \ggg \eta_{G\ d}$ を
後に見る変換が自然な同型射であることを示すために用いる。

随伴の定義を書きはしたけれどまだよく分からないので、
他の方法で定義を書いてみることで理解を深めてみたい。

まずは、おもむろに以下のような双関手を考える。

対象 $(c^{\mathrm{op}},d)$ を $\mathrm{Hom}_{\boldsymbol{D}}(F\ c,d) \in \mathrm{Obj}(\mathrm{Set})$ に対応させ
射 $(p^{\mathrm{op}},q)$ を $\mathrm{Hom}_{\boldsymbol{D}}(F\ p,q) = F\ p \ggg - \ggg q \in \mathrm{Mor}(\mathrm{Set})$
に対応させる双関手 $\mathrm{Hom}_{\boldsymbol{D}}(F\ -,-) \colon \boldsymbol{C}^{\mathrm{op}}\times\boldsymbol{D} \longrightarrow \mathbf{Set}$。

対象 $(c^{\mathrm{op}},d)$ を $\mathrm{Hom}_{\boldsymbol{C}}(c,G\ d) \in \mathrm{Obj}(\mathrm{Set})$ に対応させ
射 $(p^{\mathrm{op}},q)$ を $\mathrm{Hom}_{\boldsymbol{C}}(p,G\ q) = p \ggg - \ggg G\ q \in \mathrm{Mor}(\mathrm{Set})$
に対応させる双関手 $\mathrm{Hom}_{\boldsymbol{C}}(-,G\ -) \colon \boldsymbol{C}^{\mathrm{op}}\times\boldsymbol{D} \longrightarrow \mathbf{Set}$。

さらに、これら双関手間の変換を考える。

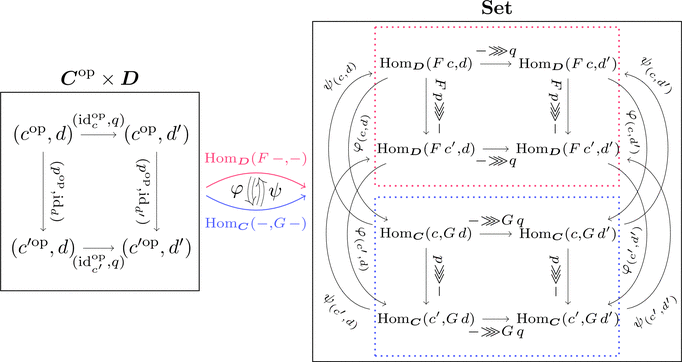
変換 $\varphi \colon \mathrm{Hom}_{\boldsymbol{D}}(F\ -,-) \Longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(-,G\ -)$ を
射の族 $\varphi_{(c,d)} = \eta_{c} \ggg G\ -$ で定義し、
変換 $\psi \colon \mathrm{Hom}_{\boldsymbol{C}}(-,G\ -) \Longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ -,-)$ を
射の族 $\psi_{(c,d)} = F\ - \ggg \varepsilon_{d}$ で定義する。

このとき $\varphi$ と $\psi$ は自然変換であることを示せる。

\begin{align}
(\mathrm{Hom}_{\boldsymbol{D}}(F\ p,q) \ggg \varphi_{(c',d')})(f)
&= \eta_{c'} \ggg G\ (F\ p \ggg f \ggg q)
\\
&=\eta_{c'} \ggg G\ (F\ p) \ggg G\ f \ggg G\ q
\\
&=(p \ggg \eta_{c}) \ggg G\ f \ggg G\ q, 
\\[2mm]
(\varphi_{(c,d)} \ggg \mathrm{Hom}_{\boldsymbol{C}}(p,G\ q))(f)
&= p \ggg (\eta_{c} \ggg G\ f) \ggg G\ q, 
\end{align}

すなわち
$\mathrm{Hom}_{\boldsymbol{D}}(F\ p,q) \ggg \varphi_{(c',d')} = \varphi_{(c,d)} \ggg \mathrm{Hom}_{\boldsymbol{C}}(p,G\ q)$
が成り立つから $\varphi$ は自然変換である。

\begin{align}
(\mathrm{Hom}_{\boldsymbol{C}}(p,G\ q) \ggg \psi_{(c',d')})(g)
&= F\ (p \ggg g \ggg G\ q) \ggg \varepsilon_{d'}
\\
&= F\ p \ggg F\ g \ggg F\ (G\ q) \ggg \varepsilon_{d'}
\\
&= F\ p \ggg F\ g \ggg (\varepsilon_{d} \ggg q), 
\\[2mm]
(\psi_{(c,d)} \ggg \mathrm{Hom}_{\boldsymbol{D}}(F\ p,q))(g)
&= F\ p \ggg (F\ g \ggg \varepsilon_{d}) \ggg q, 
\end{align}

すなわち
$\mathrm{Hom}_{\boldsymbol{C}}(p,G\ q) \ggg \psi_{(c',d')} = \psi_{(c,d)} \ggg \mathrm{Hom}_{\boldsymbol{D}}(F\ p,q)$
が成り立つから $\psi$ は自然変換である。

さらにこの $\varphi$ は自然な同型射であることを示せる。

\begin{align}
(\varphi_{(c,d)} \ggg \psi_{(c,d)})(f)
&=
F\ (\eta_{c} \ggg G\ f) \ggg \varepsilon_{d}
\\
&=
F\ \eta_{c} \ggg F\ (G\ f) \ggg \varepsilon_{d}
\\
&=
F\ \eta_{c} \ggg (\varepsilon_{F\ c} \ggg f)
\\
&=
(\eta \cdot F)_{c} \ggg (F \cdot \varepsilon)_{c} \ggg f
\\
&=
(\eta \cdot F \ggg F \cdot \varepsilon)_{c} \ggg f
\\
&=
(\mathrm{id}_{F})_{c} \ggg f
=
\mathrm{id}_{F\ c} \ggg f
=
f, 
\\[2mm]
(\psi_{(c,d)} \ggg \varphi_{(c,d)})(g)
&=
\eta_{c} \ggg G\ (F\ g \ggg \varepsilon_{d})
\\
&=
\eta_{c} \ggg G\ (F\ g) \ggg G\ \varepsilon_{d}
\\
&=
(g \ggg \eta_{G\ d}) \ggg G\ \varepsilon_{d}
\\
&=
g \ggg (G \cdot \eta)_{d} \ggg (\varepsilon \cdot G)_{d}
\\
&=
g \ggg (G \cdot \eta \ggg \varepsilon \cdot G)_{d}
\\
&=
g \ggg (\mathrm{id}_{G})_{d}
=
g \ggg \mathrm{id}_{G\ d}
=
g, 
\end{align}

すなわち
$\varphi_{(c,d)} \ggg \psi_{(c,d)}=\mathrm{id}_{\mathrm{Hom}_{\boldsymbol{D}}(F\ c,d)}$ と
$\psi_{(c,d)} \ggg \varphi_{(c,d)}=\mathrm{id}_{\mathrm{Hom}_{\boldsymbol{C}}(c, G\ d)}$ が成り立つ。

したがって
$(\varphi \ggg \psi)_{(c,d)}=\varphi_{(c,d)} \ggg \psi_{(c,d)} = \mathrm{id}_{\mathrm{Hom}_{\boldsymbol{D}}(F\ c,d)} = (\mathrm{id}_{\mathrm{Hom}_{\boldsymbol{D}}(F\ -,-)})_{(c,d)}$
$(\psi \ggg \varphi)_{(c,d)}=\psi_{(c,d)} \ggg \varphi_{(c,d)} = \mathrm{id}_{\mathrm{Hom}_{\boldsymbol{C}}(c, G\ d)} = (\mathrm{id}_{\mathrm{Hom}_{\boldsymbol{C}}(-, G\ -)})_{(c,d)}$
であり
$\mathrm{id}_{\mathrm{Hom}_{\boldsymbol{D}}(F\ -,-)}=\varphi \ggg \psi$ と $\psi \ggg \varphi=\mathrm{id}_{\mathrm{Hom}_{\boldsymbol{C}}(-, G\ -)}$
が成り立つから $\varphi$ は自然な同型射である。

別定義

関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ に対して
$\mathrm{Hom}_{\boldsymbol{D}}(F\ -,-) \cong \mathrm{Hom}_{\boldsymbol{C}}(-,G\ -)$ が成り立つ。
このとき、随伴と言い $F \dashv G$ とあらわす。

$F$ を $G$ の左随伴関手と呼び、
$G$ を $F$ の右随伴関手と呼ぶ。

関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ に対して
$F \dashv G$ が随伴であるとき以下が成り立つ。

反対圏にて定義を与えた
関手 $F^{\mathrm{op}} \colon \boldsymbol{C}^{\mathrm{op}} \longrightarrow \boldsymbol{D}^{\mathrm{op}}$ と
関手 $G^{\mathrm{op}} \colon \boldsymbol{D}^{\mathrm{op}} \longrightarrow \boldsymbol{C}^{\mathrm{op}}$ に対して、
$\mathrm{Hom}_{\boldsymbol{C}^{\mathrm{op}}}(G^{\mathrm{op}}\,-,-) \cong \mathrm{Hom}_{\boldsymbol{D}^{\mathrm{op}}}(-,F^{\mathrm{op}}\,-)$

すなわち随伴関係 $G^{\mathrm{op}} \dashv F^{\mathrm{op}}$ が成り立つ。

反対圏の定義より次の同型射が得られる。
$f_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{C}^{\mathrm{op}}}(G^{\mathrm{op}}\ d^{\mathrm{op}}, c^{\mathrm{op}}) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(c, G\ d)$
$g_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{D}}(F\ c, d) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}^{\mathrm{op}}}(d^{\mathrm{op}},F^{\mathrm{op}}\ c^{\mathrm{op}})$

$F \dashv G$ を構成する自然な同型射
すなわち写像 $\psi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{C}}(c, G\ d) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ c, d)$ を用いて、
写像 $\varphi_{(d^{\mathrm{op}},c^{\mathrm{op}})} \colon \mathrm{Hom}_{\boldsymbol{C}^{\mathrm{op}}}(G^{\mathrm{op}}\ d^{\mathrm{op}},c^{\mathrm{op}}) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}^{\mathrm{op}}}(d^{\mathrm{op}},F^{\mathrm{op}}\ c^{\mathrm{op}})$ を
射の合成 $\varphi_{(d^{\mathrm{op}},c^{\mathrm{op}})} = f_{(c,d)} \ggg \psi_{(c,d)} \ggg g_{(c,d)}$ により定義する。

$\varphi_{(d^{\mathrm{op}},c^{\mathrm{op}})}$ は自然な同型射である。

左セクション $F \cdot - \colon \boldsymbol{E}^{\boldsymbol{D}} \longrightarrow \boldsymbol{E}^{\boldsymbol{C}}$ と
左セクション $G \cdot - \colon \boldsymbol{E}^{\boldsymbol{C}} \longrightarrow \boldsymbol{E}^{\boldsymbol{D}}$ に対して、
$\mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{D}}}(G \cdot -,-) \cong \mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{C}}}(-,F \cdot -)$

すなわち随伴関係 $G \cdot - \dashv F \cdot -$ が成り立つ。

写像 $\varphi_{(C,D)} \colon \mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{D}}}(G \cdot C,D) \longrightarrow \mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{C}}}(C,F \cdot D)$ を
元の対応 $\varphi_{(C,D)} \colon \theta \longmapsto \eta \cdot C \ggg F \cdot \theta$ で定める。

このとき

\begin{align}
(\mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{D}}}(G \cdot \alpha,\beta) \ggg \varphi_{(C',D')})(\theta)
&=
\eta \cdot C' \ggg F \cdot (G \cdot \alpha \ggg \theta \ggg \beta)
\\
&=
\eta \cdot C' \ggg (F \cdot G) \cdot \alpha \ggg F \cdot \theta \ggg F \cdot \beta
\\
&=
\mathrm{id}_{\boldsymbol{C}} \cdot \alpha \ggg \eta \cdot C \ggg F \cdot \theta \ggg F \cdot \beta
\\[2mm]
(\varphi_{(C,D)} \ggg \mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{C}}}(\alpha,F \cdot \beta))(\theta)
&=
\alpha \ggg (\eta \cdot C \ggg F \cdot \theta) \ggg F \cdot \beta
\\
&=
\alpha \ggg \eta \cdot C \ggg F \cdot \theta \ggg F \cdot \beta
\\
&=
\mathrm{id}_{\boldsymbol{C}} \cdot \alpha \ggg \eta \cdot C \ggg F \cdot \theta \ggg F \cdot \beta
\end{align}

すなわち
$\mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{D}}}(G \cdot \alpha,\beta) \ggg \varphi_{(C',D')} = \varphi_{(C,D)} \ggg \mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{C}}}(\alpha,F \cdot \beta)$
が成り立つから $\varphi$ は
自然変換 $\varphi \colon \mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{D}}}(G \cdot -,-) \Longrightarrow \mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{C}}}(-,F \cdot -)$ である。

写像 $\psi_{(C,D)} \colon \mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{C}}}(C,F \cdot D) \longrightarrow \mathrm{Hom}_{\boldsymbol{E}^{\boldsymbol{D}}}(G \cdot C,D)$ を
元の対応 $\psi_{(C,D)} \colon \sigma \longmapsto G \cdot \sigma \ggg \varepsilon \cdot D$ で定めれば、

\begin{align}
(\varphi_{(C,D)} \ggg \psi_{(C,D)})(\theta)
&=
G \cdot (\eta \cdot C \ggg F \cdot \theta) \ggg \varepsilon \cdot D
\\
&=
G \cdot \eta \cdot C \ggg (G \cdot  F) \cdot \theta \ggg \varepsilon \cdot D
\\
&=
G \cdot \eta \cdot C \ggg \varepsilon \cdot (G \cdot C) \ggg \mathrm{id}_{\boldsymbol{D}} \cdot \theta
\\
&=
(G \cdot \eta \ggg \varepsilon \cdot G) \cdot C \ggg \mathrm{id}_{\boldsymbol{D}} \cdot \theta
\\
&=
\mathrm{id}_{G} \cdot C \ggg \mathrm{id}_{\boldsymbol{D}} \cdot \theta
\\
&=
\mathrm{id}_{G \cdot C} \ggg \theta = \theta
\\[2mm]
(\psi_{(C,D)} \ggg \varphi_{(C,D)})(\sigma)
&=
\eta \cdot C \ggg F \cdot (G \cdot \sigma \ggg \varepsilon \cdot D)
\\
&=
\eta \cdot C \ggg (F \cdot G) \cdot \sigma \ggg F \cdot \varepsilon \cdot D
\\
&=
\mathrm{id}_{\boldsymbol{C}} \cdot \sigma \ggg \eta \cdot (F \cdot D) \ggg F \cdot \varepsilon \cdot D
\\
&=
\mathrm{id}_{\boldsymbol{C}} \cdot \sigma \ggg (\eta \cdot F \ggg F \cdot \varepsilon) \cdot D
\\
&=
\mathrm{id}_{\boldsymbol{C}} \cdot \sigma \ggg \mathrm{id}_{F} \cdot D
\\
&=
\sigma \ggg \mathrm{id}_{F \cdot D} = \sigma
\end{align}

であるから、$\varphi_{(C,D)}$ は自然な同型射である。

右セクション $- \cdot F \colon \boldsymbol{C}^{\boldsymbol{E}} \longrightarrow \boldsymbol{D}^{\boldsymbol{E}}$ と
右セクション $- \cdot G \colon \boldsymbol{D}^{\boldsymbol{E}} \longrightarrow \boldsymbol{C}^{\boldsymbol{E}}$ に対して、
$\mathrm{Hom}_{\boldsymbol{D}^{\boldsymbol{E}}}(- \cdot F,-) \cong \mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{E}}}(-,- \cdot G)$

すなわち随伴関係 $- \cdot F \dashv - \cdot G$ が成り立つ。

写像 $\varphi_{(C,D)} \colon \mathrm{Hom}_{\boldsymbol{D}^{\boldsymbol{E}}}(C \cdot F,D) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{E}}}(C,D \cdot G)$ を
元の対応 $\varphi_{(C,D)} \colon \theta \longmapsto C \cdot \eta \ggg \theta \cdot G$ で定める。

このとき

\begin{align}
(\mathrm{Hom}_{\boldsymbol{D}^{\boldsymbol{E}}}(\alpha \cdot F,\beta) \ggg \varphi_{(C',D')})(\theta)
&=
C' \cdot \eta \ggg (\alpha \cdot F \ggg \theta \ggg \beta) \cdot G
\\
&=
C' \cdot \eta \ggg \alpha \cdot (F \cdot G) \ggg \theta \cdot G \ggg \beta \cdot G
\\
&=
\alpha \cdot \mathrm{id}_{\boldsymbol{C}} \ggg C \cdot \eta \ggg \theta \cdot G \ggg \beta \cdot G
\\[2mm]
(\varphi_{(C,D)} \ggg \mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{E}}}(\alpha,\beta \cdot G))(\theta)
&=
\alpha \ggg (C \cdot \eta \ggg \theta \cdot G) \ggg \beta \cdot G
\\
&=
\alpha \ggg C \cdot \eta \ggg \theta \cdot G \ggg \beta \cdot G
\\
&=
\alpha \cdot \mathrm{id}_{\boldsymbol{C}} \ggg C \cdot \eta \ggg \theta \cdot G \ggg \beta \cdot G
\end{align}

すなわち
$\mathrm{Hom}_{\boldsymbol{D}^{\boldsymbol{E}}}(\alpha \cdot F,\beta) \ggg \varphi_{(C',D')} = \varphi_{(C,D)} \ggg \mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{E}}}(\alpha,\beta \cdot G)$
が成り立つから $\varphi$ は
自然変換 $\varphi \colon \mathrm{Hom}_{\boldsymbol{D}^{\boldsymbol{E}}}(- \cdot F,-) \Longrightarrow \mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{E}}}(-,- \cdot G)$ である。

写像 $\psi_{(C,D)} \colon \mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{E}}}(C,D \cdot G) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}^{\boldsymbol{E}}}(C \cdot F,D)$ を
元の対応 $\psi_{(C,D)} \colon \sigma \longmapsto \sigma \cdot F \ggg D \cdot \varepsilon$ で定めれば、

\begin{align}
(\varphi_{(C,D)} \ggg \psi_{(C,D)})(\theta)
&=
(C \cdot \eta \ggg \theta \cdot G) \cdot F \ggg D \cdot \varepsilon
\\
&=
C \cdot \eta \cdot F \ggg \theta \cdot (G \cdot F) \ggg D \cdot \varepsilon
\\
&=
C \cdot \eta \cdot F \ggg (C \cdot F) \cdot \varepsilon \ggg \theta \cdot \mathrm{id}_{\boldsymbol{D}}
\\
&=
C \cdot (\eta \cdot F \ggg F \cdot \varepsilon) \ggg \theta \cdot \mathrm{id}_{\boldsymbol{D}}
\\
&=
C \cdot \mathrm{id}_{F} \ggg \theta \cdot \mathrm{id}_{\boldsymbol{D}}
\\
&=
\mathrm{id}_{C \cdot F} \ggg \theta = \theta
\\[2mm]
(\psi_{(C,D)} \ggg \varphi_{(C,D)})(\sigma)
&=
C \cdot \eta \ggg (\sigma \cdot F \ggg D \cdot \varepsilon) \cdot G
\\
&=
C \cdot \eta \ggg \sigma \cdot (F \cdot G) \ggg D \cdot \varepsilon \cdot G
\\
&=
\sigma \cdot \mathrm{id}_{\boldsymbol{C}} \ggg (D \cdot G) \cdot \eta \ggg D \cdot \varepsilon \cdot G
\\
&=
\sigma \cdot \mathrm{id}_{\boldsymbol{C}} \ggg D \cdot (G \cdot \eta \ggg \varepsilon \cdot G)
\\
&=
\sigma \cdot \mathrm{id}_{\boldsymbol{C}} \ggg D \cdot \mathrm{id}_{G}
\\
&=
\sigma \ggg \mathrm{id}_{D \cdot G} = \sigma
\end{align}

であるから、$\varphi_{(C,D)}$ は自然な同型射である。

単項演算子 ${-}^{\cap}$ と ${-}_{\cup}$ を次のように定義しよう。

圏 $\boldsymbol{D}$ の射 $f \in \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d)$ を
射の族 $\varphi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d)$ で
$f^{\cap} = \varphi_{(c,d)}(f) \in \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d)$ と変換する。

圏 $\boldsymbol{C}$ の射 $g \in \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d)$ を
射の族 $\psi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d)$ で
$g_{\cup} = \psi_{(c,d)}(g) \in \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d)$ と変換する。

$\varphi$ と $\psi$ が自然な同型射であることから
${f^{\cap}}_{\cup} = f$ と ${g_{\cup}}^{\cap} = g$ が成り立つ。
つまり ${-^{\cap}}_{\cup}$ と ${-_{\cup}}^{\cap}$ は恒等演算子である。

定義の１つめの等式により ${-^{\cap}}_{\cup}$ が恒等変換となり、
また、２つめの等式により ${-_{\cup}}^{\cap}$ が恒等変換となる。

このことは、ストリング・ダイアグラムで
随伴関手を見直せばより明らかとなるだろう。

カリー化

自然変換の具体例で見たように、
Haskell ではパラメタ多相すなわち型変数により
自然変換を定義する射の族を表現していた。

随伴の定義に用いられる自然変換は
射の族 $\eta_{c} \colon c \longrightarrow G\ (F\ c)$ と射の族 $\varepsilon_{d} \colon F\ (G\ d) \longrightarrow d$
により、もしくは
射の族 $\varphi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d)$ と
射の族 $\psi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d)$ により定まる。

Adjunction

{-# LANGUAGE MultiParamTypeClasses #-}
import Control.Category ((>>>))

class (Functor f, Functor g) => Adjunction f g where
    unit         :: c -> g (f c)
    counit       :: f (g d) -> d
    leftAdjunct  :: (f c -> d) -> (c -> g d)
    rightAdjunct :: (c -> g d) -> (f c -> d)
    {-# MINIMAL (unit, counit) | (leftAdjunct, rightAdjunct) #-}
    unit           = leftAdjunct id
    counit         = rightAdjunct id
    leftAdjunct f  = unit >>> fmap f
    rightAdjunct f = fmap f >>> counit

$\eta_{c}$ と unit、$\varepsilon_{d}$ と counit、
$\varphi_{(c,d)}$ と leftAdjunct、$\psi_{(c,d)}$ と rightAdjunct が
それぞれ対応していることが分かる。

fmap unit >>> counit = id と
unit >>> fmap counit = id が成り立つ
とき、もしくは
leftAdjunct >>> rightAdjunct = id と
rightAdjunct >>> leftAdjunct = id が成り立つ
とき、随伴と言い f $\dashv$ g とあらわす。

f = (,) a および g = (->) a とすれば

カリー化

instance Adjunction ((,) a) ((->) a) where
    unit a b      = (b, a)
    counit (a, f) = f a
    leftAdjunct   = curry >>> flip
    rightAdjunct  = flip >>> uncurry

となり、(,) a $\dashv$ (->) a の随伴関係がある。

unit はタプル生成であり、
counit は関数適用であることが分かる。

leftAdjunct と rightAdjunct はそれぞれ
curry と uncurry に相当する。

leftAdjunct  :: ((a, c) -> d) -> (c -> (a -> d))
rightAdjunct :: (c -> (a -> d)) -> ((a, c) -> d)

まとめ

自然変換の合成がとても複雑に見えて
最初はどうしても抵抗を感じてしまう。

随伴からモナドを構成できるらしいので²、
instance を作ってみると楽しいかもしれない。

これでひとまず基本は把握できたと思うので、
圏論に関する巷の文献を何となく理解できるはず。

もう諦めない圏論入門―関手と自然変換―

目次

自然変換の定義

関手と自然変換

垂直合成

水平合成

恒等変換

関手の圏

双関手

左セクション

右セクション

結合律と単位律

関手と自然変換の合成

自然変換と関手の合成

交替律

自然変換の具体例

恒等関手から List 関手への自然変換

List 関手から Maybe 関手への自然変換

Hom 関手から Hom 関手への自然変換

随伴関手

同型射

同型関手

自然同型

圏同値

定義

別定義

カリー化

まとめ