もう諦めない圏論基礎―高次元圏と変換手―

想定読者と到達目標

「モナドは単位圏から圏の圏へのラックス 2-関手」
であることをもう少しだけ深く理解したい人へ。

ストライプ・ダイアグラムで定義を見ていく。

ただ単にモナドを理解したいだけなのに、
どこか遠くへ来てしまった感はあるけれど¹、
絵を眺めるだけでどこか楽しいかもしれない。

目次

• 圏論入門前の準備運動―集合と写像―
• もう諦めない圏論入門―対象と射―
• もう諦めない圏論入門―圏と関手―
• もう諦めない圏論入門―関手と自然変換―
• もう諦めない圏論付録―ストリング・ダイアグラム―
• もう諦めない圏論基礎―極限からカン拡張へ―
• もう諦めない圏論基礎―モノイドからモナドへ―
• もう諦めない圏論基礎―高次元圏と変換手―
  • ダイアグラムで $2$-$k$-変換手の定義を確認する
  • 厳密 $n$-圏の雰囲気を理解した気になる

高次元圏

圏が対象と射で構成されるのに対して、
厳密 2-圏は対象と 1-射、2-射で構成される。

同様に、厳密 $n$-圏は
対象と 1-射、2-射、$\ldots$、$n$-射で構成される。

$n$ は圏の次元で、通常の圏は厳密 1-圏と言える。

変換手

通常の圏における関手、自然変換を
厳密 1-圏での 1-関手、1-自然変換と呼ぼう。

厳密 2-圏では 2-関手、2-自然変換、2-変更²
厳密 3-圏では 3-関手、3-自然変換、3-変更、3-摂動³
と次元 $n$ の増加と共に変換の種類が増える。

厳密 $n$-圏では $(n+1)$ 種類の変換が存在する。

	$k=0$	$k=1$	$k=2$	$k=3$
$n=1$	1-関手	1-自然変換
$n=2$	2-関手	2-自然変換	2-変更
$n=3$	3-関手	3-自然変換	3-変更	3-摂動

---

$(n+1)$ 種類の変換に $k=0$ から $k=n$ と
番号付けをして $k$-変換手と呼ぶらしい⁴。

	$k=0$	$k=1$	$k=2$	$k=3$
$n=1$	1-0-変換手	1-1-変換手
$n=2$	2-0-変換手	2-1-変換手	2-2-変換手
$n=3$	3-0-変換手	3-1-変換手	3-2-変換手	3-3-変換手

0-変換手 $=$ 関手
1-変換手 $=$ 自然変換
2-変換手 $=$ 変更
3-変換手 $=$ 摂動
のようにいつでも置換可能とする。

高次元圏の圏

圏の圏 $\mathbf{Cat}$ を考えると、
構成要素は圏と関手と自然変換である。

何を対象とし、何を射とするかに応じて
次のように色んな組み合わせで $n$-圏になる。

	圏	関手	自然変換
圏の圏	対象	射
関手の圏		対象	射
圏の 2-圏	対象	1-射	2-射

---

同様に、厳密 2-圏の圏 $2\mathbf{Cat}$ を考えると、
構成要素は 2-圏と 2-関手と 2-自然変換と 2-変更である。

何を対象とし、何を射とするかに応じて
次のように色んな組み合わせで $n$-圏になる。

	2-圏	2-関手	2-自然変換	2-変更
2-圏の圏	対象	射
2-自然変換の圏			対象	射
2-関手の 2-圏		対象	1-射	2-射
2-圏の 3-圏	対象	1-射	2-射	3-射

2-関手を対象とする場合には
2-自然変換を射としても圏にはならず、
2-ICON⁵ と呼ばれる変換を射とすると圏になる。

	2-圏	2-関手	2-ICON
2-関手の圏		対象	射
2-圏の 2-圏	対象	1-射	2-射

---

以下では厳密 2-圏の場合に焦点を当て、
$2$-$k$-変換手(すなわち 2-関手、2-自然変換、2-変更)
をストライプ・ダイアグラムで描いてみよう。

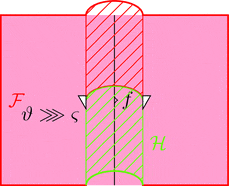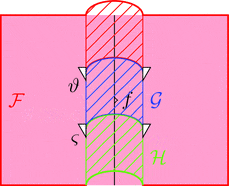
ストライプ・ダイアグラム

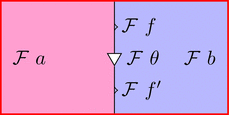
2-圏 $\boldsymbol{\mathcal{C}}$ の対象 $a,b$ および
1-射 $f,f' \colon a \longrightarrow b$ と 2-射 $\theta \colon f \Longrightarrow f'$
をストリング・ダイアグラムで描くと次のようになる。

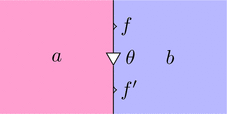
ラックス 2-関手 $(\mathcal{F},\mu,\eta)$ は $\mathcal{F}$ によって
2-圏 $\boldsymbol{\mathcal{C}}$ の対象および 1-射と 2-射を
2-圏 $\boldsymbol{\mathcal{D}}$ の対象 $\mathcal{F}\ a,\mathcal{F}\ b$ および
1-射 $\mathcal{F}\ f,\mathcal{F}\ f' \colon \mathcal{F}\ a \longrightarrow \mathcal{F}\ b$ と
2-射 $\mathcal{F}\ \theta \colon \mathcal{F}\ f \Longrightarrow \mathcal{F}\ f'$ に対応させる。

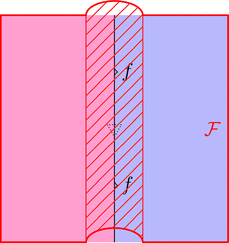
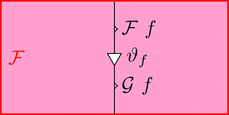
ラックス 2-関手の $\mathcal{F}$ を次のように描く。

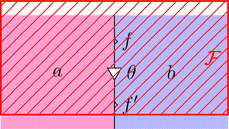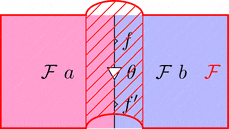
対象も 1-射も 2-射も全部対応させるので
$\mathcal{F}$ を上からかぶせるイメージだ。

ストリングが幅を持ったストライプになるので
ストライプ・ダイアグラムと呼ぶらしい⁶。

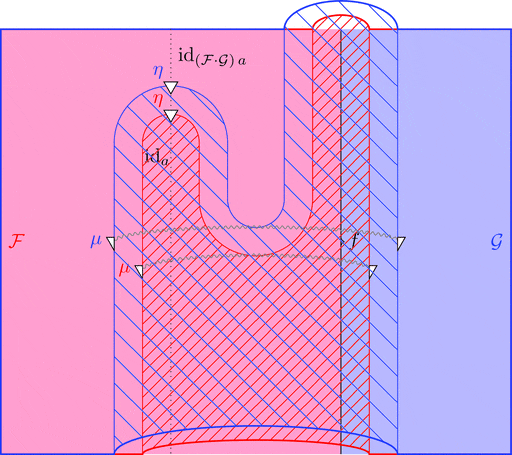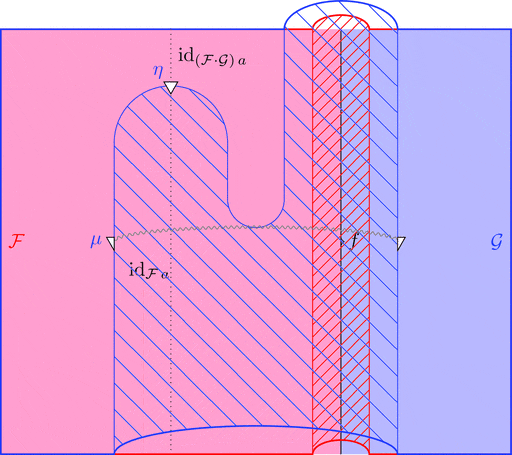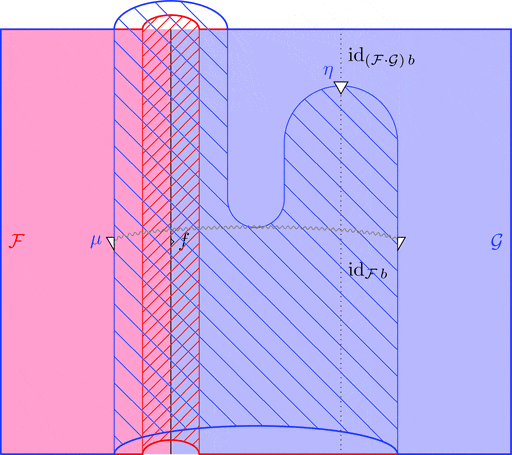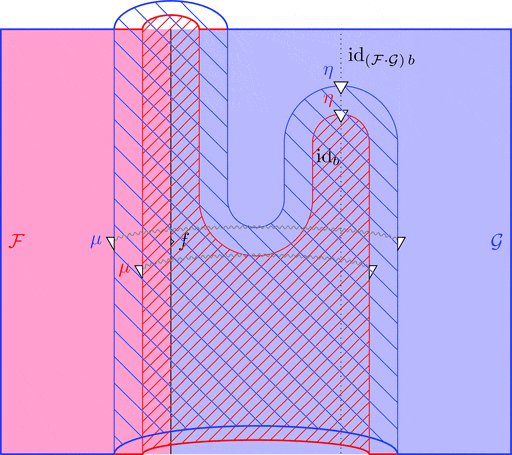
ラックス 2-関手

ラックス 2-関手 $(\mathcal{F},\mu,\eta)$ は
自然変換 $\mu \colon {\mathcal{F}\ -} \cdot {\mathcal{F}\ -} \Longrightarrow \mathcal{F}\ (- \cdot -)$ すなわち
2-射の族 $\mu_{(f,g)} \colon {\mathcal{F}\ f} \cdot {\mathcal{F}\ g} \Longrightarrow \mathcal{F}\ (f \cdot g)$

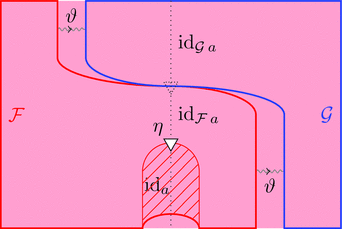
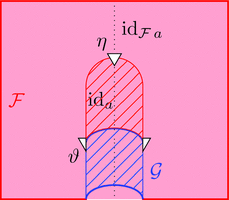
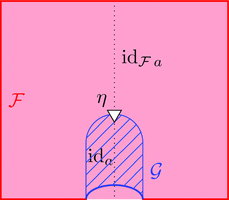
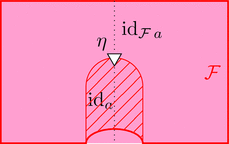
と 2-射 $\eta \colon \mathrm{id}_{\mathcal{F}\ a} \Longrightarrow \mathcal{F}\ \mathrm{id}_{a}$

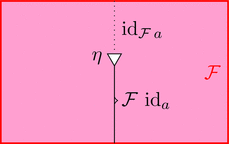
により定まる。
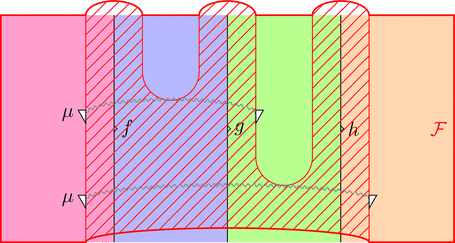
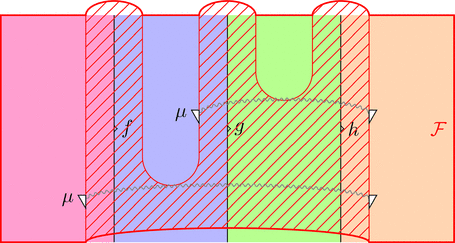
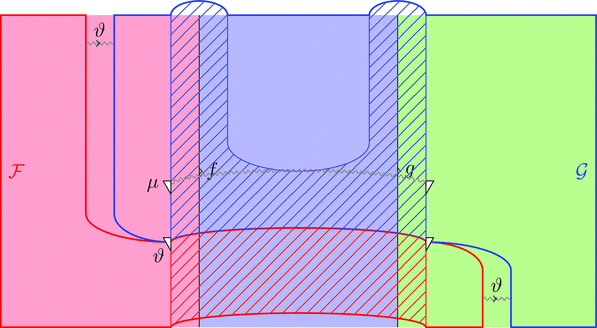
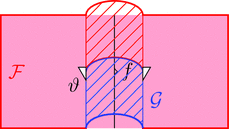
ストライプ・ダイアグラムで描くと以下となる。

ラックス 2-関手の自然変換 $\mu$ を次のように描く。

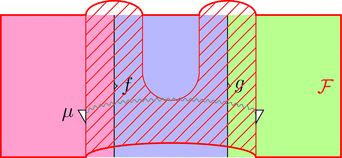
ラックス 2-関手の 2-射 $\eta$ を次のように描く。

自然性

自然変換 $\mu$ に関して、自然変換の定義より
$\mu_{(f,g)} \ggg \mathcal{F}\ (\theta \cdot \sigma) = \mathcal{F}\ \theta \cdot \mathcal{F}\ \sigma \ggg \mu_{(f',g')}$
が成り立ち、ダイアグラム計算では次の変形を行って良い。

---

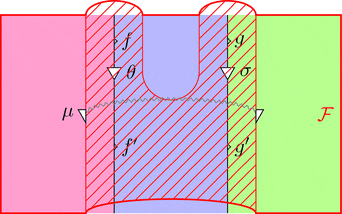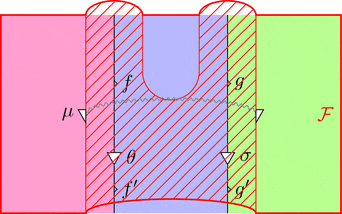
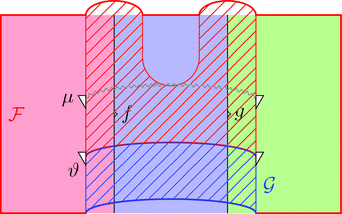
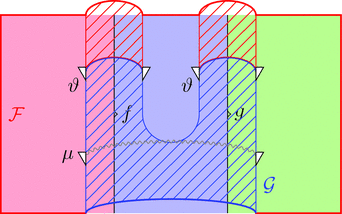
次の２つの条件を満たすとき、
組 $(\mathcal{F},\mu,\eta)$ はラックス 2-関手である。

条件 1

$=$

モナドの結合律のストリング・ダイアグラムとよく似ている。

条件 2

$=$ $=$

モナドの単位律のストリング・ダイアグラムとよく似ている。

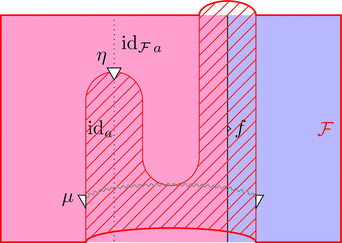
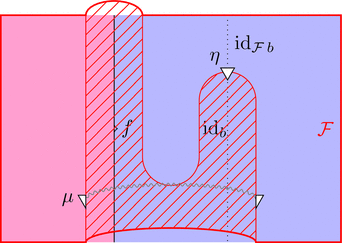
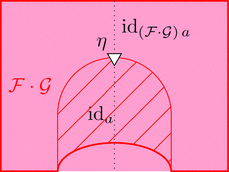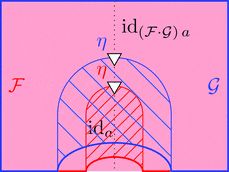
恒等 2-関手

2-関手 $\mathrm{id}_{\mathcal{C}} \colon \boldsymbol{\mathcal{C}} \longrightarrow \boldsymbol{\mathcal{C}}$ を考える。

対象および 1-射と 2-射の対応を
$\mathrm{id}_{\mathcal{C}}\ - = -$ とする。

自然変換 $\mu$ を 2-射の族により
$\mu_{(f,g)} = \mathrm{id}_{f \cdot g}$ と定義し、
2-射を $\eta = \mathrm{id}_{\mathrm{id}_{a}}$ と定義すれば、
組 $(\mathrm{id}_{\mathcal{C}},\mu,\eta)$ は恒等 2-関手である。

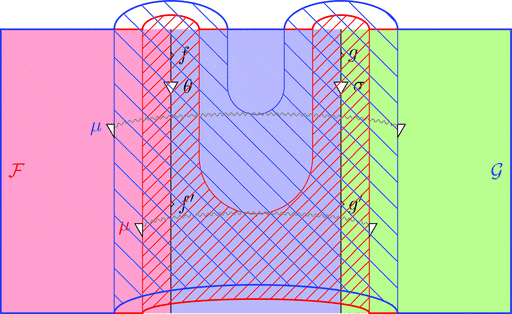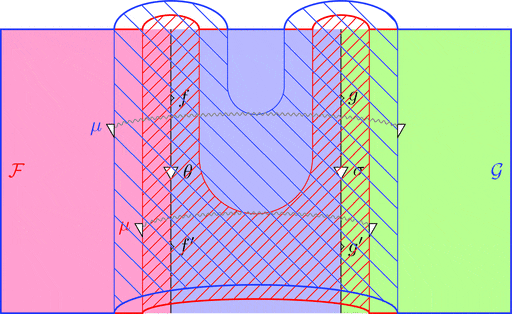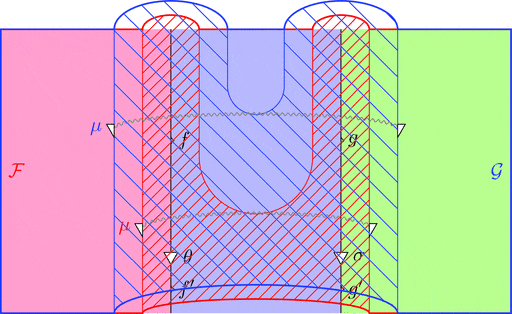
ラックス 2-関手の合成

ラックス 2-関手 $(\mathcal{F},\color{red}{\mu},\color{red}{\eta})$ と
ラックス 2-関手 $(\mathcal{G},\color{blue}{\mu},\color{blue}{\eta})$ の合成
ラックス 2-関手 $(\mathcal{F} \cdot \mathcal{G},\mu,\eta)$ を考える。

対象および 1-射と 2-射の対応を
$(\mathcal{F} \cdot \mathcal{G})\ - = \mathcal{G}\ (\mathcal{F}\ -)$ とする。

$\mu$ を 2-射の族により
$\mu_{(f,g)} = \color{blue}{\mu}_{(\mathcal{F}\ f, \mathcal{F}\ g)} \ggg \mathcal{G}\ \color{red}{\mu}_{(f,g)}$

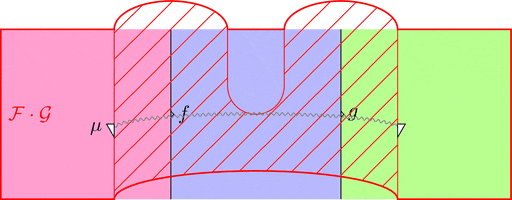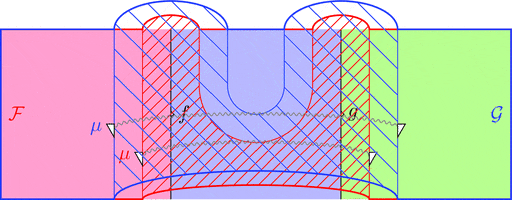
と定義し、2-射を $\eta = \color{blue}{\eta} \ggg \mathcal{G}\ \color{red}{\eta}$

と定義する。

---

次の変形により $\mu$ の自然性が分かる。

次の変形により条件 1が成り立つことが分かる。

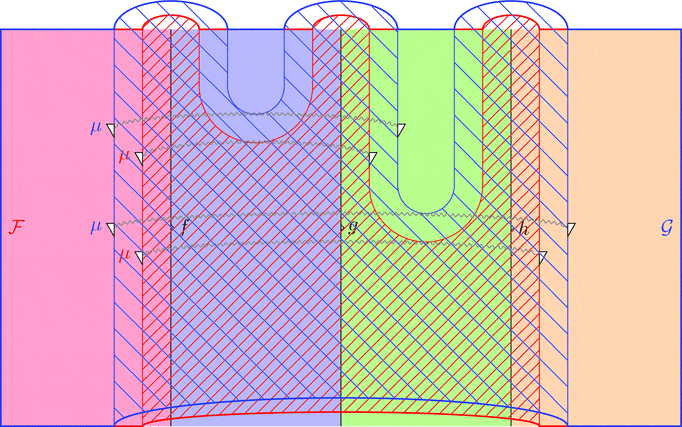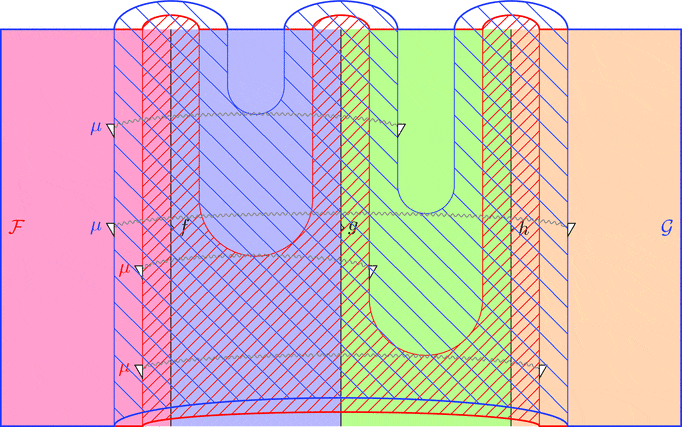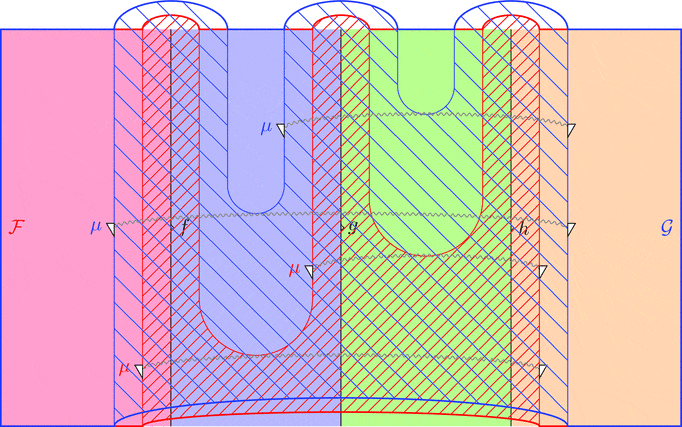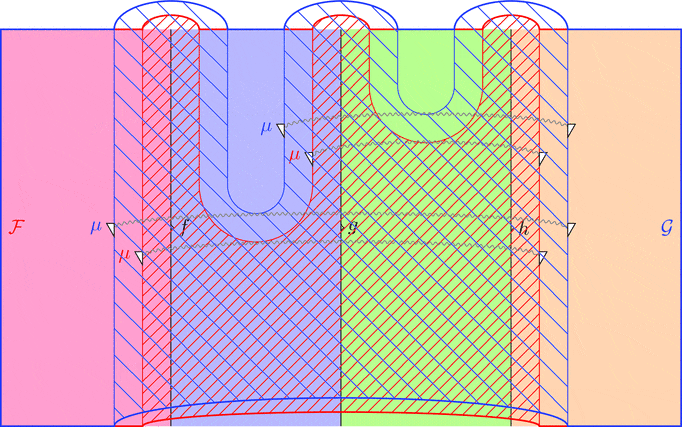
次の変形により条件 2が成り立つことが分かる。

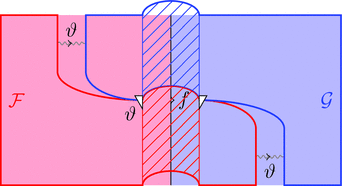
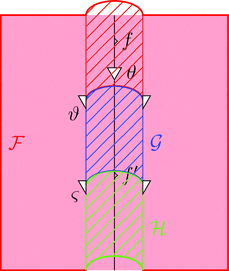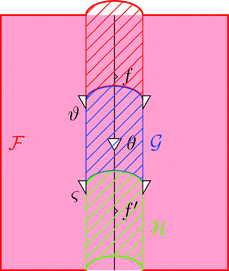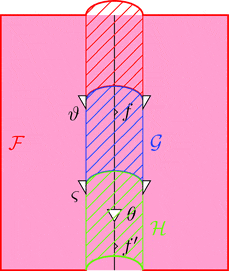
ラックス 2-自然変換

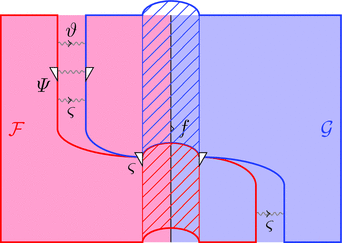
ラックス 2-自然変換 $\vartheta \colon \mathcal{F} \Longrightarrow \mathcal{G}$ は
1-射の族 $\vartheta_{a} \colon \mathcal{F}\ a \longrightarrow \mathcal{G}\ a$

と自然変換 $\vartheta \colon \vartheta_{a} \cdot {\mathcal{G}\ -} \Longrightarrow {\mathcal{F}\ -} \cdot \vartheta_{b}$ すなわち
2-射の族 $\vartheta_{f} \colon \vartheta_{a} \cdot {\mathcal{G}\ f} \Longrightarrow {\mathcal{F}\ f} \cdot \vartheta_{b}$

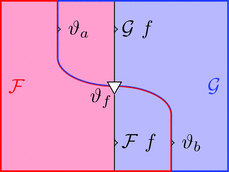
により定まる。
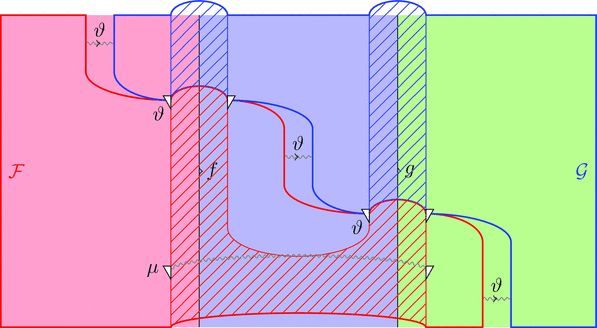
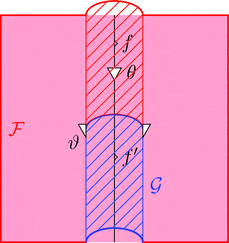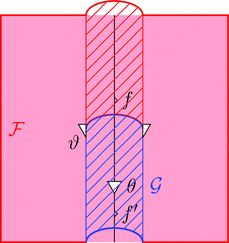
ストライプ・ダイアグラムで描くと以下となる。

ラックス 2-自然変換の 1-射の族 $\vartheta_{a}$ を次のように描く。

ラックス 2-自然変換の自然変換 $\vartheta$ を次のように描く。

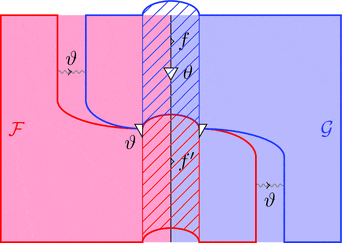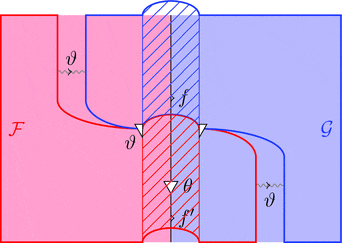
自然性

自然変換 $\vartheta$ に関して、自然変換の定義より
$\vartheta_{f} \ggg \mathcal{F}\ \theta \cdot \vartheta_{b} = \vartheta_{a} \cdot \mathcal{G}\ \theta \ggg \vartheta_{f'}$
が成り立ち、ダイアグラム計算では次の変形を行って良い。

---

次の２つの条件を満たすとき、
$\vartheta$ はラックス 2-自然変換である。

条件 1

$=$

条件 2

$=$

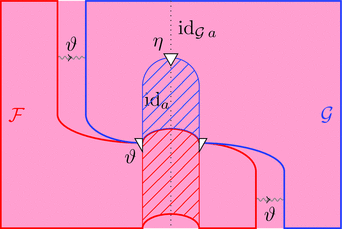
恒等 2-自然変換

2-自然変換 $\mathrm{id}_{\mathcal{F}} \colon \mathcal{F} \Longrightarrow \mathcal{F}$ を考える。

1-射の族 $(\mathrm{id}_{\mathcal{F}})_{a} = \mathrm{id}_{\mathcal{F}\ a}$ と定義し、
2-射の族 $(\mathrm{id}_{\mathcal{F}})_{f} = \mathrm{id}_{\mathcal{F}\ f}$ と定義すれば、
$\mathrm{id}_{\mathcal{F}}$ は恒等 2-自然変換である。

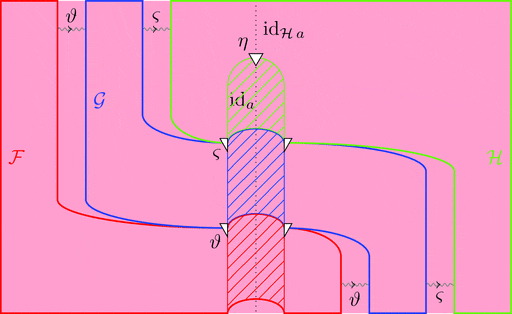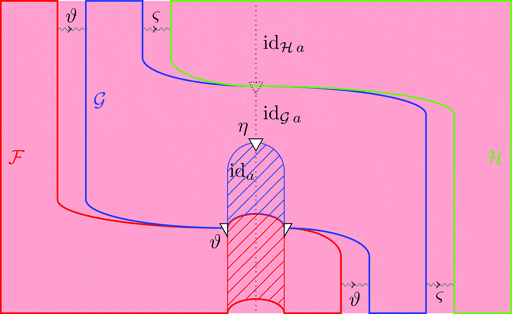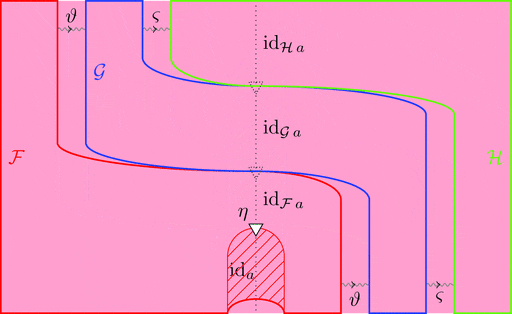
ラックス 2-自然変換の合成

ラックス 2-自然変換 $\vartheta \colon \mathcal{F} \Longrightarrow \mathcal{G}$ と
ラックス 2-自然変換 $\varsigma \colon \mathcal{G} \Longrightarrow \mathcal{H}$ の合成
ラックス 2-自然変換 $\vartheta \cdot \varsigma \colon \mathcal{F} \Longrightarrow \mathcal{H}$ を考える。

1-射の族 $(\vartheta \cdot \varsigma)_{a} = \vartheta_{a} \cdot \varsigma_{a}$ と定義し、
2-射の族 $(\vartheta \cdot \varsigma)_{f} = \vartheta_{a} \cdot \varsigma_{f} \ggg \vartheta_{f} \cdot \varsigma_{b}$ と定義する。

---

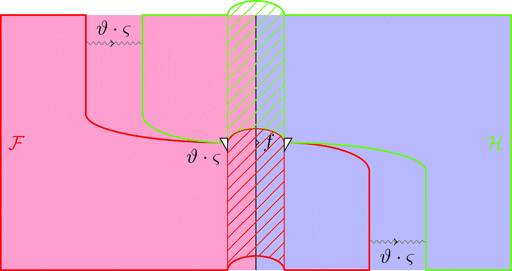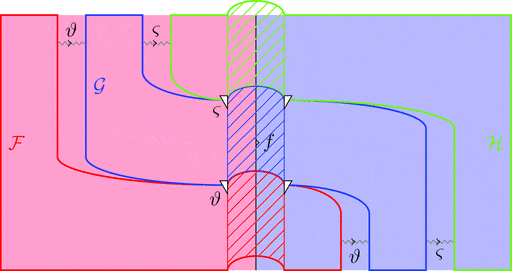
次の変形により $\vartheta \cdot \varsigma$ の自然性が分かる。

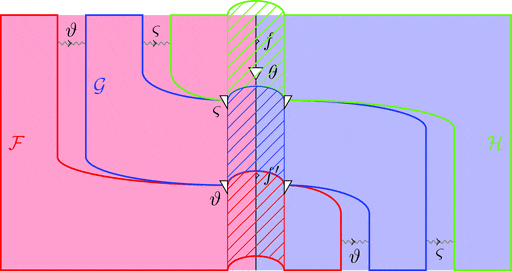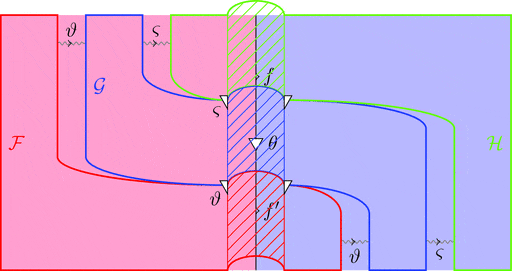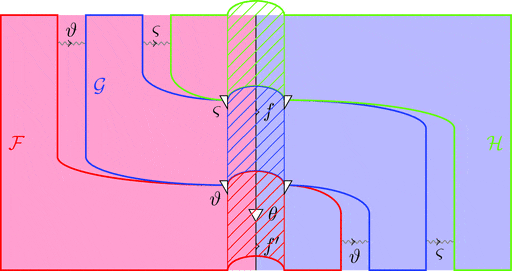
次の変形により条件 1が成り立つことが分かる。

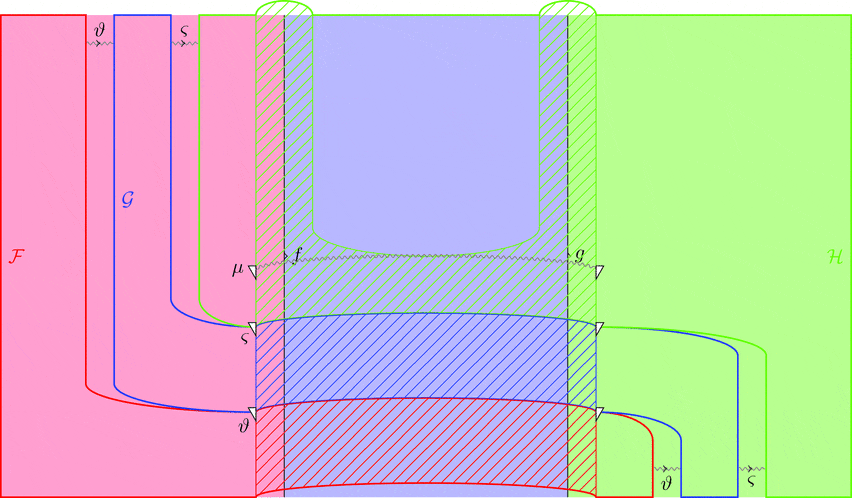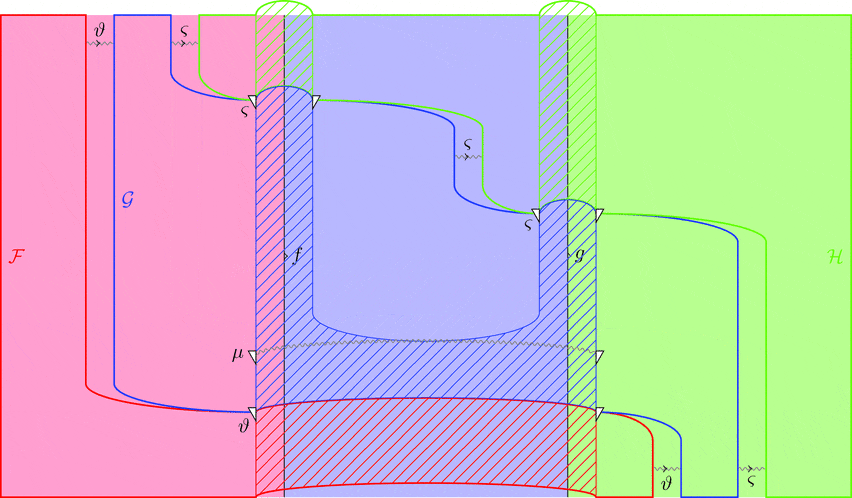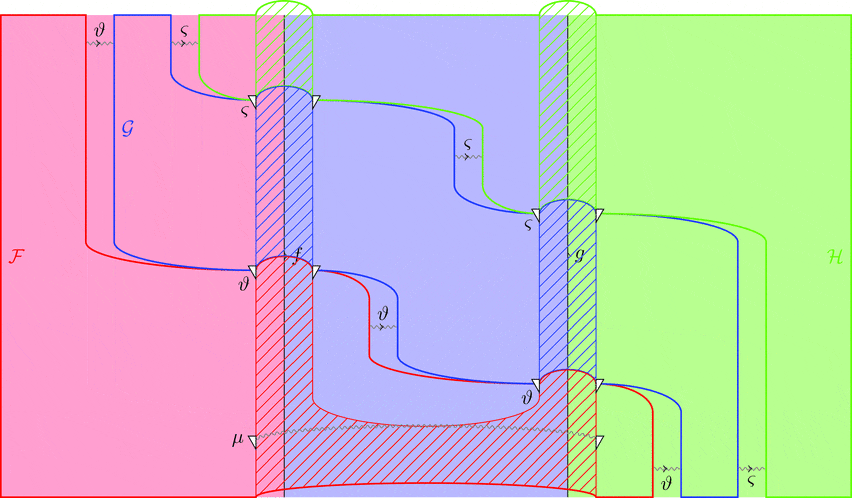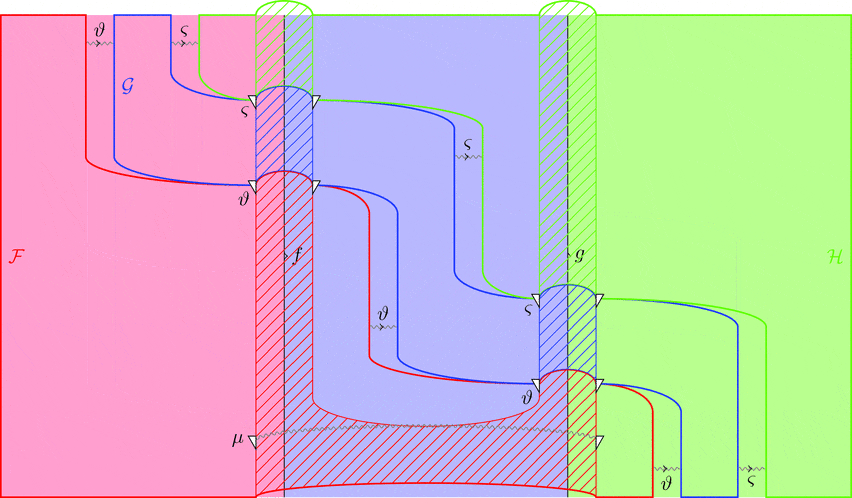
次の変形により条件 2が成り立つことが分かる。

反ラックス 2-自然変換

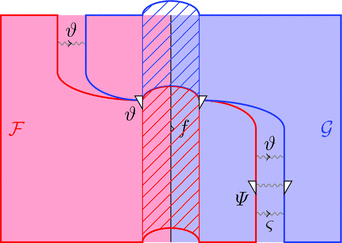
反ラックス 2-自然変換 $\vartheta \colon \mathcal{F} \Longrightarrow \mathcal{G}$ は
1-射の族 $\vartheta_{a} \colon \mathcal{F}\ a \longrightarrow \mathcal{G}\ a$ と
自然変換 $\vartheta \colon {\mathcal{F}\ -} \cdot \vartheta_{b} \Longrightarrow \vartheta_{a} \cdot {\mathcal{G}\ -}$ すなわち
2-射の族 $\vartheta_{f} \colon {\mathcal{F}\ f} \cdot \vartheta_{b} \Longrightarrow \vartheta_{a} \cdot {\mathcal{G}\ f}$

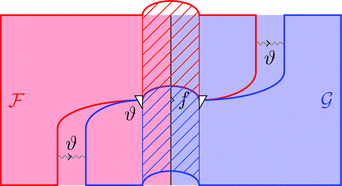
により定まる。

ラックス 2-自然変換とは自然変換 $\vartheta$ の方向が
逆になっているため、反ラックスと呼ばれる。

2-ICON

反ラックス 2-自然変換は
1-射の族 $\vartheta_{a} \colon \mathcal{F}\ a \longrightarrow \mathcal{G}\ a$ と
2-射の族 $\vartheta_{f} \colon {\mathcal{F}\ f} \cdot \vartheta_{b} \Longrightarrow \vartheta_{a} \cdot {\mathcal{G}\ f}$ により定まる。

1-射の族を恒等 1-射で
$\vartheta_{a} = \mathrm{id}_{\mathcal{F}\ a}$ と部分適用した変換を
2-ICON $\vartheta \colon \mathcal{F} \Longrightarrow \mathcal{G}$ と呼ぶ.

ラックス 2-関手による対象の対応が
$\mathcal{F}\ a = \mathcal{G}\ a$ となる。

---

2-ICON $\vartheta \colon \mathcal{F} \Longrightarrow \mathcal{G}$ は
自然変換 $\vartheta \colon \mathcal{F} \Longrightarrow \mathcal{G}$ すなわち
2-射の族 $\vartheta_{f} \colon {\mathcal{F}\ f} \Longrightarrow {\mathcal{G}\ f}$

により定まる。
ストライプ・ダイアグラムで描くと以下となる。

2-ICON の自然変換 $\vartheta$ を次のように描く。

自然性

自然変換 $\vartheta$ に関して、自然変換の定義より
$\mathcal{F}\ \theta \ggg \vartheta_{f'} = \vartheta_{f} \ggg \mathcal{G}\ \theta$
が成り立ち、ダイアグラム計算では次の変形を行って良い。

---

次の２つの条件を満たすとき、
$\vartheta$ は 2-ICON である。

条件 1

$=$

条件 2

$=$

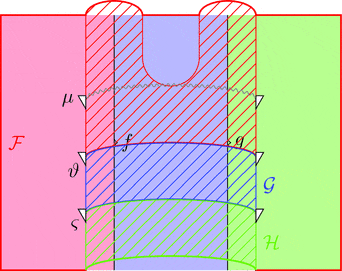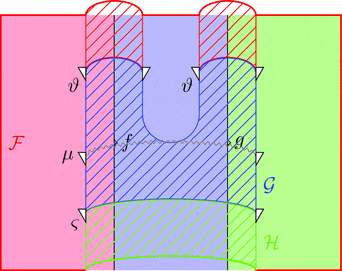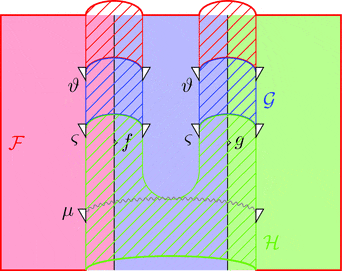
2-ICON の垂直合成

2-ICON $\vartheta \colon \mathcal{F} \Longrightarrow \mathcal{G}$ と
2-ICON $\varsigma \colon \mathcal{G} \Longrightarrow \mathcal{H}$ の垂直合成
2-ICON $\vartheta \ggg \varsigma \colon \mathcal{F} \Longrightarrow \mathcal{H}$ を考える。

2-射の族 $(\vartheta \ggg \varsigma)_{f} = \vartheta_{f} \ggg \varsigma_{f}$ と定義する。

---

次の変形により $\vartheta \ggg \varsigma$ の自然性が分かる。

次の変形により条件 1が成り立つことが分かる。

次の変形により条件 2が成り立つことが分かる。

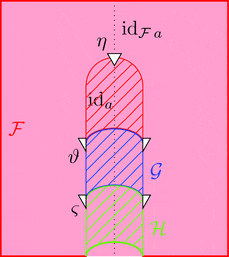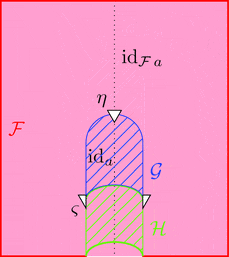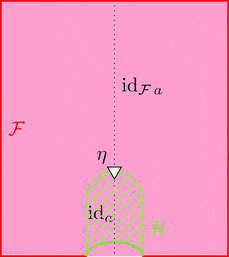
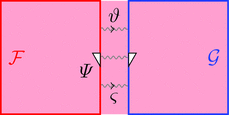
2-変更

2-変更 $\varPsi \colon \vartheta \equiv\!\Rrightarrow \varsigma$ は
2-射の族 $\varPsi_{a} \colon \vartheta_{a} \Longrightarrow \varsigma_{a}$

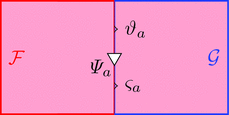
により定まる。
ストライプ・ダイアグラムで描くと以下となる。

2-変更の 2-射の族 $\varPsi_{a}$ を次のように描く。

---

次の１つの条件を満たすとき、
$\varPsi$ は 2-変更である。

条件 1

$=$

恒等 2-変更

2-変更 $\mathrm{id}_{\vartheta} \colon \vartheta \equiv\!\Rrightarrow \vartheta$ を考える。

2-射の族 $(\mathrm{id}_{\vartheta})_{a} = \mathrm{id}_{\vartheta_{a}}$ と定義すれば、
$\mathrm{id}_{\vartheta}$ は恒等 2-変更である。

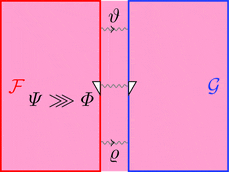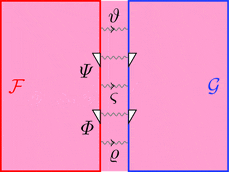
2-変更の垂直合成

2-変更 $\varPsi \colon \vartheta \equiv\!\Rrightarrow \varsigma$ と
2-変更 $\varPhi \colon \varsigma\equiv\!\Rrightarrow \varrho$ の垂直合成
2-変更 $\varPsi \ggg \varPhi \colon \vartheta \equiv\!\Rrightarrow \varrho$ を考える。

2-射の族 $(\varPsi \ggg \varPhi)_{a} = \varPsi_{a} \ggg \varPhi_{a}$ と定義する。

---

次の変形により条件 1が成り立つことが分かる。

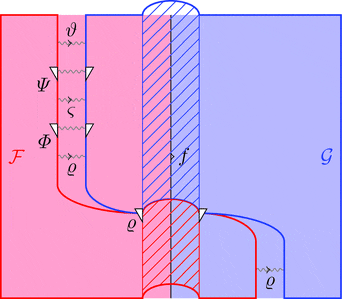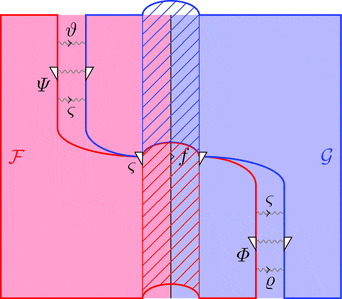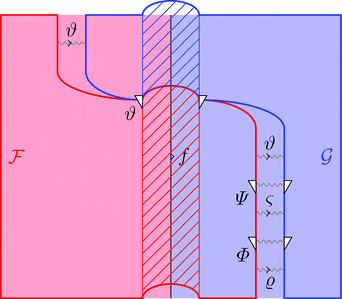
2-変更の水平合成

2-変更 $\varPsi \colon \vartheta \equiv\!\Rrightarrow \vartheta'$ と
2-変更 $\varPhi \colon \varsigma \equiv\!\Rrightarrow \varsigma'$ の水平合成
2-変更 $\varPsi \cdot \varPhi \colon \vartheta \cdot \varsigma \equiv\!\Rrightarrow \vartheta' \cdot \varsigma'$ を考える。

2-射の族 $(\varPsi \cdot \varPhi)_{a} = \varPsi_{a} \cdot \varPhi_{a}$ と定義する。

---

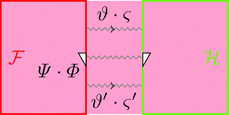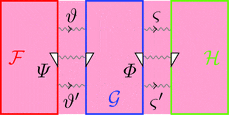
次の変形により条件 1が成り立つことが分かる。

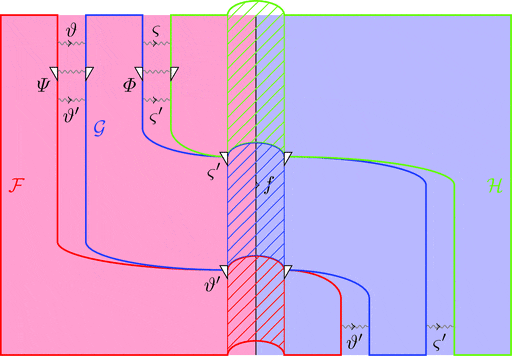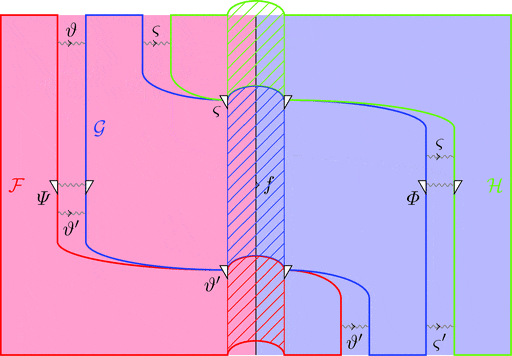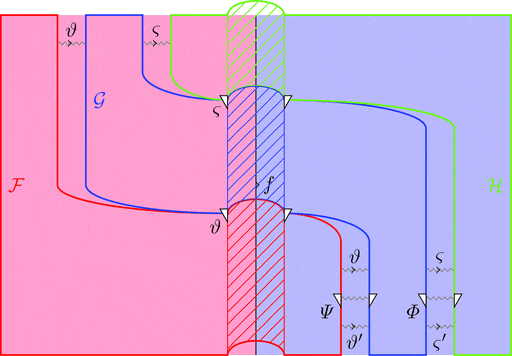
厳密 2-圏の圏

厳密 2-圏の圏 $2\mathbf{Cat}$ は
[厳密 2-圏]
(https://qiita.com/norkron/items/aff3ce925edc6be74923#厳密-2-圏)を対象とし、
ラックス 2-関手を射とする。

ラックス 2-自然変換の圏

ラックス 2-自然変換の圏 $\mathcal{D}^\mathcal{C}(\mathcal{F},\mathcal{G})$ は
ラックス 2-自然変換を対象とし、
2-変更を射とする。

ラックス 2-関手の厳密 2-圏

ラックス 2-関手の厳密 2-圏 $\mathcal{D}^\mathcal{C}$ は
ラックス 2-関手を対象とし、
各対象 $\mathcal{F}, \mathcal{G} \in \mathrm{Obj}(\mathcal{D}^\mathcal{C})$ に対して圏 $\mathcal{D}^\mathcal{C}(\mathcal{F},\mathcal{G})$ が存在し、
対象 $\vartheta,\varsigma \in \mathrm{Obj}(\mathcal{D}^\mathcal{C}(\mathcal{F},\mathcal{G}))$ を 1-射 $\vartheta,\varsigma \colon \mathcal{F} \longrightarrow \mathcal{G}$ と呼び
射 $\varPsi \in \mathrm{Mor}(\mathcal{D}^\mathcal{C}(\mathcal{F},\mathcal{G}))$ を 2-射 $\varPsi \colon \vartheta \Longrightarrow \varsigma$ と呼ぶ。

また、双関手 $-\cdot- \colon \mathcal{D}^\mathcal{C}(\mathcal{F},\mathcal{G}) \times \mathcal{D}^\mathcal{C}(\mathcal{G},\mathcal{H}) \longrightarrow \mathcal{D}^\mathcal{C}(\mathcal{F},\mathcal{H})$ と
恒等 1-射 $\mathrm{id}_{\mathcal{F}} \in \mathrm{Obj}(\mathcal{D}^\mathcal{C}(\mathcal{F},\mathcal{F}))$ が存在する。

$-\cdot-$ が関手であることを確認できる。

1. （恒等射の保存）
   $(\mathrm{id}_{\vartheta} \cdot \mathrm{id}_{\varsigma})_{a} = (\mathrm{id}_{\vartheta})_{a} \cdot (\mathrm{id}_{\varsigma})_{a} = \mathrm{id}_{\vartheta_{a}} \cdot \mathrm{id}_{\varsigma_{a}}$
   $= \mathrm{id}_{\vartheta_{a} \cdot \varsigma_{a}} = \mathrm{id}_{(\vartheta\ \cdot \varsigma)_{a}} = (\mathrm{id}_{\vartheta\ \cdot \varsigma})_{a}$
   すなわち $\mathrm{id}_{\vartheta} \cdot \mathrm{id}_{\varsigma} = \mathrm{id}_{\vartheta\ \cdot \varsigma}$ が成り立つ。

2. （合成の保存）
   $((\varPsi \ggg \varPsi') \cdot (\varPhi \ggg \varPhi'))_{a} = (\varPsi \ggg \varPsi')_{a} \cdot (\varPhi \ggg \varPhi')_{a}$
   $= (\varPsi_{a} \ggg \varPsi'_{a}) \cdot (\varPhi_{a} \ggg \varPhi'_{a}) = \varPsi_{a} \cdot \varPhi_{a} \ggg \varPsi'_{a} \cdot \varPhi'_{a}$
   $= (\varPsi \cdot \varPhi)_{a} \ggg (\varPsi' \cdot \varPhi')_{a} = (\varPsi \cdot \varPhi \ggg \varPsi' \cdot \varPhi')_{a}$
   すなわち $(\varPsi \ggg \varPsi') \cdot (\varPhi \ggg \varPhi') = \varPsi \cdot \varPhi \ggg \varPsi' \cdot \varPhi'$ が成り立つ。

結合律と単位律が成り立つ。

1. （結合律）
   $((\vartheta \cdot \varsigma) \cdot \varrho)_{a} = (\vartheta \cdot \varsigma)_{a} \cdot \varrho_{a} = (\vartheta_{a} \cdot \varsigma_{a}) \cdot \varrho_{a}$
   $= \vartheta_{a} \cdot (\varsigma_{a} \cdot \varrho_{a}) = \vartheta_{a} \cdot (\varsigma \cdot \varrho)_{a} = (\vartheta \cdot (\varsigma \cdot \varrho))_{a}$
   $((\varPsi \cdot \varPhi) \cdot \varGamma)_{a} = (\varPsi \cdot \varPhi)_{a} \cdot \varGamma_{a} = (\varPsi_{a} \cdot \varPhi_{a}) \cdot \varGamma_{a}$
   $= \varPsi_{a} \cdot (\varPhi_{a} \cdot \varGamma_{a}) = \varPsi_{a} \cdot (\varPhi \cdot \varGamma)_{a} = (\varPsi \cdot (\varPhi \cdot \varGamma))_{a}$

2. （単位律）
   $(\mathrm{id}_{\mathcal{F}} \cdot \vartheta)_{a} = (\mathrm{id}_{\mathcal{F}})_{a} \cdot \vartheta_{a} = \mathrm{id}_{\mathcal{F\ a}} \cdot \vartheta_{a} = \vartheta_{a}$
   $(\vartheta \cdot \mathrm{id}_{\mathcal{G}})_{a} = \vartheta_{a} \cdot (\mathrm{id}_{\mathcal{G}})_{a} = \vartheta_{a} \cdot \mathrm{id}_{\mathcal{G\ a}} = \vartheta_{a}$
   $(\mathrm{id}_{\mathrm{id}_{\mathcal{F}}} \cdot \varPsi)_{a} = (\mathrm{id}_{\mathrm{id}_{\mathcal{F}}})_{a} \cdot \varPsi_{a} = \mathrm{id}_{(\mathrm{id}_{\mathcal{F}})_{a}} \cdot \varPsi_{a} = \mathrm{id}_{\mathrm{id}_{\mathcal{F}\ a}} \cdot \varPsi_{a} = \varPsi_{a}$
   $(\varPsi \cdot \mathrm{id}_{\mathrm{id}_{\mathcal{G}}})_{a} = \varPsi_{a} \cdot (\mathrm{id}_{\mathrm{id}_{\mathcal{G}}})_{a} = \varPsi_{a} \cdot \mathrm{id}_{(\mathrm{id}_{\mathcal{G}})_{a}} = \varPsi_{a} \cdot \mathrm{id}_{\mathrm{id}_{\mathcal{G}\ a}} = \varPsi_{a}$

ラックス 2-関手の圏

ラックス 2-関手の圏 $\mathbf{ICON}(\boldsymbol{\mathcal{C}},\boldsymbol{\mathcal{D}})$ は
ラックス 2-関手を対象とし、
2-ICON を射とする。

まとめ

2-圏の変換手を全て把握したことで、
ラックス 2-関手に親しめた気がする。

モノイド圏は対象が１つな 2-圏なので
同様にストライプ・ダイアグラムで描ける。

モノイド関手とはラックス 2-関手で
モノイド自然変換とは 2-ICON である⁷。

1. この記事で直接的に Haskell は登場しないが、圏論を通して間接的に Haskell っぽいと考える(シリーズものは何となくタグを揃えたいので)。 ↩

2. modification ↩

3. perturbation ↩

4. 檜山正幸のキマイラ飼育記 (はてなBlog)「変換手〈transfor〉は要らないだろう」(2019-08-20) ↩

5. Identity Component Oplax Natural-transformation ↩

6. 檜山正幸のキマイラ飼育記 (はてなBlog)「モノイド関手／ラックス・モノイド関手とその実例」(2016-03-23) ↩

7. nLab「lax natural transformation」 ↩