圏論入門前の準備運動―集合と写像―

想定読者と到達目標

Haskell 覚えつつ圏論も一緒に勉強しよう
と思っていたけど結局は圏論に手も足も出ず、
Haskell はある程度できるようになった人へ¹。

圏論とは何なのかを断片的にでも理解して、
自分が何をやってるのかを多少は把握しながら
圏論に入門できるようにするための準備運動。

目次

• 圏論入門前の準備運動―集合と写像―
  • 写像とモノイドの概念を受け入れる
  • 圏論が集合論の一般化であることを理解した気になる
• もう諦めない圏論入門―対象と射―
• もう諦めない圏論入門―圏と関手―
• もう諦めない圏論入門―関手と自然変換―
• もう諦めない圏論付録―ストリング・ダイアグラム―
• もう諦めない圏論基礎―極限からカン拡張へ―
• もう諦めない圏論基礎―モノイドからモナドへ―
• もう諦めない圏論基礎―高次元圏と変換手―

集合と写像

集合や写像とは何なのか、詳細に関しては
検索すれば幾らでも出てくるので省略する。

ここでは、写像が元の対応により
次のように定められることが分かれば良い。

---

集合 $A$ と集合 $B$ があるとする。

集合 $A$ から集合 $B$ への
写像 $f \colon A \longrightarrow B$ を考える。

元 $a \in A$ と元 $b \in B$ として、
元の対応 $f \colon a \longmapsto b$ により
写像 $f$ は定められる。

型と関数

集合を型、写像を関数、元を値
にそれぞれ読み替えてみよう。

写像を定めることは、以下のように
関数を定めることと同様だと分かる。

Hask

import Data.Char

f :: Char -> Int
f = const 0

g :: Char -> Int
g = (+ (-65)) . ord

h :: Int -> Bool
h 0 = True
h _ = False

idChar :: Char -> Char
idChar = id

idInt :: Int -> Int
idInt = id

idBool :: Bool -> Bool
idBool = id

---

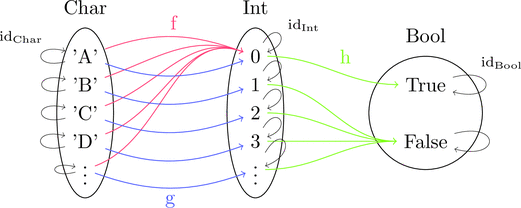
絵で描くとこんな感じになる。

id は恒等写像に相当する。

---

丸で囲まれた元の複雑な構造を潰して点 $\bullet$ とみなすと

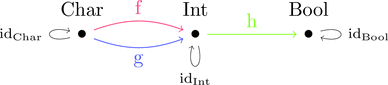
のように単純な形が浮き彫りとなる。

こうして、元(すなわち値)という内部構造に触れず
写像(すなわち関数)だけ扱う考え方が圏論といえる。

---

元の対応により写像は定義されるので、
元に触れなければ何も分からない気がする。

しかし、写像だけで意外と何とかなるもので
具体例を通してそれを確認してみようと思う。

モノイド

モノイドとは何なのか詳細に関しては
検索すれば幾らでも出てくるので省略する。

ここでは、モノイドが元を用いた記述で
次のように定義されることが分かれば良い。

---

集合 $S$ に
写像 $\diamond \colon S \times S \longrightarrow S$ と
単位元 $e \in S$ の情報を加える。

次の２つの条件を満たすとき、
組 $(S,\diamond,e)$ はモノイドである。

1. （結合律）$(a \diamond b) \diamond c = a \diamond (b \diamond c)$ が成り立つ。

2. （単位律）$e \diamond a = a \diamond e = a$ が成り立つ。

ここで、$S \times S$ は直積集合をあらわしている。

モノイド則

Haskell では、
集合(すなわち型) s に
写像(すなわち関数) (<>) :: s -> s -> s と
単位元(すなわち値) e :: s の情報を加える。

Monoid

import Prelude hiding (Monoid(..))

class Monoid s where
    (<>) :: s -> s -> s
    e    :: s

このときモノイド則は以下となる。

1. （結合律）(a <> b) <> c $=$ a <> (b <> c)

2. （単位律）e <> a $=$ a <> e $=$ a

---

上記の定義では結合律と単位律が
元(すなわち値)を用いて記述されている。

これを写像(すなわち関数)を用いて記述し、
写像だけで意外と何とかなることを感じたい。

モノイドの具体例

集合(すなわち型)として $\mathrm{Bool}$ を考える。
元(すなわち値)は $\mathrm{True}$ と $\mathrm{False}$ のみで単純だ。

写像(すなわち関数)として論理積 $\&\&$ を考えて
単位元(すなわち値)を $\mathrm{True}$ とすれば、
組 $(S,\&\&,\mathrm{True})$ はモノイドである。

---

Haskell で書くと以下となる。

All

import Prelude hiding (Monoid(..))
import Control.Arrow ((>>>), (***))

alpha :: ((a, b), c) -> (a, (b, c))
alpha ((a ,b), c) = (a, (b, c))

lambda :: ((), b) -> b
lambda (_, b) = b

rho :: (a, ()) -> a
rho (a, _) = a

class Monoid s where
    (<>) :: s -> s -> s
    e    :: s
    mu   :: (s, s) -> s
    eta  :: () -> s
    {-# MINIMAL ((<>), e) | (mu, eta) #-}
    (<>)  = curry mu
    e     = eta ()
    mu    = uncurry (<>)
    eta _ = e

instance Monoid Bool where
    e    = True
    (<>) = (&&)

結合律と単位律を関数だけで記述するために
alpha、lambda、rho、mu、eta
などの関数たちをここで準備している。

>>> は写像の合成を
*** は写像の直積をそれぞれあらわす。

---

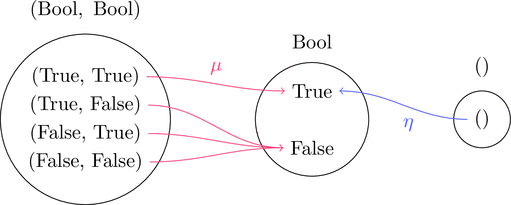
$\mu$ と $\eta$ を絵で描くとこんな感じになる。

単集合からの写像 $\eta$ が単位元を示しているのが分かる。

---

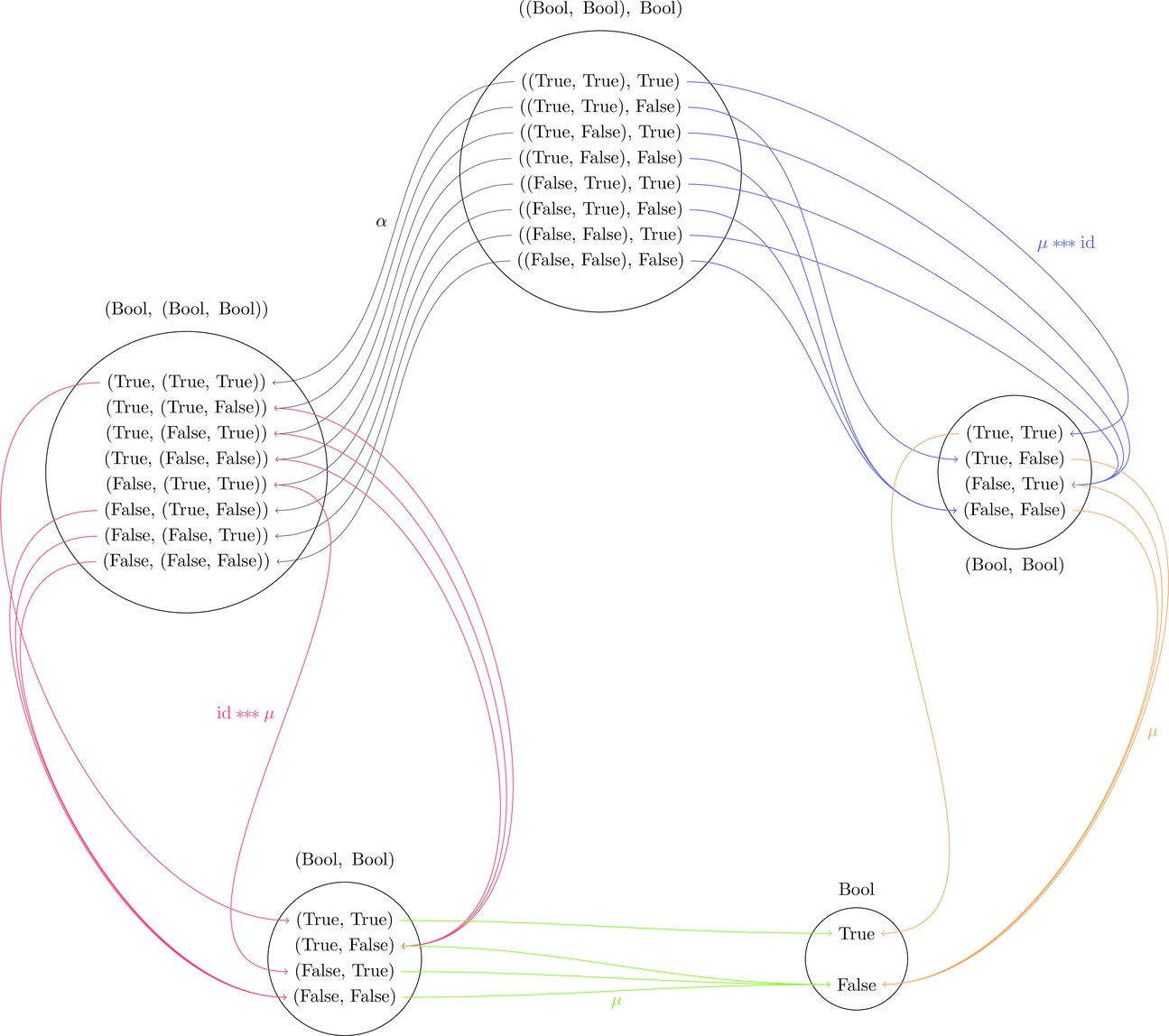
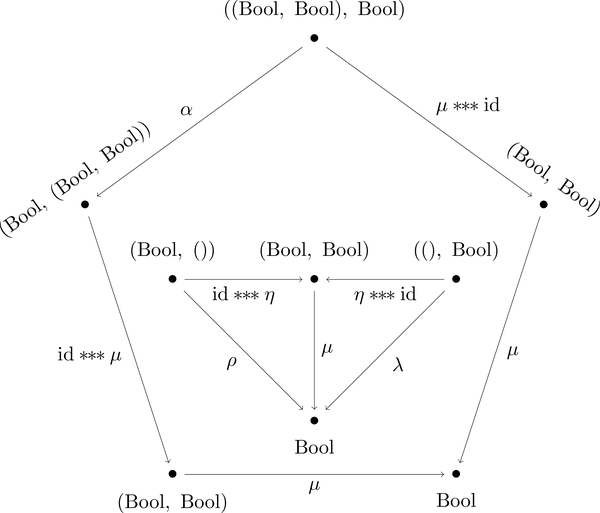
結合律を絵で描くとこんな感じになる。

五角形の一番上の頂点から左回りと右回りに矢印を辿れる。
２つの合成写像が一致することをもって結合律をあらわしている。

すなわち、次の等式が成り立つことを絵であらわしている。
mu***id >>> mu $=$ alpha >>> id***mu >>> mu

---

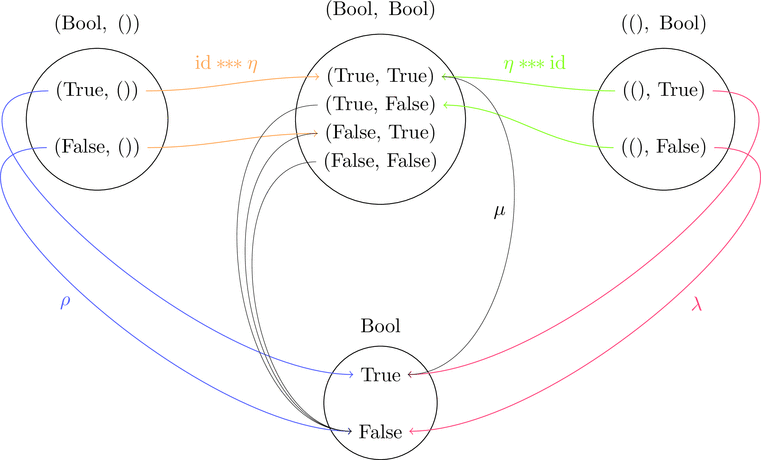
単位律を絵で描くとこんな感じになる。

写像をどのように合成しても、
始域と終域がそれぞれ同じ写像は全て一致することが分かる。

すなわち、次の等式が成り立つことを絵であらわしている。
eta***id >>> mu $=$ lambda と id***eta >>> mu $=$ rho

---

丸で囲まれた元の複雑な構造を潰して点 $\bullet$ とみなすと、
結合律と単位律をあらわす２つの図は次のようになる。

これは、次の２つの条件を図であらわしている。

1. （結合律）mu***id >>> mu $=$ alpha >>> id***mu >>> mu

2. （単位律）eta***id >>> mu $=$ lambda と id***eta >>> mu $=$ rho

---

元(すなわち値)を用いることなく、
写像(すなわち関数)だけで結合律と単位律が記述できた。

構造を潰して点 $\bullet$ とみなすことで
どんなモノイドも同じ図であらわすことができる。

集合と写像の言葉で同じことを繰り返し、
写像だけを用いてモノイドを定義してみよう。

モノイド再び

集合 $S$に
写像 $\mu \colon S \times S \longrightarrow S$ と
写像 $\eta \colon \{*\} \longrightarrow S$ の情報を加える。

次の２つの条件を満たすとき、
組 $(S,\mu,\eta)$ はモノイドである。

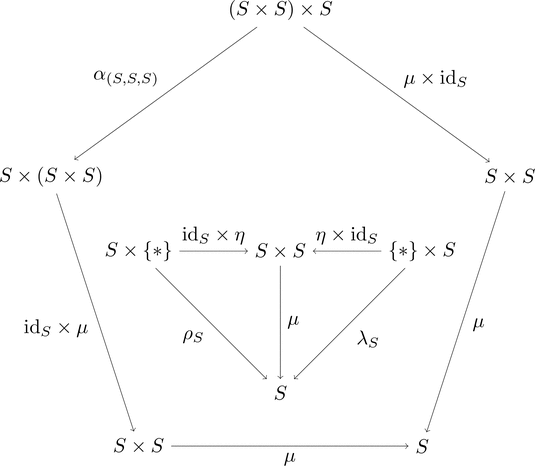
1. （結合律）$\mu \times \mathrm{id}_{S} \ggg \mu = \alpha_{(S,S,S)} \ggg \mathrm{id}_{S} \times \mu \ggg \mu$ が成り立つ。

2. （単位律）$\eta \times \mathrm{id}_{S} \ggg \mu = \lambda_{S}$ と $\mathrm{id}_{S} \times \eta \ggg \mu = \rho_{S}$ が成り立つ。

写像 $\alpha_{(S,S,S)} \colon (S \times S) \times S \longrightarrow S \times (S \times S)$ を
元の対応 $\alpha_{(S,S,S)} \colon ((a,b),c) \longmapsto (a,(b,c))$ で
写像 $\lambda_{S} \colon \{*\} \times S \longrightarrow S$ を元の対応 $\lambda_{S} \colon (*,b) \longmapsto b$ で
写像 $\rho_{S} \colon S \times \{*\} \longrightarrow S$ を元の対応 $\rho_{S} \colon (a,*) \longmapsto a$ で
それぞれ定義する。

$\{*\}$ は元が１つの集合すなわち単集合である。

$\ggg$ は写像の合成をあらわし、
$\times$ は集合または写像の直積をあらわす。

---

結合律と単位律を図で描くと次のようになる。

図中の写像を合成した結果として、
始域と終域がそれぞれ同じ写像は全て一致する。

写像の等価性

写像 $f \colon A \longrightarrow B$ と写像 $g \colon A \longrightarrow B$ が等しい
つまり $f = g$ の意味を最後に考えてみよう。

任意の元 $a \in A$ に対して $f(a) = g(a)$ が成り立つとき
写像 $f$ と $g$ は等しいと言い、これを $f = g$ と書く。

写像だけを用いて、元に触れないとは何だったのか。
誠実に言えば、元に「陽に」触れないとすべきだろう。

---

$f$ や $g$ として写像だけを考えるのであれば
元を「陽に」用いるモノイドの定義で何も問題はない。

$f$ や $g$ として $f = g$ が定まる何かを考えるとき
元を「陰に」用いるモノイド再びの定義が意味を持つ。

この何かを射と呼び、射でモノイドを記述できれば
より一般的なモノイド対象という概念を定められる。

まとめ

集合と写像のことはみんな知ってるはずなので、
圏論を集合論の一般化と捉えると良い気がする。

ただ、具体例に固執すると誤解の恐れもあるので、
抽象的に群の一般化として捉える²ことも必要かも。

	１つの集合	複数の集合
逆元あり	群	グルーポイド
逆元なし	モノイド	圏

矢印はベクトルだけどベクトルは矢印とは限らない
みたいな感じで良いんじゃないかと思います。

1. 関数の概念が分かれば良いので、特に言語は問わないような気もする。 ↩

2. 雑文集「群から圏へ」(2000-02-21) ↩