想定読者と到達目標
Data.Functor.Kan.Ranや
Data.Functor.Kan.Lanで定義されている
右カン拡張や左カン拡張を
何となく理解してみたい人へ。
圏論で重要となるらしい普遍性の概念を、
とあるコンマ圏の終対象や始対象として、
統一的に扱えるようになるかもしれない。
目次
- 圏論入門前の準備運動―集合と写像―
- もう諦めない圏論入門―対象と射―
- もう諦めない圏論入門―圏と関手―
- もう諦めない圏論入門―関手と自然変換―
- もう諦めない圏論付録―ストリング・ダイアグラム―
-
もう諦めない圏論基礎―極限からカン拡張へ―
- コンマ圏の終対象や始対象として諸概念を捉える
- カン拡張が極限であることを理解した気になる
- もう諦めない圏論基礎―モノイドからモナドへ―
- もう諦めない圏論基礎―高次元圏と変換手―
対角関手
$\boldsymbol{C}$ を圏として関手 $\varDelta \colon \boldsymbol{C} \longrightarrow \boldsymbol{C} \times \boldsymbol{C}$ を考える。
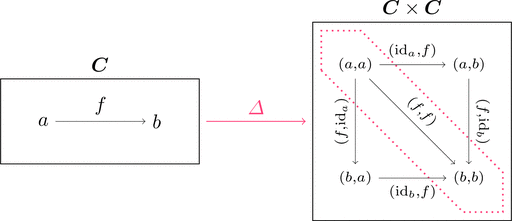
対象の対応 $\varDelta\ a = (a,a) \in \mathrm{Obj}(\boldsymbol{C} \times \boldsymbol{C})$ と
射の対応 $\varDelta\ f = (f,f) \in \mathrm{Mor}(\boldsymbol{C} \times \boldsymbol{C})$ で関手は定義される。
$\varDelta\ a$ は第1成分も第2成分も $a$ なので、
引数1と引数2に対して $a$ を返すような
定数関数と思えるだろう。$\varDelta\ f$ も同様だ。
圏の平方
格上げにより、1点離散圏を $\mathbf{1}$ として、
対象 $\mathrm{Obj}(\boldsymbol{C}) \ni a$ を
関手 $a \colon \mathbf{1} \longrightarrow \boldsymbol{C}$ とみなし、
射 $\mathrm{Mor}(\boldsymbol{C}) \ni f \colon a \longrightarrow b$ を
自然変換 $f \colon a \Longrightarrow b$ とみなせる。
同様に、2点離散圏を $\mathbf{2}$ として、
対象 $\mathrm{Obj}(\boldsymbol{C}\times\boldsymbol{C}) \ni (a_{1},a_{2})$ を
関手 $(a_{1},a_{2}) \colon \mathbf{2} \longrightarrow \boldsymbol{C}$ とみなし、
射 $\mathrm{Mor}(\boldsymbol{C}\times\boldsymbol{C}) \ni (f_{1},f_{2}) \colon (a_{1},a_{2}) \longrightarrow (b_{1},b_{2})$ を
自然変換 $(f_{1},f_{2}) \colon (a_{1},a_{2}) \Longrightarrow (b_{1},b_{2})$ とみなせる。
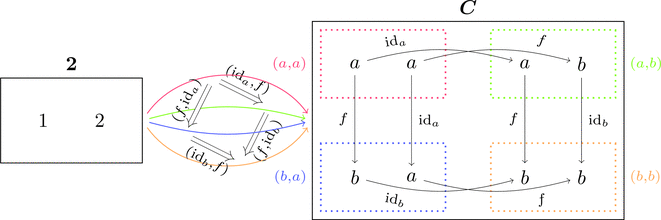
対象の対応 $(a_{1},a_{2})\ i = a_{i}$ と
射の対応 $(a_{1},a_{2})\ \mathrm{id}_{i} = \mathrm{id}_{a_{i}}$ により関手を
射の族 $(f_{1},f_{2})_{i} = f_{i}$ により自然変換を
それぞれ定める。$\mathrm{Obj}(\mathbf{2}) \ni i = 1,2$ である。
1点離散圏を $\mathbf{1}$ とすると格上げにより、
対象 $\mathrm{Obj}(\boldsymbol{C}) \ni a$ と
関手 $\mathrm{Obj}(\boldsymbol{C}^{\mathbf{1}}) \ni a \colon \mathbf{1} \longrightarrow \boldsymbol{C}$ が
射 $\mathrm{Mor}(\boldsymbol{C}) \ni f \colon a \longrightarrow b$ と
自然変換 $\mathrm{Mor}(\boldsymbol{C}^{\mathbf{1}}) \ni f \colon a \Longrightarrow b$ が
それぞれ対応し圏同型 $\boldsymbol{C} \cong \boldsymbol{C}^{\mathbf{1}}$ となる。
2点離散圏を $\mathbf{2}$ とすると圏の平方により、
対象 $\mathrm{Obj}(\boldsymbol{C}\times\boldsymbol{C}) \ni (a_{1},a_{2})$ と
関手 $\mathrm{Obj}(\boldsymbol{C}^{\mathbf{2}}) \ni (a_{1},a_{2}) \colon \mathbf{2} \longrightarrow \boldsymbol{C}$ が
射 $(f_{1},f_{2}) \colon (a_{1},a_{2}) \longrightarrow (b_{1},b_{2})$ と
自然変換 $\mathrm{Mor}(\boldsymbol{C}^{\mathbf{2}}) \ni (f_{1},f_{2}) \colon (a_{1},a_{2}) \Longrightarrow (b_{1},b_{2})$ が
それぞれ対応し圏同型 $\boldsymbol{C} \times \boldsymbol{C} \cong \boldsymbol{C}^{\mathbf{2}}$ となる。
したがって関手 $\varDelta \colon \boldsymbol{C} \longrightarrow \boldsymbol{C} \times \boldsymbol{C}$ を
関手 $\varDelta \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}^{\mathbf{2}}$ とみなすことができる。
関手 $\varDelta$ の終域 $\boldsymbol{C}^{\mathbf{2}}$ にあらわれる2点離散圏 $\mathbf{2}$ を
圏 $\boldsymbol{J}$ に一般化することを考えよう。
定義
1点離散圏 $\mathbf{1}$ には対象も射も1つしかないので、
対象 $\_ \in \mathrm{Obj}(\boldsymbol{J})$ を $F\ \_ = *$ に対応させ
射 $\_ \in \mathrm{Mor}(\boldsymbol{J})$ を $F\ \_ = \mathrm{id}_{\displaystyle *}$ に対応させることで、
圏 $\boldsymbol{J}$ に対して関手 $F \colon \boldsymbol{J} \longrightarrow \mathbf{1}$ が一意に定まる。
双関手 $- \cdot - \colon \mathbf{1}^{\boldsymbol{J}} \times \boldsymbol{C}^{\mathbf{1}} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ の
左セクション $F \cdot - \colon \boldsymbol{C}^{\mathbf{1}} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ を
この関手 $F \colon \boldsymbol{J} \longrightarrow \mathbf{1}$ に対して考えてみると、
関手 $F \cdot -$ は関数 `const` のような役割を果たす。
対象 $a \in \mathrm{Obj}(\boldsymbol{C})$ と射 $f \in \mathrm{Mor}(\boldsymbol{C})$ を格上げして
関手 $a \colon \mathbf{1} \longrightarrow \boldsymbol{C}$ と自然変換 $f \colon a \Longrightarrow b$ を考える。
対象(すなわち関手) $a \in \mathrm{Obj}(\boldsymbol{C}^{\mathbf{1}})$ と
射(すなわち自然変換) $f \in \mathrm{Mor}(\boldsymbol{C}^{\mathbf{1}})$ である。
関手 $F \cdot - \colon \boldsymbol{C}^{\mathbf{1}} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ により
対象 $a \in \mathrm{Obj}(\boldsymbol{C}^{\mathbf{1}})$ は関手 $F \cdot a \colon \boldsymbol{J} \longrightarrow \boldsymbol{C}$ すなわち
対象の対応 $(F \cdot a)\ \_ = a\ (F\ \) = a\ * = a$ と
射の対応 $(F \cdot a)\ \ = a\ (F\ \) = a\ \mathrm{id}_{\displaystyle *} = \mathrm{id}_{a}$ を、
射 $f \in \mathrm{Mor}(\boldsymbol{C}^{\mathbf{1}})$ は自然変換 $F \cdot f \colon F \cdot a \Longrightarrow F \cdot b$ すなわち
射の族 $(F \cdot f)_{\displaystyle \} = f_{F\ \_} = f_{\displaystyle *} = f$ を
それぞれ与えることが分かる。
$\boldsymbol{C} \cong \boldsymbol{C}^{\mathbf{1}}$ により $F \cdot -$ の始域 $\boldsymbol{C}^{\mathbf{1}}$ を $\boldsymbol{C}$ とし
対角関手 $\varDelta \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ を定義する。
関手 $\varDelta \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ は関数 const の型
const :: c -> (j -> c)
と類似していることが分かるだろう。
対象 $M \in \mathrm{Obj}(\boldsymbol{C}^{\boldsymbol{J}})$ は関手 $M \colon \boldsymbol{J} \longrightarrow \boldsymbol{C}$ である。
対角関手 $\varDelta \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ は $a,b \in \mathrm{Obj}(\boldsymbol{C})$ および
$\mathrm{Mor}(\boldsymbol{C}) \ni f \colon a \longrightarrow b$ とし、以下のように定まる。
$\varDelta\ a \in \mathrm{Obj}(\boldsymbol{C}^{\boldsymbol{J}})$ すなわち関手 $\varDelta\ a \colon \boldsymbol{J} \longrightarrow \boldsymbol{C}$ は
対象 $\_ \in \mathrm{Obj}(\boldsymbol{J})$ を $(\varDelta\ a)\ \_ = a$ に対応させ
射 $\_ \in \mathrm{Mor}(\boldsymbol{J})$ を $(\varDelta\ a)\ \_ = \mathrm{id}_{a}$ に対応させる。
$\varDelta\ f \in \mathrm{Mor}(\boldsymbol{C}^{\boldsymbol{J}})$ すなわち自然変換 $\varDelta\ f \colon \varDelta\ a \Longrightarrow \varDelta\ b$ は
対象 $\_ \in \mathrm{Obj}(\boldsymbol{J})$ を射 $(\varDelta\ f)_{\displaystyle \_} = f$ に対応させる。
{-# LANGUAGE Rank2Types #-}
import Control.Category ((>>>))
--対象を関手に対応させる--
newtype Const a j = Const { getConst :: a }
instance Functor (Const a) where
fmap _ = getConst >>> Const
--射を自然変換に対応させる--
class FunctorNT f where
fmapNT :: (a -> b) -> (forall j. f a j -> f b j)
instance FunctorNT Const where
fmapNT f = getConst >>> f >>> Const
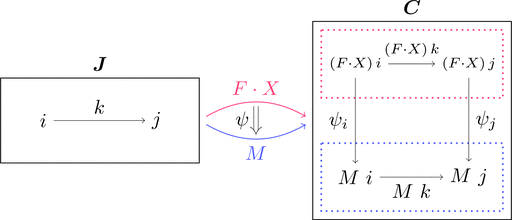
コンマ圏
$\boldsymbol{A}, \boldsymbol{B}, \boldsymbol{C}$ を圏とし、
関手 $L \colon \boldsymbol{A} \longrightarrow \boldsymbol{C}$ と 関手 $R \colon \boldsymbol{B} \longrightarrow \boldsymbol{C}$
に対してコンマ圏 $L \downarrow R$ を次のように定義する。
$a \in \mathrm{Obj}(\boldsymbol{A})$ と $b \in \mathrm{Obj}(\boldsymbol{B})$ と $h \in \mathrm{Mor}(\boldsymbol{C})$ の
組 $(a,b,h)$ を対象とし、$f \in \mathrm{Mor}(\boldsymbol{A})$ と $g \in \mathrm{Mor}(\boldsymbol{B})$ の
組 $(f,g)$ で $L\ f \ggg h' = h \ggg R\ g$ を満たすものを射とする。
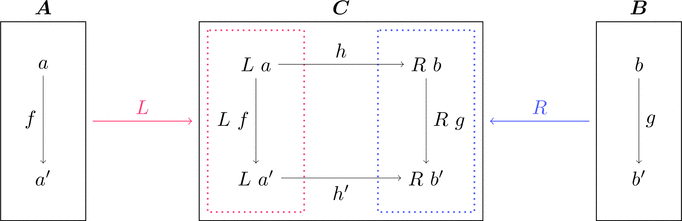
$\mathrm{Obj}(L \downarrow R)\ni (a,b,h), (a',b',h')$ と
$\mathrm{Mor}(L \downarrow R)\ni (f,g) \colon (a,b,h) \longrightarrow (a',b',h')$
であり、上図の四角形が可換図式となる。
コンマ圏 $L \downarrow R$ を始域とする2つの関手と
それに関する自然変換を次のように定義する。
関手 $P_{\mathrm{L}} \colon L \downarrow R \longrightarrow \boldsymbol{A}$ と
関手 $P_{\mathrm{R}} \colon L \downarrow R \longrightarrow \boldsymbol{B}$ と
自然変換 $\tau \colon P_{\mathrm{L}} \cdot L \Longrightarrow P_{\mathrm{R}} \cdot R$ であり、
対象の対応 $P_{\mathrm{L}}\ (a,b,h) = a$ と射の対応 $P_{\mathrm{L}}\ (f,g) = f$
対象の対応 $P_{\mathrm{R}}\ (a,b,h) = b$ と射の対応 $P_{\mathrm{R}}\ (f,g) = g$
射の族 $\tau_{(a,b,h)} = h$ とそれぞれ定める。
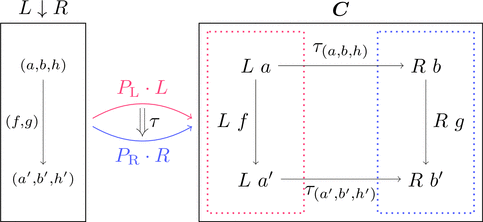
コンマ圏が満たす条件 $L\ f \ggg h' = h \ggg R\ g$ によって、
上図の四角形が可換図式となり、$\tau$ は自然変換となる。
射の圏
コンマ圏 $\mathrm{id}_{\boldsymbol{C}} \downarrow \mathrm{id}_{\boldsymbol{C}}$ を考える。
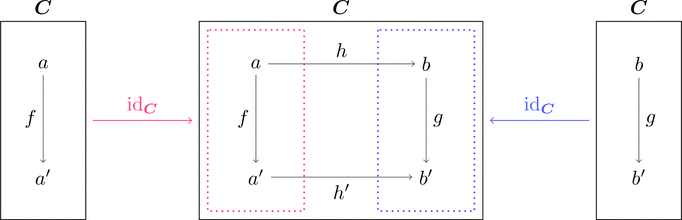
対象 $(a,b,h) = (\mathrm{dom}(h),\mathrm{cod}(h),h)$ だから
射 $h$ そのものが対象であると考えられる。
射 $(f,g) \colon (a,b,h) \longrightarrow (a',b',h')$ は
$h \ggg g = f \ggg h'$ を満たす。
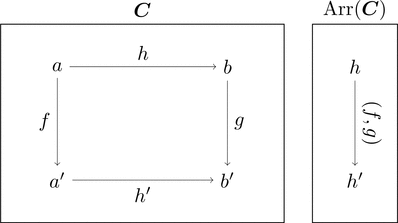
射 $h$ が対象で、上図を可換図式にするような
射の組 $(f,g) \colon h \longrightarrow h'$ が射である。
これを射(が対象)の圏1 $\mathrm{Arr}(\boldsymbol{C})$ と呼ぶ。
ねじれた射の圏
単集合 $\{*\}$ を集合の圏 $\mathbf{Set}$ の対象と考え、
格上げにより関手 $\{*\} \colon \mathbf{1} \longrightarrow \mathbf{Set}$ とみなす。
双関手 $\mathrm{Hom}_{\boldsymbol{C}}(-,-) \colon \boldsymbol{C}^{\mathrm{op}}\times\boldsymbol{C} \longrightarrow \mathbf{Set}$
に対してコンマ圏 $\{*\} \downarrow \mathrm{Hom}_{\boldsymbol{C}}(-,-)$ を考える。
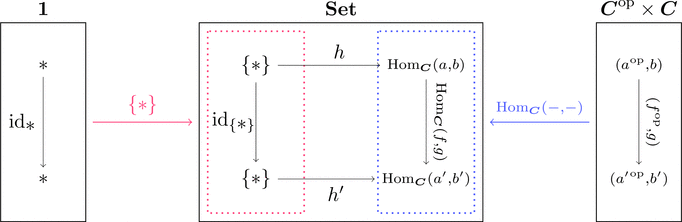
対象 $(*,(a^{\mathrm{op}},b),h) \cong (\mathrm{dom}(h),\mathrm{cod}(h),h)$ だから
射 $h$ そのものが対象であると考えられる。
$\mathrm{Hom}_{\boldsymbol{C}}(f,g) = f \ggg - \ggg g$ であるから
射 $(\mathrm{id}_{\displaystyle *},(f^{\mathrm{op}},g)) \colon (*,(a^{\mathrm{op}},b),h) \longrightarrow (*,({a'}^{\mathrm{op}},b'),h')$ は
$f \ggg h \ggg g = h'$ を満たす。
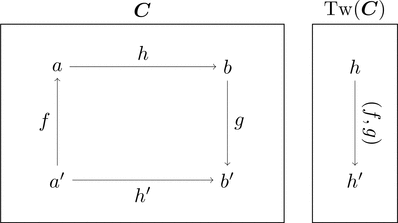
射 $h$ が対象で、上図を可換図式にするような
射の組 $(f,g) \colon h \longrightarrow h'$ が射である。
これをねじれた射の圏2 $\mathrm{Tw}(\boldsymbol{C})$ と呼ぶ。
錐と余錐
関手 $M \colon \boldsymbol{J} \longrightarrow \boldsymbol{C}$ を関手の圏 $\boldsymbol{C}^{\boldsymbol{J}}$ の対象と考え、
格上げにより関手 $M \colon \mathbf{1} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ とみなす。
この関手 $M$ と対角関手 $\varDelta \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$
に対して以下のようなコンマ圏を考える。
錐の圏
コンマ圏 $\varDelta \downarrow M$ を考える。
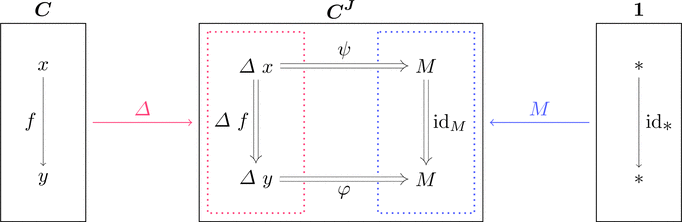
対象 $(x,*,\psi) \cong (\mathrm{dom}(\psi)\ \_,\psi)$ だから
自然変換 $\psi$ そのものが対象であると考えられる。
この自然変換を錐 $\psi \colon \varDelta\ x \Longrightarrow M$ と呼ぶ。
すなわちコンマ圏 $\varDelta \downarrow M$ は錐(が対象)の圏である。
錐 $\psi \colon \varDelta\ x \Longrightarrow M$ は次のように図示できる。
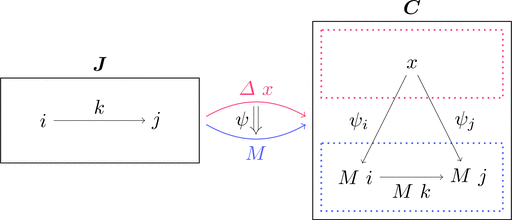
関手 $\varDelta\ x$ は全ての対象 $i \in \mathrm{Obj}(\boldsymbol{J})$ を
対象 $x \in \mathrm{Obj}(\boldsymbol{C})$ に対応させるため
射の族 $\psi_{i}$ の始域が1点に集中する。
余錐の圏
コンマ圏 $M \downarrow \varDelta$ を考える。
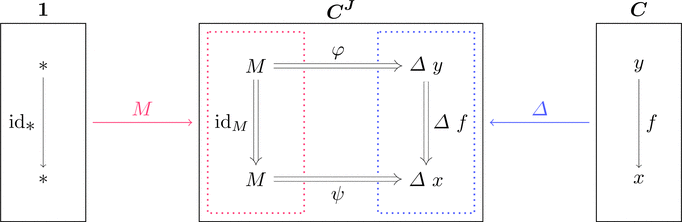
対象 $(*,x,\psi) \cong (\mathrm{cod}(\psi)\ \_,\psi)$ だから
自然変換 $\psi$ そのものが対象であると考えられる。
この自然変換を余錐 $\psi \colon M \Longrightarrow \varDelta\ x$ と呼ぶ。
すなわちコンマ圏 $M \downarrow \varDelta$ は余錐(が対象)の圏である。
余錐 $\psi \colon M \Longrightarrow \varDelta\ x$ は次のように図示できる。
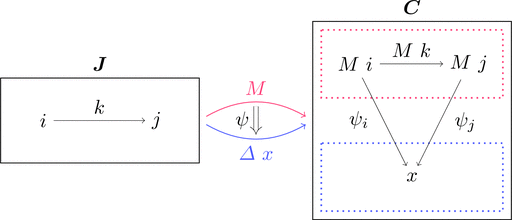
関手 $\varDelta\ x$ は全ての対象 $i \in \mathrm{Obj}(\boldsymbol{J})$ を
対象 $x \in \mathrm{Obj}(\boldsymbol{C})$ に対応させるため
射の族 $\psi_{i}$ の終域が1点に集中する。
楔と余楔
ねじれた射の圏 $\mathrm{Tw}(\boldsymbol{J})$ が始域な
関手 $P_{\mathrm{R}} \colon \mathrm{Tw}(\boldsymbol{J}) \longrightarrow \boldsymbol{J}^{\mathrm{op}}\times\boldsymbol{J}$ を
対象の対応 $P_{\mathrm{R}}\ h = (\mathrm{dom}(h)^{\mathrm{op}},\mathrm{cod}(h))$ と
射の対応 $P_{\mathrm{R}}\ (f,g) = (f^{\mathrm{op}},g)$ により定める。
$\mathrm{Obj}(\boldsymbol{J}^{\mathrm{op}}\times\boldsymbol{J}) \ni (a^{\mathrm{op}},b)$ を $T(a,b)$ に
$\mathrm{Mor}(\boldsymbol{J}^{\mathrm{op}}\times\boldsymbol{J}) \ni (f^{\mathrm{op}},g)$ を $T(f,g)$ に
対応させる双関手を $T \colon \boldsymbol{J}^{\mathrm{op}}\times\boldsymbol{J} \longrightarrow \boldsymbol{C}$ とし、
$P_{\mathrm{R}}$ との合成 $\overline{T} = P_{\mathrm{R}} \cdot T$ により
関手 $\overline{T} \colon \mathrm{Tw}(\boldsymbol{J}) \longrightarrow \boldsymbol{C}$ を定める。
対象 $\mathrm{Obj}(\mathrm{Tw}(\boldsymbol{J})) \ni h \colon a \longrightarrow b$ および
射 $\mathrm{Mor}(\mathrm{Tw}(\boldsymbol{J})) \ni (f, g)$ とすれば以下となる。
関手 $\overline{T} \colon \mathrm{Tw}(\boldsymbol{J}) \longrightarrow \boldsymbol{C}$ は
対象の対応 $\overline{T}\ h = T(a,b)$ と
射の対応 $\overline{T}\ (f,g) = T(f,g)$ である。
関手 $\overline{T^{\mathrm{op}}}^{\mathrm{op}} \colon \mathrm{Tw}(\boldsymbol{J}^{\mathrm{op}})^{\mathrm{op}} \longrightarrow \boldsymbol{C}$ は
対象の対応 $\overline{T^{\mathrm{op}}}^{\mathrm{op}}\ h = T(b,a)$ と
射の対応 $\overline{T^{\mathrm{op}}}^{\mathrm{op}}\ (f,g) = T(f,g)$ である。
関手 $\overline{T} \colon \mathrm{Tw}(\boldsymbol{J}) \longrightarrow \boldsymbol{C}$ を
関手の圏 $\boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J})}$ の対象と考えて
格上げにより関手 $\overline{T} \colon \mathbf{1} \longrightarrow \boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J})}$ とみなす。
同様に関手 $\overline{T^{\mathrm{op}}}^{\mathrm{op}} \colon \mathbf{1} \longrightarrow \boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J}^{\mathrm{op}})^{\mathrm{op}}}$ とみなす。
この関手 $\overline{T}, \overline{T^{\mathrm{op}}}^{\mathrm{op}}$ と対角関手 $\varDelta$
に対して以下のようなコンマ圏を考える。
楔の圏
コンマ圏 $\varDelta \downarrow \overline{T}$ を考える。
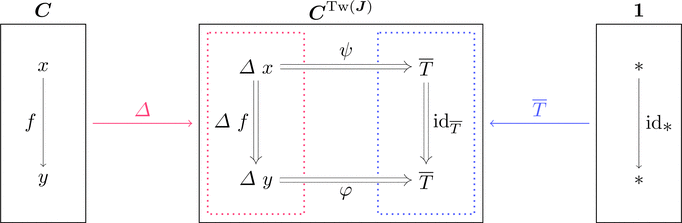
対象 $(x,*,\psi) \cong (\mathrm{dom}(\psi)\ \_,\psi)$ だから
自然変換 $\psi$ そのものが対象であると考えられる。
この自然変換を楔 $\psi \colon \varDelta\ x \Longrightarrow \overline{T}$ と呼ぶ。
すなわちコンマ圏 $\varDelta \downarrow \overline{T}$ は楔(が対象)の圏である。
任意の射 $\mathrm{Mor}(\boldsymbol{J}) \ni h \colon a \longrightarrow b$ に対して
$\mathrm{Mor}(\mathrm{Tw}(\boldsymbol{J})) \ni (\mathrm{id}_{a},h), (h,\mathrm{id}_{b})$ が存在するため、
楔 $\psi \colon \varDelta\ x \Longrightarrow \overline{T}$ は次の図式を可換とする。
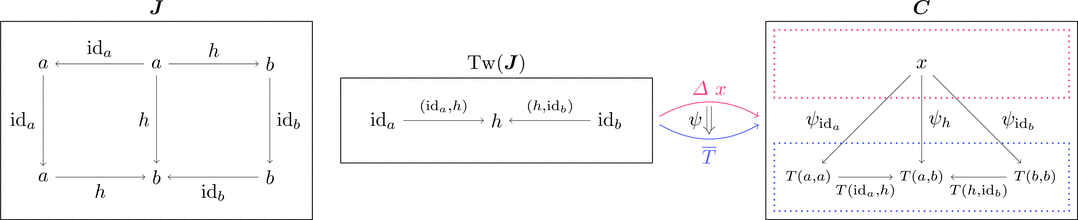
つまり、$\psi_{\mathrm{id}_{-}}$ は射の族 $\psi_{\mathrm{id}_{a}} \colon x \longrightarrow T(a,a)$ で、
任意の射 $\mathrm{Mor}(\boldsymbol{J}) \ni h \colon a \longrightarrow b$ に対して
$\psi_{\mathrm{id}_{b}} \ggg T(h,\mathrm{id}_{b}) = \psi_{\mathrm{id}_{a}} \ggg T(\mathrm{id}_{a},h)$ が成り立つ。
余楔の圏
コンマ圏 $\overline{T^{\mathrm{op}}}^{\mathrm{op}} \downarrow \varDelta$ を考える。
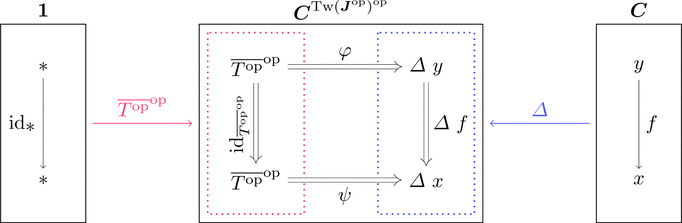
対象 $(*,x,\psi) \cong (\mathrm{cod}(\psi)\ \_,\psi)$ だから
自然変換 $\psi$ そのものが対象であると考えられる。
この自然変換を余楔 $\psi \colon \overline{T^{\mathrm{op}}}^{\mathrm{op}} \Longrightarrow \varDelta\ x$ と呼ぶ。
すなわちコンマ圏 $\overline{T^{\mathrm{op}}}^{\mathrm{op}} \downarrow \varDelta$ は余楔(が対象)の圏である。
任意の射 $\mathrm{Mor}(\boldsymbol{J}) \ni h \colon a \longrightarrow b$ に対して
$\mathrm{Mor}(\mathrm{Tw}(\boldsymbol{J}^{\mathrm{op}})^{\mathrm{op}}) \ni (h,\mathrm{id}_{a}), (\mathrm{id}_{b},h)$ が存在するため、
余楔 $\psi \colon \overline{T^{\mathrm{op}}}^{\mathrm{op}} \Longrightarrow \varDelta\ x$ は次の図式を可換とする。

つまり、$\psi_{\mathrm{id}_{-}}$ は射の族 $\psi_{\mathrm{id}_{a}} \colon T(a,a) \longrightarrow x$ で、
任意の射 $\mathrm{Mor}(\boldsymbol{J}) \ni h \colon a \longrightarrow b$ に対して
$T(\mathrm{id}_{b},h) \ggg \psi_{\mathrm{id}_{b}} = T(h,\mathrm{id}_{a}) \ggg \psi_{\mathrm{id}_{a}}$ が成り立つ。
柱と余柱
対角関手 $\varDelta \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ とは、
一意に定まる関手を $F \colon \boldsymbol{J} \longrightarrow \mathbf{1}$ として、
双関手 $- \cdot - \colon \mathbf{1}^{\boldsymbol{J}} \times \boldsymbol{C}^{\mathbf{1}} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ の
左セクション $F \cdot - \colon \boldsymbol{C}^{\mathbf{1}} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ である。
関手を $F \colon \boldsymbol{J} \longrightarrow \boldsymbol{D}$ と一般化して、
双関手 $- \cdot - \colon \boldsymbol{D}^{\boldsymbol{J}} \times \boldsymbol{C}^{\boldsymbol{D}} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ の
左セクション $F \cdot - \colon \boldsymbol{C}^{\boldsymbol{D}} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ を考えよう。
関手 $M \colon \boldsymbol{J} \longrightarrow \boldsymbol{C}$ を関手の圏 $\boldsymbol{C}^{\boldsymbol{J}}$ の対象と考え、
格上げにより関手 $M \colon \mathbf{1} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$ とみなす。
この関手 $M$ と関手 $F \cdot - \colon \boldsymbol{C}^{\boldsymbol{D}} \longrightarrow \boldsymbol{C}^{\boldsymbol{J}}$
に対して以下のようなコンマ圏を考える。
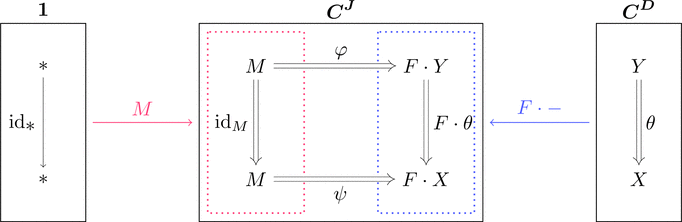
柱の圏
コンマ圏 $F \cdot - \downarrow M$ を考える。
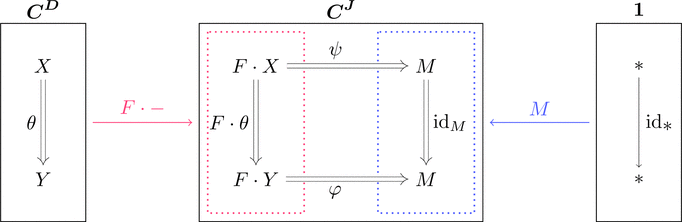
対象 $(X,*,\psi) \cong (X,\psi)$ だから
関手と自然変換の組 $(X,\psi)$ が対象であると考えられる。
この組を柱 $(X,\psi)$ と呼ぶ。$\psi \colon F \cdot X \Longrightarrow M$ である。
すなわちコンマ圏 $F \cdot - \downarrow M$ は柱(が対象)の圏である。
自然変換 $\psi \colon F \cdot X \Longrightarrow M$ は次のように図示できる。
錐の圏とは異なり、対象 $i \in \mathrm{Obj}(\boldsymbol{J})$ として、
射の族 $\psi_{i}$ の始域も終域も1点に集中しない。
余柱の圏
コンマ圏 $M \downarrow F \cdot -$ を考える。
対象 $(*,X,\psi) \cong (X,\psi)$ だから
関手と自然変換の組 $(X,\psi)$ が対象であると考えられる。
この組を余柱 $(X,\psi)$ と呼ぶ。$\psi \colon M \Longrightarrow F \cdot X$ である。
すなわちコンマ圏 $M \downarrow F \cdot -$ は余柱(が対象)の圏である。
自然変換 $\psi \colon M \Longrightarrow F \cdot X$ は次のように図示できる。
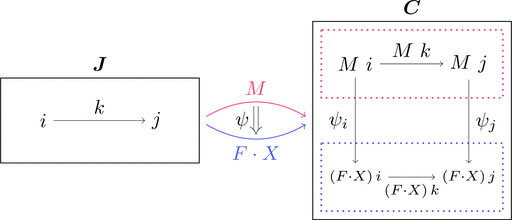
余錐の圏とは異なり、対象 $i \in \mathrm{Obj}(\boldsymbol{J})$ として、
射の族 $\psi_{i}$ の始域も終域も1点に集中しない。
普遍性
終対象と始対象の普遍性が
おそらく例として最も簡単だろう。
「一意に存在する」と言う
普遍性の概念に慣れるため、
随伴関手を構成する全単射を考えて
一意性の雰囲気を感じてみよう。
終対象
1点離散圏を $\mathbf{1}$ として、
一意に定まる関手 $! \colon \boldsymbol{C} \longrightarrow \mathbf{1}$ の右随伴関手 $1 \colon \mathbf{1} \longrightarrow \boldsymbol{C}$
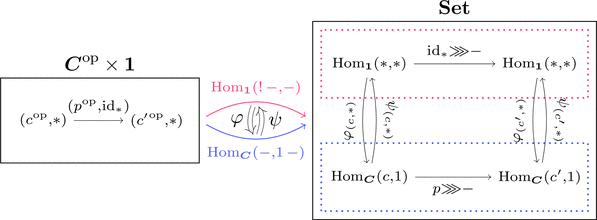
すなわち対象 $\mathrm{Obj}(\boldsymbol{C}) \ni 1 = 1\ *$ を終対象 $1$ と呼ぶ。
随伴関係 $! \dashv 1$ すなわち
$\mathrm{Hom}_{\mathbf{1}}(!\ -,-) \cong \mathrm{Hom}_{\boldsymbol{C}}(-,1\ -)$ が
成り立つとき、次の自然な同型射が存在する。
$\varphi_{(c,*)} \colon \mathrm{Hom}_{\mathbf{1}}(*,*) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(c,1)$
$\psi_{(c,*)} \colon \mathrm{Hom}_{\boldsymbol{C}}(c,1) \longrightarrow \mathrm{Hom}_{\mathbf{1}}(*,*)$
任意の対象 $c \in \mathrm{Obj}(\boldsymbol{C})$ に対して
射 $\mathrm{Mor}(\boldsymbol{C}) \ni g \colon c \longrightarrow 1$ が、
元の対応 $\varphi_{(c,*)} \colon \mathrm{id}_{\displaystyle *} \longmapsto g$ により、
一意に存在することが分かる。
終対象とは以下を満たす対象 $1 \in \mathrm{Obj}(\boldsymbol{C})$ である。
任意の対象 $c \in \mathrm{Obj}(\boldsymbol{C})$ に対して
射 $\mathrm{Mor}(\boldsymbol{C}) \ni g \colon c \longrightarrow 1$ が一意に存在する。
始対象
1点離散圏を $\mathbf{1}$ として、
一意に定まる関手 $! \colon \boldsymbol{D} \longrightarrow \mathbf{1}$ の左随伴関手 $0 \colon \mathbf{1} \longrightarrow \boldsymbol{D}$
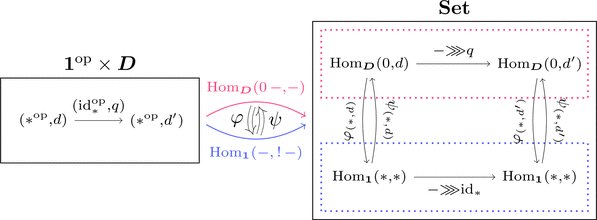
すなわち対象 $\mathrm{Obj}(\boldsymbol{D}) \ni 0 = 0\ *$ を始対象 $0$ と呼ぶ。
随伴関係 $0 \dashv~!$ すなわち
$\mathrm{Hom}_{\boldsymbol{D}}(0\ -,-) \cong \mathrm{Hom}_{\mathbf{1}}(-,!\ -)$ が
成り立つとき、次の自然な同型射が存在する。
$\varphi_{(*,d)} \colon \mathrm{Hom}_{\boldsymbol{D}}(0,d) \longrightarrow \mathrm{Hom}_{\mathbf{1}}(*,*)$
$\psi_{(*,d)} \colon \mathrm{Hom}_{\mathbf{1}}(*,*) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(0,d)$
任意の対象 $d \in \mathrm{Obj}(\boldsymbol{D})$ に対して
射 $\mathrm{Mor}(\boldsymbol{D}) \ni f \colon 0 \longrightarrow d$ が、
元の対応 $\psi_{(*,d)} \colon \mathrm{id}_{\displaystyle *} \longmapsto f$ により、
一意に存在することが分かる。
始対象とは以下を満たす対象 $0 \in \mathrm{Obj}(\boldsymbol{D})$ である。
任意の対象 $d \in \mathrm{Obj}(\boldsymbol{D})$ に対して
射 $\mathrm{Mor}(\boldsymbol{D}) \ni f \colon 0 \longrightarrow d$ が一意に存在する。
普遍射
格上げにより
対象 $c \in \mathrm{Obj}(\boldsymbol{C})$ を関手 $c \colon \mathbf{1} \longrightarrow \boldsymbol{C}$ とみなし、
対象 $d \in \mathrm{Obj}(\boldsymbol{D})$ を関手 $d \colon \mathbf{1} \longrightarrow \boldsymbol{D}$ とみなす。
また、すべての対象に対する普遍射を
集めることで随伴関手を定められる。
余単位
ある $d \in \mathrm{Obj}(\boldsymbol{D})$ に対して定まる対象と射を
それぞれ $G\ d \in \mathrm{Obj}(\boldsymbol{C})$ と $\varepsilon_{d} \in \mathrm{Mor}(\boldsymbol{D})$ とする。
関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と対象 $d \colon \mathbf{1} \longrightarrow \boldsymbol{D}$ に対して、
コンマ圏 $F \downarrow d$ の終対象 $(G\ d,*,\varepsilon_{d})$
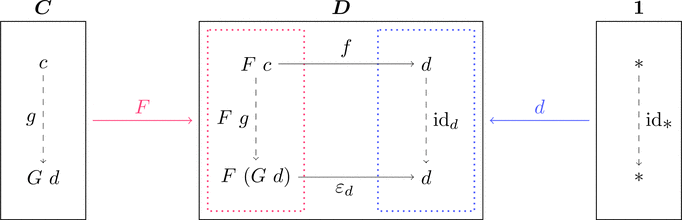
すなわち $(G\ d,\varepsilon_{d})$ を $F$ から $d$ への普遍射と呼ぶ。
各対象 $d \in \mathrm{Obj}(\boldsymbol{D})$ に対して普遍射 $(G\ d,\varepsilon_{d})$ が存在するとき、
関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ と自然変換 $\varepsilon \colon G \cdot F \Longrightarrow \mathrm{id}_{\boldsymbol{D}}$ が定義できて、
$G$ による射 $q \colon d \longrightarrow d'$ の対応を考える。
まずコンマ圏 $F \downarrow d$ の終対象 $(G\ d,*,\varepsilon_{d})$
すなわち普遍射 $\varepsilon_{d} \colon F\ (G\ d) \longrightarrow d$ を用いて
合成射 $\varepsilon_{d} \ggg q \colon F\ (G\ d) \longrightarrow d'$ すなわち
コンマ圏 $F \downarrow d'$ の対象 $(G\ d,*,\varepsilon_{d} \ggg q)$ を用意する。
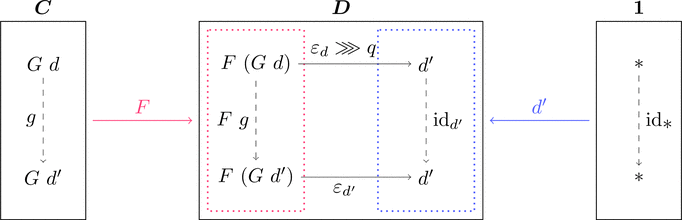
コンマ圏 $F \downarrow d'$ には終対象 $(G\ d',*,\varepsilon_{d'})$ が
存在するため、射 $g \colon G\ d \longrightarrow G\ d'$ すなわち
コンマ圏 $F \downarrow d'$ の射 $(g,\mathrm{id}_{\displaystyle *})$ が一意に存在する。
これにより射の対応 $G\ q = g$ を定める。
また、コンマ圏 $F \downarrow d'$ の射 $(g,\mathrm{id}_{\displaystyle *})$ が満たす条件は
$(G \cdot F)\ q \ggg \varepsilon_{d'} = \varepsilon_{d} \ggg \mathrm{id}_{\boldsymbol{D}}\ q$ となっており、
自然変換 $\varepsilon \colon G \cdot F \Longrightarrow \mathrm{id}_{\boldsymbol{D}}$ が満たす条件と一致する。
随伴関係 $F \dashv G$ すなわち次式が成り立つ。
写像 $\psi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d)$ を
元の対応 $\psi_{(c,d)} \colon g \longmapsto F\ g \ggg \varepsilon_{d}$ で定める。
このとき
\begin{align}
(\mathrm{Hom}_{\boldsymbol{C}}(p,G\ q) \ggg \psi_{(c',d')})(g)
&=
F\ (p \ggg g \ggg G\ q) \ggg \varepsilon_{d'}
\\
&=
F\ p \ggg F\ g \ggg (G \cdot F)\ q \ggg \varepsilon_{d'}
\\
&=
F\ p \ggg F\ g \ggg \varepsilon_{d} \ggg \mathrm{id}_{\boldsymbol{D}}\ q
\\[2mm]
(\psi_{(c,d)} \ggg \mathrm{Hom}_{\boldsymbol{D}}(F\ p,q))(g)
&=
F\ p \ggg (F\ g \ggg \varepsilon_{d}) \ggg q
\\
&=
F\ p \ggg F\ g \ggg \varepsilon_{d} \ggg q
\\
&=
F\ p \ggg F\ g \ggg \varepsilon_{d} \ggg \mathrm{id}_{\boldsymbol{D}}\ q
\end{align}
すなわち
$\mathrm{Hom}_{\boldsymbol{C}}(p,G\ q) \ggg \psi_{(c',d')} = \psi_{(c,d)} \ggg \mathrm{Hom}_{\boldsymbol{D}}(F\ p,q)$
が成り立つから $\psi$ は
自然変換 $\psi \colon \mathrm{Hom}_{\boldsymbol{C}}(-,G\ -) \Longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ -,-)$ である。
写像 $\varphi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d)$ を
考えて写像 $\psi_{(c,d)}$ が同型射であることを示そう。
任意の射 $f \in \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d)$ に対して、
組 $(c,*,f)$ はコンマ圏 $F \downarrow d$ の対象であるから
コンマ圏 $F \downarrow d$ の射 $(g,\mathrm{id}_{\displaystyle *})$ が一意に存在する。
つまり、$F\ g \ggg \varepsilon_{d} = f$ を満たす射 $g$ が一意に存在する。
これにより元の対応 $\varphi_{(c,d)} \colon f \longmapsto g$ を定める。
このとき
\begin{align}
(\varphi_{(c,d)} \ggg \psi_{(c,d)})(f)
&=
F\ \varphi_{(c,d)}(f) \ggg \varepsilon_{d}
\\
&=
F\ g \ggg \varepsilon_{d} = f
\\[2mm]
(\psi_{(c,d)} \ggg \varphi_{(c,d)})(g)
&=
\varphi_{(c,d)}(F\ g \ggg \varepsilon_{d})
\\
&= g
\end{align}
であるから、$\psi_{(c,d)}$ は自然な同型射である。
単位
ある $c \in \mathrm{Obj}(\boldsymbol{C})$ に対して定まる対象と射を
それぞれ $F\ c \in \mathrm{Obj}(\boldsymbol{D})$ と $\eta_{c} \in \mathrm{Mor}(\boldsymbol{C})$ とする。
対象 $c \colon \mathbf{1} \longrightarrow \boldsymbol{C}$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ に対して、
コンマ圏 $c \downarrow G$ の始対象 $(*,F\ c,\eta_{c})$
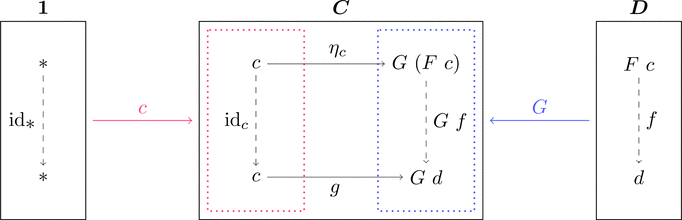
すなわち $(F\ c,\eta_{c})$ を $c$ から $G$ への普遍射と呼ぶ。
各対象 $c \in \mathrm{Obj}(\boldsymbol{C})$ に対して普遍射 $(F\ c,\eta_{c})$ が存在するとき、
関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と自然変換 $\eta \colon \mathrm{id}_{\boldsymbol{C}} \Longrightarrow F \cdot G$ が定義できて、
$F$ による射 $p \colon c' \longrightarrow c$ の対応を考える。
まずコンマ圏 $c \downarrow G$ の始対象 $(*,F\ c,\eta_{c})$
すなわち普遍射 $\eta_{c} \colon c \longrightarrow G\ (F\ c)$ を用いて
合成射 $p \ggg \eta_{c} \colon c' \longrightarrow G\ (F\ c)$ すなわち
コンマ圏 $c' \downarrow G$ の対象 $(*,F\ c,p \ggg \eta_{c})$ を用意する。
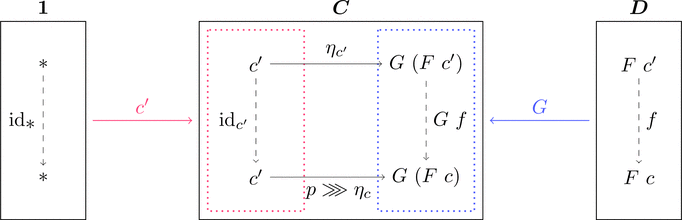
コンマ圏 $c' \downarrow G$ には始対象 $(*,F\ c',\eta_{c'})$ が
存在するため、射 $f \colon F\ c' \longrightarrow F\ c$ すなわち
コンマ圏 $c' \downarrow G$ の射 $(\mathrm{id}_{\displaystyle *},f)$ が一意に存在する。
これにより射の対応 $F\ p = f$ を定める。
また、コンマ圏 $c' \downarrow G$ の射 $(\mathrm{id}_{\displaystyle *},f)$ が満たす条件は
$\mathrm{id}_{\boldsymbol{C}}\ p \ggg \eta_{c} = \eta_{c'} \ggg (F \cdot G)\ p$ となっており、
自然変換 $\eta \colon \mathrm{id}_{\boldsymbol{C}} \Longrightarrow F \cdot G$ が満たす条件と一致する。
随伴関係 $F \dashv G$ すなわち次式が成り立つ。
写像 $\varphi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d)$ を
元の対応 $\varphi_{(c,d)} \colon f \longmapsto \eta_{c} \ggg G\ f$ で定める。
このとき
\begin{align}
(\mathrm{Hom}_{\boldsymbol{D}}(F\ p,q) \ggg \varphi_{(c',d')})(f)
&=
\eta_{c'} \ggg G\ (F\ p \ggg f \ggg q)
\\
&=
\eta_{c'} \ggg (F \cdot G)\ p \ggg G\ f \ggg G\ q
\\
&=
\mathrm{id}_{\boldsymbol{C}}\ p \ggg \eta_{c} \ggg G\ f \ggg G\ q
\\[2mm]
(\varphi_{(c,d)} \ggg \mathrm{Hom}_{\boldsymbol{C}}(p,G\ q))(f)
&=
p \ggg (\eta_{c} \ggg G\ f) \ggg G\ q
\\
&=
p \ggg \eta_{c} \ggg G\ f \ggg G\ q
\\
&=
\mathrm{id}_{\boldsymbol{C}}\ p \ggg \eta_{c} \ggg G\ f \ggg G\ q
\end{align}
すなわち
$\mathrm{Hom}_{\boldsymbol{D}}(F\ p,q) \ggg \varphi_{(c',d')} = \varphi_{(c,d)} \ggg \mathrm{Hom}_{\boldsymbol{C}}(p,G\ q)$
が成り立つから $\varphi$ は
自然変換 $\varphi \colon \mathrm{Hom}_{\boldsymbol{D}}(F\ -,-) \Longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(-,G\ -)$ である。
写像 $\psi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ c,d)$ を
考えて写像 $\varphi_{(c,d)}$ が同型射であることを示そう。
任意の射 $g \in \mathrm{Hom}_{\boldsymbol{C}}(c,G\ d)$ に対して、
組 $(*,d,g)$ はコンマ圏 $c \downarrow G$ の対象であるから
コンマ圏 $c \downarrow G$ の射 $(\mathrm{id}_{\displaystyle *},f)$ が一意に存在する。
つまり、$\eta_{c} \ggg G\ f = g$ を満たす射 $f$ が一意に存在する。
これにより元の対応 $\psi_{(c,d)} \colon g \longmapsto f$ を定める。
このとき
\begin{align}
(\varphi_{(c,d)} \ggg \psi_{(c,d)})(f)
&=
\psi_{(c,d)}(\eta_{c} \ggg G\ f)
\\
&= f
\\[2mm]
(\psi_{(c,d)} \ggg \varphi_{(c,d)})(g)
&=
\eta_{c} \ggg G\ \psi_{(c,d)}(g)
\\
&=
\eta_{c} \ggg G\ f = g
\end{align}
であるから、$\varphi_{(c,d)}$ は自然な同型射である。
テンソル関手
次のHom 関手
関手 $\mathrm{Hom}_{\boldsymbol{C}}^{\mathrm{op}}(-,c) \colon \boldsymbol{C} \longrightarrow \mathbf{Set}^{\mathrm{op}}$ と
関手 $\mathrm{Hom}_{\boldsymbol{C}}(b,-) \colon \boldsymbol{C} \longrightarrow \mathbf{Set}$ に関して
普遍射および随伴関手を考える。
エンドとしての右カン拡張や
コエンドとしての左カン拡張を
考える際に以下の概念が必要となる。
余テンソル対象
コンマ圏 $\mathrm{Hom}_{\boldsymbol{C}}^{\mathrm{op}}(-,c) \downarrow B^{\mathrm{op}}$ の終対象 $(B \pitchfork c,*,\varepsilon_{B^{\mathrm{op}}})$
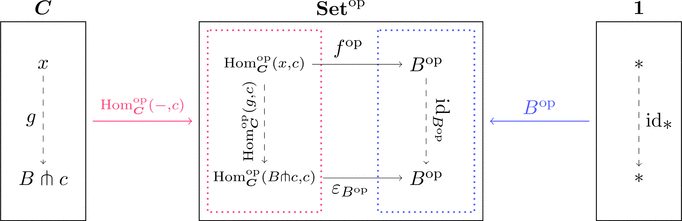
すなわち $(B \pitchfork c,\varepsilon_{B^{\mathrm{op}}})$ は $\mathrm{Hom}_{\boldsymbol{C}}^{\mathrm{op}}(-,c)$ から $B^{\mathrm{op}}$ への普遍射であり、
余テンソル対象 $B \pitchfork c$ と呼ぶ。
各対象 $B^{\mathrm{op}} \in \mathrm{Obj}(\mathbf{Set}^{\mathrm{op}})$ に対して普遍射 $(B \pitchfork c,\varepsilon_{B^{\mathrm{op}}})$
が存在するとき、関手 $- \pitchfork c \colon \mathbf{Set}^{\mathrm{op}} \longrightarrow \boldsymbol{C}$ と
自然変換 $\varepsilon \colon \mathrm{Hom}_{\boldsymbol{C}}^{\mathrm{op}}(- \pitchfork c,c) \Longrightarrow \mathrm{id}_{\mathbf{Set}^{\mathrm{op}}}$ が定義できて、
随伴関係 $\mathrm{Hom}_{\boldsymbol{C}}^{\mathrm{op}}(-,c) \dashv - \pitchfork c$ すなわち次式が成り立つ。
$\mathrm{Hom}_{\mathbf{Set}^{\mathrm{op}}}(\mathrm{Hom}_{\boldsymbol{C}}^{\mathrm{op}}(-,c),-) \cong \mathrm{Hom}_{\boldsymbol{C}}(-,- \pitchfork c)$
各対象 $c \in \mathrm{Obj}(\boldsymbol{C})$ に対しても余テンソル対象 $B \pitchfork c$
が存在するとき、双関手 $- \pitchfork - \colon \mathbf{Set}^{\mathrm{op}} \times \boldsymbol{C} \longrightarrow \boldsymbol{C}$ が定まり
射の族 $\psi_{(x,B,c)} \colon \mathrm{Hom}_{\boldsymbol{C}}(x,B \pitchfork c) \longrightarrow \mathrm{Hom}_{\mathbf{Set}}(B,\mathrm{Hom}_{\boldsymbol{C}}(x,c))$
により自然同型 $\psi$ を定義することができる4。
$\mathrm{Mor}(\boldsymbol{C}) \ni g \colon x \longrightarrow B \pitchfork c$ と
$\mathrm{Mor}(\mathbf{Set}) \ni f \colon B \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(x,c)$ であり、
射の族 $\psi_{(x,B,c)}$ は関数 flip の型
flip :: (x -> (b -> c)) -> (b -> (x -> c))
と類似していることが分かるだろう。
テンソル対象
コンマ圏 $A \downarrow \mathrm{Hom}_{\boldsymbol{C}}(b,-)$ の始対象 $(*,A \odot b,\eta_{A})$
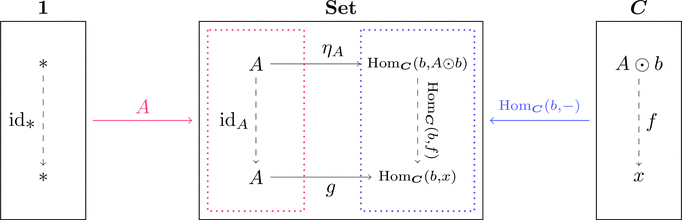
すなわち $(A \odot b,\eta_{A})$ は $A$ から $\mathrm{Hom}_{\boldsymbol{C}}(b,-)$ への普遍射であり、
テンソル対象 $A \odot b$ と呼ぶ。
各対象 $A \in \mathrm{Obj}(\mathbf{Set})$ に対して普遍射 $(A \odot b,\eta_{A})$
が存在するとき、関手 $- \odot b \colon \mathbf{Set} \longrightarrow \boldsymbol{C}$ と
自然変換 $\eta \colon \mathrm{id}_{\mathbf{Set}} \Longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(b,- \odot b)$ が定義できて、
随伴関係 $- \odot b \dashv \mathrm{Hom}_{\boldsymbol{C}}(b,-)$ すなわち次式が成り立つ。
$\mathrm{Hom}_{\boldsymbol{C}}(- \odot b,-) \cong \mathrm{Hom}_{\mathbf{Set}}(-,\mathrm{Hom}_{\boldsymbol{C}}(b,-))$
各対象 $b \in \mathrm{Obj}(\boldsymbol{C})$ に対してもテンソル対象 $A \odot b$
が存在するとき、双関手 $- \odot - \colon \mathbf{Set} \times \boldsymbol{C} \longrightarrow \boldsymbol{C}$ が定まり
射の族 $\varphi_{(A,b,x)} \colon \mathrm{Hom}_{\boldsymbol{C}}(A \odot b,x) \longrightarrow \mathrm{Hom}_{\mathbf{Set}}(A,\mathrm{Hom}_{\boldsymbol{C}}(b,x))$
により自然同型 $\varphi$ を定義することができる4。
$\mathrm{Mor}(\boldsymbol{C}) \ni f \colon A \odot b \longrightarrow x$ と
$\mathrm{Mor}(\mathbf{Set}) \ni g \colon A \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(b,x)$ であり、
射の族 $\varphi_{(A,b,x)}$ は関数 curry の型
curry :: ((a, b) -> x) -> (a -> (b -> x))
と類似していることが分かるだろう。
極限と余極限
極限と余極限で見た概念を
関手や自然変換を用いて定義する。
錐の圏の終対象が極限であり、
余錐の圏の始対象が余極限である。
極限
錐の圏 $\varDelta \downarrow M$ の終対象 $(\mathrm{lim}_{\boldsymbol{J}}M,*,\varepsilon_{M})$
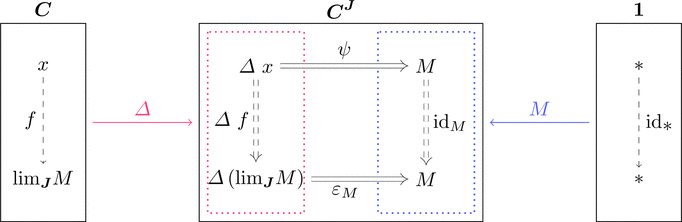
すなわち $(\mathrm{lim}_{\boldsymbol{J}}M,\varepsilon_{M})$ は $\varDelta$ から $M$ への普遍射であり、
これを関手 $M \colon \boldsymbol{J} \longrightarrow \boldsymbol{C}$ の極限 $\mathrm{lim}_{\boldsymbol{J}}M$ と呼ぶ。
各対象 $M \in \mathrm{Obj}(\boldsymbol{C}^{\boldsymbol{J}})$ に対して普遍射 $(\mathrm{lim}_{\boldsymbol{J}}M,\varepsilon_{M})$
が存在するとき、関手 $\mathrm{lim}_{\boldsymbol{J}} \colon \boldsymbol{C}^{\boldsymbol{J}} \longrightarrow \boldsymbol{C}$ と
自然変換 $\varepsilon \colon \mathrm{lim}_{\boldsymbol{J}} \cdot \varDelta \Longrightarrow \mathrm{id}_{\boldsymbol{C}^{\boldsymbol{J}}}$ が定義できて、
随伴関係 $\varDelta \dashv \mathrm{lim}_{\boldsymbol{J}}$ すなわち次式が成り立つ。
$\mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{J}}}(\varDelta\ -,-) \cong \mathrm{Hom}_{\boldsymbol{C}}(-,\mathrm{lim}_{\boldsymbol{J}},-)$
圏の平方にて定義を与えた関手 $(a,b) \colon \mathbf{2} \longrightarrow \boldsymbol{C}$ の
極限 $\mathrm{lim}_{\mathbf{2}}(a,b) \cong a \times b$ が直積である。
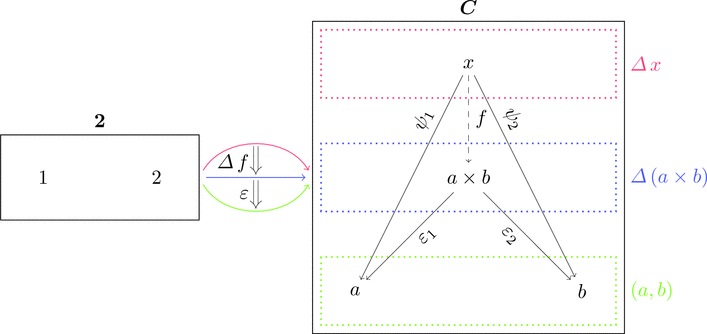
$\mathrm{Obj}(\mathbf{2}) \ni i = 1,2$ として、$\psi_{i} = f \ggg \varepsilon_{i}$ である。
ここでは $\varepsilon_{(a,b)}$ を $\varepsilon$ と略記している。
右随伴関手との交換
関手 $F \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ と関手 $G \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ に対して
$F \dashv G$ が随伴であるとき以下が成り立つ。
圏 $\boldsymbol{C}$ の終対象 $1 \in \mathrm{Obj}(\boldsymbol{C})$ が存在すれば、
圏 $\boldsymbol{D}$ の終対象 $G\ 1 \in \mathrm{Obj}(\boldsymbol{D})$ が定まる。
すなわち、右随伴関手 $G$ は[__終対象__](#終対象)を保つ。
$F \dashv G$ より次の自然な同型射が存在する。
$\varphi_{(d,c)} \colon \mathrm{Hom}_{\boldsymbol{C}}(F\ d, c) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(d, G\ c)$
$\psi_{(d,c)} \colon \mathrm{Hom}_{\boldsymbol{D}}(d, G\ c) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(F\ d, c)$
終対象 $1 \in \mathrm{Obj}(\boldsymbol{C})$ が存在すれば、
任意の対象 $d \in \mathrm{Obj}(\boldsymbol{D})$ に対して
射 $\mathrm{Mor}(\boldsymbol{D}) \ni g \colon d \longrightarrow G\ 1$ が、
写像 $\varphi_{(d,1)} \colon \mathrm{Hom}_{\boldsymbol{C}}(F\ d, 1) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(d, G\ 1)$ により、
一意に存在することが分かる。
$F_{\displaystyle*} \dashv G_{\displaystyle*}$ が随伴となるような
関手 $F_{\displaystyle*} \colon \varDelta \downarrow M \cdot G \longrightarrow \varDelta \downarrow M$ と
関手 $G_{\displaystyle*} \colon \varDelta \downarrow M \longrightarrow \varDelta \downarrow M \cdot G $ を
構成することができる。
対象の対応 $F_{\displaystyle*}\ (d,*,\beta) = (F\ d,*,\beta_{\cup})$ と
射の対応 $F_{\displaystyle*}\ (q,\mathrm{id}_{\displaystyle*}) = (F\ q,\mathrm{id}_{\displaystyle*})$ を
対象の対応 $G_{\displaystyle*}\ (c,*,\alpha) = (G\ c,*,\alpha \cdot G)$ と
射の対応 $G_{\displaystyle*}\ (p,\mathrm{id}_{\displaystyle*}) = (G\ p,\mathrm{id}_{\displaystyle*})$ を
それぞれ定める。
ここで $\beta_{\cup} = \beta \cdot F \ggg M \cdot \varepsilon$ であり、
${\beta_{\cup}}^{\cap} = \varDelta\ \eta_{d} \ggg \beta_{\cup} \cdot G = \beta$ である。
写像 $\varphi_{((d,*,\beta),(c,*,\alpha))} \colon \mathrm{Hom}_{\varDelta \downarrow M}(F_{\displaystyle*}\ (d,*,\beta),(c,*,\alpha)) \longrightarrow \mathrm{Hom}_{\varDelta \downarrow M \cdot G}((d,*,\beta),G_{\displaystyle*}\ (c,*,\alpha))$ を
元の対応 $\varphi_{((d,*,\beta),(c,*,\alpha))} \colon (f,\mathrm{id}_{\displaystyle*}) \longmapsto (\eta_{d} \ggg G\ f,\mathrm{id}_{\displaystyle*})$ で定める。
コンマ圏 $\varDelta \downarrow M$ の射 $(f,\mathrm{id}_{\displaystyle*})$ が満たす条件
$\beta_{\cup} = \varDelta\ f \ggg \alpha$ により
\begin{align}
\beta
&=
(\varDelta\ f \ggg \alpha)^{\cap}
\\
&=
\varDelta\ \eta_{d} \ggg (\varDelta\ f \ggg \alpha) \cdot G
\\
&=
\varDelta\ \eta_{d} \ggg \varDelta\ (G\ f) \ggg \alpha \cdot G
\\
&=
\varDelta\ (\eta_{d} \ggg G\ f) \ggg \alpha \cdot G
\end{align}
コンマ圏 $\varDelta \downarrow M \cdot G$ の射 $(\eta_{d} \ggg G\ f,\mathrm{id}_{\displaystyle*})$ が満たす条件
$\beta = \varDelta\ (\eta_{d} \ggg G\ f) \ggg \alpha \cdot G$ が成り立つ。
写像 $\psi_{((d,*,\beta),(c,*,\alpha))} \colon \mathrm{Hom}_{\varDelta \downarrow M \cdot G}((d,*,\beta),G_{\displaystyle*}\ (c,*,\alpha)) \longrightarrow \mathrm{Hom}_{\varDelta \downarrow M}(F_{\displaystyle*}\ (d,*,\beta),(c,*,\alpha))$ を
元の対応 $\psi_{((d,*,\beta),(c,*,\alpha))} \colon (g,\mathrm{id}_{\displaystyle*}) \longmapsto (F\ g \ggg \varepsilon_{c},\mathrm{id}_{\displaystyle*})$ で定める。
コンマ圏 $\varDelta \downarrow M \cdot G$ の射 $(g,\mathrm{id}_{\displaystyle*})$ が満たす条件
$\beta = \varDelta\ g \ggg \alpha \cdot G$ により
\begin{align}
\beta_{\cup}
&=
(\varDelta\ g \ggg \alpha \cdot G)_{\cup}
\\
&=
(\varDelta\ g \ggg \alpha \cdot G) \cdot F \ggg M \cdot \varepsilon
\\
&=
\varDelta\ (F\ g) \ggg \alpha \cdot (G \cdot F) \ggg M \cdot \varepsilon
\\
&=
\varDelta\ (F\ g) \ggg \varDelta\ c \cdot \varepsilon \ggg \alpha \cdot \mathrm{id}_{\boldsymbol{C}}
\\
&=
\varDelta\ (F\ g) \ggg \varDelta\ \varepsilon_{c} \ggg \alpha
\\
&=
\varDelta\ (F\ g \ggg \varepsilon_{c}) \ggg \alpha
\end{align}
コンマ圏 $\varDelta \downarrow M$ の射 $(F\ g \ggg \varepsilon_{c},\mathrm{id}_{\displaystyle*})$ が満たす条件
$\beta_{\cup} = \varDelta\ (F\ g \ggg \varepsilon_{c}) \ggg \alpha$ が成り立つ。
この写像 $\varphi_{((d,*,\beta),(c,*,\alpha))}$ と写像 $\psi_{((d,*,\beta),
(c,*,\alpha))}$ は、
1点離散圏 $\mathbf{1}$ の射 $\mathrm{id}_{\displaystyle*}$ を除き第1成分だけを見れば、
随伴関手の定義にて自然な同型射であることを示した
写像 $\varphi_{(d,c)}$ と写像 $\psi_{(d,c)}$ に等しい。
したがって、$\varphi_{((d,*,\beta),(c,*,\alpha))}$ は自然な同型射である
右随伴関手 $G_{\displaystyle*}$ は極限(錐の圏 $\varDelta \downarrow M$ の終対象)を保つ。
関手 $M$ の極限 $(\mathrm{lim}_{\boldsymbol{J}}M,\varepsilon_{M})$ が存在すれば、
関手 $M \cdot G$ の極限 $(G\ (\mathrm{lim}_{\boldsymbol{J}}M),\varepsilon_{M} \cdot G)$ が定まる。
右随伴関手 $G$ は極限と交換する。
$G\ (\mathrm{lim}_{\boldsymbol{J}}M) \cong \mathrm{lim}_{\boldsymbol{J}}(M \cdot G)$
余極限
余錐の圏 $M \downarrow \varDelta$ の始対象 $(*,\mathrm{colim}^{\boldsymbol{J}}\!M,\eta_{M})$
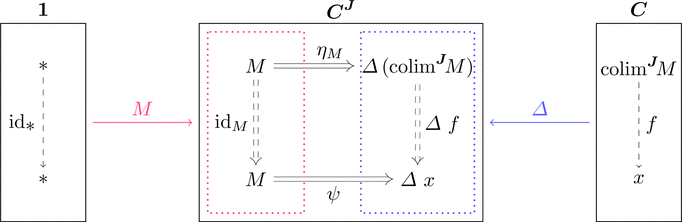
すなわち $(\mathrm{colim}^{\boldsymbol{J}}\!M,\eta_{M})$ は $M$ から $\varDelta$ への普遍射であり、
これを関手 $M \colon \boldsymbol{J} \longrightarrow \boldsymbol{C}$ の余極限 $\mathrm{colim}^{\boldsymbol{J}}\!M$ と呼ぶ。
各対象 $M \in \mathrm{Obj}(\boldsymbol{C}^{\boldsymbol{J}})$ に対して普遍射 $(\mathrm{colim}^{\boldsymbol{J}}\!M,\eta_{M})$
が存在するとき、関手 $\mathrm{colim}^{\boldsymbol{J}} \colon \boldsymbol{C}^{\boldsymbol{J}} \longrightarrow \boldsymbol{C}$ と
自然変換 $\eta \colon \mathrm{id}_{\boldsymbol{C}^{\boldsymbol{J}}} \Longrightarrow \mathrm{colim}^{\boldsymbol{J}} \cdot \varDelta$ が定義できて、
随伴関係 $\mathrm{colim}^{\boldsymbol{J}} \dashv \varDelta$ すなわち次式が成り立つ。
$\mathrm{Hom}_{\boldsymbol{C}}(\mathrm{colim}^{\boldsymbol{J}}-,-) \cong \mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{J}}}(-,\varDelta\ -)$
圏の平方にて定義を与えた関手 $(a,b) \colon \mathbf{2} \longrightarrow \boldsymbol{C}$ の
余極限 $\mathrm{colim}_{\mathbf{2}}(a,b) \cong a + b$ が余直積である。
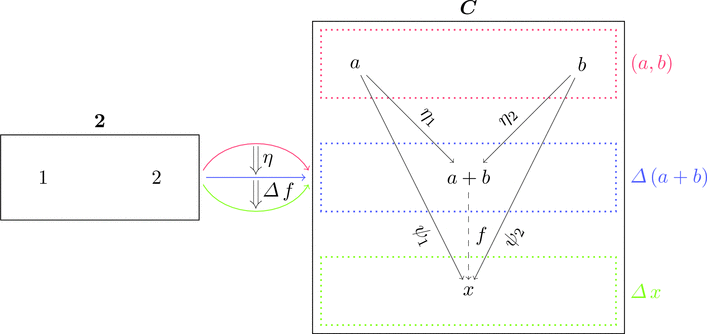
$\mathrm{Obj}(\mathbf{2}) \ni i = 1,2$ として、$\psi_{i} = \eta_{i} \ggg f$ である。
ここでは $\eta_{(a,b)}$ を $\eta$ と略記している。
左随伴関手との交換
関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{C}$ に対して
$F \dashv G$ が随伴であるとき以下が成り立つ。
圏 $\boldsymbol{C}$ の始対象 $0 \in \mathrm{Obj}(\boldsymbol{C})$ が存在すれば、
圏 $\boldsymbol{D}$ の始対象 $F\ 0 \in \mathrm{Obj}(\boldsymbol{D})$ が定まる。
すなわち、左随伴関手 $F$ は[__始対象__](#始対象)を保つ。
$F \dashv G$ より次の自然な同型射が存在する。
$\varphi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{D}}(F\ c, d) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(c, G\ d)$
$\psi_{(c,d)} \colon \mathrm{Hom}_{\boldsymbol{C}}(c, G\ d) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ c, d)$
始対象 $0 \in \mathrm{Obj}(\boldsymbol{C})$ が存在すれば、
任意の対象 $d \in \mathrm{Obj}(\boldsymbol{D})$ に対して
射 $\mathrm{Mor}(\boldsymbol{D}) \ni f \colon F\ 0 \longrightarrow d$ が、
写像 $\psi_{(0,d)} \colon \mathrm{Hom}_{\boldsymbol{C}}(0, G\ d) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ 0, d)$ により、
一意に存在することが分かる。
$F^{\displaystyle*} \dashv G^{\displaystyle*}$ が随伴となるような
関手 $F^{\displaystyle*} \colon M \downarrow \varDelta \longrightarrow M \cdot F \downarrow \varDelta$ と
関手 $G^{\displaystyle*} \colon M \cdot F \downarrow \varDelta \longrightarrow M \downarrow \varDelta$ を
構成することができる。
対象の対応 $F^{\displaystyle*}\ (*,c,\alpha) = (*,F\ c,\alpha \cdot F)$ と
射の対応 $F^{\displaystyle*}\ (\mathrm{id}_{\displaystyle*},p) = (\mathrm{id}_{\displaystyle*},F\ p)$ を
対象の対応 $G^{\displaystyle*}\ (*,d,\beta) = (*,G\ d,\beta^{\cap})$ と
射の対応 $G^{\displaystyle*}\ (\mathrm{id}_{\displaystyle*},q) = (\mathrm{id}_{\displaystyle*},G\ q)$ を
それぞれ定める。
ここで $\beta^{\cap} = M \cdot \eta \ggg \beta \cdot G$ であり、
${\beta^{\cap}}_{\cup} = \beta^{\cap} \cdot F \ggg \varDelta\ \varepsilon_{d} = \beta$ である。
写像 $\varphi_{((*,c,\alpha),(*,d,\beta))} \colon \mathrm{Hom}_{M \cdot F \downarrow \varDelta}(F^{\displaystyle*}\ (*,c,\alpha),(*,d,\beta)) \longrightarrow \mathrm{Hom}_{M \downarrow \varDelta}((*,c,\alpha),G^{\displaystyle*}\ (*,d,\beta))$ を
元の対応 $\varphi_{((*,c,\alpha),(*,d,\beta))} \colon (\mathrm{id}_{\displaystyle*},f) \longmapsto (\mathrm{id}_{\displaystyle*},\eta_{c} \ggg G\ f)$ で定める。
コンマ圏 $M \cdot F \downarrow \varDelta$ の射 $(\mathrm{id}_{\displaystyle*},f)$ が満たす条件
$\beta = \alpha \cdot F \ggg \varDelta\ f$ により
\begin{align}
\beta^{\cap}
&=
(\alpha \cdot F \ggg \varDelta\ f)^{\cap}
\\
&=
M \cdot \eta \ggg (\alpha \cdot F \ggg \varDelta\ f) \cdot G
\\
&=
M \cdot \eta \ggg \alpha \cdot (F \cdot G) \ggg \varDelta\ (G\ f)
\\
&=
\alpha \cdot \mathrm{id}_{\boldsymbol{C}} \ggg \varDelta\ c \cdot \eta \ggg \varDelta\ (G\ f)
\\
&=
\alpha \ggg \varDelta\ \eta_{c} \ggg \varDelta\ (G\ f)
\\
&=
\alpha \ggg \varDelta\ (\eta_{c} \ggg G\ f)
\end{align}
コンマ圏 $M \downarrow \varDelta$ の射 $(\mathrm{id}_{\displaystyle*},\eta_{c} \ggg G\ f)$ が満たす条件
$\beta^{\cap} = \alpha \ggg \varDelta\ (\eta_{c} \ggg G\ f)$ が成り立つ。
写像 $\psi_{((*,c,\alpha),(*,d,\beta))} \colon \mathrm{Hom}_{M \downarrow \varDelta}((*,c,\alpha),G^{\displaystyle*}\ (*,d,\beta)) \longrightarrow \mathrm{Hom}_{M \cdot F \downarrow \varDelta}(F^{\displaystyle*}\ (*,c,\alpha),(*,d,\beta))$ を
元の対応 $\psi_{((*,c,\alpha),(*,d,\beta))} \colon (\mathrm{id}_{\displaystyle*},g) \longmapsto (\mathrm{id}_{\displaystyle*},F\ g \ggg \varepsilon_{d})$ で定める。
コンマ圏 $M \downarrow \varDelta$ の射 $(\mathrm{id}_{\displaystyle*},g)$ が満たす条件
$\beta^{\cap} = \alpha \ggg \varDelta\ g$ により
\begin{align}
\beta
&=
(\alpha \ggg \varDelta\ g)_{\cup}
\\
&=
(\alpha \ggg \varDelta\ g) \cdot F \ggg \varDelta\ \varepsilon_{d}
\\
&=
\alpha \cdot F \ggg \varDelta\ (F\ g) \ggg \varDelta\ \varepsilon_{d}
\\
&=
\alpha \cdot F \ggg \varDelta\ (F\ g \ggg \varepsilon_{d})
\end{align}
コンマ圏 $M \cdot F \downarrow \varDelta$ の射 $(\mathrm{id}_{\displaystyle*},F\ g \ggg \varepsilon_{d})$ が満たす条件
$\beta = \alpha \cdot F \ggg \varDelta\ (F\ g \ggg \varepsilon_{d})$ が成り立つ。
この写像 $\varphi_{((*,c,\alpha),(*,d,\beta))}$ と写像 $\psi_{((*,c,\alpha),
(*,d,\beta))}$ は、
1点離散圏 $\mathbf{1}$ の射 $\mathrm{id}_{\displaystyle*}$ を除き第2成分だけを見れば、
随伴関手の定義にて自然な同型射であることを示した
写像 $\varphi_{(c,d)}$ と写像 $\psi_{(c,d)}$ に等しい。
したがって、$\varphi_{((*,c,\alpha),(*,d,\beta))}$ は自然な同型射である
左随伴関手 $F^{\displaystyle*}$ は余極限(余錐の圏 $M \downarrow \varDelta$ の始対象)を保つ。
関手 $M$ の余極限 $(\mathrm{colim}^{\boldsymbol{J}}M,\eta_{M})$ が存在すれば、
関手 $M \cdot F$ の余極限 $(F\ (\mathrm{colim}^{\boldsymbol{J}}M),\eta_{M} \cdot F)$ が定まる。
左随伴関手 $F$ は余極限と交換する。
$F\ (\mathrm{colim}^{\boldsymbol{J}}M) \cong \mathrm{colim}^{\boldsymbol{J}}(M \cdot F)$
エンドとコエンド
Haskell では
Data.Functor.Kan.Ranまたは
Data.Functor.Kan.Lanにて、
右カン拡張または左カン拡張を
エンドとしてまたはコエンドとして
それぞれ記述している。
楔の圏の終対象がエンドであり、
余楔の圏の始対象がコエンドである。
エンド
楔の圏 $\varDelta \downarrow \overline{T}$ の終対象 $(\int_{\boldsymbol{J}}T,*,\varepsilon_{\overline{T}})$
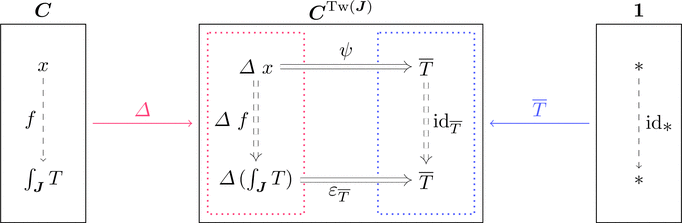
すなわち $(\int_{\boldsymbol{J}}T,\varepsilon_{\overline{T}})$ は $\varDelta$ から $\overline{T}$ への普遍射
もしくは関手 $\overline{T} \colon \mathrm{Tw}(\boldsymbol{J}) \longrightarrow \boldsymbol{C}$ の極限 $\mathrm{lim}_{\mathrm{Tw}(\boldsymbol{J})}\overline{T}$ であり、
双関手 $T \colon \boldsymbol{J}^{\mathrm{op}}\times\boldsymbol{J} \longrightarrow \boldsymbol{C}$ のエンド $\int_{\boldsymbol{J}}T$ と呼ぶ。
各対象 $\overline{T} \in \mathrm{Obj}(\boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J})})$ に対して普遍射 $(\int_{\boldsymbol{J}}T,\varepsilon_{\overline{T}})$
が存在するとき、関手 $\int_{\boldsymbol{J}} \colon \boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J})} \longrightarrow \boldsymbol{C}$ と
自然変換 $\varepsilon \colon \int_{\boldsymbol{J}} \cdot \varDelta \Longrightarrow \mathrm{id}_{\boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J})}}$ が定義できて、
随伴関係 $\varDelta \dashv \int_{\boldsymbol{J}}$ すなわち次式が成り立つ。
$\mathrm{Hom}_{\boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J})}}(\varDelta\ -,-) \cong \mathrm{Hom}_{\boldsymbol{C}}(-,\int_{\boldsymbol{J}}-)$
全称量化子
双関手 $\mathrm{Hom}_{\boldsymbol{D}}(F\ -,G\ -) \colon \boldsymbol{C}^{\mathrm{op}}\times\boldsymbol{C} \longrightarrow \mathbf{Set}$ の
エンドに関して、次の式が成り立つ。
$T = \mathrm{Hom}_{\boldsymbol{D}}(F\ -,G\ -)$ とする。
楔 $\psi \colon \varDelta\ X \Longrightarrow \overline{T}$ を考えると、
各対象 $\mathrm{Obj}(\mathrm{Tw}(\boldsymbol{C})) \ni h \colon a \longrightarrow b$ に対して
射 $\mathrm{Mor}(\mathbf{Set}) \ni \psi_{h} \colon X \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ a,G\ b)$
すなわち写像 $\psi_{h}$ が存在する。
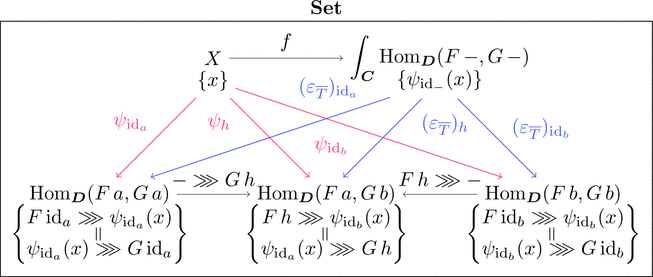
写像 $\psi_{h}$ は元の対応で次のように定義される。
$\psi_{h} \colon x \longmapsto F\ h \ggg \psi_{\mathrm{id}_{b}}(x) = \psi_{\mathrm{id}_{a}}(x) \ggg G\ h$
各対象 $a \in \mathrm{Obj}(\boldsymbol{C})$ に対して射 $\psi_{\mathrm{id}_{a}}(x) \colon F\ a \longrightarrow G\ a$
が存在するため $\psi_{\mathrm{id}_{-}}(x)$ は射の族であり、また
条件 $F\ h \ggg \psi_{\mathrm{id}_{b}}(x) = \psi_{\mathrm{id}_{a}}(x) \ggg G\ h$
を満たすため自然変換 $\psi_{\mathrm{id}_{-}}(x) \colon F \Longrightarrow G$ である。
楔 $\varepsilon_{\overline{T}} \colon \varDelta,\left(\mathrm{Hom}_{\boldsymbol{D}^\boldsymbol{C}}(F,G)\right) \Longrightarrow \overline{T}$ を
写像 $(\varepsilon_{\overline{T}})_{h} \colon \mathrm{Hom}_{\boldsymbol{D}^\boldsymbol{C}}(F,G) \longrightarrow \mathrm{Hom}_{\boldsymbol{D}}(F\ a,G\ b)$ すなわち
元の対応 $(\varepsilon_{\overline{T}})_{h} \colon \psi_{\mathrm{id}_{-}}(x) \longmapsto F\ h \ggg \psi_{\mathrm{id}_{b}}(x) = \psi_{\mathrm{id}_{a}}(x) \ggg G\ h$
として定義することができる。
このとき、任意の楔 $\psi$ に対して、
射(すなわち写像) $f \colon X \longrightarrow \mathrm{Hom}_{\boldsymbol{D}^\boldsymbol{C}}(F,G)$ が
元の対応 $f \colon x \longmapsto \psi_{\mathrm{id}_{-}}(x)$ により定まり、
$f \ggg (\varepsilon_{\overline{T}})_{h} = \psi_{h}$ すなわち $\varDelta\ f \ggg \varepsilon_{\overline{T}} = \psi$ を満たす。
$\displaystyle \mathrm{Hom}_{\boldsymbol{D}^\boldsymbol{C}}(F,G) \cong \int_{\boldsymbol{C}}\mathrm{Hom}_{\boldsymbol{D}}(F\ -,G\ -)$
{-# LANGUAGE Rank2Types #-}
{-# LANGUAGE TypeOperators #-}
type f ~> g = forall c. f c -> g c
自然変換とはすべての対象(すなわち型)に対して
存在する射(すなわち関数)を集めたものである。
エンドの記法として、対象 $c \in \mathrm{Obj}(\boldsymbol{C})$ を明示し
$\displaystyle \mathrm{Hom}_{\boldsymbol{D}^\boldsymbol{C}}(F,G) \cong \int_{c \in \boldsymbol{C}}\mathrm{Hom}_{\boldsymbol{D}}(F\ c,G\ c)$
と書く場合もある。コエンドでも同様の記法を用いる。
ある双関手 $T \colon \mathbf{Set}^{\mathrm{op}}\times\mathbf{Set} \longrightarrow \mathbf{Set}$ の
エンド $\int_{j\in\mathbf{Set}}T(j,j)$ は Haskell で次のように書ける。
{-# LANGUAGE Rank2Types #-}
data End t = End (forall j. t j j)
積分記号 $\int_{j\in\mathbf{Set}}$ と全称量化子 forall j が対応している。
コエンド
余楔の圏 $\overline{T^{\mathrm{op}}}^{\mathrm{op}} \downarrow \varDelta$ の始対象 $(*,\int^{\boldsymbol{J}}T,\eta_{\overline{T^{\mathrm{op}}}^{\mathrm{op}}})$
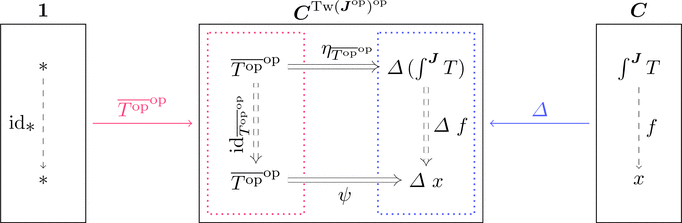
すなわち $(\int^{\boldsymbol{J}}T,\eta_{\overline{T^{\mathrm{op}}}^{\mathrm{op}}})$ は $\overline{T^{\mathrm{op}}}^{\mathrm{op}}$ から $\varDelta$ への普遍射
もしくは関手 $\overline{T^{\mathrm{op}}}^{\mathrm{op}} \colon \mathrm{Tw}(\boldsymbol{J}^{\mathrm{op}})^{\mathrm{op}} \longrightarrow \boldsymbol{C}$ の余極限 $\mathrm{colim}^{\mathrm{Tw}(\boldsymbol{J}^{\mathrm{op}})^{\mathrm{op}}}\overline{T^{\mathrm{op}}}^{\mathrm{op}}$ であり、
双関手 $T \colon \boldsymbol{J}^{\mathrm{op}}\times\boldsymbol{J} \longrightarrow \boldsymbol{C}$ のコエンド $\int^{\boldsymbol{J}}T$ と呼ぶ。
各対象 $\overline{T^{\mathrm{op}}}^{\mathrm{op}} \in \mathrm{Obj}(\boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J}^{\mathrm{op}})^{\mathrm{op}}})$ に対して普遍射 $(\int^{\boldsymbol{J}}T,\eta_{\overline{T^{\mathrm{op}}}^{\mathrm{op}}})$
が存在するとき、関手 $\int^{\boldsymbol{J}} \colon \boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J}^{\mathrm{op}})^{\mathrm{op}}} \longrightarrow \boldsymbol{C}$ と
自然変換 $\eta \colon \mathrm{id}_{\boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J}^{\mathrm{op}})^{\mathrm{op}}}} \Longrightarrow \int^{\boldsymbol{J}} \cdot \varDelta$ が定義できて、
随伴関係 $\int^{\boldsymbol{J}} \dashv \varDelta$ すなわち次式が成り立つ。
$\mathrm{Hom}_{\boldsymbol{C}}(\int^{\boldsymbol{J}}-,-) \cong \mathrm{Hom}_{\boldsymbol{C}^{\mathrm{Tw}(\boldsymbol{J}^{\mathrm{op}})^{\mathrm{op}}}}(-,\varDelta\ -)$
存在量化子
ある双関手 $T \colon \mathbf{Set}^{\mathrm{op}}\times\mathbf{Set} \longrightarrow \mathbf{Set}$ の
コエンド $\int^{j\in\mathbf{Set}}T(j,j)$ は Haskell で次のように書ける。
{-# LANGUAGE ExistentialQuantification #-}
data CoEnd t = forall j. CoEnd (t j j)
積分記号 $\int^{j\in\mathbf{Set}}$ と存在量化子 forall j が対応している。
全称量化子と同じく forall j なのでややこしいが、
一般化代数的データ型(__G__eneralized __A__lgebraic __D__ata __T__ype)
を考えれば両者の違いを思い出せるだろう。
{-# LANGUAGE GADTs #-}
{-# LANGUAGE ExplicitForAll #-}
data T = forall a. T a
data T' where
T' :: forall a. a -> T'
T と T' は型として同じものをあらわし、
すべての型 a から1つの型 T が作れる。
また一方で、型 T の中身はある型 a である。
直和型も同様に複数の型から1つの型が作れる。
data CB = C Char | B Bool
型 CB の中身はある型(Char か Bool)である。
カン拡張
全ての概念5と呼ばれる
カン拡張を最後に定義する。
柱の圏の終対象が右カン拡張であり、
余柱の圏の始対象が左カン拡張である。
関手 $F \colon \boldsymbol{J} \longrightarrow \boldsymbol{D}$ の終域 $\boldsymbol{D}$ が
1点離散圏 $\mathbf{1}$ であるならば、
関手 $F \cdot -$ は対角関手 $\varDelta$ となるため、
極限と余極限に帰着することを注意しよう。
右カン拡張
柱の圏 $F \cdot - \downarrow M$ の終対象 $(\mathrm{Ran}_{F}M,*,\varepsilon_{M})$
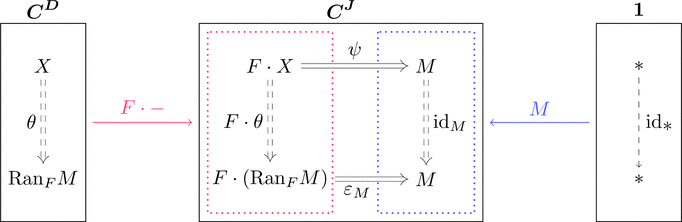
すなわち $(\mathrm{Ran}_{F}M,\varepsilon_{M})$ は $F \cdot -$ から $M$ への普遍射であり、
$F$ に沿った $M$ の右カン拡張 $\mathrm{Ran}_{F}M$ と呼ぶ。
各対象 $M \in \mathrm{Obj}(\boldsymbol{C}^{\boldsymbol{J}})$ に対して普遍射 $(\mathrm{Ran}_{F}M,\varepsilon_{M})$
が存在するとき、関手 $\mathrm{Ran}_{F} \colon \boldsymbol{C}^{\boldsymbol{J}} \longrightarrow \boldsymbol{C}^{\boldsymbol{D}}$ と
自然変換 $\varepsilon \colon F \cdot (\mathrm{Ran}_{F},-) \Longrightarrow \mathrm{id}_{\boldsymbol{C}^{\boldsymbol{J}}}$ が定義できて、
随伴関係 $F \cdot - \dashv \mathrm{Ran}_{F}$ すなわち次式が成り立つ。
$\mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{J}}}(F \cdot -,-) \cong \mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{D}}}(-,\mathrm{Ran}_{F},-)$
極限として
コンマ圏 $d \downarrow F$ を考えることで次の図式を得る。
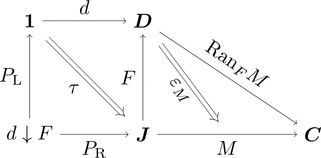
双関手 $- \cdot - \colon \mathbf{1}^{d \downarrow F} \times \boldsymbol{C}^{\mathbf{1}} \longrightarrow \boldsymbol{C}^{d \downarrow F}$ の
左セクション $P_{\mathrm{L}} \cdot - \colon \boldsymbol{C}^{\mathbf{1}} \longrightarrow \boldsymbol{C}^{d \downarrow F}$ は
対角関手 $\varDelta \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}^{d \downarrow F}$ となる。
$P_{\mathrm{L}}$ に沿った $P_{\mathrm{R}} \cdot M$ の右カン拡張は
関手 $P_{\mathrm{R}} \cdot M \colon d \downarrow F \longrightarrow \boldsymbol{C}$ の極限である4。
$(\mathrm{Ran}_{F}M)\ d \cong \mathrm{lim}_{d \downarrow F}(P_{\mathrm{R}} \cdot M)$
エンドとして
双関手 $\mathrm{Hom}_{\boldsymbol{D}}(d,F\ -) \pitchfork M\ - \colon \boldsymbol{J}^{\mathrm{op}}\times\boldsymbol{J} \longrightarrow \boldsymbol{C}$ の
エンドとして、右カン拡張を
$\displaystyle \mathrm{Ran}_{F}M\ d \cong \int_{j\in\boldsymbol{J}} \mathrm{Hom}_{\boldsymbol{D}}(d,F\ j) \pitchfork M\ j$
と書くことができる。
以下の式変形により示すことができる4。
\begin{align}
\mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{D}}}(X,\mathrm{Ran}_{F}M)
&\cong
\int_{d\in\boldsymbol{D}}\mathrm{Hom}_{\boldsymbol{C}}(X\ d,\mathrm{Ran}_{F}M\ d)
\\
&\cong
\int_{d\in\boldsymbol{D}}\mathrm{Hom}_{\boldsymbol{C}}\left(X\ d,\int_{j\in\boldsymbol{J}} \mathrm{Hom}_{\boldsymbol{D}}(d,F\ j) \pitchfork M\ j\right)
\\
&\cong
\int_{d\in\boldsymbol{D}}\int_{j\in\boldsymbol{J}}\mathrm{Hom}_{\boldsymbol{C}}(X\ d,\mathrm{Hom}_{\boldsymbol{D}}(d,F\ j) \pitchfork M\ j)
\\
&\cong
\int_{d\in\boldsymbol{D}}\int_{j\in\boldsymbol{J}}\mathrm{Hom}_{\mathbf{Set}^{\mathrm{op}}}(\mathrm{Hom}_{\boldsymbol{C}}^{\mathrm{op}}(X\ d,M\ j),\mathrm{Hom}_{\boldsymbol{D}}^{\mathrm{op}}(d,F\ j))
\\
&\cong
\int_{j\in\boldsymbol{J}}\int_{d\in\boldsymbol{D}}\mathrm{Hom}_{\mathbf{Set}^{\mathrm{op}}}(\mathrm{Hom}_{\boldsymbol{C}}^{\mathrm{op}}(X\ d,M\ j),\mathrm{Hom}_{\boldsymbol{D}}^{\mathrm{op}}(d,F\ j))
\\
&\cong
\int_{j\in\boldsymbol{J}}\mathrm{Hom}_{{\mathbf{Set}^{\mathrm{op}}}^{\boldsymbol{D}}}(\mathrm{Hom}_{\boldsymbol{C}}^{\mathrm{op}}(X\ -,M\ j),\mathrm{Hom}_{\boldsymbol{D}}^{\mathrm{op}}(-,F\ j))
\\
&\cong
\int_{j\in\boldsymbol{J}}\mathrm{Hom}_{\boldsymbol{C}}((F \cdot X)\ j,M\ j)
\\
&\cong
\mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{J}}}(F \cdot X,M)
\end{align}
圏 $\boldsymbol{C}$ を集合の圏 $\mathbf{Set}$ (すなわち圏 $\mathbf{Hask}$)とすれば
余テンソル対象 $B \pitchfork C$ は $\mathrm{Hom}_{\mathbf{Set}}(B, C)$ であり4、
圏 $\boldsymbol{J},\boldsymbol{D}$ も集合の圏 $\mathbf{Set}$ のときは以下となる。
$\displaystyle \mathrm{Ran}_{F}M\ d \cong \int_{j\in\mathbf{Set}} \mathrm{Hom}_{\mathbf{Set}}(\mathrm{Hom}_{\mathbf{Set}}(d,F\ j), M\ j)$
{-# LANGUAGE Rank2Types #-}
data Ran f m d = Ran (forall j. (d -> f j) -> m j)
左カン拡張
余柱の圏 $M \downarrow F \cdot -$ の始対象 $(*,\mathrm{Lan}_{F}M,\eta_{M})$
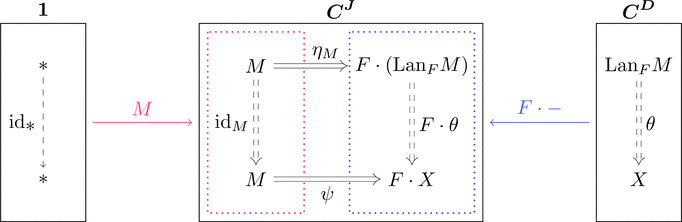
すなわち $(\mathrm{Lan}_{F}M,\eta_{M})$ は $M$ から $F \cdot -$ への普遍射であり、
$F$ に沿った $M$ の左カン拡張 $\mathrm{Lan}_{F}M$ と呼ぶ。
各対象 $M \in \mathrm{Obj}(\boldsymbol{C}^{\boldsymbol{J}})$ に対して普遍射 $(\mathrm{Lan}_{F}M,\eta_{M})$
が存在するとき、関手 $\mathrm{Lan}_{F} \colon \boldsymbol{C}^{\boldsymbol{J}} \longrightarrow \boldsymbol{C}^{\boldsymbol{D}}$ と
自然変換 $\eta \colon \mathrm{id}_{\boldsymbol{C}^{\boldsymbol{J}}} \Longrightarrow F \cdot (\mathrm{Lan}_{F},-)$ が定義できて、
随伴関係 $\mathrm{Lan}_{F} \dashv F \cdot -$ すなわち次式が成り立つ。
$\mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{D}}}(\mathrm{Lan}_{F},-,-) \cong \mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{J}}}(-,F \cdot -)$
余極限として
コンマ圏 $F \downarrow d$ を考えることで次の図式を得る。
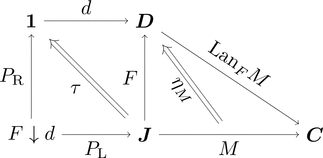
双関手 $- \cdot - \colon \mathbf{1}^{F \downarrow d} \times \boldsymbol{C}^{\mathbf{1}} \longrightarrow \boldsymbol{C}^{F \downarrow d}$ の
左セクション $P_{\mathrm{R}} \cdot - \colon \boldsymbol{C}^{\mathbf{1}} \longrightarrow \boldsymbol{C}^{F \downarrow d}$ は
対角関手 $\varDelta \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}^{F \downarrow d}$ となる。
$P_{\mathrm{R}}$ に沿った $P_{\mathrm{L}} \cdot M$ の左カン拡張は
関手 $P_{\mathrm{L}} \cdot M \colon F \downarrow d \longrightarrow \boldsymbol{C}$ の余極限である4。
$(\mathrm{Lan}_{F}M)\ d \cong \mathrm{colim}^{F \downarrow d}(P_{\mathrm{L}} \cdot M)$
コエンドとして
双関手 $\mathrm{Hom}_{\boldsymbol{D}}(F\ -, d) \odot M\ - \colon \boldsymbol{J}^{\mathrm{op}}\times\boldsymbol{J} \longrightarrow \boldsymbol{C}$ の
コエンドとして、左カン拡張を
$\displaystyle \mathrm{Lan}_{F}M\ d \cong \int^{j\in\boldsymbol{J}}\!\!\mathrm{Hom}_{\boldsymbol{D}}(F\ j, d) \odot M\ j$
と書くことができる。
以下の式変形により示すことができる4。
\begin{align}
\mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{D}}}(\mathrm{Lan}_{F}M,X)
&\cong
\int_{d\in\boldsymbol{D}}\mathrm{Hom}_{\boldsymbol{C}}(\mathrm{Lan}_{F}M\ d,X\ d)
\\
&\cong
\int_{d\in\boldsymbol{D}}\mathrm{Hom}_{\boldsymbol{C}}\left(\int^{j\in\boldsymbol{J}}\!\!\mathrm{Hom}_{\boldsymbol{D}}(F\ j, d) \odot M\ j,X\ d\right)
\\
&\cong
\int_{d\in\boldsymbol{D}}\int_{j\in\boldsymbol{J}}\mathrm{Hom}_{\boldsymbol{C}}\left(\mathrm{Hom}_{\boldsymbol{D}}(F\ j, d) \odot M\ j,X\ d\right)
\\
&\cong
\int_{d\in\boldsymbol{D}}\int_{j\in\boldsymbol{J}}\mathrm{Hom}_{\mathbf{Set}}(\mathrm{Hom}_{\boldsymbol{D}}(F\ j, d),\mathrm{Hom}_{\boldsymbol{C}}(M\ j,X\ d))
\\
&\cong
\int_{j\in\boldsymbol{J}}\int_{d\in\boldsymbol{D}}\mathrm{Hom}_{\mathbf{Set}}(\mathrm{Hom}_{\boldsymbol{D}}(F\ j, d),\mathrm{Hom}_{\boldsymbol{C}}(M\ j,X\ d))
\\
&\cong
\int_{j\in\boldsymbol{J}}\mathrm{Hom}_{\mathbf{Set}^{\boldsymbol{D}}}(\mathrm{Hom}_{\boldsymbol{D}}(F\ j, -),\mathrm{Hom}_{\boldsymbol{C}}(M\ j,X\ -))
\\
&\cong
\int_{j\in\boldsymbol{J}}\mathrm{Hom}_{\boldsymbol{C}}(M\ j,(F \cdot X)\ j)
\\
&\cong
\mathrm{Hom}_{\boldsymbol{C}^{\boldsymbol{J}}}(M,F \cdot X)
\end{align}
圏 $\boldsymbol{C}$ を集合の圏 $\mathbf{Set}$ (すなわち圏 $\mathbf{Hask}$)とすれば
テンソル対象 $A \odot B$ は直積 $A \times B$ であり4、
圏 $\boldsymbol{J},\boldsymbol{D}$ も集合の圏 のときは以下となる。
$\displaystyle \mathrm{Lan}_{F}M\ d \cong \int^{j\in\mathbf{Set}}\!\!\mathrm{Hom}_{\mathbf{Set}}(F\ j, d) \times M\ j$
{-# LANGUAGE ExistentialQuantification #-}
data Lan f m d = forall j. Lan (f j -> d, m j)
まとめ
普遍性による定義が分かりづらいのは
「満たすべき条件」や「可換性」や「一意性」
などの諸概念が同時に押し寄せるからだろう。
ここでは「満たすべき条件」や「可換性」を
自然変換やコンマ圏が満たす条件として、
また「一意性」を終対象や始対象として、
それぞれ分離することで単純化を試みた。
カン拡張を結局どう使うのかは
現時点で分からないけれども、
極限からカン拡張への雰囲気は
把握できたのではないかと思う。