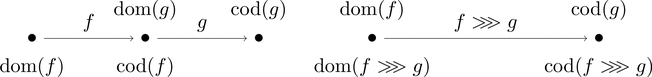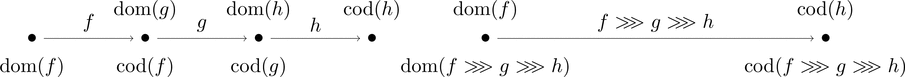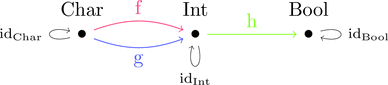Go to Qiita Advent Calendar 2024 Top
LoginSignup
99
83

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 3 years have passed since last update.

@norkron

もう諦めない圏論入門―対象と射―

Last updated at Posted at 2019-02-13

想定読者と到達目標

圏論に入門しようと定義などを眺めてみたものの
それより先に進む方法が分からない人へ向けて。

具体例を通して、抽象的な定義を受け入れつつ、
自分が何を分かっていないか分かるようにする。

大学数学の知識は特に仮定していないつもりなので、
「圏論を理解できないのは○○が分からないからだ」
みたいな自分自身に対する言い訳を排除したい所存。

ひとまず細かいことは気にせず雰囲気を掴んでおいて、
必要の際1に詳細文献を読めるような下地作りが目標。

目次

圏の定義

まずは定義を見てみましょう。
具体例を考えたとき、それが圏の定義を満たしているのか、
確認したくなったらここに戻ってくれば良い。

確認を重ねるうちに定義には慣れてくるはずだ。

対象と射

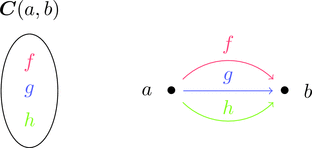
対象2の集まり $\mathrm{Obj}(\boldsymbol{C})$ と
射3の集まり $\mathrm{Mor}(\boldsymbol{C})$ で構成される $\boldsymbol{C}$ を考える。

有向グラフ

対象を $\bullet$ で射を $\longrightarrow$ で描いている。

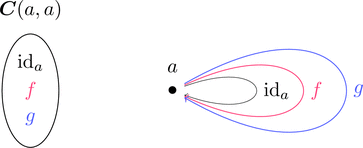
各々の対象 $a,b \in \mathrm{Obj}(\boldsymbol{C})$ に対して集合 $\boldsymbol{C}(a,b)$ が存在し、
その元 $f \in \boldsymbol{C}(a,b)$ を射 $f \colon a \longrightarrow b$ と呼ぶ。

集合と射

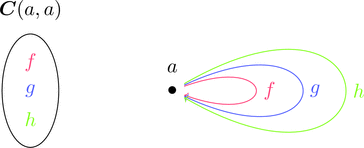
左図と右図は同じものを表している。

集合と自己射

のように集合 $\boldsymbol{C}(a,a)$ も存在するし、

空集合

のように集合 $\boldsymbol{C}(a,b)$ は空集合でも良い。

つまり、各々の射 $f\in\mathrm{Mor}(\boldsymbol{C})$ に対して
始域4 $\mathrm{dom}(f)\in\mathrm{Obj}(\boldsymbol{C})$ と呼ばれる対象と
終域5 $\mathrm{cod}(f)\in\mathrm{Obj}(\boldsymbol{C})$ と呼ばれる対象が存在する。

射

射 $\longrightarrow$ を描いたときは必ず矢尻と矢頭に対象 $\bullet$ が存在する。

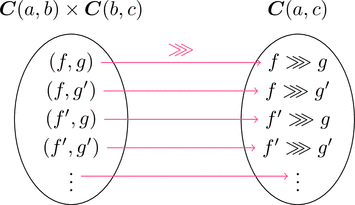
合成射

直積集合 $\boldsymbol{C}(a,b) \times \boldsymbol{C}(b,c)$ から集合 $\boldsymbol{C}(a,c)$ への
写像 $\ggg \colon \boldsymbol{C}(a,b) \times \boldsymbol{C}(b,c) \longrightarrow \boldsymbol{C}(a,c)$ が存在する。

射を合成する写像

元の対応を $\ggg \colon (f,g)\longmapsto f \ggg g$ と書く。

つまり、射 $f, g$ が $\mathrm{cod}(f)=\mathrm{dom}(g)$ を満たすとき合成射 $f \ggg g$ が存在し、
$\mathrm{dom}(f)=\mathrm{dom}(f \ggg g)$ かつ $\mathrm{cod}(f \ggg g)=\mathrm{cod}(g)$ である。

射の合成

左図を描いたときは必ず右図のような合成射が存在する。
圏なら合成射は必ず存在するので図を描くときに省略してよい。

恒等射

集合 $\boldsymbol{C}(a,a)$ には恒等射6と呼ばれる元 $\mathrm{id}_{a}$ が必ず存在する。
つまり、各対象 $a \in \mathrm{Obj}(\boldsymbol{C})$ に恒等射 $\mathrm{id}_{a} \colon a \longrightarrow a$ が存在する。

恒等射

単位元的なものが複数あることを最初は不思議に思った気がする。
圏なら恒等射は必ず存在するので図を描くときに省略してよい。

集合 $\boldsymbol{C}(a,a)$ の中に恒等射 $\mathrm{id}_{a}$ が存在すれば良いだけなので、
恒等射以外に他の射があっても構わないことに注意しよう。

恒等射と自己射

また、集合 $\boldsymbol{C}(a,a)$ の元だからと言って
それが恒等射であるとは限らないことにも注意。

後に示す条件(単位律)を満たす射を恒等射 $\mathrm{id}_{a}$ と呼ぶ。

圏

射 $f,g,h,\mathrm{id}_{a},\mathrm{id}_{b} \in\mathrm{Mor}(\boldsymbol{C})$ と対象 $a,b\in\mathrm{Obj}(\boldsymbol{C})$ に対して、
次の２つの条件を満たすとき、$\boldsymbol{C}$ は圏である。

  1. （結合律）$(f \ggg g) \ggg h=f \ggg (g \ggg h)$ が成り立つ。
  2. （単位律）$\mathrm{id}_{a} \ggg f = f \ggg \mathrm{id}_{b} = f$ が成り立つ。

モノイドでは単一の集合 $S$ に関して
写像 $\diamond \colon S \times S \longrightarrow S$ や単位元 $e \in S$ を考えていたが、
圏では複数の集合 $\boldsymbol{C}(a,b),\boldsymbol{C}(b,c),\boldsymbol{C}(a,c),\boldsymbol{C}(a,a)$ に関して
写像 $\ggg \colon \boldsymbol{C}(a,b) \times \boldsymbol{C}(b,c) \longrightarrow \boldsymbol{C}(a,c)$ や
恒等射 $\mathrm{id}_{a} \in \boldsymbol{C}(a,a)$ を考えることになる。

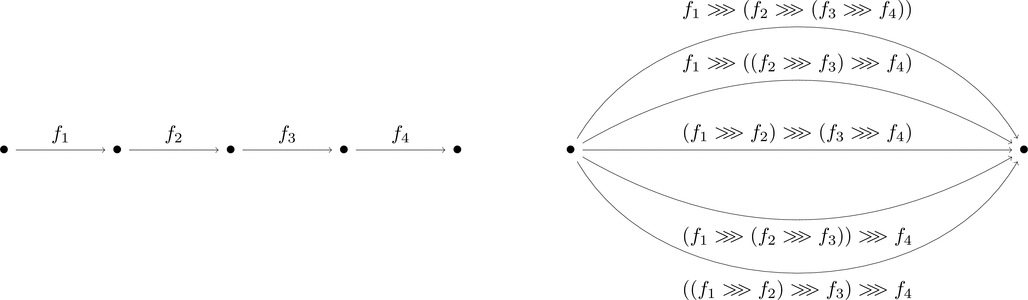
結合律は合成を施す順序が自由なことを意味する。
$f \ggg g = g \ggg f$ が成り立つ交換律との違いに注意しよう。

結合律

左図を描いたときは右図のような合成射を１つ考えればよい。
合成する射の数が増えても同様である。

合成の順序

もし結合律が無ければこれらの射を区別しなければならない。
射の数が増えるとさらにやばい。ありがとう結合律。

圏の具体例

定義ばかりじゃ何も見えてこないので、
具体例を通して定義の理解を深める。

圏が定義できると何が嬉しいのかは置いておいて、
以下の例が圏なことを定義と照らし合わせ考えよう。

対象が型で射が関数な圏

Haskell の型を対象、Haskell の関数を射にすると圏になる
と言うのはどこかで見聞きしたことがあるかもしれない。

全ての型や関数を考えると理解が追いつかないので、
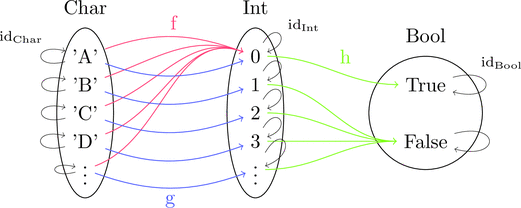
型は $\mathrm{Char}$ と $\mathrm{Int}$ と $\mathrm{Bool}$、関数は次の $\mathrm{f}$ と $\mathrm{g}$ と $\mathrm{h}$ に限定して考える。

Haskell の関数は Category の instance に標準でなっている。

Hask
import Prelude hiding (id)
import Control.Category (id,(>>>))
import Data.Char

f :: Char -> Int
f = const 0

g :: Char -> Int
g = (+ (-65)) . ord

h :: Int -> Bool
h 0 = True
h _ = False

idChar :: Char -> Char
idChar = id

idInt :: Int -> Int
idInt = id

idBool :: Bool -> Bool
idBool = id

射の合成 >>> は関数合成で定義されている。

絵で描くとこんな感じになる。

対象が型で射が関数な圏の内部構造

関数の定義と絵がだいたい対応しているのが分かると思う。
この絵からは集合と写像が思い出されることだろう。

丸で囲まれた集合的な部分の複雑な構造を潰して点 $\bullet$ とみなすと

対象が型で射が関数な圏

のように単純な形が浮き彫りとなる。圏っぽさが増したと主張したい。
このように内部構造を気にせず済む感じがきっと大切なんだろうと思う。

合成射 $\mathrm{f} \ggg \mathrm{h}$ などを矢印 $\rightarrow$ として陽に描いてはいないが、
合成射で見たように、一意に存在するため描画を省略している。

対象が自然数で射が自然数倍の圏

前の例は、値の集合からなる型が対象で、内部構造が複雑だった。
ここでは値がそのまま１つの対象となるような単純な圏を考える。

射を Category の instance にしようとすると対象は型である必要があるため、
圏としては単純でも Haskell 的な意味では少し難しくなってしまう。

「GHCの型レベル自然数を理解する」(2020-04-20)などを参考に、
自然数の値を１つの型として、それを自然数倍する関数を考える。

f (Proxy :: Proxy 2) >>> f (Proxy :: Proxy 5) $$$ (Proxy :: Proxy 2)
とすれば2を2倍の5倍した20が返って来ることを確認できるはずだ。

Nat
{-# LANGUAGE TypeOperators #-}
{-# LANGUAGE DataKinds #-}

import Prelude hiding (id,(.))
import Control.Category
import GHC.TypeLits
import Data.Proxy

data Mor a b = Mor (a -> b)
($$$) (Mor f) = natVal . f
infixr 0 $$$

f :: Proxy i -> Mor (Proxy n) (Proxy (i*n))
f i = Mor $ \n -> Proxy

instance Category Mor where
    id = Mor $ \n -> n
    Mor g . Mor f = Mor $ \n -> g (f n)

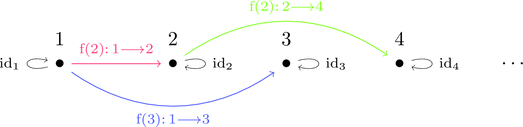
絵で描くとこんな感じになる。

対象が自然数で射が自然数倍の圏

$1$ や $2$ などの数字は、それぞれ Proxy 1 や Proxy 2 などの型をあらわしている。
Int 値の集合である Int 型が対象となる場合との違いに注意すれば、
自然数と自然数倍が圏なことを理解できるのではないだろうか。

図中に $\mathrm{f}(2)$ と言う同じ名前の射が２つあるけれども、
ここでは型(すなわち始域と終域)が異なる射を別の射とみなす。
$\mathrm{f}(i)$ は射の族で、各対象 $n$ に対して射 $\mathrm{f}(i)_{n} \colon n \longrightarrow i*n$ が存在する。

対象１つで射が整数値の圏

これまでの例ではいずれも対象が型で射は関数だった。
ここでは射が関数ではないような圏を考える。

Haskell のユニット型 $()$ を唯一の対象、
Haskell の Integer 値を射とする。

Integer 型のある値を $i$ とすると、
$\mathrm{f}(i) \colon () \longrightarrow ()$ という射がたくさんある。

射の合成が加法で、恒等射は加法の単位元 $0$ とする。

Monoid
import Prelude hiding (id,(.))
import Control.Category

data Mor a b = Mor Integer deriving Show

f :: Integer -> Mor () ()
f = Mor

instance Category Mor where
    id = Mor 0
    Mor i1 . Mor i2 = Mor $ i1 + i2

絵で描くとこんな感じになる。

対象１つで射が整数値の圏

恒等射以外にも、自分自身に戻ってくるような射がたくさんある。

ただし、この例では $\mathrm{id}_{()} = \mathrm{f}(-1) \ggg \mathrm{f}(1)$ および
$\mathrm{f}(2) = \mathrm{f}(1) \ggg \mathrm{f}(1)$ や
$\mathrm{f}(3) = \mathrm{f}(1) \ggg \mathrm{f}(1) \ggg \mathrm{f}(1)$ などが成り立つため、
合成射を陽に描かない場合には射が $\mathrm{f}(-1)$ と $\mathrm{f}(1)$ だけとなり、
射がたくさんあるというのは誤解を招くかもしれない。

Haskell のユニット型 $()$ を対象、
Haskell の String 値を射として、
射の合成が文字列の連結、恒等射は空文字
とする例が適切であったかもしれない7。

いずれにせよ mempty = id、(<>) = (.)とすれば
射を Monoid の instance にすることができるはずだ。

直積と余直積

圏の定義をある程度は理解したところで、
圏があると何が嬉しいのか、その片鱗を見てみたい。

圏がある場合に定義が可能となる直積8と
その双対概念9である余直積を通して圏論を感じよう。

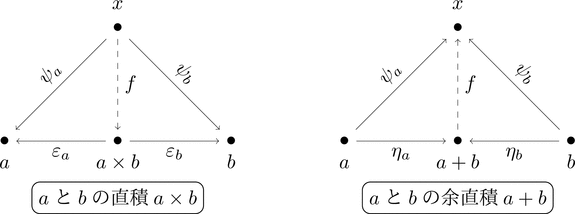
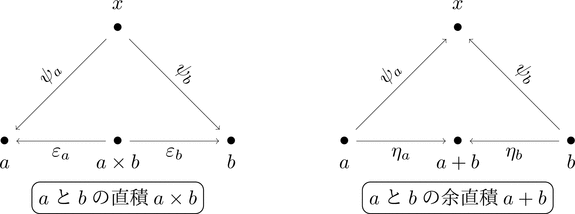
定義

直積(product)
対象 $a \times b$ および射 $\varepsilon_{a} \colon a \times b \longrightarrow a$ と $\varepsilon_{b} \colon a \times b \longrightarrow b$ の組であり、
任意の対象 $x$ および２つの射 $\psi_{a} \colon x \longrightarrow a$と$\psi_{b} \colon x \longrightarrow b$ の組に対して、
点線の射 $f \colon x \longrightarrow a \times b$ が一意に存在し次の図式が可換になる。
余直積(coproduct)
対象 $a + b$ および射 $\eta_{a} \colon a \longrightarrow a + b$ と $\eta_{b} \colon b \longrightarrow a + b$ の組であり、
任意の対象 $x$ および２つの射 $\psi_{a} \colon a \longrightarrow x$ と $\psi_{b} \colon b \longrightarrow x$ の組に対して、
点線の射 $f \colon a + b \longrightarrow x$ が一意に存在し次の図式が可換になる。

直積と余直積の可換図式

直積集合と直和集合

急に絵を持ち出されて、可換になると言われても困るし、
そもそも可換が何を意味するのかすら分からない。

それでも、とにかく具体的な圏を考えて、
上記の定義が何を意味するのか探り当てよう。

まずは、対象が型で射が関数な圏の場合からだ。

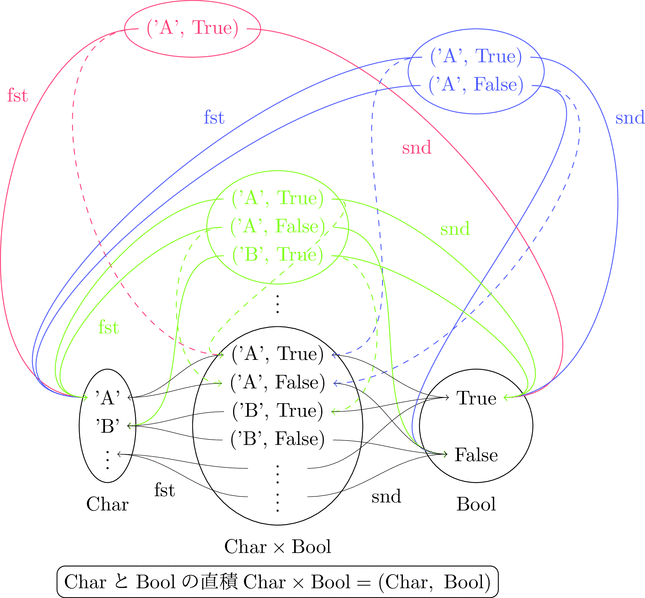
直積の定義は直積集合を意味し、絵で描くとこんな感じになる。

直積集合の内部構造

直積集合の下位集合たちが赤や青や緑で描かれている。
任意の下位集合、すなわち任意の対象 $x$ に対し定義のような射が存在する。
実線の射が存在すれば、点線の射が一意に存在することが分かるだろう。

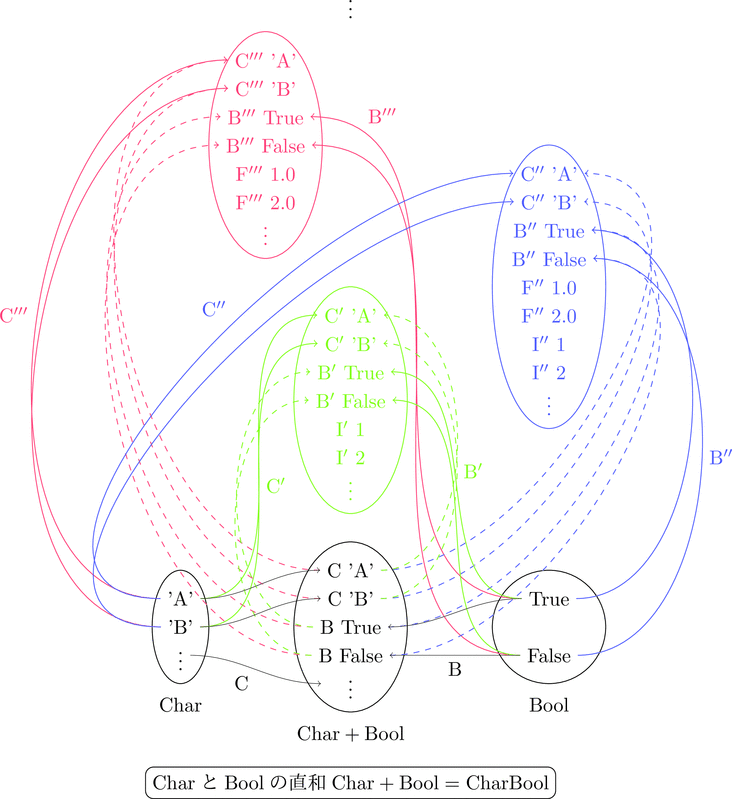
直積集合はタプルで済ませたが、直和集合は以下のデータ型を定義する。

coproduct
data CharBoolFloat = C''' Char | B''' Bool | F''' Float deriving Show

data CharBoolFloatInt = C'' Char | B'' Bool | F'' Float | I'' Int deriving Show

data CharBoolInt = C' Char | B' Bool | I' Char deriving Show

data CharBool = C Char | B Bool deriving Show

余直積の定義は直和集合を意味し、絵で描くとこんな感じになる。

直和集合の内部構造

直和集合の上位集合たちが赤や青や緑で描かれている。
任意の上位集合、すなわち任意の対象 $x$ に対し定義のような射が存在する。
実線の射が存在すれば、点線の射が一意に存在することが分かるだろう。

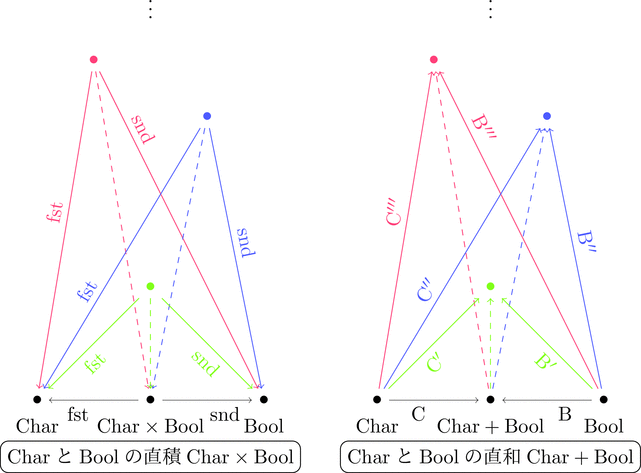
例によって、丸で囲まれた集合的な部分の複雑な構造を潰して点 $\bullet$ とみなすと

直積集合と直和集合

のように、直積集合と直和集合が内部構造に触れることなく定義される。
直積集合と直和集合は、矢印を逆にした、互いに双対となっている。
まだ良くは分からないけど何か凄いことが起きているような気がしてくる。
矢印を逆にした、というと逆射かな？と思ってしまうがそれとは何か違う模様10。

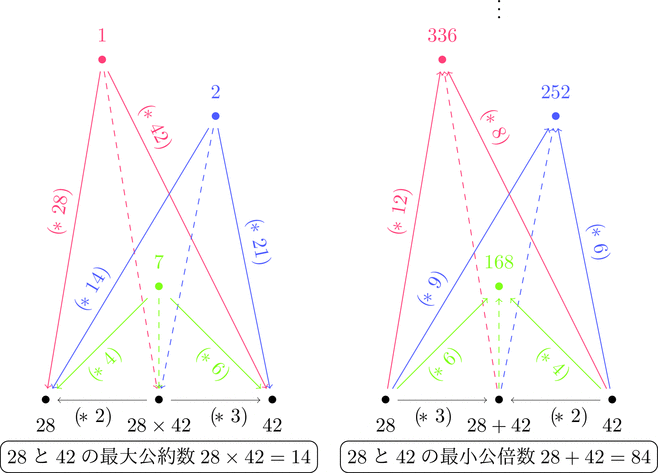
最大公約数と最小公倍数

次に、対象が自然数で射が自然数倍の圏を考えよう。
直積は最大公約数を意味し11、余直積は最小公倍数を意味する。
これ、分かりやすいと思うし、面白いと思うんですよね。

絵で描くとこんな感じになる。

最大公約数と最小公倍数

なんと最大公約数と最小公倍数は互いに双対の関係だった。
直積が最大を、余直積が最小を、それぞれ絞り込む様が良く分かると思います。

可換図式

具体例を見て図式が可換になる雰囲気を感じたところで、
定義を振り返りつつ、可換図式が意味する所を理解したい。

図式を用いないで直積と余直積の定義を書くと以下となる。

直積(product)
対象 $a \times b$ および射 $\varepsilon_{a} \colon a \times b \longrightarrow a$ と $\varepsilon_{b} \colon a \times b \longrightarrow b$ の組であり、
任意の対象 $x$ および２つの射 $\psi_{a} \colon x \longrightarrow a$と$\psi_{b} \colon x \longrightarrow b$ の組に対して、
射 $f \colon x \longrightarrow a \times b$ が一意に存在し $\psi_{a} = f \ggg \varepsilon_{a}$ かつ $\psi_{b} = f \ggg \varepsilon_{b}$。
余直積(coproduct)
対象 $a + b$ および射 $\eta_{a} \colon a \longrightarrow a + b$ と $\eta_{b} \colon b \longrightarrow a + b$ の組であり、
任意の対象 $x$ および２つの射 $\psi_{a} \colon a \longrightarrow x$ と $\psi_{b} \colon b \longrightarrow x$ の組に対して、
射 $f \colon a + b \longrightarrow x$ が一意に存在し $\psi_{a} = \eta_{a} \ggg f$ かつ $\psi_{b} = \eta_{b} \ggg f$。

図を用いる定義とはそれぞれ最終行だけが異なり、
１つの可換図式が２つの等式をあらわしていることになる。

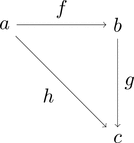
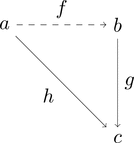
つまり、下記の図を可換図式として見る場合には、
等式 $h = f \ggg g$ が成り立つということを意味し、
また、単に図としてみる場合には、始域 $a$ で終域 $c$ な
異なる２つの射 $h$ と $f \ggg g$ が存在することを意味する。

射の合成

今になって思えばただそれだけのことではあるけれども、
圏の定義を理解していない状態だと難しく感じた気がする。

上記の図では対象をあらわす点 $\bullet$ を描くことを省いているが、
これで十分に事足りることが分かるのではないかと思います。

また、下記の図のように射が点線になっている可換図式は、
等式 $h = f \ggg g$ を満たす $f$ を求めよという問いに対して
その答えがひとつだけ存在すると言うことを意味する。

射の分解

これを、射 $h$ の分解と言ったりするらしい。

極限と余極限

定義に従って具体例を考えてみたところ
確かに直積と余直積を感じることができた気がする。

でもまだ定義がややこしく思えて覚えられる気はしない。
そこで、次のように図を段階的に捉えてみよう。

  1. 最初に対象 $a,b\in\mathrm{Obj}(\boldsymbol{C})$ を考える。
    極限と余極限1

  2. ある対象をひとつ加え、1. の各対象への射(各対象からの射)を考える。
    (射の向きに応じて２つのパターン考えることができる。)
    極限と余極限2

  3. 別の対象をひとつ加え、2. と同様な射を考える。
    極限と余極限3

  4. ある対象と別の対象との間に点線の射を考える。
    (3. で加えた射を分解するような向きの射を考える。)
    極限と余極限4

この捉え方をどうやら極限12や余極限と言うらしい。
最初の 1. を他の図に変えると他の概念が定義できる。

例えば、最初に対象 $a,b,c\in\mathrm{Obj}(\boldsymbol{C})$ を考えれば
直積 $a \times b \times c$ や直和 $a + b + c$ が定義できるはずだ。

極限の正式な定義13には関手や自然変換の理解が必要となる。

まとめ

図を描くことに疲れ、かなり投げやりな感はあるけれど、
圏の定義を理解する助けには間違いなくなると信じたい。

大学数学の知識は特に仮定していないとは言いつつも、
抽象的な定義に触れた経験がないと厳しいと思われる。

ベクトルのことはみんな知ってるはずなので、
自分の知ってるベクトルがベクトル空間の定義を
満たしていることを確認してみると良いかもしれない。

  1. そのような状況が訪れるかどうかについては考えないものとする。 ↩

  2. Object ↩

  3. Morphism ↩

  4. domain ↩

  5. codomain ↩

  6. identity morphism ↩

  7. これは読者への宿題としておく(これが言いたい)。 ↩

  8. bitterharvest's diary「極限－圏論の積」(2017-11-25) ↩

  9. 圏論 | 壱大整域「双対」(2019-03-27) ↩

  10. tnomuraのブログ「双対 dual」(2014-07-14) ↩

  11. bitterharvest's diary「極限－例：最大公約数」(2017-12-04) ↩

  12. 圏論 | 壱大整域「普遍性」(2019-03-30) ↩

  13. 圏論 | 壱大整域「極限」(2020-01-19) ↩

99
83
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
99
83

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?