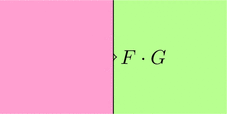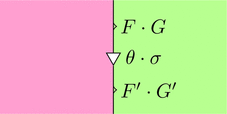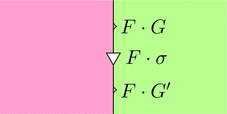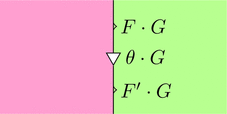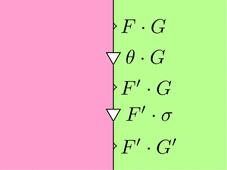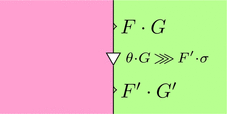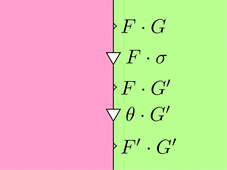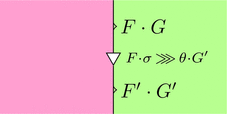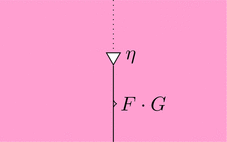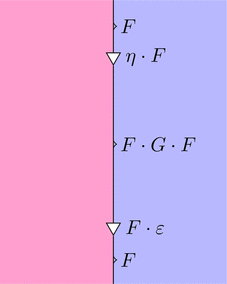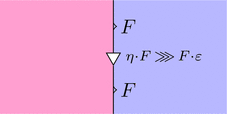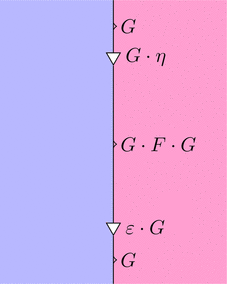想定読者と到達目標
圏、関手、自然変換、
それぞれの定義をひとまず把握した人へ。
ダイアグラム計算を通して
圏論してる雰囲気を醸し出す。
無くて困るものじゃないけど、
ダイアグラムって何かカッコいいし、
後で使うかもしれないのでここに記す1。
目次
- 圏論入門前の準備運動―集合と写像―
- もう諦めない圏論入門―対象と射―
- もう諦めない圏論入門―圏と関手―
- もう諦めない圏論入門―関手と自然変換―
-
もう諦めない圏論付録―ストリング・ダイアグラム―
- 可換図式とストリング・ダイアグラムの関係を受け入れる
- ポアンカレ双対を理解した気になる
- もう諦めない圏論基礎―極限からカン拡張へ―
- もう諦めない圏論基礎―モノイドからモナドへ―
- もう諦めない圏論基礎―高次元圏と変換手―
ストリング・ダイアグラム
可換図式をストリング・ダイアグラム
で表現するためのルールを定める。
射の射という概念を扱いたいので、
ここでは圏の圏 $\mathbf{Cat}$ を考える。
圏と関手
関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ を考える。
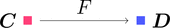
ストリング・ダイアグラムで描くと次となる。
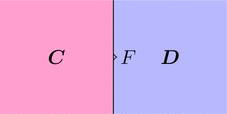
合成関手
関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{E}$ を考える。

ストリング・ダイアグラムで描くと次となる。

このストリング・ダイアグラムを用いて、
合成関手 $F \cdot G \colon \boldsymbol{C} \longrightarrow \boldsymbol{E}$ を計算しよう。
スライドモードで見れば、計算が進む様子を
パラパラ漫画的に把握できるだろう。たぶん。
恒等関手
恒等関手 $\mathrm{id}_{\boldsymbol{C}} \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}$ を考える。
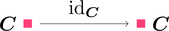
ストリング・ダイアグラムで描くと次となる。
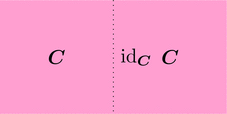
左単位律
恒等関手 $\mathrm{id}_{\boldsymbol{C}} \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}$ と 関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ を考える。

ストリング・ダイアグラムで描くと次となる。

このストリング・ダイアグラムを用いて、
恒等関手 $\mathrm{id}_{\boldsymbol{C}}$ と関手 $F$ を合成してみよう。
合成の結果はもちろん関手 $F$ となるわけで、
恒等関手が点線な気持ちが分かるだろう。
右単位律
関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と 恒等関手 $\mathrm{id}_{\boldsymbol{D}} \colon \boldsymbol{D} \longrightarrow \boldsymbol{D}$ を考える。
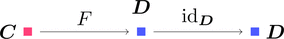
ストリング・ダイアグラムで描くと次となる。

このストリング・ダイアグラムを用いて、
関手 $F$ と恒等関手 $\mathrm{id}_{\boldsymbol{D}}$ を合成してみよう。
合成の結果はもちろん関手 $F$ となるわけで、
恒等関手が点線な気持ちが分かるだろう。
関手と自然変換
自然変換 $\theta \colon F \Longrightarrow G$ を考える。
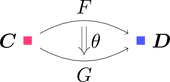
ストリング・ダイアグラムで描くと次となる。
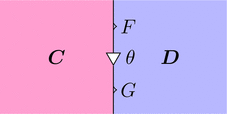
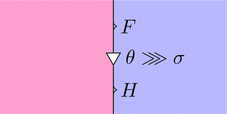
垂直合成
自然変換 $\theta \colon F \Longrightarrow G$ と自然変換 $\sigma \colon G \Longrightarrow H$ を考える。
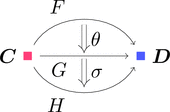
ストリング・ダイアグラムで描くと次となる。
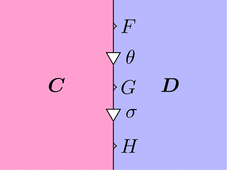
このストリング・ダイアグラムを用いて、
垂直合成 $\theta \ggg \sigma \colon F \Longrightarrow H$ を計算しよう。
スライドモードで見れば、計算が進む様子を
パラパラ漫画的に把握できるだろう。たぶん。
水平合成
自然変換 $\theta \colon F \Longrightarrow F'$ と自然変換 $\sigma \colon G \Longrightarrow G'$ を考える。
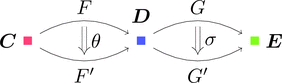
ストリング・ダイアグラムで描くと次となる。
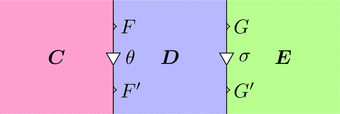
このストリング・ダイアグラムを用いて、
水平合成 $\theta \cdot \sigma \colon F \cdot G \Longrightarrow F' \cdot G'$ を計算しよう。
スライドモードで見れば、計算が進む様子を
パラパラ漫画的に把握できるだろう。たぶん。
恒等変換
恒等変換 $\mathrm{id}_{F} \colon F \Longrightarrow F$ を考える。
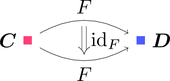
ストリング・ダイアグラムで描くと次となる。
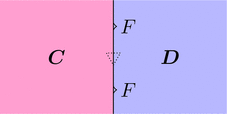
上単位律
恒等変換 $\mathrm{id}_{F} \colon F \Longrightarrow F$ と自然変換 $\theta \colon F \Longrightarrow G$ を考える。
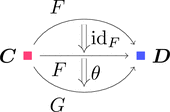
ストリング・ダイアグラムで描くと次となる。
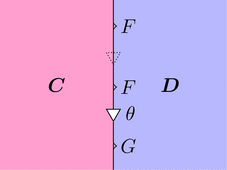
このストリング・ダイアグラムを用いて、
恒等変換 $\mathrm{id}_{F}$ と自然変換 $\theta$ を合成してみよう。
合成の結果はもちろん自然変換 $\theta$ となるわけで、
恒等変換が点線な気持ちが分かるだろう。
下単位律
自然変換 $\theta \colon F \Longrightarrow G$ と恒等変換 $\mathrm{id}_{G} \colon G \Longrightarrow G$ を考える。
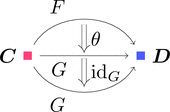
ストリング・ダイアグラムで描くと次となる。
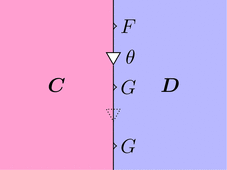
このストリング・ダイアグラムを用いて、
自然変換 $\theta$ と恒等変換 $\mathrm{id}_{G}$ を合成してみよう。
合成の結果はもちろん自然変換 $\theta$ となるわけで、
恒等変換が点線な気持ちが分かるだろう。
関手の圏
双関手 $- \cdot - \colon \boldsymbol{D}^\boldsymbol{C} \times \boldsymbol{E}^\boldsymbol{D} \longrightarrow \boldsymbol{E}^\boldsymbol{C}$ が関わる計算は
ストリング・ダイアグラムで描けば楽になる。
結合律と単位律や交替律などの性質を
図の変形として直感的に取り扱えるからだろう。
関手と自然変換の合成
関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ と自然変換 $\sigma \colon G \Longrightarrow G'$ を考える。
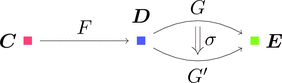
ストリング・ダイアグラムで描くと次となる。

このストリング・ダイアグラムを用いて、
関手 $F$ と自然変換 $\sigma$ の合成を計算しよう。
スライドモードで見れば、計算が進む様子を
パラパラ漫画的に把握できるだろう。たぶん。
自然変換と関手の合成
自然変換 $\theta \colon F \Longrightarrow F'$ と関手 $G \colon \boldsymbol{D} \longrightarrow \boldsymbol{E}$ を考える。
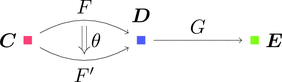
ストリング・ダイアグラムで描くと次となる。

このストリング・ダイアグラムを用いて、
自然変換 $\theta$ と関手 $G$ の合成を計算しよう。
スライドモードで見れば、計算が進む様子を
パラパラ漫画的に把握できるだろう。たぶん。
交替律
水平合成は次のように書けるのであった。
$\theta \cdot \sigma = \theta \cdot G \ggg F' \cdot \sigma = F \cdot \sigma \ggg \theta \cdot G'$
ストリング・ダイアグラムにより
この式を視覚的に捉えることができる。
まず、
自然変換 $\theta$ と関手 $G$ の合成
関手 $F'$ と自然変換 $\sigma$ の合成
を計算してみよう。
また、
関手 $F$ と自然変換 $\sigma$ の合成
自然変換 $\theta$ と関手 $G'$ の合成
を計算してみよう。
したがって、水平合成の交替律
$\theta \cdot \sigma = \theta \cdot G \ggg F' \cdot \sigma = F \cdot \sigma \ggg \theta \cdot G'$
は次の変形を行って良いことをあらわす。
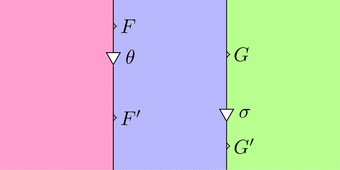 $=$
$=$ 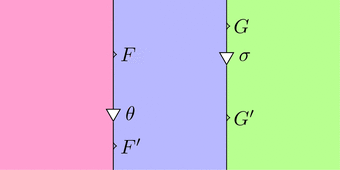
対象と射
圏 $\boldsymbol{C}$ の射 $f \colon a \longrightarrow b$ を考える。

ストリング・ダイアグラムで描くために
対象と射を関手と自然変換とみなす2。
格上げ
対象が1つ $\{*\} = \mathrm{Obj}(\mathbf{1})$ で
射が1つ $\{\mathrm{id}_{\displaystyle *}\} = \mathrm{Mor}(\mathbf{1})$ な単位圏 $\mathbf{1}$ から
圏 $\boldsymbol{C}$ への関手 $\widetilde{a}, \widetilde{b} \colon \mathbf{1} \longrightarrow \boldsymbol{C}$ と
自然変換 $\widetilde{f} \colon \widetilde{a} \Longrightarrow \widetilde{b}$ を考える。
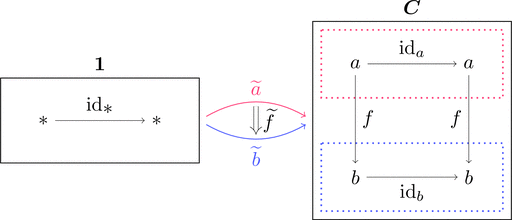
$f \colon a \longrightarrow b$ と $\widetilde{f} \colon \widetilde{a} \Longrightarrow \widetilde{b}$ を同一視して
チルダを陽には書かないことにする。
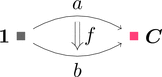
ストリング・ダイアグラムで描くと次となる。
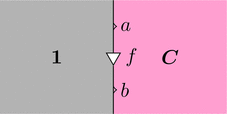
自然性
自然変換 $f \colon a \Longrightarrow b$ と自然変換 $\theta \colon F \Longrightarrow G$ を考えると、
$f \cdot \theta = f \cdot F \ggg b \cdot \theta = a \cdot \theta \ggg f \cdot G$ であり
ダイアグラム計算で次の変形を行って良い。
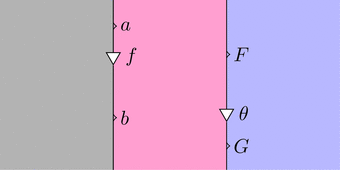 $=$
$=$ 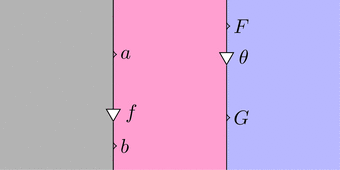
これは、対象 $\{*\} = \mathrm{Obj}(\mathbf{1})$ として
$(f \cdot \theta)_{\displaystyle *} = F\ f_{\displaystyle *} \ggg \theta_{b,{\displaystyle*}} = \theta_{a,{\displaystyle*}} \ggg G\ f_{\displaystyle *}$
すなわち、自然変換 $\theta$ が満たすべき式
$(f \cdot \theta)_{\displaystyle *} = F\ f \ggg \theta_{b} = \theta_{a} \ggg G\ f$
をあらわしており、何か上手くできてる。
随伴関手
これでルールは定まったので、
ストリング・ダイアグラムを用いて
随伴について考えてみよう。
単位
自然変換 $\eta \colon \mathrm{id}_{\boldsymbol{C}} \Longrightarrow F \cdot G$ を考える。
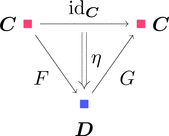
ストリング・ダイアグラムで描くと次となる。
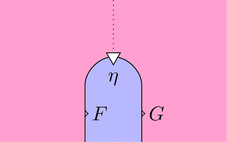
このストリング・ダイアグラムを用いて、
関手 $F$ と関手 $G$ を合成してみよう。
余単位
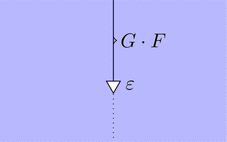
自然変換 $\varepsilon \colon G \cdot F \Longrightarrow \mathrm{id}_{\boldsymbol{D}}$ を考える。
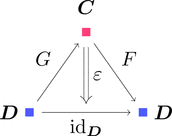
ストリング・ダイアグラムで描くと次となる。
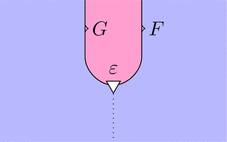
このストリング・ダイアグラムを用いて、
関手 $G$ と関手 $F$ を合成してみよう。
単位と余単位
自然変換 $\eta \colon \mathrm{id}_{\boldsymbol{C}} \Longrightarrow F \cdot G$ と
自然変換 $\varepsilon \colon G \cdot F \Longrightarrow \mathrm{id}_{\boldsymbol{D}}$ を考える。
ストリング・ダイアグラムで描くと次となる。

このストリング・ダイアグラムを用いて、
関手や自然変換の計算してみよう。
余単位と単位
自然変換 $\varepsilon \colon G \cdot F \Longrightarrow \mathrm{id}_{\boldsymbol{D}}$ と
自然変換 $\eta \colon \mathrm{id}_{\boldsymbol{C}} \Longrightarrow F \cdot G$ を考える。
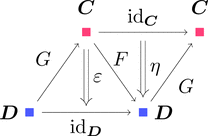
ストリング・ダイアグラムで描くと次となる。
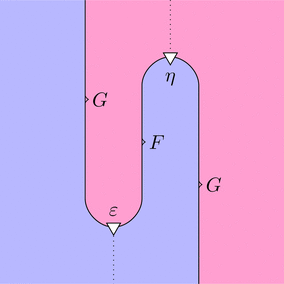
このストリング・ダイアグラムを用いて、
関手や自然変換の計算してみよう。
可換図式とストリング・ダイアグラム
したがって、以下のように可換図式と
ストリング・ダイアグラムが対応することが分かる。
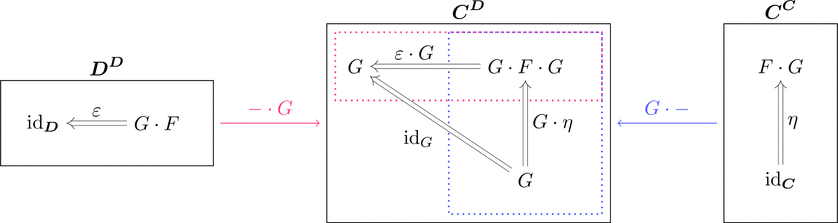
可換図式
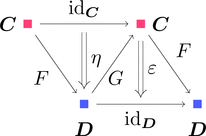
次図、三角形の可換図式が $\eta \cdot F \ggg F \cdot \varepsilon = \mathrm{id}_{F}$ をあらわし、

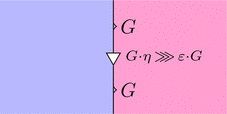
次図、三角形の可換図式が $G \cdot \eta \ggg \varepsilon \cdot G = \mathrm{id}_{G}$ をあらわす。
ストリング・ダイアグラム
次図、ストリング・ダイアグラムが $\eta \cdot F \ggg F \cdot \varepsilon = \mathrm{id}_{F}$ をあらわし、
 $=$
$=$ 
次図、ストリング・ダイアグラムが $G \cdot \eta \ggg \varepsilon \cdot G = \mathrm{id}_{G}$ をあらわす。
 $=$
$=$ 
まとめ
ペースティング・ダイアグラム

をストリング・ダイアグラム
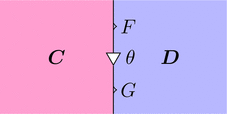
に書き換えることで、
点 $\scriptstyle \blacksquare$ であらわされていた圏が面となり、
面であらわされていた自然変換が点 $\scriptstyle \bigtriangledown$ となる。
ポアンカレ双対
$0$ 次元の圏は $2-0=2$ 次元の面に
$1$ 次元の関手は $2-1=1$ 次元の線に
$2$ 次元の自然変換が $2-2=0$ 次元の点に
それぞれ対応し、これをポアンカレ双対と言うらしい3。
高次元である自然変換を主に考えたいときは
たぶんストリング・ダイアグラムが便利なのだろう。
-
この記事で直接的に Haskell は登場しないが、圏論を通して間接的に Haskell っぽいと考える(シリーズものは何となくタグを揃えたいので)。 ↩
-
檜山正幸のキマイラ飼育記 (はてなBlog)「圏論の随伴をちゃんと抑えよう: お絵描き完全解説」(2018-03-02) ↩