More than 3 years have passed since last update.

もう諦めない圏論基礎―モノイドからモナドへ―

Last updated at 2020-03-18Posted at 2019-08-31

想定読者と到達目標

モノイドの定義および
集合と写像を知っていて、
モナドに関するパワー・ワードを
どうしても理解したい人へ。

モナドは
「自己関手の圏におけるモノイド対象」
「単位圏から自己関手の圏へのラックス・モノイド関手」
「単位圏から圏の圏へのラックス 2-関手」
であることが分かるはず。

圏論入門前の準備運動―集合と写像―
もう諦めない圏論入門―対象と射―
もう諦めない圏論入門―圏と関手―
もう諦めない圏論入門―関手と自然変換―
もう諦めない圏論付録―ストリング・ダイアグラム―
もう諦めない圏論基礎―極限からカン拡張へ―
もう諦めない圏論基礎―モノイドからモナドへ―
- モノイド圏と 2-圏の概念を受け入れる
- モナドがモノイドであることを理解した気になる
もう諦めない圏論基礎―高次元圏と変換手―

モノイド集合

集合 $S$ に
写像 $\diamond \colon S \times S \longrightarrow S$ と
単位元 $e \in S$ の情報を加える。

次の２つの条件を満たすとき、
組 $(S,\diamond,e)$ はモノイド集合である。

（結合律）$(a \diamond b) \diamond c = a \diamond (b \diamond c)$ が成り立つ。
（単位律）$e \diamond a = a \diamond e = a$ が成り立つ。

モノイド則

Haskell では、
集合(すなわち型) s に
写像(すなわち関数) (<>) :: s -> s -> s と
単位元(すなわち値) e :: s の情報を加える。

Monoid

import Prelude hiding (Monoid(..))

class Monoid s where
    e    :: s
    (<>) :: s -> s -> s

このときモノイド則は以下となる。

（結合律）(a <> b) <> c $=$ a <> (b <> c)
（単位律）e <> a $=$ a <> e $=$ a

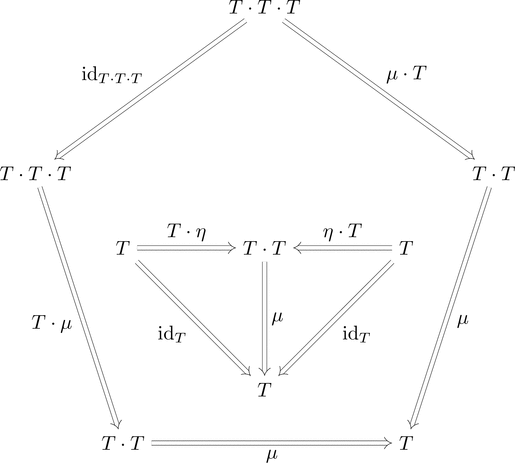
モナド

関手 $T \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}$ に
自然変換 $\mu \colon T \cdot T \Longrightarrow T$ と
自然変換 $\eta \colon \mathrm{id}_{\boldsymbol{C}} \Longrightarrow T$ の情報を加える。

次の２つの条件を満たすとき、
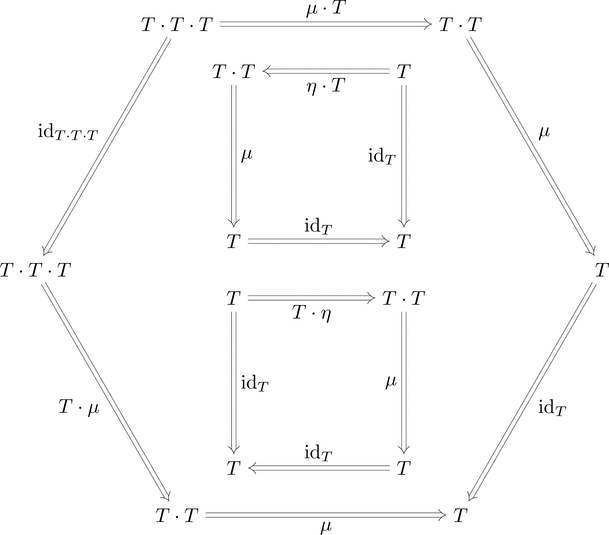
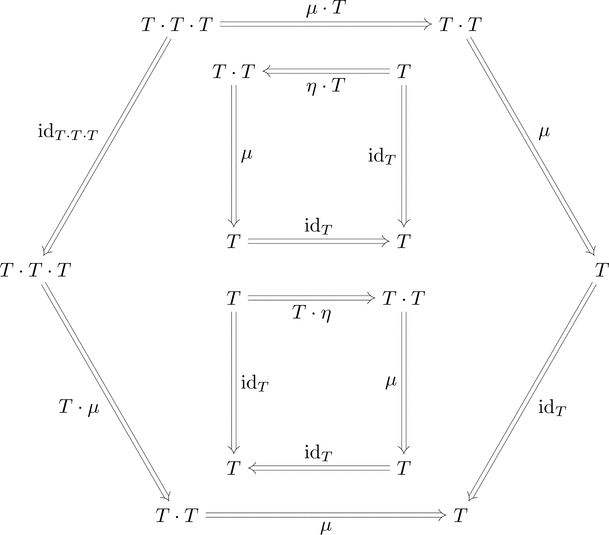
組 $(T,\mu,\eta)$ はモナドである。

（結合律）$\mu \cdot T \ggg \mu = T \cdot \mu \ggg \mu$ が成り立つ。
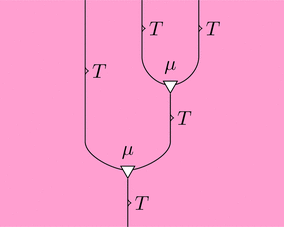
可換図式とストリング・ダイアグラムでそれぞれ以下のように描ける。

$=$
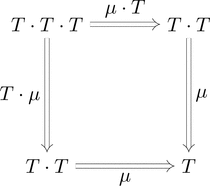
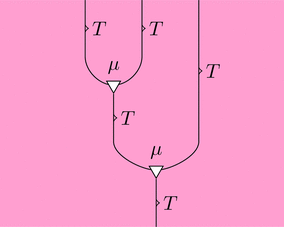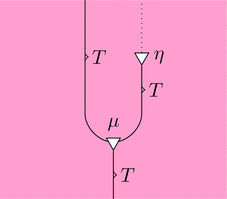
（単位律）$\eta \cdot T \ggg \mu = T \cdot \eta \ggg \mu = \mathrm{id}_{T}$ が成り立つ。
可換図式とストリング・ダイアグラムでそれぞれ以下のように描ける。

$=$ $=$

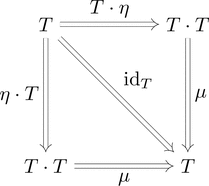
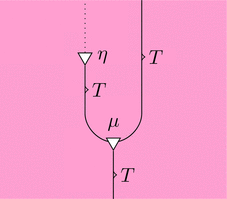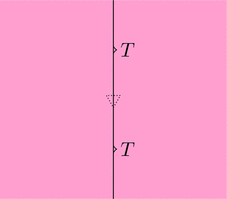
モナド則

関手の具体例でみたように、Haskell では、
対象(すなわち型)の対応 t :: * -> * と
射(すなわち関数)の対応 fmap :: (a -> b) -> (f a -> f b)
で関手を定義する。

関手 $t \colon \mathbf{Hask} \longrightarrow \mathbf{Hask}$ に
自然変換(すなわち多相関数) join :: t (t a) -> t a と
自然変換(すなわち多相関数) return :: a -> t a の情報を加える。

Monad

import Prelude hiding (Monad(..),(=<<))
import Control.Category ((>>>))

class Functor t => Monad t where
    join   :: t (t a) -> t a
    return :: a -> t a

(=<<) :: Monad t => (a -> t b) -> (t a -> t b)
(=<<) f = fmap f >>> join

(>>=) :: Monad t => t a -> (a -> t b) -> t b
(>>=) = flip (=<<)

このときモナド則は以下となる。

（結合律）fmap join >>> join $=$ join >>> join
（単位律）fmap return >>> join $=$ return >>> join $=$ id
（$\mu$ の自然性）fmap (fmap f) >>> join $=$ join >>> fmap f
（$\eta$ の自然性）f >>> return = return >>> fmap f

可換図式はただの等式なので恐れる必要はない。

自然変換の垂直合成と水平合成を理解しないと
$\mu \cdot T, T \cdot \mu, \eta \cdot T, T \cdot \eta$ の意味が分からないのでつらい。

ここではモナド則を join で記述しているが、

`>>=` を用いたよく見る形式を導出できる[^宿題]。

$\mu$ が自然変換であることから
$(T \cdot T)\ f \ggg \mu_{b} = \mu_{a} \ggg T\ f$ が成り立つ。

Haskell では次のようになる。
fmap (fmap f) >>> join $=$ join >>> fmap f

自然変換の等式 $\mu \cdot T \ggg \mu = T \cdot \mu \ggg \mu$ は
射の族の等式 $T\ \mu_{a} \ggg \mu_{a} = \mu_{T\ a} \ggg \mu_{a}$ である。

左辺
fmap join >>> join :: Monad t => t (t (t a)) -> t a
$=$ fmap join >>> join $ fmap (fmap g) (fmap f m)
$=$ fmap (fmap g) >>> fmap join >>> join $ fmap f m
$=$ fmap f >>> fmap (fmap g) >>> fmap join >>> join $ m
$=$ fmap (f >>> fmap g >>> join) >>> join $ m
$=$ fmap (\x -> fmap g >>> join $ f x) >>> join $ m
$=$ fmap (\x -> f x >>= g) >>> join $ m
$=$ m >>= (\x -> f x >>= g)

右辺
join >>> join :: Monad t => t (t (t a)) -> t a
$=$ join >>> join $ fmap (fmap g) (fmap f m)
$=$ fmap (fmap g) >>> join >>> join $ fmap f m
$=$ (join >>> fmap g) >>> join $ fmap f m
$=$ fmap g >>> join $ join (fmap f m)
$=$ join (fmap f m) >>= g
$=$ (fmap f >>> join $ m) >>= g
$=$ (m >>= f) >>= g

したがって
m >>= (\x -> f x >>= g) $=$ (m >>= f) >>= g

$\eta$ が自然変換であることから
$f \ggg \eta_{b} = \eta_{a} \ggg T\ f$ が成り立つ。

Haskell では次のようになる。
f >>> return = return >>> fmap f

自然変換の等式 $T \cdot \eta \ggg \mu = \mathrm{id}_{T}$ は
射の族の等式 $\eta_{T\ a} \ggg \mu_{a} = \mathrm{id}_{T\ a}$ である。

左辺
return >>> join :: Monad t => t a -> t a
return >>> join $ f x
$=$ f >>> return >>> join $ x
$=$ (return >>> fmap f) >>> join $ x
$=$ fmap f >>> join $ return x
$=$ return x >>= f

右辺
id :: Monad t => t a -> t a
id $ f x $=$ f x

したがって
return x >>= f $=$ f x

自然変換の等式 $\eta \cdot T \ggg \mu = \mathrm{id}_{T}$ は
射の族の等式 $T\ \eta_{a} \ggg \mu_{a} = \mathrm{id}_{T\ a}$ である。

fmap return >>> join $=$ id

左辺
fmap return >>> join :: Monad t => t a -> t a
fmap return >>> join $ m $=$ m >>= return

右辺
id :: Monad t => t a -> t a
id m $=$ m

したがって
m >>= return $=$ m

単対象圏

対象１つで射が整数値の圏でみたように、
単対象圏はモノイドと関係がある。

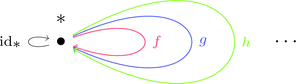
対象が１つ $\{*\} = \mathrm{Obj}(\boldsymbol{C})$ な圏 $\boldsymbol{C}$ を考える。
射 $f,g,h \colon * \longrightarrow *$ はいくつあっても良い。

Hom 集合は集合の圏 $\mathbf{Set}$ の対象(すなわち集合)であるから、
射の合成 $\ggg$ を集合の圏 $\mathbf{Set}$ の射(すなわち写像)
$\ggg \colon \mathrm{Hom}_{\boldsymbol{C}}(a,b) \times \mathrm{Hom}_{\boldsymbol{C}}(b,c) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(a,c)$
とみなすことができる。

集合 $\mathrm{Hom}_{\boldsymbol{C}}(*,*)$ に
射の合成 $\ggg \colon \mathrm{Hom}_{\boldsymbol{C}}(*,*) \times \mathrm{Hom}_{\boldsymbol{C}}(*,*) \longrightarrow \mathrm{Hom}_{\boldsymbol{C}}(*,*)$ と
恒等射 $\mathrm{id}_{\displaystyle *} \in \mathrm{Hom}_{\boldsymbol{C}}(*,*)$ の情報を加える。

圏の定義より結合律と単位律が成り立つ。

組 $(\mathrm{Hom}_{\boldsymbol{C}}(*,*),\ggg,\mathrm{id}_{\displaystyle *})$ はモノイド集合である。

対象ではなく、射の集合がモノイドになっている。

圏の圏

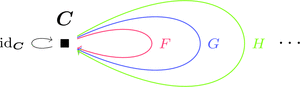
同様に、対象が１つな圏の圏 $\mathbf{Cat}$ を考える。

対象は圏 $\boldsymbol{C}$ のみとし、
射(すなわち関手) $F,G,H \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}$ はいくつあっても良い。

集合 $\mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{C})$ に
関手の合成 $\cdot \colon \mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{C}) \times \mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{C}) \longrightarrow \mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{C})$ と
恒等関手 $\mathrm{id}_{\boldsymbol{C}} \in \mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{C})$ の情報を加える。

圏の圏においても結合律と単位律が成り立つ。

組 $(\mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{C}) ,\cdot,\mathrm{id}_{\boldsymbol{C}})$ はモノイド集合である。

対象ではなく、射(すなわち関手)の集合がモノイドになっている。

圏の圏 $\mathbf{Cat}$ は圏であるから、
対象 $\boldsymbol{C},\boldsymbol{D} \in \mathrm{Obj}(\mathbf{Cat})$ に対して集合 $\mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{D})$ が存在し、
関手の合成 $\cdot \colon \mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{D}) \times \mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{D},\boldsymbol{E}) \longrightarrow \mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{E})$
によりモノイド集合を構成することができた。

圏の圏 $\mathbf{Cat}$ の場合にはそれに加えて、
対象 $\boldsymbol{C},\boldsymbol{D} \in \mathrm{Obj}(\mathbf{Cat})$ に対して関手の圏 $\boldsymbol{D}^\boldsymbol{C}$ が存在する。

自己関手の圏

関手の圏にて定義を与えた
対象(すなわち関手)を合成関手 $\cdot$ で対応させ
射(すなわち自然変換)を水平合成 $\cdot$ で対応させる
双関手 $- \cdot - \colon \boldsymbol{D}^\boldsymbol{C} \times \boldsymbol{E}^\boldsymbol{D} \longrightarrow \boldsymbol{E}^\boldsymbol{C}$ を考える。

$\boldsymbol{D}^\boldsymbol{C}$ を $\mathbf{Cat}(\boldsymbol{C},\boldsymbol{D})$ と書くことにして、
双関手 $- \cdot - \colon \mathbf{Cat}(\boldsymbol{C},\boldsymbol{D}) \times \mathbf{Cat}(\boldsymbol{D},\boldsymbol{E}) \longrightarrow \mathbf{Cat}(\boldsymbol{C},\boldsymbol{E})$
と書けば、関手の合成 $\cdot$ の場合とよく似ている。

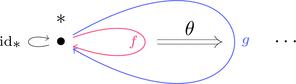
自己関手の圏 $\boldsymbol{C}^{\boldsymbol{C}}$ は、これまでと異なり、
対象が１つの圏とは限らないことに注意しよう。

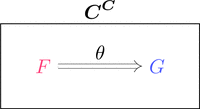
対象は関手 $F,G \colon \boldsymbol{C} \longrightarrow \boldsymbol{C}$ で
射は自然変換 $\theta \colon F \Longrightarrow G$ である。

関手の合成 $\cdot \colon \mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{C}) \times \mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{C}) \longrightarrow \mathrm{Hom}_{\mathbf{Cat}}(\boldsymbol{C},\boldsymbol{C})$
は圏の圏 $\mathbf{Cat}$ における射(すなわち関手)に対する演算とみなせる。

双関手 $- \cdot - \colon \boldsymbol{C}^\boldsymbol{C}\times\boldsymbol{C}^\boldsymbol{C}\longrightarrow\boldsymbol{C}^\boldsymbol{C}$
は関手の圏 $\boldsymbol{C}^\boldsymbol{C}$ における対象(すなわち関手)に対する演算とみなせる。

圏 $\boldsymbol{C}^\boldsymbol{C}$ に
双関手 $- \cdot - \colon \boldsymbol{C}^\boldsymbol{C}\times\boldsymbol{C}^\boldsymbol{C}\longrightarrow\boldsymbol{C}^\boldsymbol{C}$ と
恒等関手 $\mathrm{id}_{\boldsymbol{C}} \in \mathrm{Obj}(\boldsymbol{C}^{\boldsymbol{C}})$ の情報を加える。

双関手 $- \cdot -$ に対して結合律と単位律が成り立つ。

組 $(\boldsymbol{C}^\boldsymbol{C},\cdot,\mathrm{id}_{\boldsymbol{C}})$ はモノイドっぽいけど集合ではない。

集合ではなく圏がモノイドっぽくなってしまった。
これはモノイド集合ではなくてモノイド圏といえる。

厳密モノイド圏

圏 $\boldsymbol{C}$ に
双関手 $- \diamond - \colon \boldsymbol{C}\times\boldsymbol{C}\longrightarrow\boldsymbol{C}$ と
単位対象 $e \in \mathrm{Obj}(\boldsymbol{C})$ の情報を加える。

次の２つの条件を満たすとき、
組 $(\boldsymbol{C},\diamond,e)$ は厳密モノイド圏である。

（結合律）$(- \diamond -) \diamond - = - \diamond (- \diamond -)$ が成り立つ。
（単位律）$e \diamond - = - \diamond e = \mathrm{id}_{\boldsymbol{C}}$ が成り立つ。

ここで、関手 $a \diamond - \colon \boldsymbol{C}\longrightarrow\boldsymbol{C}$ は
$b \in \mathrm{Obj}(\boldsymbol{C})$ を $a \diamond b \in \mathrm{Obj}(\boldsymbol{C})$ に対応させ
$g \in \mathrm{Mor}(\boldsymbol{C})$ を $\mathrm{id}_{a} \diamond g \in \mathrm{Mor}(\boldsymbol{C})$ に対応させる。

同様に、関手 $- \diamond b \colon \boldsymbol{C}\longrightarrow\boldsymbol{C}$ は
$a \in \mathrm{Obj}(\boldsymbol{C})$ を $a \diamond b \in \mathrm{Obj}(\boldsymbol{C})$ に対応させ
$f \in \mathrm{Mor}(\boldsymbol{C})$ を $f \diamond \mathrm{id}_{b} \in \mathrm{Mor}(\boldsymbol{C})$ に対応させる。

自己関手の圏を一般化すると厳密モノイド圏になる。
厳密というのは満たすべき条件(結合律と単位律)が
等号 $=$ により記述されていることを意味する。

随伴関手の定義のように、関手が一致すると言う条件を
等号 $=$ から同型 $\cong$ に変えることで少し緩めよう。

モノイド圏

圏 $\boldsymbol{C}$ に
双関手 $- \diamond - \colon \boldsymbol{C}\times\boldsymbol{C}\longrightarrow\boldsymbol{C}$ と
単位対象 $e \in \mathrm{Obj}(\boldsymbol{C})$ の情報を加える。

次の３つの条件を満たすとき、
組 $(\boldsymbol{C},\diamond,e)$ はモノイド圏である。

（結合律）$(- \diamond -) \diamond - \cong - \diamond (- \diamond -)$ が成り立つ。
（単位律）$e \diamond - \cong - \diamond e \cong \mathrm{id}_{\boldsymbol{C}}$ が成り立つ。
（一貫性条件）２つの図式が可換となる。

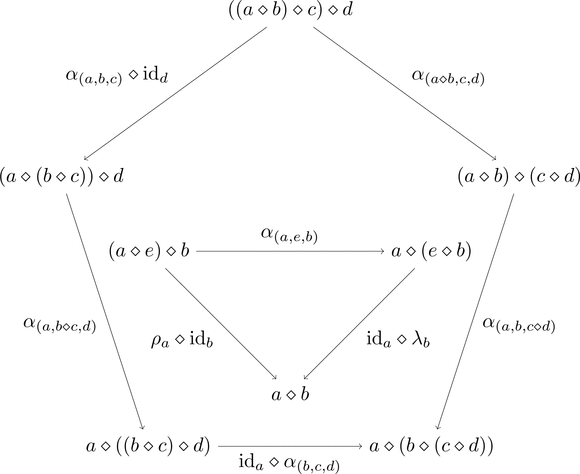
自然同型 $\alpha \colon (- \diamond -) \diamond - \Longrightarrow - \diamond (- \diamond -)$
自然同型 $\lambda \colon e \diamond - \Longrightarrow \mathrm{id}_{\boldsymbol{C}}$
自然同型 $\rho \colon - \diamond e \Longrightarrow \mathrm{id}_{\boldsymbol{C}}$

４つ以上の引数を持つ関手 $((-\diamond-)\diamond-)\diamond-$ などに
結合律と単位律が成り立つよう一貫性条件が加わるらしい。

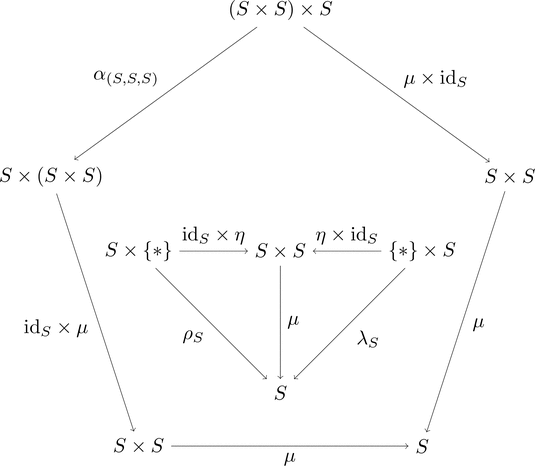
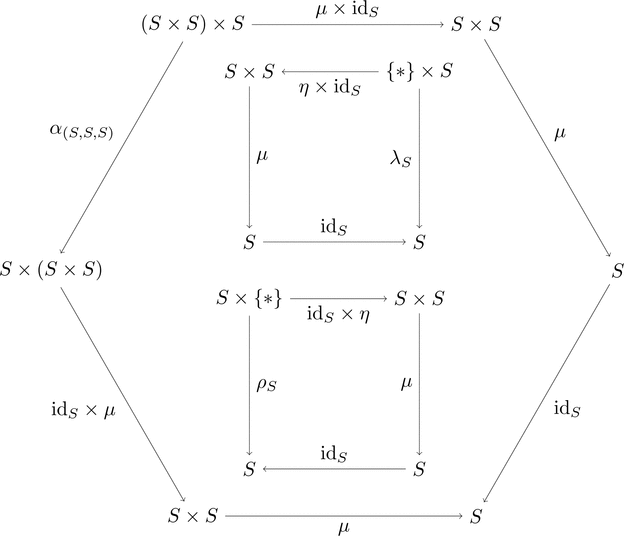
集合の圏を $\mathbf{Set}$ として
組 $(\mathbf{Set},\times,\{*\})$ がモノイド圏であることを確認すれば、
条件を同型 $\cong$ に緩めた気持ちが分かるかもしれない。

圏の圏を $\mathbf{Cat}$ として、同様に、
組 $(\mathbf{Cat},\times,\mathbf{1})$ がモノイド圏であることを確認できる。

圏 $\mathbf{Set}$ に
双関手 $- \diamond - \colon \mathbf{Set}\times\mathbf{Set}\longrightarrow\mathbf{Set}$ と
単位対象 $\{*\} \in \mathrm{Obj}(\mathbf{Set})$ の情報を加える。

集合 $A,B \in \mathrm{Obj}(\mathbf{Set})$ と
写像 $f,g \in \mathrm{Mor}(\mathbf{Set})$ に対して、
対象(すなわち集合)の対応 $A \diamond B = A \times B$ と
射(すなわち写像)の対応 $f \diamond g = f \times g$ のように、
直積 $\times$ を用いて双関手 $- \diamond -$ を定義する。

$\{*\}$ は元が１つの集合すなわち単集合である。

（結合律）

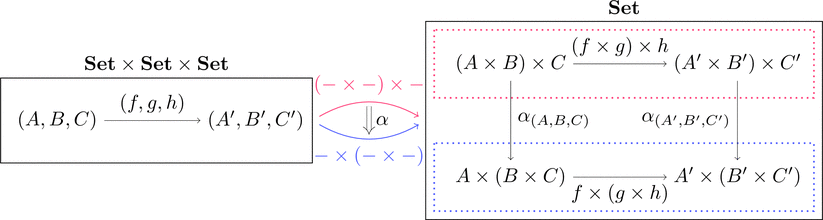
写像 $\alpha_{(A,B,C)} \colon (A \times B) \times C \longrightarrow A \times (B \times C)$ を
元の対応 $\alpha_{(A,B,C)} \colon ((a,b),c) \longmapsto (a,(b,c))$
により定義すれば、$\alpha$ は自然同型となる。
（単位律）

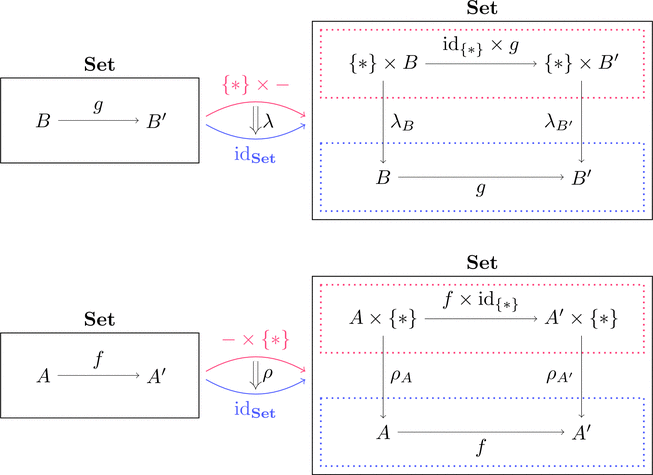
写像 $\lambda_{B} \colon \{*\} \times B \longrightarrow B$ を元の対応 $\lambda_{B} \colon (*,b) \longmapsto b$
により定義すれば、$\lambda$ は自然同型となる。
写像 $\rho_{A} \colon A \times \{*\} \longrightarrow A$ を元の対応 $\rho_{A} \colon (a,*) \longmapsto a$
により定義すれば、$\rho$ は自然同型となる。

組 $(\mathbf{Set},\times,\{*\})$ はモノイド圏である¹。

等号 $=$ から同型 $\cong$ に緩めたことで
集合の圏におけるモノイド構造をあらわせた。

集合 $A,B,C$ に対して
$(A \times B) \times C \cong A \times (B \times C)$ や
$\{*\} \times A \cong A \times \{*\} \cong A$ が
成り立つことになる。

圏 $\mathbf{Set}$ の対象は集合であるから、
モノイド対象を考えることができれば
通常の意味におけるモノイド集合が得られる。

モノイド対象

集合の圏 $\mathbf{Set}$ の対象(すなわち集合)が
モノイド集合となる条件を、集合の要素ではなく、
射(すなわち写像)により表現することができる。

モノイド再びにおいて集合を対象に、写像を射
と読み替えることでモノイド対象を定義できる。

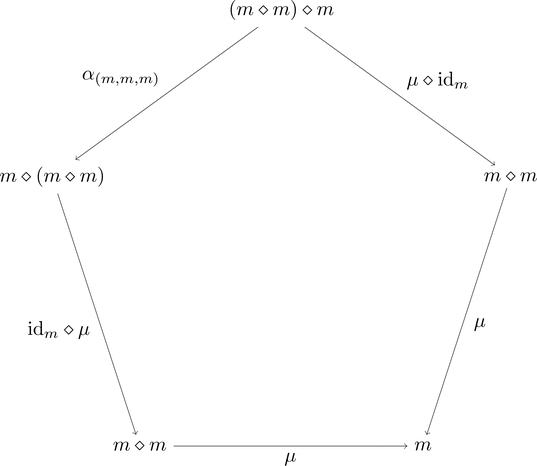
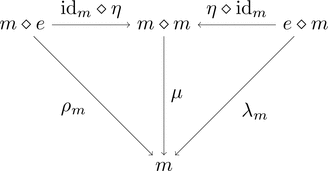
モノイド圏 $(\boldsymbol{C},\diamond,e)$ があるとする。

対象 $m \in \mathrm{Obj}(\boldsymbol{C})$に
射 $\mu \colon m \diamond m \longrightarrow m$ と
射 $\eta \colon e \longrightarrow m$ の情報を加える。

次の２つの条件を満たすとき、
組 $(m,\mu,\eta)$ はモノイド対象である。

（結合律）図式が可換となる。
（単位律）図式が可換となる。

対象 $S \in \mathrm{Obj}(\mathbf{Set})$に
射 $\mu \colon S \times S \longrightarrow S$ と
射 $\eta \colon \{*\} \longrightarrow S$ の情報を加える。

$\eta \colon * \longmapsto e$ により $e \in S$ が単位元となることに注意する。

次の２つの図式が可換となるとき、
組 $(S,\mu,\eta)$ はモノイド対象である。

集合の圏におけるモノイド対象はモノイド集合だ。

自己関手の圏におけるモノイド対象

対象 $T \in \mathrm{Obj}(\boldsymbol{C}^\boldsymbol{C})$に
射 $\mu \colon T \cdot T \Longrightarrow T$ と
射 $\eta \colon \mathrm{id}_{\boldsymbol{C}} \Longrightarrow T$ の情報を加える。

$\mathrm{id}_{T} \cdot \theta = T \cdot \theta$ と $\theta \cdot \mathrm{id}_{T} = \theta \cdot T$ に注意する。

次の２つの図式が可換となるとき、
組 $(T,\mu,\eta)$ はモノイド対象である。

自己関手の圏におけるモノイド対象はモナドだ。

ラックス・モノイド関手

モノイド圏を定義したのでモノイド関手も定義しよう。

モノイド圏とは圏に双関手と単位対象
の情報を加えたものであったので、
モノイド関手も関手に情報を加えたものだ。

唐突なラックス○○○○に驚きを禁じえないが、
ラックスは条件が緩いことをあらわしている。

色んな言葉遣いがあるみたいだけれど、
ここでは次のように考えてみることにする。

条件が等号 $=$	条件が同型 $\cong$	条件がそれ以外
厳密○○○○	○○○○	ラックス○○○○

モノイド圏 $(\boldsymbol{C},\diamond,e)$ と
モノイド圏 $(\boldsymbol{D},\diamond,e)$ の対応を考える。

関手 $F \colon \boldsymbol{C} \longrightarrow \boldsymbol{D}$ を考える。

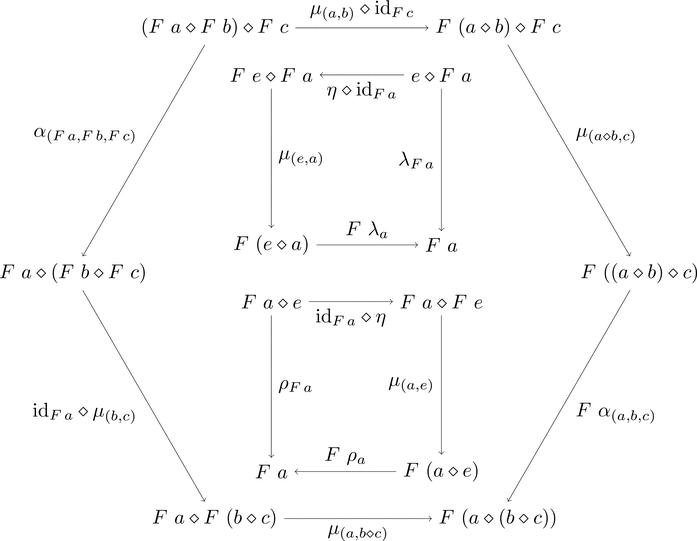
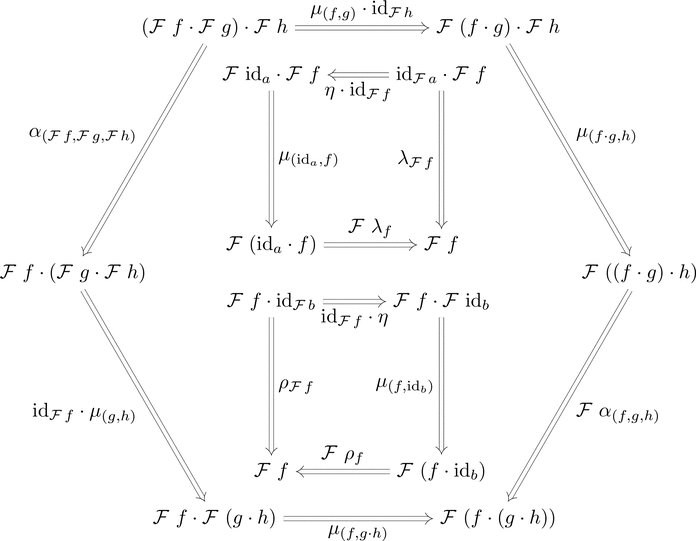
次の３つの条件を満たすとき、
組 $(F,\mu,\eta)$ はラックス・モノイド関手である。

（結合律）自然変換 $\mu \colon {F\ -} \diamond {F\ -} \Longrightarrow F\ (- \diamond -)$ が存在する
（単位律）射 $\eta \colon e \longrightarrow F\ e$ が存在する。
（一貫性条件）３つの図式が可換となる。

格上げ

圏 $\boldsymbol{C}$ の対象は、格上げにより、
単位圏 $\mathbf{1}$ から圏 $\boldsymbol{C}$ への関手とみなせた。

モノイド圏 $(\boldsymbol{C},\diamond,e)$ の「対象」は
単位圏 $(\mathbf{1},\diamond,*)$ からモノイド圏 $(\boldsymbol{C},\diamond,e)$ への
ラックス・モノイド関手とみなせるだろうか。

ここで、単位圏 $(\mathbf{1},\diamond,*)$ とは
対象が１つ $\{*\} = \mathrm{Obj}(\mathbf{1})$ で
射が１つ $\{\mathrm{id}_{\displaystyle *}\} = \mathrm{Mor}(\mathbf{1})$ な厳密モノイド圏である。

双関手 $- \diamond - \colon \mathbf{1}\times\mathbf{1}\longrightarrow\mathbf{1}$ は
対象の対応 $* \diamond * = *$ と
射の対応 $\mathrm{id}_{\displaystyle *} \diamond \mathrm{id}_{\displaystyle *} = \mathrm{id}_{\displaystyle *}$ で一意に定まる。

単位圏 $(\mathbf{1},\diamond,*)$ からモノイド圏 $(\boldsymbol{C},\diamond,e)$ への
ラックス・モノイド関手 $(m,\mu,\eta)$ を考える。

関手 $m \colon \mathbf{1} \longrightarrow \boldsymbol{C}$ すなわち対象 $m\ * \in \mathrm{Obj}(\boldsymbol{C})$ および
射 $\mu_{(*,*)} \colon {m\ *} \diamond {m\ *} \longrightarrow {m\ *}$ と射 $\eta \colon e \longrightarrow {m\ *}$ より
モノイド対象 $({m\ *},\mu_{(*,*)},\eta)$ が定まる。

単位圏 $(\mathbf{1},\diamond,*)$ から
集合の圏 $(\mathbf{Set},\times,\{*\})$ への
ラックス・モノイド関手を考える。

次の３つの図式が可換となるとき、
組 $(F,\mu,\eta)$ はラックス・モノイド関手である。

単位圏から集合の圏へのラックス・モノイド関手はモノイド集合だ。

単位圏から自己関手の圏へのラックス・モノイド関手

単位圏 $(\mathbf{1},\diamond,*)$ から
自己関手の圏へのラックス・モノイド関手を考える。

$\mathrm{id}_{T} \cdot \theta = T \cdot \theta$ と $\theta \cdot \mathrm{id}_{T} = \theta \cdot T$ に注意する。

次の３つの図式が可換となるとき、
組 $(F,\mu,\eta)$ はラックス・モノイド関手である。

単位圏から自己関手の圏へのラックス・モノイド関手はモナドだ。

対象が１つな圏の圏 $\mathbf{Cat}$ からはじめ、
自己関手の圏を一般化したモノイド圏
およびモノイド関手の概念をみてきた。

対象を１つに制限せず、
圏の圏 $\mathbf{Cat}$ を一般化できないだろうか。

厳密 2-圏

対象の集合 $\mathrm{Obj}(\boldsymbol{\mathcal{C}})$ があるとする。

各対象 $a,b \in \mathrm{Obj}(\boldsymbol{\mathcal{C}})$ に対して圏 $\boldsymbol{\mathcal{C}}(a,b)$ が存在し、
対象 $f,g \in \mathrm{Obj}(\boldsymbol{\mathcal{C}}(a,b))$ を 1-射 $f,g \colon a \longrightarrow b$ と呼び
射 $\theta \in \mathrm{Mor}(\boldsymbol{\mathcal{C}}(a,b))$ を 2-射 $\theta \colon f \Longrightarrow g$ と呼ぶ。

また、双関手 $- \cdot - \colon \boldsymbol{\mathcal{C}}(a,b) \times \boldsymbol{\mathcal{C}}(b,c) \longrightarrow \boldsymbol{\mathcal{C}}(a,c)$ と
恒等 1-射 $\mathrm{id}_{a} \in \mathrm{Obj}(\boldsymbol{\mathcal{C}}(a,a))$ が各対象に存在する。

次の２つの条件を満たすとき、$\boldsymbol{\mathcal{C}}$ は厳密 2-圏である。

（結合律）$(- \cdot -) \cdot - = - \cdot (- \cdot -)$ が成り立つ。
すなわち、恒等変換 $\alpha \colon (- \cdot -) \cdot - \Longrightarrow - \cdot (- \cdot -)$ が存在する。
（単位律）$\mathrm{id}_{a} \cdot - = - \cdot \mathrm{id}_{b} = \mathrm{id}_{\boldsymbol{\mathcal{C}}(a,b)}$ が成り立つ。
すなわち、恒等変換 $\lambda \colon \mathrm{id}_{a} \cdot - \Longrightarrow \mathrm{id}_{\boldsymbol{\mathcal{C}}(a,b)}$ と
恒等変換 $\rho \colon - \cdot \mathrm{id}_{b} \Longrightarrow \mathrm{id}_{\boldsymbol{\mathcal{C}}(a,b)}$ が存在する。

ここで、関手 $f \cdot - \colon \boldsymbol{\mathcal{C}}(b,c) \longrightarrow \boldsymbol{\mathcal{C}}(a,c)$ は
$g \in \mathrm{Obj}(\boldsymbol{\mathcal{C}}(b,c))$ を $f \cdot g \in \mathrm{Obj}(\boldsymbol{\mathcal{C}}(a,c))$ に対応させ
$\sigma \in \mathrm{Mor}(\boldsymbol{\mathcal{C}}(b,c))$ を $\mathrm{id}_{f} \cdot \sigma \in \mathrm{Mor}(\boldsymbol{\mathcal{C}}(a,c))$ に対応させる。

同様に、関手 $- \cdot g \colon \boldsymbol{\mathcal{C}}(a,b) \longrightarrow \boldsymbol{\mathcal{C}}(a,c)$ は
$f \in \mathrm{Obj}(\boldsymbol{\mathcal{C}}(a,b))$ を $f \cdot g \in \mathrm{Obj}(\boldsymbol{\mathcal{C}}(a,c))$ に対応させ
$\theta \in \mathrm{Mor}(\boldsymbol{\mathcal{C}}(a,b))$ を $\theta \cdot \mathrm{id}_{g} \in \mathrm{Mor}(\boldsymbol{\mathcal{C}}(a,c))$ に対応させる。

圏の圏を一般化すると厳密 2-圏になる。
厳密というのは満たすべき条件(結合律と単位律)が
等号 $=$ により記述されていることを意味する。

自己関手の圏すなわち対象が１つな圏の圏
を一般化すると厳密モノイド圏になったが、
厳密 2-圏で対象が１つな場合はどうなるだろう。

対象が１つ $\{*\} = \mathrm{Obj}(\boldsymbol{\mathcal{C}})$ な厳密 2-圏を考える。
1-射 $f,g \in \mathrm{Obj}(\boldsymbol{\mathcal{C}}(*,*))$ や
2-射 $\theta \in \mathrm{Mor}(\boldsymbol{\mathcal{C}}(*,*))$ はいくつあっても良い。

圏 $\boldsymbol{\mathcal{C}}(*,*)$ に
双関手 $- \cdot - \colon \boldsymbol{\mathcal{C}}(*,*) \times \boldsymbol{\mathcal{C}}(*,*) \longrightarrow \boldsymbol{\mathcal{C}}(*,*)$ と
恒等 1-射 $\mathrm{id}_{\displaystyle *} \in \mathrm{Obj}(\boldsymbol{\mathcal{C}}(*,*))$ の情報を加える。

厳密 2-圏の定義より結合律と単位律が成り立つ。

組 $(\boldsymbol{\mathcal{C}}(*,*),\cdot,\mathrm{id}_{\displaystyle *})$ は厳密モノイド圏である。

ラックス 2-関手

2-圏を定義したので 2-関手を考えよう。

2-圏とは対象と各対象に存在する圏からなるので、
2-関手は対象と各対象に存在する圏をそれぞれ対応させる。

2-圏 $\boldsymbol{\mathcal{C}}$ と 2-圏 $\boldsymbol{\mathcal{D}}$ があるとする。

対象の対応 $\mathcal{F} \colon \mathrm{Obj}(\boldsymbol{\mathcal{C}}) \longrightarrow \mathrm{Obj}(\boldsymbol{\mathcal{D}})$ および
関手 $\mathcal{F} \colon \boldsymbol{\mathcal{C}}(a,b) \longrightarrow \boldsymbol{\mathcal{D}}(\mathcal{F}\ a,\mathcal{F}\ b)$ を考える。

次の３つの条件を満たすとき、
組 $(\mathcal{F},\mu,\eta)$ はラックス 2-関手である。

（結合律）自然変換 $\mu \colon {\mathcal{F}\ -} \cdot {\mathcal{F}\ -} \Longrightarrow \mathcal{F}\ (- \cdot -)$ が存在する。
（単位律）2-射 $\eta \colon \mathrm{id}_{\mathcal{F}\ a} \Longrightarrow \mathcal{F}\ \mathrm{id}_{a}$ が存在する。
（一貫性条件）３つの図式が可換となる。

格上げ

圏 $\boldsymbol{C}$ の対象は、格上げにより、
単位圏 $\mathbf{1}$ から圏 $\boldsymbol{C}$ への関手とみなせた。

2-圏 $\boldsymbol{\mathcal{C}}$ の「対象」は
単位圏 $\mathbf{1}$ から 2-圏 $\boldsymbol{\mathcal{C}}$ への
ラックス 2-関手とみなせるだろうか。

ここで、単位圏 $\mathbf{1}$ とは
対象が１つ $\{*\} = \mathrm{Obj}(\mathbf{1})$ で
1-射が１つ $\{\mathrm{id}_{\displaystyle *}\} = \mathrm{Obj}(\mathbf{1}(*,*))$ で
2-射が１つ $\{\mathrm{id}_{\mathrm{id}_{\scriptstyle *}}\} = \mathrm{Mor}(\mathbf{1}(*,*))$ な厳密 2-圏である。

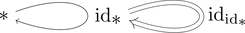
双関手 $- \cdot - \colon \mathbf{1}(*,*) \times \mathbf{1}(*,*) \longrightarrow \mathbf{1}(*,*)$ は
対象の対応 $\mathrm{id}_{\displaystyle *} \cdot \mathrm{id}_{\displaystyle *} = \mathrm{id}_{\displaystyle *}$ と
射の対応 $\mathrm{id}_{\mathrm{id}_{\scriptstyle *}} \cdot \mathrm{id}_{\mathrm{id}_{\scriptstyle *}} = \mathrm{id}_{\mathrm{id}_{\scriptstyle *}}$ で一意に定まる。

単位圏 $\mathbf{1}$ から 2-圏 $\boldsymbol{\mathcal{C}}$ への
ラックス 2-関手 $(\mathcal{F},\mu,\eta)$ を考える。

対象の対応 $\mathcal{F} \colon \mathrm{Obj}(\mathbf{1}) \longrightarrow \mathrm{Obj}(\boldsymbol{\mathcal{C}})$ より
対象 $\mathcal{F}\ * \in \mathrm{Obj}(\boldsymbol{\mathcal{C}})$ すなわち
モノイド圏 $(\boldsymbol{\mathcal{C}}(\mathcal{F}\ *,\mathcal{F}\ *),\cdot,\mathrm{id}_{\mathcal{F}\ {\displaystyle *}})$ が定まる。

関手 $\mathcal{F} \colon \mathbf{1}(*,*) \longrightarrow \boldsymbol{\mathcal{C}}(\mathcal{F}\ *,\mathcal{F}\ *)$
すなわち 1-射 $\mathcal{F}\ \mathrm{id}_{\displaystyle *} \in \mathrm{Obj}(\boldsymbol{\mathcal{C}}(\mathcal{F}\ *,\mathcal{F}\ *))$ および
2-射 $\mu_{(\mathrm{id}_{\scriptstyle *},\mathrm{id}_{\scriptstyle *})} \colon {\mathcal{F}\ \mathrm{id}_{\displaystyle *}} \cdot {\mathcal{F}\ \mathrm{id}_{\displaystyle *}} \Longrightarrow \mathcal{F}\ \mathrm{id}_{\displaystyle *}$ と
2-射 $\eta \colon \mathrm{id}_{\mathcal{F}\ {\displaystyle *}} \Longrightarrow \mathcal{F}\ \mathrm{id}_{\displaystyle *}$ より
モノイド対象 $(\mathcal{F}\ \mathrm{id}_{\displaystyle *},\mu_{(\mathrm{id}_{\scriptstyle *},\mathrm{id}_{\scriptstyle *})},\eta)$ が定まる。

単位圏から圏の圏へのラックス 2-関手

単位圏 $\mathbf{1}$ から
圏の圏へのラックス 2-関手を考える。

次の３つの図式が可換となるとき、
$(\mathcal{F},\mu,\eta)$ はラックス 2-関手である。

単位圏から圏の圏へのラックス 2-関手はモナドだ。

まとめ

モナドは自己関手の圏におけるモノイド対象だった。

ひたすらに結合律と単位律との戦いだった。

Haskell との関連においては
アプリカティブ関手を理解したい。

一貫性条件に関してはあとでいつかきっとそのうち確認する。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up